An Image Encryption Method Based on a Two-Dimensional Cross-Coupled Chaotic System

Abstract

Chaotic systems have demonstrated significant potential in the field of image encryption due to their extreme sensitivity to initial conditions, inherent unpredictability, and pseudo-random behavior. However, existing chaos-based encryption schemes still face several limitations, including narrow chaotic regions, discontinuous chaotic ranges, uneven trajectory distributions, and fixed pixel processing sequences. These issues substantially hinder the security and efficiency of such algorithms. To address these challenges, this paper proposes a novel hyperchaotic map, termed the two-dimensional cross-coupled chaotic map (2D-CFCM), derived from a newly designed 2D cross-coupled chaotic system. The proposed 2D-CFCM exhibits enhanced randomness, greater sensitivity to initial values, a broader chaotic region, and a more uniform trajectory distribution, thereby offering stronger security guarantees for image encryption applications. Based on the 2D-CFCM, an innovative image encryption method was further developed, incorporating efficient scrambling and forward and reverse random multidirectional diffusion operations with symmetrical properties. Through simulation tests on images of varying sizes and resolutions, including color images, the results demonstrate the strong security performance of the proposed method. This method has several remarkable features, including an extremely large key space (greater than $2^{912}$), extremely high key sensitivity, nearly ideal entropy value (greater than 7.997), extremely low pixel correlation (less than 0.04), and excellent resistance to differential attacks (with the average values of NPCR and UACI being $99.6050\%$ and $33.4643\%$, respectively). Compared to existing encryption algorithms, the proposed method provides significantly enhanced security.

1. Introduction

With the rapid growth of digital communication technologies and the increasing reliance on cloud storage and online data transfer, protecting sensitive data has become a major concern. Images, in particular, are vulnerable to breaches and attacks due to their ability to contain personal, confidential, or national security-related information. As a result, image encryption has become essential for safeguarding images during storage and transmission [1,2,3,4]. In the domain of image encryption for large datasets, traditional algorithms such as the Data Encryption Standard (DES) [5], Advanced Encryption Standard (AES) [6], and Rivest–Shamir–Adleman (RSA) system [7] have been largely replaced by newer methods. A variety of innovative image encryption methods, using DNA coding [8], RNA coding [9,10], neural networks [11,12], cellular automata [13], Fourier transform [14], compressed sensing [15,16], chaos theory [17], or others [18,19], have emerged. Notably, encryption systems based on chaos theory have demonstrated significant advantages in enhancing the overall performance of cryptographic algorithms.

The effectiveness of chaotic image encryption algorithms largely relies on the specific attributes of the chaotic system employed. Owing to the sensitivity to initial conditions, ergodic properties, and intrinsic stochasticity, chaotic systems can significantly enhance encryption performance [20,21]. Consequently, chaotic systems have found widespread applications across various scientific disciplines, including cryptography, secure communications, information technology, mathematics, biology, medicine, economics, engineering, and physics [17,22,23,24,25,26,27,28]. Depending on their complexity, chaotic systems are typically divided into single-variable (one-dimensional) and multi-variable (high-dimensional) categories. One-dimensional discrete chaotic systems, characterized by their simplicity, fewer control parameters, and relatively quick generation of chaotic sequences, offer advantages in terms of efficiency. However, limited key space and lower pseudo-randomness make them more susceptible to attacks. In contrast, high-dimensional chaotic systems possess a more extensive key space and more robust chaotic behavior, providing enhanced security. Nevertheless, high-dimensional chaotic systems come with increased computational burden and higher implementation costs.

The two-dimensional (2D) chaotic system combines the simplicity of one-dimensional systems with the complexity of higher-dimensional systems, providing strong performance while maintaining efficiency. In recent years, the use of various 2D chaotic systems for image encryption has been growing. For example, Wu [24] used a 2D logical map with a complex basin structure and attractor. Hua [25] introduced a new 2D sine logistic modulated map (2D-SLMM). Zhu [26] presented a 2D chaotic map based on sine modulation and logistic coupling, called the logical modulated sine coupling logistic map (LSMCL). In addition to developing new chaotic systems and encryption algorithms, it is equally crucial to consider the role of cryptanalysis in evaluating the robustness of these methods. Recent studies have conducted in-depth cryptanalysis of various image encryption schemes [27,28]. These analyses not only revealed the potential weaknesses but also proposed significant improvement measures to enhance the security of the algorithm.

In this study, a new 2D chaotic system with cross-coupling is introduced to enhance system performance. Furthermore, a novel hyperchaotic system (2D-CFCM) was developed by combining Chebyshev, Fuch, sine, and cosine mappings. Analysis of phase diagrams, fractal diagrams (also known as bifurcation diagrams), Lyapunov exponents, and information entropy reveals that the proposed system demonstrates more extensive chaotic behaviors and increased complexity, significantly improving both the security and efficiency of encryption methods. An effective image encryption algorithm is proposed, which utilizes chaotic matrices and an enhanced Zigzag transformation. The algorithm incorporates both forward and reverse random multidirectional diffusion. The chaotic matrix-based permutation simultaneously scrambles pixel positions across both rows and columns, significantly boosting the randomness of the scrambling process and minimizing pixel correlation. The forward and reverse random multidirectional diffusion process selects diffusion directions from multiple orientations in both forward and reverse directions, thus increasing diffusion randomness and enhancing encryption security. To accommodate color image encryption, the approach was extended to process the R, G, and B components individually. The experimental results demonstrate that the proposed algorithm ensures strong security, as confirmed by key space, information entropy, pixel correlation, and histogram analyses.

The key contributions of this work are outlined as follows:

(1)

A new 2D cross-coupled chaotic system is proposed, capable of generating multiple chaotic maps. Specifically, a hyperchaotic system was developed by combining Chebyshev mapping, the Fuch map, sine mapping, and cosine mapping.

(2)

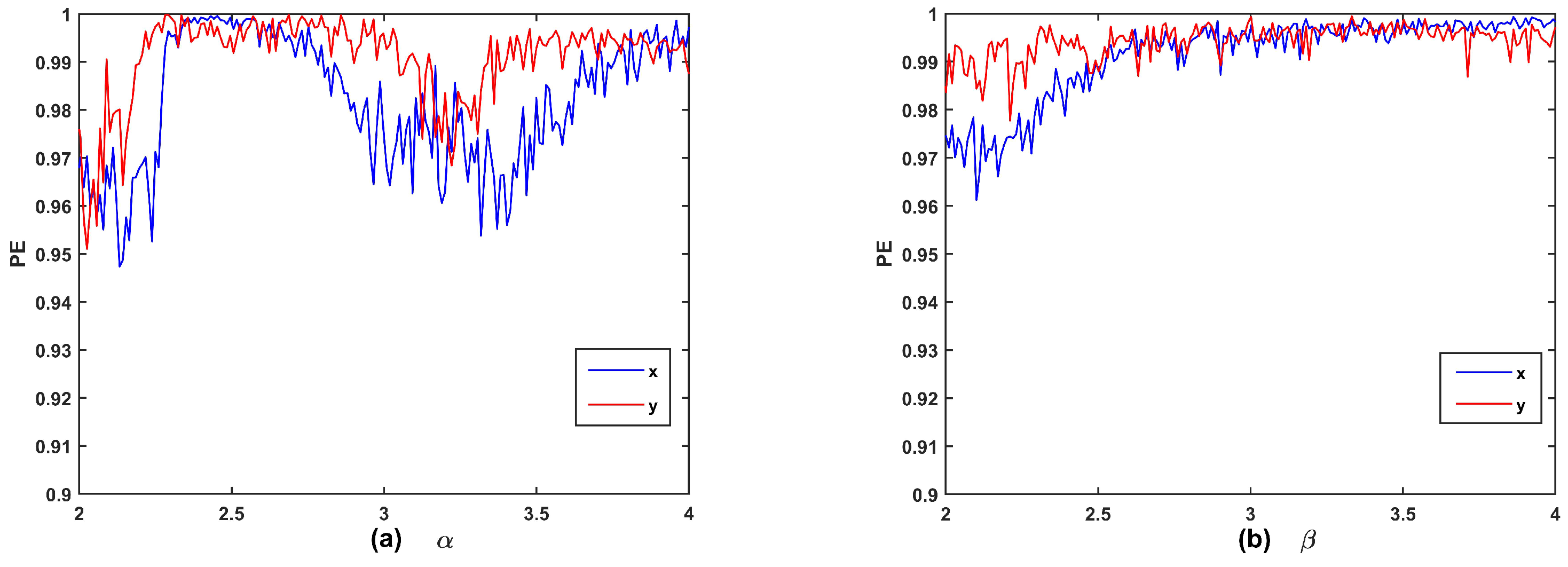
The analysis of bifurcation diagrams, phase diagrams, Lyapunov exponents, and permutation entropy reveals that the proposed system exhibits a larger key space, enhanced ergodicity, and increased unpredictability, leading to more complex chaotic dynamics.

(3)

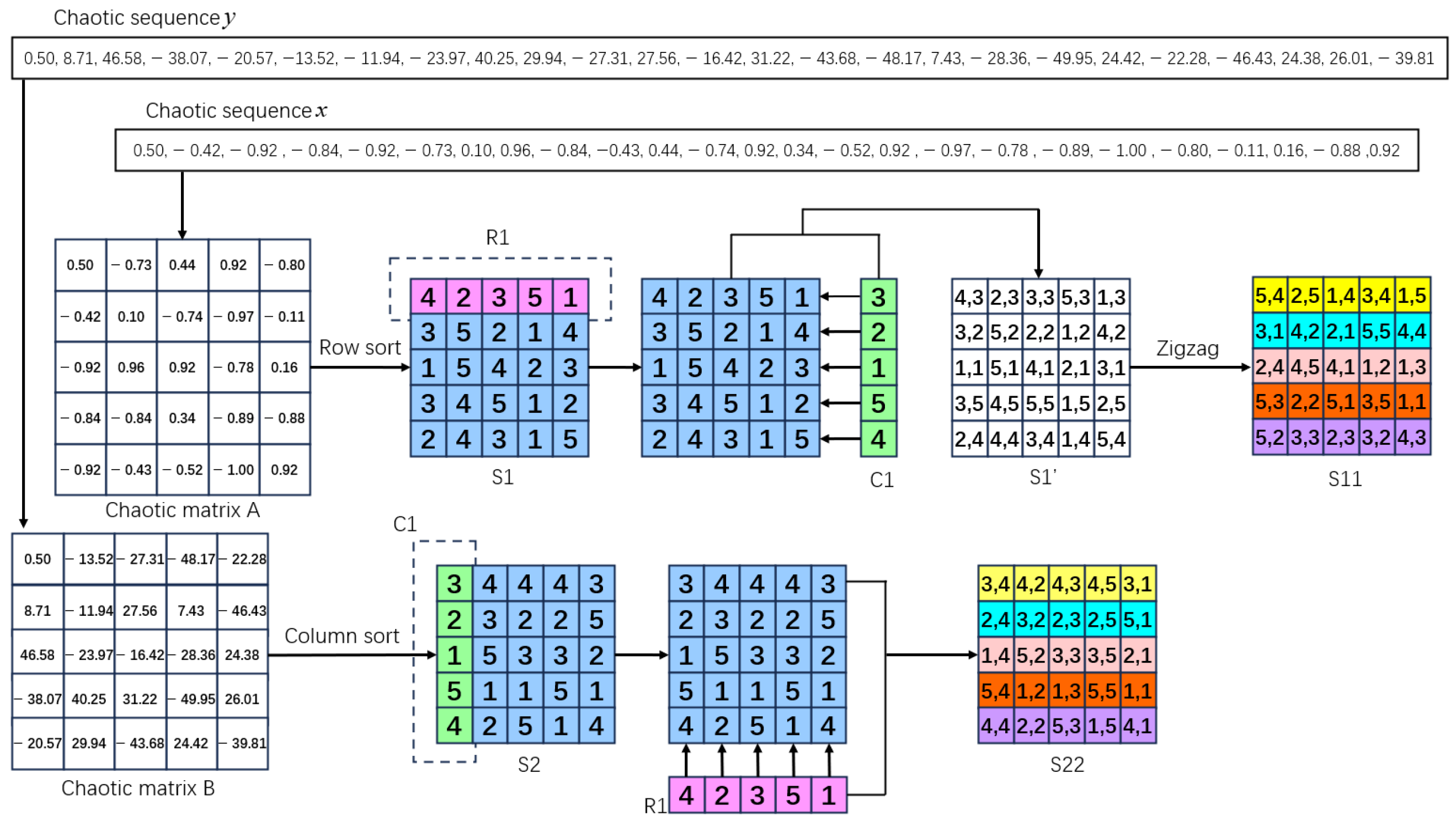
An efficient image encryption scheme is introduced, which utilizes a chaotic matrix in conjunction with a Zigzag transformation for effective permutation and forward and reverse random multidirectional diffusion operations with symmetrical significance. The chaotic matrix-based permutation disrupts pixel positions by simultaneously scrambling both rows and columns in a random order. The symmetric forward and backward random multi-directional diffusion is achieved by conducting two rounds of random diffusion in multiple directions.

(4)

A comprehensive evaluation of the encryption algorithm’s performance is conducted, covering aspects such as key space, histogram analysis, variance, entropy, and correlation coefficient.

The organization of this paper is as follows. Section 2 presents the novel two-dimensional hyperchaotic map, 2D-CFCM. Section 3 discusses the dynamical behavior of the map with comparative performance analysis. Section 4 describes the design of the image encryption algorithm based on the proposed chaotic system. Section 5 provides simulation results and evaluates this security performance of the proposed method. Finally, Section 6 concludes the study.

2. Definition of 2D-CFCM

The chaotic properties of chaotic systems are crucial in encryption communication. Some classical chaotic mappings exhibit limited attractor distribution, low ergodicity, and insufficient unpredictability of chaotic sequences, leading to security vulnerabilities. In response to these drawbacks, this study introduces a newly developed two-dimensional cross-coupled chaotic system, which introduces two inputs and a cross-coupling mechanism to construct a more complex hyperchaotic map, as illustrated in Figure 1.

As shown in Figure 1, the system consists of two independent variables, $x_n$ and $y_n$, as inputs, and two dependent variables, $x_{n+1}$ and $y_{n+1}$, as outputs. F and J represent one-dimensional chaotic maps. The operations ⊕ and ⊖ correspond to addition and subtraction applied to the signals, respectively. To improve the unpredictability and pseudorandomness of the two-dimensional chaotic map, functions f and j are introduced to modulate the system, leading to the two-dimensional cross-coupled chaotic system. The system is defined as follows.

$$\left\{\begin{array}{c}{x}_{n+1}=F\left(f(f\left(y_n\right)-j\left(x_n\right))\right),\hfill \\ y_{n+1}=J(f\left(x_n\right)+j\left(y_n\right)).\hfill \end{array}\right.$$

(1)

In the cross-coupling system, the function f is defined as the sine function, while j is selected as the cosine function. The chaotic maps F and J are represented by the Chebyshev map and the Fuch map, respectively. Both the Chebyshev and Fuch maps are well-established chaotic functions, and their respective formulations are presented in Equations (2) and (3).

$$x_{n+1}=cos\left(\alpha {cos}^{-1}\left(x_n\right)\right).$$

(2)

$$y_{n+1}=cos(1/y_n^2).$$

(3)

A novel, two-dimensional Chebyshev–Fuchs coupled map (2D-CFCM) is obtained through subtle modifications based on Equations (2) and (3).

$$\left\{\begin{array}{c}{x}_{n+1}=cos(\alpha ·{cos}^{-1}(sin(sin{y}_n-cos{x}_n))),\hfill \\ y_{n+1}=\beta ·cos(9/{(sin{x}_n+cos{y}_n)}^2).\hfill \end{array}\right.$$

(4)

$\alpha$, $\beta$ are control parameters and $\alpha$, $\beta$$\in [1,+\infty )$.

3. Chaotic Property Evaluation of 2D-CFCM

To analyze the chaotic properties of 2D-CFCM, such as ergodicity, complexity, and unpredictability, we employed various analytical techniques, including phase portraits, bifurcation diagrams, Lyapunov exponents, and permutation entropy. Additionally, we compared the characteristics of 2D-CFCM with those of traditional one-dimensional chaotic maps (e.g., logistic map, sine map, and ICMIC) and two-dimensional chaotic maps (e.g., 2D-SIMM, 2D-LSMCL, 2D-logistic map, and 2D-SLMM).

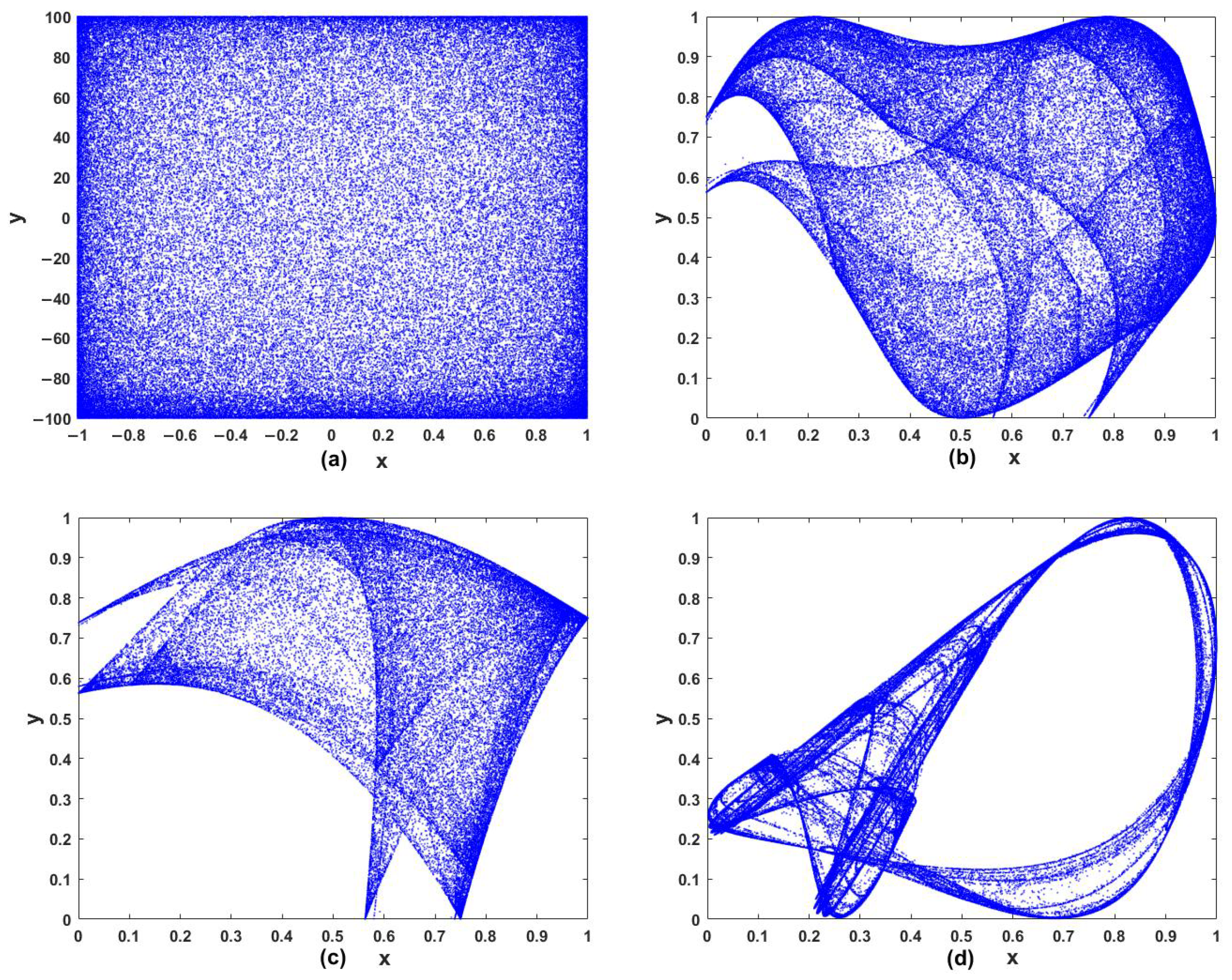
3.1. Phase Diagram

The phase diagram serves as an essential analytical tool for visualizing and characterizing the dynamical behaviors of chaotic systems. The phase trajectories of chaotic motion typically form non-closed curves, a characteristic that is clearly exhibited in phase plane plots. Systems displaying prominent chaotic behavior often have attractors that cover a considerable area in the phase diagram, revealing intricate and complex structures. In order to ensure the comparability of the experiments and the optimal performance of the system, the initial values of all systems in this study were set as ($x_0,y_0$) = (0.1, 0.1). To balance the optimal performance and practical feasibility of 2D-CFCM, the system parameters were set as $\alpha$ = 100 and $\beta$ = 100, resulting in the phase diagram shown in Figure 2a. Figure 2b–d are the phase diagrams of 2D-LSMCL ($\alpha$ = 0.75, $\beta$ = 3), 2D-SLMM ($\alpha$ = 1, $\beta$ = 3), and 2D-Logistic (r = 1.19) obtained based on the selection of the optimal parameters from the existing literature. Compared with this, the trajectory of 2D-CFCM covers the entire phase plane. Therefore, 2D-CFCM exhibits superior ergodicity and a broader chaotic distribution.

3.2. Bifurcation Diagram

The bifurcation diagram is an essential analytical tool for analyzing and understanding the various dynamical behavior of chaotic systems. It demonstrates how a system’s motion evolves with varying control parameters and investigates its stability, periodic behavior, and whether it reaches the chaotic state [29]. Figure 3 presents the bifurcation diagram of the 2D-CFCM, where (a) illustrates the bifurcation diagram of x as it depends on system parameters $\alpha$ and $\beta$, with both parameters varying within the range (0, 100). (b) shows the bifurcation diagram of y as it depends on $\alpha$ and $\beta$, also within the range (0, 100). As observed in Figure 3, both bifurcation diagrams of the 2D-CFCM system exhibit chaotic behavior across broad range of parameter values, with no periodic states emerging. This indicates that the chaotic regime of the 2D-CFCM system is extensive.

3.3. Lyapunov Exponent

The Lyapunov exponent ($LE$) is a key measure for determining the chaotic nature of a dynamical system and assessing its chaotic behavior. It quantifies how the system’s trajectory responds to variations in initial conditions over time. A positive $LE$ indicates sensitivity to initial conditions, where even small perturbations lead to rapid divergence [30]. Multiple positive $LE$ signify a hyperchaotic state in the system. The calculation method for the $LE$ of a two-dimensional chaotic system is described as follows. $f(x,y)=(f_1(x,y),f_2(x,y))$, i.e., for any $i\in \mathbb{N}$,

$$\left\{\begin{array}{c}{x}_{i+1}=f_1(x_i,y_i)=cos(\alpha ·{cos}^{-1}(sin(sin{y}_n-cos{x}_n))),\hfill \\ y_{i+1}=f_2(x_i,y_i)=\beta ·cos(9/{(sin{x}_n+cos{y}_n)}^2),\hfill \end{array}\right.$$

(5)

$$J\left(x_i,y_i\right)=\left(\begin{array}{cc}{\displaystyle \frac{\partial f_1(x,y)}{\partial x}}& {\displaystyle \frac{\partial f_1(x,y)}{\partial y}}\\ {\displaystyle \frac{\partial f_2(x,y)}{\partial x}}& {\displaystyle \frac{\partial f_2(x,y)}{\partial y}}\end{array}\right),$$

(6)

where $f(x,y)$ represents the two-dimensional chaotic map. $J(x_i,y_i)$ denotes the Jacobian matrix of $f(x,y)$.

Assuming the Jacobian matrix J has eigenvalues ${\lambda }_1\left(J\right)$ and ${\lambda }_2\left(J\right)$, the $LE$ can be computed using the following approach.

$$LE=\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\sum _{i=0}^{n-1}ln\left|{\lambda }_i\left(J\right)\right|.$$

(7)

Figure 4 displays the $LE$ for 2D-CFCM. Panel (a) shows the variation of the first Lyapunov exponent ($L{E}_1$) as a function of the system parameters $\alpha$ and $\beta$, while panel (b) presents the second Lyapunov exponent ($L{E}_2$) for the same set of parameters. It is evident that when $\alpha >1$ and $\beta >1$, both Lyapunov exponents are positive; this implies a hyperchaotic state for the system. With increasing $\alpha$ and $\beta$, the system’s Lyapunov exponents ($LEs$) also increase, suggesting an enhancement in the chaotic behavior as the system parameters grow. Additionally, the system exhibits a heightened sensitivity to initial conditions, suggesting the presence of complex dynamical behavior; thus, it is appropriate for cryptographic applications.

3.4. Complexity

The complexity measure of chaotic systems serves as a critical indicator for assessing the degree of resemblance between the system-generated chaotic sequences and purely random sequences. Due to the inherent uncertainty and nonlinearity of chaotic systems, the sequences they generate often exhibit characteristics similar to those of random sequences. The complexity of chaotic sequences significantly affects their performance in encryption tasks. The higher the value of complexity, the more the statistical properties of the chaotic sequence resemble those of a random sequence and the higher the cryptographic security. There are many methods used to analyze the complexity. In this section, we will use replacement entropy (PE) to evaluate the complexity situation of 2D-CFCM.

Figure 5 shows the replacement entropy (PE) complexity plots of the mapped 2D-CFCM with respect to the control parameters $\alpha$ and $\beta$, respectively. In Figure 6a, the PE complexity of the 2D-CFCM chaotic system is compared with the PE complexity of several classical 1D chaotic systems, such as logistic maps, sinusoidal maps, and ICMIC. Figure 6b shows the PE complexity comparison of 2D-CFCM with three 2D chaotic systems: 2D-SLMM, 2D-logistic map, and 2D-LSMCL.The results show that 2D-CFCM generates chaotic sequences with a complexity value close to 1, which indicates that it has a good complexity and unpredictability. This suggests that it is well suited for generating more secure image encryption key sequences.

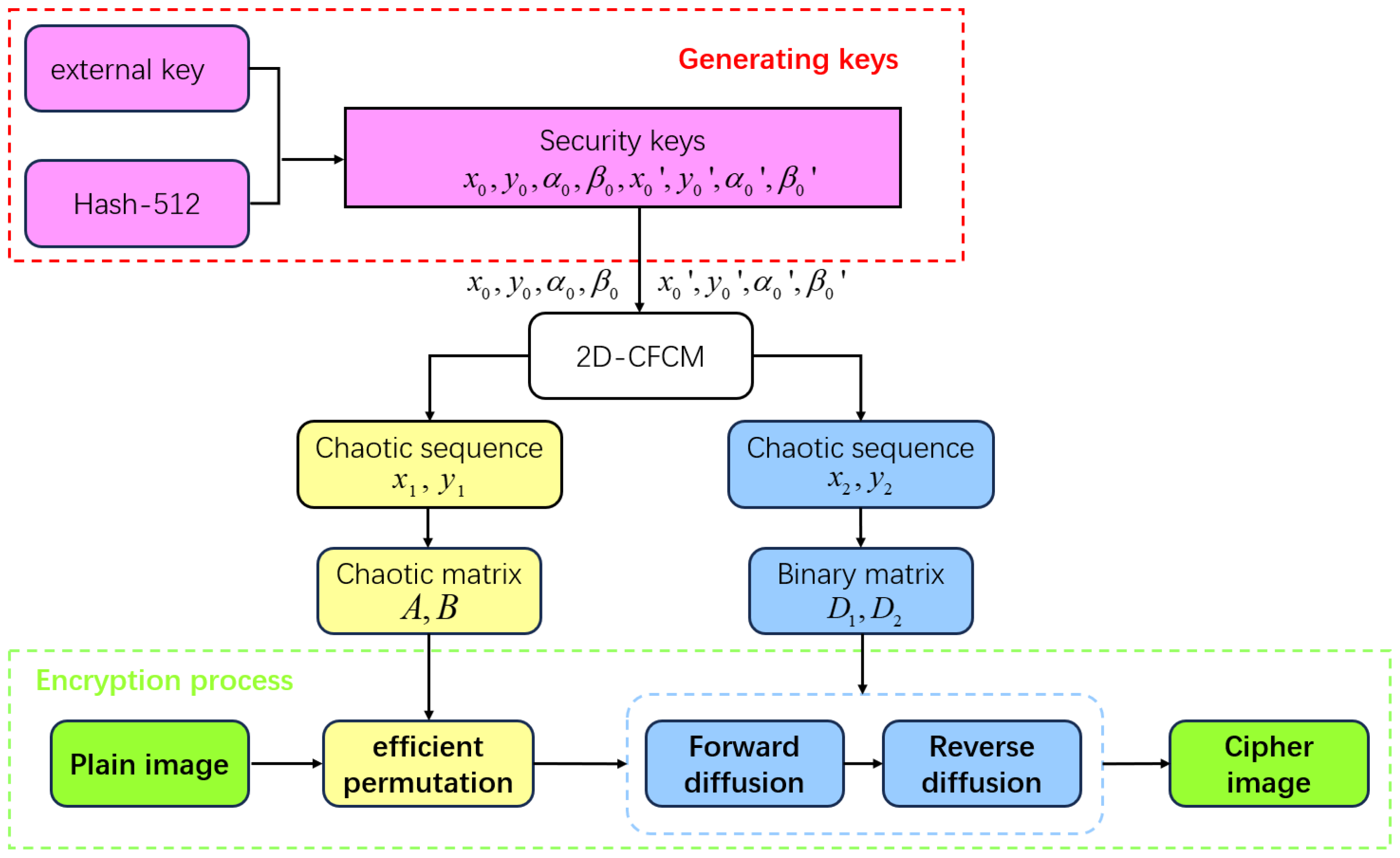
4. Image Encryption Method

This section primarily introduces the preparatory work and the proposed encryption method. The aforementioned two-dimensional chaotic system, 2D-CFCM, possesses an extensive chaotic range, strong unpredictability, and complex chaotic characteristics, which offers a robust basis for the development of secure encryption schemes. Based on 2D-CFCM, a new image encryption method is introduced in this section. The comprehensive flowchart outlining the algorithm is depicted in Figure 7. The algorithm consists of three stages: (1) generating keys related to the plane image; (2) performing scrambling operations based on the chaotic matrix and Zigzag transformation; (3) implementing forward and backward random multidirectional diffusion operations.

4.1. Generating Keys

The hash algorithm exhibits an extremely high sensitivity to input variations, where even a minor change results in a drastically different output, thus effectively resisting plaintext attacks. Furthermore, the result of the hash algorithm is non-reversible, meaning that the original input cannot be reconstructed from the output, ensuring strong one-way functionality and security [31,32]. Consequently, the cryptographic algorithm proposed in this paper utilizes a hash algorithm to generate keys, thus improving system security.

The 512 bit hash output, denoted as $Hash$, is generated using the SHA-512 algorithm. This hash is subsequently segmented into 64 groups of 8 bits each, represented as $h_1,h_2,\dots ,h_{63},h_{64}$. The SHA-512 hash function can generate a unique subkey derived from the original image, thereby ensuring that distinct images produce different encryption keys. The detailed procedure of the SHA-512 algorithm is outlined as follows: $Hash=h_1,h_2,\dots ,h_{63},h_{64}$.

By combining $h_1,h_2,\dots ,h_{63},h_{64}$, 16 hash combinations $H_1,H_2,\dots ,H_{16}$ are obtained, which are derived from the equations outlined below.

$$\left\{\begin{array}{cc}\hfill & H_1=min\left(h_1,h_2,\dots ,h_{15},h_{16}\right),\hfill \\ \hfill & H_2=max\left(h_1,h_2,\dots ,h_{15},h_{16}\right),\hfill \\ \hfill & H_3=h_1+h_2+\dots +h_{15}+h_{16},\hfill \\ \hfill & H_4=h_1\oplus h_2\oplus \dots \oplus h_{15}\oplus h_{16},\hfill \\ \hfill & H_5=min\left(h_{17},h_{18},\dots ,h_{31},h_{32}\right),\hfill \\ \hfill & H_6=max\left(h_{17},h_{18},\dots ,h_{31},h_{32}\right),\hfill \\ \hfill & H_7=h_{17}+h_{18}+\dots +h_{31}+h_{32},\hfill \\ \hfill & H_8=h_{17}\oplus h_{18}\oplus \dots \oplus h_{31}\oplus h_{32},\hfill \\ \hfill & H_9=min\left(h_{33},h_{34},\dots ,h_{47},h_{48}\right),\hfill \\ \hfill & H_{10}=max(h_{33},h_{34},\dots ,h_{47},h_{48}),\hfill \\ \hfill & H_{11}=h_{33}+h_{34}+\dots +h_{47}+h_{48},\hfill \\ \hfill & H_{12}=h_{33}\oplus h_{34}\oplus \dots \oplus h_{47}\oplus h_{48},\hfill \\ \hfill & H_{13}=min\left(h_{49},h_{50},\dots ,h_{63},h_{64}\right),\hfill \\ \hfill & H_{14}=max\left(h_{49},h_{50},\dots ,h_{63},h_{64}\right),\hfill \\ \hfill & H_{15}=h_{49}+h_{50}+\dots +h_{63}+h_{64},\hfill \\ \hfill & H_{16}=h_{49}\oplus h_{50}\oplus \dots \oplus h_{63}\oplus h_{64}.\hfill \end{array}\right.$$

(8)

The intermediate keys $R_1,R_2,\dots ,R_8$ are calculated by $H_1,H_2,\dots ,H_{16}$ and the external keys $t_1,t_2,\dots ,t_7,t_8(t_i\in [0,1])$, which are described as

$$\left\{\begin{array}{cc}\hfill & R_1=(t_1\times t_3+t_7)+{\displaystyle \frac{1}{2\times 512}}\times {\displaystyle \frac{H_1}{H_2}},\hfill \\ \hfill & R_2=(t_2+t_6\times t_7+t_8)+t_7\times {\displaystyle \frac{H_4}{H_3}},\hfill \\ \hfill & R_3=(t_1+t_3+t_5)\times {\displaystyle \frac{H_8}{H_7}},\hfill \\ \hfill & R_4=(t_4\times t_7)\times \left({\displaystyle \frac{H_5}{H_6}}-H_5\right),\hfill \\ \hfill & R_5=(t_1\times t_7+t_5)-{\displaystyle \frac{1}{2\times 512}}\times {\displaystyle \frac{H_9}{H_{10}}},\hfill \\ \hfill & R_6=(t_2\times t_3+t_6)-{\displaystyle \frac{1}{2\times 512}}\times {\displaystyle \frac{H_{11}}{H_{12}}},\hfill \\ \hfill & R_7=(t_1\times t_7+t_2)+t_4\times {\displaystyle \frac{H_{13}}{H_{14}}},\hfill \\ \hfill & R_8=(t_2\times t_3+t_8)+{\displaystyle \frac{1}{3\times 512}}\times {\displaystyle \frac{H_{15}}{H_{16}}}.\hfill \end{array}\right.$$

(9)

Further keys ($x_0$, $y_0$, ${\alpha }_0$, ${\beta }_0$) and ($x_0^{\prime }$, $y_0^{\prime }$, ${\alpha }_0^{\prime }$, ${\beta }_0^{\prime }$) of the 2D-CFCM chaotic map are generated according to the following equations:

$$\left\{\begin{array}{cc}\hfill & {\alpha }_0=mod\left(\left|(R_1\times R_2+R_5)\times {10}^{16}\right|,10\right),\hfill \\ \hfill & {\beta }_0=mod\left(\left|(R_3\times R_4+R_6)\times {10}^{16}\right|,10\right),\hfill \\ \hfill & x_0=mod\left(\right|R_1+R_2|,1),\hfill \\ \hfill & y_0=mod\left(\right|R_3+R_4|,{\beta }_0),\hfill \end{array}\right.$$

(10)

and

$$\left\{\begin{array}{cc}\hfill & {\alpha }_0^{\prime }=mod\left(\left|(R_5\times R_6+R_7)\times {10}^{16}\right|,10\right),\hfill \\ \hfill & {\beta }_0^{\prime }=mod\left(\left|(R_7\times R_8+R_8)\times {10}^{16}\right|,10\right),\hfill \\ \hfill & x_0^{\prime }=mod\left(\right|R_5+R_6|,1),\hfill \\ \hfill & y_0^{\prime }=mod\left(\right|R_7+R_8|,{\beta }_0^{\prime }).\hfill \end{array}\right.$$

(11)

Since the key is inherently associated with the plaintext image, even a single bit alteration in the plaintext causes a substantially different key to be generated. Therefore, the key generation algorithm exhibits a high level of security.

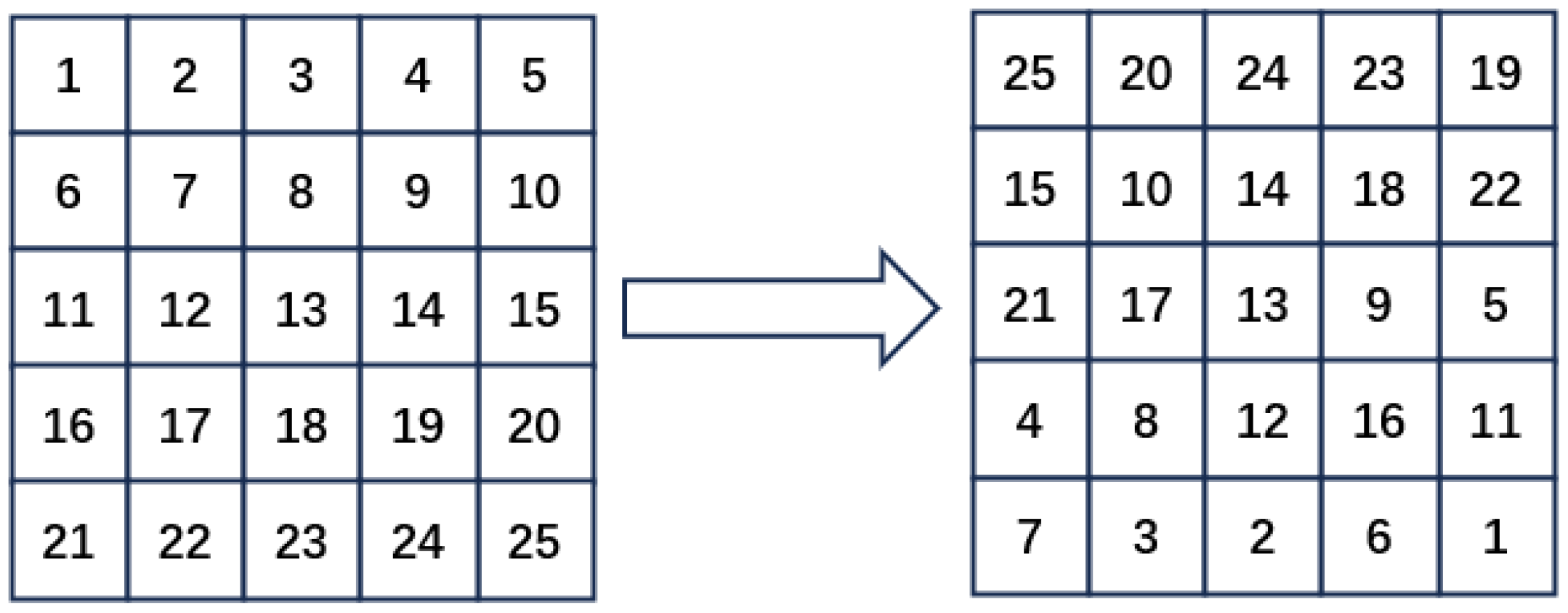
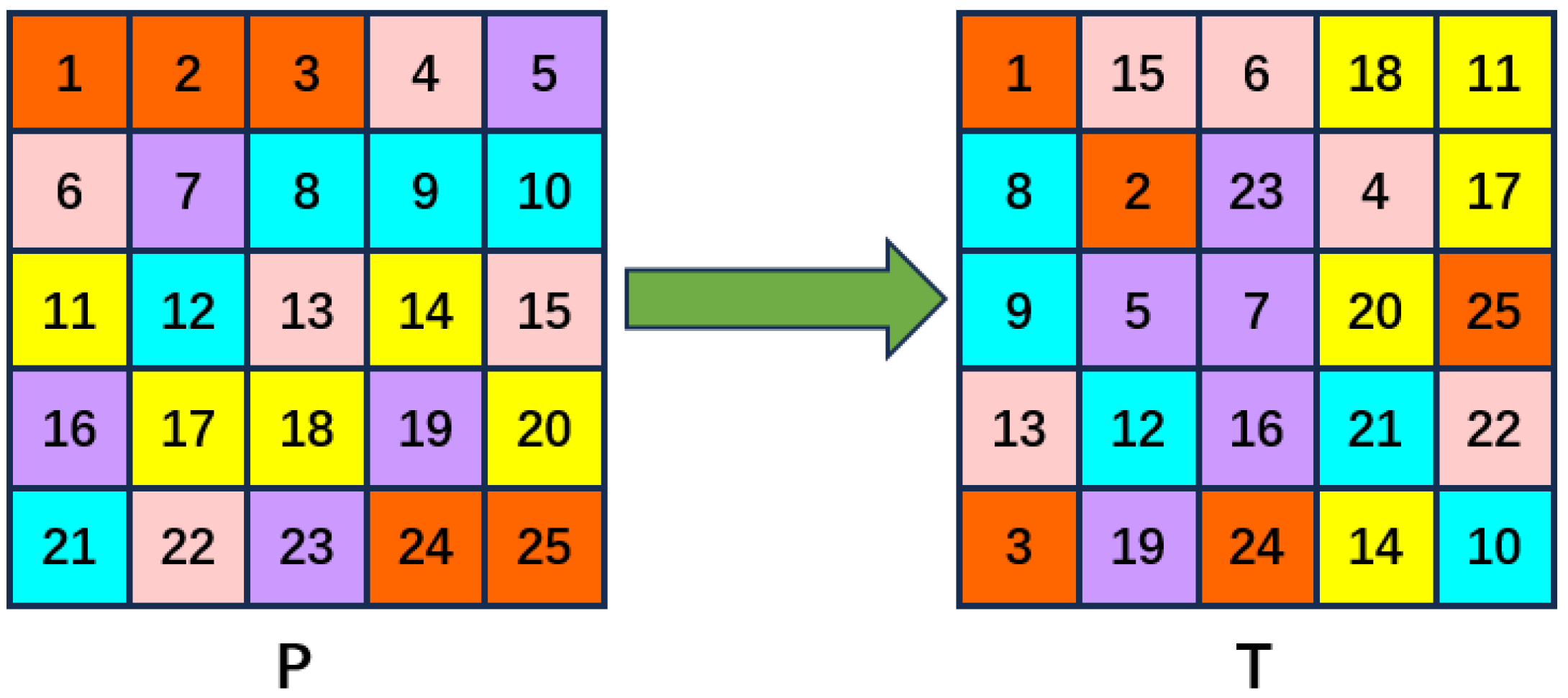
4.2. Chaotic Efficient Permutation

Many current image encryption methods use fixed pixel arrangements, whether in rows or columns, which may leave predictable patterns that can be exploited by attackers, and the construction of chaotic matrices is simple, thereby endangering the security of the encryption [33,34]. To improve both security and randomness, a novel image encryption algorithm that combines chaotic matrices with a Zigzag transformation is introduced. This approach randomizes the pixel positions using a secret order, enhancing the encryption’s complexity. Additionally, the algorithm modifies pixel locations in both the horizontal and vertical directions simultaneously. Following the permutation, the pixels are relocated within the image, greatly diminishing their correlation. A comprehensive explanation of this chaotic permutation process is provided below.

Figure 8 shows the generation of the row matrix $a_1$, the column matrix $b_1$, and the coordinate matrices $a_2$ and $b_2$. The corresponding coordinates of the rows with the same color are changed. The elements of each row of the $a_1$ matrix are combined with the corresponding elements of each row of n to form the coordinates and then a modified Zigzag transformation is performed to obtain the coordinate matrix $a_2$. The modified Zigzag transformation is shown in Figure 9. For example, the elements of the first row of $a_1$ in horizontal coordinates are combined with the first element of n in column coordinates to obtain the first row of the coordinate matrix $a_2$: (4, 3), (2, 3), (3, 3), (5, 3), (1, 3). The elements of the first column of the matrix $b_1$ are combined with the corresponding elements of the first column of n to form the coordinates, and the coordinate matrix $b_2$ is obtained. For example, the horizontal coordinates of the first column element of $b_1$ are combined with the column coordinates of each column element of m to obtain the first column of the coordinate matrix $b_2$: (3, 4), (2, 4), (1, 4), (5, 4), (4, 4).

As shown in Figure 10, the pixel positions in the image P are numbered sequentially from 1 to 25. After one disarrangement operation proposed in this paper, a chaotic matrix T is obtained. Each pixel in the image is completely rearranged depending on the coordinate matrices $a_2$ and $b_2$. Different colors are chosen to make the scrambling effect more intuitive. Without knowing the coordinate matrices, it becomes extremely challenging for an attacker to decrypt the image, which greatly improves the security of the encryption scheme.

The detailed procedure of the image scrambling operation is described as follows.

Step 1. Select the pixels corresponding to all the coordinates in the first row of $b_2$ from the image P and move these corresponding pixels to different positions corresponding to all the coordinates corresponding to the first row of $a_2$. For example, T(5, 4) = P(3, 4), T(2, 5) = P(4, 2), T(1, 4) = P(4, 3), T(3, 4) = P(4, 5), and T(1, 5) = P(3,1), as shown in Figure 11a.

Step 2. Select the pixels corresponding to all the coordinates in the second row of $b_2$ from the image P. Move these corresponding pixels to different positions corresponding to all the coordinates corresponding to the second row of $a_2$. For example, T(3, 1) = P(2, 4), T(4, 2) = P(3, 2), T(2, 1) = P(2, 3), T(5, 5) = P(2, 5), and T(4, 4) = P(5, 1), as shown in Figure 11b.

Step 3. Select the pixels corresponding to all the coordinates in the third row of $b_2$ from the image P and move these corresponding pixels to different positions corresponding to all the coordinates corresponding to the third row of $a_2$. For example, T(2, 4) = P(1, 4), T(4, 5) = P(5, 2), T(4, 1) = P(3, 3), T(1, 2) = P(3, 5), and T(1, 3) = P(2, 1), as shown in Figure 11c.

Step 4. Select the pixels corresponding to all the coordinates in the fourth row of $b_2$ from the image P. Move these corresponding pixels to different positions corresponding to all the coordinates corresponding to the fourth row of $a_2$. For example, T(5, 3) = P(5, 4), T(2, 2) = P(1, 2), T(5, 1) = P(1, 3), T(3, 5) = P(5, 5), and T(1, 1) = P(1, 1), as shown in Figure 11d.

Step 5. Select the pixels corresponding to all the coordinates in the fifth row of $b_2$ from the image P. Move these corresponding pixels to different positions corresponding to all the coordinates corresponding to the fifth row of $a_2$. For example, T(5, 2) = P(4, 4), T(3, 3) = P(2, 2), T(2, 3) = P(5, 3), T(3, 2) = P(1, 5), and T(4, 3) = P(4, 1), as shown in Figure 11e.

The permutation process used in the encryption stage is inherently reversible. During decryption, the same initial keys and parameters of the 2D cross-coupled chaotic map (2D-CFCM) are employed to regenerate the identical chaotic sequences. These sequences are then used to reconstruct the original permutation index. Based on this index, an inverse permutation operation is performed on the encrypted image, whereby the scrambled pixels are remapped to their original positions, thus restoring the original spatial structure of the image. This inverse permutation procedure is highly sensitive to the correctness of the secret keys. Even a minute deviation in the key values will result in an incorrect chaotic sequence, ultimately causing the decryption to fail. This high key sensitivity ensures the security and confidentiality of the encrypted image data.

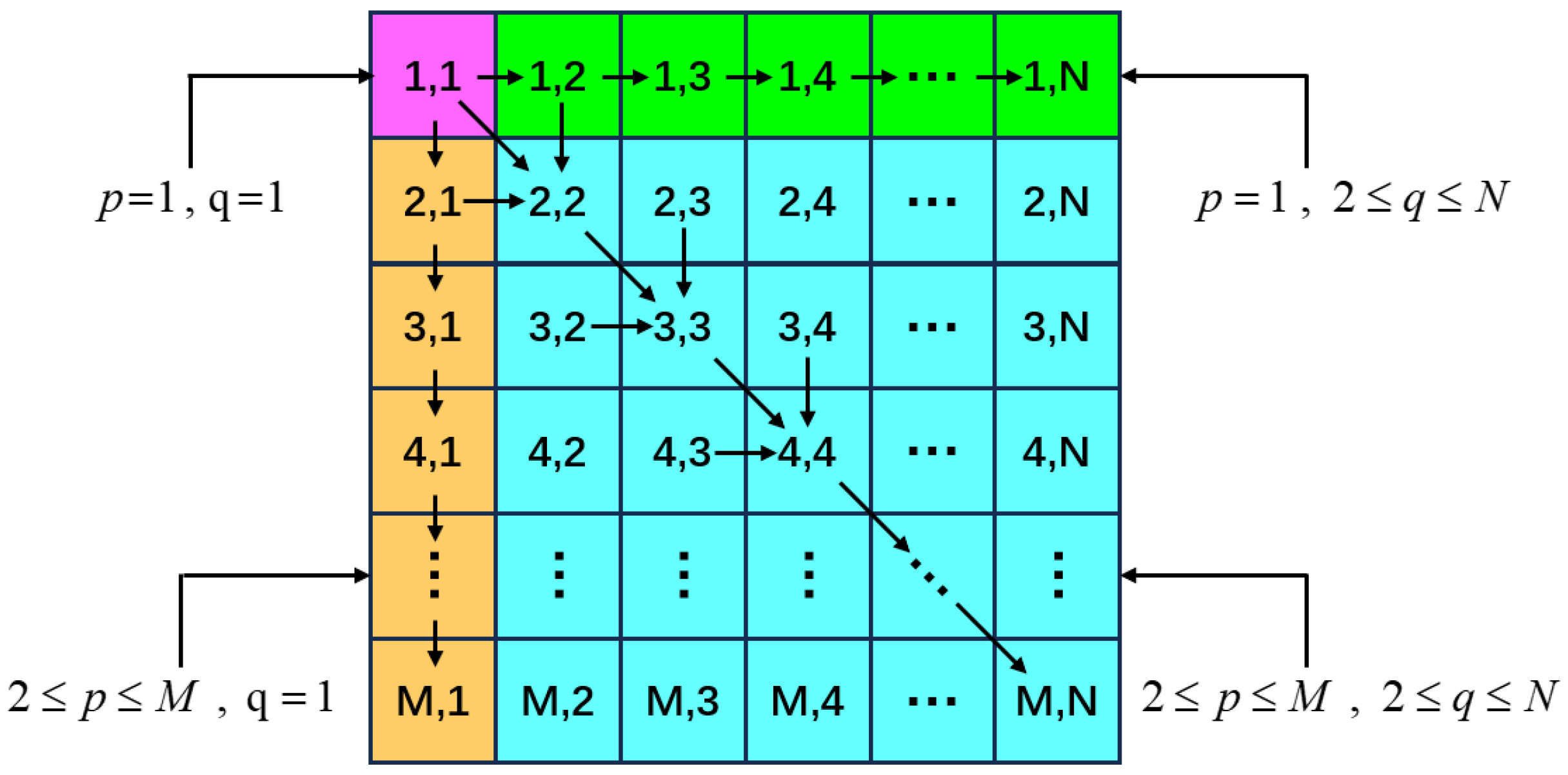
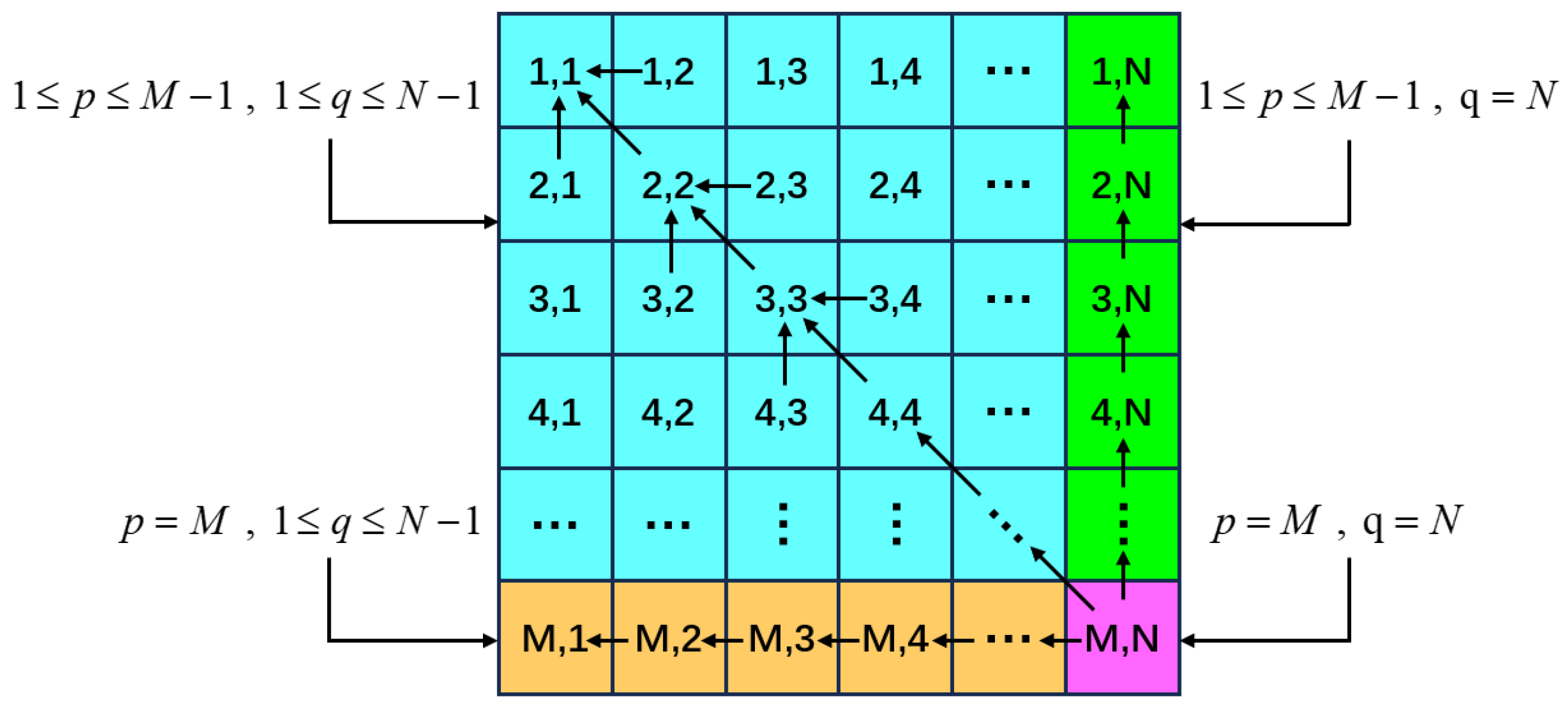
4.3. Forward and Reverse Random Multidirectional Diffusion

The core objective of diffusion is to propagate the effect of a pixel’s change to other pixel locations, thereby enhancing the encryption system’s sensitivity to variations in the plaintext. An ideal encryption algorithm should demonstrate strong diffusion properties, ensuring that minor modifications to the plaintext image induce widespread alterations in the ciphertext image. Currently, most diffusion methods adopt a fixed pixel processing order, where each pixel is only influenced by its preceding pixel. This approach somewhat weakens the encryption effectiveness. To address this issue, we propose a forward and backward random multi-directional diffusion method with symmetrical characteristics. This method selects the diffusion direction based on different chaotic matrices. It is achieved through two rounds of random diffusion in multiple directions. The forward diffusion and the backward diffusion are symmetrically related in structure and mechanism. This diffusion algorithm can modify pixels in each direction at each position, thereby improving the performance of this diffusion method. A detailed description of the forward and reverse random multidirectional diffusion process is provided below.

Assume that the dimension of the matrix T is $M\times N$. The initial values $x_0^{\prime },y_0^{\prime },{\alpha }_0^{\prime },{\beta }_0^{\prime }$ are obtained from Equation (11). Two chaotic sequences, {$x_p^{\prime }$} and {$y_q^{\prime }$}, each of length $M\times N$, are generated according to Equation (4). Then, the matrices $B_1$ and $B_2$ are constructed by the following Equations (12) and (13):

$$\begin{array}{c}\hfill X^{\prime }=\mathrm{mod}(\mathrm{floor}(x_p^{\prime }\times {10}^{25}),256),\\ \hfill Y^{\prime }=\mathrm{mod}(\mathrm{floor}(y_q^{\prime }\times {10}^{25}),256).\end{array}$$

(12)

$$\begin{array}{c}\hfill B_1=\mathrm{reshape}(X^{\prime },[M,N]),\\ \hfill B_2=\mathrm{reshape}(Y^{\prime },[M,N]).\end{array}$$

(13)

where ‘floor’ represents rounding down and ‘reshape’ represents reshaping.

The iterative equation for the forward random multidirectional diffusion process is as follows:

$$R(p,q)=\left\{\begin{array}{cc}\mathrm{mod}\left(T(1,1)\oplus B_1(1,1),256\right)\hfill & (p=1,q=1);\hfill \\ \mathrm{mod}\left(T(1,q)\oplus B_1(1,q)\oplus R(1,q-1),256\right)\hfill & (p=1,2\le q\le N);\hfill \\ \mathrm{mod}\left(T(p,1)\oplus B_1(p,1)\oplus R(p-1,1),256\right)\hfill & (2\le p\le M,q=1);\hfill \\ \mathrm{mod}\left(\begin{array}{c}T(p,q)\oplus B_1(p,q)\oplus R(p-1,q-1)\hfill \\ \oplus R(p,q-1)\oplus R(p-1,q)\hfill \end{array},256\right)\hfill & (2\le p\le M,2\le q\le N).\hfill \end{array}\right.$$

(14)

where T is the input variable of forward diffusion, R is the output variable of forward diffusion, $B_1$ is the key used for forward diffusion, and symbol ⊕ denotes the bit-level XOR operation.

The schematic diagram of forward stochastic multidirectional diffusion is shown in Figure 12. Different colors represent the different equations used in the encryption process, and the arrows indicate that the pixels at this coordinate are related to the pixels at other coordinates. Therefore, the decryption equation for forward stochastic multidirectional diffusion can be obtained by the following computational procedure.

Step 1. Remove the ‘mod’ operation in the forward random multinomial diffusion equation.

$$R(p,q)=\left\{\begin{array}{cc}\mathrm{mod}\left(T(1,1)\oplus B_1(1,1),256\right)\hfill & (p=1,q=1);\hfill \\ \mathrm{mod}\left(T(1,q)\oplus B_1(1,q)\oplus R(1,q-1),256\right)\hfill & (p=1,2\le q\le N);\hfill \\ \mathrm{mod}\left(T(p,1)\oplus B_1(p,1)\oplus R(p-1,1),256\right)\hfill & (2\le p\le M,q=1);\hfill \\ \mathrm{mod}\left(\begin{array}{c}T(p,q)\oplus B_1(p,q)\oplus R(p-1,q-1)\hfill \\ \oplus R(p,q-1)\oplus R(p-1,q)\hfill \end{array},256\right)\hfill & (2\le p\le M,2\le q\le N).\hfill \end{array}\right.$$

(15)

$$=\left\{\begin{array}{cc}T(1,1)\oplus B_1(1,1)+256n_{1,1}\hfill & (p=1,q=1);\hfill \\ T(1,q)\oplus B_1(1,q)\oplus R(1,q-1)+256n_{1,q}\hfill & (p=1,2\le q\le N);\hfill \\ T(p,1)\oplus B_1(p,1)\oplus R(p-1,1)+256n_{p,1}\hfill & (2\le p\le M,q=1);\hfill \\ \left(\begin{array}{c}\hfill T(p,q)\oplus B_1(p,q)\oplus R(p-1,q-1)\\ \hfill \oplus R(p,q-1)\oplus R(p-1,q)+256n_{p,q}\end{array}\right)\hfill & (2\le p\le M,2\le q\le N).\hfill \end{array}\right.$$

(16)

Step 2. Calculate the diffusion input matrix $T(p,q)$.

$$T(p,q)=\left\{\begin{array}{cc}R(1,1)\oplus B_1(1,1)+256n_{1,1}\hfill & (p=1,q=1);\hfill \\ R(1,q)\oplus B_1(1,q)\oplus R(1,q-1)+256n_{1,q}\hfill & (p=1,2\le q\le N);\hfill \\ R(p,1)\oplus B_1(p,1)\oplus R(p-1,1)+256n_{p,1}\hfill & (2\le p\le M,q=1);\hfill \\ \left(\begin{array}{c}\hfill R(p,q)\oplus B_1(p,q)\oplus R(p-1,q-1)\\ \hfill \oplus R(p,q-1)\oplus S(p-1,q)+256n_{p,q}\end{array}\right)\hfill & (2\le p\le M,2\le q\le N).\hfill \end{array}\right.$$

(17)

$$=\left\{\begin{array}{cc}\mathrm{mod}\left(R(1,1)\oplus B_1(1,1),256\right)\hfill & (p=1,q=1);\hfill \\ \mathrm{mod}\left(R(1,q)\oplus B_1(1,q)\oplus R(1,q-1),256\right)\hfill & (p=1,2\le q\le N);\hfill \\ \mathrm{mod}\left(R(p,1)\oplus B_1(p,1)\oplus R(p-1,1),256\right)\hfill & (2\le p\le M,q=1);\hfill \\ \mathrm{mod}\left(\begin{array}{c}R(p,q)\oplus B_1(p,q)\oplus R(p-1,q-1)\hfill \\ \oplus R(p,q-1)\oplus R(p-1,q)\hfill \end{array},256\right)\hfill & (2\le p\le M,2\le q\le N).\hfill \end{array}\right.$$

(18)

The reverse random multinomial diffusion operation is described as follows:

$$C(p,q)=\left\{\begin{array}{cc}\mathrm{mod}\left(R(M,N)\oplus B_2(M,N),256\right)\hfill & (p=M,q=N);\hfill \\ \mathrm{mod}\left(R(M,q)\oplus B_2(M,q)\oplus C(M,q+1),256\right)\hfill & (p=M,1\le q\le N-1);\hfill \\ \mathrm{mod}\left(R(p,N)\oplus B_2(p,N)\oplus C(p+1,N),256\right)\hfill & (1\le p\le M-1,q=N);\hfill \\ \mathrm{mod}\left(\begin{array}{c}R(p,q)\oplus B_2(p,q)\oplus C(p+1,q+1)\hfill \\ \oplus C(p+1,q)\oplus C(p,q+1)\hfill \end{array},256\right)\hfill & (1\le p\le M-1,1\le q\le N-1).\hfill \end{array}\right.$$

(19)

where R is the input variable of the reverse diffusion, C is the output variable of the reverse diffusion, $B_2$ is the reverse diffusion key, and symbol ⊕ denotes the bit-level XOR operation.

The schematic diagram of reverse random multidirectional diffusion is shown in Figure 13. The meanings of the colors and arrows are the same as those in Figure 12. Similar to the decryption process of forward stochastic multidirectional diffusion, the decryption equation of reverse stochastic multidirectional diffusion can also be described by the following equation.

Step 1. Remove the ‘mod’ operation in the reverse random multinomial diffusion equation.

Step 2. Calculate the diffusion input matrix $R(p,q)$.

$$R(p,q)=\left\{\begin{array}{cc}\mathrm{mod}\left(C(M,N)\oplus B_2(M,N),256\right)\hfill & (p=M,q=N);\hfill \\ \mathrm{mod}\left(C(M,q)\oplus B_2(M,q)\oplus C(M,q+1),256\right)\hfill & (p=M,1\le q\le N-1);\hfill \\ \mathrm{mod}\left(C(p,N)\oplus B_2(p,N)\oplus C(p+1,N),256\right)\hfill & (1\le p\le M-1,q=N);\hfill \\ \mathrm{mod}\left(\begin{array}{c}C(p,q)\oplus B_2(p,q)\oplus C(p+1,q+1)\hfill \\ \oplus C(p+1,q)\oplus C(p,q+1)\hfill \end{array},256\right)\hfill & (1\le p\le M-1,1\le q\le N-1).\hfill \end{array}\right.$$

(20)

5. Simulation Results and Performance Analysis

This section comprehensively evaluates the encryption performance and security of the proposed algorithm through various testing methods applied to color images of different sizes. These simulation experiments were all conducted on MATLAB 2020b on a compatible Windows-10-operating-system computer (with 8.00 GB of memory and an Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz). All the experimental images were sourced from three renowned benchmark databases: https://sipi.usc.edu/database/ (accessed on 22 July 2025) USC-SIPI, https://www.imageprocessingplace.com/root_files_V3/image_databases.htm (accessed on 22 July 2025) IPP, and https://www.cs.cmu.edu/~cil/v-images.html (accessed on 22 July 2025) CVIT. The test images selected included a 256 × 256 Lena image, a 512 × 512 Aircraft image, a 512 × 512 Sailboat image, a 1024 × 1024 Satellite map image, and a 768 × 512 Butterfly image. The simulation results, as illustrated in Figure 14, demonstrate that the encrypted images effectively conceal the plaintext information. In addition to performing encryption tests on these images, a comprehensive security analysis of the encryption method was performed, including key space analysis, entropy, histogram analysis, chi-squared test, and correlation analysis. Through this comprehensive analysis, it was demonstrated that the proposed encryption method delivers effective security performance when applied to color images across a range of different sizes and resolutions.

5.1. Key Space Analysis

Brute-force attacks involve systematically attempting to crack a cryptographic key by exhaustively trying all possible combinations of passwords or passphrases until the correct one is found. Over time, images encrypted with shorter keys become more vulnerable to such attacks, while longer keys provide stronger protection, making short-term decryption nearly impossible. Evaluating the size of the key space is crucial for assessing the strength of encryption systems against brute-force attacks. A key space larger than $2^{100}$ is typically regarded as robust enough to resist such attacks [35].

The keys used in this scheme are $t_1,t_2,\dots ,t_7,t_8$, along with SHA-512. Assuming the precision accuracy to be ${10}^{-16}$, the key total space of the eight input keys can be approximated as ${10}^{16\times 8}={10}^{128}$, which is greater than ${10}^{120}\approx 2^{10\times 40}$. In contrast, the key space is generated during the key creation stage using $2^{512}$. As such, the total key space is greater than $2^{912}$, which is significantly greater than $2^{100}$, thus meeting the required security level. A comparison of the key space of this scheme with that of several previous schemes is presented in

Table 1. Key space comparison.

Scheme	Key Space	Scheme	Key Space	Scheme	Key Space
Ref. [36]	$2^{209}$	Ref. [37]	${10}^{64}$	Ref. [38]	$2^{128}$
Ref. [39]	$2^{260}$	Ref. [40]	$2^{512}$	Ref. [41]	$2^{168}$
Ref. [42]	$2^{398}$	Ref. [43]	$2^{512}$	Proposed	>$2^{912}$

. As shown, compared with the reference method, this scheme has a better key space, thereby providing a stronger capability to withstand brute-force attacks.

5.2. Histogram Analysis

Histograms are commonly used to statistically evaluate image encryption algorithms. They graphically show the distribution of pixel intensities across grayscale levels, reflecting the image’s grayscale characteristics. A plaintext image typically has distinct statistical patterns, while an ideally encrypted image disrupts these patterns, resulting in a uniform grayscale distribution in the ciphertext, effectively concealing the original image’s information.

Experimental evaluations on standard test images with different resolutions (e.g., Lena, airplane, sailboat, satellite, and butterfly) showed that the image encryption method in this study significantly destroyed the original grayscale distribution. As shown in Figure 14, where red, green, and blue correspond to the R, G, and B channels respectively, the histogram distribution of the image after encryption was very homogeneous, indicating an equal frequency of gray levels. This uniformity indicated that the image content was completely obfuscated and, therefore, statistical analysis could not extract meaningful information. Thus, the algorithm exhibits strong resistance to statistical attacks.

5.3. Variance and Chi-Square Analysis

An uneven pixel value distribution in an image typically indicates the presence of important structural or feature details. This distribution characteristic can enable an attacker to obtain relevant data. In contrast, when the pixel values exhibit a uniform distribution, the statistical nature of the original image can be effectively hidden, thus enhancing the resistance of this encryption algorithm to statistical attacks. The variance var(X) and the Chi-square ${\chi }^2$ tests for a grayscale image can be calculated using Equations (21) and (22), respectively.

$$var\left(X\right)={\displaystyle \frac{1}{n^2}}\sum _{i=0}^n\sum _{j=1}^n{\displaystyle \frac{1}{2}}{(x_i-x_j)}^2,$$

(21)

$${\chi }^2=\sum _{i=0}^{255}{\displaystyle \frac{{(n_i-n/256)}^2}{n/256}},$$

(22)

where $X=\{x_1,x_2,\dots ,x_{256}\}$ represents the vector of tonal values in the histogram. $x_i$ and $x_j$ indicate the pixel counts for gray levels i and j, respectively. Let $n_i$ denote the frequency of tonal value i and n the total pixel count. Thus, the expected frequency for each tonal value is $n/256$. A significance level of $\alpha =0.05$ is typically used. If chi-square score ${\chi }_{0.05}^2\left(255\right)=293.248$, this suggests that the pixel distribution is exceptionally uniform [44]. To achieve greater uniformity, the variance should be made as small as possible. The variance and ${\chi }^2$ test results for the original and encrypted images under the histogram analysis in Figure 14 are presented in

Table 2. Analysis of variance and ${\chi }^2$ test results for the images.

Images	P/E	Size	Variance	Chi-Square
Lena	Plain	256 $\times$256	1.9329 $\times {10}^5$	6.4430 $\times {10}^4$
	Encrypted	256 $\times$256	666.9725	221.4557
Aircraft	Plain	512 $\times$512	2.7718 $\times {10}^7$	2.3098 $\times {10}^6$
	Encrypted	512 $\times$512	2714.8	225.3457
Sailboat	Plain	512 $\times$512	2.6723 $\times {10}^6$	2.2269 $\times {10}^5$
	Encrypted	512 $\times$512	2955.1	245.2995
Satellite	Plain	1024 $\times$1024	6.8016 $\times {10}^7$	1.4170 $\times {10}^6$
	Encrypted	1024 $\times$1024	11,434	237.2786
Butterfly	Plain	768 $\times$512	1.4687 $\times {10}^7$	8.1595 $\times {10}^5$
	Encrypted	768 $\times$512	4145.3	229.3971

.

5.4. Correlation Analysis

In plaintext images, pixels usually exhibit strong correlations among themselves. Therefore, efficient image encryption algorithms should greatly reduce inter-pixel correlation through effective substitution operations. To quantify the correlation between pixels, the correlation coefficient $r_{xy}$ between pixels can be computed using Equation (23).

$$r_{xy}={\displaystyle \frac{E[x-E(x\left)\right][y-E(y\left)\right]}{\sqrt{var\left(x\right)\sqrt{var\left(y\right)}}}},$$

(23)

where $E\left(x\right)={\displaystyle \frac{1}{N}}{\Sigma }_{i=1}^N{x}_i$, $var\left(x\right)={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N[{(x_i-E\left(x\right)]}^2$, $x_i$, and $y_i$ denote the hue value of the i pairs of neighboring pixels and N denotes the number of pixel samples. In this study, 3000 pixel samples were analyzed by extracting them from encrypted images. The original and encrypted images of Lena, airplane, sailboat, satellite, and butterfly were analyzed along with their correlation coefficients in horizontal, vertical, and diagonal directions for R, G, and B channels. Figure 15 shows the correlations in the three directions of the experimental pictures, where the horizontal, vertical, and diagonal correspond to red, blue, and green respectively and

Table 3. The correlation coefficient of adjacent pixels in the image.

Images	Channels	Plaintext Image			Ciphertext Image
		H	V	D	H	V	D
Lena	R	0.9403	0.9742	0.9255	0.0127	−0.0252	0.0022
	G	0.9500	0.9669	0.9279	−0.0238	0.0003	0.0066
	B	0.9431	0.9634	0.9203	−0.0080	−0.0130	−0.0020
Aircraft	R	0.9686	0.9733	0.9447	−0.0107	0.0033	0.0008
	G	0.9646	0.9722	0.9458	0.0392	−0.0076	0.0086
	B	0.9591	0.9570	0.9274	−0.0369	0.0096	−0.0092
Sailboat	R	0.9632	0.9594	0.9483	−0.0113	0.0069	0.0001
	G	0.9716	0.9689	0.9586	0.0295	−0.0111	−0.0093
	B	0.9748	0.9719	0.9560	−0.0006	−0.0015	0.0044
Satellite	R	0.9560	0.9192	0.9027	0.0004	−0.0102	0.0248
	G	0.9208	0.9242	0.9038	−0.0001	−0.0005	0.0256
	B	0.8902	0.9128	0.8902	−0.0228	0.0034	0.0017
Butterfly	R	0.9721	0.9612	0.9535	0.0207	−0.0263	0.0023
	G	0.9411	0.9478	0.9091	0.0061	0.0193	−0.0093
	B	0.9590	0.9470	0.9455	−0.0062	0.0030	0.0311

presents the corresponding correlation numbers. The results show that while the original images showed significant pixel correlation, the encrypted images showed negligible correlation between neighboring pixels. The reduction of the correlation coefficient tended to zero, which proves that the proposed encryption method effectively improves the randomness and security of encryption and further confirms the efficiency of the algorithm.

5.5. Information Entropy Analysis

Information entropy is a fundamental measure of uncertainty and randomness in image data. Higher entropy values indicate greater unpredictability in an image’s content. An entropy value near eight typically signifies that the encrypted image exhibits enhanced security and randomness [45]. As a crucial tool for evaluating ciphertext properties, information entropy is widely applied to assess the performance of encryption algorithms and the resilience of encryption schemes. By using formula (24), entropy can be quantified, providing a clear standard for evaluating the security of an encryption system.

$$H\left(x\right)=\sum _{i=0}^{2^n-1}p\left(x_i\right)lo{g}_2{\displaystyle \frac{1}{p\left(x_i\right)}}.$$

(24)

Let x represent the information source, with the probability of $x_i$ denoted as $p\left(x_i\right)$. The total number of possible states is $2^n$. For color images with 256 grayscale levels,

Table 4. Information entropy analysis.

Images	Size	Plaintext Image			Ciphertext Image
		R	G	B	R	G	B
Lena	256 × 256 × 3	7.2353	7.5683	6.9176	7.9974	7.9976	7.9972
Aircraft	512 × 512 × 3	6.7178	6.799	6.2138	7.9994	7.9993	7.9994
Sailboat	512 × 512 × 3	7.3124	7.6461	7.2137	7.9993	7.9994	7.9993
Satellite	1024 × 1024 × 3	7.7229	7.5289	6.8318	7.9998	7.9998	7.9998
Butterfly	768 × 512 × 3	7.4042	7.0843	6.9801	7.9996	7.9995	7.9996
Ref. [34]	512 × 512 × 3	–	–	–	7.9971	7.9975	7.9974
Ref. [36]	512 × 512 × 3	–	–	–	7.9912	7.9913	7.9914
Ref. [38]	512 × 512 × 3	–	–	–	7.9974	7.9974	7.9974

lists the entropy values of R, G, and B channels of plaintext and ciphertext images according to the encryption method proposed in this paper and compares them with the entropy values obtained by other encryption techniques. The results show that the entropy values of the R, G, and B channels of the ciphertext image are almost equal to the ideal value eight.

5.6. Differential Attack Analysis

In the field of image encryption, differential analysis is commonly employed to assess the robustness of encryption algorithms against differential attacks. This approach involves introducing slight perturbations to the input image and then observing how these small changes propagate within the ciphertext, thereby evaluating whether the encryption algorithm possesses strong security. Ideally, a secure image encryption system should exhibit high plaintext sensitivity, meaning that even a single pixel change in the input image should lead to a significant alteration in the overall structure of the ciphertext.

To quantify the performance of encryption algorithms under such conditions, two key metrics are commonly introduced: the Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI). NPCR measures the proportion of pixel position changes between two ciphertext images before and after encryption, reflecting the extent to which local disturbances are diffused in the ciphertext. UACI, on the other hand, captures the average intensity differences between two ciphertext images, indicating the response of the encryption output to perturbations at the numerical level. Together, these two metrics allow for a comprehensive assessment of an algorithm’s resistance to differential attacks from both the spatial distribution and intensity change perspectives. Therefore, NPCR and UACI have become essential standards for evaluating the security of image encryption algorithms and are widely used in the verification of modern encryption schemes. The calculation formulas for NPCR and UACI are defined in Equations (25)–(27).

$$\mathrm{NPCR}={\displaystyle \frac{{\sum }_{i=1}^M{\sum }_{j=1}^{N}D(i,j)}{M\times N}}\times 100\%,$$

(25)

$$D(i,j)=\left\{\begin{array}{c}1,T_1(i,j)\ne T_2(i,j)\hfill \\ 0,T_1(i,j)=T_2(i,j)\hfill \end{array}\right.,$$

(26)

$$\mathrm{UACI}={\displaystyle \frac{1}{M\times N}}\left[\sum _{i=1}^M\sum _{j=1}^N{\displaystyle \frac{|T_1(i,j)-T_2(i,j)|}{255}}\right]\times 100\%,$$

(27)

where $T_1(i,j)$ and $T_2(i,j)$ respectively represent the pixel values at the same coordinate positions in the encrypted images obtained by the encryption algorithm from the original images that have slight differences. M and N indicate the number of rows and columns of the ciphertext image, respectively. The NPCR and UACI results for images of various sizes used in the experiments are presented in

Table 5. Results of NPCR and UACI performance.

Images	NPCR(%)			UACI(%)
	R	G	B	R	G	B
Lena	99.6156	99.5965	99.5978	33.4829	33.4759	33.4573
Aircraft	99.6046	99.6107	99.6116	33.3912	33.4616	33.4250
Sailboat	99.5964	99.6064	99.6075	33.4997	33.4976	33.4578
Satellite	99.6076	99.5987	99.5989	33.4419	33.5068	33.5038
Butterfly	99.5921	99.6242	99.6056	33.4480	33.4497	33.4656
Ref. [46]	99.5461	99.7066	99.6070	35.9229	36.6366	36.2376
Ref. [47]	99.5925	99.6294	99.6140	33.4226	33.4344	33.4698
Ref. [48]	99.6048	99.6010	99.5987	33.4481	33.4886	33.5094

. Notably, the experimental results are in close proximity to the ideal NPCR value of 99.6094% and the ideal UACI value of 33.4635%. The comparative analysis shows that the performance of our algorithm in terms of NPCR and UACI is basically closer to the theoretical ideal values. This indicates that our algorithm exhibits stronger resistance to differential attacks.

6. Conclusions and Outlook

This paper introduced a novel hyperchaotic system developed from a two-dimensional cross-coupled chaotic system. By combining Chebyshev mapping, Fuch mapping, and nonlinear functions $sin\left(x\right)$ and $cos\left(x\right)$, a two-dimensional Chebyshev–Fuch coupled map (2D-CFCM) was established. The proposed chaotic system exhibits significant chaotic behavior, highlighted by enhanced phase diagrams, bifurcation diagrams, Lyapunov exponents, and complexity. The resulting chaotic sequences demonstrate a greater degree of randomness, and the chaotic parameter space is notably expanded. In order to check the performance of the 2D chaotic system, an image encryption scheme based on 2D-CFCM was introduced. The algorithm derives a key from the original image using the SHA-512 function and then applies both obfuscation and diffusion via a chaotic matrix coupled with the I-Zigzag transformation, achieving multi-directional randomness. Simulation outcomes show that the encryption method performs exceptionally well, provides a large key space, and exhibits significant sensitivity to key alterations. However, the encryption method’s efficiency, especially for larger images, requires further optimization. Future research could explore the integration of this encryption method with emerging technologies like quantum computing and machine learning to enable more advanced encryption solutions. Additionally, testing the algorithm’s applicability in real-world scenarios, such as cloud storage and digital media transmission, would demonstrate its practical potential.