Imperialist Competitive Algorithm with Three Empires for Energy-Efficient Parallel Batch Processing Machine Scheduling with Preventive Maintenance

Abstract

Batch processing machines (BPMs) are extensively present in high energy-consuming manufacturing processes such as casting, and they show some symmetries on adjacent batches and jobs within each batch. Preventive maintenance (PM) is very important for the stable running and energy saving of BPMs; however, PM in a parallel BPM shop is seldom studied. In this study, the energy-efficient parallel BPM scheduling problem with PM is considered and an imperialist competitive algorithm with three empires (TEICA) is presented to minimize makespan and total energy consumption. To obtain high-quality solutions, the number of empires is not used as a parameter and fixed at 3, a new way is applied to construct three initial empires, each of which has a new structure like two imperialists, a new assimilation is given, and an adaptive imperialist competition is implemented based on historical competition data. A number of computational experiments are conducted on 108 instances. The computational results show that the new strategies of TEICA are effective; TEICA can provide better results than all comparative methods on more than 90% instances of the considered BPM scheduling problem, and TEICA may be an effective way to solve other BPM scheduling problem.

1. Introduction

As a typical batch processing machine (BPM) scheduling problem, parallel BPM scheduling has attracted much attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. As the main approaches, meta-heuristics such as genetic algorithm (GA) [1,5], differential evolution (DE) [2,8], particle swarm optimization (PSO) [3] are often used, and heuristics [4,7] are also applied to solve the scheduling problem in parallel BPM shop.

There are some works on the uniform problem [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23], which use algorithms based on linear programming and integer programming [9] and heuristic [9,10]. Some meta-heuristics are also applied, which are Pareto-based ant colony system [11], non-dominated sorting genetic algorithm-II (NSGA-II) and multi-objective imperialist competitive algorithm [12], DE [13], ant colony optimization [14,15], artificial immune system [16] and evolutionary algorithm [17]. Non-identical parallel BPM scheduling problem is solved by PSO [18], GA [19], fruit fly optimization algorithm [20], artificial bee colony (ABC) [21], shuffled frog-leaping algorithm (SFLA) [22], and teaching–learning-based optimization [23].

Many results are also obtained on unrelated parallel BPM scheduling. Shahidi-Zadeh et al. [24] proposed a harmony search algorithm to solve a multi-objective problem. A hybrid ABC with tabu search is applied to solve the problem with maintenance and deteriorating jobs [25]. A problem with different capacities and arbitrary job sizes is solved by a random key GA [26]. Sadati et al. [27] proposed fuzzy multi-objective discrete teaching–learning-based optimization and fuzzy NSGA-II. Zarook et al. [28] constructed an MILP model and provided six heuristics and a random key GA. To handle the problem in production systems under carbon reduction policies, Fallahi et al. [29] developed an MILP model, NSGA-II, and a multi-objective gray wolf optimizer. An SFLA with variable neighborhood search is designed for solving problems with nonlinear processing time [30]. A tabu-based adaptive large neighborhood search algorithm is presented by Xiao et al. [31], which renews the best known solutions of 55 instances. A problem with 2D packing constraint, non-identical sizes, unequal release dates, and due dates is solved by using an adaptive large neighborhood search [32].

BPMs are often present in high energy-consuming processes such as casting and energy-efficient BPM scheduling has attracted much attention in recent years [23,29,33,34,35,36,37,38,39,40,41,42]. With respect to the energy-efficient parallel BPM scheduling problem, Jia et al. [33] and Wang et al. [34] proposed a bi-objective ant colony optimization and a three-population co-evolutionary algorithm to minimize makespan and total energy consumption. For the problem with time-of-use electricity tariffs, Zhou et al. [35] developed a multi-objective DE algorithm for the problem with dynamic job arrivals, and Tian and Zheng [36] constructed a mixed-integer linear programming formulation and proposed a branch and price algorithm. Li et al. [17,37] developed a multi-objective evolutionary algorithm for uniform and non-identical problems with different job sizes and release times. Yang [38] presented an online algorithm for problems in the steel making process. Jiang et al. [39] proposed a modified benders decomposition and meta-heuristics for problems in the semiconductor burn-in test process. Schorn et al. [40] solved the problem with release time by genetic programming. Abedi et al. [41] developed a tabu search method for problems with incompatible families and release times. Wang et al. [23] dealt with a fuzzy problem with machine eligibility and sequence-dependent setup time in fabric dyeing processing using a dynamical teaching–learning-based optimization. Wang et al. [42] presented a multi-objective mixed-integer programming model and a multi-objective evolutionary algorithm based on decomposition combined with variable neighborhood search for problems with preventive maintenance (PM).

As stated above, many results are obtained on parallel BPM scheduling; uniform problem, non-identical problem, unrelated problem, and energy-efficient problem are often considered; scheduling of parallel BPMs in real-life manufacturing processes such as fabric dyeing and semiconductor burn-in test is frequently investigated; various processing conditions and constraints, including machine eligibility, are also handled. However, some constraints are seldom dealt with, for example, PM is often applied to prevent potential failures and serious accidents in parallel machines, and the parallel machine scheduling problem (PMSP) with PM is frequently addressed [43,44,45]. To the best of our knowledge, related works on PM in parallel BPM shops are seldom conducted. A BPM is often a furnace for heating and melting and a high energy-consuming machine; its stable running and avoidance of failure and accidents can directly affect the production efficiency and energy consumption of a manufacturing process, so it is necessary to the solve energy-efficient parallel BPM scheduling problem with PM.

The imperialist competitive algorithm (ICA) is a meta-heuristic illuminated by the historical phenomena of imperialism and colonialism. Unlike the existing meta-heuristics such as GA and SFLA, ICA has good neighborhood search ability, effective global search property, good convergence rate, and flexible structure [46]. In recent years, ICA has been extensively applied to solve various production scheduling problems such as PMSP [47], flexible job shop scheduling [48,49], hybrid flow shop scheduling [50,51], and assembly scheduling [52]; however, ICA is seldom applied to solve parallel BPM scheduling. ICA has successfully been applied to solve PMSP and results revealed that ICA has a strong exploration–exploitation balance and significantly outperforms the best-performing algorithms in the literature. When all machines of PMSP are replaced with BPMs, PMSP is extended to the parallel BPM scheduling problem. The advantages of ICA in solving PMSP show that ICA has a potential advantage in handling parallel BPM scheduling, so ICA is chosen in this study.

In this paper, the energy-efficient parallel BPM scheduling problem with PM is considered, and a new imperialist competitive algorithm with three empires (TEICA) is presented to minimize makespan and total energy consumption. In TEICA, the number of empires is fixed at 3 and not used as a parameter. A new way is applied to construct three initial empires, each of which has a new structure resembling two imperialists, and exploration ability can be intensified. A new assimilation is given and an adaptive imperialist competition is implemented. A number of computational experiments are conducted on 108 instances. The computational results demonstrate that new strategies, such as a new empire structure, are effective, and TEICA has promising advantages in solving the BPM scheduling problem being considered.

2. Problem Description

The parallel BPM scheduling problem with PM is shown below. There are n jobs $J_1,J_2,\cdots ,J_n$ and m unrelated parallel BPMs $M_1,M_2,\cdots ,M_m$. Each job can be processed on any BPM. Table 1 describes some notations. $p_{ki}$ indicates the processing time of $J_i$ on $M_k$. $S_i$ may be size, weight. Size means the number of $J_i$, $S_i$ is the weight in the fabric dyeing process. Jobs can be grouped into a batch according to the type of job and the capacity of the BPM. In batch $B_{kv}$, all jobs belong to the same type and capacity constraint is met, that is, the sum of index of all jobs in the batch cannot exceed $q_k$, for example, the sum of size or weight of all jobs is less than or equal to $q_k$. $P{T}_{kv}=max\left\{p_{ki},i\in B_{kv}\right\}$. In a batch, all jobs of the batch start at the same time and also end at the same time.

Table 1. Notation and description.

Notation	Description	Notation	Description
n	number of jobs	m	number of machines
$p_{ki}$	the processing time of $J_i$ on $M_k$	$S_i$	index of $J_i$
$t_i$	the type of $J_i$	$q_k$	capacity of $M_k$
$B_{kv}$	the $v$-th batch on $M_k$	$P{T}_{kv}$	the processing time of $B_{kv}$
$C_i$	completion time of $J_i$	$C_{max}$	maximum completion time of all jobs
$TEC$	total energy consumption	$N{U}_k$	the number of batches processed on $M_k$
N	population scale	$N_{col}$	total number of colonies
$N{C}_k$	total number of colonies in empire k	$T{C}_k$	total cost of empire k
$NT{C}_k$	normalized total cost of empire k	$E{P}_k$	power of empire k

PM is considered. There is a time interval between two consecutive PMs, during which jobs are processed. For $M_k$, $u_k$ indicates the length of the interval, $w_k$ denotes the duration of PM, and the start time of the g-th PM is $g\times u_k$, that is, the processing of a job cannot be finished when time $g\times u_k$ reaches, PM will be first handled and then the job is processed.

The following constraints on jobs and machines are considered:

• Each batch can be processed on only one machine at a time.
• Each machine handles at most one batch at a time.
• The operations cannot be interrupted.
• All the machines are available at time zero.

The problem is composed of three sub-problems: machine assignment, batch formation, and scheduling. The goal of the problem is to minimize makespan and total energy consumption when all sub-problems are solved and all constraints are met.

$$C_{max}=\underset{i=1,2,\cdots n}{max}\left\{C_i\right\}$$

(1)

$$TEC={\sum }_{k=1}^m{\sum }_{i=1}^{N{U}_k}P{T}_{ki}·e_k+{\sum }_{k=1}^m\left(I{T}_k·i{e}_k+PM{T}_k·pm{e}_k\right)$$

(2)

where $e_k,i{e}_k,pm{e}_k$ indicates energy consumption per unit time when $M_k$ is in processing mode, idle mode and maintenance mode respectively, $I{T}_k$, $PM{T}_k$ are total idle time and total maintenance time.

There are some symmetries on each BPM. On the BPM $M_k$, two adjacent batches between two processing machines are exchanged with each other. Two objectives are kept invariant, which is symmetry, but when two batches on different BPM are swapped, objectives will vary and no symmetry exists. For two objectives, the conflict means that when one objective is improved, the other objective may deteriorate. For parallel BPM scheduling, for a given $C_{max}$, there exist many different schedules with the same $C_{max}$, and these schedules have different $TEC$. When $C_{max}$ diminishes, $TEC$ may increase, so $C_{max}$ and $TEC$ conflict each other.

Figure 1 shows a schedule for an example with 20 jobs and 2 BPMs, $q_1=17$, $q_2=15$.

$${\left(t_i\right)}_{1\times 20}=\left[\begin{array}{cccccccccccccccccccc}1& 2& 2& 2& 1& 1& 1& 1& 1& 2& 2& 1& 1& 2& 2& 1& 2& 1& 1& 1\end{array}\right]$$

(3)

$${\left(S_i\right)}_{1\times 20}=\left[\begin{array}{cccccccccccccccccccc}4& 10& 9& 3& 3& 1& 10& 7& 5& 3& 5& 2& 10& 4& 10& 1& 8& 5& 5& 9\end{array}\right]$$

(4)

$$\begin{array}{c}{\left(p_{ki}\right)}_{2\times 20}={\left[\begin{array}{cccccccccc}36\hfill & 33\hfill & 50\hfill & 43\hfill & 40\hfill & 59\hfill & 62\hfill & 30\hfill & 32\hfill & 34\hfill \\ 63\hfill & 51\hfill & 56\hfill & 31\hfill & 39\hfill & 46\hfill & 42\hfill & 43\hfill & 52\hfill & 61\hfill \end{array}\right]}_{1-10}\hfill \\ {\left(p_{ki}\right)}_{2\times 20}={\left[\begin{array}{cccccccccc}51\hfill & 59\hfill & 69\hfill & 59\hfill & 46\hfill & 34\hfill & 58\hfill & 31\hfill & 53\hfill & 46\hfill \\ 39\hfill & 62\hfill & 57\hfill & 36\hfill & 32\hfill & 40\hfill & 39\hfill & 62\hfill & 37\hfill & 38\hfill \end{array}\right]}_{11-20}\hfill \end{array}$$

(5)

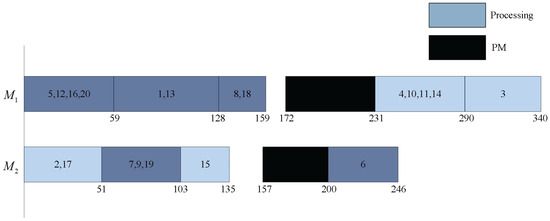
Figure 1. A schedule of the example.

In the above equation, the first part is about jobs $J_1-J_{10}$ and the second is about the remaining jobs. Figure 1 shows a schedule of the example. The numbers in each box represent the jobs in a batch; for example, the first batch on $M_1$ is composed of jobs 5, 12, 16, 20.

For the problem with $T_{tot}$ and $TEC$, $x\succ y$ indicates x dominates y and is defined as follows: if $T_{tot}\left(x\right)\le T_{tot}\left(y\right)$, $TEC\left(x\right)\le TEC\left(y\right)$, and $T_{tot}\left(x\right)<T_{tot}\left(y\right)$ or $TEC\left(x\right)<TEC\left(y\right)$, then $x\succ y$. If $x\succ y$ and $y\succ x$ are not met, then $x,y$ are non-dominated by each other.

3. TEICA for Energy-Efficient Parallel BPM Scheduling with PM

ICA is composed of initial empire formation, assimilation, revolution, and imperialist updating in each empire and imperialist competition. In TEICA, there are three fixed empires, each of which has two imperialists, and new assimilation and imperialist competition are given because of the fixed number of empires. Figure 2 shows the flow chart of TEICA, in which initial empire formation is used to construct initial empires, assimilation and revolution are main steps to produce new solutions, and imperialist competition is used to move colonies between empires. The stopping condition is often the running time of an algorithm.

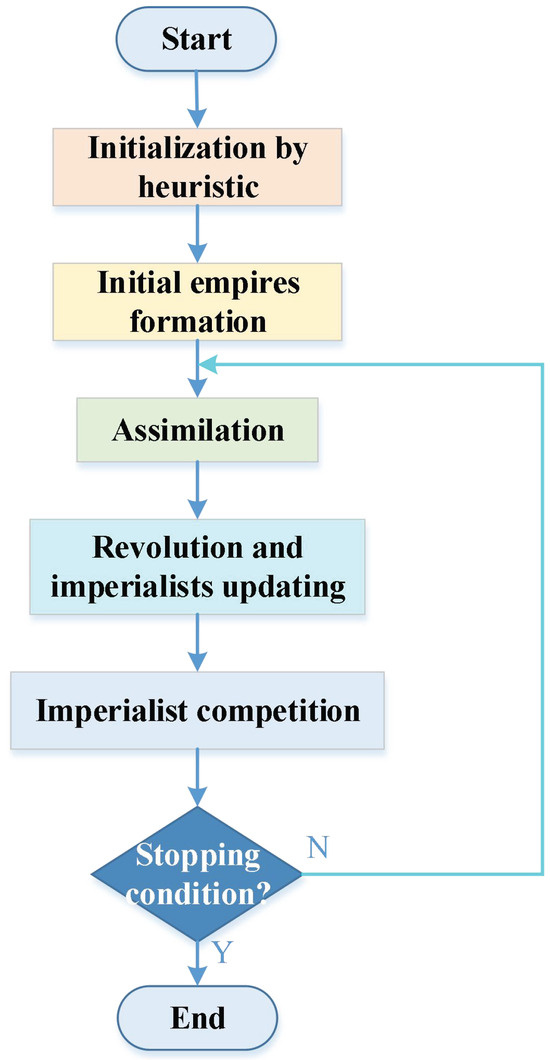
Figure 2. Flow chart of TEICA.

3.1. Initialization and Initial Empires

Two-string representation is used. For the problem with n jobs and m BPMs, its solution is represented as a machine assignment string $\left[M_{h_1},M_{h_2},\cdots ,M_{h_n}\right]$ and a scheduling string $\left[{\theta }_1,{\theta }_2,\cdots ,{\theta }_n\right]$, where $M_{h_i}$ and ${\theta }_i$ are the assigned BPM and a real number for job $J_i$.

The decoding process is shown below. For each BPM $M_k$, decide all jobs assigned on $M_k$ according to machine assignment string and sort all jobs on $M_k$ in the ascending order of their ${\theta }_i$, obtain a permutation of all jobs, construct a empty batch $B_{kv},v=1$, repeat the following steps until the permutation is empty: for the first job $J_i$ on the permutation, $B_{kv}=B_{kv}\cup \left\{J_i\right\}$, delete $J_i$ from the permutation, then choose all jobs with the type of $t_i$ from the permutation sequentially under capacity constraint and add all chosen jobs into $B_{kv}$ and delete the chosen jobs from the permutation, $v=v+1$, let $B_{kv}$ be empty. After batches $B_{k1},B_{k2},\cdots ,B_{kv}$ are formed, then all batches are processed on $M_k$ according to sequence $B_{k1},B_{k2},\cdots ,B_{kv}$.

For the example in Section 2, a possible solution is $[M_1,M_2,M_1,M_1,M_1,M_2,M_2,M_1,$$M_2,M_1,M_1,M_1,M_1,M_1,M_2,M_1,M_2,M_1,M_2,M_1]$ and $[0.82,0.02,0.95,0.65,0.66,0.94,0.3,$$0.29,0.9,0.91,$$\left.0.72,0.25,0.27,0.74,0.55,0.31,0.51,0.83,0.07,0.19\right]$. On $M_2$, jobs $J_2,J_{17},J_7,J_9,$$J_{19},J_{15},J_6$ are assigned on $M_2$, a permutation $[2,19,7,17,15,9,6]$ is obtained, then $B_{21}=\left\{J_2,J_{17}\right\}$, $B_{22}=\left\{J_{19},J_7,J_9\right\}$, $B_{23}=\left\{J_{15}\right\}$, $B_{24}=\left\{J_6\right\}$.

A simple heuristic is used, in which for each job $J_i$, a BPM $M_k$ with the smallest $p_{ki}$ is chosen as $M_{h_i}$, and a scheduling string is randomly produced. The initial population P is generated as follows. The heuristic is applied to produce six initial solutions, and $N-6$ initial solutions are produced stochastically.

In general ICA, each country corresponds to a solution of the problem and cost $c_x$ [46] is defined for each x. The better the solution is, the smaller the cost is. In population P, there are $N_{im}$ imperialists and $N_{col}$ colonies, $N_{col}=N-N_{im}$. There are $N_{im}$ empires, each of which is composed of an imperialist and $N{C}_k$ colonies. When initial empires are constructed, $N_{im}$ solutions with the smallest cost are first chosen as imperialists, then for each imperialist $I{M}_k,k=1,2,\cdots ,N_{im}$, its normalized cost ${\overline{c}}_{I{M}_k}$, power $po{w}_k$, $N{C}_k$ [46] are given; $N{C}_k$ colonies are randomly selected for $I{M}_k$ and empire k is obtained with $I{M}_k$ and its colonies.

$${\overline{c}}_{I{M}_k}=\underset{I{M}_l\in \left\{I{M}_1,I{M}_2,\cdots ,I{M}_{N_{im}}\right\}}{max}{c}_{I{M}_l}-c_{I{M}_k}$$

(6)

$$po{w}_k={\overline{c}}_k/\phantom{{\overline{c}}_k{\sum }_{I{M}_l\in \left\{I{M}_1,I{M}_2,\cdots ,I{M}_{N_{im}}\right\}}{\overline{c}}_l}{\sum }_{I{M}_l\in \left\{I{M}_1,I{M}_2,\cdots ,I{M}_{N_{im}}\right\}}{\overline{c}}_l$$

(7)

$$N{C}_k=round\left(po{w}_k\times N_{col}\right)$$

(8)

where $round\left(x\right)$ is an integer being closet to x.

A new way is proposed to produce three initial empires, as shown below.

(1) Define six solutions produced by the heuristic as imperialists $I{M}_1,I{M}_2,\cdots ,I{M}_6$, randomly choose two imperialists and add them into empire 1, then stochastically select the other two imperialists and include them into empire 2, and add the remaining two imperialists into empire 3.

(2) Execute non-dominated sorting [53] on all solutions of population P, define ${\overline{c}}_{I{M}_k}$ for each $I{M}_k$.

(3) Compute ${\overline{pow}}_1,{\overline{pow}}_2,{\overline{pow}}_3$ and $N{C}_1,N{C}_2,N{C}_3$ and randomly select colonies for empires 1,2,3.

Suppose that $I{M}_1,I{M}_2$ are in empire 1, $I{M}_3,I{M}_4$ are in empire 2 and $I{M}_5,I{M}_6$ are in empire 3, then ${\overline{pow}}_1$ is computed below.

$${\overline{c}}_{I{M}_k}=\underset{x\in P}{max}\left\{ran{k}_x\right\}-ran{k}_{I{M}_k}+dis{t}_{I{M}_k}/\phantom{dis{t}_{I{M}_k}{\sum }_{x\in P}dis{t}_x}{\sum }_{x\in P}dis{t}_x$$

(9)

where $ran{k}_x$ and $dis{t}_x$ are rank value and crowding distance of x obtained by non-dominated sorting.

$${\overline{pow}}_1=\left({\overline{c}}_{I{M}_1}+{\overline{c}}_{I{M}_2}\right)/\phantom{\left({\overline{c}}_1+{\overline{c}}_2\right){\sum }_{k=1}^6{\overline{c}}_{I{M}_k}}{\sum }_{k=1}^6{\overline{c}}_k$$

(10)

When ${\overline{pow}}_2$ and ${\overline{pow}}_3$ are computed, ${\overline{c}}_3,{\overline{c}}_4$ and ${\overline{c}}_5,{\overline{c}}_6$ substitute for ${\overline{c}}_1,{\overline{c}}_2$ respectively. When $N{C}_1,N{C}_2,N{C}_3$ are calculated, $po{w}_k$ of Equation (6) is replaced with ${\overline{pow}}_k$.

Unlike the existing ICA, TEICA only has three empires, and each empire has two fixed imperialists; this is a new structure. Moreover, $N_{im}$ is fixed at 3, and a parameter is reduced. After three empires are constructed, new assimilation and revolution are applied to improve solutions for each empire, and communication between empires is executed by imperialist competition; as a result, two objectives can be minimized continuously.

3.2. New Assimilation and Revolution

Assimilation is the main step for producing new solutions. In the assimilation process, a colony in each empire moves $\epsilon$ along with e direction toward its imperialist. The moving distance $\epsilon$ is a random number gotten by random distribution in interval $\left[0,s\times e\right]$, where $s\in \left(1,2\right)$ and e is the distance between the colony and the imperialist. Setting $s>1$ causes the colony to move toward the imperialist direction. However, imperialist cannot absorb their colonies in direct movement, resulting in a deviation from the direct line. The deviation is represented by $\theta$, which follows a uniform distribution in $\left[-\phi ,\phi \right]$, where $\phi$ is an arbitrary parameter.

To solve production scheduling problems, including parallel BPM scheduling, the above assimilation is often discretized because coding strings of scheduling problems often have special meaning and constraints; for example, in machine assignment, $M_{h_i}$ is a BPM and cannot be updated by using the above method.

In general ICA, each empire has only one imperialist. If the imperialist of an empire cannot be updated in some generations, the solution diversity in the empire will diminish greatly and search may stagnate. In TEICA, two imperialists are allocated in each empire, and colonies move to two imperialists; the above stagnation can be avoided effectively. A new assimilation is given because of the new structure of empires.

A new assimilation is described below for empire k.

(1)

For each colony x of empire k, randomly choose an imperialist, suppose $I{M}_{1+2(k-1)}$ is chosen, execute two-point crossover on machine assignment strings of $x,I{M}_{1+2(k-1)}$, obtain a new solution $x_{new}$, if $x_{new}\succ x$ or $x_{new},x$ are non-dominated each other, then $x=x_{new}$ and update external archive $\Omega$ with x; otherwise, produce $x_{new}$ by two-point crossover on scheduling string of $x, I{M}_{1+2(k-1)}$ and update $x,\Omega$ according to the above condition.

(2)

For imperialist $I{M}_{1+2(k-1)}$, execute two-point crossover on machine assignment string and scheduling string on $I{M}_{1+2(k-1)}$, $I{M}_{2+2(k-1)}$ respectively and update $I{M}_{1+2(k-1)}$ and $\Omega$ using the same way of step (1); then perform the same step for $I{M}_{2+2(k-1)}$.

In Step 2, for $I{M}_{2+2(k-1)}$, two-point crossovers on $I{M}_{2+2(k-1)}$, $I{M}_{1+2(k-1)}$ are performed and $I{M}_{2+2(k-1)}$ is renewed. When imperialists are improved continuously in each empire, exploration ability will be intensified.

$\Omega$ is used to store non-dominated solutions produced by TEICA and updated in the following way: add x into $\Omega$, compare all solutions of $\Omega$ based on Pareto dominance and delete all dominated solutions.

Revolution is a step of ICA, which is similar with the mutation of GA. It is applied to increase exploration and prevents the early convergence to local optima. Revolution is shown as follows. For empire k, for each colony x of empire k, if random number $rand<U_R$, then perform multiple neighborhood search on x, where $rand$ follows a uniform distribution on [0, 1].

Seven neighborhood structures are used. ${\mathcal{N}}_1$ is shown below: randomly choose a BPM $M_k$ with $N{U}_k>1$ and a BPM $M_l$, then randomly choose a job $J_i$ from $M_k$ and move it to $M_l$, that is, let $M_{h_i}(=M_k)$ be $M_l$. ${\mathcal{N}}_2,{\mathcal{N}}_3$ are similar with ${\mathcal{N}}_1$, in ${\mathcal{N}}_2$, $M_k$ is the BPM with the biggest completion time and $M_l$ is the BPM with the smallest completion time; in ${\mathcal{N}}_3$, $M_k$ is the BPM with the biggest energy consumption and $M_l$ indicates the BPM with the smallest energy consumption. ${\mathcal{N}}_4$ is described below: randomly select two BPMs $M_k,M_l$, $N{U}_k>0,N{U}_l>0$, exchange a randomly chosen batch $B_{kv}$ of $M_k$ and a stochastically chosen batch $B_{lu}$ on $M_l$, that is, all jobs of $B_{kv}$ are assigned to $M_l$ and all jobs of $B_{lu}$ are allocated to $M_k$. ${\mathcal{N}}_5$, ${\mathcal{N}}_6$, ${\mathcal{N}}_7$ are swap operator, insertion operator and invert operator of scheduling string.

Two using sequences of seven neighborhood structures are applied, which are ${\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3,{\mathcal{N}}_4,{\mathcal{N}}_5,{\mathcal{N}}_6,{\mathcal{N}}_7$ and ${\mathcal{N}}_5,{\mathcal{N}}_6,{\mathcal{N}}_7,{\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3,{\mathcal{N}}_4$.

Multiple neighborhood search is depicted as follows: for solution x, randomly choose a using sequence, let $\omega =1$, repeat the following steps until $\omega =8$: produce a new solution z by using the $\omega -$th neighborhood structure in the chosen sequence, if $z\succ x$ or $z,x$ are non-dominated each other, then $x=z$ and update $\Omega$; otherwise, $\omega =\omega +1$.

After assimilation and revolution are completed, in each empire k, non-dominated sorting [53] is performed on all solutions; choose two solutions with the smallest rank and the biggest crowding distance as new imperialists.

3.3. Imperialist Competition

Imperialist competition is an important step based on the total cost of empire.

The steps of imperialist competition are shown as follows:

(1)

Calculate total cost $T{C}_k$, $NT{C}_k$ [46] for each empire k;

(2)

Compute the power $E{P}_k$ [46] for each empire k;

(3)

Construct a vector $\left[E{P}_1-s_1,E{P}_2-s_2,\cdots ,E{P}_{N_{im}}-s_{N_{im}}\right]$ and choose an empire k with the biggest $E{P}_k-s_k$;

(4)

Assign the weakest colony from the weakest empire to the chosen empire.

In the above,

$$T{C}_k=c_k+\zeta ·\mathrm{mean}\left\{\mathrm{Cost}\right(\mathrm{colonies}\mathrm{of}\mathrm{empire}k\left)\right\}$$

(11)

$$NT{C}_k=\underset{l}{max}\left\{T{C}_l\right\}-T{C}_k$$

(12)

$$E{P}_k=\left|NT{C}_k/{\sum }_{v=1}^{N_{im}}NT{C}_v\right|$$

(13)

where in Equation (11), $mean\left\{Cost\right(coloniesofempirek)$ indicates average cost of all colonies in empire k, $\zeta$ is a positive number between 0 and 1 and close to 0. $s_i$ denotes a random number following the uniform distribution in [0, 1].

In the existing ICA, the number of empires diminishes when imperialist competition is performed continuously. In TEICA, there are three fixed empires in the whole search procedure and no movement of the colony is performed; a new imperialist competition is presented to adapt to the above new situations.

$r_k$ is an integer for empire k, if empire k cannot win, than $r_k=r_k+1$; otherwise, $r_k=0$.

The new imperialist competition is shown below:

(1)

Calculate $NT{C}_k$, $E{P}_k$ and decide the winning empire in terms of the above steps, suppose empire 1 wins.

(2)

For empire 1, choose R colonies with the smallest rank and the biggest crowding distance, for each chosen colony x, execute two-point crossover on machine assignment string and scheduling string like step 1 of assimilation, then perform multiple neighborhood search on x.

(3)

For empire k with $r_k\ge A$, suppose that $r_3\ge A$, choose the best $round(R·E{P}_1/(E{P}_1+E{P}_2)$ solutions from empire 1 and the best $R-round(R·E{P}_1/(E{P}_1+E{P}_2)$ solutions from empire 2, then for each chosen solution, perform multiple neighborhood search on it and the newly produced solution substitutes for the worst R solutions of empire 3.

In step (1), $NT{C}_k$ is defined directly. In step (2), R best colonies can be improved by crossover and multiple neighborhood search acts, and exploration ability can be intensified.

$$NT{C}_k={\overline{c}}_{I{M}_{1+2\left(k-1\right)}}+{\overline{c}}_{I{M}_{2+2\left(k-1\right)}}+\zeta {\sum }_{x\in H_k}{\overline{c}}_x$$

(14)

where $\zeta =0.1$, $H_k$ is the set of all colonies of empire k.

In step (3), when multiple neighborhood solutions exist on x, the new solution is compared with the worst R solution of empire 3 and substitutes for one of the worst R solutions in empire 3 if the condition in the above neighborhood search is met.

In step (3), $r_3\ge A$ means that empire 3 cannot win in steps (1) (2) in continuous A generation, empire 3 cannot win and R extra searches are also cannot be obtained and the winning possibility of empire 3 will greatly diminish, in this case, historical competition results of each empire are used, excessive competition also occurs. To avoid this case, empire 3 is intensified by using some of the best solutions from empires 1 and 2.

If just two initial empires are constructed, a vector based on $E{P}_k$ will just have two elements and the worst empire will be eliminated in the limited generations, as a result, diversity of population will diminish and the effect of imperialist competition is limited. When three empires are used, there are good balance on diversity of population and effect of imperialist competition between two empires and $N_{im}(>3)$ empires; no elimination and the avoidance of excessive competition can keep high diversity and good effect of imperialist competition, so $N_{im}$ is fixed at 3.

3.4. Algorithm Description

The main steps of TEICA are shown below:

(1)

Produce initial population P by heuristic and random way; let $gen=1$.

(2)

Construct three initial empires; let $r_k=0$, $k=1,2,3$.

(3)

Perform new assimilation in each empire.

(4)

Execute revolution and update two imperialists in each empire.

(5)

Perform new imperialist competition.

(6)

$gen=gen+1$; if stopping condition is met, then stop the search. Otherwise, go to step (3).

Unlike the existing ICAs, TEICA has the following features. Only three empires are constructed and $N_{im}$ is fixed at three and not used as parameter, to adapt this new situation, each empire has new structure with two imperialists and a novel assimilation is presented to adapt to this structure; no elimination of empire is considered, new imperialist competition and an effective way for excessive competition are given. On the other hand, some new things are added into TEICA, and its implementation is more difficult than the standard ICA.

4. Computational Experiments

Extensive experiments are conducted to test the performance of TEICA for the considered problem. Experiments are implemented by using Microsoft Visual C++ 2019 and run on 8.0G RAM 2.4GHz CPU PC.

4.1. Instances, Metrics and Comparative Algorithms

One hundred eight instances are used, which have the following data: $n\in \left\{10,50,100,150,250,500\right\}$, $m\in \left\{2,5,8\right\}$, $t_i\in \left\{2,4,6\right\}$, $S_i\in \left[1,10\right]$, when $m=2$, ${\left(q_k\right)}_{1\times 2}=\left[1015\right]$; when $m=5$, ${\left(q_k\right)}_{1\times 5}=\left[1010151520\right]$; when $m=8$, ${\left(q_k\right)}_{1\times 8}=\left[1010101515152020\right]$. $p_{ki}$ is given by Li et al. [16].

Li et al. [17] proposed an algorithm named C-NSGA-A for minimizing maximum lateness and total pollution emission cost. Jia et al. [33] presented bi-objective ant colony optimization (BOACO) to minimize total energy consumption and makespan. When PM is added into the decoding procedure of C-NSGA-A and BOACO, two algorithms can be directly applied to solve our problem, so they are chosen as comparative algorithms.

To show the effectiveness of new strategies of TEICA, an ICA is constructed, which has the same steps as the standard ICA [46]. In ICA, $N_{im}$ is a parameter, $N_{im}$ empires, assimilation, revolution, imperialist competition are implemented according to reference [46], When colony moves its imperialist, global search is executed in the same way as assimilation of TEICA.

Three metrics are used. Metric $\mathcal{C}$ [54] is applied to compare the approximate Pareto optimal set obtained by algorithms.

$$\mathcal{C}\left(L,B\right)={\displaystyle \frac{\left|\left\{b\in B:\exists h\in L,h\succ b\right\}\right|}{\left|B\right|}}$$

(15)

Metric $\rho$ [55] is the ratio of $|\left\{x\in {\Omega }_l\left|x\in {\Omega }^{*}\right.\right\}|$ to $\left|{\Omega }^{*}\right|$, where ${\Omega }_l$ is the non-dominated set of Algorithm l, the reference set ${\Omega }^{*}$ consists of the non-dominated solutions in the union of non-dominated sets of all algorithms.

$IGD$ [56] is used to calculate the distance of the non-dominated set ${\Omega }_l$ relative to a reference set ${\Omega }^{*}$.

$$IGD({\Omega }_l,{\Omega }^{*})={\displaystyle \frac{1}{\left|{\Omega }^{*}\right|}}\sum _{x\in {\Omega }^{*}}\underset{y\in {\Omega }_l}{min}d(x,y)$$

(16)

where $d(x,y)$ is the distance between a solution x and a reference solution y in the normalized objective space.

4.2. Parameter Settings

TEICA has the following parameters: $N,R,U_R,A$, and the stopping condition. In this study, CPU time is adopted as the stopping condition. We found through experiments that TEICA, ICA, C-NSGA-A, and BOACO can reach a stable set of solutions on all instances when the second CPU time reaches $0.3\times n$, so this CPU time is used as the stopping condition for four algorithms.

To decide the settings for other parameters, the Taguchi method [57] is applied on instance 37. Table 2 describes the levels of each parameter. The orthogonal array $L_{16}\left(4^4\right)$ is executed. TEICA with each parameter combination runs 10 times for the chosen instance.

Table 2. Level of the parameters.

	Factor Level
Parameters	1	2	3	4
N	60	80	100	120
$U_R$	0.2	0.3	0.4	0.5
R	4	5	6	7
A	2	3	4	5

Figure 3 shows the results of $\rho$ and S/N ratio, which is $-10{log}_{10}\left({\rho }^2\right)$. It can be found from Figure 3 that TEICA with the following combination $N=80,U_R=0.3,R=5,A=3$ can obtain better results than TEICA with other combinations, so the above parameter settings are adopted.

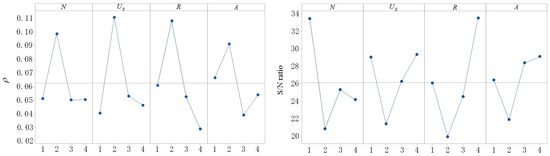
Figure 3. Main effect plot for $\rho$ and S/N ratio.

ICA has $N=80,U_R=0.3,N_{im}=5$ and the above stopping condition. These settings are obtained by experiments.

With respect to C-NSGA-A and BOACO, their parameter settings, except the stopping condition, are directly chosen from references [17,33] and used in this study. Experiments are conducted to decide the parameters of references [17,33] under the above CPU time as stopping condition, the experimental results show that the parameter settings of each comparative algorithm are still effective, so they are kept.

4.3. Results and Discussions

TEICA, ICA, BOACO, and C-NSGA-A are compared. Each algorithm randomly runs 10 times for each instance. Table 3, Table 4 and Table 5 describe the corresponding results of four algorithms. T, I, C, B represent TEICA, ICA, C-NSGA-A, and BOACO. Figure 4 shows distributions of non-dominated solutions, each point indicates the non-dominated solution of an algorithm. Table 6 gives results of paired sample t-test, where p-value being less than 0.05 for t-test (A,B) means that A performs better than B in the statistical sense. Figure 5 gives mean plot with 95% confidence interval.

Table 3. Computational results of four algorithms on metric $IGD$.

No.	TEICA	ICA	C-NSGA-A	BOACO	No.	TEICA	ICA	C-NSGA-A	BOACO
1	0.000	0.000	0.000	0.000	55	0.054	0.461	0.031	0.712
2	0.064	0.239	0.173	0.000	56	0.000	0.505	0.245	0.984
3	0.000	0.010	0.241	0.137	57	0.000	0.184	0.432	0.902
4	0.000	0.030	0.094	0.255	58	0.000	0.240	0.357	1.050
5	0.000	0.000	0.328	0.509	59	0.000	0.272	0.394	1.003
6	0.000	0.205	0.590	0.597	60	0.000	0.311	0.470	1.130
7	0.000	0.000	0.000	0.000	61	0.000	0.331	0.260	0.997
8	0.000	0.115	0.006	0.000	62	0.000	0.380	0.239	0.801
9	0.000	0.029	0.211	0.173	63	0.000	0.219	0.251	0.976
10	0.019	0.103	0.036	0.159	64	0.000	0.263	0.306	0.975
11	0.000	0.000	0.189	0.871	65	0.000	0.267	0.507	1.179
12	0.000	0.000	0.679	0.568	66	0.000	0.244	0.405	1.113
13	0.000	0.000	0.038	0.000	67	0.000	0.355	0.214	1.024
14	0.004	0.086	0.001	0.000	68	0.000	0.203	0.171	0.898
15	0.078	0.191	0.131	0.213	69	0.000	0.168	0.392	1.134
16	0.000	0.000	0.867	0.946	70	0.000	0.159	0.232	0.972
17	0.000	0.000	0.415	0.642	71	0.000	0.251	0.345	1.230
18	0.000	0.016	0.247	0.365	72	0.000	0.230	0.360	1.178
19	0.018	0.088	0.213	0.600	73	0.000	0.871	0.158	0.969
20	0.147	0.210	0.202	0.909	74	0.082	0.619	0.280	0.797
21	0.000	0.120	0.172	0.882	75	0.000	0.531	0.553	1.216
22	0.000	0.150	0.223	0.807	76	0.000	0.456	0.434	0.969
23	0.000	0.149	0.259	0.921	77	0.000	0.456	1.001	1.225
24	0.000	0.157	0.155	0.295	78	0.000	0.374	0.687	1.169
25	0.000	0.114	0.177	0.859	79	0.101	0.392	0.154	0.704
26	0.000	0.179	0.337	1.141	80	0.000	0.481	0.088	0.949
27	0.000	0.156	0.208	1.075	81	0.000	0.369	0.536	1.321
28	0.000	0.108	0.261	0.906	82	0.001	0.144	0.232	0.865
29	0.000	0.111	0.375	0.895	83	0.000	0.223	0.649	1.177
30	0.000	0.067	0.183	0.810	84	0.000	0.314	0.655	1.127
31	0.019	0.036	0.210	0.899	85	0.056	0.324	0.005	1.109
32	0.018	0.085	0.384	0.946	86	0.000	0.385	0.081	0.978
33	0.000	0.059	0.288	0.876	87	0.000	0.290	0.412	1.029
34	0.000	0.042	0.223	0.902	88	0.000	0.266	0.532	1.172
35	0.000	0.052	0.276	0.931	89	0.000	0.332	0.854	1.322
36	0.032	0.071	0.196	0.963	90	0.000	0.284	0.630	1.217
37	0.000	0.187	0.137	0.994	91	0.083	0.984	0.159	0.761
38	0.000	0.558	0.109	1.163	92	0.366	1.049	0.000	0.875
39	0.000	0.283	0.402	1.019	93	0.000	0.659	0.580	0.956
40	0.000	0.190	0.179	1.018	94	0.000	0.726	0.919	1.078
41	0.000	0.168	0.408	0.871	95	0.000	0.692	0.982	1.113
42	0.000	0.196	0.443	1.016	96	0.000	0.716	1.024	1.164
43	0.008	0.239	0.081	0.825	97	0.183	0.824	0.120	0.815
44	0.000	0.254	0.152	0.928	98	0.000	0.868	0.318	0.922
45	0.000	0.133	0.411	1.048	99	0.000	0.608	0.904	1.105
46	0.000	0.188	0.300	1.088	100	0.000	0.730	0.807	1.185
47	0.000	0.142	0.228	0.977	101	0.000	0.583	1.111	1.098
48	0.000	0.137	0.277	0.913	102	0.000	0.552	0.940	1.133
49	0.000	0.156	0.091	0.921	103	0.117	0.544	0.176	0.705
50	0.000	0.156	0.304	0.816	104	0.000	0.699	0.194	0.783
51	0.000	0.142	0.320	1.077	105	0.000	0.561	0.842	1.192
52	0.000	0.116	0.191	0.916	106	0.000	0.494	0.716	1.005
53	0.000	0.185	0.330	1.029	107	0.000	0.541	0.945	1.168
54	0.000	0.186	0.266	1.091	108	0.000	0.495	0.812	1.135

Table 4. Computational results of four algorithms on metric $\rho$.

No.	TEICA	ICA	C-NSGA-A	BOACO	No.	TEICA	ICA	C-NSGA-A	BOACO
1	1.000	1.000	1.000	1.000	55	0.500	0.000	0.500	0.000
2	0.857	0.571	0.143	1.000	56	1.000	0.000	0.000	0.000
3	1.000	0.889	0.000	0.222	57	1.000	0.000	0.000	0.000
4	1.000	0.714	0.286	0.000	58	1.000	0.000	0.000	0.000
5	1.000	1.000	0.000	0.000	59	1.000	0.000	0.000	0.000
6	1.000	0.250	0.000	0.000	60	1.000	0.000	0.000	0.000
7	1.000	1.000	1.000	1.000	61	1.000	0.000	0.000	0.000
8	1.000	0.750	0.750	1.000	62	1.000	0.000	0.000	0.000
9	1.000	0.500	0.167	0.000	63	1.000	0.000	0.000	0.000
10	0.857	0.286	0.571	0.000	64	1.000	0.000	0.000	0.000
11	1.000	1.000	0.000	0.000	65	1.000	0.000	0.000	0.000
12	1.000	1.000	0.000	0.000	66	1.000	0.000	0.000	0.000
13	1.000	1.000	0.500	1.000	67	1.000	0.000	0.000	0.000
14	0.875	0.750	0.875	1.000	68	1.000	0.000	0.000	0.000
15	0.750	0.250	0.250	0.250	69	1.000	0.000	0.000	0.000
16	1.000	1.000	0.000	0.000	70	1.000	0.000	0.000	0.000
17	1.000	1.000	0.000	0.000	71	1.000	0.000	0.000	0.000
18	1.000	0.750	0.000	0.000	72	1.000	0.000	0.000	0.000
19	0.600	0.200	0.200	0.000	73	1.000	0.000	0.000	0.000
20	0.667	0.333	0.000	0.000	74	0.750	0.000	0.250	0.000
21	1.000	0.000	0.000	0.000	75	1.000	0.000	0.000	0.000
22	1.000	0.000	0.000	0.000	76	1.000	0.000	0.000	0.000
23	1.000	0.000	0.000	0.000	77	1.000	0.000	0.000	0.000
24	1.000	0.000	0.000	0.000	78	1.000	0.000	0.000	0.000
25	1.000	0.000	0.000	0.000	79	0.364	0.000	0.636	0.000
26	1.000	0.000	0.000	0.000	80	1.000	0.000	0.000	0.000
27	1.000	0.000	0.000	0.000	81	1.000	0.000	0.000	0.000
28	1.000	0.000	0.000	0.000	82	0.900	0.100	0.000	0.000
29	1.000	0.000	0.000	0.000	83	1.000	0.000	0.000	0.000
30	1.000	0.000	0.000	0.000	84	1.000	0.000	0.000	0.000
31	0.500	0.500	0.000	0.000	85	0.167	0.000	0.833	0.000
32	0.800	0.200	0.000	0.000	86	1.000	0.000	0.000	0.000
33	1.000	0.000	0.000	0.000	87	1.000	0.000	0.000	0.000
34	1.000	0.000	0.000	0.000	88	1.000	0.000	0.000	0.000
35	1.000	0.000	0.000	0.000	89	1.000	0.000	0.000	0.000
36	0.667	0.333	0.000	0.000	90	1.000	0.000	0.000	0.000
37	1.000	0.000	0.000	0.000	91	0.600	0.000	0.400	0.000
38	1.000	0.000	0.000	0.000	92	0.000	0.000	1.000	0.000
39	1.000	0.000	0.000	0.000	93	1.000	0.000	0.000	0.000
40	1.000	0.000	0.000	0.000	94	1.000	0.000	0.000	0.000
41	1.000	0.000	0.000	0.000	95	1.000	0.000	0.000	0.000
42	1.000	0.000	0.000	0.000	96	1.000	0.000	0.000	0.000
43	0.900	0.000	0.100	0.000	97	0.400	0.000	0.600	0.000
44	1.000	0.000	0.000	0.000	98	1.000	0.000	0.000	0.000
45	1.000	0.000	0.000	0.000	99	1.000	0.000	0.000	0.000
46	1.000	0.000	0.000	0.000	100	1.000	0.000	0.000	0.000
47	1.000	0.000	0.000	0.000	101	1.000	0.000	0.000	0.000
48	1.000	0.000	0.000	0.000	102	1.000	0.000	0.000	0.000
49	1.000	0.000	0.000	0.000	103	0.556	0.000	0.444	0.000
50	1.000	0.000	0.000	0.000	104	1.000	0.000	0.000	0.000
51	1.000	0.000	0.000	0.000	105	1.000	0.000	0.000	0.000
52	1.000	0.000	0.000	0.000	106	1.000	0.000	0.000	0.000
53	1.000	0.000	0.000	0.000	107	1.000	0.000	0.000	0.000
54	1.000	0.000	0.000	0.000	108	1.000	0.000	0.000	0.000

Table 5. Computational results of four algorithms on metric $\mathcal{C}$.

No.	$\mathcal{C}(\mathit{T},\mathit{I})$	$\mathcal{C}(\mathit{I},\mathit{T})$	$\mathcal{C}(\mathit{T},\mathit{C})$	$\mathcal{C}(\mathit{C},\mathit{T})$	$\mathcal{C}(\mathit{T},\mathit{B})$	$\mathcal{C}(\mathit{B},\mathit{T})$	No.	$\mathcal{C}(\mathit{T},\mathit{I})$	$\mathcal{C}(\mathit{I},\mathit{T})$	$\mathcal{C}(\mathit{T},\mathit{C})$	$\mathcal{C}(\mathit{C},\mathit{T})$	$\mathcal{C}(\mathit{T},\mathit{B})$	$\mathcal{C}(\mathit{B},\mathit{T})$
1	0.000	0.000	0.000	0.000	0.000	0.000	55	1.000	0.000	0.400	0.400	1.000	0.000
2	0.000	0.000	0.800	0.000	0.000	0.000	56	1.000	0.000	1.000	0.000	1.000	0.000
3	0.000	0.000	1.000	0.000	0.500	0.000	57	1.000	0.000	1.000	0.000	1.000	0.000
4	0.167	0.000	0.600	0.000	1.000	0.000	58	1.000	0.000	1.000	0.000	1.000	0.000
5	0.000	0.000	1.000	0.000	1.000	0.000	59	1.000	0.000	1.000	0.000	1.000	0.000
6	0.500	0.000	1.000	0.000	1.000	0.000	60	1.000	0.000	1.000	0.000	1.000	0.000
7	0.000	0.000	0.000	0.000	0.000	0.000	61	1.000	0.000	1.000	0.000	1.000	0.000
8	0.250	0.000	0.250	0.000	0.000	0.000	62	1.000	0.000	1.000	0.000	1.000	0.000
9	0.400	0.000	0.800	0.000	1.000	0.000	63	1.000	0.000	1.000	0.000	1.000	0.000
10	0.600	0.000	0.200	0.000	0.875	0.000	64	1.000	0.000	1.000	0.000	1.000	0.000
11	0.000	0.000	1.000	0.000	1.000	0.000	65	1.000	0.000	1.000	0.000	1.000	0.000
12	0.000	0.000	1.000	0.000	1.000	0.000	66	1.000	0.000	1.000	0.000	1.000	0.000
13	0.000	0.000	0.500	0.000	0.000	0.000	67	1.000	0.000	1.000	0.000	1.000	0.000
14	0.000	0.000	0.222	0.125	0.000	0.125	68	1.000	0.000	1.000	0.000	1.000	0.000
15	0.600	0.000	0.333	0.000	0.600	0.000	69	1.000	0.000	1.000	0.000	1.000	0.000
16	0.000	0.000	1.000	0.000	1.000	0.000	70	1.000	0.000	1.000	0.000	1.000	0.000
17	0.000	0.000	1.000	0.000	1.000	0.000	71	1.000	0.000	1.000	0.000	1.000	0.000
18	0.250	0.000	1.000	0.000	1.000	0.000	72	1.000	0.000	1.000	0.000	1.000	0.000
19	0.800	0.250	0.000	0.375	1.000	0.000	73	1.000	0.000	1.000	0.000	1.000	0.000
20	0.833	0.000	1.000	0.000	1.000	0.000	74	1.000	0.000	0.000	0.000	1.000	0.000
21	1.000	0.000	1.000	0.000	1.000	0.000	75	1.000	0.000	1.000	0.000	1.000	0.000
22	1.000	0.000	1.000	0.000	1.000	0.000	76	1.000	0.000	1.000	0.000	1.000	0.000
23	1.000	0.000	1.000	0.000	1.000	0.000	77	1.000	0.000	1.000	0.000	1.000	0.000
24	1.000	0.000	1.000	0.000	1.000	0.000	78	1.000	0.000	1.000	0.000	1.000	0.000
25	1.000	0.000	1.000	0.000	1.000	0.000	79	1.000	0.000	0.125	0.200	1.000	0.000
26	1.000	0.000	1.000	0.000	1.000	0.000	80	1.000	0.000	1.000	0.000	1.000	0.000
27	1.000	0.000	1.000	0.000	1.000	0.000	81	1.000	0.000	1.000	0.000	1.000	0.000
28	1.000	0.000	1.000	0.000	1.000	0.000	82	0.750	0.000	1.000	0.000	1.000	0.000
29	1.000	0.000	1.000	0.000	1.000	0.000	83	1.000	0.000	1.000	0.000	1.000	0.000
30	1.000	0.000	1.000	0.000	1.000	0.000	84	1.000	0.000	1.000	0.000	1.000	0.000
31	0.250	0.625	1.000	0.000	1.000	0.000	85	1.000	0.000	0.000	0.000	1.000	0.000
32	0.667	0.000	1.000	0.000	1.000	0.000	86	1.000	0.000	1.000	0.000	1.000	0.000
33	1.000	0.000	1.000	0.000	1.000	0.000	87	1.000	0.000	1.000	0.000	1.000	0.000
34	1.000	0.000	1.000	0.000	1.000	0.000	88	1.000	0.000	1.000	0.000	1.000	0.000
35	1.000	0.000	1.000	0.000	1.000	0.000	89	1.000	0.000	1.000	0.000	1.000	0.000
36	0.800	0.000	1.000	0.000	1.000	0.000	90	1.000	0.000	1.000	0.000	1.000	0.000
37	1.000	0.000	1.000	0.000	1.000	0.000	91	1.000	0.000	0.000	0.000	1.000	0.000
38	1.000	0.000	1.000	0.000	1.000	0.000	92	1.000	0.000	0.000	1.000	1.000	0.000
39	1.000	0.000	1.000	0.000	1.000	0.000	93	1.000	0.000	1.000	0.000	1.000	0.000
40	1.000	0.000	1.000	0.000	1.000	0.000	94	1.000	0.000	1.000	0.000	1.000	0.000
41	1.000	0.000	1.000	0.000	1.000	0.000	95	1.000	0.000	1.000	0.000	1.000	0.000
42	1.000	0.000	1.000	0.000	1.000	0.000	96	1.000	0.000	1.000	0.000	1.000	0.000
43	1.000	0.000	0.750	0.000	1.000	0.000	97	1.000	0.000	0.000	0.000	1.000	0.000
44	1.000	0.000	1.000	0.000	1.000	0.000	98	1.000	0.000	1.000	0.000	1.000	0.000
45	1.000	0.000	1.000	0.000	1.000	0.000	99	1.000	0.000	1.000	0.000	1.000	0.000
46	1.000	0.000	1.000	0.000	1.000	0.000	100	1.000	0.000	1.000	0.000	1.000	0.000
47	1.000	0.000	0.750	0.000	1.000	0.000	101	1.000	0.000	1.000	0.000	1.000	0.000
48	1.000	0.000	1.000	0.000	1.000	0.000	102	1.000	0.000	1.000	0.000	1.000	0.000
49	1.000	0.000	1.000	0.000	1.000	0.000	103	1.000	0.000	0.000	0.286	1.000	0.000
50	1.000	0.000	1.000	0.000	1.000	0.000	104	1.000	0.000	1.000	0.000	1.000	0.000
51	1.000	0.000	0.750	0.000	1.000	0.000	105	1.000	0.000	1.000	0.000	1.000	0.000
52	1.000	0.000	1.000	0.000	1.000	0.000	106	1.000	0.000	1.000	0.000	1.000	0.000
53	1.000	0.000	1.000	0.000	1.000	0.000	107	1.000	0.000	1.000	0.000	1.000	0.000
54	1.000	0.000	0.750	0.000	1.000	0.000	108	1.000	0.000	1.000	0.000	1.000	0.000

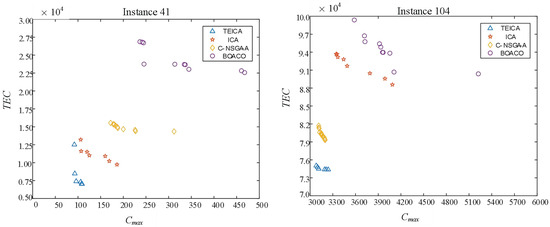
Figure 4. Distribution of non-dominated solutions of four algorithms.

Table 6. Results of paired sample t-test.

t-Test	p-Value (IGD)	p-Value ($\mathit{C}$)	p-Value ($\mathit{\rho }$)
t-test (TEICA, ICA)	0.000	0.000	0.000
t-test (TEICA, C-NSGA-A)	0.000	0.000	0.000
t-test (TEICA, BOACO)	0.000	0.000	0.000

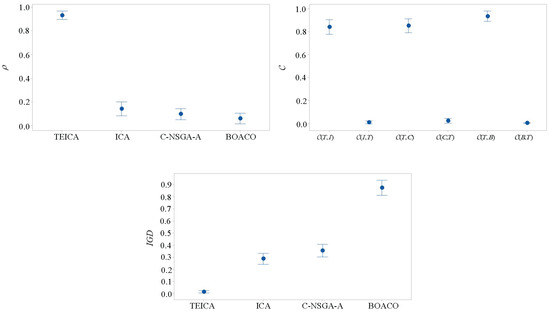
Figure 5. Mean plot with 95% confidence interval.

Table 3 shows that TEICA obtains a smaller $IGD$ than ICA on 101 instances. The significant performance differences between TEICA and ICA can be found in Figure 4 and Figure 5. It can be seen from Table 4 that $\rho$ of TEICA is better than that of ABC on more than 90% instances, and $\rho$ of TEICA is 1 on 89 instances, that is, TEICA provides all members for reference set ${\Omega }^{*}$. As shown in Table 5, TEICA produces smaller $\mathcal{C}$(I,T) than $\mathcal{C}$(T,I) on 97 of 108 instances and obtains $\mathcal{C}$(T,I) of 1 on 84 instances. These results show that all solutions of ICA are dominated by non-dominated solutions of TEICA on most of the instances, and TEICA converges significantly better than ICA. The new strategies of TEICA really have a positive impact on the performance, so the new strategies are effective.

When TEICA is compared with C-NSGA-A, it can be found that TEICA performs better than C-NSGA-A on most of instances. As shown in Table 4, TEICA obtains a bigger $\rho$ than C-NSGA-A on 101 instances, and the $\rho$ of TEICA is 1.0 on 90 instances, that is, all members of reference set ${\Omega }^{*}$ are generated by TEICA. TEICA also performs better than C-NSGA-A on $IGD$ because TEICA obtains a better $IGD$ than C-NSGA-A on 101 instances. Table 5 shows that TEICA provides smaller $\mathcal{C}$(C,T) than $\mathcal{C}$(T,C) on 99 of 108 instances and obtains $\mathcal{C}$(T,C) of 1 on 84 instances. The above analyses show that TEICA can provide better results than C-NSGA-A. Table 6 reveals that performance difference between TEICA and C-NSGA-A is significant in the statistical sense. Figure 4 and Figure 5 also show that the above conclusion is still effective.

It can also be concluded from Table 3 to Table 5 that TEICA outperforms BOACO on three metrics. TEICA obtains smaller $\mathcal{C}$(B,T) than $\mathcal{C}$(T,B) on 103 instances, gets bigger $\rho$ than BOACO on nearly all instances and better $IGD$ than TICA on 102 instances. On the other hand, TEICA has $IGD$ of 0, $\rho$ of 1 and $\mathcal{C}$(T,B) of 1 on most of instances, that is, there exist notable performance differences between TEICA and BOACO. This conclusion can also be drawn from Table 6 and Figure 4 and Figure 5, thus, based on the above analyses, it can be concluded that TEICA can provide better results than the two comparative algorithms.

The good performance of TEICA mainly result from its new strategies. Three empires with new structures exist in the whole search procedure of TEICA, and their competition is implemented fully; as a result, high diversity of population can be kept and exploration ability is intensified because of new assimilation. Thus, TEICA is a very competitive method for the considered BPM scheduling problem.

5. Conclusions

PM and energy-efficient scheduling are seldom considered in a parallel BPM shop. In this study, energy-efficient parallel BPM scheduling with PM is considered, and a novel algorithm named TEICA is presented to minimize makespan and total energy consumption. In TEICA, the number of empires is not used as a parameter and is fixed at 3. To adapt to this new situation, a new way is applied to construct three initial empires with a new structure, a new assimilation is given, and an adaptive imperialist competition is implemented. This is a new path to designing ICA, and this path also has limitations such as the increase of implementation difficulty. A number of computational experiments are conducted on 108 instances. The computational results show that the new strategies of TEICA are effective, and TEICA has promising advantages in solving the considered BPM scheduling problem.

The BPM is frequently used in real-world manufacturing industries such as casting and textiles. The BPM scheduling problem has higher complexity than the classical scheduling problem; batch formation is added. In real-life factories, hybrid flow shop scheduling problems with BPMs and flexible job shop scheduling with BPMs extensively exist in casting, textile, semiconductor, and steel making, in which batch production is part of the factories. This feature leads to great challenges in solving them. We will try to solve them by using meta-heuristics with new optimization mechanisms including learning, cooperation, feedback, and competition. BPM scheduling problems in real-life manufacturing processes are also our future topic. We will try to refine and solve BPM scheduling for production processes in manufacturing companies.