The Analysis of Three-Dimensional Time-Fractional Helmholtz Model Using a New İterative Method
Abstract
1. Introduction
2. Preliminaries
3. Methods and Materials
4. Convergence Analysis
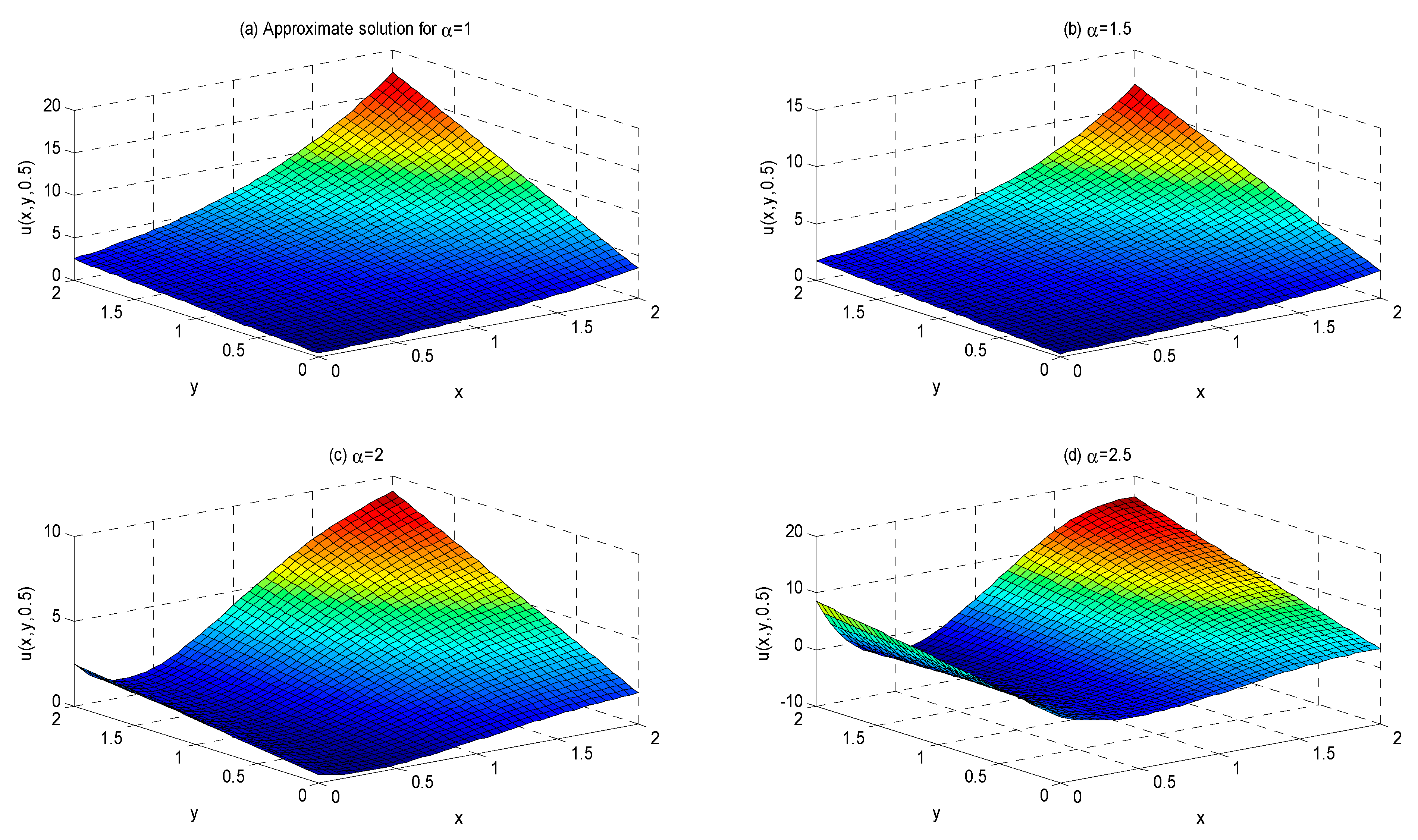
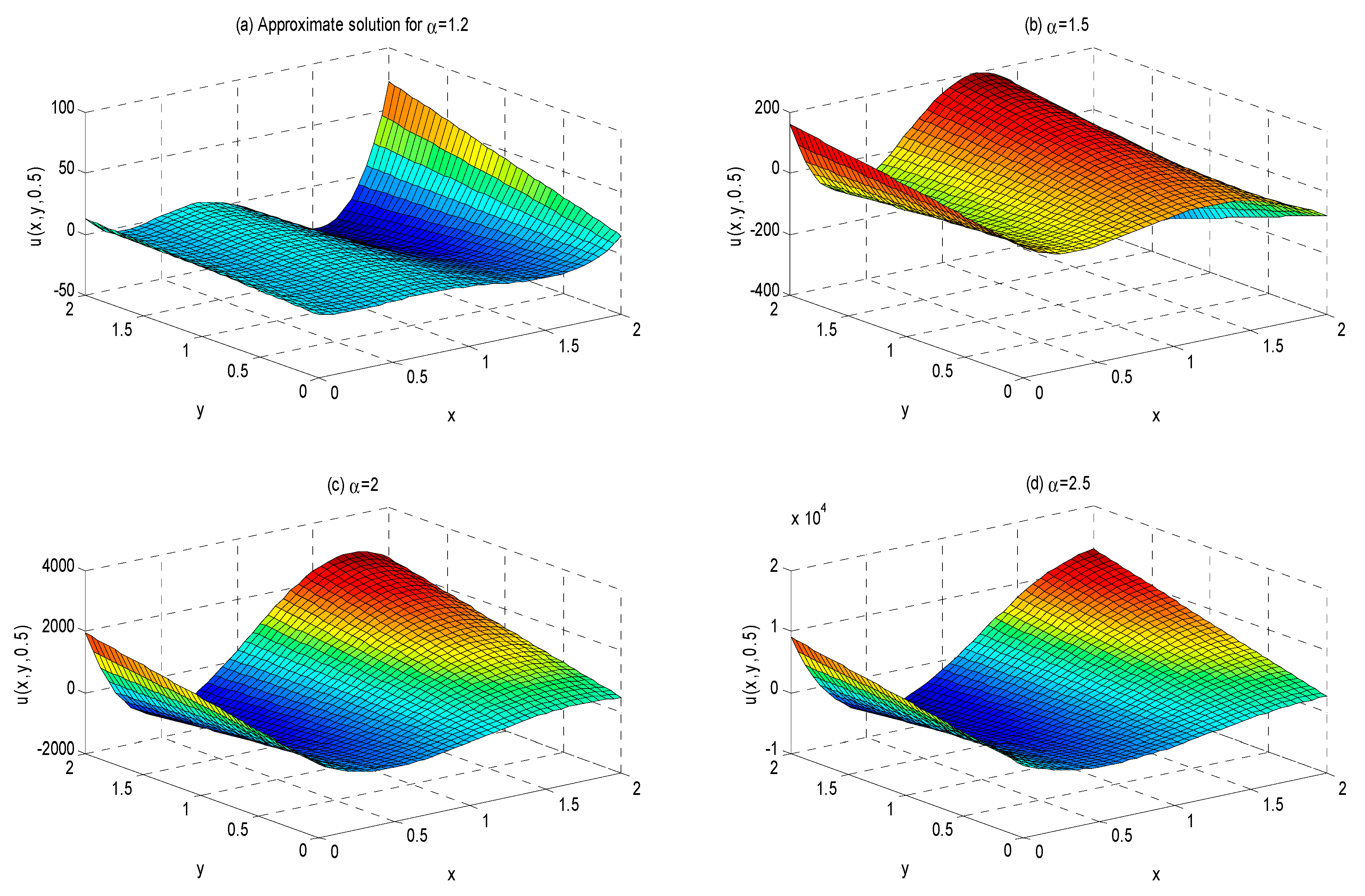
5. Applications of ATDM
- Solution.
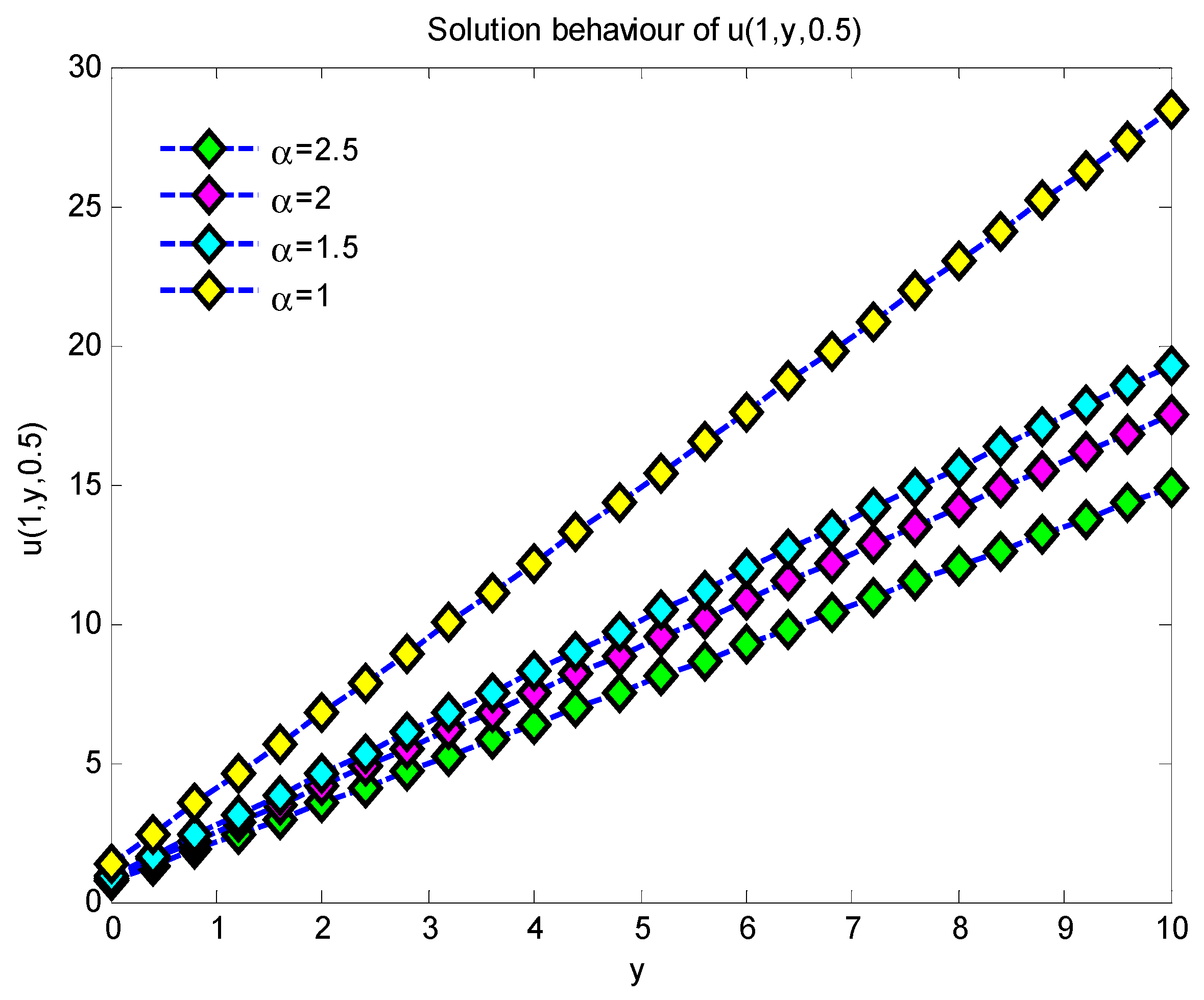
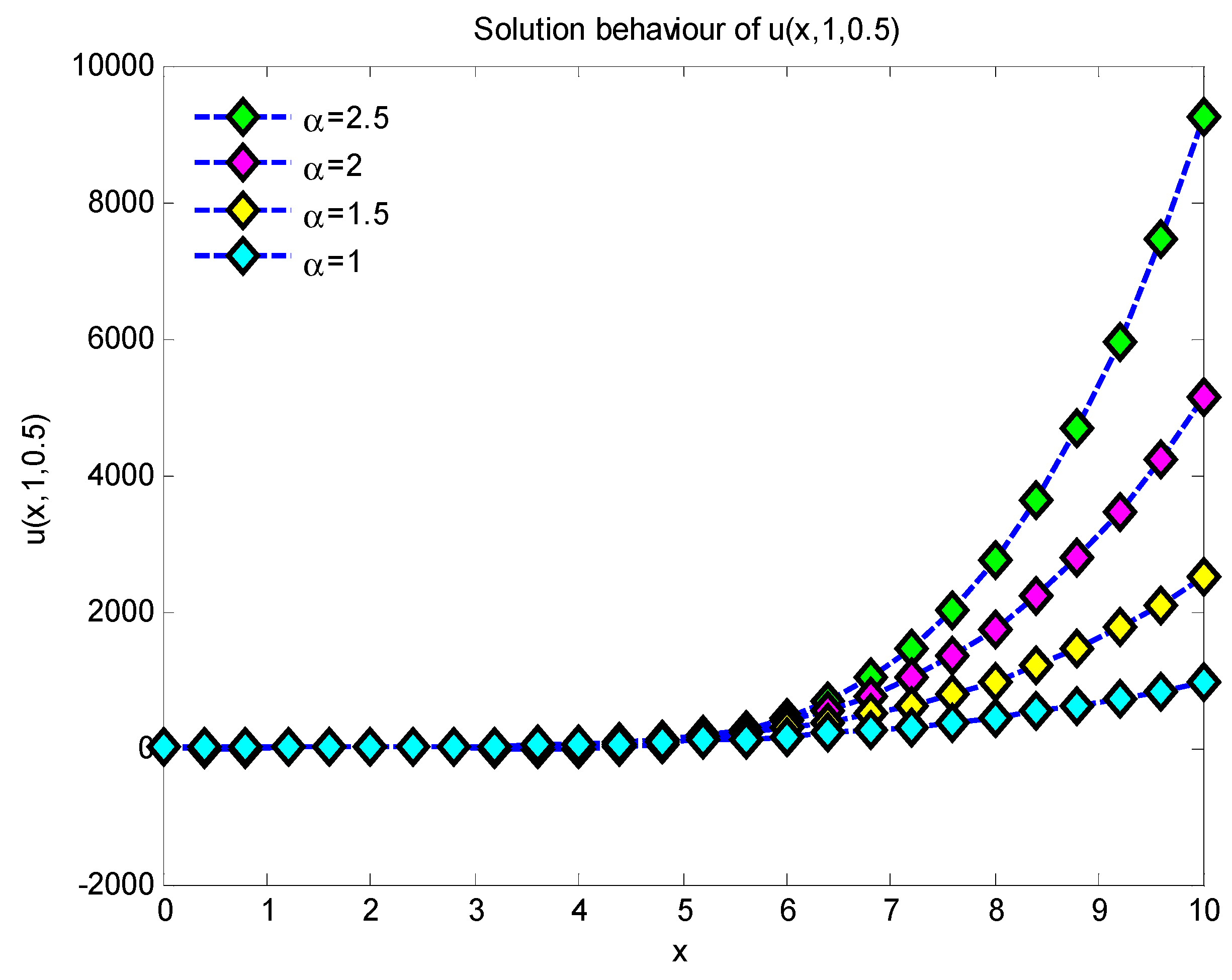
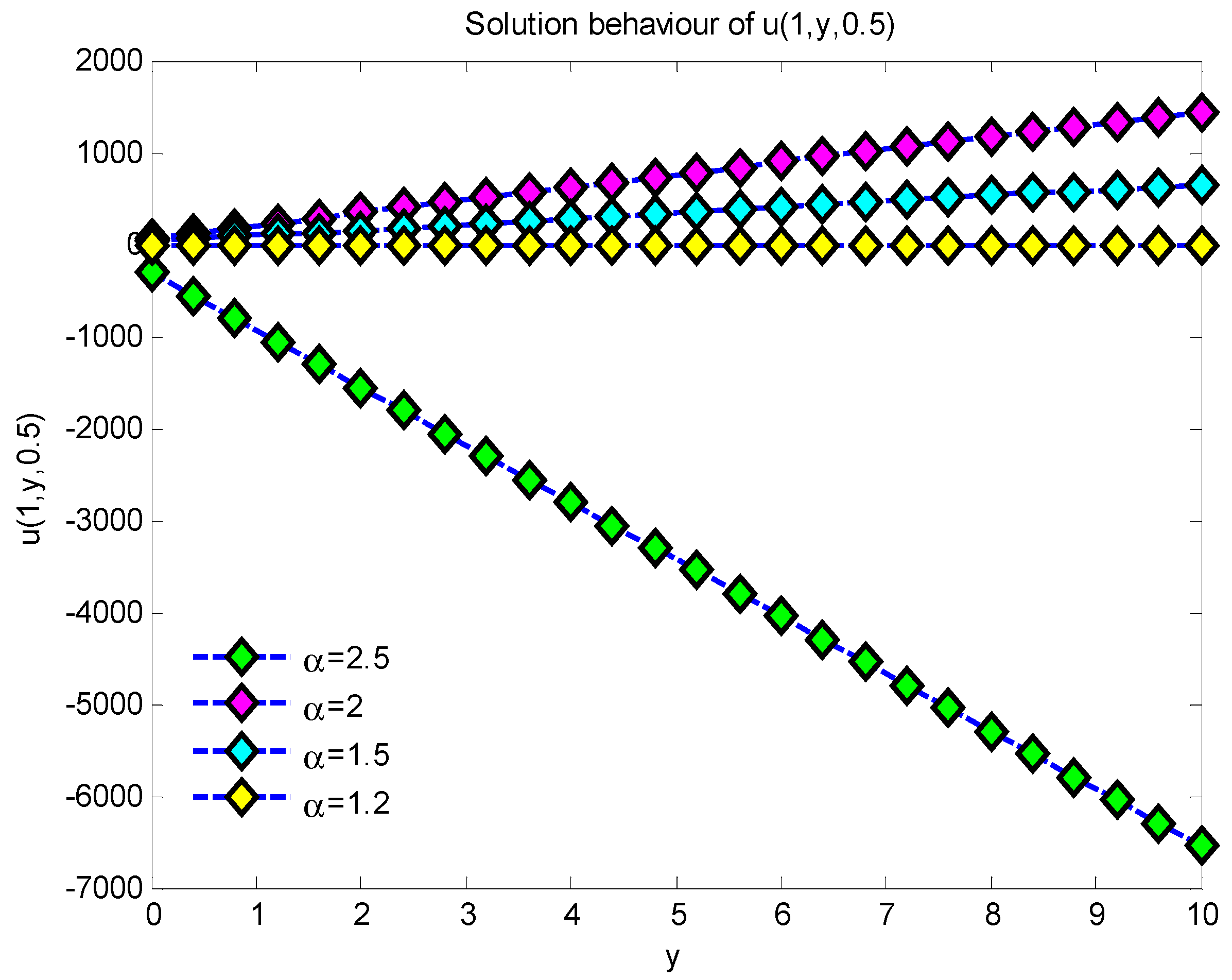
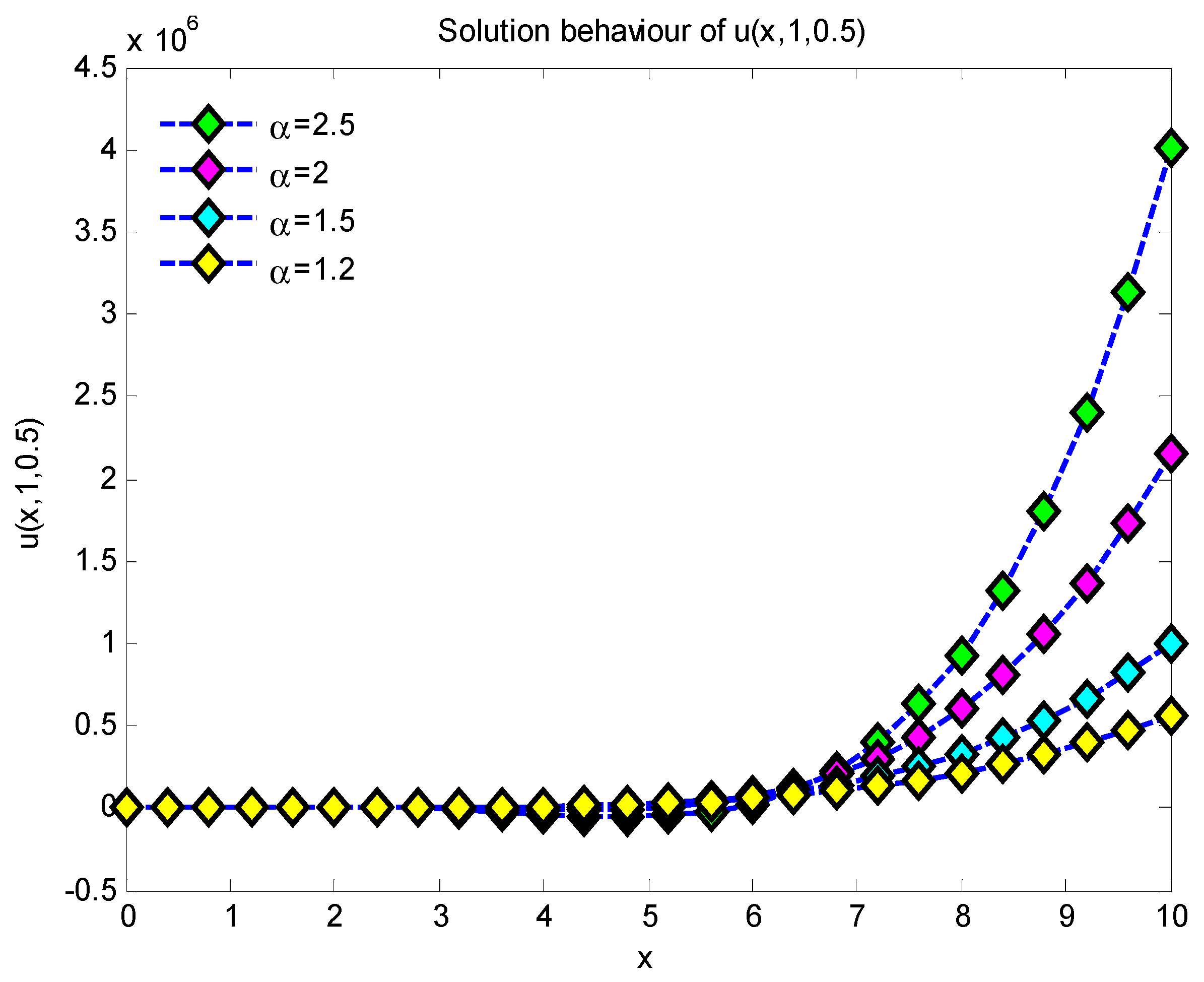
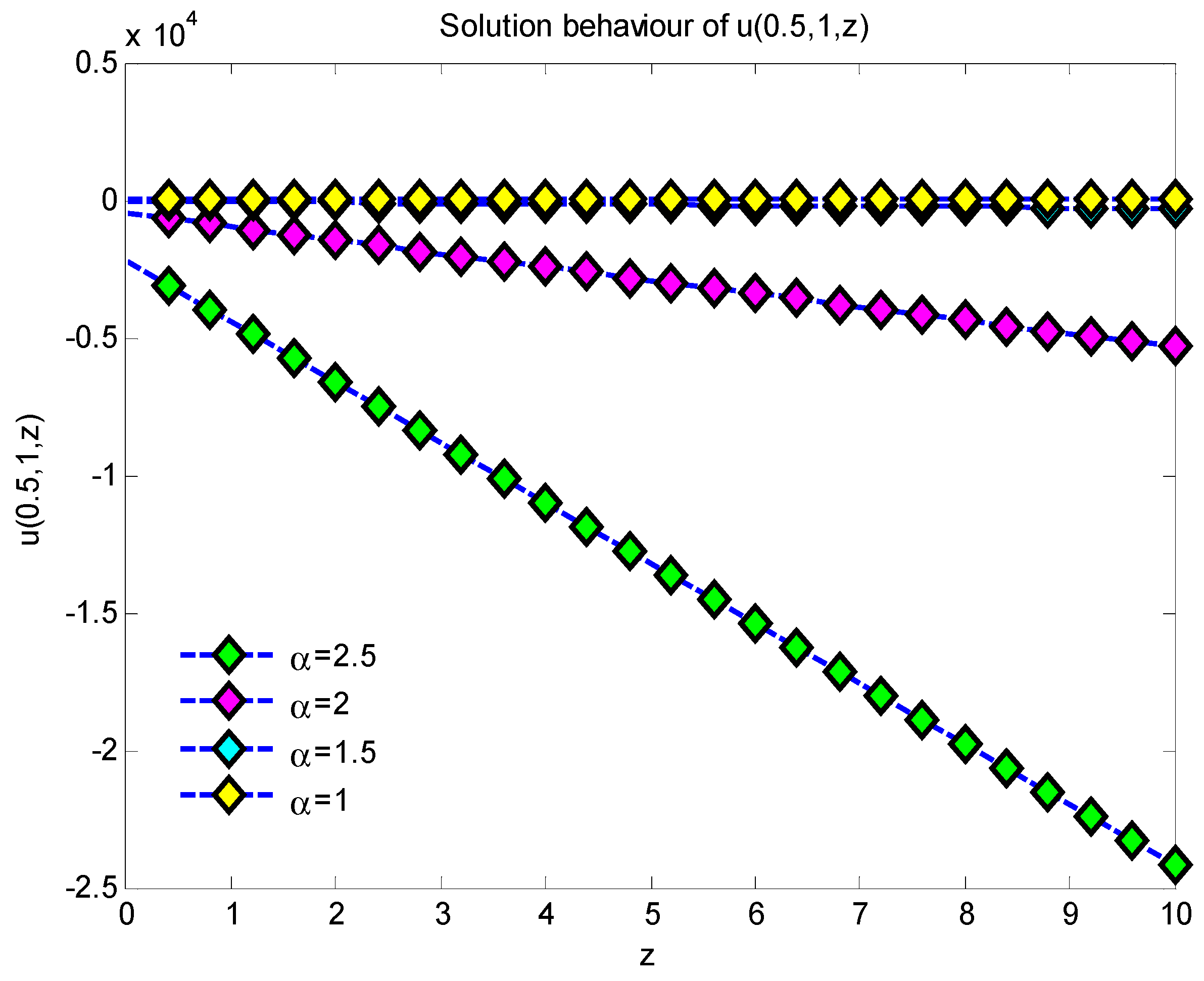
6. Results and Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abuasad, S.; Moaddy, K.; Hashim, I. Analytical treatment of two-dimensional fractional Helmholtz equations. J. King Saud Univ. Sci. 2019, 31, 659–666. [Google Scholar] [CrossRef]
- Ghaffar, F.; Badshah, N.; Islam, S. Multigrid method for solution of 3d helmholtz equation based on hoc schemes. Abstr. Appl. Anal. 2014, 14, 954658. [Google Scholar] [CrossRef]
- Gupta, P.K.; Yildirim, A.; Rai, K. Application of he’s homotopy perturbation method for multi-dimensional fractional helmholtz equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 424–435. [Google Scholar] [CrossRef]
- Li, W. A fast singular boundary method for 3d helmholtz equation. Comp. Math. Appl. 2019, 77, 525–535. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Fu, Z.; Qin, Q.-A. A regularized approach evaluating the near-boundary and boundary solutions for three-dimensional helmholtz equation with wideband wave-Numbers. Appl. Math. Lett. 2019, 91, 55–60. [Google Scholar] [CrossRef]
- Bespalov, A.; Betcke, T.; Haberl, A.; Praetorius, D. Adaptive bem with optimal convergence rates for the helmholtz equation. Comput. Methods Appl. Mech. Eng. 2019, 346, 260–287. [Google Scholar] [CrossRef]
- Wang, K.; Wong, Y.S.; Deng, J. Efficient and accurate numerical solutions for helmholtz equation in polar and spherical coordinates. Commun. Comp. Phys. 2015, 17, 779–807. [Google Scholar] [CrossRef]
- Qu, W.; Chen, W.; Gu, Y. Fast multipole accelerated singular boundary method for the 3d helmholtz equation in low frequency regime. Comp. Math. Appl. 2015, 70, 679–690. [Google Scholar] [CrossRef]
- Alshammari, S.; Abuasad, S. Exact Solutions of the 3D Fractional Helmholtz Equation by Fractional Differential Transform Method. J. Func. Spac. 2022, 2022, 374751. [Google Scholar] [CrossRef]
- Nadeem, M.; Abu Arqub, O.; Iambor, L.F.; Hussien, M.; Ebraheem Alzahrani, E. The Prospective Analysis of Three-Dimensional Time-Fractional Helmholtz Model using a New İterative Method. Fractals 2025, 33, 1–12. [Google Scholar] [CrossRef]
- Nadeem, M.; Sharaf, M.; Mahamad, S. Numerical investigation of two-dimensional fractional Helmholtz equation using Aboodh transform scheme. Int. J. Heat Fluid Flow 2024, 34, 4520–4534. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Aljoufi, M.D.; Chung, J.D. An efficient approach for solution of fractional-order Helmholtz equations. Adv. Differ. Equ. 2021, 1, 14. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A New Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 2, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a New Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 2, 87–92. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Nonlocal and Non-Singular Kernel. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Mitkowski, W.; Gawin, E.; Dziedzic, K. The Caputo vs. Caputo-Fabrizio operators in modeling of heat transfer process. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 4. [Google Scholar]
- Aboodh, K.S. The New Integral Transform Aboodh Transform. Glob. J. Pure Appl. Math. 2013, 1, 35–43. [Google Scholar]
- Aboodh, K.S. Application of New Transform Aboodh Transform to Partial Differential Equations. Glob. J. Pure Appl. Math. 2014, 2, 249–254. [Google Scholar]
- Benattia, M.E.; Belghaba, K. Application of The Aboodh Transform for Solving Fractional Delay Differential Equations. Univ. J. Math. Appl. 2020, 3, 93–101. [Google Scholar] [CrossRef]
- Şahin, Y.; Merdan, M.; Açıkgöz, P. The Novel Numerical Solutions for Caputo-Fabrizio Fractional Newell–Whitehead–Segel Equation by Using Aboodh-ADM. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Yasmin, H. Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators. Symmetry 2023, 15, 453. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Yasmin, H.; Shah, R.; Ali, A.; Khan, I. Fractional-order view analysis of Fisher’s and foam drainage equations within Aboodh transform. Eng. Comput. 2024, 41, 489–515. [Google Scholar] [CrossRef]
- Iqbal, N.; Hussain, S.; Hamza, A.E.; Abdullah, A.; Mohammed, W.W.; Yar, M. Fractional dynamics study: Analytical solutions of modified Kordeweg-de Vries equation and coupled Burger’s equations using Aboodh transform. Sci. Rep. 2024, 14, 12751. [Google Scholar] [CrossRef] [PubMed]
- Ojo, G.O.; Mahmudov, N.I. Aboodh Transform Iterative Method for Spatial Diffusion of a Biological Population with Fractional-Order. Mathematics 2021, 9, 155. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of New Time and Spatial Fractional Derivatives with Exponential Kernels. Progr. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Qureshi, S.; Rangaig, N.A.; Baleanu, D. New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics 2019, 7, 374. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Analysis and Application of New Fractional Adams–Bashforth Scheme With Caputo–Fabrizio Derivative. Chaos Solitons Fractal 2017, 109, 111–119. [Google Scholar] [CrossRef]
- Al-Refai, M.; Pal, K. New Aspects of Caputo-Fabrizio Fractional Derivative. Progr. Fract. Differ. Appl. 2019, 5, 157–166. [Google Scholar] [CrossRef]
- Bhangale, N.; Kachhia, K.; Gómez-Aguilar, J.F. A New Iterative Method with ρ Laplace Transform for Solving Fractional Differential Equations with Caputo Generalized Fractional Derivative. Eng. Comput. 2022, 38, 2125–2138. [Google Scholar] [CrossRef]
- Mboro Nchama, G.A. Properties of Caputo-Fabrizio Fractional Operators. New Trends Math. Sci. 2020, 1, 1–25. [Google Scholar] [CrossRef]
- Oyewumi, A.A.; Oderinu, R.A.; Ogunsola, A.W.; Taiwo, M.; Yahaya, A.A. A Numerical Solution of the Fractional Navier-Stokes Equation Using The Caputo-Fabrizio Aboodh Transform Method with the Reduced Differential Polynomials. Adv. Math. Sci. J. 2024, 13, 61–84. [Google Scholar] [CrossRef]
- Ziane, D.; Belgacem, R.; Bokhari, A. A New Modified Adomian Decomposition Method for Nonlinear Partial Differential Equations. Open J. Math. Anal. 2019, 3, 81–90. [Google Scholar] [CrossRef]
- Şahin, Y.; Merdan, M. The Solutions of Caputo-Fabrizio Random Fractional Ordinary Differential Equations by Aboodh Transform Method. Erzincan Üniversitesi Fen Bilim. Enstitüsü Derg. 2025, 18, 149–170. [Google Scholar] [CrossRef]
- Şahin, Y. Solutions of Random Fractional Differential Equations Using Aboodh and Aboodh-Adomian Decomposition Method. Master’s Thesis, Gumushane University, Gümüşhane, Turkey, 2024. [Google Scholar]
- Şahin, Y.; Merdan, M. New Numerical Solutions for Caputo–Fabrizio Fractional Differential Multidimensional Diffusion Problems. Int. J. Math. Mathemat. Sci. 2025, 1, 5554516. [Google Scholar] [CrossRef]
- Bekela, A.S.; Deresse, A.T. A hybrid yang transform adomian decomposition method for solving time-fractional nonlinear partial differential equation. BMC Rese. Not. 2024, 17, 226. [Google Scholar] [CrossRef] [PubMed]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis for fractional model of regularized long-wave equation arising in ionacoustic plasma waves. Math. Methods Appl. Sci. 2017, 40, 5642–5653. [Google Scholar] [CrossRef]
- Magreñán, Á.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]
- Kırane, M.; Turmetovand, B.K.H.; Torebek, T.B. A Nonlocal Fractional Helmholtz Equation. Fract. Differ. Calc. 2017, 7, 225–234. [Google Scholar] [CrossRef]
- Khan, A.; Liaqat, M.İ.; Mushtaq, A. Analytical Analysis for Space Fractional Helmholtz Equations by Using the Hybrid Efficient Approach. Acta Mech. Autom. 2024, 18, 4. [Google Scholar] [CrossRef]
- Juraev, D.A.; Agarwal, P.; Elsayed, E.E.; Targyn, N. Helmholtz Equations and Their Applications in Solving Physical Problems. Adv. Eng. Sci. 2024, 4, 54–64. [Google Scholar]
- Alesemi, M.; Iqbal, N.; Wyal, N. Novel Evaluation of Fuzzy Fractional Helmholtz Equations. J. Funct. Spaces 2022, 2022, 8165019. [Google Scholar] [CrossRef]
- Wang, K. New computational approaches to the fractional coupled nonlinear Helmholtz equation. Eng. Comput. 2024, 41, 1285–1300. [Google Scholar] [CrossRef]
- Nadeem, M.; Li, Z.; Kumar, D.; Alsayaad, Y. A Robust Approach for Computing Solutions of Fractional-Order two-Dimensional Helmholtz Equation. Sci. Rep. 2024, 14, 4152. [Google Scholar] [CrossRef] [PubMed]
- Hoana, L.V.C.; Korpinar, Z.; Inc, M.; Chue, Y.-M.; Almohseng, B. On Convergence Analysis and Numerical Solutions of Local Fractional Helmholtz Equation. Alex. Eng. J. 2020, 59, 4335–4341. [Google Scholar] [CrossRef]
- Samuel, M.S.; Thomas, A. On Fractional Helmholtz Equations. Fract. Calc. Appl. Anal. 2010, 13, 295–308. [Google Scholar]
- Baleanu, D.; Jassim, H.K.; Al Qurash, M. Solving Helmholtz Equation with Local Fractional Derivative Operators. Fractal Fract. 2019, 3, 43. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, R.; Khan, H.; Arif, M. Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions. Math. Meth. Appl. Sci. 2020, 1, 199–212. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şahin, Y.; Merdan, M.; Açıkgöz, P. The Analysis of Three-Dimensional Time-Fractional Helmholtz Model Using a New İterative Method. Symmetry 2025, 17, 1219. https://doi.org/10.3390/sym17081219
Şahin Y, Merdan M, Açıkgöz P. The Analysis of Three-Dimensional Time-Fractional Helmholtz Model Using a New İterative Method. Symmetry. 2025; 17(8):1219. https://doi.org/10.3390/sym17081219
Chicago/Turabian StyleŞahin, Yasin, Mehmet Merdan, and Pınar Açıkgöz. 2025. "The Analysis of Three-Dimensional Time-Fractional Helmholtz Model Using a New İterative Method" Symmetry 17, no. 8: 1219. https://doi.org/10.3390/sym17081219
APA StyleŞahin, Y., Merdan, M., & Açıkgöz, P. (2025). The Analysis of Three-Dimensional Time-Fractional Helmholtz Model Using a New İterative Method. Symmetry, 17(8), 1219. https://doi.org/10.3390/sym17081219






