Abstract
This research presents the development of a type-2 fuzzy-controlled autonomous mobile robot specifically designed for monitoring and actively maintaining indoor air quality. The core of this system is the proposed type-2 fuzzy PID dual-mode controller used for stably patrolling rooms along the walls of the environment. The design method ingeniously merges the fast error correction capability of PID control with the robust adaptability of type-2 fuzzy logic control, which utilizes interval type-2 fuzzy sets. Furthermore, the type-2 fuzzy rule table of the right wall-following controller can be extended from the first designed fuzzy left wall-following controller in a symmetrical design manner. As a result, this study eliminates the drawbacks of excessive oscillations arising from PID control and sluggish response to large initial errors in typical traditional fuzzy control. The following of the stable wall and obstacle is facilitated with ensured accuracy and easy implementation so that effective air quality monitoring and active PM2.5 filtering are achieved in a movable manner. Furthermore, the augmented reality (AR) interface overlays real-time PM2.5 data directly onto a user’s visual field, enhancing situational awareness and enabling an immediate and intuitive assessment of air quality. As this type of control is different from that used in traditional fixed sensor networks, both broader area coverage and efficient air filtering are achieved. Finally, the experimental results demonstrate the controller’s superior performance and its potential to significantly improve indoor air quality.
1. Introduction
Particulate matter 2.5 (PM2.5), with its microscopic size and hazardous health effects, poses significant risks to respiratory and cardiovascular health [1]. Traditional air filtering methods, including electrostatic precipitation, high-efficiency particulate air (HEPA) filtration, and photocatalysis, can effectively capture PM2.5 but remain limited to fixed locations, making them inadequate for dynamic and uneven pollutant distributions [2]. Internet of Things (IoT)-enabled air quality systems provide remote monitoring but often face challenges, for example, high energy consumption and limited spatial coverage [3,4,5]. To overcome these constraints, mobile robotic systems integrated with IoT-based sensors offer a flexible solution for real-time PM2.5 monitoring and mobile sensing in indoor environments [6]. However, a patrolling strategy for the mobile robot is still lacking in terms of high working efficiency. An active air-cleaning function is required for the mobile robot.
Many control methods have been proposed for controlling autonomous mobile robots, for example, nonlinear control [7,8], learning-based control [9,10], fuzzy logic control (FLC) [11,12], etc. Although nonlinear control and learning-based control ensure good control performance and robustness, these control laws are complex and difficult to implement. As humans are conscious beings, FLC is easily applied to mobile robots, so fuzzy control methods have high potential to be applied to various complex applications for mobile robots. However, their performance is dependent on the design of fuzzy rules. To ensure control precision, proportional–integral–derivative (PID) control has been integrated with FLC in some studies [13,14,15]. These fuzzy PID controllers yield both stability and easier implementation. Additionally, FLC is also applied to the wall-following control [16,17,18,19,20] of mobile robots for the objective of exploring or patrolling rooms, etc. One benefit of this is that it can be used in complex environments with irregular walls and obstacles because of the well-designed knowledge inherent in FLC. As a result, the wall-following–control approaches outlined in the literature can possibly be used to solve the active air-cleaning problem in a mobile manner. Unfortunately, these approaches highlight the trade-offs between precision, adaptability, and computational efficiency, so their implementation is limited to specific environmental requirements.
Conversely, type-2 FLC has been applied to mobile robots [21,22,23]. Since type-2 fuzzy logic controllers improve adaptability by representing the footprint of the uncertainty in fuzzy sets, they are able to handle noise, imprecision, and dynamic environmental variations effectively. This advantage makes them particularly suited for wall-following robots in complex environments with obstacles [24,25,26,27]. Compared with type-1 FLC, there are fewer type-2 fuzzy rules. However, the response is slower because of the limited operational range of the fuzzy sets. Furthermore, these type-2 fuzzy logic controllers require significant computational resources. A comparative table of the current literature is given in Table 1. Based on Table 1, it is reasonable to combine type-2 FLC and PID controllers to achieve both easy implementation and high control performance.

Table 1.
Comparison of relative control strategies.
From the aforementioned research background, this study will propose a new type-2 fuzzy wall-following controller to develop an air-cleaning mobile robot (AMR) to remove PM2.5 in an active and mobile manner. To achieve fast convergence and high robustness, we combine the advantages of type-2 FLC and PID control. Indeed, the proposed type-2 fuzzy FLC uses interval type-2 fuzzy membership functions, which allows for straightforward fuzzy inference reduction. Since the interval type-2 fuzzy logic system can inherently represent uncertainties in the footprint of uncertainty (FOU) of membership functions, this capability makes it particularly suitable for the robust control of mobile robots. Being different to type-1 FLC, the interval type-2 FLC will have lower sensitivity on the design of rule base. Then, the adaptability of type-2 FLC and the fast control capability of PID control are integrated via dual-mode control configuration. When the two control modes are individually fine-tuned, a proper switching rule allows for better integration without excessive oscillations and slow responses to large initial errors. Compared with other type-2 FLC, the proposed method allows for simpler system adjustment to deal with complex wall-following environments. Based on the type-2 fuzzy wall-following control, an active air-cleaning system is designed by integrating the movable PM2.5 sensing and air filtering subsystems on the AMR accompanying an indoor positioning system and an augmented reality (AR) system. The air-cleaning efficiency and coverage area are improved in comparison to traditional fixed air-cleaning systems. Furthermore, the air quality can be monitored in real time through a user-friendly interface. The experimental results will verify the validity of the designed AMR system.
The remainder of this paper is organized as follows. First, Section 2 describes the sensors, system platform, and motion model of the air-cleaning mobile robot. Section 3 proposes the control design for the wall-following navigation. Then, the system implementation is stated in Section 4. In Section 5, experiments validate the effectiveness of the proposed controller and overall system in different scenarios. Finally, some conclusions are made in Section 6.
2. Air-Cleaning Mobile Robot
The main function of the air-cleaning mobile robot (AMR) is to perform mobile sensing of air and actively clean dusty air. Additionally, this study develops both the air-cleaning system and the motion controller for the AMR, as described below. In this section, the mobile robot platform and basic elements are introduced below.
2.1. Mobile Robot Platform
This study utilizes the P3-DX mobile platform [28] to develop the AMR. The P3-DX robot is a compact platform consisting of a two-wheel drive system, eight fixed sonar sensors, and a data acquisition system. The robot’s configuration is represented by its position in Cartesian space, as shown in Figure 1, with coordinates defined as ( in the X-Y plane. The kinematic model of the mobile robot is given as follows:
where represents the average moving speed, is the speed difference between the right and left wheels, is the sampling time of the controller, is the body angle, H is the distance between the two drive wheels, and ‘’ is the discrete time index. Let denote the speeds of the left and right wheels, respectively. The average moving speed of the robot is obtained as:
while the speed difference is defined by
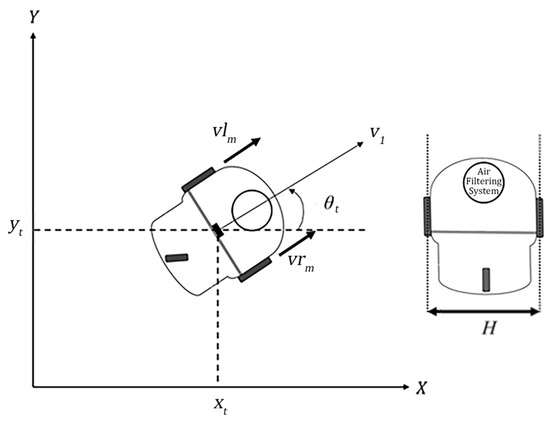
Figure 1.
Configuration of a two-wheeled air-cleaning mobile robot.
In this study, the average moving speed will be preset to a desired value. Thus, motion control can be achieved by properly designing the wheel speed difference. This means that the angle of the robot is adjusted by the control input as follows:
Since the motion is controlled by adjusting the differential speed between the two drive wheels, the motion control process is straightforward. Note that the speed on the left and right wheels belongs to the range [−100, 100] mm/s. The body angle of the AMR is constrained within [].
2.2. Air Filtering System
The air filtering system, located in the circular disk area at the top of the mobile robot, as shown in Figure 1, integrates multiple advanced filtration methods to ensure effective air purification. Specifically, it employs a high-efficiency particulate air (HEPA) filter, which can capture particles as small as 0.3 microns with a filtration efficiency exceeding 99.97%. Additionally, the system includes antimicrobial and antiviral filters designed to neutralize bacteria and viruses, thereby enhancing overall air quality. For real-time air quality assessment, the system is equipped with a PM2.5 sensor, which continuously monitors particulate matter levels and provides dynamic feedback for controlling the air filtering operation. This integrated AMR system can effectively reduce airborne contaminants and improve indoor environmental health.
2.3. Sonar Sensors
In addition to the PM2.5 sensor, ultrasonic (sonar) sensors are essential components of the AMR for distance measurement and obstacle detection. As illustrated in Figure 2, each sonar sensor is positioned on the forward side of the robot and spaced 20 degrees apart. These sensors typically have a detection range of 3 to 250 cm, making them highly suitable for near-range environmental perception. The sonar sensor data from each transducer are collected every 40 milliseconds. It should be noted that measurement deviations due to environmental uncertainty should be considered in controller design. The data retrieved from the eight sonar sensors, denoted as [], are used to facilitate the automated navigation of the mobile robot.
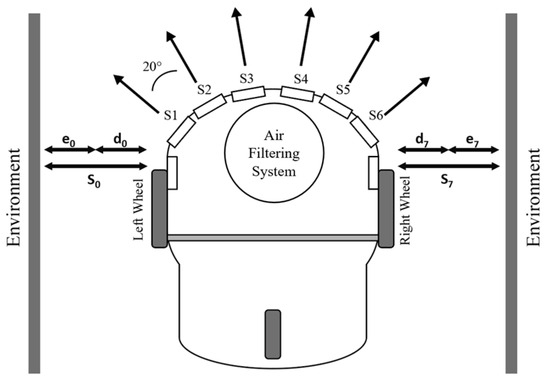
Figure 2.
Ultrasonic sensing configuration.
3. Wall-Following Control of the AMR
To drive the AMR to perform mobile sensing and active air cleaning in indoor environments, this section proposes a type-2 fuzzy wall-following controller. This approach simplifies the patrolling motion control of the robot, eliminating the need for complex path planning or SLAM algorithms. The detailed design is described below.
3.1. Error Notation
The following variable notations are introduced. To maintain a fixed distance between the AMR and the environmental wall, the measured values and (see Figure 2) are crucial for determining the distance control errors:
where and are the desired reference distances to the left and right walls, respectively. At the same time, the measured distances , , and are used to keep the AMR parallel to the left wall. The errors for left wall following are defined as:
where and are the reference values for and , respectively. Similarly, the distances , , and are used to keep the AMR parallel to the right wall, in a symmetrical manner. The errors for right wall following are defined as and , with respect to the reference values and . Since sonar sensors may produce inaccurate measurements due to environmental noise or unknown objects, type-2 fuzzy logic control is utilized to address these uncertainties.
3.2. Type-2 Fuzzy Logic System
Type-0 and type-1 fuzzy logic systems are known for their simple structures and ease of implementation. However, traditional fuzzy logic systems exhibit limited robustness and are highly sensitive to the selection of rules. When faced with noise and uncertainty—commonly encountered in wall-following control, such as sensor noise or environmental variations—the design process can become complex and challenging. In contrast, type-2 fuzzy logic systems inherently accommodate uncertainties, thus offering superior performance in such scenarios. The design of fuzzy rules and membership functions can be achieved with relative ease, making this approach particularly well suited for the robust control required in the proposed mobile robot system.
As described in [29], the interval type-2 fuzzy logic system is based on a type-2 fuzzy set , characterized by a type-2 membership function for , defined as follows:
where denotes the union over all admissible or ; is the primary membership of , and ⊆ [0, 1] for all ∀; is the secondary grade of the secondary membership function. Due to the uncertainty in the primary memberships of the type-2 fuzzy set , a bounded region known as the footprint of uncertainty (FOU) is defined by the union of all primary memberships, . For simplification, all secondary grades are assumed to equal one, so the resulting type-2 fuzzy set is referred to as an interval type-2 fuzzy set. The FOU, thus, becomes a two-dimensional shaded region between the upper and lower primary memberships, allowing the system to represent the uncertainty in the input .
The type-2 fuzzy logic system can then be described in the following rule form:
where is the j-th input; , for , are interval type-2 fuzzy sets; is a type-1 fuzzy set; y is the output; and is the number of rules. The consequent control action is selected from a predefined control action set . For the type-2 fuzzy logic system (9), the FOU of can be represented as a bounded interval in terms of the upper membership function and the lower membership function . For simplicity, the lower membership function is defined as , where is an adjustable numerical constant. An example of interval type-2 fuzzy sets is shown in Figure 3, where the solid and dashed curves represent the upper and lower membership functions, respectively. The trapezoidal membership functions of the type-2 fuzzy sets are as follows:
where a, b, c are suitable parameters. The corresponding lower membership functions are obtained via . It should be noted that symmetrical interval type-2 fuzzy membership functions are used here to simplify the fuzzy inference process.
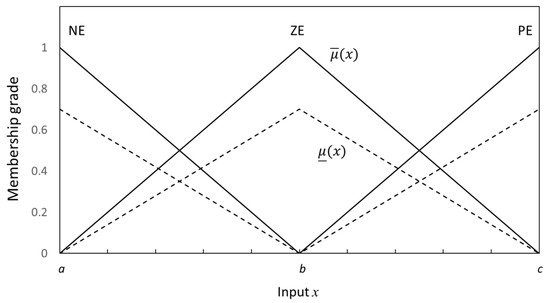
Figure 3.
Interval type-2 fuzzy sets.
For the type-2 fuzzy logic system (9), the computation process consists of fuzzification, inference, type reduction, and defuzzification. During fuzzification, the crisp input (, ) is converted into a fuzzy singleton and mapped to an appropriate fuzzy set with interval degrees of membership functions (), for . Due to the use of symmetrical interval fuzzy membership functions, the inference engine can be efficiently implemented via a fuzzy t-norm operation using algebraic products. The firing strength of the i-th rule, , is accordingly computed by the upper and lower membership functions as follows:
where
Although various fuzzy inference methods have been proposed in the literature, this study utilizes upper and lower extreme fuzzy inference for simplification (i.e., the iterative Karnik–Mendel procedure [30] is not employed). Instead, the Nagar–Bardini type-reduction method [31,32] is adopted. As the type-2 fuzzy system (9) is based on interval type-2 fuzzy membership functions, the inference process uses only the specific upper and lower rule firing strengths, rather than all possible combinations. The final output is obtained through a type-reduction process, yielding two fuzzy singletons, and , defined as:
where is the center of the fuzzy set . The final output of the type-2 fuzzy system is then computed by directly averaging these two values:
Equation (14) greatly simplifies the type-reduction procedure compared to the original Karnik–Mendel process. This simplified type-reduction fuzzy inference avoids the computational complexity of combining all possible fuzzy inferences from the primary memberships, enabling easier implementation. Meanwhile, the input uncertainty is represented using the symmetrical interval type-2 fuzzy membership functions, as shown in Figure 4.
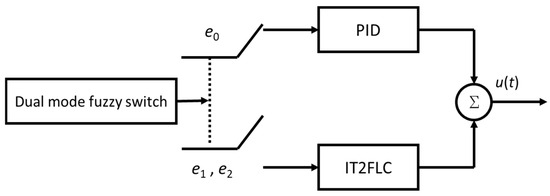
Figure 4.
The schematic diagram of the T2FPDC.
3.3. Type-2 Fuzzy-PID Dual-Mode Controller
3.3.1. Controller Design Art
Given that type-2 fuzzy sets accommodate the footprint of uncertainty (FOU), an interval type-2 fuzzy logic controller (IT2FLC) is particularly well suited for wall-following tasks involving large curvatures and for obstacle avoidance—scenarios often characterized by significant uncertainty. The IT2FLC enables the robot to more easily follow the outer contours of a wall compared to a conventional PID controller. In contrast, the traditional PID controller offers higher control precision and faster convergence when tracking straight paths or gentle curves.
To leverage the strengths of both IT2FLC and PID control, this study proposes a type-2 fuzzy-PID dual-mode controller (T2FPDC), as illustrated in Figure 5. This controller adopts an adaptive dual-mode hybrid structure, in which either the PID or the type-2 FLC is activated based on current sensor input. In this setup, the distance to the wall is regulated by the PID control mode, while the IT2FLC mode maintains the AMR parallel to the wall. By combining both control modes, the AMR can smoothly follow either the right or left wall.
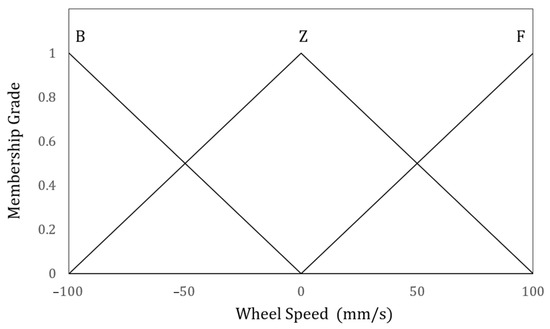
Figure 5.
Membership functions for the outputs of IT2FLC.
The design is first illustrated for left wall following. To mutually complement the two control modes, T2FPDC switches modes according to the minimum distance measured by the signals , , and , which represent the closest lateral distance from the AMR to an environmental obstacle or wall. The dual-mode switching rule is defined as follows:
THEN PID is OFF and IT2FLC is ON
ELSE PID is ON and IT2FLC is OFF
Remark 1: Although it might appear that the switching mechanism in Equation (15) could lead to abrupt transitions, such as chattering or instability, this behavior is addressed in the design. By using the minimum value among the three sensors as the switching variable, sensor fusion helps prevent the state from remaining near the switching threshold K. If the parameter K is set significantly larger than the desired distance , both the PID controller and IT2FLC will drive the system in the same direction toward the target distance, further reducing the chance of instability. Additionally, the switching rule in Equation (15) can be further refined with several fuzzy rules to smooth any abrupt transitions.
Then, the detailed designs of the IT2FLC and PID controller are presented in the following subsections.
3.3.2. IT2FLC for Wall Following
For wall-following control, the interval type-2 fuzzy logic controller (IT2FLC) is introduced in this section. To achieve left wall following by regulating the parallel orientation between the AMR and the wall, the errors and (defined in Equations (6) and (7)) are selected as the inputs to the IT2FLC. The control variables—the speeds of the left and right wheels, —serve as the outputs of the fuzzy controller.
The IT2FLC is governed by the following fuzzy rules:
for i = 1,…, M, where , for are interval type-2 fuzzy sets, and (for are type-1 fuzzy sets. The input fuzzy sets are selected from Figure 3 for and , where three interval type-2 triangular membership functions—NE (Negative Error), ZE (Zero Error), and PE (Positive Error)—are employed. These membership functions, with their respective FOUs, are crucial for generating appropriate control outputs and ensuring responsive wall-following performance under varying environmental conditions.
The outputs, , are defined by the type-1 fuzzy sets illustrated in Figure 5. The speed range for both wheels (−100 mm/s to 100 mm/s) is partitioned into three fuzzy sets: B (Backward), Z (Zero), and F (Forward). Each set is represented by a singleton value of −100 mm/s, 0 mm/s, and 100 mm/s, respectively, for use in fuzzy inference.
Meanwhile, the IT2FLC adopts the same processes for fuzzification, inference, type reduction, and defuzzification, as outlined for the type-2 fuzzy logic system in Section 3.2. Because the interval type-2 fuzzy logic system effectively handles input uncertainty, only nine fuzzy rules are needed in the IT2FLC controller. These rules are designed to adjust the wheel speeds to keep the AMR moving parallel to the wall, driving the errors and quickly to zero. When the errors converge rapidly, robust wall following and obstacle avoidance are achieved. Compared to other type-2 FLC approaches [24], the proposed IT2FLC does not require specific training for different indoor environments, making it highly adaptable. The fuzzy control rules used for the IT2FLC are summarized in Table 2.

Table 2.
Fuzzy rules of IT2FLC.
3.3.3. PID Controller for Distance Keeping
The objective of the PID control mode is to maintain a fixed parallel distance to the wall, that is, to drive the error toward zero. The differential speed of the AMR’s two wheels is used as the control input. The PID controller is expressed as follows:
where ‘’ is the discrete time index, is the sampling period, and are the proportional, integral, and derivative control gains, respectively.
In practice, the PID controller can be implemented in the following discrete difference form:
Here, the proportional gain determines the immediate response to the current error—larger values yield a more aggressive correction. The integral gain accumulates past errors to provide a correction based on the cumulative deviation. The derivative gain anticipates future errors, helping to reduce overshoot and enhance system stability. Appropriate gain tuning leads to rapid convergence and high precision in tracking the error
By integrating the above IT2FLC and PID controller designs, the system achieves robust wall following and close-range obstacle avoidance through the IT2FLC and accurate straight-line wall following via the PID controller. Consequently, the overall T2FPDC provides seamless adaptability in dynamic environments, benefiting from dual-mode switching as well as the well-designed IT2FLC and PID controller. In addition, to clarify the explanation of the proposed method, the variable natation is given as shown in Appendix A.
Remark 2: Right wall following can be realized symmetrically using the same design strategy as left wall following. Specifically, the error is used for designing the PID distance-keeping controller as in Equation (18). The errors and serve as inputs for the right wall-following IT2FLC, with the same rule structure as in Equation (16). Here, the type-2 fuzzy sets illustrated in Figure 3 and the type-1 fuzzy sets in Figure 5 are used for the input , , and the output velocities , respectively. The fuzzy rules for right wall following are designed using the symmetry property described at the end of Table 1. As a result, the T2FPDC for right wall following can be directly constructed from the same PID controller and IT2FLC configurations. Overall, left and right wall following is achieved with straightforward implementation and a symmetrical design concept.
4. System Implementation
The complete AMR system is constructed as illustrated in Figure 6. In addition to the proposed type-2 fuzzy wall-following controller, the system integrates an indoor positioning system (IPS), an augmented reality (AR) system, and an air filtering subsystem to develop a fully functional active air filtering robot. Specifically, the air filtering subsystem consists of a HANLIN-CarPM module with a HEPA filter and an intake fan, both of which ensure reliable performance in capturing fine particulate matter and maintaining effective air purification during the robot’s operation.
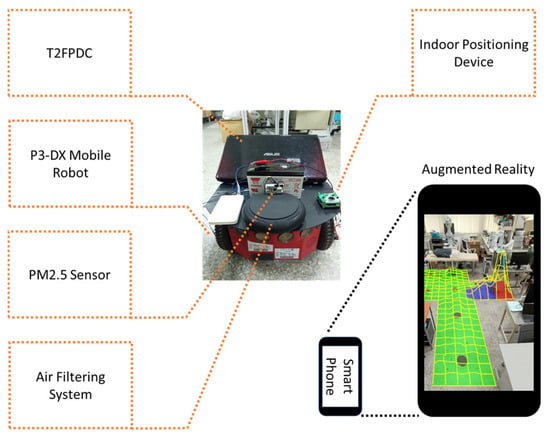
Figure 6.
Configuration of the AMR system.
Leveraging the type-2 fuzzy wall-following controller, the AMR is able to actively sense air quality throughout its environment. The measured air quality data are mapped to the position of the AMR, allowing the spatial distribution of PM2.5 to be analyzed and visualized for users. If the PM2.5 concentration at any location exceeds the safety threshold, the air filtering subsystem is immediately activated, that is, the intake fan is turned on. The overall system architecture and decision-making flowchart are shown in Figure 7. The T2FPDC wall-following controller enables the AMR to patrol indoor environments, while the mobile PM2.5 sensing yields actively filtering the air to maintain high air quality. In the following subsections, the IPS and AR system are introduced, followed by the details of the controller implementation.
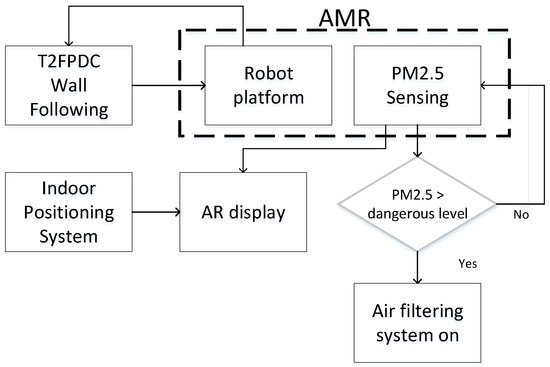
Figure 7.
System architecture and decision-making flowchart.
4.1. Indoor Positioning System
To localize the AMR, the StarGazer IPS [33] is utilized in this system. Based on infrared detection technology, the StarGazer IPS comprises an infrared projector, several ID landmarks, and an image processing unit. The IPS interprets the reflected infrared images emitted from passive landmarks attached to the indoor ceiling. Each landmark has a unique ID, encoded with a specific positioning pattern, that provides information on both the distance and orientation relative to the AMR. The acquired landmark data are then transformed into defined world coordinates. Figure 8a displays the StarGazer device, while Figure 8b shows the passive landmarks installed on the ceiling. The StarGazer IPS minimizes the impact of environmental noise on positioning accuracy, offering high precision in both heading angle and localized position. Therefore, it is well suited for accurate localization of the AMR in indoor environments.

Figure 8.
(a) StarGazer indoor positioning device; (b) a passive landmark.
4.2. Hardware and Software Settings for the AR System
The AR system is designed to provide a convenient user interface for monitoring both the status of the AMR and the spatial distribution of air quality. To reliably measure PM2.5 concentrations in a given environment or room, a Sharp GP2Y0 dust sensor is employed. The measured PM2.5 concentration is correlated with the AMR’s location, as determined by the StarGazer IPS, allowing the distribution of PM2.5 to be visualized through an AR interface on a mobile phone.
The AR system overlays real-time sensor data onto the live environmental image captured by the mobile phone camera [5,34]. To accomplish this, the AR system requires high-performance image processing hardware and real-time software algorithms. In this implementation, AR visualization is performed on an Android 10 smartphone equipped with a 50 MP camera, offering latency below 0.2 s and a frame rate up to 30 fps. The average delay from sensor data acquisition to AR visualization is approximately 0.15 s, enabling real-time display on the user interface.
Both the coverage and detail levels of the AR system can be flexibly adjusted according to monitoring conditions and user needs. After integrating air quality sensing and indoor localization systems, PM2.5 data are mapped onto the environmental image. This AR display helps users intuitively understand the spatial distribution of air quality, thereby enhancing the overall user experience with the developed AR system.
4.3. T2FPDC Implementation
The proposed T2FPDC is implemented on a notebook computer, as shown in Figure 7, and all plots and figures were generated using MATLAB R2022b. To ensure optimal wall-following performance, both the IT2FLC (Equation (16)) and the PID controller (Equation (18)) were individually and carefully tuned. The sensor and controller update sampling time was set to to ensure system stability and consistent control performance.
The proportional, integral, and derivative gains of the PID controller (Equation (18)) were tuned to balance stability and convergence speed while minimizing overshoot. The selected gains are:
To apply the PID control law (Equation (18)) to the AMR’s wheel speeds, the average moving speed in Equation (1) was set to 100 mm/s. With this setting, the wall-following error can be rapidly corrected, ensuring a consistent trajectory.
For the IT2FLC, the antecedent (IF-part) fuzzy rules (Equation (16)) are based on interval type-2 fuzzy sets (see Figure 3), with the parameters , , , and . That is, the upper membership function is related to the lower membership function by . The FOU of these type-2 fuzzy membership functions effectively captures the uncertainty in the measured distances. The consequent (THEN-part) of the rules uses the type-1 fuzzy sets shown in Figure 5, while the fuzzy rules in Table 1 are adopted for the IT2FLC. The simplified type-reduction fuzzy inference method (Equations (12)–(14)) is applied for efficient computation. These settings provide optimal performance for wall following after a series of parameter adjustments and experimental tests. The tuning strategy aims for minimal tracking error and robust transitions.
To enable smooth dual-mode switching, the parameter K should be set significantly larger than the desired distance , ensuring that both the PID controller and IT2FLC drive the robot in the same direction to maintain the desired distance and follow the wall. In the experimental case, = 200 mm and K is set to 450 mm. Empirically, setting K to approximately twice delivers optimal performance for both obstacle avoidance and wall-following precision. Notably, the same design and parameter settings can be used to implement the T2FPDC for right wall following.
A significant advantage of the proposed dual-mode system (T2FPDC) is its inherent adaptability: even if the fuzzy rules are not optimally tuned, the integrated PID controller ensures effective convergence and stable performance. Unlike existing methods, which often depend on precise rule tuning for specific layouts, this approach maintains robustness due to the complementary behavior of the PID controller, providing stability regardless of the fuzzy rule precision.
5. Experimental Results
5.1. Controller Validation
To validate the effectiveness of the proposed T2FPDC wall-following controller, several experiments were conducted in this section. The overall functions of the AMR are also demonstrated. For comprehensive comparison, the PID controller, a traditional fuzzy logic controller (FLC), and the proposed T2FPDC were all evaluated under identical environmental scenarios involving linear paths, obstacles, and corners. The implementation details for the PID controller and T2FPDC are described in Section 4. The configuration of the traditional FLC for wall following is described below.
The eight sonar sensors of the AMR are grouped into three sets: (left sonar sensors), (front sonar sensors), and (right sonar sensors). For simplification, the minimum distance measured by each group is used as the input variable for the traditional FLC, denoted as DL (distance left), DF (distance forward), and DR (distance right), respectively.
If the input space is considered to range from 0 to 1000 mm, the fuzzy membership distributions for the variables DL, DF, and DR are illustrated in Figure 9. Each variable is classified into three fuzzy sets: Near (N), Quite-Near (QN), and Far (F). The outputs of the traditional FLC wall-following controller are the left wheel speed ( and right wheel speed (. When the wheel speed range is set from −100 to 100 mm/s, it is further partitioned into five fuzzy subsets: backward fast (BF), backward (B), zero (Z), forward (F), and fast forward (FF). These membership functions are depicted in Figure 10. Unlike the IT2FLC described in Equation (16), a greater number of fuzzy sets are used in the traditional FLC to achieve finer control performance.
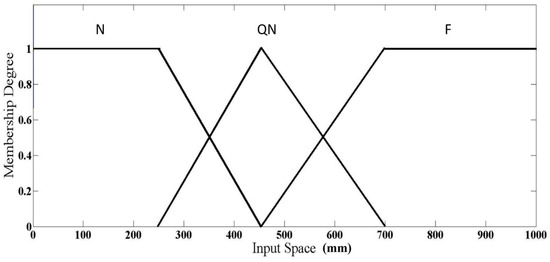
Figure 9.
Fuzzy membership functions for DL, DF, and DR.
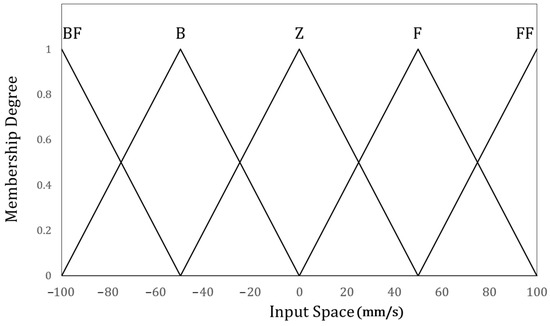
Figure 10.
Membership functions for velocities and .
Based on the above-defined fuzzy membership functions, the fuzzy rules for the traditional FLC are designed and listed in Table 3. Maximum-product fuzzy inference is used to evaluate these rules. The membership functions and rule base have been fine-tuned through experimental testing to achieve optimal controller performance. This well-tuned fuzzy controller enables a rapid control response and stable wall following.

Table 3.
Rules of traditional fuzzy logic controller.
To demonstrate the effectiveness of the proposed T2FPDC, three experimental scenarios are considered:
- Motion inside a rectangular room without obstacles;
- Motion inside a rectangular room with a single obstacle;
- Following the outside perimeter of a rectangular room with two obstacles.
For scenarios 1 and 2, the rectangular room has dimensions of 1400 mm × 1800 mm, with concrete walls and smooth vinyl floors; the obstacles consist of 200 mm × 100 mm cartons. In scenario 3, the room measures 600 mm × 1300 mm, and two obstacles are placed outside the room. In each scenario, the AMR follows the left wall to patrol the environment. The detailed layouts for these three environments are shown in Figure 11, Figure 12 and Figure 13, respectively.
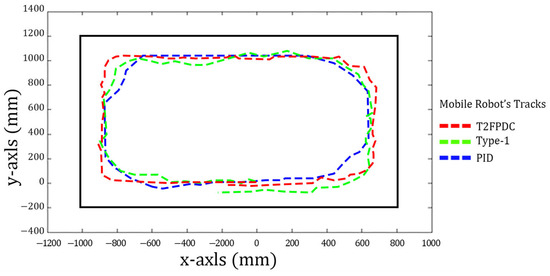
Figure 11.
Comparative control results of the three controllers in a rectangular room without obstacles (red dashed: T2FPDC; green dashed: type-1 fuzzy; blue dashed: PID).
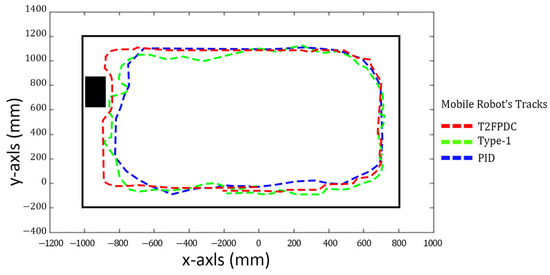
Figure 12.
Comparative control results of the three controllers in a rectangular room with a single obstacle (red dashed: T2FPDC; green dashed: type-1 fuzzy; blue dashed: PID).
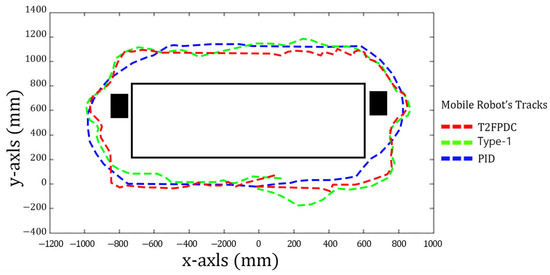
Figure 13.
Control trajectories following the outside of a rectangular room with two obstacles (red dashed: T2FPDC; green dashed: type-1 fuzzy; blue dashed: PID).
To compare the wall-following and obstacle avoidance performance of all three controllers under identical experimental conditions, the control trajectories for the PID controller, type-1 fuzzy logic controller, and the proposed T2FPDC are shown in Figure 11, Figure 12 and Figure 13 for each scenario. The results indicate that the T2FPDC achieves the most stable and accurate wall-following trajectories, effectively balancing both precision and adaptability. The type-1 fuzzy logic controller exhibits moderate adaptability but larger tracking deviations, especially near corners and obstacles. The PID controller, by contrast, tends to maintain a greater distance from obstacles and corners, resulting in less effective area coverage and mapping. This integrated comparison visually highlights the superior performance and robustness of the T2FPDC controller.
For further comparison, the response for the third experimental scenario is examined in more detail. The responses of the control error for the traditional FLC and the T2FPDC are shown in Figure 14 and Figure 15, respectively. After analyzing the steady-state responses from the experiments in all three scenarios, detailed performance metrics are summarized in Table 4. The error is maintained close to zero in all scenarios.
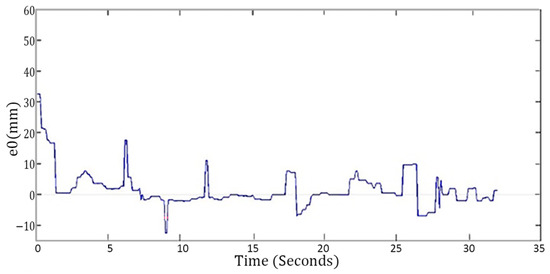
Figure 14.
Error response for the traditional FLC.
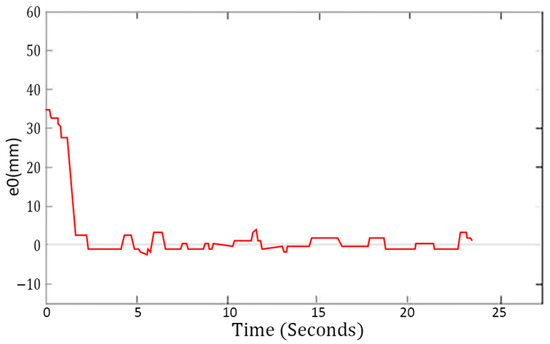
Figure 15.
Error response for the T2FPDC.

Table 4.
Statistical performance over experimental runs.
Clearly, the PID controller exhibits a fast response but lower accuracy. The traditional FLC achieves lower tracking error but tends to result in over-control. The T2FPDC, by combining the strengths of both the PID controller and traditional FLC, achieves superior wall-following control. The results demonstrate that T2FPDC offers the best overall control performance in terms of accuracy, stability, and response speed.
Furthermore, compared with existing methods in the literature—where the PID baseline controller or the traditional FLC may be enhanced by techniques such as genetic algorithms [19] or reinforcement learning [18,24]—the resulting controller design can become quite complex and difficult to implement. In contrast, the dual-mode switching strategy proposed here enables the T2FPDC to be easily implemented while still delivering outstanding control performance. This makes the proposed method more suitable for wall-following control across a wide range of environments.
Additionally, the control velocities of the two wheels are shown in Figure 16 and Figure 17. The results indicate that the traditional FLC causes the wheel velocities to fluctuate continuously, while the T2FPDC results in smoother changes in wheel velocity. In Figure 17, the upward arrow (“↑”) indicates the switching to PID control mode, and the downward arrow (“↓”) indicates switching to the IT2FLC mode. The switching law (15) does not result in abrupt transitions, such as chattering or instability, and efficient wall-following performance is achieved. As a result, the T2FPDC maintains high performance even in complex scenarios involving obstacles.
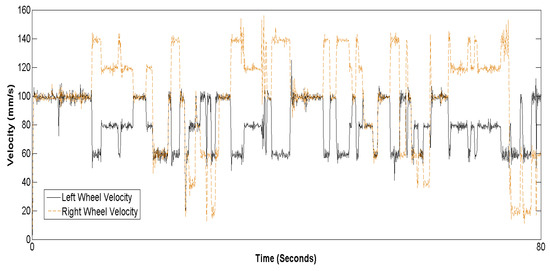
Figure 16.
Left and right wheel velocity generated by the traditional FLC.
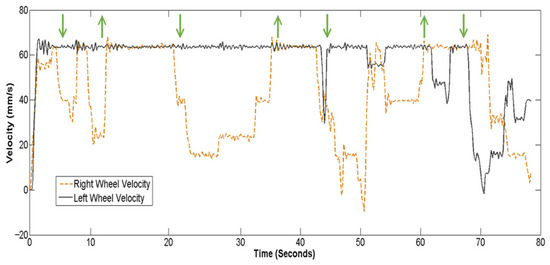
Figure 17.
Left and right wheel velocity generated by the T2FPDC (dashed line: right wheel velocity; solid line: left wheel velocity).
5.2. Demonstration of AR Display
After performing mobile sensing of environmental air quality, the spatial distribution of PM2.5 can be visualized by mapping the data to the AMR’s location. One such result is shown in Figure 18, where green regions indicate safe zones with PM2.5 concentrations ranging from 0.00 to 0.05 mg/m3, blue areas represent semi-safe zones (0.06 to 0.12 mg/m3), and red areas denote dangerous zones with concentrations exceeding 0.13 mg/m3. Augmented reality (AR) technology has been integrated into the autonomous mobile robot system, as illustrated in Figure 19, to enhance the intuitiveness and interactivity of indoor air quality monitoring. This visual presentation not only improves the user experience but also makes monitoring data easier to interpret. In complex indoor environments, AR enables more efficient interaction between the robot and users and assists designers in improving the accuracy of air quality control. Therefore, the AR display tool not only enriches the functionality of the AMR but also offers a new perspective for indoor air quality monitoring.
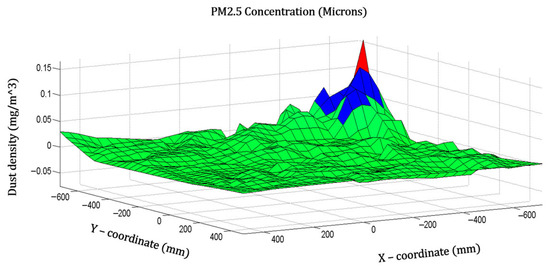
Figure 18.
Distribution of PM2.5 concentration (the PM2.5 concentration is visualized by colors, where green, blue, and red represent low, moderate, and high concentrations, respectively).

Figure 19.
AR representation of the PM2.5 concentration map (the PM2.5 concentration is visualized by colors, where green, blue, and red represent low, moderate, and high concentrations, respectively).
5.3. Function Verification of Active Air Filtering System
Based on the collected air quality data, the spatial distribution of PM2.5 can also be visualized in two dimensions. Using the color definitions for different PM2.5 levels, as shown in Figure 18, Figure 20 provides an example after the AMR conducts mobile sensing by T2FPDC wall following. If the PM2.5 concentration exceeds the dangerous level, the AMR automatically moves to the hazardous zone and activates the air filter, which remains on until the concentration drops below 0.13 mg/m3. Figure 21 shows the control signal response of the air filter when the threshold is reached. The PM2.5 concentration is quickly reduced to a safe level. Compared with traditional fixed-position HEPA air purifiers, the developed AMR provides rapid and mobile air purification over a wide area—capabilities difficult to achieve with conventional circulation-based air purifiers.
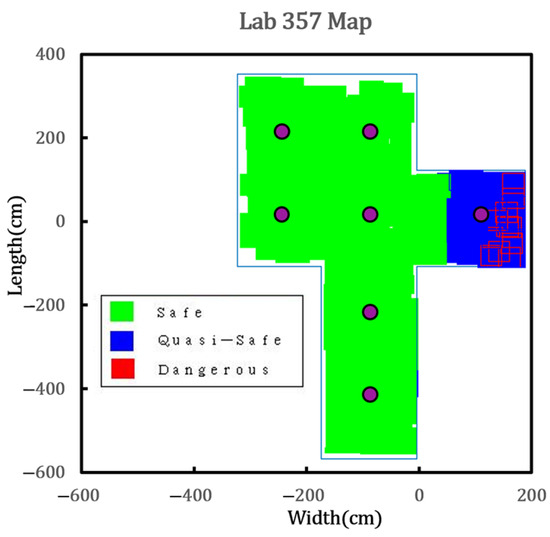
Figure 20.
A 2D visualization of PM2.5 and the active path of the AMR.
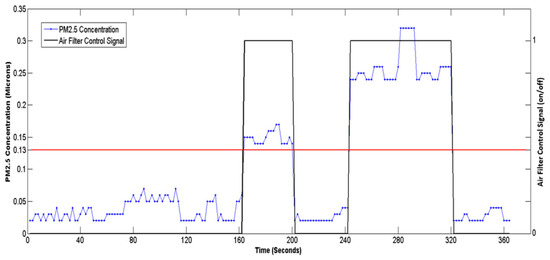
Figure 21.
Air PM2.5 response and filter control signal (red line is the limit threshold of PM2.5 concentration).
6. Conclusions
This study proposed the T2FPDC for the AMR, enabling effective mobile air quality sensing using a wall-following strategy. The T2FPDC offers enhanced robustness in the presence of rule design and measurement uncertainty, resulting in better control performance compared to traditional fuzzy logic control. By integrating the advantages of type-2 fuzzy logic and PID control, the T2FPDC addresses the limitations of conventional fuzzy logic controllers, such as reduced robustness and a greater dependency on rule complexity. Furthermore, the left and right wall-following controllers were designed symmetrically. As a result, the mobile sensing system for monitoring and maintaining air quality is easily realized using the type-2 fuzzy-controlled mobile robot. Supported by the proposed indoor positioning system and AR display interface, the AMR enables effective visualization of air quality data, thereby providing a better user experience. This not only improves the efficiency of air quality management but also reduces the operational complexity for users. The effectiveness of the proposed AMR system was validated via several experiments.
In the future, the developed AMR can be applied to a variety of environments to enhance the monitoring of hazardous air quality and to promote human health, such as detecting CO2 or VOC levels. These applications can be realized by integrating new air sensors, while advanced AR human–robot interfaces can be developed to provide richer and more interactive information. Moreover, detailed air quality analysis can be conducted, leading to significant real-world applications.
Author Contributions
Writing—review and editing, C.-S.C.; software, methodology, writing, original draft preparation, S.-Y.Y.; software, hardware, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council, R.O.C., and the project number is NSTC 113-2221-E-033-033.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Table of Symbols
| Symbol | Definition |
| average moving speed of robot | |
| speed difference between the right and left wheels | |
| speed on the left and right wheels | |
| body angle of the robot | |
| ( | coordinator of the robot |
| distance between the two drive wheels | |
| sampling time period | |
| Value of -th sonar sensor | |
| switching threshold for dual-mode control | |
| reference value for | |
| error for wall following | |
| interval type-2 fuzzy sets | |
| upper membership function for type-2 fuzzy set | |
| lower membership function for type-2 fuzzy set | |
| relative parameter between upper and lower membership functions | |
| a, b, c | parameters of interval type-2 membership functions in Figure 3 |
| the center of the fuzzy set | |
| proportional gain of PID controller | |
| integral gain of PID controller | |
| derivative gain of PID controller | |
| NE, ZE, PE | interval type-2 fuzzy sets. |
| B, Z, F | fuzzy sets for wheel speed |
| N, QN, F | Fuzzy sets for distances DL, DF, and DR |
| BF, B, Z, F, FF | fuzzy sets for wheel speed in type-1 FLC |
References
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the global burden of diseases study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Robert, B.; Nallathambi, G. A concise review on electrospun nanofibres/nanonets for filtration of gaseous and solid constituents (PM2.5) from polluted air. Colloid Interface Sci. Commun. 2020, 37, 100275. [Google Scholar] [CrossRef]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef]
- Nižetić, S.; Šolić, P.; López-de-Ipiña González-de-Artaza, D.; Patrono, L. Internet of Things (IoT): Opportunities, issues and challenges towards a smart and sustainable future. J. Clean. Prod. 2020, 274, 122877. [Google Scholar] [CrossRef]
- Katsiokalis, M.; Tsekeri, E.; Lilli, A.; Gobakis, K.; Kolokotsa, D.; Mania, K. GoNature AR: Air quality & noise visualization through a multimodal and interactive augmented reality experience. In Proceedings of the 2023 ACM International Conference on Interactive Media Experiences, Nantes, France, 12–15 June 2023; pp. 366–369. [Google Scholar]
- Jin, M.; Liu, S.; Schiavon, S.; Spanos, C. Automated mobile sensing: Towards high-granularity agile indoor environmental quality monitoring. Build. Environ. 2018, 127, 268–276. [Google Scholar] [CrossRef]
- Veselov, G.E.; Sklyarov, A.A. Nonlinear control system of mobile robot for avoiding obstacles. In Proceedings of the 2019 III International Conference on Control in Technical Systems (CTS), St. Petersburg, Russia, 30 October–1 November 2019; pp. 281–284. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Peng, H.; Hu, Y.; Su, H. Fuzzy-torque approximation-enhanced sliding mode control for lateral stability of mobile robot. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 2491–2500. [Google Scholar] [CrossRef]
- Gökbulut, M.; Top, A. Real-time deep learning-based position control of a mobile robot. Eng. Appl. Artif. Intell. 2024, 138, 109373. [Google Scholar] [CrossRef]
- Sierra-Garcia, J.E.; Santos, M. Combining reinforcement learning and conventional control to improve automatic guided vehicles tracking of complex trajectories. Expert Syst. 2024, 41, e13076. [Google Scholar] [CrossRef]
- Abdelwahab, M.; Parque, V.; Fath Elbab, A.M.R.; Abouelsoud, A.A.; Sugano, S. Trajectory tracking of wheeled mobile robots using z-number based fuzzy logic. IEEE Access 2020, 8, 18426–18441. [Google Scholar] [CrossRef]
- Batti, H.; Jabeur, C.B.; Fourati, H.; Seddik, H. Fuzzy logic based control for autonomous mobile robot navigation and obstacles avoidance. In Proceedings of the 2022 IEEE Information Technologies & Smart Industrial Systems (ITSIS), Paris, France, 15–17 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Q.; Kan, J.; Chen, S.; Yan, S. Fuzzy PID based trajectory tracking control of mobile robot and its simulation in Simulink. Int. J. Control. Autom. 2014, 7, 233–244. [Google Scholar] [CrossRef]
- Tiep, D.K.; Lee, K.; Im, D.-Y.; Kwak, B.; Ryoo, Y.-J. Design of Fuzzy-PID Controller for Path Tracking of Mobile Robot with Differential Drive. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 220–228. [Google Scholar] [CrossRef]
- Wondosen, A.; Shiferaw, D. Fuzzy Logic Controller Design for Mobile Robot Outdoor Navigation. arXiv 2024, arXiv:2401.01756. [Google Scholar]
- Hanafi, D.; Abueejela, Y.M.; Zakaria, M.F. Wall follower autonomous robot development applying fuzzy incremental controller. Intell. Control. Autom. 2013, 4, 18–25. [Google Scholar] [CrossRef]
- Zaki, A.A.; Mulyana, E.; Mardiati, R. Modeling wall tracer robot motion based on fuzzy logic control. In Proceedings of the 2020 6th International Conference on Wireless and Telematics (ICWT), Bandung, Indonesia, 3–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.-H.; Jeng, S.-Y.; Lin, C.-J. Mobile robot wall-following control using fuzzy logic controller with improved differential search and reinforcement learning. Mathematics 2020, 8, 1254. [Google Scholar] [CrossRef]
- Suwoyo, H.; Tian, Y.; Deng, C.; Adriansyah, A. Improving a wall-following robot performance with a PID-genetic algorithm controller. In Proceedings of the 2018 5th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Malang, Indonesia, 16–18 October 2018; pp. 314–318. [Google Scholar] [CrossRef]
- Riman, C.F.; Abi-Char, P.E. Fuzzy logic control for mobile robot navigation in automated storage. Int. J. Mech. Eng. Robot Res. 2023, 12, 313–323. [Google Scholar] [CrossRef]
- Cherroun, L.; Nadour, M.; Kouzou, A. Type-1 and type-2 fuzzy logic controllers for autonomous robotic motion. In Proceedings of the 2019 International Conference on Applied Automation and Industrial Diagnostics (ICAAID), Elazig, Turkey, 25–27 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Thuong, T.T.; Ha, V.T.; Truc, L.N. Intelligent control for mobile robots based on fuzzy logic controller. In Intelligent Systems and Networks. ICISN 2023; Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2023; Volume 752, pp. 566–573. [Google Scholar] [CrossRef]
- Al-Mahturi, A.; Santoso, F.; Garratt, M.A.; Anavatti, S.G. A Novel Evolving Type-2 Fuzzy System for Controlling a Mobile Robot under Large Uncertainties. Robotics 2023, 12, 40. [Google Scholar] [CrossRef]
- Juang, C.-F.; Huang, C.-H. Reinforcement ant optimized fuzzy controller for mobile-robot wall-following control. IEEE Trans. Ind. Electron. 2009, 56, 3931–3940. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Juang, C.-F. Evolutionary robot wall-following control using type-2 fuzzy controller with species-de-activated continuous ACO. IEEE Trans. Fuzzy Syst. 2013, 21, 100–112. [Google Scholar] [CrossRef]
- Santiago, C.; Chiu, C.-S. Interval type-2 fuzzy and PID dual-mode controller for an autonomous mobile robot. In Proceedings of the 2018 International Conference on System Science and Engineering (ICSSE), New Taipei, Taiwan, 28–30 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Al-Mallah, M.; Ali, M.; Al-Khawaldeh, M. Obstacles avoidance for mobile robot using type-2 fuzzy logic controller. Robotics 2022, 11, 130. [Google Scholar] [CrossRef]
- Fareh, R.; Baziyad, M.; Rabie, T.; Bettayeb, M. Enhancing path quality of real-time path planning algorithms for mobile robots: A sequential linear paths approach. IEEE Access 2020, 8, 167090–167104. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Chen, C.; Wu, D.; Garibaldi, J.M.; John, R.I.; Twycross, J.; Mendel, J.M. A comprehensive study of the efficiency of type-reduction algorithms. IEEE Trans. Fuzzy Syst. 2021, 29, 1556–1566. [Google Scholar] [CrossRef]
- Chen, Y. Study on centroid type-reduction of interval type-2 fuzzy logic system based on noniterative algorithms. Complexity 2019, 9, 7325053. [Google Scholar] [CrossRef]
- El-Nagar, A.M.; El-Bardini, M. Simplified interval type 2 fuzzy logic system based on new type-reduction. J. Intell. Fuzzy Syst. 2014, 27, 1999–2010. [Google Scholar] [CrossRef]
- Huang, J.; Junginger, S.; Liu, H.; Thurow, K. Indoor positioning systems of mobile robots: A Review. Robotics 2023, 12, 47. [Google Scholar] [CrossRef]
- Sanità, M.; Fratini, J.; Muralikrishna, N.; Pierdicca, R.; Malinverni, E.S. Augmented reality for air quality monitoring: Case study in the marche region (Italy). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 48, 389–395. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).