Plume Characterization of Electrodeless Plasma Thruster with Configurable Exhaust
Abstract
1. Introduction
2. Experimental Setup
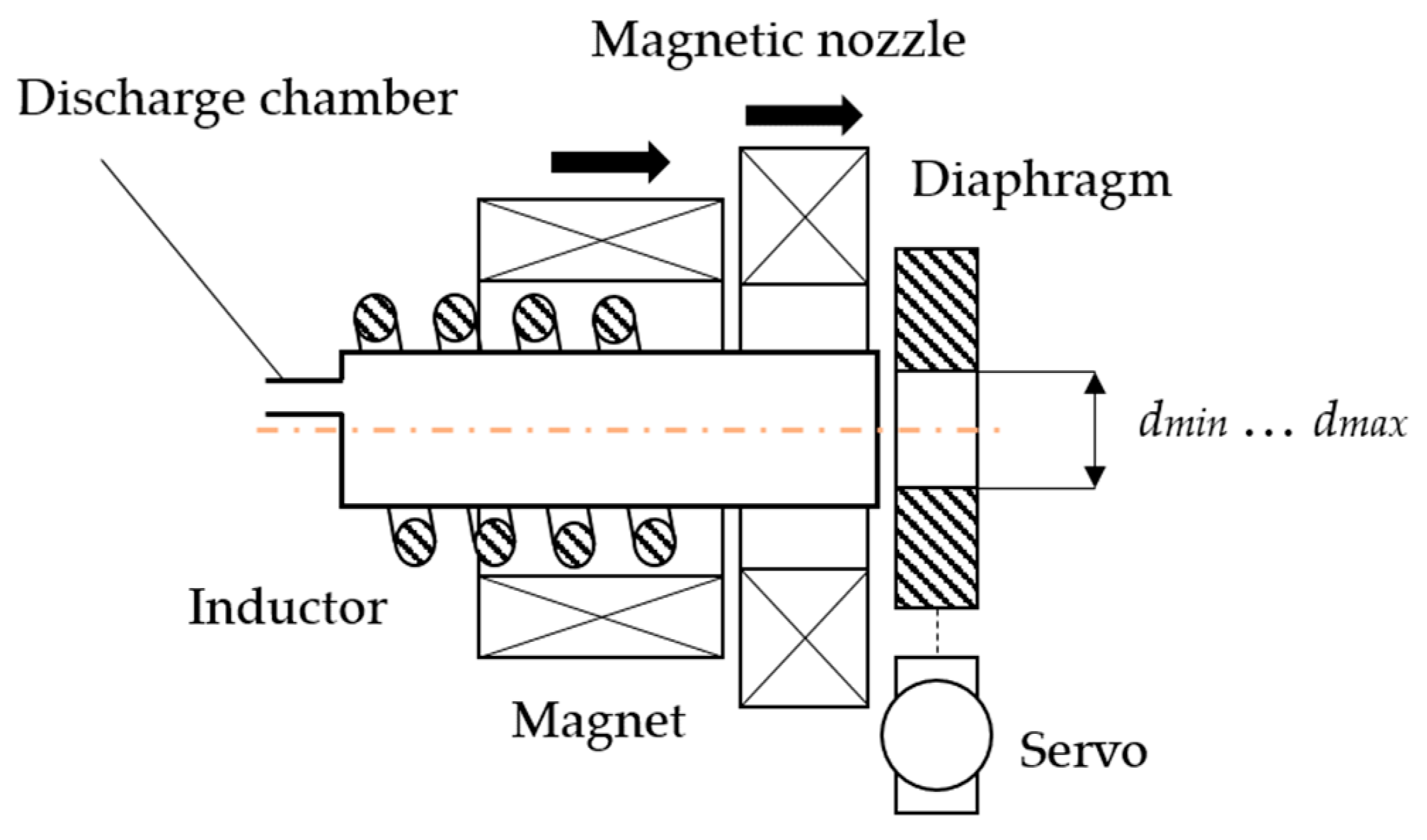
2.1. Electrodeless Plasma Thruster
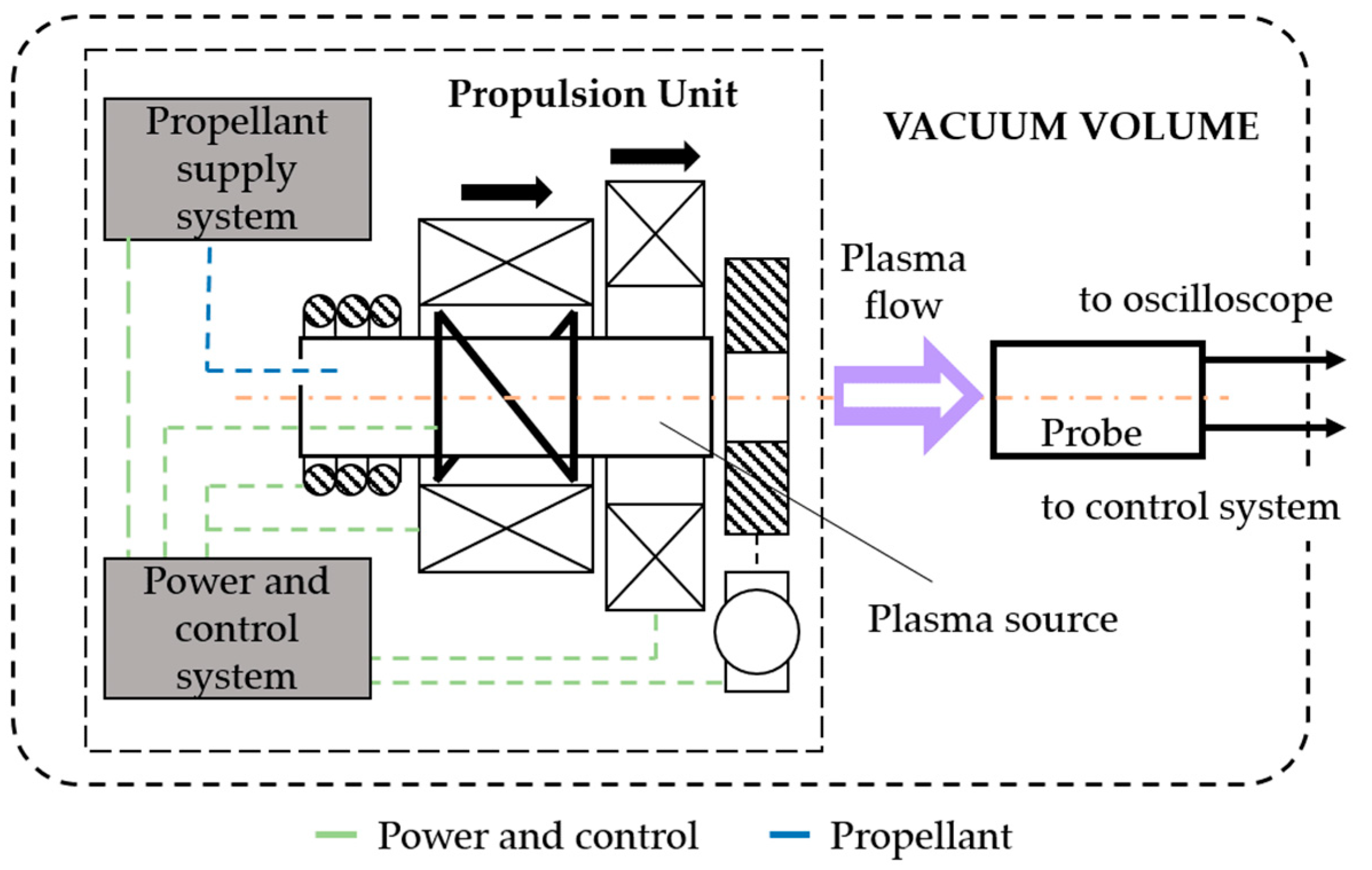
2.2. Experimental Design
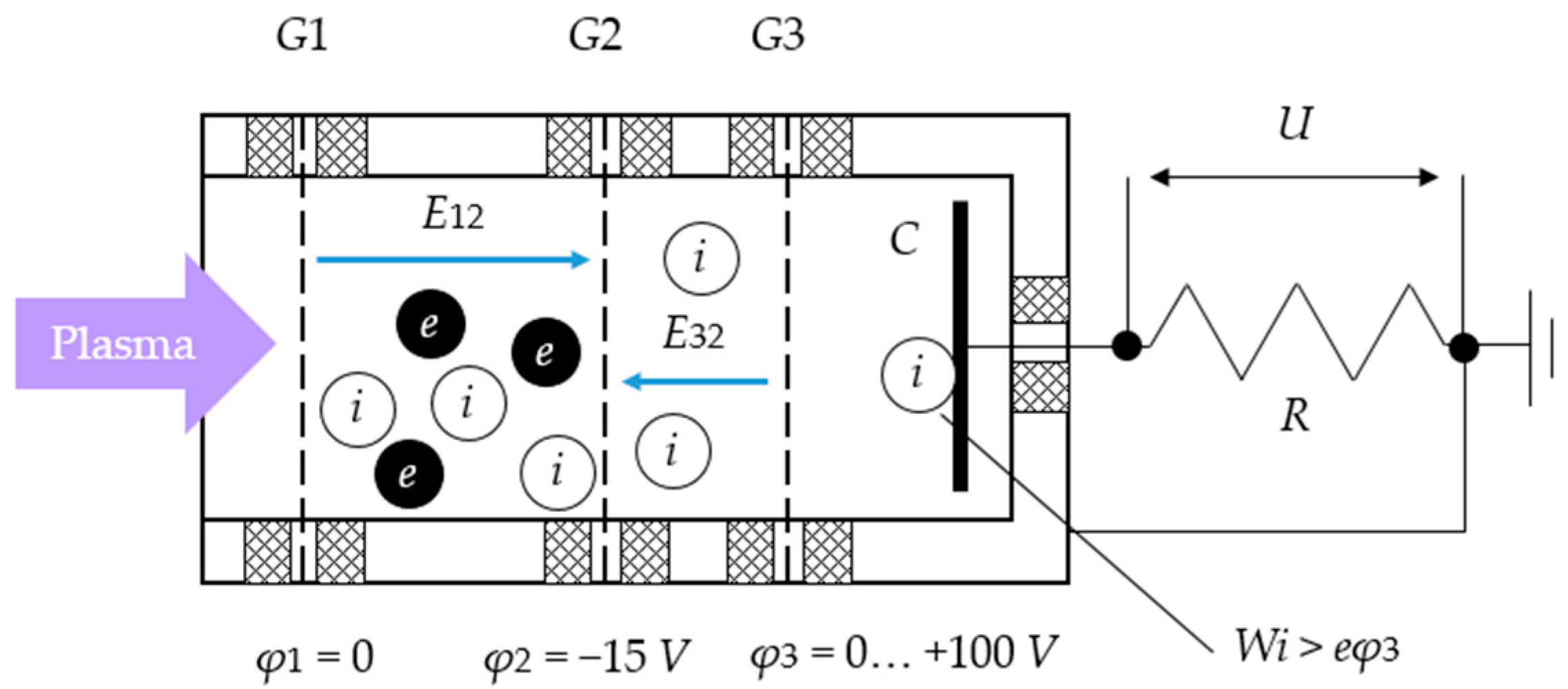
2.3. Diagnostic Probe
3. Experimental Data and Processing
3.1. Operating Modes
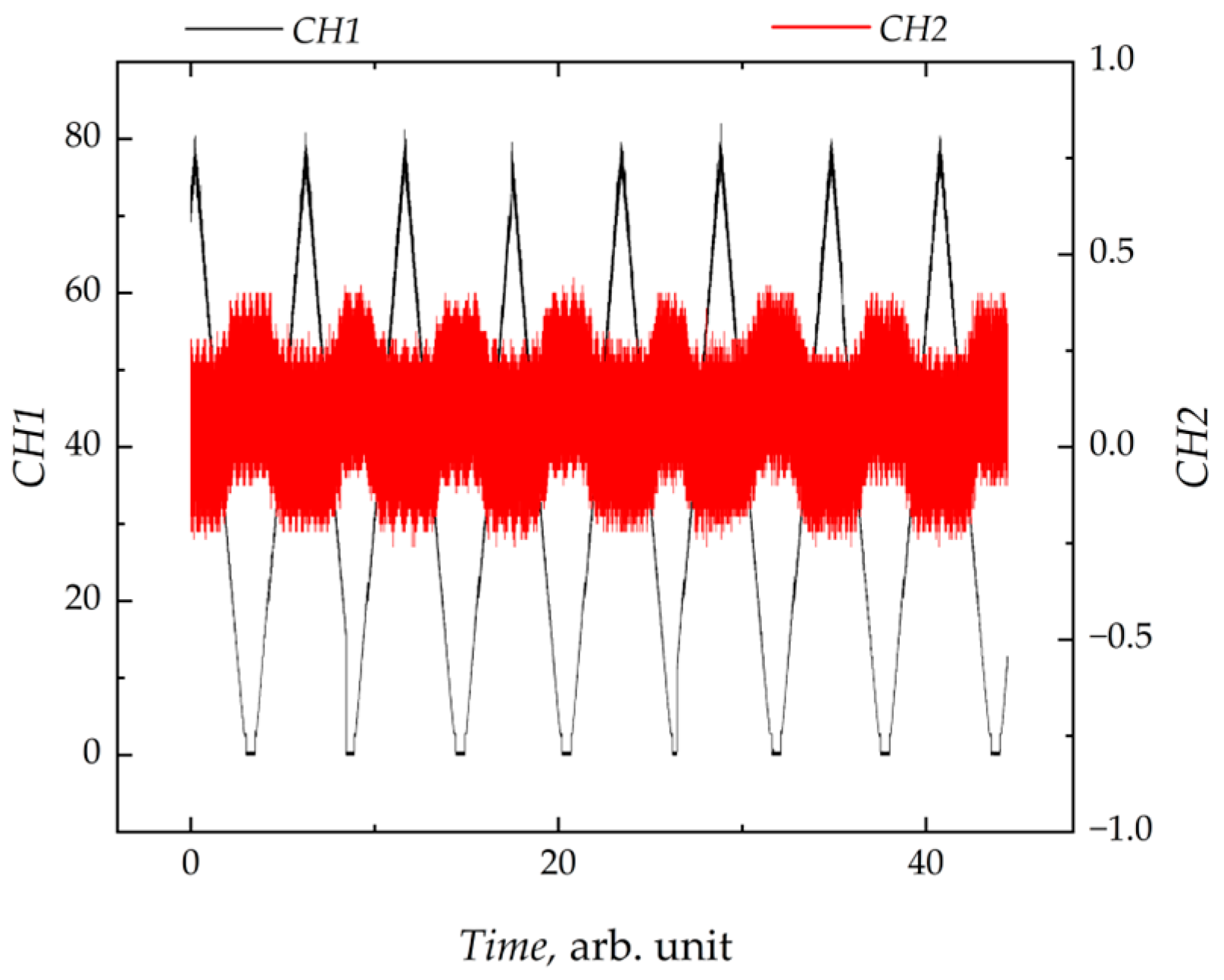
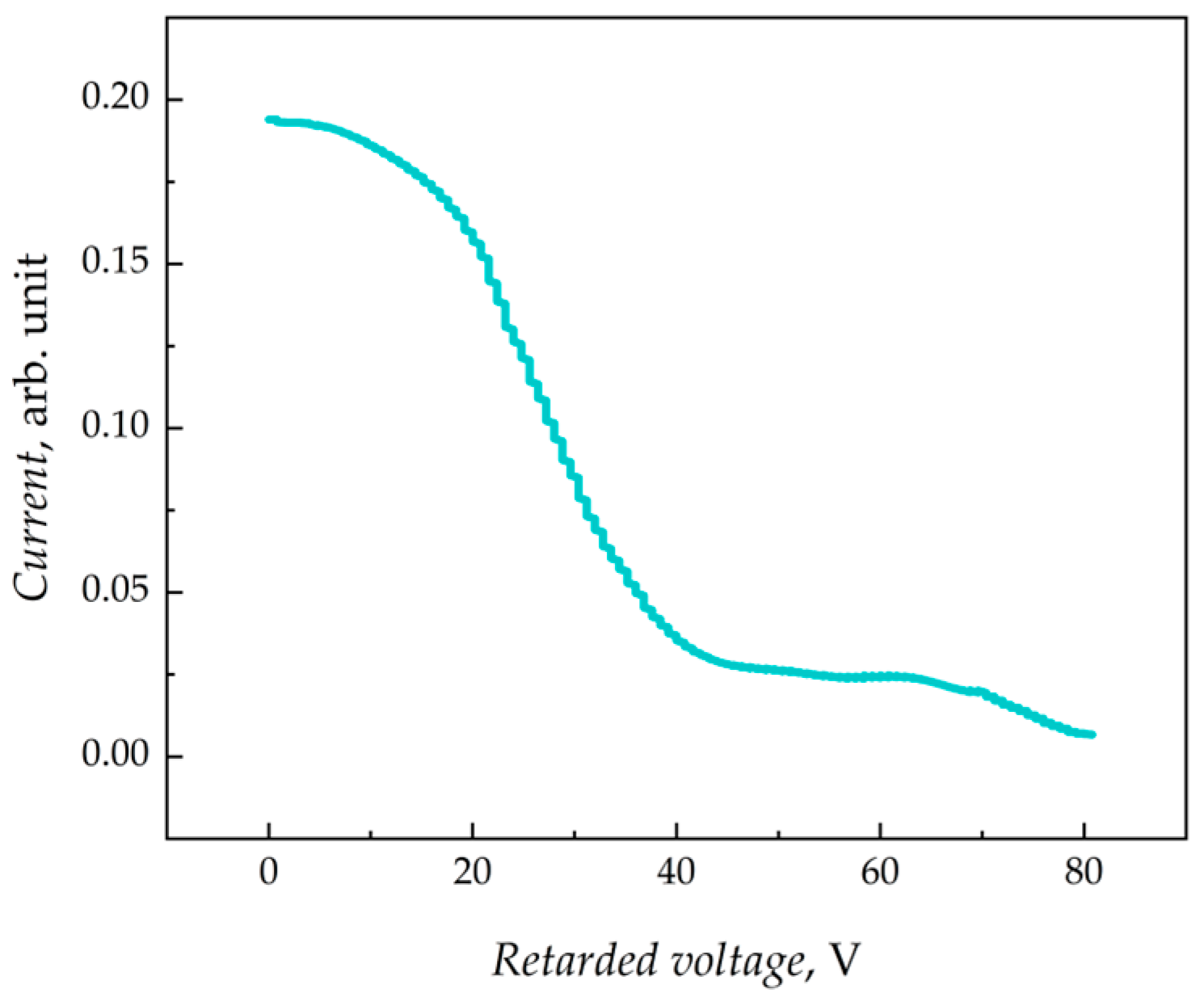
3.2. Experimental Data
3.3. Data Processing Methodology
4. Results and Discussion
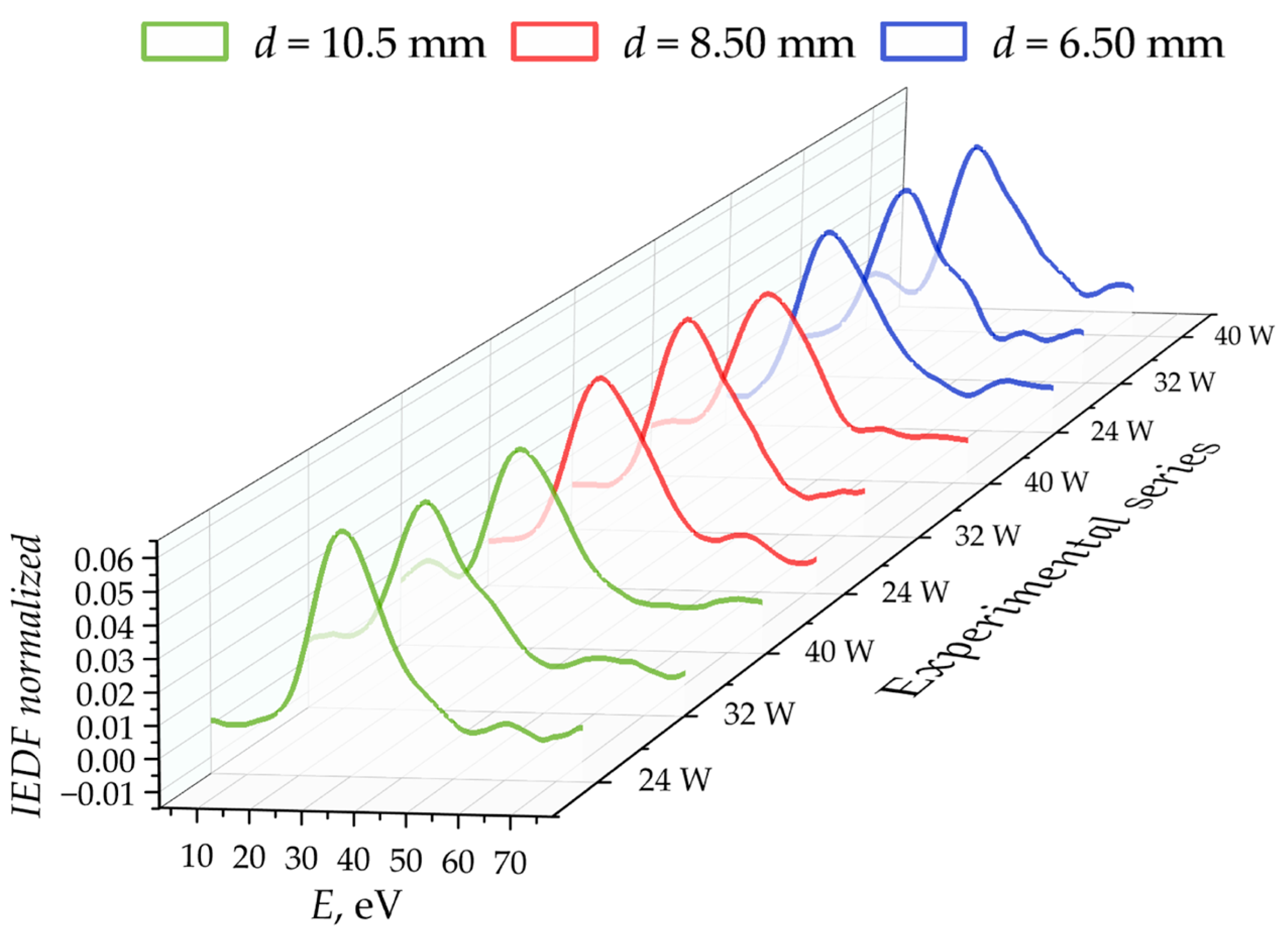
4.1. Experimental IEDF
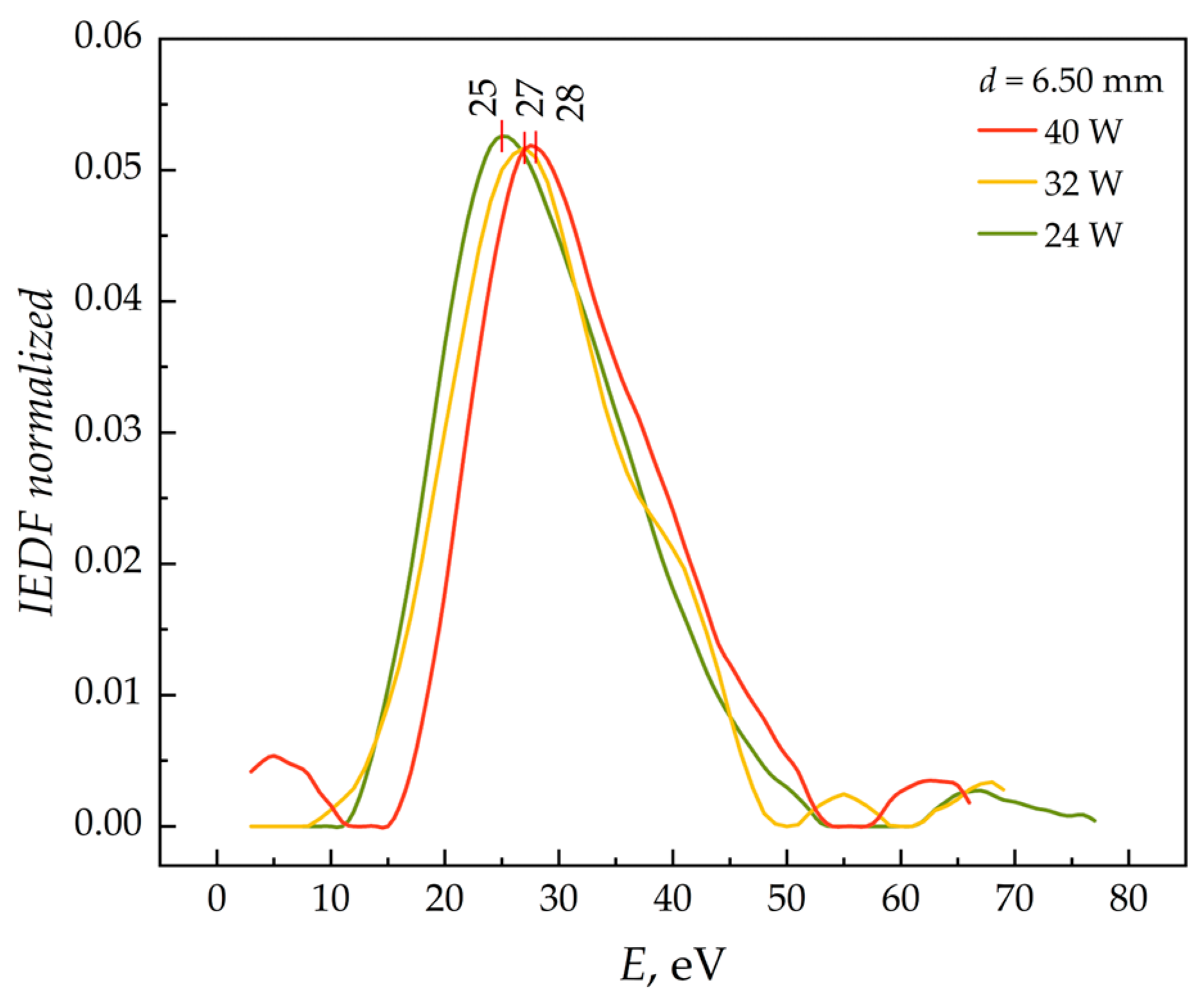
4.2. Analysis of Series with Constant Diameter
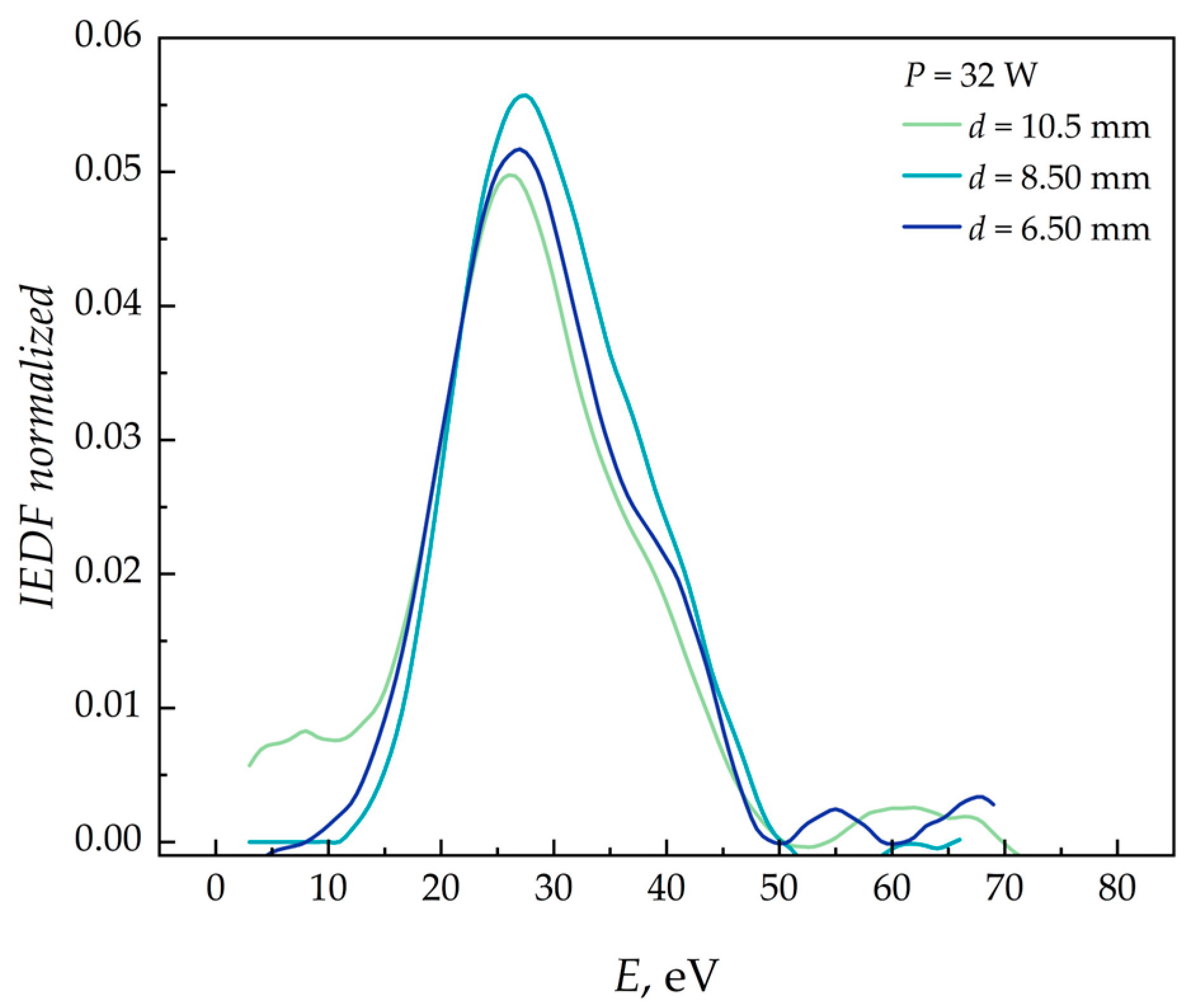
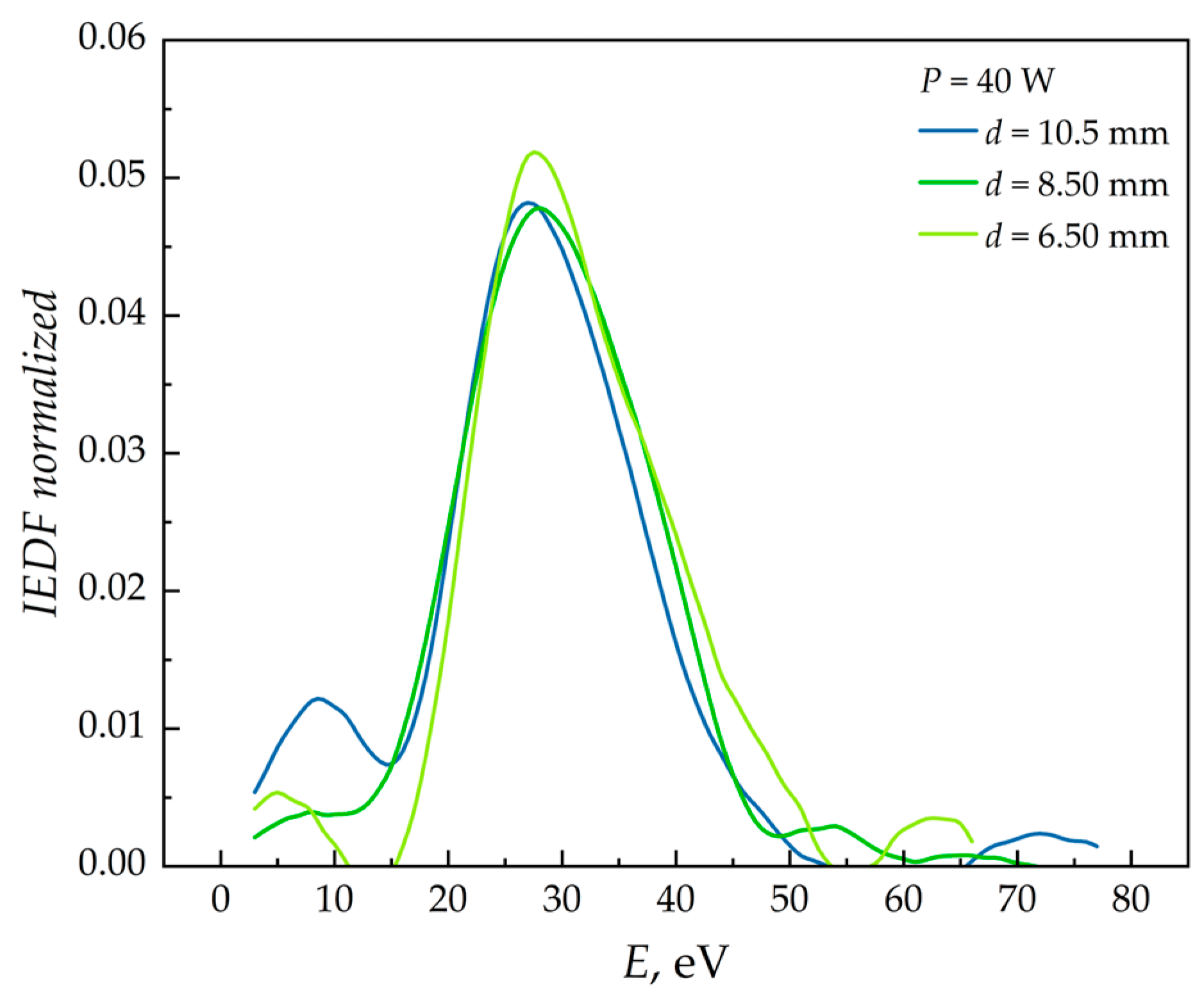
4.3. Investigating the Effect of Diaphragm Diameter
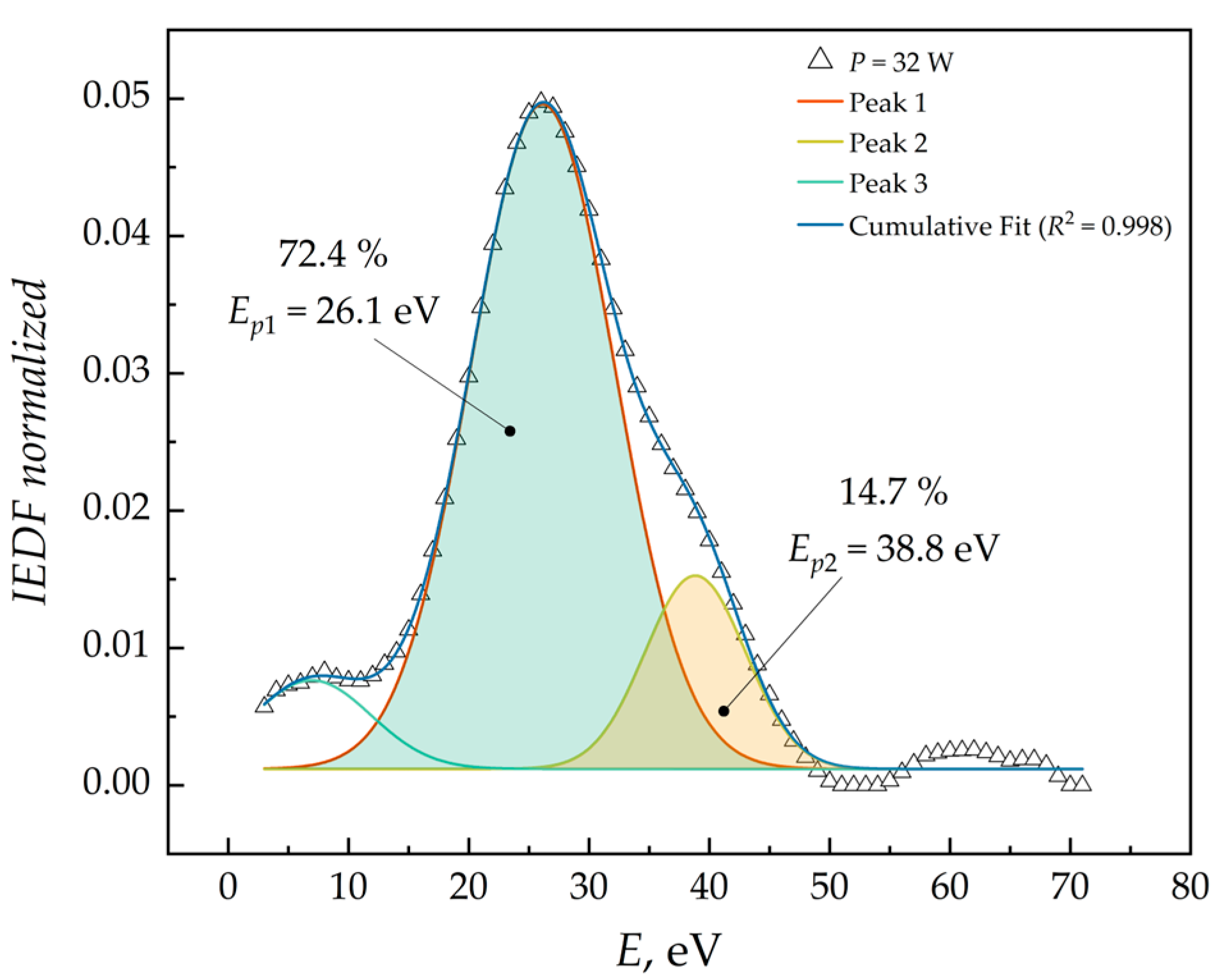
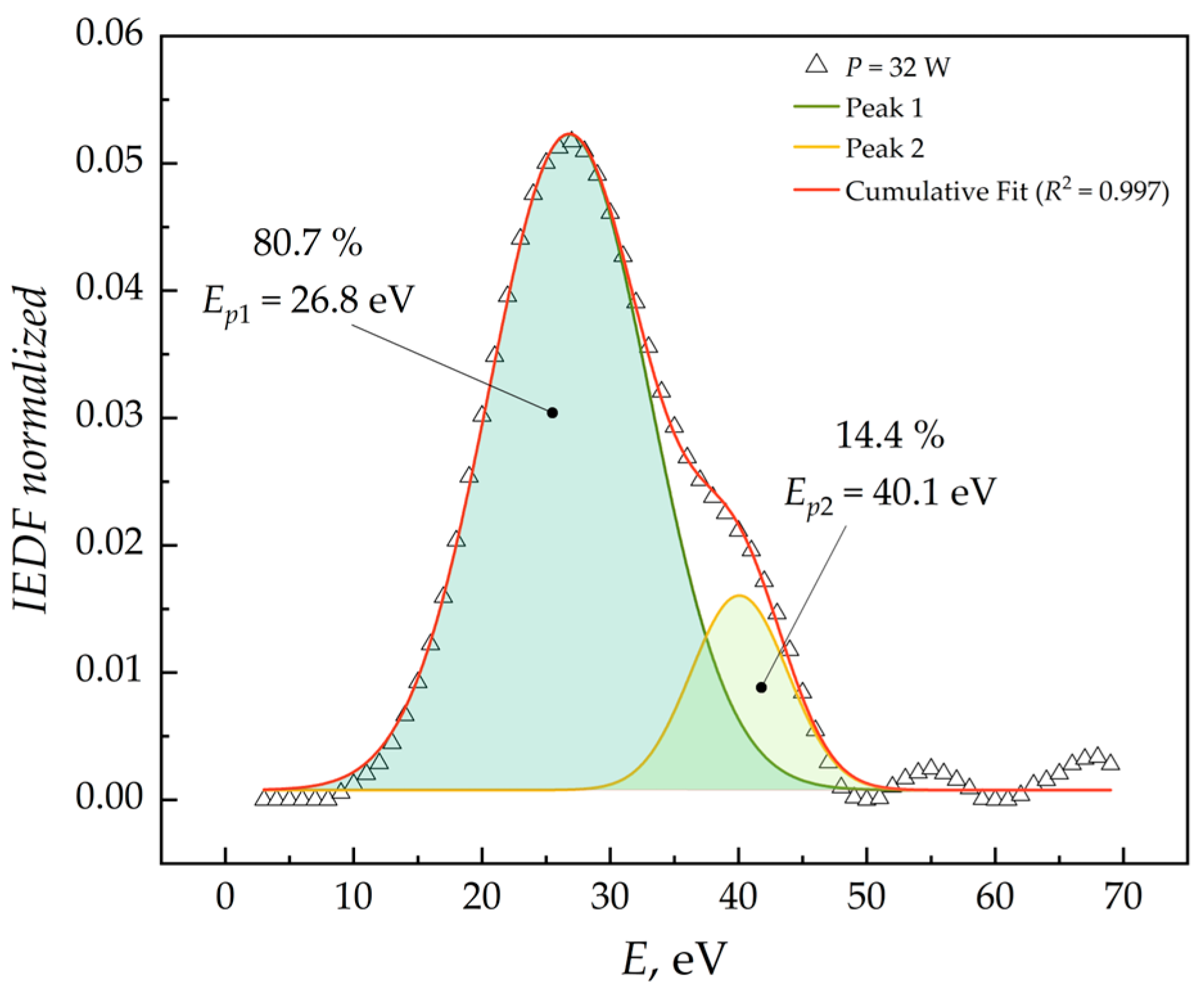
4.4. Asymmetry of Energy Distribution Functions
4.5. Theoretical Analysis of Exhaust Velocity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garzaniti, N.; Tekic, Z.; Kukolj, D.; Golkar, A. Review of technology trends in new space missions using a patent analytics approach. Prog. Aerosp. Sci. 2021, 125, 100727. [Google Scholar] [CrossRef]
- Choueiri, E.Y. A Critical History of Electric Propulsion: The First 50 Years (1906–1956). J. Prop. Power 2004, 20, 193–203. [Google Scholar] [CrossRef]
- Pashaev, A.D.; Shumeiko, A.I.; Telekh, V.D. Determination of the minimum size of a small spacecraft of the cubesat standard for the possibility of using modern propulsion systems. AIP Conf. Proc. 2023, 2549, 050002. [Google Scholar] [CrossRef]
- Rafalskyi, D.; Martínez, J.M.; Habl, L.; Rossi, E.Z.; Proynov, P.; Boré, A.; Baret, T.; Poyet, A.; Lafleur, T.; Dudin, S.; et al. In-orbit demonstration of an iodine electric propulsion system. Nature 2021, 599, 411–415. [Google Scholar] [CrossRef]
- Douglas Liddle, J.; Holt, A.P.; Jason, S.J.; O’Donnell, K.A.; Stevens, E.J. Space science with CubeSats and nanosatellites. Nat. Astron. 2020, 4, 1026–1030. [Google Scholar] [CrossRef]
- Massey, R.; Lucatello, S.; Benvenuti, P. The challenge of satellite megaconstellations. Nat. Astron. 2020, 4, 1022–1023. [Google Scholar] [CrossRef]
- Levchenko, I.; Keidar, M.; Cantrell, J.; Wu, Y.; Kuninaka, H.; Bazaka, K.; Xu, S. Explore space using swarms of tiny satellites. Nature 2018, 562, 185–187. [Google Scholar] [CrossRef]
- Shkolnik, E.L. On the verge of an astronomy CubeSat revolution. Nat. Astron. 2018, 2, 374–378. [Google Scholar] [CrossRef]
- Lev, D.; Myers, R.M.; Lemmer, K.M.; Kolbeck, J.; Koizumi, H.; Palzin, K. The technological and commercial expansion of electric propulsion. Acta Astronaut. 2019, 159, 213–227. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Mayorova, V.I. Development of a novel wave plasma propulsion module with six-directional thrust vectoring capability. Acta Astronaut. 2022, 191, 431–437. [Google Scholar] [CrossRef]
- Resta, E.; Marsilio, R.; Ferlauto, M. Thrust vectoring of a fixed axisymmetric supersonic nozzle using the shock-vector control method. Fluids 2022, 6, 441. [Google Scholar] [CrossRef]
- Afridi, S.; Khan, T.A.; Shah, S.I.A.; Shams, T.A.; Mohiuddin, K.; Kukulka, D.J. Techniques of fluidic thrust vectoring in jet engine nozzles: A review. Energies 2022, 16, 5721. [Google Scholar] [CrossRef]
- Lee, E. Kang, H.; Kwon, S. Demonstration of thrust vector control by hydrogen peroxide injection in hybrid rockets. J. Prop. Power 2019, 35, 109–114. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Li, M.; Wu, P.; Wang, Y.; Lu, S.; Zhang, G.; Ren, J.; Tang, H. Plume deflection using an asymmetrical magnetic nozzle for an applied-field magnetoplasmadynamic thruster—An experimental demonstration and numerical analysis. Acta Astronaut. 2023, 209, 82–94. [Google Scholar] [CrossRef]
- Takahashi, K.; Imai, R. Two-dimensional deflection of a plasma plume exhausted from a magnetically steered radiofrequency plasma thruster. Phys. Plasm. 2022, 29, 054501. [Google Scholar] [CrossRef]
- Caldarelli, A.; Filleul, F.; Charles, C.; Boswell, R.; Rattenbury, N.; Cater, J. Radial characterization of an ion beam in a deflected magnetic nozzle. J. Electr. Prop. 2022, 1, 10. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Jarrar, F.S.; Swei, S.S. Advanced wave plasma thruster with multiple thrust vectoring capability. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2190. [Google Scholar] [CrossRef]
- Merino, M.; Ahedo, E. Contactless steering of a plasma jet with a 3D magnetic nozzle. Plasm. Sources Sci. Technol. 2017, 26, 095001. [Google Scholar] [CrossRef]
- Stark, W.; Gondol, N.; Tajmar, M. Concept and design of a hall-effect thruster with integrated thrust vector control. J. Electr. Prop. 2022, 1, 21. [Google Scholar] [CrossRef]
- Ding, M.; Li, H.; Ding, Y.; Wei, L.; Mao, W.; Yu, D.; Cao, Y. Performance and plume characteristics of a Hall-effect thruster with asymmetrical gas supply. Vacuum 2021, 190, 110285. [Google Scholar] [CrossRef]
- Gozhaya, E.; Kudriavtzev, S.; Nikulin, N. SPT thrust vector control. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit AIAA-1998-3643 (AIAA, 1998), Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Garrigues, L.; Boniface, C.; Hagelaar, G.J.M.; Boeuf, J.P.; Duchemin, O. Performance modeling of a thrust vectoring device for hall effect thrusters. J. Prop. Power 2009, 25, 1003–1012. [Google Scholar] [CrossRef]
- Brophy, J.R.; Garner, C.E.; Mikes, S.C. Dawn ion propulsion system: Initial checkout after launch. J. Prop. Power 2009, 25, 1189–1202. [Google Scholar] [CrossRef]
- Savytskyy, I.; Jugroot, M. Design and Modeling of a Vectored Electrospray Thruster. In Proceedings of the ASCEND 2022 AIAA-2022-4271 (AIAA, 2022), Las Vegas, NV, USA, 24–26 October 2022. [Google Scholar] [CrossRef]
- Luke, J.R.; James, R.; Phipps, C.R.; McDuff, G.G. Laser plasma thruster. Appl. Phys. A 2003, 77, 343–348. [Google Scholar] [CrossRef]
- Fedorova, D.K.; Shumeiko, A.I.; Egoshin, D.A.; Pavlov, A.V. Granted Patent in Russia RU2823975C1 Coaxial Ablation Pulse Plasma Engine with Thrust Vectoring. RU2823975C1, 30 November 2023. [Google Scholar]
- Shumeiko, A.I.; Telekh, V.D. Direct thrust measurements of 2U-sized bi-directional wave plasma thruster. AIP Adv. 2023, 2171, 170019. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Ryzhkov, S.V. Starting Modes of Bi-Directional Plasma Thruster Utilizing Krypton. Symmetry 2023, 15, 1705. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Ryzhkov, S.V. Probe Diagnostics and Optical Emission Spectroscopy of Wave Plasma Source Exhaust. Symmetry 2022, 14, 1983. [Google Scholar] [CrossRef]
- Imai, R.; Takahashi, K. Demonstrating a magnetic steering of the thrust imparted by the magnetic nozzle radiofrequency plasma thruster. Appl. Phys. Lett. 2021, 118, 264102. [Google Scholar] [CrossRef]
- Zakrzwski, C.; Sanneman, P.; Hunt, T.; Blackman, K. Design of the EO-1 pulsed plasma thruster attitude control experiment. In Proceedings of the 37th Joint Propulsion Conference and Exhibit AIAA-2001-3637, (AIAA, 2001), Salt Lake City, UT, USA, 8–11 July 2001. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Ryzhkov, S.V. Thrust-vectoring schemes for electric propulsion systems: A review. Chin. J. Aeronaut. 2025, in press. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Pashaev, A.D.; Savelev, P.O.; Telekh, V.D. In-Orbit Demonstration of Bi-directional Electrodeless Plasma Thruster. In Proceedings of the IAF Space Propulsion Symposium, Milan, Italy, 14–18 October 2024; pp. 358–366. [Google Scholar] [CrossRef]
- Takahashi, K. Thirty percent conversion efficiency from radiofrequency power to thrust energy in a magnetic nozzle plasma thruster. Sci. Rep. 2022, 12, 18618. [Google Scholar] [CrossRef]
- Charles, C.; Boswell, R.W. Laboratory evidence of a supersonic ion beam generated by a current-free “helicon” double-layer. Phys. Plasmas 2004, 11, 1706–1714. [Google Scholar] [CrossRef]
- Lynden, W.; Andriulli, R.; Souhair, N.; Ponti, F.; Magarotto, M. Coupling of Fluid and Particle-in-Cell Simulations of Ambipolar Plasma Thrusters. Aerospace 2024, 11, 880. [Google Scholar] [CrossRef]
- Charles, C.; Boswell, R.W.; Laine, R.; MacLellan, P. An experimental investigation of alternative propellants for the helicon double layer thruster. App. Phys. 2008, 41, 175–213. [Google Scholar] [CrossRef]
- Zhurin, V.V. Industrial Ion Sources. Broadbeam Gridless Ion Source Technolog; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Shumeiko, A.I. Development and flight-testing of the bi-directional wave plasma accelerator. Ph.D. Thesis, Kazan National Research Technical University, Tatarstan, Russia, 2025. Available online: https://bmstu.ru/svedendoc/disser/index.php?q=dissertation&id=1006&ysclid=m9cs7cdr3q922287555 (accessed on 16 April 2025).
- Sumikawa, S.; Takahashi, K. Measurement of a force imparted to a magnetic nozzle by electron diamagnetism. Phys. Plasmas 2024, 31, 034501. [Google Scholar] [CrossRef]
- Takahashi, K. Helicon-type radiofrequency plasma thrusters and magnetic plasma nozzles. Rev. Mod. Plasm. Phys. 2019, 3, 3. [Google Scholar] [CrossRef]
- Fruchtman, A. Electric field in a double layer and the imparted momentum. Phys. Rev. Lett. 2006, 96, 065002. [Google Scholar] [CrossRef]
- Thakur, S.C.; Hansen, A.; Scime, E.E. Threshold for formation of a stable double layer in an expanding helicon plasma. Plasma Sources Sci. Technol. 2010, 19, 025008. [Google Scholar] [CrossRef]

| d, mm | 24 W | 32 W | 40 W |
|---|---|---|---|
| 10.5 | Mode 1 | Mode 2 | Mode 3 |
| 8.50 | Mode 4 | Mode 5 | Mode 6 |
| 6.50 | Mode 7 | Mode 7 | Mode 8 |
| Mass Flow m, mg/s | I, A (Magnetic Nozzle) | Gas |
|---|---|---|
| 3.70 | 5.00 | Krypton |
| R, kΩ | Aperture d, mm | K | A |
|---|---|---|---|
| 30.0 | 2.50 | 2.21 | 25.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andronov, A.A.; Shumeiko, A.I.; Pashaev, A.D.; Tsygankov, P.A.; Kovalev, S.V.; Telekh, V.D. Plume Characterization of Electrodeless Plasma Thruster with Configurable Exhaust. Symmetry 2025, 17, 661. https://doi.org/10.3390/sym17050661
Andronov AA, Shumeiko AI, Pashaev AD, Tsygankov PA, Kovalev SV, Telekh VD. Plume Characterization of Electrodeless Plasma Thruster with Configurable Exhaust. Symmetry. 2025; 17(5):661. https://doi.org/10.3390/sym17050661
Chicago/Turabian StyleAndronov, Artur A., Andrei I. Shumeiko, Aslan D. Pashaev, Petr A. Tsygankov, Sergei V. Kovalev, and Victor D. Telekh. 2025. "Plume Characterization of Electrodeless Plasma Thruster with Configurable Exhaust" Symmetry 17, no. 5: 661. https://doi.org/10.3390/sym17050661
APA StyleAndronov, A. A., Shumeiko, A. I., Pashaev, A. D., Tsygankov, P. A., Kovalev, S. V., & Telekh, V. D. (2025). Plume Characterization of Electrodeless Plasma Thruster with Configurable Exhaust. Symmetry, 17(5), 661. https://doi.org/10.3390/sym17050661








