Abstract
The Tree–Seed Algorithm (TSA) is a symmetry-driven metaheuristic algorithm that shows potential for complex optimization problems, but it suffers from local optimum entrapment and slow convergence. To address these limitations, we propose the ADTSA algorithm. First, ADTSA adopts a symmetry-driven dual-layer framework for seed generation, which promotes effective information exchange between subpopulations and accelerates convergence speed. In later iterations, ADTSA enhances the population’s exploitation ability through a population fusion mechanism, further improving the convergence speed. Moreover, we propose a historical optimal solution archiving and replacement mechanism, along with a t-distribution perturbation mechanism, to enhance the algorithm’s ability to escape local optima. ADTSA also strengthens population diversity and avoids local optima through convex lens symmetric reverse generation based on the optimal solution. With these mechanisms, ADTSA converges more effectively to the global optimum during the evolutionary process. Tests on the IEEE CEC 2014 benchmark functions showed that ADTSA outperformed several top-performing algorithms, such as LSHADE, JADE, LSHADE-RSP, and the latest TSA variants, and it also excelled in comparison with other optimization algorithms, including GWO, PSO, BOA, GA, and RSA, underscoring its robust performance across diverse testing scenarios. The proposed ADTSA’s applicability in solving complex constrained problems was also validated, with the results showing that ADTSA achieved the best solutions for these complex problems.
1. Introduction
In the modeling and management of complex systems, optimization problems undoubtedly play a central role [1]. From engineering design, resource allocation, and traffic scheduling to supply chain management and the performance regulation of anthill clay-bonded sand mold systems in foundry processes [2], optimization is virtually ubiquitous. Whether it is developing more energy-efficient mechanical equipment [3], or optimizing process parameters for CO2 laser cutting of 3D-printed PLA-CF composites [4], seeking optimal or near-optimal solutions has become a necessary step. However, traditional analytical methods such as linear programming [5] and gradient descent [6] often struggle to effectively solve complex nonlinear and large-scale systems due to high computational complexity. These methods rely on analytical solutions or iterative calculations, and as the scale expands, computational costs rise rapidly, limiting their applicability in practical scenarios.
Inspired by natural intelligence, population-based metaheuristic algorithms offer fresh perspectives for tackling intricate optimization challenges. These algorithms encompass a variety of approaches, such as evolutionary strategies, swarm intelligence methods, human-inspired algorithms, and physics-based techniques [7]. This method sacrifices the theoretical guarantee of global optimality in exchange for higher computational efficiency and scalability [8]. The No Free Lunch (NFL) theorem [9] makes it clear that no one-size-fits-all algorithm exists for tackling every optimization problem effectively. Because of this limitation, researchers are constantly pushing the boundaries by developing novel optimization techniques and hybrid approaches to improve algorithmic performance.
The Tree–Seed Algorithm (TSA), proposed by Kiran [10], is an effective metaheuristic based on the natural connection between trees and their seeds. Known for its simple design and strong robustness, TSA performs excellently in complex problem spaces and can find solutions that are either optimal or close to optimal [7]. It simulates the distribution and growth of trees and seeds to explore potential optimal solution regions. Many researchers have applied TSA to solve complex optimization problems. Table 1 lists typical examples of the application of TSA in complex optimization scenarios. However, TSA suffers from the issues of local optimum entrapment and slow convergence [7].

Table 1.
TSA variants and their applications.
Therefore, this research aims to address these limitations by introducing a symmetric dual-layer update framework, which divides the population into two subpopulations. These two subpopulations focus on exploitation and exploration, respectively, accelerating the convergence speed. Additionally, a population fusion mechanism is proposed to further enhance the population’s exploitation ability in the later stages, thereby speeding up the convergence in the final iterations. ADTSA archives historical optimal solutions and dynamically updates the archive via K-means clustering [15]. In later stages, the algorithm adaptively selects individuals from the archive to replace underperforming solutions, providing better guidance and enhancing the ability to escape local optima. Furthermore, ADTSA employs convex lens symmetric reverse learning, which enhances population diversity and strengthens the algorithm’s capability to avoid local optima. Through the aforementioned hybrid strategies and improvements to the initial design, this study further enhances TSA’s ability to avoid local optima and achieve rapid convergence.
1.1. Motivations
TSA is an evolutionary algorithm that simulates the natural process of trees propagating through the dispersal of seeds. It has shown effectiveness in solving optimization problems due to its simplicity, low number of parameters, and easy-to-understand concepts [10]. Despite its merits, it also faces some challenges. For example, the existing heuristic mechanism is unable to escape from local optimal solutions and cannot quickly converge to the global optimal solution. In addition, the algorithm does not make full use of the optimal solutions generated in each iteration, which may lead to the algorithm converging to suboptimal results, thus limiting its search ability. Furthermore, the Tree–Seed Algorithm has difficulties in maintaining population diversity, making it prone to falling into local optima. Population diversity is a crucial factor. When diversity is low, the algorithm’s exploration ability diminishes, raising the likelihood of settling into local optima. However, these limitations drove us to refine our approach. The study’s key motivations are as follows:
- TSA’s approach to seed generation blends the current tree, the top-performing tree, and the random tree. When a particular tree becomes stuck in a local optimum, the seeds it produces tend to follow suit, reinforcing that same suboptimal peak and influencing the overall search trajectory of the population. This approach ignores guidance towards potentially promising regions and lacks an effective mechanism for identifying and exploring potential areas in the search space, thus limiting its global exploration capability. Existing studies have demonstrated that adopting hybrid strategies can significantly enhance algorithm performance [16]. To tackle this challenge, this research introduces a symmetric dual-layer architecture designed for dynamic interaction. This innovative approach skillfully navigates the trade-off between exploration and exploitation, allowing the TSA algorithm to efficiently reach the global optimum with remarkable speed.
- The seed generation of TSA depends on the distance between the current tree, the optimal tree, and the random tree to update the seed position. However, over time, if the distance between these three trees gradually decreases, the search space of the population shrinks, and the trees converge, leading to a reduction in population diversity. This reduces the convergence speed and performance of the algorithm. Therefore, methods must be developed to help TSA preserve diversity, ensuring comprehensive exploration of the solution space and preventing convergence to local optima.
- TSA fails to fully mine key information from historical evolutionary stages during the iterative process, which easily causes the algorithm to lose its evolutionary direction. This results in reduced exploration of the solution space and increased likelihood of becoming trapped in local optima, particularly in high-dimensional, complex optimization problems. Therefore, it is urgent to construct a variant of TSA to provide better heuristic guidance for population iteration by effectively reusing historical evolutionary information.
- TSA typically uses uniform random initialization of the population, which can result in low initial diversity, thus impacting the search performance, especially in complex optimization tasks. To boost the quality of the initial population, this research adopts a Bernoulli chaotic mapping method [17] for initialization, paired with reverse symmetric learning strategies [18]. By greedily selecting the most promising starting points, the approach guarantees a diverse and high-quality initial pool, which in turn strengthens the algorithm’s resilience and flexibility across different optimization tasks.
1.2. Contributions
This study aims to improve TSA’s exploration ability to escape local optima and accelerate convergence to the global optimum. To achieve this, the following four innovative mechanisms are proposed and integrated into the TSA, aimed at enhancing the balance between exploration and exploitation. This study improves the algorithm’s efficiency and robustness by introducing new optimization strategies that prevent local optima and accelerate convergence to the global solution. Key contributions include
- Adaptive and Dynamic Updated Dual-Population Mechanism: This study proposes an symmetric dual-layer framework for dynamic interaction that divides the population into high- and low-fitness subpopulations, adopting different update strategies to balance global exploration and local exploitation. In the high-fitness subpopulation, the original algorithm’s formula is combined with the Golden Sine Algorithm (Gold-SA) update formula [19], incorporating an adaptive step size. This guides the seeds to perform fine-grained exploration around the initialization point, using a smaller step size in the early stages. As iterations progress, the step size gradually increases to enhance global exploration. In the later stages, the focus shifts to finer adjustments for local exploitation, and occasionally, larger steps are introduced in the final stage to alleviate the risk of falling into local optima, significantly improving the solution quality. The low-fitness subpopulation is updated based on both the current best solution and random solutions, avoiding excessive reliance on historical information and enhancing internal information exchange within the population. This ensures that the algorithm maintains a global exploration capability, while improving convergence accuracy at different stages. When population diversity decreases or fitness stagnates, the ratio of the two subpopulations is adaptively adjusted, helping to balance exploration and exploitation.
- Population Fusion and Reverse Recovery Perturbation Mechanism: To prevent a decline in population diversity and a deficiency in local exploitation capabilities in the later stages of the algorithm, this study designs and incorporates a population fusion and reverse recovery perturbation mechanism. When two subpopulations approach each other, seeds from low-fitness individuals are allocated to high-fitness individuals. Simultaneously, the updating of low-fitness parent individuals is halted and stored as memory solutions, helping to escape local optima. When the population diversity decreases, a convex lens reverse symmetric learning strategy based on the global best solution is implemented to replace the memory solution and restore the number of seeds [18]. Additionally, t-distribution perturbation is used to enhance diversity [20], enabling the algorithm to avoid local optima, maintain a strong global search capability, and accelerate convergence.
- Dynamic Clustering Archive Replacement Mechanism: To address the issue of premature convergence, this research proposes a dynamic clustering archive replacement mechanism. In each generation, the best solutions are stored in the archive. When the archive becomes full, the K-means clustering algorithm is employed to select the best individuals from each cluster [15], discarding the others, and subsequently update the archive, thus maintaining the diversity of solutions and preventing premature convergence. Whenever the population diversity declines or the fitness stagnates, new individuals are randomly introduced from the candidate pool of the archive to replace the worst individuals in the current population, ensuring continuous and effective search, sustaining the vitality of the algorithm, and achieving a balance between exploration and exploitation.
- Chaotic Mapping Initialization and Greedy Strategy: This study employs Bernoulli chaotic mapping initialization [17] to enhance the initial population diversity. Compared to traditional uniform random initialization, chaotic mapping provides a more dynamic exploration of the search space, which helps the algorithm escape local optima. Using reverse learning and a greedy selection method [18], the best initial solution is chosen, boosting population quality and increasing robustness and adaptability in complex optimization problems.
To assess its effectiveness, the proposed ADTSA algorithm was rigorously tested using the IEEE CEC 2014 benchmark suite, which includes four distinct function types—unimodal, multimodal, hybrid, and composite—along with a selection of challenging real-world engineering optimization problems. The source code of ADTSA is available at www.jianhuajiang.com.
This paper is structured as follows: Section 2 provides an overview of the traditional TSA and related algorithms. Section 3 presents the motivation behind our approach and introduces the proposed method. In Section 4, we analyze both qualitative and quantitative outcomes, benchmarking ADTSA against competing algorithms on benchmark functions with 30, 50, and 100 dimensions, as well as real-world optimization scenarios. Finally, Section 5 concludes the work and outlines future research directions.
2. Related Work
2.1. Foundation for TSA
The Tree-Seed Algorithm (TSA) draws inspiration from the symbiotic relationship between trees and their seeds in nature, embodying core concepts of swarm intelligence [10]. This metaheuristic approach was specifically developed to tackle continuous optimization challenges, proving particularly effective for population-based search methods and heuristic problem-solving. The algorithm operates on several fundamental principles:
- Initialization: Each tree’s starting position is randomly set within the boundaries of the search space, as shown in Equation (1).
- Core Mechanism: The seed-generation process is governed by two key equations that determine the position of new seeds based on the current location of each tree and population-level knowledge, as shown in Equations (2) and (3).In these expressions, denotes the j-th coordinate of the seed generated by the i-th tree. The term corresponds to the current position of the i-th tree in the j-th dimension, while represents the best-known coordinate in the j-th dimension within the population. refers to the same coordinate dimension of a randomly selected peer tree r. The factor is randomly drawn from the range and controls the extent of perturbation, promoting either exploration or exploitation depending on its value.
2.2. Overview of Golden-SA
The Golden Sine Algorithm (Golden-SA) [19] integrates the golden ratio with sine functions to enhance local search efficiency. It adaptively adjusts step sizes to better explore promising regions, as defined in Equations (4)–(6).
In the above formulations, denotes the j-th coordinate of agent i, and is the corresponding target position. and are random variables. The scalar is based on the golden ratio. Constants and are set to and .
2.3. Literature Review
The TSA is widely studied in swarm intelligence due to its simplicity, precision, and reliability, making it a leading algorithm in the field. TSA employs tree–seed propagation to efficiently explore global and local search areas, showing strong adaptability. In recent years, researchers have introduced numerous enhancements to TSA, focusing on refining seed generation strategies, improving tree migration mechanisms, and expanding the algorithm’s applicability across diverse domains, to further boost its performance.
- Tree Migration Mechanism: Researchers have proposed various tree migration variants to enhance TSA’s performance. The Migration Tree–Seed Algorithm (MTSA), inspired by the Grey Wolf Optimizer, combines hierarchical gravity learning with random-based migration strategies, significantly improving TSA’s search balance and stability [21]. SATSA enhances population dynamic renewal ability by setting a maximum retention count for trees to prevent the search stagnation caused by prolonged tree retention [22]. The Triple Tree–Seed Algorithm (TiTSA) employs a triple learning approach that combines migration strategies with sine-distributed randomness, boosting its global search ability [23]. These advancements can not only optimize TSA’s search efficiency in complex search spaces, but also provide new insights for addressing high-dimensional and dynamic optimization problems.
- On Seed Generation Mechanism: Seed generation is a critical factor in TSA’s optimization performance. To improve seed generation efficacy and optimization efficiency, researchers have developed various innovative methods. For instance, the Sine Cosine Tree–Seed Algorithm (TSASC) integrates the Sine Cosine Algorithm into TSA, enhancing exploration by refining the seed position update mechanism and adjusting weight factors [24]. MS-TSA enhances TSA’s ability to avoid population diversity loss through adaptive weighting, chaotic elite learning, and experience-based learning mechanisms [11]. The Sine Tree–Seed Algorithm (STSA) adapts seed numbers dynamically, producing more seeds initially for broader exploration and fewer later for intensification, thus enhancing the balance between global and local search [25]. ITSA variants incorporate an acceleration coefficient for quicker updates [26], whereas EST-TSA improves local search by utilizing the current best position [27]. The Feedback Tree–Seed Algorithm (fb-TSA) improves the integration between seeds and search tendencies through a feedback mechanism [28]. DTSA, inspired by Particle Swarm Optimization (PSO), incorporates a dynamic velocity vector adjustment to strengthen the balance between exploration and exploitation in the search space [7]. These innovations can enhance TSA’s flexibility under uncertain conditions, enabling it to adapt better to dynamic search space demands.
Given the above considerations, scholars have focused on optimizing tree migration and seed generation mechanisms to enhance the overall performance of TSA. However, existing mechanisms still have room for improvement in several areas, such as slow convergence to the global optimal solution, insufficient utilization of the optimal seeds in each generation, and limited seed diversity. This paper aims to address these shortcomings and further enhance TSA’s ability to avoid local optima and rapidly converge to the global optimal solution.
3. Methods
3.1. Adaptive and Dynamic Updated Dual-Subpopulation Mechanism
The original tree–seed algorithm lacks flexibility, as its update mechanism typically depends on the overall fitness of the population, without distinguishing individuals with different fitness levels. This results in a lack of diversity within the population, increasing the likelihood of becoming trapped in local optima.
In the improved approach, the original population is divided into two subpopulations based on fitness levels. The top 50% of individuals in terms of fitness are considered the subpopulation with higher fitness values. For this subpopulation, the golden sine update formula, combined with an adaptive step size, is applied to guide the optimization process:
In Figure 1, the step size strategy begins with fine-grained exploration around initialization points using smaller step sizes in the early stages, gradually increasing step sizes as iterations progress, to intensify global exploration. In the later stages, the focus shifts to local exploitation with finer adjustments, while the occasional introduction of large steps in the final phase alleviates the risk of becoming trapped in local optima. This adaptive approach balances exploration and exploitation, speeding up convergence and boosting the algorithm’s global optimization in complex search spaces.
where , , and are defined as in the original TSA [10]. and are sine perturbation parameters from Golden-SA [19]. is the search tendency coefficient, set to 0.1.
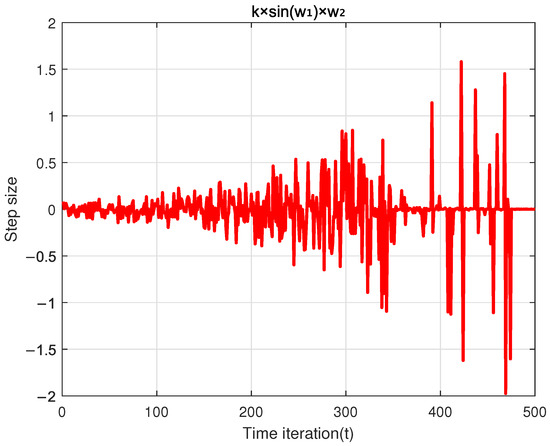
Figure 1.
The variation in step size with iterations.
For the subpopulation with lower fitness values, the following update formula is applied:
Using as the basis for updating the lower-fitness subpopulation offers a significant advantage over directly updating based on . Since represents the current optimal solution, it guides the lower-fitness individuals toward potential optima, speeding up convergence.
Updating based on instead of brings the additional benefit of random selection of individuals, avoiding dependence on each individual’s historical information. This encourages information exchange within the population and promotes diversity, allowing low-fitness individuals to learn from others’ exploration. This improves global exploration and prevents the population from settling in local optima.
In Figure 2, after each iteration, the fitness of the population is evaluated and sorted from the best to the worst. The individuals of the two populations are updated dynamically, which facilitates communication between the populations. When the diversity decreases or the convergence flattens out, a counter is triggered. If the counter reaches ten consecutively, the proportions of the two sub-populations are adjusted adaptively to maintain the balance between exploration and exploitation.
where psize represents the proportion of the elite subpopulation.
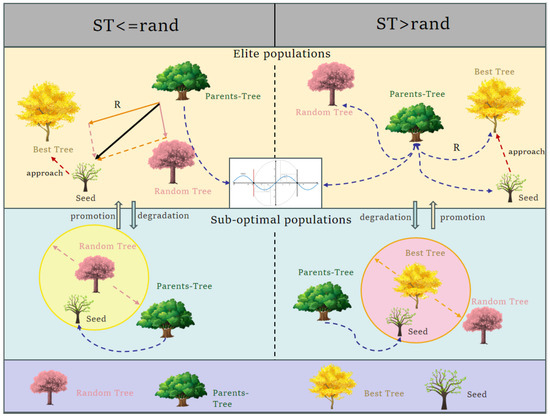
Figure 2.
The principle of dual-subpopulation dynamic update mechanism.
3.2. Population Fusion and Reverse Recovery Perturbation Mechanism
In the later stages, the diversity of the population tends to decrease, which slows down the convergence rate. To address this issue, a population fusion mechanism is employed. When the distance between two subpopulations becomes small, they are merged, allowing seeds from lower-fitness individuals to be fully allocated to higher-fitness individuals. To accelerate convergence, the top 20% of elite individuals are selected to absorb seeds. This method helps in the development of the best individuals and speeds up the convergence process. Lower-fitness parent individuals are paused from updating and preserved as memory. This memory mechanism sustains the algorithm’s global exploration, even after convergence to local optima. These memory individuals still hold the potential for further exploration, facilitating the algorithm’s escape from local optima.
When two subpopulations are close to each other, the number of seeds(ns) in the best subpopulation is updated by combining it with the number of seeds from the worse subpopulation, as shown in Figure 3.
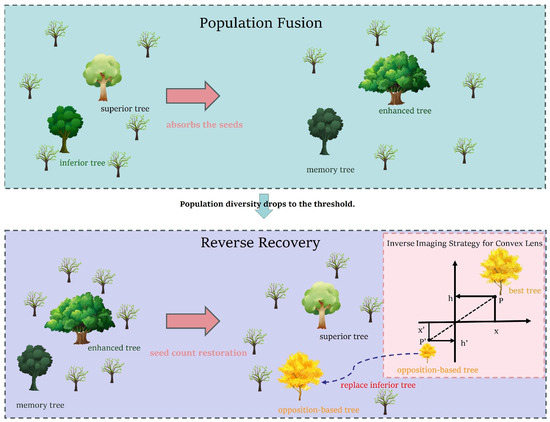
Figure 3.
Principle of population fusion and reverse recovery perturbation mechanism.
When the population size decreases sharply, this can lead to reduced diversity, resulting in entrapment within local optima. Therefore, when the population is reduced to a certain extent, a convex lens symmetric reverse learning strategy based on the global optimal solution can be used to replace the memory solutions, while restoring the number of seeds. Additionally, when the population stagnates in a certain region, t-distribution perturbations can be applied with a certain probability to increase diversity and help escape from local optima.
In Equations (15) and (16), the variable m is used to scale the search space based on the current iteration t, gradually reducing the step size as the algorithm progresses. If more than a third of the population remains stagnant, this triggers an update to the positions of the trees. Additionally, is a parameter that controls the t-distribution for sampling [20], which introduces randomness and allows for exploration. represents generating a random sample from a t-distribution with degrees of freedom , where changes with the iteration count, introducing randomness and allowing the algorithm to explore more broadly. represents the randomly drawn perturbation value from the t-distribution with degree of freedom , which controls the magnitude and frequency of the perturbations.
In this experiment, , meaning that there is a 10% probability of using the t-distribution for perturbations. The algorithm uses Opposition-Based Learning (OBL) to improve population diversity, exploring new search areas by evaluating solutions alongside their opposites. These elements work together to prevent the algorithm from becoming trapped in local optima as it progresses.
3.3. Dynamic Clustering Archive Replacement Mechanism
In this section, we present the dynamic clustering archive replacement strategy aimed at improving population diversity and algorithm efficiency. This mechanism involves storing the best solutions from each generation into an archive, creating a candidate pool. When the pool reaches its capacity, a K-means clustering algorithm is employed to retain the best individuals from each cluster, while discarding the rest. This process not only preserves the diversity of solutions, but also mitigates the problem of becoming trapped in local optima.
When the population diversity decreases or when the fitness values stagnate over several generations, individuals from the candidate pool are randomly introduced to replace the worst-performing individuals in the current population, as shown in Figure 4. This integration fosters a continuous influx of new solutions, thus rejuvenating the search process. Maintaining historical optimal solutions preserves essential exploration paths, effectively balancing exploration and exploitation.
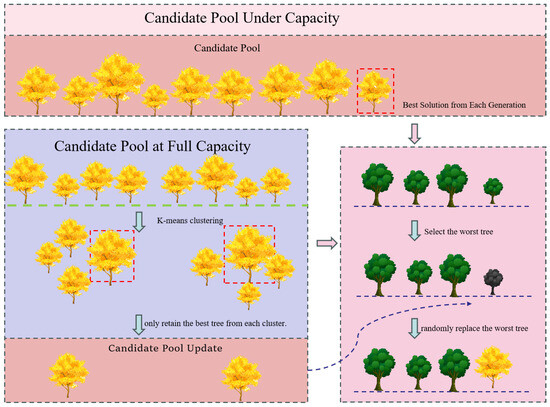
Figure 4.
Principle of dynamic clustering archive replacement mechanism.
This dynamic clustering archive replacement mechanism not only enhances the overall performance of the algorithm, but also ensures long-term stability by maintaining a diverse set of candidate solutions, ultimately leading to improved convergence toward the global optimum.
3.4. ADTSA: An Adaptive Dual-Subpopulation Tree–Seed Algorithm
The revised algorithm significantly improves the Tree–Seed Algorithm’s performance. Firstly, a reverse symmetric learning-based Bernoulli chaotic mapping initialization strategy is adopted to lay the foundation for symmetric search, where the algorithm generates an initial solution and its reverse symmetric counterpart simultaneously, followed by greedy selection of fitter solutions to expand the initial solution space coverage and avoid local clustering. Secondly, the Symmetric Dual-layer Framework for Dynamic Interaction is adopted to divide the population into high-fitness and low-fitness subpopulations, with each subpopulation employing distinct update strategies. The population ratio is adaptively adjusted according to the search status, thereby enhancing information exchange between subpopulations. This helps maintain a balance between global exploration and local exploitation, reducing the risk of premature convergence.
Secondly, a population fusion and reverse recovery mechanism allows for the merging of subpopulations in the later stages of iteration when they become close, reallocating seeds and preserving low-fitness individuals as memory. When the diversity decreases below a threshold, the reverse learning strategy based on the optimal solution is applied to re-explore the search space. This design expands the search scope from the “current optimal neighborhood” to its symmetric region, thus maintaining the global search capability and helping the algorithm escape local optima.
Lastly, a dynamic clustering archive replacement mechanism stores the best solutions from each generation. When the diversity declines, individuals from the archive are used to replace the worst-performing individuals, sustaining diversity and maintaining an effective balance between exploration and exploitation. These innovations collectively enhance the algorithm’s optimization performance, achieving faster convergence and higher solution quality compared to the original TSA.
3.5. Analyzing the Time Complexity of ADTSA
To assess the computational complexity of ADTSA, it is necessary to consider its main components and their execution frequencies. The algorithm comprises several stages, including initialization, iterative updates, fusion, reverse generation, and archive replacement, each with distinct time costs.
During initialization, a Bernoulli chaotic map is used to produce random values across all dimensions for each tree. A reverse learning strategy is also employed to select an initial solution. The time complexity of the reverse learning strategy for selecting the initial solution is . This phase involves nested loops—N trees and D dimensions—leading to a complexity of .
The update stage repeats for a maximum of MaxIters iterations. Key operations include adaptive step-size adjustment (), seed generation (), tree updates with best-solution tracking (), counter updates (), t-distribution perturbation (), and fitness ranking via sorting (). The total time complexity for this stage is approximately .
In later iterations, population fusion compares elite and suboptimal groups, costing . If the population falls below two-thirds of N, reverse generation is triggered at , giving this part an overall cost of .
The archive mechanism is updated when a better solution is found, with a per-iteration complexity of . Once the archive is full, k-means clustering divides the archive into groups, requiring . If the population diversity declines or the fitness stagnates, new individuals from the archive are reintroduced to replace weaker ones, which also takes . Thus, the archive mechanism contributes a total complexity of .
Overall, ADTSA’s time complexity is higher than that of TSA due to additional mechanisms such as population sorting and archive clustering, which introduce extra overhead. Specifically, the population sorting operation has a time complexity of O(N log N), and the K-means computation in archive clustering involves a quadratic term N, making the population size N have a more significant impact on the complexity compared to the dimension. However, ADTSA’s archive clustering is only triggered when the threshold condition is met, reducing redundant computations across multiple iterations. The full algorithm process is illustrated in Figure 5 and detailed in the pseudo-code of Algorithm 1.
| Algorithm 1 Pseudo-code of the ADTSA algorithm |
|
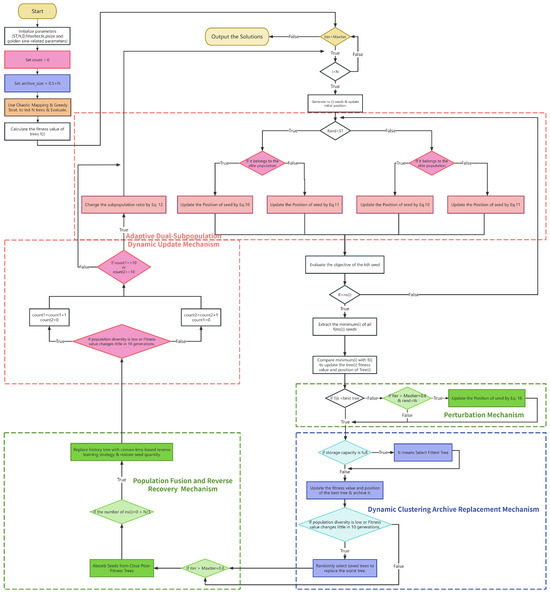
Figure 5.
The flowchart for the ADTSA.
4. Results and Discussion
This section presents a series of experiments aimed at assessing the efficacy of the proposed ADTSA. To highlight its strengths, we rely on five in-depth experimental results. Section 4.1 details the parameter settings used throughout our tests, providing a clear picture of the experimental framework. Moving on, Section 4.2 offers a qualitative review of ADTSA’s behavior, while Section 4.3 dives into the quantitative analysis. To further demonstrate its practical value, Section 4.4 applies ADTSA to tackle three real-world challenges, expanding the scope of the validation. Finally, in Section 4.5, we tested ADTSA on the Split Delivery Vehicle Routing Problem (SDVRP), emphasizing its robust performance across three benchmark scenarios that grew in complexity.
4.1. Experiment Setting
ADTSA underwent an extensive performance evaluation by competing against several advanced algorithms and various modifications. Key competitors included TSA [10], STSA [25], MTSA [21], EST-TSA [27], fb-TSA [28], PSO [1], GWO [29], LSHADE [30], JADE [31], lshade-rsp [32], BOA [33], RSA [34], and GA [35]. To ensure a level playing field across the experiments, this research meticulously logged the datasets and parameters leveraged by the comparative algorithms, as detailed in the foundational study—summarized in Table 2. The experimental data hailed from the IEEE CEC 2014 benchmark. According to their statistical categorization, F1-F3 are single peak functions, F4-F16 exhibit straightforward multiple peaks, F17-F23 represent a blend of both, and F24-F30 consist of composite peaks.

Table 2.
Initial settings of the comparison algorithms.
4.2. Qualitative Analysis
To assess the algorithm, we examined its convergence, diversity, and balance between exploration and exploitation. We used F2 for exploitation and F14 for exploration, as depicted in Figure 6.

Figure 6.
Visualizing parameter spaces.
4.2.1. Convergence Behavior Analysis
The study presents four convergence plots (Figure 7 and Figure 8) demonstrating ADTSA’s performance across various functions. These graphs are analyzed as follows:
- The first graph illustrates ADTSA’s optimization path, with black dots showing explored areas and the red dot indicating the best solution. The concentration of black points near the red dot illustrates the algorithm’s convergence through iteration.
- The second graph shows ADTSA’s rapid convergence to the optimal solution, with the steep decline indicating its efficiency in quickly identifying optimal results.
- The third graph illustrates the algorithm’s avoidance of early convergence to local optima, indicating ADTSA’s ability to effectively navigate past local traps and explore comprehensively.
- The fourth graph shows the average convergence across iterations, with the steep decline indicating ADTSA’s robust convergence performance and its strong optimization effectiveness.
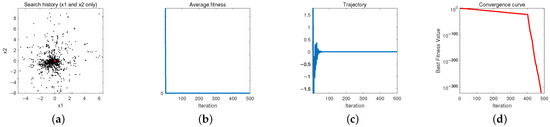
Figure 7.
Qualitative assessment of ADTSA in F2: (a) search process, (b) mean fitness over iterations, (c) trajectory path, (d) convergence trend.
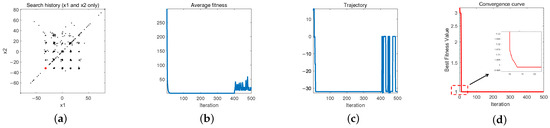
Figure 8.
Qualitativeassessment of ADTSA in F14: (a) search process, (b) mean fitness over iterations, (c) trajectory path, (d) convergence trend.
4.2.2. Evaluation of Population Diversity
Swarm intelligence algorithms rely on population diversity for effective global search and convergence. Higher diversity prevents individuals from prematurely converging to local optima and deepens exploration within the search space, providing a foundation for solving complex problems. Thus, maintaining an appropriate population diversity is crucial for enhancing algorithm robustness and global optimization capability. The diversity level of the population is evaluated via centroid-based dispersion, and the definition of the diversity index is as described by Jiang et al. [7].
Figure 9 and Figure 10 show that, for function , both ADTSA and TSA quickly reduced the population diversity, indicating strong local search. ADTSA converged faster than TSA and sustained higher diversity, enhancing the global optimization efficiency. ADTSA optimized ’s multimodal function with dual-population strategies and inter-population information, enhancing the diversity throughout the iterations. Although the population diversity rapidly decreased in later stages due to the fusion mechanism aimed at enhancing exploitation, ADTSA leveraged reverse learning perturbations and a dynamic clustering archiving strategy to further strengthen diversity, enabling it to escape local optima effectively.
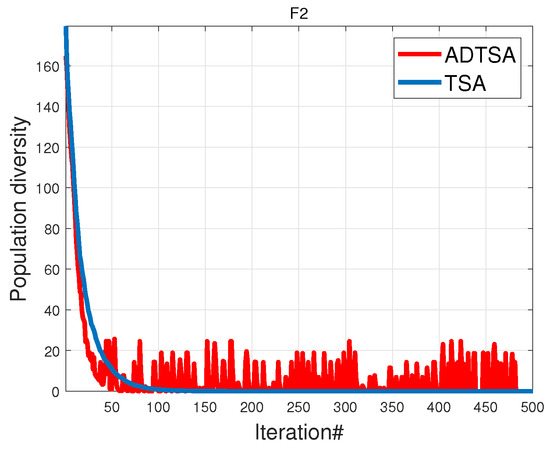
Figure 9.
Population diversity for F2.
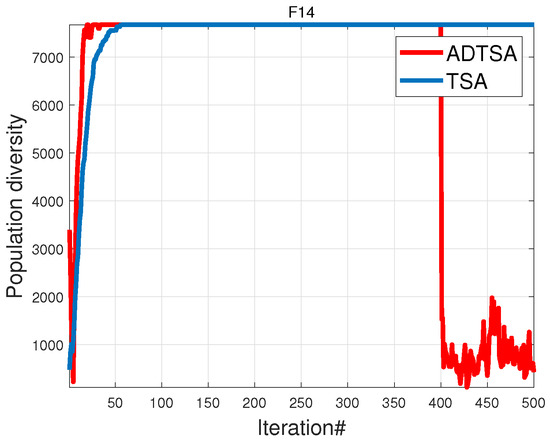
Figure 10.
Population diversity for F14.
4.2.3. Exploration and Exploitation Evaluation
To evaluate the balance between exploration and exploitation in swarm-based algorithms, this study analyzes the population’s spatial diversity across iterations; as seeen in Jiang et al. [7], the diversity value at iteration t, denoted as , is calculated as the mean distance between individuals in the population, which captures the average inter-individual distance within the swarm and is formulated in Equation (19), and the exploration–exploitation relationship is quantified by comparing the current diversity to the maximum observed value, as shown in Equations (20) and (21).
In Figure 11 and Figure 12, a higher exploration value indicates a stronger global search capability, while a higher exploitation value reflects a stronger focus on local exploitation in the t-th iteration. ADTSA outperformed the original algorithm, showing faster convergence to the global optimum for the unimodal function and a better balance between exploration and exploitation for the multimodal function . By the 11th iteration, ADTSA achieved equilibrium through population fusion and reverse learning, sustaining robust global and local search capabilities to avoid local optima. In contrast, TSA briefly balanced at the 19th iteration but struggled with adaptability, leading to exploration–exploitation imbalances and poorer performance for complex multimodal functions.
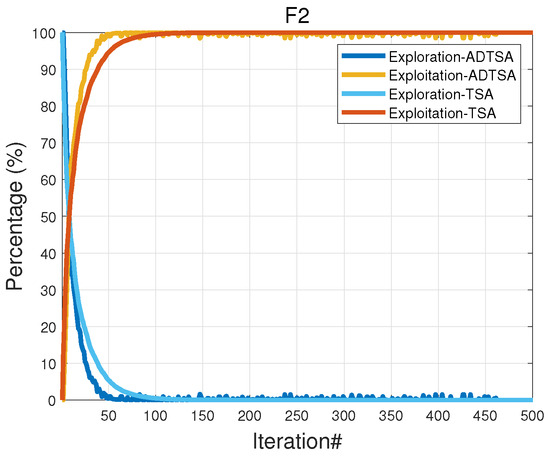
Figure 11.
Analysis for F2.
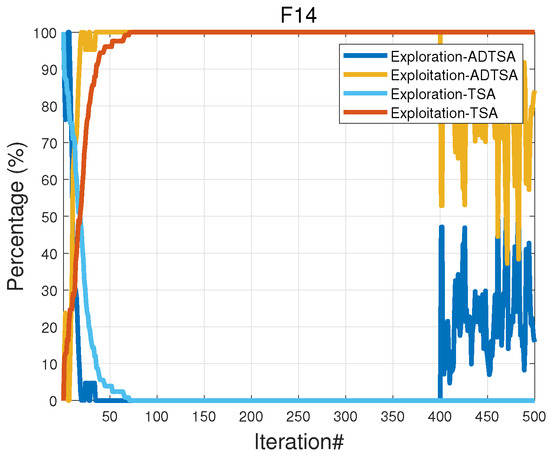
Figure 12.
Analysis for F14.
4.3. Quantitative Analysis
This section demonstrates the excellent performance of ADTSA through three meticulously designed experiments. In Section 4.3.1, an ablation experiment of ADTSA was carried out, with the aim of verifying the effectiveness of the innovative points of the algorithm and exploring the synergy among different innovative points. Section 4.3.2 expands the scope of the comparison by incorporating other meta-heuristic algorithms and their variants, emphasizing the unique ability of ADTSA in handling complex problems. Section 4.3.3 presents box plots based on the results of 30 experimental runs, providing insights into the stability of ADTSA across multiple iterations.
4.3.1. Contrastive Experiment 1: Ablation Experiments of ADTSA
To verify the effectiveness of the four key innovations of ADTSA, this study conducted an ablation experiment in the initial comparative analysis, where each innovation was sequentially added to the original TSA, to form several improved versions. Specifically, ADTSA1 introduced reverse symmetric learning-based Bernoulli chaotic mapping initialization strategy to enhance initial population diversity; ADTSA2 employed an adaptive dual-subgroup dynamic update mechanism to balance global exploration and local exploitation; ADTSA3 integrated population fusion and reverse recovery perturbation mechanisms to prevent the algorithm from falling into local optima; and ADTSA4 incorporated a dynamic clustering archive replacement mechanism to maintain solution diversity and search stability. Comparing each variant to TSA and the full ADTSA revealed each innovation’s impact and their combined effectiveness in enhancing optimization.
Figure 13, Figure 14 and Figure 15 illustrate the convergence curves of each algorithm, providing a visual comparison of their convergence characteristics. In addition, Table 3, Table 4 and Table 5 present a comparative analysis of ADTSA across 30, 50, and 100 dimensions, as well as comparisons with other improved versions. The tables present the average optimal values from 30 runs of 500 iterations each, where the color markers indicate the best value of the corresponding function among the algorithms, highlighting each algorithm’s convergence and enabling comparison of their performance.
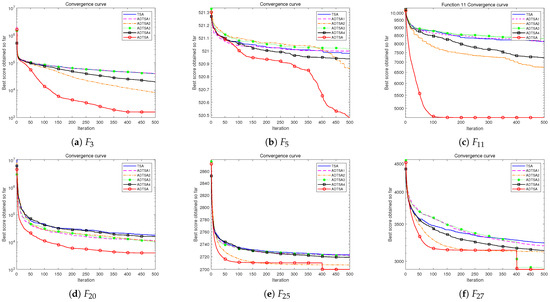
Figure 13.
Convergence curve of ADTSA, TSA, ADTSA1, and other variants for 30D.
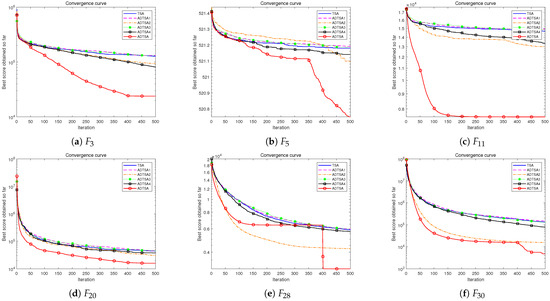
Figure 14.
Convergence curve of ADTSA, TSA, ADTSA1, and other variants for 50D.
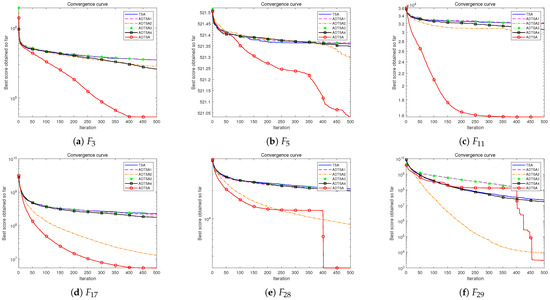
Figure 15.
Convergence curve of ADTSA, TSA, ADTSA1, and other variants for 100D.

Table 3.
Average values for the ADTSA, TSA, ADTSA1, and other variants for 30D.

Table 4.
Average values for the ADTSA, TSA, ADTSA1, and other variants for 50D.

Table 5.
Average values for the ADTSA, TSA, ADTSA1, and other variants for 100D.
The experimental results show that integrating the four novel mechanisms significantly improved ADTSA’s performance in complex optimization. The reverse symmetric Bernoulli chaotic map boosts initial diversity, while the adaptive dual-subgroup balances exploration and exploitation. Population fusion and reverse recovery further prevent local optima by maintaining diversity, and the dynamic clustering archive preserves high-quality solutions. These improvements boost ADTSA’s overall performance and adaptability.
Additionally, we calculated the time consumption of each ADTSA branch under 100 dimensions and 30 individuals: ADTSA1 and ADTSA4 showed nearly the same time as TSA, as ADTSA1’s initialization strategy did not significantly add to the computations, and the archiving mechanism in ADTSA4 was rarely triggered in a single branch, with its overhead overshadowed by core processes. ADTSA2, due to population sorting and adaptive parameter calculations, and ADTSA3, due to additional computations like population diversity evaluation, took 1.02 times the time of TSA. The fully integrated ADTSA, with the superposition of multiple mechanisms, required frequent balancing of exploitation and exploration in the later population stage, leading to an increased trigger probability, thus taking 1.2 times the time of TSA.
4.3.2. Contrastive Experiment 2: ADTSA Versus TSA Variants and Established and Novel Heuristic Optimization Algorithms
The experiment compared the basic TSA [10] with its recent variants and traditional heuristic algorithms such as GA [35], PSO [1], RSA [34], BOA [33], LSHADE [30], lshade-rsp [32], and JADE [31] to assess their performance.
The experimental setup followed Section 4.3.1, with 30 runs of 500 iterations each across 30, 50, and 100 dimensions. Table 6, Table 7 and Table 8 report mean optimal values and average rankings, demonstrating ADTSA’s robust performance for multimodal problems. Figure 16, Figure 17 and Figure 18 display the convergence trends of all algorithms. From the convergence trends, it can be seen that the proposed innovative mechanisms significantly enhanced TSA’s ability to escape local optima and achieve rapid convergence. Particularly for high-dimensional Composition Functions, ADTSA’s convergence curve maintains a downward trend in the later stage, effectively avoiding the issue where TSA often becomes trapped in local optima.

Table 6.
Average values for ADTSA and other heuristics for 30D.

Table 7.
Average values for ADTSA and other heuristics for 50D.

Table 8.
Average values for ADTSA and other heuristics for 100D.
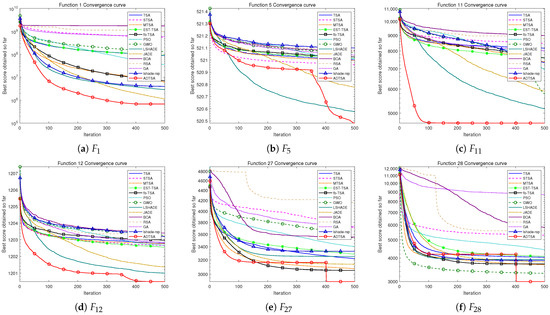
Figure 16.
Convergence curve of the ADTSA and other heuristic for 30D.
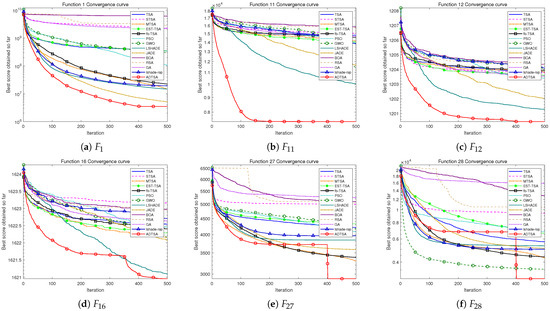
Figure 17.
Convergence curve of the ADTSA and other heuristics for 50D.
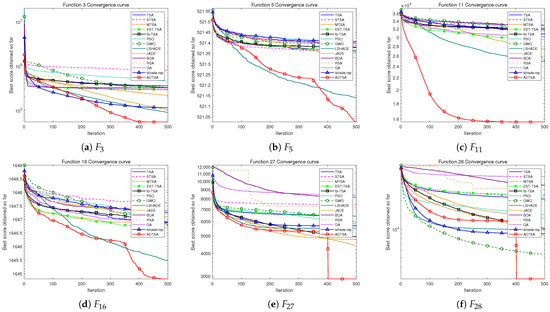
Figure 18.
Convergence curve of the ADTSA and other heuristics for 100D.
4.3.3. Contrastive Experiment 3: ADTSA Stability Assessment
The box plots (Figure 19, Figure 20 and Figure 21) display ADTSA’s stability compared to the other algorithms. The x-axis identifies each method, while the y-axis represents objective function evaluations (30 runs each). Black lines indicate ranges, boxes show quartiles, red lines mark medians, and plus signs denote outliers, enabling stability comparisons across multiple executions.

Figure 19.
Box plots of all tested algorithms for 30D.
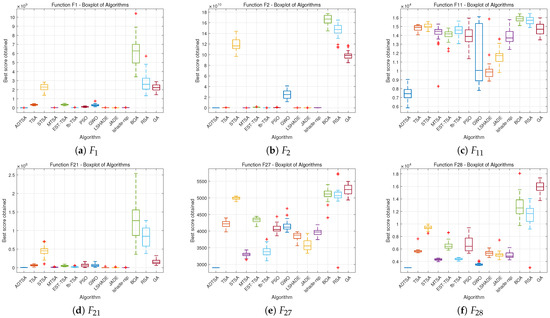
Figure 20.
Box plots of all tested algorithms for 50D.
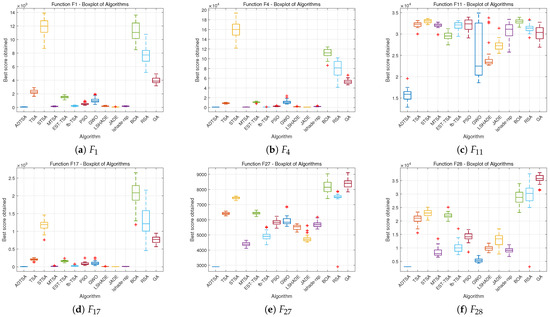
Figure 21.
Box plots of all tested algorithms for 100D.
An in-depth analysis of these box plots reveals that ADTSA demonstrated excellent performance stability across the various experimental settings, showcasing notable robustness. The box plot for ADTSA displays consistent results, with few outliers, confirming its ability to achieve reliable outcomes across the different testing scenarios. However, in the simpler unimodal function tests, where the problem complexity was lower, all algorithms could effortlessly reach the optimal solution, making ADTSA’s performance enhancement less apparent. The relative superiority of each algorithm inherently depended on the specific complexity and characteristics embedded in each problem. Therefore, ADTSA inevitably exhibits varying levels of effectiveness according to the complexity and dimensionality of the tasks it encounters.
4.4. Applied Engineering Challenges in Mathematical Modeling
This section evaluates ADTSA’s performance on complex constrained optimization problems using three benchmarks: tension spring, three-bar truss, and welded beam designs [36,37,38]. Table 9, Table 10 and Table 11 report the statistical metrics (Best, Average, Standard Deviation, Worst, and optimal x-value) from 30 runs, enabling rigorous assessment of ADTSA’s solving capability. Bold values indicate the optimal solution.

Table 9.
Tension/compression spring design problem.

Table 10.
Design problem of three-bar truss.

Table 11.
Design problem of welded beam.
4.4.1. Example 1: The Tension/Compression Spring Design
The tension/compression spring design problem is a constrained optimization task focused on minimizing spring volume, while meeting load requirements [36]. It involves three variables: active coil count, coil diameter, and wire diameter. Optimization must satisfy physical and geometric constraints to preserve load capacity and elasticity, while reducing material use and space. Its moderate complexity and engineering applicability make it a common benchmark for testing optimization algorithms. Table 9 shows the tension/compression spring design results, highlighting ADTSA’s superior performance over the other approaches.
4.4.2. Example 2: Design Problem of Three-Bar Truss
In Test 2, the algorithm was validated on a three-bar truss optimization problem [37]. The goal was to minimize the truss volume by optimizing cross-sectional areas and , subject to three nonlinear inequality constraints. The nonlinear objective function aimed to find optimal design variables. This test demonstrated the algorithm’s ability to handle complex design spaces, while balancing material use and stability, providing insights into multi-dimensional optimization challenges. Table 10 shows the outcomes for the design problem of three-bar truss, highlighting ADTSA’s enhanced effectiveness.
4.4.3. Example 3: Design Problem of Welded Beam
The Welded Beam Design (WBD) challenge represents a well-known optimization problem in engineering [38], where the primary goal is to cut production expenses by fine-tuning four key parameters: the beam’s length (l), height (t), width (b), and weld size (h). The goal is to achieve cost minimization, while satisfying constraints on shear stress (), bending stress (), buckling load (), and end deflection (). As a key practical challenge and a paradigmatic nonlinear programming problem, WBD involves a cost function tightly coupled with multiple interdependent constraints, making it a benchmark for evaluating optimization algorithms. Table 11 displays the outcomes of the design problem of the welded beam, highlighting ADTSA’s exceptional performance.
4.5. Split Delivery Vehicle Routing Problem
This section assesses the ADTSA algorithm’s performance in addressing the SDVRP [39]. We assessed its performance using a set of benchmark SDVRP instances that involved complex objective functions and various constraints. These benchmark problems covered the gil262, Loggi-n401-k23, and Loggi-n1001-k31 datasets. Table 12, Table 13 and Table 14 report statistical metrics (Best: optimal solution from 30 runs; Average: mean result; Standard: deviation (variability); Worst: poorest outcome) over 1000 iterations per run, evaluating ADTSA’s SDVRP-solving capability and validating its effectiveness.

Table 12.
Results for gil262 for the SDVRP.

Table 13.
Results for Loggi-n401-k23 for the SDVRP.

Table 14.
Results for Loggi-n1001-k31 for the SDVRP.
The results of ADTSA solving the SDVRP on benchmarks (gil262, Loggi-n401-k23, Loggi-n1001-k31) are shown in Table 12, Table 13 and Table 14, with convergence curves in Figure 22. Bold values indicate the optimal solution. The research revealed that ADTSA consistently delivered better results when tackling SDVRP scenarios, effectively meeting the key goal of reducing the overall travel distance. Compared to the alternative algorithms, it stood out by producing higher-quality solutions and reaching optimal outcomes more efficiently. Especially in the late iteration stage, its optimization capability was further enhanced by the population fusion and reverse generation mechanisms. Compared to the other algorithms, ADTSA consistently achieved lower costs and faster convergence, thus validating its effectiveness and robustness in real-world SDVRP problems.
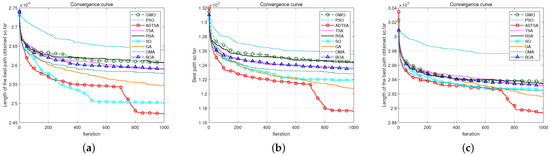
Figure 22.
Convergence curves of all experimental algorithms on three datasets. (a) Convergence curve for gil262. (b) Convergence curve for Loggi-n401-k23. (c) Convergence curve for Loggi-n1001-k31.
5. Summary and Prospective Work
This study introduced four optimization strategies to enhance the algorithm’s efficiency in escaping local optima and accelerating convergence to the global optimum. The experimental results showed that after implementing these strategies, the optimization performance of ADTSA significantly improved in solving complex optimization problems. Therefore, several key conclusions can be drawn from this study:
- Performance enhancement: ADTSA was rigorously benchmarked against leading algorithms such as LSHADE, JADE, lshade-rsp, TSA variants, and other methods. The results showed ADTSA reliably outperformed the other methods across various dimensions and function types in IEEE CEC 2014 tests.
- Convergence Speed and Local Optima Avoidance: Figure 18 reveals that ADTSA converged faster and escaped local optima more effectively, particularly for high-dimensional hybrid and composite functions. This advantage arises from the four novel mechanisms that optimize exploration–exploitation balance, enhancing solution speed and precision.
- Engineering Applications: When tackling practical engineering challenges like tension spring design, three-bar truss optimization, welded beam layout refinement, or the Split Delivery Vehicle Routing Problem (SDVRP) in offline optimization scenarios, ADTSA consistently delivered optimal results, as shown in Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14. This underscores its effectiveness and reliability in solving complex, constrained offline optimization problems.
Overall, the implementation of these enhanced strategies dramatically boosted ADTSA’s performance, enabling it to escape local optima traps and rapidly reach globally optimal solutions for complex challenges. However, the algorithm still has certain limitations, particularly when dealing with low-dimensional problems. Future studies should focus on refining the application of the adaptive mechanism and multi-level elitism strategy, strive to reduce algorithm complexity and develop a lightweight version, and explore additional mechanisms to overcome these limitations, thereby further improving the algorithm’s efficiency and continuously enhancing its applicability across diverse dimensions.
Author Contributions
Conceptualization, H.L. and J.J.; Data curation, H.L.; Formal analysis, H.L. and J.J.; Funding acquisition, J.J.; Investigation, H.L. and Z.M.; Methodology, H.L., J.J., J.L., C.L. and Z.Y.; Project administration, J.J. and Z.M.; Resources, J.J.; Software, H.L.; Supervision, J.J. and Z.M.; Validation, H.L. and L.L.; Visualization, H.L.; Writing—original draft, H.L.; Writing—review and editing, J.J. and Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the financial support from the Foundation of the Jilin Provincial Department of Science and Technology (No. YDZJ202201ZYTS565).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Radwan, M.; Elsayed, S.; Sarker, R.; Essam, D.; Coello, C.C. Neuro-PSO algorithm for large-scale dynamic optimization. Swarm Evol. Comput. 2025, 94, 101865. [Google Scholar] [CrossRef]
- Prasad Chandran, N.; Manjunath Patel, G.C.; Chate, G.R.; Der, O.; Selvan, C.P. Multi-Input Multi-Output Modeling of Anthill Clay-Bonded Sand Mold System Using Artificial Neural Networks: Forward and Reverse Predictions. Eng. Rep. 2025, 7, e70224. [Google Scholar] [CrossRef]
- Huang, X.; Yan, J.; Zhou, X.; Yang, Z.; Huang, X.F. Energy-efficient optimization method for air conditioning terminal systems in IDC based on genetic algorithm. Energy 2025, 333, 137502. [Google Scholar] [CrossRef]
- Basar, G.; Der, O.; Guvenc, M.A. AI-powered hybrid metaheuristic optimization for predicting surface roughness and kerf width in CO2 laser cutting of 3D-printed PLA-CF composites. J. Thermoplast. Compos. Mater. 2025, 08927057251344183. [Google Scholar] [CrossRef]
- Sarkar, B.; Kugele, A.S.H.; Sarkar, M. Two non-linear programming models for the multi-stage multi-cycle smart production system with autonomation and remanufacturing in same and different cycles to reduce wastes. J. Ind. Inf. Integr. 2025, 44, 100749. [Google Scholar] [CrossRef]
- Zhou, X.; You, Z.; Sun, W.; Zhao, D.; Yan, S. Fractional-order stochastic gradient descent method with momentum and energy for deep neural networks. Neural Netw. 2025, 181, 106810. [Google Scholar] [CrossRef]
- Jiang, J.; Huang, J.; Wu, J.; Luo, J.; Yang, X.; Li, W. DTSA: Dynamic Tree-Seed Algorithm with Velocity-Driven Seed Generation and Count-Based Adaptive Strategies. Symmetry 2024, 16, 795. [Google Scholar] [CrossRef]
- Li, X.; He, D.; Zhang, X. Efficient Algorithms for Approximate k-Radius Coverage Query on Large-Scale Road Networks. IEEE Trans. Intell. Transp. Syst. 2024, 26, 1631–1644. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ.; Kiran, M.S. A tree seed algorithm with multi-strategy for parameter estimation of solar photovoltaic models. Appl. Soft Comput. 2024, 167, 112220. [Google Scholar] [CrossRef]
- Zhou, Q.; Dai, R.; Zhou, G.; Ma, S.; Luo, S. An Enhanced Tree-Seed Algorithm for Function Optimization and Production Optimization. Biomimetics 2024, 9, 334. [Google Scholar] [CrossRef]
- Qiao, Z.; Wu, L.; Heidari, A.A.; Zhao, X.; Chen, H. An enhanced tree-seed algorithm for global optimization and neural architecture search optimization in medical image segmentation. Biomed. Signal Process. Control 2025, 104, 107457. [Google Scholar] [CrossRef]
- Aslan, M.F.; Sabanci, K.; Ropelewska, E. A new approach to COVID-19 detection: An ANN proposal optimized through tree-seed algorithm. Symmetry 2022, 14, 1310. [Google Scholar] [CrossRef]
- Lu, J.; Luo, T.; Li, K. A forward k-means algorithm for regression clustering. Inf. Sci. 2025, 711, 122105. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, J.; Jia, C.; Liu, Y.; Fu, M. A Hybrid Black-Winged Kite Algorithm with PSO and Differential Mutation for Superior Global Optimization and Engineering Applications. Biomimetics 2025, 10, 236. [Google Scholar] [CrossRef]
- García-Grimaldo, C.; Campos-Cantón, E. Exploring a family of Bernoulli-like shift chaotic maps and its amplitude control. Chaos Soliton. Fract. 2023, 175, 113951. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Wang, Y.; Sun, J. Military UCAV 3D path planning based on multi-strategy developed human evolutionary optimization algorithm. IEEE Internet Things J. 2025, 12, 16735–16747. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, M.; Yang, K.; Shang, C.; Luo, Y. Research and implementation of fault data recovery method for dry-type transformer temperature control sensor based on ISSA-LSTM algorithm. Measurement 2024, 228, 114333. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Qian, L.; Wang, H. Enhance tree-seed algorithm using hierarchy mechanism for constrained optimization problems. Expert Syst. Appl. 2022, 209, 118311. [Google Scholar] [CrossRef]
- Liu, J.; Hou, Y.; Li, Y.; Zhou, H. Advanced strategies on update mechanism of tree-seed algorithm for function optimization and engineering design problems. Expert Syst. Appl. 2024, 236, 121312. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, Y.; Zhao, Z. TriTSA: Triple Tree-Seed Algorithm for dimensional continuous optimization and constrained engineering problems. Eng. Appl. Artif. Intell. 2021, 104, 104303. [Google Scholar] [CrossRef]
- Jiang, J.; Han, R.; Meng, X.; Li, K. TSASC: Tree–seed algorithm with sine–cosine enhancement for continuous optimization problems. Soft Comput. 2020, 24, 18627–18646. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, M.; Meng, X.; Li, K. STSA: A sine Tree-Seed Algorithm for complex continuous optimization problems. Phys. A 2020, 537, 122802. [Google Scholar] [CrossRef]
- Linden, A. ITSA: Stata Module to Perform Interrupted Time Series Analysis for Single and Multiple Groups. 2021. Available online: https://ideas.repec.org/c/boc/bocode/s457793.html (accessed on 1 June 2024).
- Jiang, J.; Jiang, S.; Meng, X.; Qiu, C. EST-TSA: An effective search tendency based to tree seed algorithm. Physica A 2019, 534, 122323. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Chen, Y.; Qiu, C.; Liu, Y.; Li, K. Enhancing tree-seed algorithm via feed-back mechanism for optimizing continuous problems. Appl. Soft Comput. 2020, 92, 106314. [Google Scholar] [CrossRef]
- Wang, Z.; Shu, L.; Yang, S.; Zeng, Z.; He, D.; Chan, S. Multi-population dynamic grey wolf optimizer based on dimension learning and Laplace Mutation for global optimization. Expert Syst. Appl. 2025, 265, 125863. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. LSHADE algorithm with rank-based selective pressure strategy for solving CEC 2017 benchmark problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Zhang, T.; Yin, Q.; Li, S.; Guo, T.; Fan, Z. An Optimized Genetic Algorithm-Based Wavelet Image Fusion Technique for PCB Detection. Appl. Sci. 2025, 15, 3217. [Google Scholar] [CrossRef]
- Tzanetos, A.; Blondin, M. A qualitative systematic review of metaheuristics applied to tension/compression spring design problem: Current situation, recommendations, and research direction. Eng. Appl. Artif. Intell. 2023, 118, 105521. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Liu, J. Dimension by dimension dynamic sine cosine algorithm for global optimization problems. Appl. Soft Comput. 2021, 98, 106933. [Google Scholar] [CrossRef]
- Chun, Y.; Hua, X.; Qi, C.; Yao, Y.X. Improved marine predators algorithm for engineering design optimization problems. Sci. Rep. 2024, 14, 13000. [Google Scholar] [CrossRef]
- Ferreira, K.M.; de Queiroz, T.A.; Munari, P.; Toledo, F.M.B. A variable neighborhood search for the green vehicle routing problem with two-dimensional loading constraints and split delivery. Eur. J. Oper. Res. 2024, 316, 597–616. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).