The Inhomogeneous Road to Chiral Symmetry Breaking: A Ginzburg–Landau–Langevin Analysis
Abstract
1. Introduction
2. Inhomogeneous Phases
3. The Model
4. Archetypes of the Condensate’s Evolution
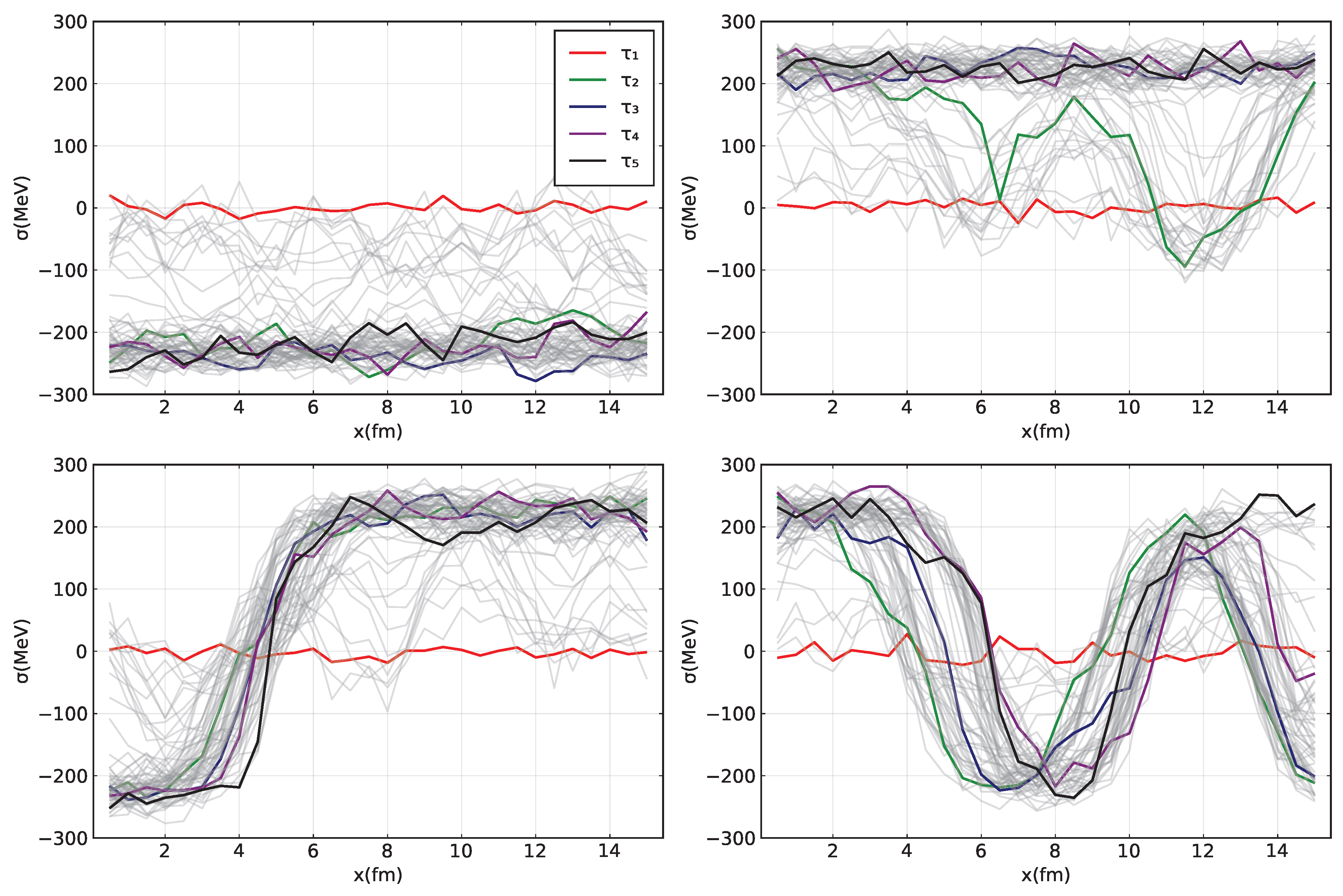
4.1. 1 + 1 Dimensions
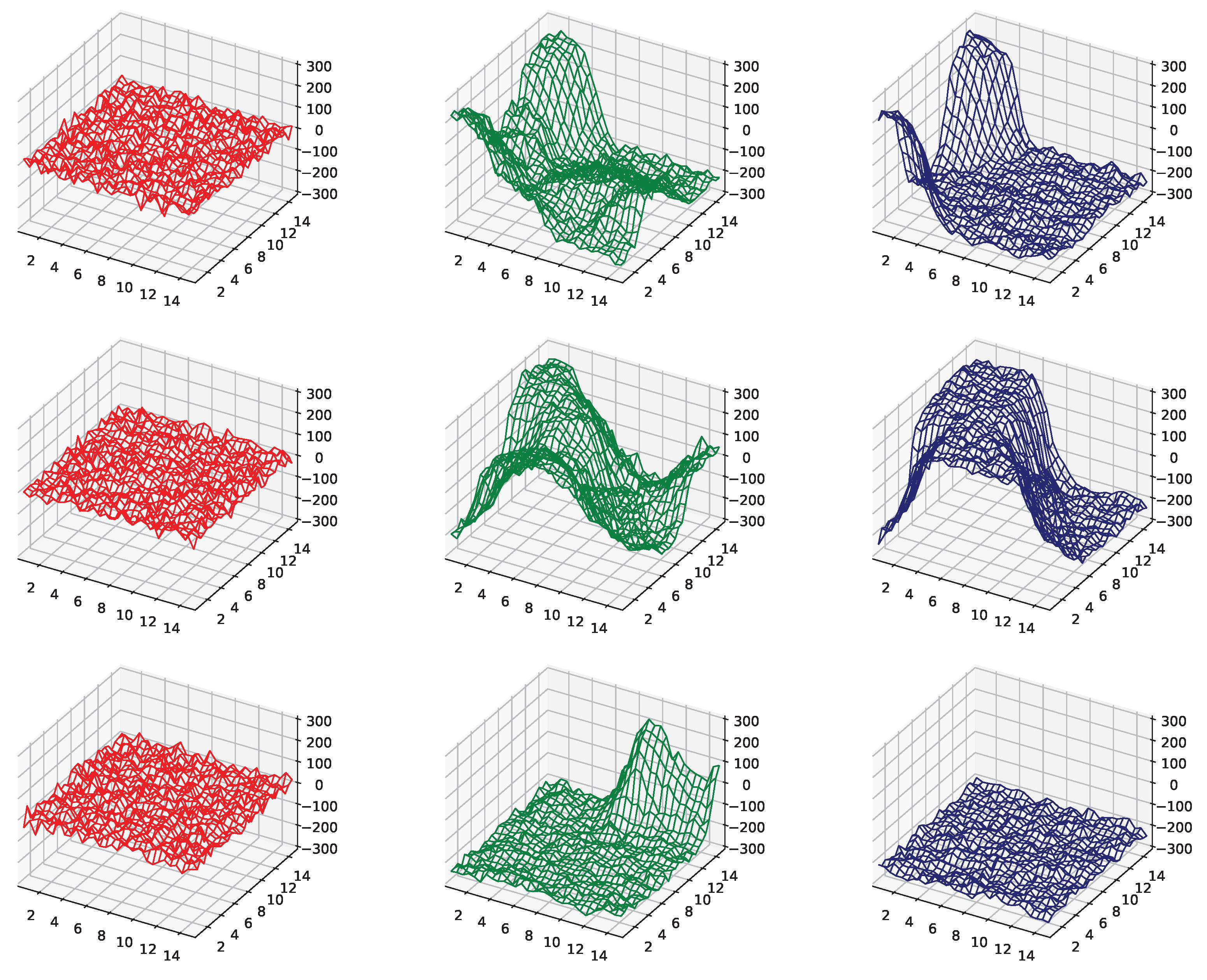
4.2. 2 + 1 Dimensions
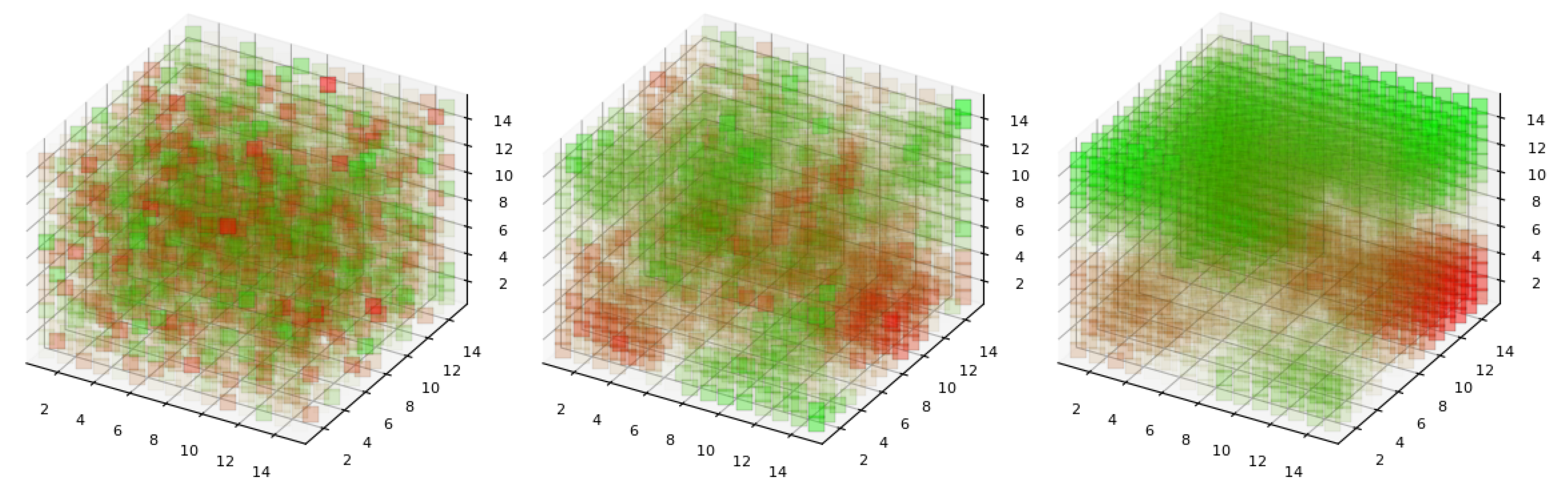
4.3. 3 + 1 Dimensions
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Overhauser, A.W. Structure of Nuclear Matter. Phys. Rev. Lett. 1960, 4, 415–418. [Google Scholar] [CrossRef]
- Motta, T.F.; Bernhardt, J.; Buballa, M.; Fischer, C.S. Inhomogenuous instabilities at large chemical potential in a rainbow-ladder QCD model. arXiv 2024, arXiv:2406.00205. [Google Scholar] [CrossRef]
- Motta, T.F.; Bernhardt, J.; Buballa, M.; Fischer, C.S. Toward a stability analysis of inhomogeneous phases in QCD. Phys. Rev. D 2023, 108, 114019. [Google Scholar] [CrossRef]
- Motta, T.F.; Buballa, M.; Fischer, C.S. New Tool to Detect Inhomogeneous Chiral Symmetry Breaking. arXiv 2024, arXiv:2411.02285. [Google Scholar]
- Thies, M. From relativistic quantum fields to condensed matter and back again: Updating the Gross-Neveu phase diagram. J. Phys. A 2006, 39, 12707–12734. [Google Scholar] [CrossRef]
- Koenigstein, A.; Pannullo, L.; Rechenberger, S.; Steil, M.J.; Winstel, M. Detecting inhomogeneous chiral condensation from the bosonic two-point function in the (1 + 1)-dimensional Gross–Neveu model in the mean-field approximation. J. Phys. A 2022, 55, 375402. [Google Scholar] [CrossRef]
- Ciccone, R.; Pietro, L.D.; Serone, M. Inhomogeneous Phase of the Chiral Gross-Neveu Model. Phys. Rev. Lett. 2022, 129, 071603. [Google Scholar] [CrossRef]
- Koenigstein, A.; Winstel, M. Revisiting the spatially inhomogeneous condensates in the (1 + 1)-dimensional chiral Gross–Neveu model via the bosonic two-point function in the infinite-N limit. J. Phys. A 2024, 57, 335401. [Google Scholar] [CrossRef]
- Buballa, M.; Carignano, S. Inhomogeneous chiral phases away from the chiral limit. Phys. Lett. B 2019, 791, 361–366. [Google Scholar] [CrossRef]
- Buballa, M.; Carignano, S. Inhomogeneous chiral condensates. Prog. Part. Nucl. Phys. 2015, 81, 39–96. [Google Scholar] [CrossRef]
- Buballa, M.; Carignano, S.; Kurth, L. Inhomogeneous phases in the quark-meson model with explicit chiral-symmetry breaking. Eur. Phys. J. Spec. Top. 2020, 229, 3371–3385. [Google Scholar] [CrossRef]
- Tripolt, R.A.; Schaefer, B.J.; von Smekal, L.; Wambach, J. Low-temperature behavior of the quark-meson model. Phys. Rev. D 2018, 97, 034022. [Google Scholar] [CrossRef]
- Nickel, D. Inhomogeneous phases in the Nambu-Jona-Lasino and quark-meson model. Phys. Rev. D 2009, 80, 074025. [Google Scholar] [CrossRef]
- Thies, M. Nonperturbative phase boundaries in the Gross-Neveu model from a stability analysis. Phys. Rev. D 2024, 110, 096012. [Google Scholar] [CrossRef]
- Pannullo, L.; Wagner, M.; Winstel, M. Inhomogeneous Phases in the Chirally Imbalanced 2 + 1-Dimensional Gross-Neveu Model and Their Absence in the Continuum Limit. Symmetry 2022, 14, 265. [Google Scholar] [CrossRef]
- Winstel, M.; Pannullo, L. Stability of homogeneous chiral phases against inhomogeneous perturbations in 2 + 1 dimensions. PoS 2023, LATTICE2022, 195. [Google Scholar] [CrossRef]
- Pannullo, L. Inhomogeneous condensation in the Gross-Neveu model in noninteger spatial dimensions 1 ≤ d < 3. Phys. Rev. D 2023, 108, 036022. [Google Scholar] [CrossRef]
- Koenigstein, A.; Pannullo, L. Inhomogeneous condensation in the Gross-Neveu model in noninteger spatial dimensions 1 ≤ d < 3. II. Nonzero temperature and chemical potential. arXiv 2023, arXiv:2312.04904. [Google Scholar]
- Buballa, M.; Kurth, L.; Wagner, M.; Winstel, M. Regulator dependence of inhomogeneous phases in the (2 + 1)-dimensional Gross-Neveu model. Phys. Rev. D 2021, 103, 034503. [Google Scholar] [CrossRef]
- Pannullo, L.; Wagner, M.; Winstel, M. Inhomogeneous phases in the 3 + 1-dimensional Nambu-Jona-Lasinio model and their dependence on the regularization scheme. PoS 2023, LATTICE2022, 156. [Google Scholar] [CrossRef]
- Pannullo, L.; Wagner, M.; Winstel, M. Regularization effects in the Nambu-Jona-Lasinio model: Strong scheme dependence of inhomogeneous phases and persistence of the moat regime. arXiv 2024, arXiv:2406.11312. [Google Scholar] [CrossRef]
- Pannullo, L. Inhomogeneous Phases and the Moat Regime in Nambu-Jona-Lasinio-Type Models. Ph.D. Thesis, Frankfurt Uiversity, Frankfurt am Main, Germany, 2024. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Tsvelik, A.M.; Valgushev, S. How transverse thermal fluctuations disorder a condensate of chiral spirals into a quantum spin liquid. Phys. Rev. D 2020, 102, 016015. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Skokov, V.V.; Tsvelik, A.M. Fluctuations in cool quark matter and the phase diagram of Quantum Chromodynamics. Phys. Rev. D 2019, 99, 074025. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; Perseus Books: Reading, UK, 1992. [Google Scholar]
- Onuki, A. Phase Transition Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Carlomagno, J.P.; Gomez Dumm, D.; Scoccola, N.N. Generalized Ginzburg-Landau approach to inhomogeneous phases in nonlocal chiral quark models. Phys. Lett. B 2015, 745, 1–4. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Gómez Dumm, D.; Scoccola, N.N. Inhomogeneous phases in nonlocal chiral quark models. Phys. Rev. D 2015, 92, 056007. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Krein, G. Time-dependent Ginzburg-Landau approach to the dynamics of inhomogeneous chiral condensates in a nonlocal Nambu–Jona-Lasinio model. Phys. Rev. D 2018, 98, 014015. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Krein, G.; Kroff, D.; Peixoto, T. Dynamics of inhomogeneous chiral condensates. EPJ Web Conf. 2018, 172, 03005. [Google Scholar] [CrossRef][Green Version]
- Rischke, D.H. Forming disoriented chiral condensates through fluctuations. Phys. Rev. C 1998, 58, 2331–2357. [Google Scholar] [CrossRef][Green Version]
- Nahrgang, M.; Leupold, S.; Herold, C.; Bleicher, M. Nonequilibrium chiral fluid dynamics including dissipation and noise. Phys. Rev. C 2011, 84, 024912. [Google Scholar] [CrossRef]
- Krein, G.; Miller, C. Nonequilibrium Dynamics of the Chiral Quark Condensate under a Strong Magnetic Field. Symmetry 2021, 13, 551. [Google Scholar] [CrossRef]
- Ferrer, E.J.; de la Incera, V. Magnetic Dual Chiral Density Wave: A Candidate Quark Matter Phase for the Interior of Neutron Stars. Universe 2021, 7, 458. [Google Scholar] [CrossRef]
- Nakano, E.; Tatsumi, T. Chiral symmetry and density wave in quark matter. Phys. Rev. D 2005, 71, 114006. [Google Scholar] [CrossRef]
- Müller, D.; Buballa, M.; Wambach, J. Dyson-Schwinger study of chiral density waves in QCD. Phys. Lett. B 2013, 727, 240–243. [Google Scholar] [CrossRef]
- Kojo, T.; Hidaka, Y.; McLerran, L.; Pisarski, R.D. Quarkyonic Chiral Spirals. Nucl. Phys. A 2009, 843, 37–58. [Google Scholar] [CrossRef]
- Nishiyama, K.; Karasawa, S.; Tatsumi, T. Hybrid chiral condensate in the external magnetic field. Phys. Rev. D 2015, 92, 036008. [Google Scholar] [CrossRef]
- Başar, G.; Dunne, G.V. Twisted kink crystal in the chiral Gross-Neveu model. Physical Review D 2008, 78, 065022. [Google Scholar] [CrossRef]
- Basar, G.; Dunne, G.V.; Thies, M. Inhomogeneous Condensates in the Thermodynamics of the Chiral NJL(2) model. Phys. Rev. D 2009, 79, 105012. [Google Scholar] [CrossRef]
- Colangelo, G.; Durr, S. The Pion mass in finite volume. Eur. Phys. J. C 2004, 33, 543–553. [Google Scholar] [CrossRef]
- FLAG Working Group; Aoki, S.; Bernard, C.; Blum, T.; Colangelo, G.; Della Morte, M.; Dürr, S.; El-Khadra, A.X.; Fukaya, H.; Horsley, R.; et al. Review of Lattice Results Concerning Low-Energy Particle Physics. Eur. Phys. J. C 2014, 74, 2890. [Google Scholar] [CrossRef]
- Bowler, R.D.; Birse, M.C. A Nonlocal, covariant generalization of the NJL model. Nucl. Phys. A 1995, 582, 655–664. [Google Scholar] [CrossRef]
- Diakonov, D.; Petrov, V.Y. Meson Current Correlation Functions in Instanton Vacuum. Sov. Phys. JETP 1985, 62, 431–437. [Google Scholar]
- Diakonov, D.; Petrov, V.Y.; Pobylitsa, P.V. A Chiral Theory of Nucleons. Nucl. Phys. B 1988, 306, 809. [Google Scholar] [CrossRef]
- Calzetta, E.A.; Hu, B.L.B. Nonequilibrium Quantum Field Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Blaschke, D.; Aichelin, J.; Bratkovskaya, E.; Friese, V.; Gazdzicki, M.; Randrup, J.; Rogachevsky, O.; Teryaev, O.; Toneev, V. Topical issue on Exploring Strongly Interacting Matter at High Densities—NICA White Paper. Eur. Phys. J. A 2016, 52, 267. [Google Scholar] [CrossRef]
- Agarwal, K. The compressed baryonic matter (CBM) experiment at FAIR—physics, status and prospects. Phys. Scr. 2023, 98, 034006. [Google Scholar] [CrossRef]
- Aoki, K.; Fujioka, H.; Gogami, T.; Hidaka, Y.; Hiyama, E.; Honda, R.; Hosaka, A.; Ichikawa, Y.; Ieiri, M.; Isaka, M.; et al. Extension of the J-PARC Hadron Experimental Facility: Third White Paper. arXiv 2021, arXiv:2110.04462. [Google Scholar]
- Carignano, S.; Nickel, D.; Buballa, M. Influence of vector interaction and Polyakov loop dynamics on inhomogeneous chiral symmetry breaking phases. Phys. Rev. D 2010, 82, 054009. [Google Scholar] [CrossRef]
- Nickel, D. How many phases meet at the chiral critical point? Phys. Rev. Lett. 2009, 103, 072301. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Rennecke, F. Signatures of Moat Regimes in Heavy-Ion Collisions. Phys. Rev. Lett. 2021, 127, 152302. [Google Scholar] [CrossRef]
- Rennecke, F.; Pisarski, R.D. Moat Regimes in QCD and their Signatures in Heavy-Ion Collisions. PoS 2022, CPOD2021, 016. [Google Scholar] [CrossRef]
- Winstel, M.; Valgushev, S. Lattice study of disordering of inhomogeneous condensates and the Quantum Pion Liquid in effective O(N) model. In Proceedings of the Excited QCD 2024 Workshop, Benasque, Spain, 14–20 January 2024. [Google Scholar]
- Nussinov, Z.; Ogilvie, M.C.; Pannullo, L.; Pisarski, R.D.; Rennecke, F.; Schindler, S.T.; Winstel, M. Dilepton production from moaton quasiparticles. arXiv 2024, arXiv:2410.22418. [Google Scholar]
- Rennecke, F.; Pisarski, R.D.; Rischke, D.H. Particle interferometry in a moat regime. Phys. Rev. D 2023, 107, 116011. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motta, T.F.; Krein, G. The Inhomogeneous Road to Chiral Symmetry Breaking: A Ginzburg–Landau–Langevin Analysis. Symmetry 2025, 17, 568. https://doi.org/10.3390/sym17040568
Motta TF, Krein G. The Inhomogeneous Road to Chiral Symmetry Breaking: A Ginzburg–Landau–Langevin Analysis. Symmetry. 2025; 17(4):568. https://doi.org/10.3390/sym17040568
Chicago/Turabian StyleMotta, Theo F., and Gastão Krein. 2025. "The Inhomogeneous Road to Chiral Symmetry Breaking: A Ginzburg–Landau–Langevin Analysis" Symmetry 17, no. 4: 568. https://doi.org/10.3390/sym17040568
APA StyleMotta, T. F., & Krein, G. (2025). The Inhomogeneous Road to Chiral Symmetry Breaking: A Ginzburg–Landau–Langevin Analysis. Symmetry, 17(4), 568. https://doi.org/10.3390/sym17040568





