Reflections on Chiral Symmetry Within QCD
Abstract
1. Introduction
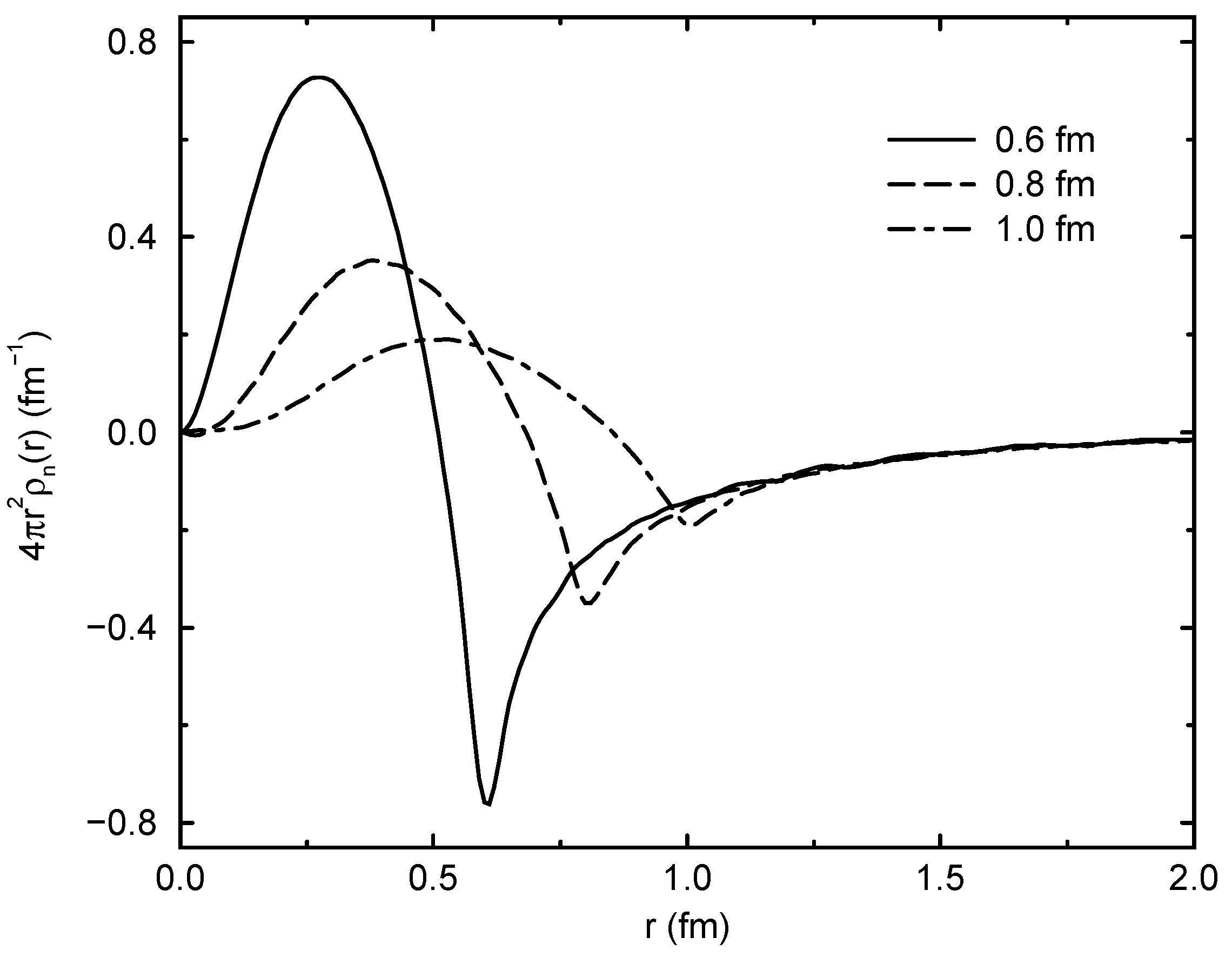
2. Anti-Matter in the Proton
Asymmetry in the Strange Sea
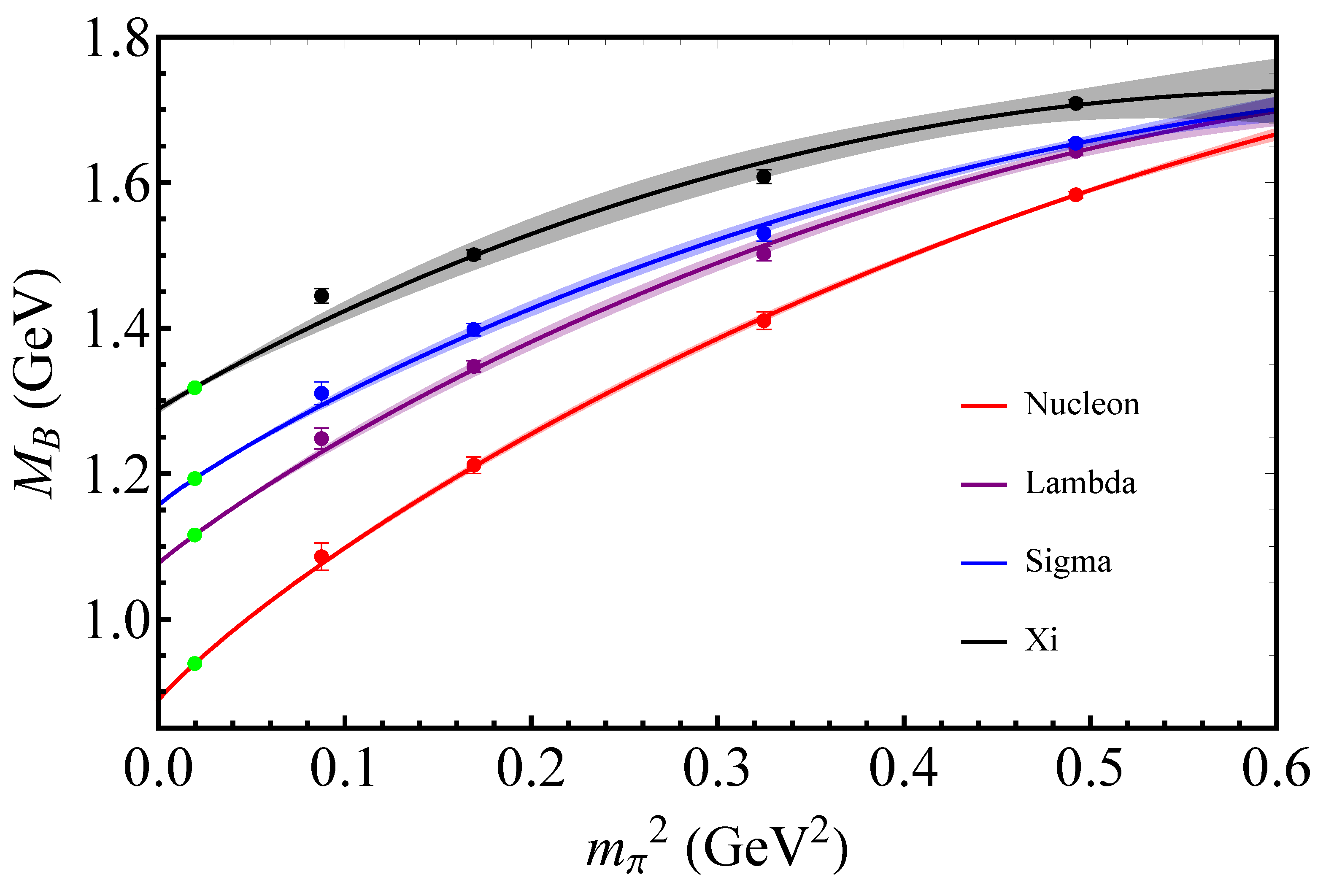
3. QCD Predictions as a Function of Quark Mass
Strangeness Content of the Nucleon
4. The “Spin Crisis”
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Gross, F.; Klempt, E.; Brodsky, S.J.; Buras, A.J.; Burkert, V.D.; Heinrich, G.; Jakobs, K.; Meyer, C.A.; Orginos, K.; Strickland, M.; et al. 50 Years of Quantum Chromodynamics. Eur. Phys. J. C 2023, 83, 1125. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetries of baryons and mesons. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef]
- Zweig, G. An SU(3) Model for Strong Interaction Symmetry and Its Breaking, Version 1; 1964. Available online: https://cds.cern.ch/record/352337 (accessed on 1 March 2025). [CrossRef]
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. B 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Aubert, J.J.; Becker, U.; Biggs, P.J.; Burger, J.; Chen, M.; Everhart, G.; Goldhagen, P.; Leong, J.; McCorriston, T.; Rhoades, T.G.; et al. Experimental Observation of a Heavy Particle. J. Phys. Rev. Lett. 1974, 33, 1404–1406. [Google Scholar] [CrossRef]
- Augustin, J.E.; Boyarski, A.M.; Breidenbach, M.; Bulos, F.; Dakin, J.T.; Feldman, G.J.; Fischer, G.E.; Fryberger, D.; Hanson, G.; Jean-Marie, B.; et al. Discovery of a Narrow Resonance in e+e− Annihilation. Phys. Rev. Lett. 1974, 33, 1406–1408. [Google Scholar] [CrossRef]
- Rinat, A.S.; Thomas, A.W. A Relativistic Description of pi d Scattering in the (3,3) Resonance Region. Nucl. Phys. A 1977, 282, 365–388. [Google Scholar] [CrossRef]
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak Interactions with Lepton-Hadron Symmetry. Phys. Rev. D 1970, 2, 1285–1292. [Google Scholar] [CrossRef]
- Brandelik, R.; Braunschweig, W.; Gather, K.; Kadansky, V.; Kirschfink, F.J.; Lübelsmeyer, K.; Martyn, H.U.; Peise, G.; Rimkus, J.; Sander, H.G.; et al. Evidence for a Spin One Gluon in Three Jet Events. Phys. Lett. B 1980, 97, 453–458. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B. Baryon Structure in the Bag Theory. Phys. Rev. D 1974, 10, 2599. [Google Scholar] [CrossRef]
- Pagels, H. Departures from Chiral Symmetry: A Review. Phys. Rep. 1975, 16, 219. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Levy, M. The axial vector current in beta decay. Nuovo C. 1960, 16, 705. [Google Scholar] [CrossRef]
- Glashow, S.L.; Weinberg, S. Breaking chiral symmetry. Phys. Rev. Lett. 1968, 20, 224–227. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Symmetry group of vector and axial vector currents. Phys. Phys. Fiz. 1964, 1, 63–75. [Google Scholar] [CrossRef]
- Adler, S.L. Consistency conditions on the strong interactions implied by a partially conserved axial vector current. Phys. Rev. 1965, 137, B1022–B1033. [Google Scholar] [CrossRef]
- Weinberg, S. Pion scattering lengths. Phys. Rev. Lett. 1966, 17, 616–621. [Google Scholar] [CrossRef]
- Chodos, A.; Thorn, C.B. Chiral Hedgehogs in the Bag Theory. Phys. Rev. D 1975, 12, 2733. [Google Scholar] [CrossRef]
- Brown, G.E.; Rho, M.; Vento, V. Little Bag Dynamics. Phys. Lett. B 1979, 84, 383–388. [Google Scholar] [CrossRef]
- Chew, G.F.; Low, F.E. Effective range approach to the low-energy p wave pion—Nucleon interaction. Phys. Rev. 1956, 101, 1570–1579. [Google Scholar] [CrossRef]
- Miller, G.A.; Thomas, A.W.; Theberge, S. Pion-Nucleon Scattering in the Cloudy Bag Model. Phys. Lett. B 1980, 91, 192–195. [Google Scholar] [CrossRef]
- Thomas, A.W. Chiral Symmetry and the Bag Model: A New Starting Point for Nuclear Physics. Adv. Nucl. Phys. 1984, 13, 1–137. [Google Scholar] [CrossRef]
- Theberge, S.; Thomas, A.W.; Miller, G.A. The Cloudy Bag Model. 1. The (3,3) Resonance. Phys. Rev. D 1980, 22, 2838, Erratum in Phys. Rev. D 1981, 23, 2106. [Google Scholar] [CrossRef]
- Dodd, L.R.; Thomas, A.W.; Alvarez-Estrada, R.F. The Cloudy Bag Model. 3. Convergent Perturbation Expansion for the Nucleon. Phys. Rev. D 1981, 24, 1961. [Google Scholar] [CrossRef]
- Thomas, A.W.; Theberge, S.; Miller, G.A. The Cloudy Bag Model of the Nucleon. Phys. Rev. D 1981, 24, 216. [Google Scholar] [CrossRef]
- Hofstadter, R.; Herman, R. Electric and Magnetic Structure of the Proton and Neutron. Phys. Rev. Lett. 1961, 6, 293–296. [Google Scholar] [CrossRef]
- Galster, S.; Klein, H.; Moritz, J.; Schmidt, K.H.; Wegener, D.; Bleckwenn, J. Elastic electron-deuteron scattering and the electric neutron form factor at four-momentum transfers 5fm−2 < q2 < 14fm−2. Nucl. Phys. B 1971, 32, 221–237. [Google Scholar] [CrossRef]
- Bartel, W.; Busser, F.W.; Dix, W.R.; Felst, R.; Harms, D.; Krehbiel, H.; Kuhlmann, P.E.; McElroy, J.; Meyer, J.; Weber, G. Measurement of proton and neutron electromagnetic form-factors at squared four momentum transfers up to 3-GeV/c2. Nucl. Phys. B 1973, 58, 429–475. [Google Scholar] [CrossRef]
- Platchkov, S.; Amroun, A.; Auffret, S.; Cavedon, J.M.; Dreux, P.; Duclos, J.; Frois, B.; Goutte, D.; Hachemi, H.; Martino, J.; et al. Deuteron A (Q2) Structure Function and the Neutron Electric Form-Factor. Nucl. Phys. A 1990, 510, 740–758. [Google Scholar] [CrossRef]
- Miller, G.A. Charge Density of the Neutron. Phys. Rev. Lett. 2007, 99, 112001. [Google Scholar] [CrossRef] [PubMed]
- Lorcé, C. Charge Distributions of Moving Nucleons. Phys. Rev. Lett. 2020, 125, 232002. [Google Scholar] [CrossRef] [PubMed]
- Theberge, S.; Thomas, A.W. The Magnetic Moments of the Nucleon Octet Calculated in the Cloudy Bag Model. Phys. Rev. D 1982, 25, 284. [Google Scholar] [CrossRef]
- Theberge, S.; Thomas, A.W. Magnetic Moments of the Nucleon Octet Calculated in the Cloudy Bag Model. Nucl. Phys. A 1983, 393, 252–282. [Google Scholar] [CrossRef]
- Zenczykowski, P. Kaon Cloud Contribution to the Magnetic Moments of the Nucleon Octet. Phys. Rev. D 1984, 29, 577. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Miller, G.A.; Thomas, A.W. The Axial Form-factor of the Nucleon and the Pion-Nucleon Vertex Function. Phys. Lett. B 1983, 124, 109–112. [Google Scholar] [CrossRef][Green Version]
- Aubert, J.J.; Bassompierre, G.; Becks, K.H.; Best, C.; Böhm, E.; de Bouard, X.; Brasse, F.W.; Broll, C.; Brown, S.; Carr, J.; et al. The ratio of the nucleon structure functions F2n for iron and deuterium. Phys. Lett. B 1983, 123, 275–278. [Google Scholar] [CrossRef]
- European Muon Collaboration; Ashman, J.; Badelek, B.; Baum, G.; Beaufays, J.; Bee, C.P.; Benchouk, C.; Bird, I.G.; Brown, S.C.; Caputo, M.C.; et al. A Measurement of the ratio of the nucleon structure function in copper and deuterium. Z. Phys. C Part. Fields 1993, 57, 211–218. [Google Scholar] [CrossRef]
- Bari, G.; Benvenuti, A.C.; Bollini, D.; Bruni, G.; Camporesi, T.; Heiman, G.; Monari, L.; Navarria, F.L.; Argento, A.; Cvach, J.; et al. A Measurement of Nuclear Effects in Deep Inelastic Muon Scattering on Deuterium, Nitrogen and Iron Targets. Phys. Lett. B 1985, 163, 282. [Google Scholar] [CrossRef]
- Arrington, J.; Bane, J.; Daniel, A.; Fomin, N.; Gaskell, D.; Seely, J.; Asaturyan, R.; Benmokhtar, F.; Boeglin, W.; Bosted, P.; et al. Measurement of the EMC effect in light and heavy nuclei. Phys. Rev. C 2021, 104, 065203. [Google Scholar] [CrossRef]
- Geesaman, D.F.; Saito, K.; Thomas, A.W. The nuclear EMC effect. Ann. Rev. Nucl. Part. Sci. 1995, 45, 337–390. [Google Scholar] [CrossRef]
- Hen, O.; Miller, G.A.; Piasetzky, E.; Weinstein, L.B. Nucleon-Nucleon Correlations, Short-lived Excitations, and the Quarks Within. Rev. Mod. Phys. 2017, 89, 045002. [Google Scholar] [CrossRef]
- Thomas, A.W. Reflections on the Origin of the EMC Effect. Int. J. Mod. Phys. E 2019, 27, 1840001. [Google Scholar] [CrossRef]
- Ericson, M.; Thomas, A.W. Pionic Corrections and the EMC Enhancement of the Sea in Iron. Phys. Lett. B 1983, 128, 112–116. [Google Scholar] [CrossRef]
- Llewellyn Smith, C.H. A Possible Explanation of the Difference Between the Structure Functions of Iron and Deuterium. Phys. Lett. B 1983, 128, 107–111. [Google Scholar] [CrossRef]
- Sullivan, J.D. One pion exchange and deep inelastic electron—Nucleon scattering. Phys. Rev. D 1972, 5, 1732–1737. [Google Scholar] [CrossRef]
- Thomas, A.W. A Limit on the Pionic Component of the Nucleon Through SU(3) Flavor Breaking in the Sea. Phys. Lett. B 1983, 126, 97–100. [Google Scholar] [CrossRef]
- Amaudruz, P.; Arneodo, M.; Arvidson, A.; Badelek, B.; Baum, G.; Beaufays, J.; Bird, I.G.; Botje, M.; Broggini, C.; Brückner, W.; et al. The Gottfried sum from the ratio F2(n)/F2(p). Phys. Rev. Lett. 1991, 66, 2712–2715. [Google Scholar] [CrossRef]
- Towell, R.S.; McGaughey, P.L.; Awes, T.C.; Beddo, M.E.; Brooks, M.L.; Brown, C.N.; Bush, J.D.; Carey, T.A.; Chang, T.H.; Cooper, W.E.; et al. Improved measurement of the anti-d/anti-u asymmetry in the nucleon sea. Phys. Rev. D 2001, 64, 052002. [Google Scholar] [CrossRef]
- Dove, J.; Kerns, B.; Leung, C.; McClellan, R.E.; Miyasaka, S.; Morton, D.H.; Nagai, K.; Prasad, S.; Sanftl, F.; Scott, M.B.C.; et al. Measurement of flavor asymmetry of the light-quark sea in the proton with Drell-Yan dimuon production in p+p and p+d collisions at 120 GeV. Phys. Rev. C 2023, 108, 035202. [Google Scholar] [CrossRef]
- Melnitchouk, W.; Thomas, A.W.; Signal, A.I. Gottfried sum rule and the shape of F2(p)-F2(n). Z. Phys. A Hadron. Nucl. 1991, 340, 85–92. [Google Scholar] [CrossRef]
- Melnitchouk, W.; Speth, J.; Thomas, A.W. Dynamics of light anti-quarks in the proton. Phys. Rev. D 1998, 59, 014033. [Google Scholar] [CrossRef]
- Signal, A.I.; Thomas, A.W. Possible Strength of the Nonperturbative Strange Sea of the Nucleon. Phys. Lett. B 1987, 191, 205. [Google Scholar] [CrossRef]
- Wang, X.G.; Ji, C.R.; Melnitchouk, W.; Salamu, Y.; Thomas, A.W.; Wang, P. Strange quark asymmetry in the proton in chiral effective theory. Phys. Rev. D 2016, 94, 094035. [Google Scholar] [CrossRef]
- Wang, X.G.; Ji, C.R.; Melnitchouk, W.; Salamu, Y.; Thomas, A.W.; Wang, P. Constraints on s − asymmetry of the proton in chiral effective theory. Phys. Lett. B 2016, 762, 52–56. [Google Scholar] [CrossRef]
- Thomas, A.W.; Melnitchouk, W.; Steffens, F.M. Dynamical symmetry breaking in the sea of the nucleon. Phys. Rev. Lett. 2000, 85, 2892–2894. [Google Scholar] [CrossRef]
- Ball, R.D.; Carrazza, S.; Cruz-Martinez, J.; Del Debbio, L.; Forte, S.; Giani, T.; Iranipour, S.; Kassabov, Z.; Latorre, J.I.; Nocera, E.R.; et al. The path to proton structure at 1% accuracy. Eur. Phys. J. C 2022, 82, 428. [Google Scholar] [CrossRef]
- Ablat, A.; Courtoy, A.; Dulat, S.; Guzzi, M.; Hobbs, T.; Hou, T.J.; Huston, J.; Mohan, K.; Lin, H.W.; Nadolsky, P.; et al. New results in the CTEQ-TEA global analysis of parton distributions in the nucleon. Eur. Phys. J. Plus 2024, 139, 1063. [Google Scholar] [CrossRef]
- Melnitchouk, W.; Owens, J.F. Deep-inelastic scattering with positron beams. Eur. Phys. J. A 2021, 57, 311. [Google Scholar] [CrossRef]
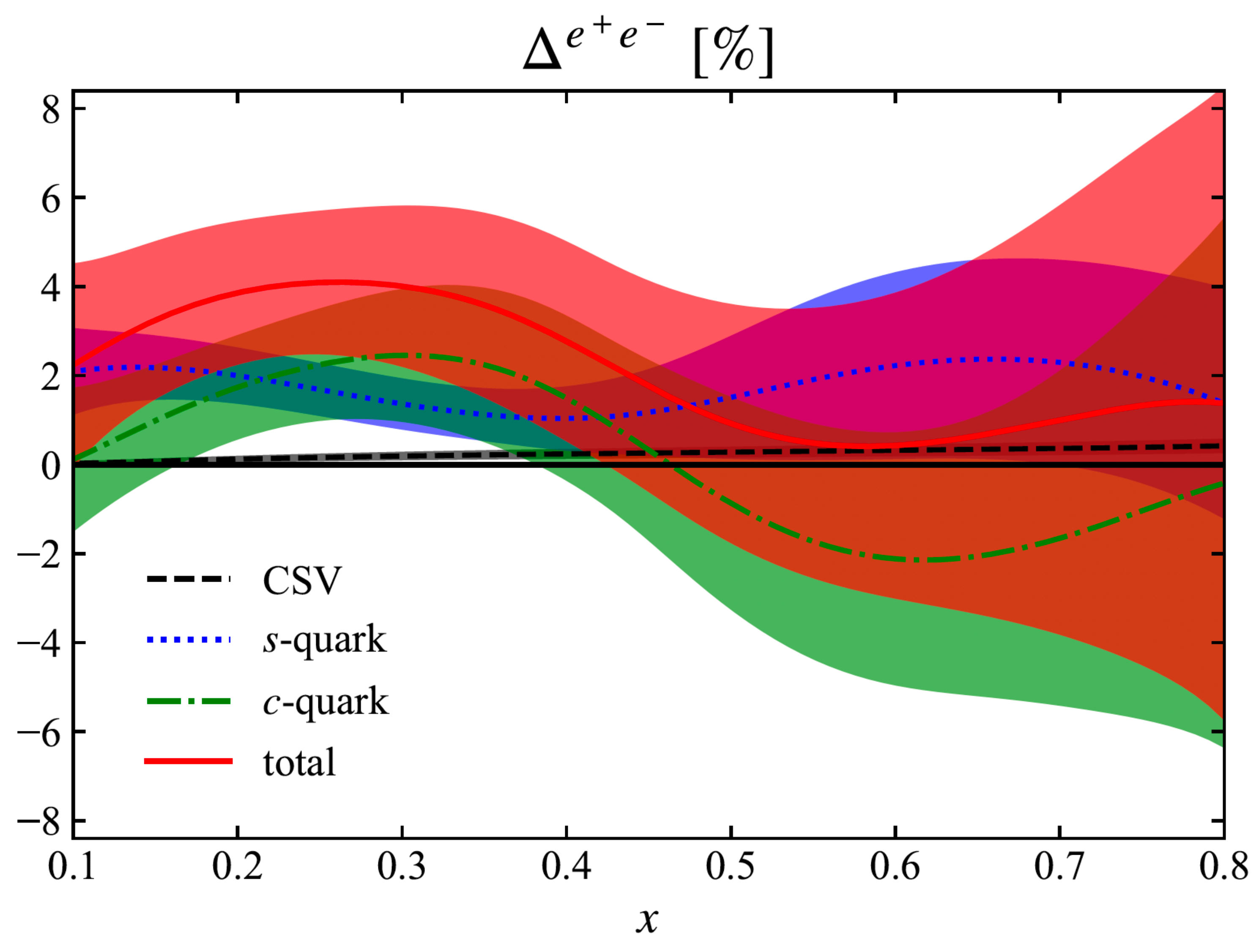
- Wang, X.G.; Thomas, A.W. Challenges in the extraction of physics beyond the Standard Model from electron scattering. J. Phys. G 2025, 52, 015006. [Google Scholar] [CrossRef]
- Rodionov, E.N.; Thomas, A.W.; Londergan, J.T. Charge asymmetry of parton distributions. Mod. Phys. Lett. A 1994, 9, 1799–1806. [Google Scholar] [CrossRef]
- Sather, E. Isospin violating quark distributions in the nucleon. Phys. Lett. B 1992, 274, 433–438. [Google Scholar] [CrossRef]
- Zheng, X.; Erler, J.; Liu, Q.; Spiesberger, H. Accessing weak neutral-current coupling using positron and electron beams at Jefferson Lab. Eur. Phys. J. A 2021, 57, 173. [Google Scholar] [CrossRef]
- Wilson, K.G. Confinement of Quarks. Phys. Rev. D 1974, 10, 2445–2459. [Google Scholar] [CrossRef]
- Durr, S.; Fodor, Z.; Frison, J.; Hoelbling, C.; Hoffmann, R.; Katz, S.D.; Krieg, S.; Kurth, T.; Lellouch, L.; Lippert, T.; et al. Ab-Initio Determination of Light Hadron Masses. Science 2008, 322, 1224–1227. [Google Scholar] [CrossRef]
- Borsanyi, S.; Dürr, S.; Fodor, Z.; Frison, J.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Kurth, T.; Lellouch, L.; Lippert, T.; et al. Isospin splittings in the light baryon octet from lattice QCD and QED. Phys. Rev. Lett. 2013, 111, 252001. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142. [Google Scholar] [CrossRef]
- Leutwyler, H. On the foundations of chiral perturbation theory. Ann. Phys. 1994, 235, 165–203. [Google Scholar] [CrossRef]
- Meissner, U.G. Recent developments in chiral perturbation theory. Rep. Prog. Phys. 1993, 56, 903–996. [Google Scholar] [CrossRef]
- Ecker, G. Chiral perturbation theory. Prog. Part. Nucl. Phys. 1995, 35, 1–80. [Google Scholar] [CrossRef]
- Pich, A. Chiral perturbation theory. Rep. Prog. Phys. 1995, 58, 563–610. [Google Scholar] [CrossRef]
- Young, R.D.; Leinweber, D.B.; Thomas, A.W. Convergence of chiral effective field theory. Prog. Part. Nucl. Phys. 2003, 50, 399–417. [Google Scholar] [CrossRef]
- Leinweber, D.B.; Thomas, A.W.; Tsushima, K.; Wright, S.V. Baryon masses from lattice QCD: Beyond the perturbative chiral regime. Phys. Rev. D 2000, 61, 074502. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Holstein, B.R.; Borasoy, B. SU(3) baryon chiral perturbation theory and long distance regularization. Phys. Rev. D 1999, 59, 036002. [Google Scholar] [CrossRef]
- Owa, S.; Leinweber, D.B.; Thomas, A.W.; Wang, X.G. Chiral analysis of the nucleon mass and sigma commutator. Phys. Rev. D 2024, 109, 116022. [Google Scholar] [CrossRef]
- Aoki, S.; Ishikawa, K.I.; Ishizuka, N.; Izubuchi, T.; Kadoh, D.; Kanaya, K.; Kuramashi, Y.; Namekawa, Y.; Okawa, M.; Taniguchi, Y.; et al. 2+1 flavor lattice QCD toward the physical point. Phys. Rev. D 2009, 79, 034503. [Google Scholar] [CrossRef]
- Alarcón, J.M. Brief history of the pion–nucleon sigma term. Eur. Phys. J. Spec. Top. 2021, 230, 1609–1622. [Google Scholar] [CrossRef]
- Hoferichter, M.; Ruiz de Elvira, J.; Kubis, B.; Meißner, U.G. High-Precision Determination of the Pion-Nucleon σ Term from Roy-Steiner Equations. Phys. Rev. Lett. 2015, 115, 092301. [Google Scholar] [CrossRef]
- Hoferichter, M.; de Elvira, J.R.; Kubis, B.; Meißner, U.G. On the role of isospin violation in the pion–nucleon σ-term. Phys. Lett. B 2023, 843, 138001. [Google Scholar] [CrossRef]
- Ruiz de Elvira, J.; Hoferichter, M.; Kubis, B.; Meißner, U.G. Extracting the σ-term from low-energy pion-nucleon scattering. J. Phys. G 2018, 45, 024001. [Google Scholar] [CrossRef]
- Yang, Y.B.; Alexandru, A.; Draper, T.; Liang, J.; Liu, K.F. πN and strangeness sigma terms at the physical point with chiral fermions. Phys. Rev. D 2016, 94, 054503. [Google Scholar] [CrossRef]
- Aoki, Y.; Blum, T.; Collins, S.; Del Debbio, L.; Della Morte, M.; Dimopoulos, P.; Feng, X.; Golterman, M.; Gottlieb, S.; Gupta, R.; et al. FLAG Review 2024. arXiv 2024, arXiv:2411.04268. [Google Scholar]
- Bali, G.S.; Collins, S.; Richtmann, D.; Schäfer, A.; Söldner, W.; Sternbeck, A. Direct determinations of the nucleon and pion σ terms at nearly physical quark masses. Phys. Rev. D 2016, 93, 094504. [Google Scholar] [CrossRef]
- Ottnad, K.; Djukanovic, D.; Meyer, H.B.; von Hippel, G.; Wittig, H. Mass and isovector matrix elements of the nucleon at zero-momentum transfer. In Proceedings of the 39th International Symposium on Lattice Field Theory (Lattice2022), Bonn, Germany, 8–13 August 2022. [Google Scholar] [CrossRef]
- Ellis, J.R.; Olive, K.A.; Savage, C. Hadronic Uncertainties in the Elastic Scattering of Supersymmetric Dark Matter. Phys. Rev. D 2008, 77, 065026. [Google Scholar] [CrossRef]
- Giedt, J.; Thomas, A.W.; Young, R.D. Dark matter, the CMSSM and lattice QCD. Phys. Rev. Lett. 2009, 103, 201802. [Google Scholar] [CrossRef]
- Young, R.D.; Thomas, A.W. Octet baryon masses and sigma terms from an SU(3) chiral extrapolation. Phys. Rev. D 2010, 81, 014503. [Google Scholar] [CrossRef]
- Shanahan, P.E.; Thomas, A.W.; Young, R.D. Sigma terms from an SU(3) chiral extrapolation. Phys. Rev. D 2013, 87, 074503. [Google Scholar] [CrossRef]
- Nelson, A.E.; Kaplan, D.B. Strange Condensate Realignment in Relativistic Heavy Ion Collisions. Phys. Lett. B 1987, 192, 193. [Google Scholar] [CrossRef]
- Thomas, A.W. Chiral extrapolation of hadronic observables. Nucl. Phys. B Proc. Suppl. 2003, 119, 50–58. [Google Scholar] [CrossRef]
- Dalitz, R.H.; Tuan, S.F. The phenomenological description of -K -nucleon reaction processes. Ann. Phys. 1960, 10, 307–351. [Google Scholar] [CrossRef]
- Veit, E.A.; Jennings, B.K.; Thomas, A.W.; Barrett, R.C. S-Wave Meson-Nucleon Scattering in an SU(3) Cloudy Bag Model. Phys. Rev. D 1985, 31, 1033. [Google Scholar] [CrossRef]
- Thomas, A.W. Low-energy Pion Scattering in the Cloudy Bag Model. J. Phys. G 1981, 7, L283. [Google Scholar] [CrossRef]
- Tomozawa, Y. Proton Decay Rate. Phys. Rev. Lett. 1981, 46, 463, Erratum in Phys. Rev. Lett. 1982, 49, 507. [Google Scholar] [CrossRef]
- Hall, J.M.M.; Hsu, A.C.P.; Leinweber, D.B.; Thomas, A.W.; Young, R.D. Finite-volume matrix Hamiltonian model for a Δ→Nπ system. Phys. Rev. D 2013, 87, 094510. [Google Scholar] [CrossRef]
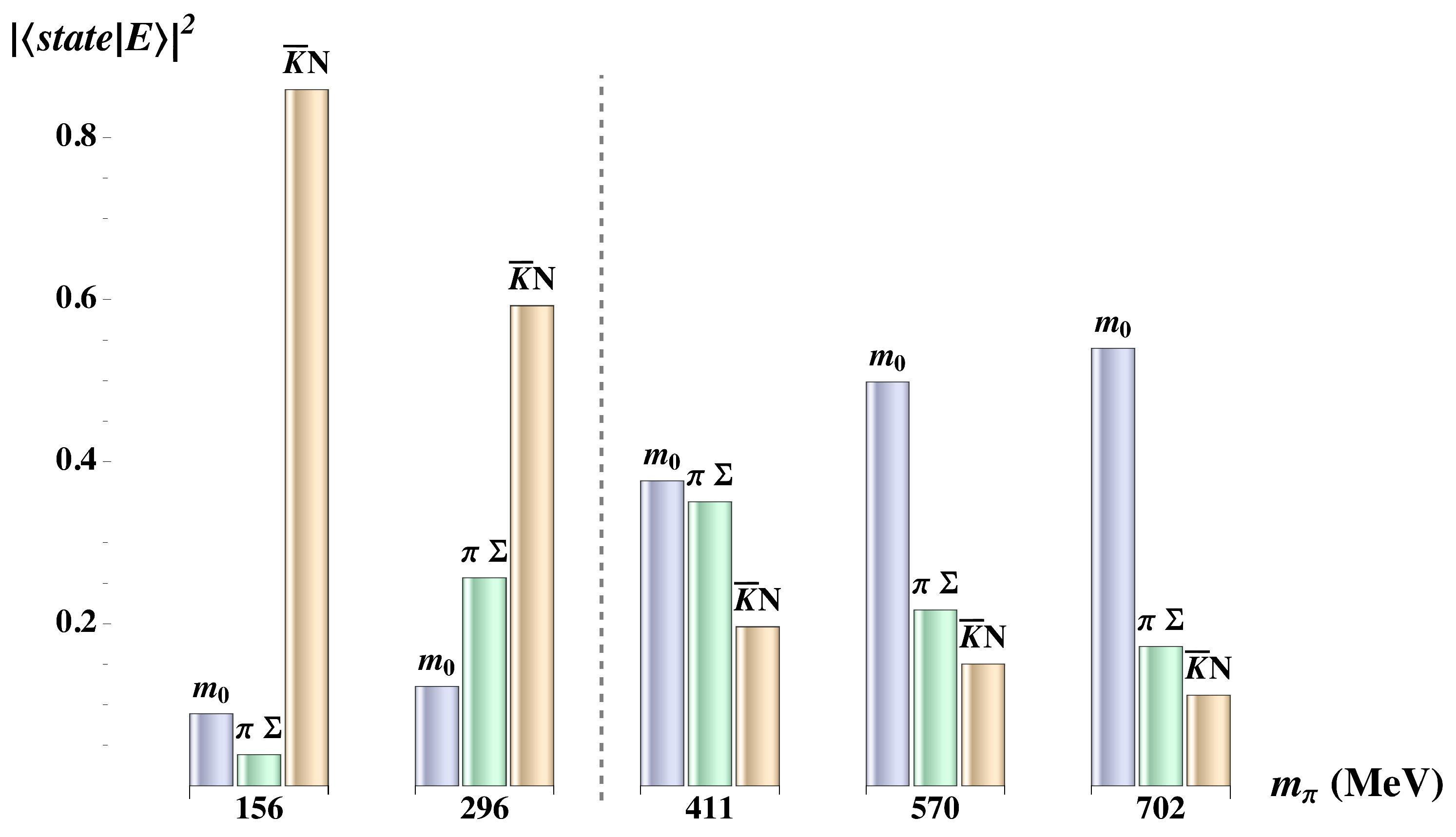
- Hall, J.M.M.; Kamleh, W.; Leinweber, D.B.; Menadue, B.J.; Owen, B.J.; Thomas, A.W.; Young, R.D. Lattice QCD Evidence that the Λ(1405) Resonance is an Antikaon-Nucleon Molecule. Phys. Rev. Lett. 2015, 114, 132002. [Google Scholar] [CrossRef]
- Hall, J.M.M.; Kamleh, W.; Leinweber, D.B.; Menadue, B.J.; Owen, B.J.; Thomas, A.W. Light-quark contributions to the magnetic form factor of the Lambda(1405). Phys. Rev. D 2017, 95, 054510. [Google Scholar] [CrossRef]
- Veneziano, G. Is There a QCD Spin Crisis? Mod. Phys. Lett. A 1989, 4, 1605. [Google Scholar] [CrossRef]
- Leader, E.; Anselmino, M. A crisis in the parton model: Where, oh where is the proton’s spin? Z. Phys. C Part. Fields 1988, 41, 239. [Google Scholar] [CrossRef]
- Ellis, J.R.; Jaffe, R.L. A Sum Rule for Deep Inelastic Electroproduction from Polarized Protons. Phys. Rev. D 1974, 9, 1444, Erratum in Phys. Rev. D 1974, 10, 1669. [Google Scholar] [CrossRef]
- Ashman, J.; Badelek, B.; Baum, G.; Beaufays, J.; Bee, C.P.; Benchouk, C.; Bird, I.G.; Brown, S.C.; Caputo, M.C.; Cheung, H.W.K. et al. A Measurement of the Spin Asymmetry and Determination of the Structure Function g(1) in Deep Inelastic Muon-Proton Scattering. Phys. Lett. B 1988, 206, 364. [Google Scholar] [CrossRef]
- Erler, J.; Su, S. The Weak Neutral Current. Prog. Part. Nucl. Phys. 2013, 71, 119–149. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Manohar, A. Strange Matrix Elements in the Proton from Neutral Current Experiments. Nucl. Phys. B 1988, 310, 527–547. [Google Scholar] [CrossRef]
- Leinweber, D.B. Quark contributions to baryon magnetic moments in full, quenched and partially quenched QCD. Phys. Rev. D 2004, 69, 014005. [Google Scholar] [CrossRef]
- Leinweber, D.B.; Boinepalli, S.; Cloet, I.C.; Thomas, A.W.; Williams, A.G.; Young, R.D.; Zanotti, J.M.; Zhang, J.B. Precise determination of the strangeness magnetic moment of the nucleon. Phys. Rev. Lett. 2005, 94, 212001. [Google Scholar] [CrossRef]
- Leinweber, D.B.; Boinepalli, S.; Thomas, A.W.; Wang, P.; Williams, A.G.; Young, R.D.; Zanotti, J.M.; Zhang, J.B. Strange electric form-factor of the proton. Phys. Rev. Lett. 2006, 97, 022001. [Google Scholar] [CrossRef]
- Acha, A.; Aniol, K.A.; Armstrong, D.S.; Arrington, J.; Averett, T.; Bailey, S.L.; Barber, J.; Beck, A.; Benaoum, H.; Benesch, J.; et al. Precision Measurements of the Nucleon Strange Form Factors at Q2 ~ 0.1-GeV 2. Phys. Rev. Lett. 2007, 98, 032301. [Google Scholar] [CrossRef]
- Androić, D.; Armstrong, D.S.; Arvieux, J.; Bailey, S.L.; Beck, D.H.; Beise, E.J.; Benesch, J.; Benmokhtar, F.; Bimbot, L.; Birchall, J.; et al. Strange Quark Contributions to Parity-Violating Asymmetries in the Backward Angle G0 Electron Scattering Experiment. Phys. Rev. Lett. 2010, 104, 012001. [Google Scholar] [CrossRef]
- Ahmed, Z.; Allada, K.; Aniol, K.; Armstrong, D.; Arrington, J.; Baturin, P.; Bellini, V.; Benesch, J.; Beminiwattha, R.; Benmokhtar, F.; et al. New Precision Limit on the Strange Vector Form Factors of the Proton. Phys. Rev. Lett. 2012, 108, 102001. [Google Scholar] [CrossRef]
- Alexandrou, C.; Bacchio, S.; Constantinou, M.; Finkenrath, J.; Hadjiyiannakou, K.; Jansen, K.; Koutsou, G. Nucleon strange electromagnetic form factors. Phys. Rev. D 2020, 101, 031501. [Google Scholar] [CrossRef]
- Hughes, V.W.; Papavassiliou, V.; Piegaia, R.; Schuler, K.P.; Baum, G. The Integral of the Spin Dependent Structure Function G(1)p and the Ellis-Jaffe Sum Rule. Phys. Lett. B 1988, 212, 511–514. [Google Scholar] [CrossRef][Green Version]
- Jaffe, R.L. The Axial Anomaly and the Sum Rules for Spin Dependent Electroproduction. Phys. Lett. B 1987, 193, 101–104. [Google Scholar] [CrossRef]
- Carlitz, R.D.; Collins, J.C.; Mueller, A.H. The Role of the Axial Anomaly in Measuring Spin Dependent Parton Distributions. Phys. Lett. B 1988, 214, 229–236. [Google Scholar] [CrossRef]
- Bodwin, G.T.; Qiu, J.W. The Gluonic Contribution to G(1) and Its Relationship to the Spin Dependent Parton Distributions. Phys. Rev. D 1990, 41, 2755. [Google Scholar] [CrossRef]
- Efremov, A.V.; Soffer, J.; Teryaev, O.V. Spin Structure of Nucleon and the Axial Anomaly. Nucl. Phys. B 1990, 346, 97–114. [Google Scholar] [CrossRef]
- Shore, G.M.; Veneziano, G. The U(1) Goldberger-Treiman Relation and the Two Components of the Proton ‘Spin’. Phys. Lett. B 1990, 244, 75–82. [Google Scholar] [CrossRef][Green Version]
- Bass, S.D.; Ioffe, B.L.; Nikolaev, N.N.; Thomas, A.W. On the infrared contribution to the photon-gluon scattering and the proton spin content. J. Moscow. Phys. Soc. 1991, 1, 317–333. [Google Scholar]
- Schreiber, A.W.; Thomas, A.W. Spin Dependent Structure Functions in the Cloudy Bag Model. Phys. Lett. B 1988, 215, 141–144. [Google Scholar] [CrossRef]
- Bazilevsky, A. The RHIC Spin Program Overview. J. Phys. Conf. Ser. 2016, 678, 012059. [Google Scholar] [CrossRef]
- de Florian, D.; Sassot, R.; Stratmann, M.; Vogelsang, W. Evidence for polarization of gluons in the proton. Phys. Rev. Lett. 2014, 113, 012001. [Google Scholar] [CrossRef]
- Abdallah, M.S.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, I.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; et al. Longitudinal double-spin asymmetry for inclusive jet and dijet production in polarized proton collisions at = 510 GeV. Phys. Rev. D 2022, 105, 092011. [Google Scholar] [CrossRef]
- Acharya, U.; Adare, A.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Alfred, M.; Apadula, N.; Aramaki, Y.; Asano, H.; et al. Measurement of charged pion double spin asymmetries at midrapidity in longitudinally polarized p + p collisions at = 510 GeV. Phys. Rev. D 2020, 102, 032001. [Google Scholar] [CrossRef]
- Myhrer, F.; Thomas, A.W. A possible resolution of the proton spin problem. Phys. Lett. B 2008, 663, 302–305. [Google Scholar] [CrossRef]
- Hogaasen, H.; Myhrer, F. SU(6) violations due to One Gluon Exchange. Phys. Rev. D 1988, 37, 1950. [Google Scholar] [CrossRef] [PubMed]
- Myhrer, F.; Thomas, A.W. Understanding the proton’s spin structure. J. Phys. G 2010, 37, 023101. [Google Scholar] [CrossRef][Green Version]
- Thomas, A.W. Interplay of Spin and Orbital Angular Momentum in the Proton. Phys. Rev. Lett. 2008, 101, 102003. [Google Scholar] [CrossRef]
- Arrington, J.; Battaglieri, M.; Boehnlein, A.; Bogacz, S.A.; Brooks, W.K.; Chudakov, E.; Cloët, I.; Ent, R.; Gao, H.; Grames, J.; et al. Physics with CEBAF at 12 GeV and future opportunities. Prog. Part. Nucl. Phys. 2022, 127, 103985. [Google Scholar] [CrossRef]
- Willeke, F. Electron Ion Collider Conceptual Design Report 2021; 2021. Available online: https://www.osti.gov/servlets/purl/1765663/ (accessed on 1 March 2025). [CrossRef]
- Khalek, R.A.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-Bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science Requirements and Detector Concepts for the Electron-Ion Collider: EIC Yellow Report. Nucl. Phys. A 2022, 1026, 122447. [Google Scholar] [CrossRef]
- Anderle, D.P.; Bertone, V.; Cao, X.; Chang, L.; Chang, N.; Chen, G.; Chen, X.; Chen, Z.; Cui, Z.; Dai, L.; et al. Electron-ion collider in China. Front. Phys. 2021, 16, 64701. [Google Scholar] [CrossRef]
- Ji, X.D. Breakup of hadron masses and energy—Momentum tensor of QCD. Phys. Rev. D 1995, 52, 271–281. [Google Scholar] [CrossRef]
- Balitsky, I.; Ji, X.D. How much of the nucleon spin is carried by glue? Phys. Rev. Lett. 1997, 79, 1225–1228. [Google Scholar] [CrossRef]
- Ji, X.D. Gauge-Invariant Decomposition of Nucleon Spin. Phys. Rev. Lett. 1997, 78, 610–613. [Google Scholar] [CrossRef]
- Ji, X.D. Off forward parton distributions. J. Phys. G 1998, 24, 1181–1205. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Radyushkin, A.V. Unraveling hadron structure with generalized parton distributions. Phys. Rep. 2005, 418, 1–387. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Müller, D.; Ji, Y. Compton scattering: From deeply virtual to quasi-real. Nucl. Phys. B 2014, 878, 214–268. [Google Scholar] [CrossRef]
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.B.; et al. Electron Ion Collider: The Next QCD Frontier: Understanding the glue that binds us all. Eur. Phys. J. A 2016, 52, 268. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomas, A. Reflections on Chiral Symmetry Within QCD. Symmetry 2025, 17, 512. https://doi.org/10.3390/sym17040512
Thomas A. Reflections on Chiral Symmetry Within QCD. Symmetry. 2025; 17(4):512. https://doi.org/10.3390/sym17040512
Chicago/Turabian StyleThomas, Anthony. 2025. "Reflections on Chiral Symmetry Within QCD" Symmetry 17, no. 4: 512. https://doi.org/10.3390/sym17040512
APA StyleThomas, A. (2025). Reflections on Chiral Symmetry Within QCD. Symmetry, 17(4), 512. https://doi.org/10.3390/sym17040512





