1. Introduction
Metaheuristics have become essential for solving complex computational problems that are otherwise intractable using exact methods within practical time constraints [
1,
2]. By drawing inspiration from natural phenomena such as evolution, swarm intelligence, and adaptive behaviors, metaheuristics offer flexible, high-level frameworks for navigating vast and dynamic solution spaces [
3]. This adaptability and robustness have made them indispensable in diverse fields—from logistics and engineering design to machine learning and data analytics—spurring continuous innovation and the hybridization of established approaches.
The recent shifts toward multi-cloud environments have introduced additional layers of complexity, particularly in security. In such environments, organizations rely on multiple cloud service providers to avoid vendor lock-in, enhance reliability, and optimize costs [
4,
5]. However, each provider presents unique operational protocols, cost structures, and compliance standards, making the harmonization of security measures both intricate and critical [
6]. The need to maintain consistent security configurations, identity and access controls, data encryption protocols, and disaster recovery strategies across different platforms presents a multi-objective optimization challenge that often involves conflicting requirements for cost, performance, and compliance [
7,
8]. Traditional optimization methods frequently encounter difficulties in these large-scale, high-dimensional, and discrete problem spaces [
9], whereas metaheuristics excel at escaping local optima and adapting to evolving constraints [
10,
11].
In this context, this paper introduces a novel JADEGMO algorithm for multi-cloud security optimization. The proposed method leverages the self-adaptive control parameters of JADE (an adaptive differential evolution technique) and the intensification–diversification strengths often associated with GMO-inspired frameworks (e.g., variants of grey wolf optimization or genetic multi-objective search). By uniting these complementary features, JADEGMO balances exploration and exploitation, allowing it to respond dynamically to shifting security threats and changing performance requirements. This adaptive balance is vital in multi-cloud security scenarios, where real-time updates to workloads, cost models, and regulatory demands necessitate continuous, near-optimal reconfiguration.
Beyond the technical aspects, this research is motivated by the growing complexity of hybrid and multi-cloud infrastructure, which increasingly integrates on-premises resources, legacy systems, and various public or private clouds. Addressing security in these heterogeneous settings demands advanced optimization algorithms capable of encompassing additional factors such as latency, interoperability, data locality, and resiliency. The new JADEGMO method aims to fill this gap by providing a robust, scalable, and adaptive approach that can holistically optimize security while balancing multiple, often competing, objectives.
Motivation and Contributions
Novel hybrid metaheuristic: We propose a new method—JADEGMO—that combines JADE’s self-adaptive properties with GMO-based global search techniques. Multi-cloud security optimization: The algorithm is specifically tailored to handle security requirements, cost constraints, performance trade-offs, and regulatory factors in multi-cloud environments. Adaptive and scalable: By blending exploration and exploitation, JADEGMO is designed to adapt to dynamic changes in workload demands and evolving cyber threats, offering robust performance in large-scale scenarios. Benchmarking and validation: Comprehensive experiments, using both synthetic and real-world multi-cloud case studies, demonstrate JADEGMO’s effectiveness compared to existing metaheuristics and mathematical programming approaches.
2. Literature Review
The optimization of resource allocation and task scheduling within multi-cloud environments has garnered significant attention in recent years due to the rapid growth in cloud computing and its diverse applications. Several research works have addressed the challenges associated with ensuring efficiency, security, and cost-effectiveness in such environments [
12].
2.1. Multi-Cloud Optimization
The problem of service composition across multiple clouds has been widely studied. Various decision-making algorithms have been proposed to select and integrate cloud services while minimizing cost and satisfying quality of service (QoS) constraints. Shirvani [
13] introduced a bi-objective genetic optimization algorithm for web service composition in multi-cloud environments, optimizing cost and performance. Similarly, Amirthayogam et al. [
14] proposed a hybrid optimization algorithm to enhance QoS-aware service composition. Other researchers, such as Wang et al. [
15], explored game-theoretic approaches for scheduling workflows in heterogeneous cloud environments. These studies demonstrate that multi-cloud service composition can reduce costs and improve performance by intelligently distributing components. However, real-world validation remains a challenge, and adapting these methods to dynamic environments like edge-cloud computing is an open issue.
2.2. Scheduling and Resource Allocation
Scheduling in multi-cloud environments is a complex problem that has been addressed through various optimization techniques. Toinard et al. [
16] proposed a cloud brokering framework using the PROMETHEE method, incorporating trust and assurance criteria. Díaz et al. [
17] focused on the optimal allocation of virtual machines (VMs) with pricing considerations, while Peng et al. [
18] addressed cost minimization for cloudlet-based workflows. More recently, Kaur et al. [
19] explored bio-inspired algorithms for scheduling in multi-cloud environments. Machine learning techniques have also been integrated into scheduling frameworks, as demonstrated by Cui et al. [
20], who proposed a dynamic load-balancing approach based on learning mechanisms. Despite these advances, real-time adaptability and fault tolerance in scheduling remain ongoing research challenges.
2.3. Security and Trust in Multiple Clouds
Security remains a major concern in multi-cloud environments. Casola et al. [
21] proposed an optimization approach for security-by-design in multi-cloud applications, ensuring compliance with security policies. John et al. [
22] examined attribute-based access control for secure collaborations between multiple clouds, addressing dynamic authorization challenges. Similarly, Yang et al. [
23] introduced a secure and cost-effective storage policy using NSGA-II-C optimization. These studies highlight the need for robust security frameworks to ensure trust and confidentiality in multi-cloud operations. However, interoperability and compliance issues continue to pose challenges, requiring further standardization efforts.
2.4. Cloud Brokering and Resource Management
Cloud brokering is a critical aspect of multi-cloud management. Ramamurthy et al. [
24] investigated the selection of cloud service providers for web applications in a multi-cloud setting. Pandey et al. [
25] developed a knowledge-engineered multi-cloud resource broker to optimize application workflows. Additionally, Addya et al. [
26] explored optimal VM coalition strategies for multi-tier applications. While these studies have provided efficient resource management strategies, seamless interoperability between different cloud providers remains a significant challenge. Comparative summary of the key literature on multi-cloud environment strategies is presented in
Table 1.
In [
27], the authors propose an optimized encryption-integrated container scheduling framework to enhance the orchestration of the containers in multi-cloud data centers. The study formulated container scheduling as an optimization problem, incorporating constraints related to energy consumption and server consolidation. A novel encryption model based on container attributes was introduced to ensure the security of the migrated containers, while the cost implications of encryption were carefully integrated into the scheduling process. The experimental results demonstrated substantial reductions in the number of active servers and power consumption, alongside balanced server loads, showcasing the efficacy of the proposed approach in real-world scenarios.
The significance of secure data sharing and task management in distributed systems was also emphasized in [
28], where a range of methodologies were explored to address data security and privacy concerns. The work highlighted advancements in information flow containment, cooperative data access in multi-cloud settings, and privacy-preserving data mining. Such efforts underline the growing need for integrated security policies and multi-party authorization frameworks to foster trust and collaboration in distributed systems.
Furthermore, the optimization of task scheduling in multi-cloud environments was explored [
29], where an improved optimization theory was applied to address the complexities of task allocation among multiple cloud service providers (CSPs). The proposed framework introduces a secure task scheduling paradigm that ensures collaboration among the CSPs while overcoming the limitations of the existing solutions. By addressing interoperability and security concerns, the work contributed to the development of robust scheduling mechanisms tailored to the multi-cloud landscape. Jawade and Ramachandram [
30] introduced a secure task scheduling scheme for multi-cloud environments, addressing the issue of risk probability during task execution. The study utilized a hybrid dragon-aided grey wolf optimization (DAGWO) technique to optimize task allocation while considering metrics such as makespan, execution time, utilization cost, and security constraints. The experimental results highlighted the effectiveness of DAGWO in achieving optimal resource utilization and improved security compared to existing methods.
Massonet et al. [
31] explored the integration of industrial standard security control frameworks into the multi-cloud deployment process. The study emphasized the importance of selecting cloud service providers (CSPs) based on their security capabilities, including their ability to monitor and meet predefined security requirements. By modeling security requirements as constraints within deployment objectives, the proposed approach aimed to generate optimal deployment plans. The research underscored the critical role of cloud security standards in achieving efficient and secure deployments across multiple CSPs.
Jogdand et al. [
32] addressed the security challenges associated with cloud storage, specifically focusing on data integrity, public verifiability, and availability in multi-cloud environments. The proposed solution combined the Merkle Hash Tree with the DepSky system model to ensure robust verification mechanisms and reliable data availability. The work advanced the field by incorporating inter-cloud collaboration to tackle the pressing issue of trustworthy and secure data management in multi-cloud systems.
Ref. [
33] provided a platform for diverse studies in cloud computing and related fields. The topics discussed included dynamic resource allocation, image-based password mechanisms, and innovative cloud computing models. These contributions highlight the ongoing efforts to address the multifaceted challenges of cloud computing, particularly in environments that require secure and efficient communication and data management.
2.5. Metaheuristic Algorithms in Edge and Cloud Computing
Metaheuristic algorithms have been extensively employed in edge and cloud computing environments to address a wide range of optimization challenges [
34]. These challenges include resource allocation, task scheduling, data routing, and service deployment. The inherent ability of metaheuristics to explore large and complex search spaces efficiently makes them particularly suitable for scenarios where traditional or exact methods are often infeasible due to high computational cost, frequent system reconfigurations, or rapidly changing problem constraints.
Differential evolution (DE) stands out among these metaheuristic techniques because of its simplicity, robustness, and powerful exploration capabilities [
35]. One noteworthy variation of DE involves adapting its population size dynamically (i.e., a variable population size), which helps to maintain a balance between the exploration of new solutions and the exploitation of high-quality solutions [
36]. This approach is especially useful in UAV-assisted IoT data collection systems, where deployment optimization frequently revolves around determining optimal UAV trajectories and placements. These optimizations aim to maximize data throughput or minimize energy consumption while respecting constraints such as UAV battery limitations and heterogeneous IoT device distributions [
37].
Beyond differential evolution, computational intelligence (CI) techniques (e.g., fuzzy systems, neural networks, evolutionary algorithms, and swarm intelligence) have also played a significant role in tackling issues specific to cloud and edge computing [
38]. For instance, resource management and scheduling solutions that incorporate CI-based approaches (e.g., genetic algorithms, deep reinforcement learning) can effectively balance energy consumption, latency requirements, and service-level agreements [
39]. Similarly, evolutionary strategies for service placement and migration in cloud-edge hierarchies can dynamically reposition services or virtual machines based on changing user demands [
40]. Swarm-based techniques, such as ant colony optimization and particle swarm optimization, have proven valuable in optimizing network paths, mitigating congestion, and achieving load balancing in distributed and often volatile edge networks [
41].
3. Proposed JADEGMO Hybrid Algorithm
The hybrid algorithm combines the strengths of JADE (adaptive differential evolution with optional external archive) [
42] and GMO (geometric mean optimizer) to create an efficient and robust optimization method. JADE is known for its adaptive parameter control and the use of an external archive to maintain diversity in the population, which helps with avoiding premature convergence. GMO, on the other hand, utilizes the concept of the geometric mean for guiding the search process and employs velocity updates similar to particle swarm optimization (PSO) to explore the solution space effectively.
By leveraging the adaptive mutation and crossover mechanisms from JADE along with the elite-guided search and velocity updates from GMO, the algorithm aims to optimize complex functions more effectively. This hybrid approach seeks to enhance both the exploration and exploitation capabilities of the optimization process. The adaptive parameters in JADE ensure a dynamic response to the current state of the search process, while the elite-guided mechanism in GMO helps with focusing the search around the promising regions of the solution space.
Initialization: The initial population P of size N is generated randomly within the bounds . Each individual is a potential solution in the search space.
Fitness evaluation: The fitness of each individual is evaluated using an objective function .
Adaptive parameter control: The crossover rate
and scaling factor
for each individual are adapted using normal and Cauchy distributions, as shown in Equations (
1) and (
2):
where
and
are the mean crossover rate and scaling factor, respectively.
Mutation: The mutant vector
for each individual
is generated as shown in Equation (
3):
where
is the best individual, and
and
are randomly selected individuals from the population or archive.
Crossover: The trial vector
is created by combining
and
, as shown in Equation (
4):
where
is the crossover rate, and
is a randomly chosen index.
Selection: The individual
is replaced if
has a better fitness, as we can see in Equation (
5):
Initialization: The initial positions and velocities of the particles are generated randomly within their respective bounds and .
Fitness evaluation: The fitness of each particle is evaluated using an objective function .
Elite selection: The best individuals (elite solutions) are selected based on their fitness values. The number of elite solutions
k decreases linearly from
to
over the iterations, as shown in Equation (
6):
where
t is the current iteration number.
Dual-fitness index (DFI): The DFI for each solution is calculated to assess its quality, as shown in Equation (
7):
where
is the standard deviation of the fitness values,
is the mean fitness, and
is the fitness of the
l-th solution.
Guide solution calculation: The guide solution
is computed as shown in Equation (
8):
where
are the dual-fitness indices, and
k is the number of elite solutions.
Velocity update: The velocity
of each particle is updated as shown in Equation (
9):
where
is the mutated guide solution, and
w is an inertia weight factor.
Position update: The position
is updated using the new velocity, as shown in Equation (
10):
3.1. Algorithm Description and Pseudocode
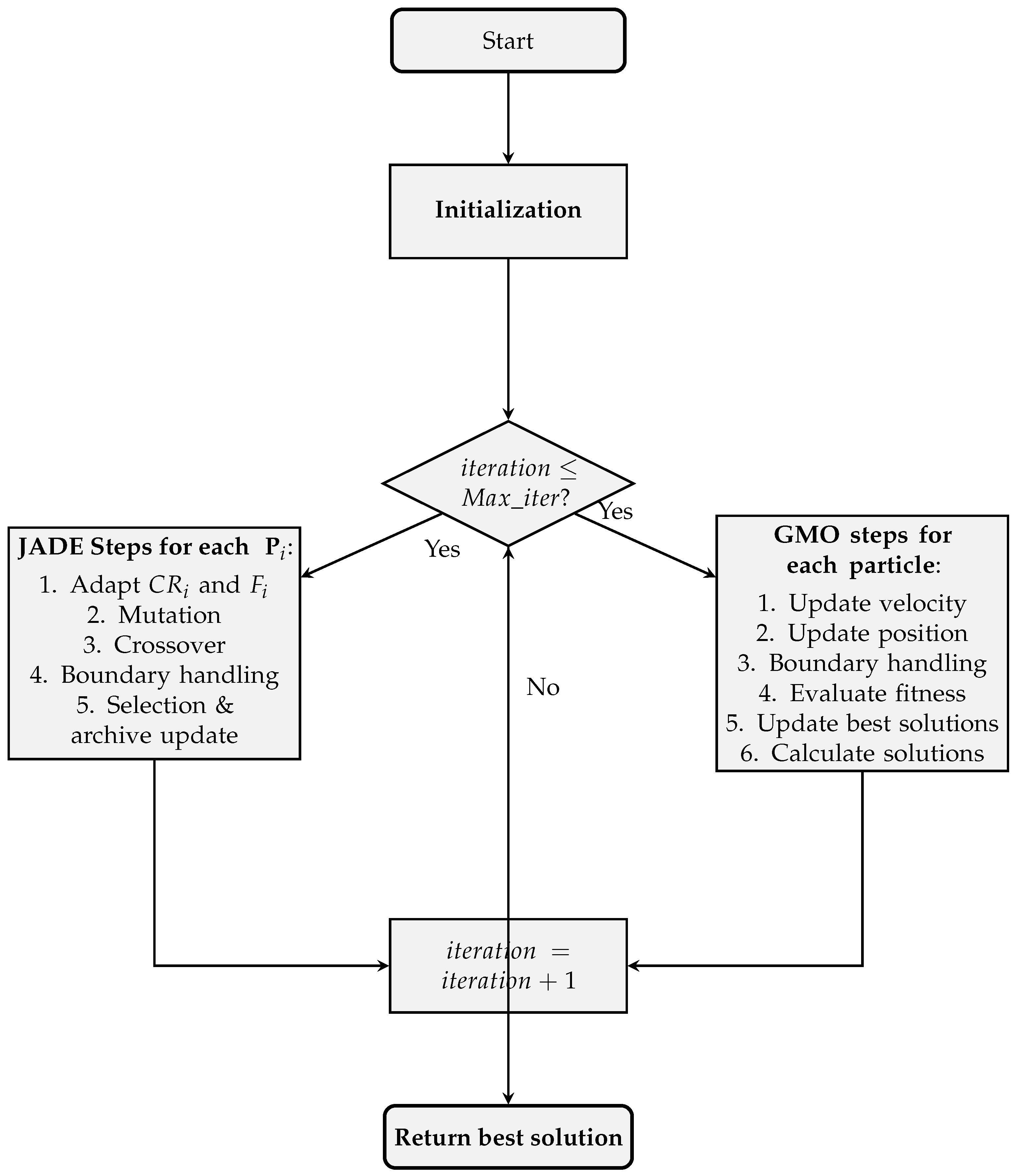
JADEGMO integrates JADE and GMO operations into a cohesive optimization process. The pseudocode outlining the main steps of the algorithm as shown in Algorithm 1 and the flow chart steps are shown in
Figure 1.
JADEGMO begins with the initialization of the population and velocities within predefined bounds. It then evaluates the fitness of the initial population and initializes an external archive. During each iteration, the JADE operations adaptively adjust the crossover rate and scaling factor, perform mutation and crossover to generate trial vectors, handle boundary conditions, and select better solutions to replace the current population, updating the archive accordingly. Concurrently, the GMO operations update particle velocities and positions, handle boundary conditions, evaluate fitness, and calculate guide solutions based on elite individuals. This iterative process continues until the maximum number of iterations is reached, ultimately returning the best solution found. The hybrid approach effectively explores the solution space, maintains diversity, and improves convergence towards optimal solutions. The source code is available at
https://www.mathworks.com/matlabcentral/fileexchange/180068-hybrid-jade-gmo-optimizer (accessed on 20 January 2025).
| Algorithm 1 Hybrid JADE-GMO algorithm. |
- 1:
Initialize population and velocities randomly within bounds - 2:
Evaluate initial fitness of population - 3:
Initialize archive - 4:
for to do - 5:
for each individual i in do - 6:
Adapt and according to Equations ( 1) and ( 2) - 7:
Mutation: Generate using best individual and random individuals as in Equation ( 3) - 8:
Crossover: Generate by combining and according to Equation ( 4) - 9:
Boundary handling for - 10:
Selection: Update if is better according to Equation ( 5) - 11:
Add replaced individuals to archive - 12:
end for - 13:
for each particle i in do - 14:
Update velocities using guide solutions and inertia weight as in Equation ( 9) - 15:
Update positions using new velocities according to Equation ( 10) - 16:
Boundary handling for updated positions - 17:
Evaluate fitness of updated positions - 18:
Update best-so-far solutions and objectives - 19:
Calculate guide solutions using elite solutions as in Equation ( 8) - 20:
end for - 21:
end for - 22:
return The best solution found
|
3.2. Exploration and Exploitation Behavior of JADEGMO
The exploration phase of JADEGMO is primarily driven by the JADE component. JADE’s adaptive parameter control and external archive significantly contribute to maintaining diversity in the population and preventing premature convergence. JADE dynamically adjusts the crossover rate
and scaling factor
for each individual using normal and Cauchy distributions, as described in Equations (
1) and (
2). This adaptability allows the algorithm to explore different regions of the search space effectively.
The mutation process, as shown in Equation (
3), generates mutant vectors by combining the best individual and randomly selected individuals from the population or archive. This helps with exploring new solutions that are not confined to the vicinity of the current population. Additionally, JADE maintains an external archive
of superior solutions that are not part of the current population. This archive enhances the algorithm’s exploratory capability by providing a diverse set of solutions that can be used in the mutation process, ensuring that the search does not become stuck in local optima. During the mutation process, the algorithm randomly selects individuals from the population and the archive. This random selection introduces variability and helps with exploring a wide range of solutions.
Exploitation Behavior
The exploitation phase of JADEGMO is significantly enhanced by the GMO component, which focuses on refining the search around the promising regions of the solution space. GMO selects the best individuals (elite solutions) based on their fitness values. The number of elite solutions decreases linearly from
to
over the iterations, as shown in Equation (
6). This focus on elite solutions ensures that the algorithm exploits the most promising areas of the search space.
The guide solutions
, computed using the dual-fitness indices (DFIs) as shown in Equation (
8), direct the search towards regions with high potential. These guide solutions help refine the search and improve the quality of the solutions. GMO updates the velocities of the particles using an inertia weight factor
w and the difference between the mutated guide solutions and current positions, as shown in Equation (
9). This mechanism ensures that the particles are directed towards better solutions, enhancing the exploitation of the search space. The position update, as described in Equation (
10), moves the particles closer to the guide solutions, further refining the search around the best-found solutions.
The DFI, calculated as shown in Equation (
7), assesses the quality of each solution by considering the fitness values of the other solutions in the population. This index helps with identifying the most promising solutions for exploitation, ensuring that the algorithm focuses its efforts on the best areas of the search space.
3.3. Rationale for Hybridizing JADE and GMO
In this section, we detail the theoretical and empirical justifications for combining JADE (adaptive differential evolution with optional external archive [
42] with GMO (geometric mean optimizer) to form the proposed hybrid algorithm. This design choice stemmed from our objective of achieving a robust balance between exploration and exploitation, while minimizing extensive parameter tuning and avoiding premature convergence.
3.3.1. Adaptive Parameter Control in JADE
JADE is distinguished from classic differential evolution (DE) by its built-in adaptive mechanism for parameter tuning. Specifically, JADE updates the mutation factor (F) and crossover rate () through a feedback process that relies on the performance of successful mutations. This adaptation reduces the dependency on manual parameter selection and enables JADE to effectively navigate different problem landscapes. As a result, JADE demonstrates an aptitude for refining candidate solutions around promising regions, which strengthens the exploitation phase of the search process.
3.3.2. Diversity Preservation in GMO
GMO introduces geometric strategies aimed at maintaining a diverse set of solutions. Its mutation operators are designed to mitigate premature convergence by introducing higher levels of variation in the population. This mechanism is particularly beneficial in multi-modal and complex optimization problems where the risk of stagnation is significant. By preserving a broad search horizon, GMO ensures that the global search capability of JADEGMO remains potent.
3.3.3. Strengths and Synergy
Combining JADE and GMO leverages the complementary strengths of these two algorithms:
Adaptive exploitation (JADE): The adaptive parameter control in JADE helps fine-tune solutions once promising regions of the search space are located.
Enhanced exploration (GMO): GMO’s diverse mutation strategies promote continuous exploration across the search space, reducing the likelihood of local optima entrapment.
When integrated, JADE’s feedback-driven refinements and GMO’s diversity-oriented approach reinforce one another, forming a balanced hybrid that can adapt to both simple and complex problem landscapes.
3.3.4. Empirical Evidence from Preliminary Studies
Prior to finalizing the proposed hybrid algorithm, we conducted several pilot experiments to evaluate different potential pairings of evolutionary optimizers. In these preliminary studies, the JADEGMO combination consistently achieved superior performance in terms of convergence speed and solution quality. We attribute this efficacy to the effective interplay between JADE’s adaptive parameter adjustments and GMO’s population diversity mechanisms. These findings informed our decision to focus on the JADEGMO hybrid for the main experimental phase of this research.
4. Experimental Results and Testing
4.1. Overview of IEEE Congress on Evolutionary Computation
(CEC2022)
The IEEE Congress on Evolutionary Computation (CEC2022) ( See
Figure 2) is a premier international event dedicated to the advancement and dissemination of research in evolutionary computation. Held annually, CEC2022 brings together researchers, practitioners, and industry experts from diverse fields to present their latest findings, exchange ideas, and discuss emerging trends and challenges in the domain. The conference covers a wide range of topics, including genetic algorithms, swarm intelligence, evolutionary multi-objective optimization, and real-world applications of evolutionary computation.
4.2. Results of CEC2022
As it can be seen in
Table 2 and
Table 3, JADEGMO consistently shows strong performance across a range of test functions. For instance, on functions F1, F2, F3, and F6, it achieves very low mean values and attains top-two overall ranks, reflecting its robustness in both unimodal and multi-modal landscapes. Notably, JADEGMO ranks forst on F2, underscoring its ability to escape local optima and converge effectively under that function’s conditions. Even on more challenging problems, such as F4 or F7, JADEGMO’s rankings remain near the upper quartile, indicating that its adaptive differential evolution strategies enable it to maintain competitiveness against a wide array of powerful modern optimizers (e.g., MFO, CMAES, and L_SHADE).
In comparison with the other optimizers, JADEGMO often outperforms prominent metaheuristics including FLO, STOA, and SPBO, which frequently obtain larger mean values or rank lower. However, a few algorithms occasionally outperform JADEGMO on selected test functions (e.g., L_SHADE on F1 and F3), illustrating that no single optimizer is universally dominant. Nevertheless, JADEGMO’s consistently low standard deviations and standard errors demonstrate stable convergence behavior. Overall, the results highlight JADEGMO as a top-tier method, exhibiting both reliability and strong optimization capability across a diverse set of benchmark functions.
4.3. JADE MGO Convergence Diagram
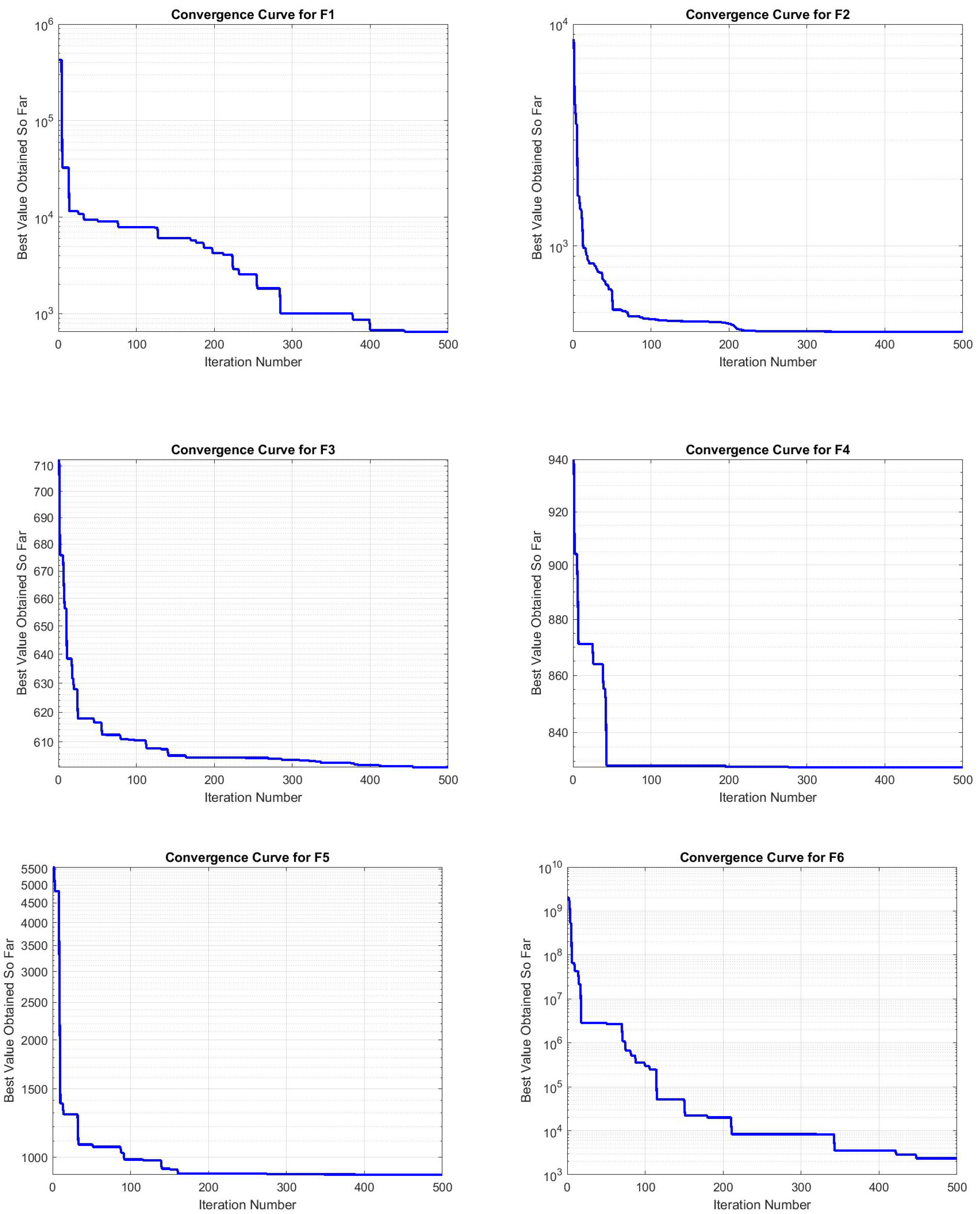
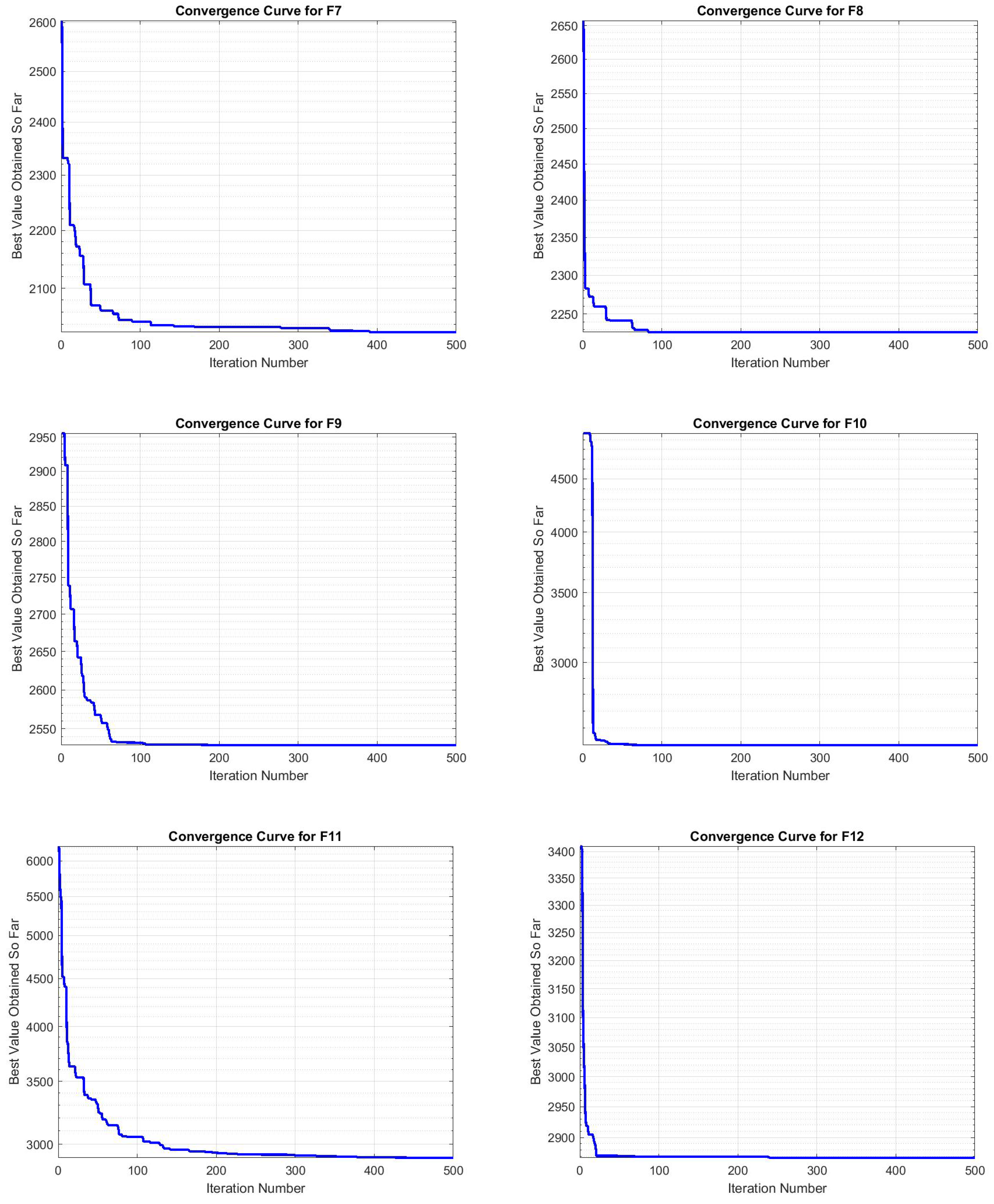
In
Figure 3 and
Figure 4, the convergence curves of functions F3, F5, and F6 demonstrate a pattern characterized by an initial rapid decrease in the objective function value, followed by phases of stagnation. This behavior suggests that the JADEGMO algorithm encounters challenges in further refining the solution after achieving an initial improvement, which is indicative of complex landscapes with numerous local optima. The intermittent plateaus observed in these curves imply that the algorithm might benefit from enhanced diversification strategies to avoid premature convergence. Moreover, the gradual downward trend seen in the later stages highlights the need for adaptive parameter tuning mechanisms that can dynamically adjust the exploration–exploitation balance to sustain progress and achieve better final solutions.
The convergence curves for JADEGMO JADEGMO from functions F1 to F12 on the CEC2022 benchmark exhibit a general pattern of rapid initial improvement, which stabilizes as the iterations increase. Specifically, the sharp initial drop observed in the curves suggests that JADEGMO efficiently identifies regions of significant improvement early in the search process. Functions F1, F2, and F3 show very steep declines within the first few iterations, indicating that the algorithm quickly approaches near-optimal solutions. This is indicative of JADEGMO’s effectiveness in exploring and exploiting the search space for functions with simpler landscapes or fewer local optima.
As the function indices increase, particularly from to , the convergence curves become gradually smoother after the initial drop, reflecting a slower rate of improvement as the algorithm fine-tunes the solutions in more complex problem landscapes. This variance across different function types highlights JADEGMO’s adaptive capability but also underscores challenges in handling functions with potentially deceptive or rugged landscapes.
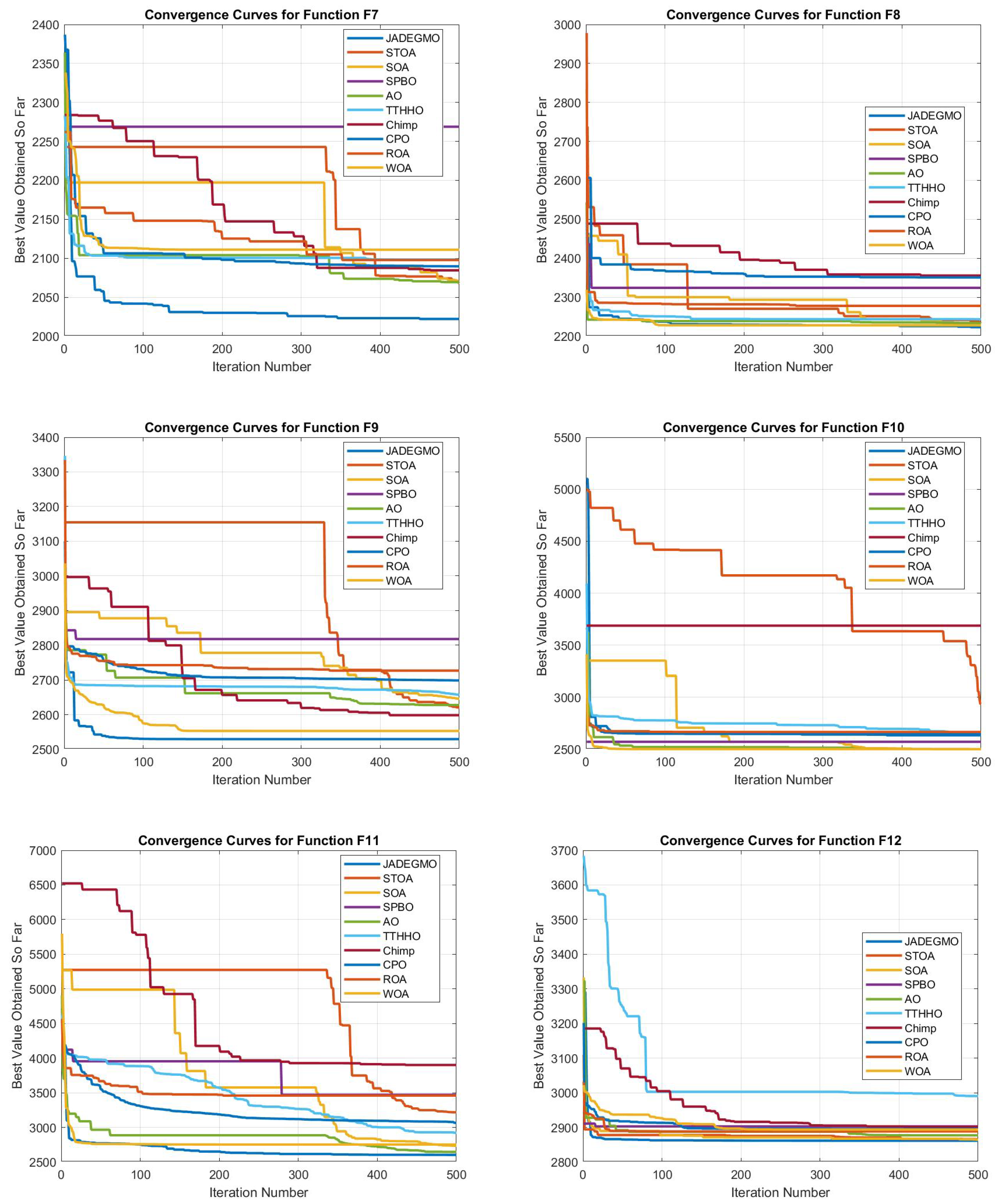
Comparison of JADEGMO Convergence with Other Optimizers
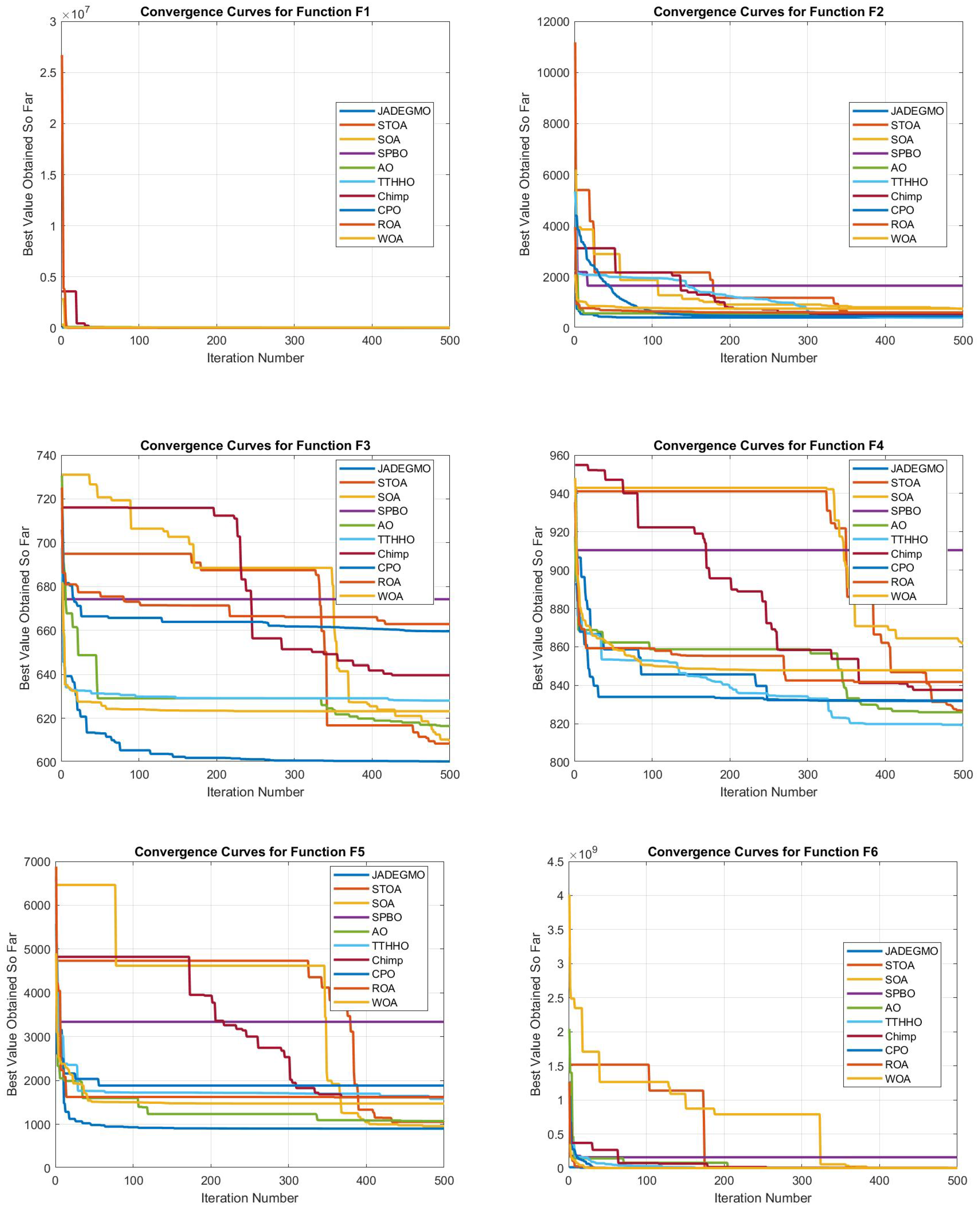
In
Figure 5 and
Figure 6, JADEGMO demonstrates superior convergence characteristics compared to most of the other optimizers across multiple test functions. The convergence plots indicate that JADEGMO consistently achieves a rapid decline in the objective function value within the initial iterations, suggesting strong exploration capabilities. Unlike some other optimizers such as STOA and SPBO, which exhibit stagnation in certain iterations, JADEGMO maintains a smooth and steady decline, indicating a balanced trade-off between exploration and exploitation. For instance, in functions such as F12 and F11, JADEGMO reaches an optimal value significantly faster than TTHHO and Chimp, which show delayed improvements or premature convergence. This suggests that JADEGMO is more resilient in navigating complex landscapes, avoiding local minima more effectively. Additionally, its final optimized values remain competitive, often outperforming traditional optimizers like ROA and WOA.
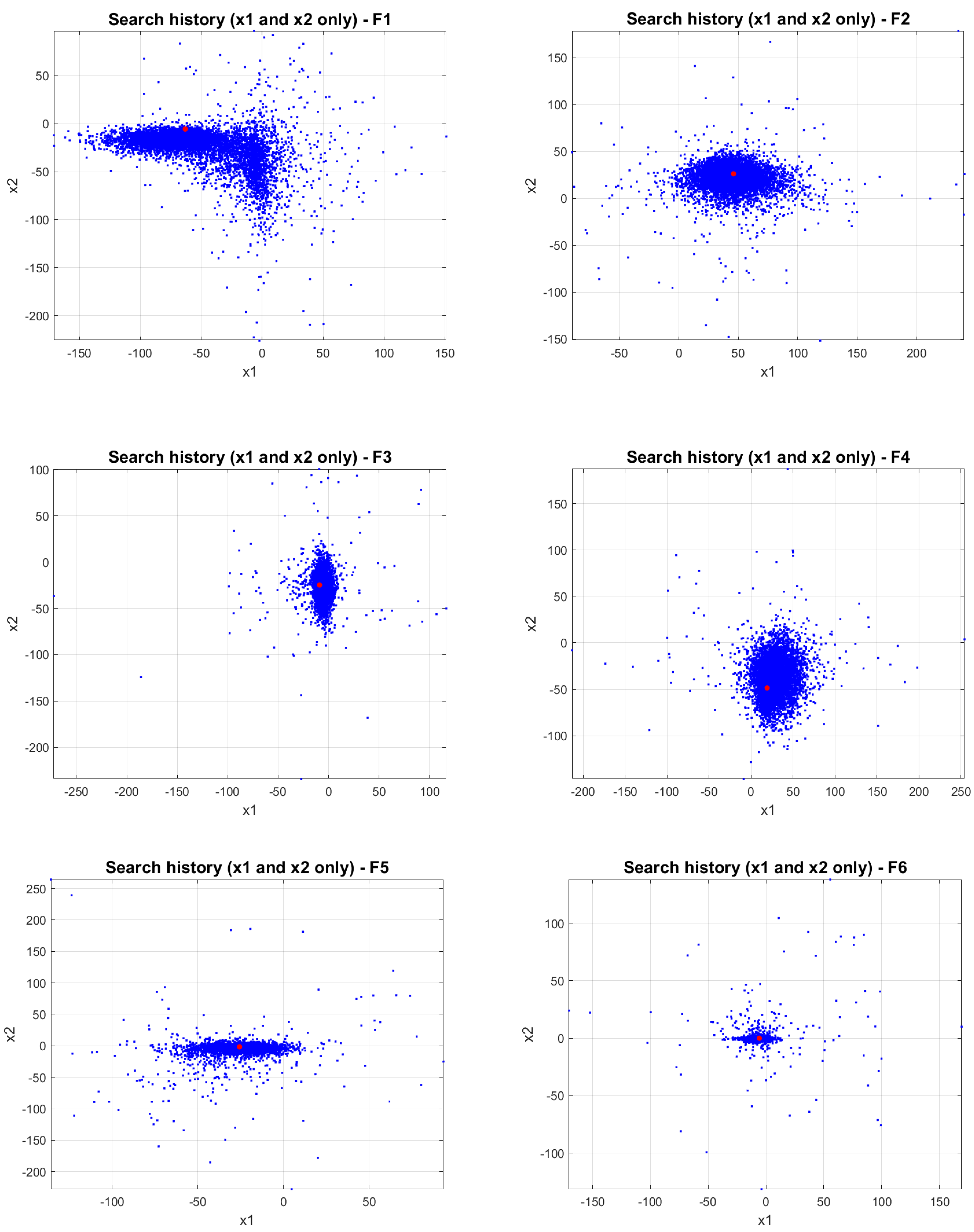
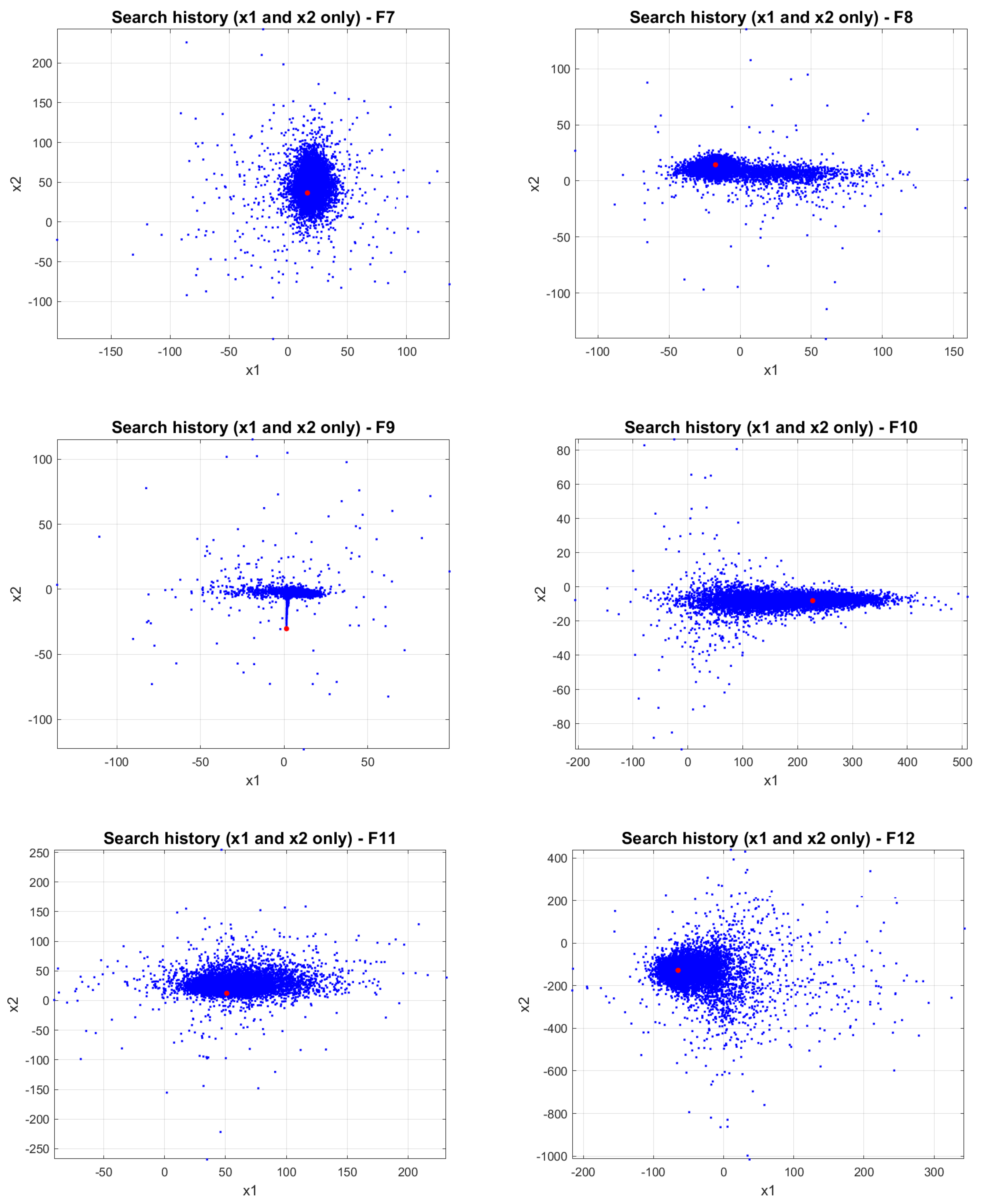
4.4. JADEGMO Search History Diagram
In
Figure 7 and
Figure 8, the search history plots of JADEGMO JADEGMO on CEC2022 functions
to
demonstrate varied explorative and exploitative behaviors across two-dimensional search spaces. For
and
, the algorithm disperses widely, suggesting a broad exploratory strategy, possibly due to flatter landscapes or deceptive optima. Contrastingly,
,
, and
exhibit dense clustering around the optimum, indicating strong local exploitation and possibly smoother landscapes.
shows more focused exploration, hinting at the presence of narrower global optima.
and
indicate targeted explorative behavior with notable spread, suggesting a mix of landscape features. Finally,
and
show a denser, centralized search pattern, reflecting effective exploitation amidst potentially challenging search landscapes with multiple local optima.
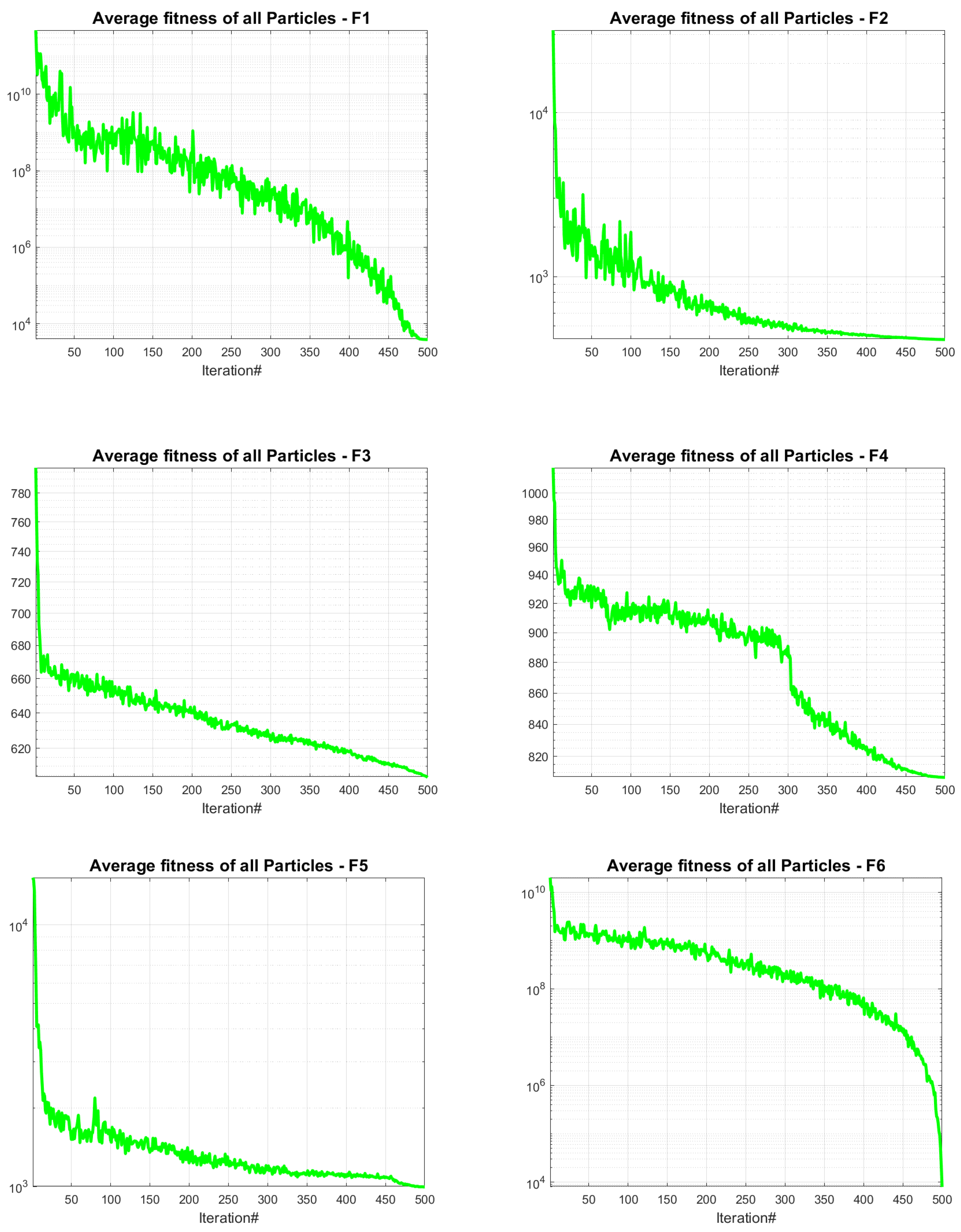
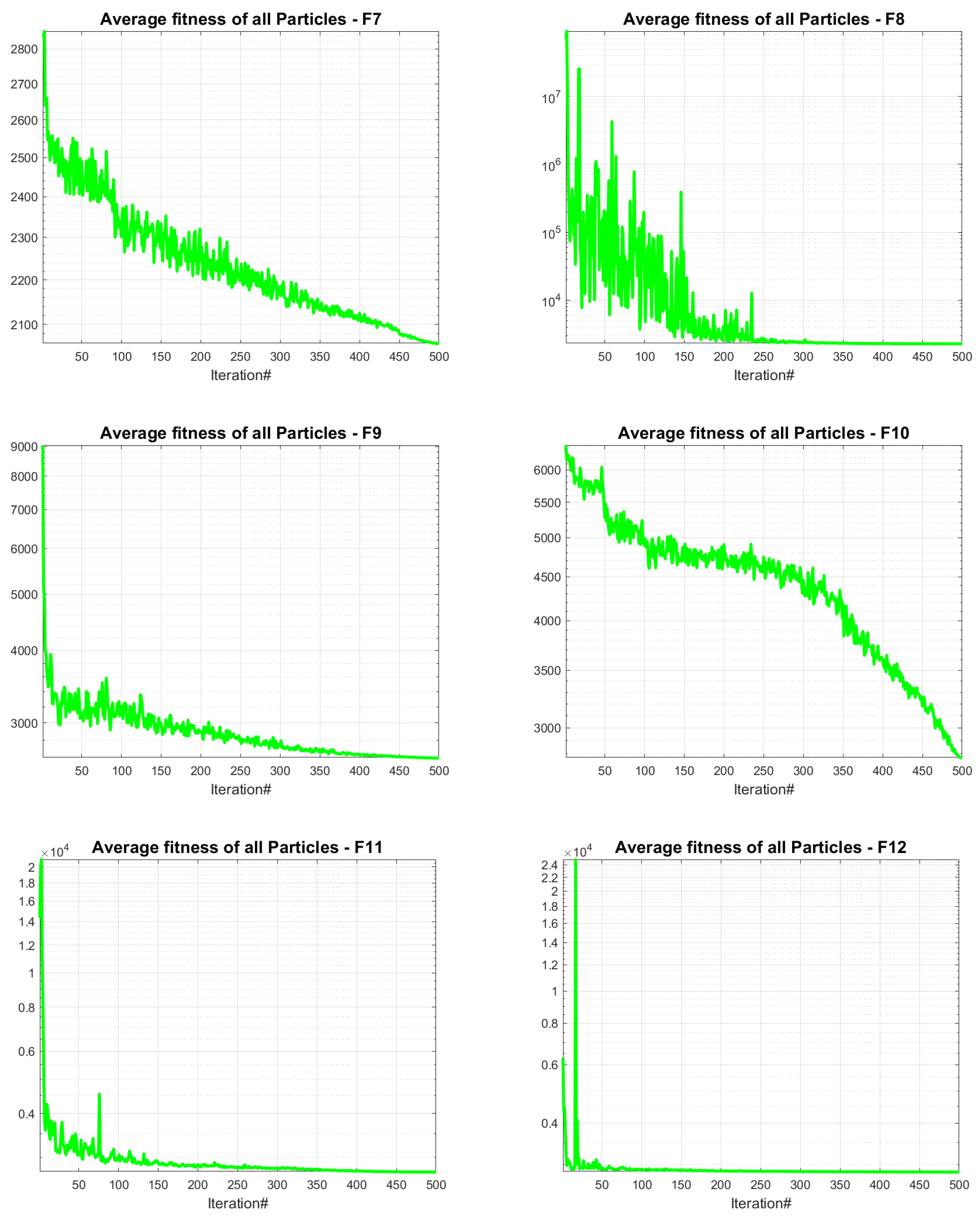
4.5. JADEGMO Average Fitness Diagram
In
Figure 9 and
Figure 10, the progression of the average fitness for JADEGMO JADEGMO from functions
to
on the CEC2022 benchmark demonstrates varied rates of convergence and stabilization. Functions
,
, and
display rapid initial decreases in average fitness, indicating a swift convergence towards better solutions in the early iterations. The steady decline through the subsequent iterations suggests continuous improvement, albeit at a decreasing rate, pointing towards the algorithm’s efficiency in refining solutions. In contrast, functions
and
exhibit a more gradual descent, potentially highlighting a more challenging landscape or slower optimization progress. Functions
and
show significant fluctuations, which may indicate the algorithm’s struggle with complex landscapes characterized by multiple local optima or steep gradients. Functions
,
, and
reveal a more consistent decrease after an initial steep drop, suggesting effective exploitation of the search space after rapidly escaping inferior regions.
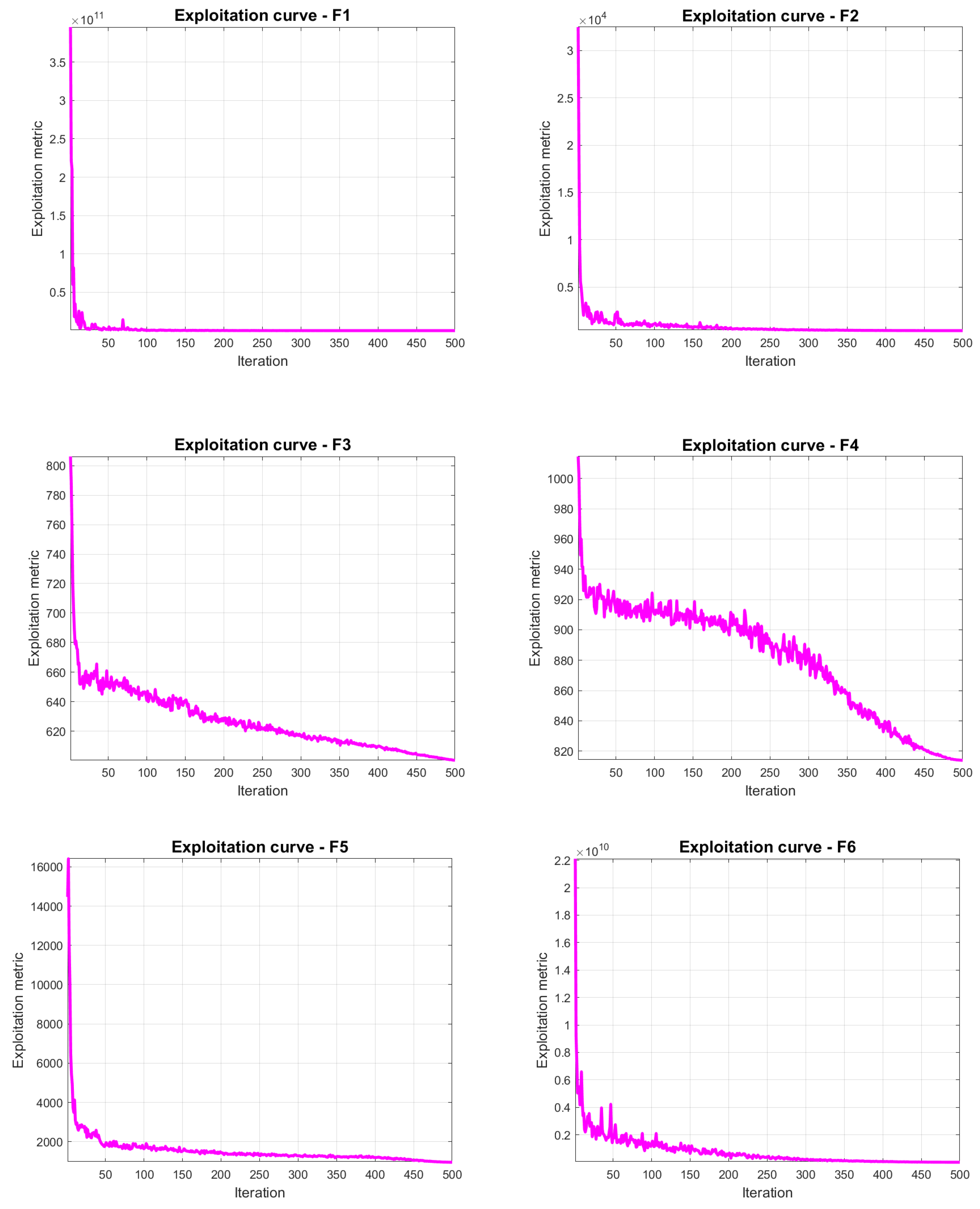
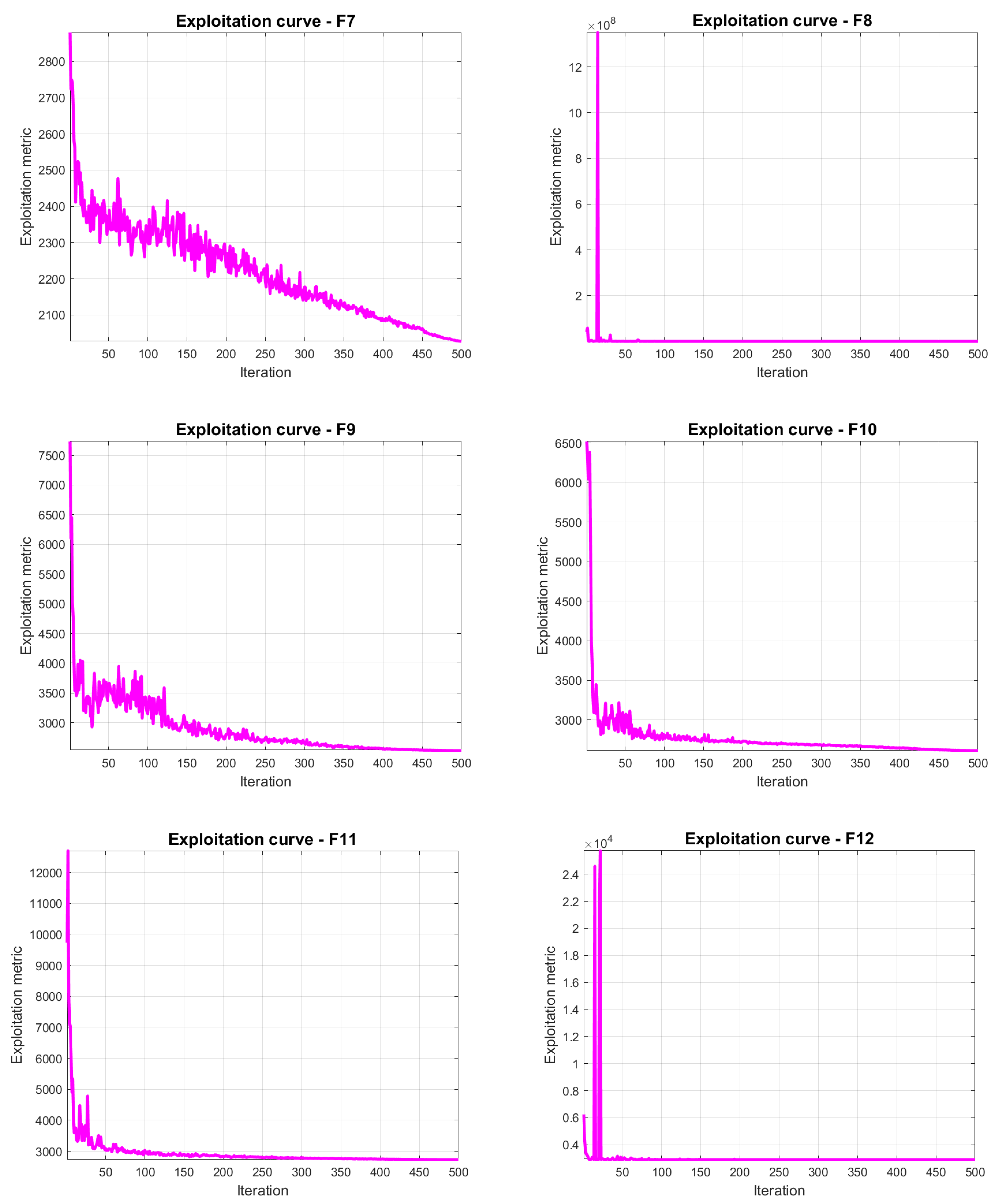
4.6. JADEGMO Exploitation Diagram
In
Figure 11 and
Figure 12, the exploitation metrics of JADEGMO JADEGMO over the CEC2022 benchmark for functions F1 to F12 reveal significant insights into its performance dynamics. Initially, for all functions, there is a steep drop in the exploitation metric, indicating rapid convergence towards regions of higher exploitation in the search space. This is particularly evident in the initial iterations where the algorithm aggressively exploits the potential solutions. As the iterations progress, the curves tend to flatten, suggesting a reduction in the rate of exploitation improvement. This behavior is consistent across all functions, with F1 and F2 showing a sharp initial decline before stabilizing, while functions like F5 and F11 display occasional spikes in later iterations, indicating intermittent explorations that potentially escape local optima.
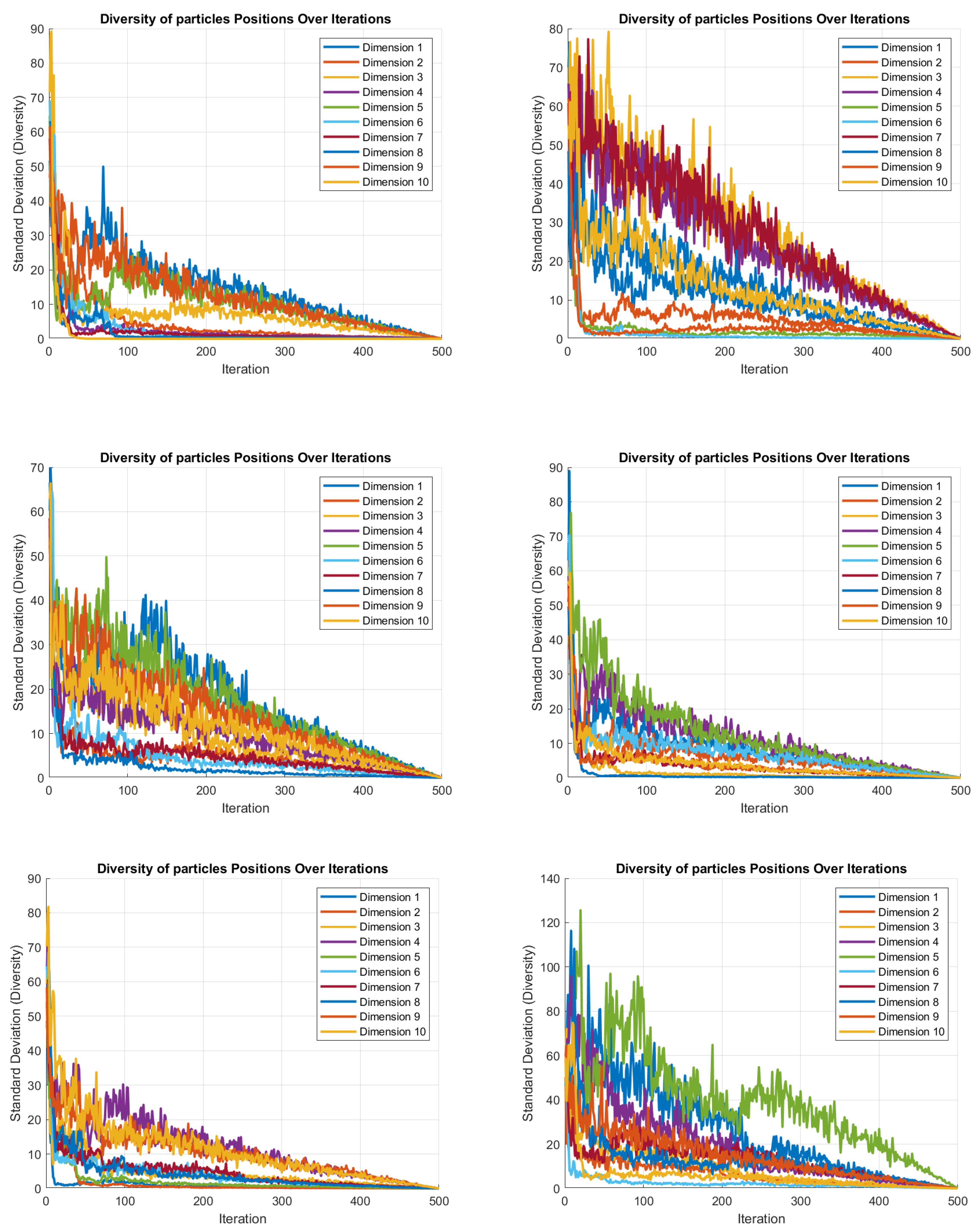
4.7. JADEGMO Diversity Diagram
In
Figure 13 and
Figure 14, the hybrid JADEGMO algorithm’s behavior on the CEC2022 benchmark for functions F1 to F12 illustrates a pronounced trend in diversity decay across all dimensions, as observed in the standard deviation of the particles’ positions over iterations. The diversity within the swarm shows a steep drop within the initial iterations, reflecting a quick convergence towards regions of interest. This pattern is most prominent in the dimensions where the initial diversity is the highest; typically, these initial high values indicate exploration, where the algorithm tests a wide variety of possible solutions. As the iterations progress, the decrease in standard deviation across all dimensions signifies a shift from exploration to exploitation, narrowing the search to promising regions. This transition is visible across all test functions, suggesting the consistent performance characteristic of JADEGMO in maintaining sufficient exploration before converging, which is critical for avoiding local minima in complex optimization landscapes.
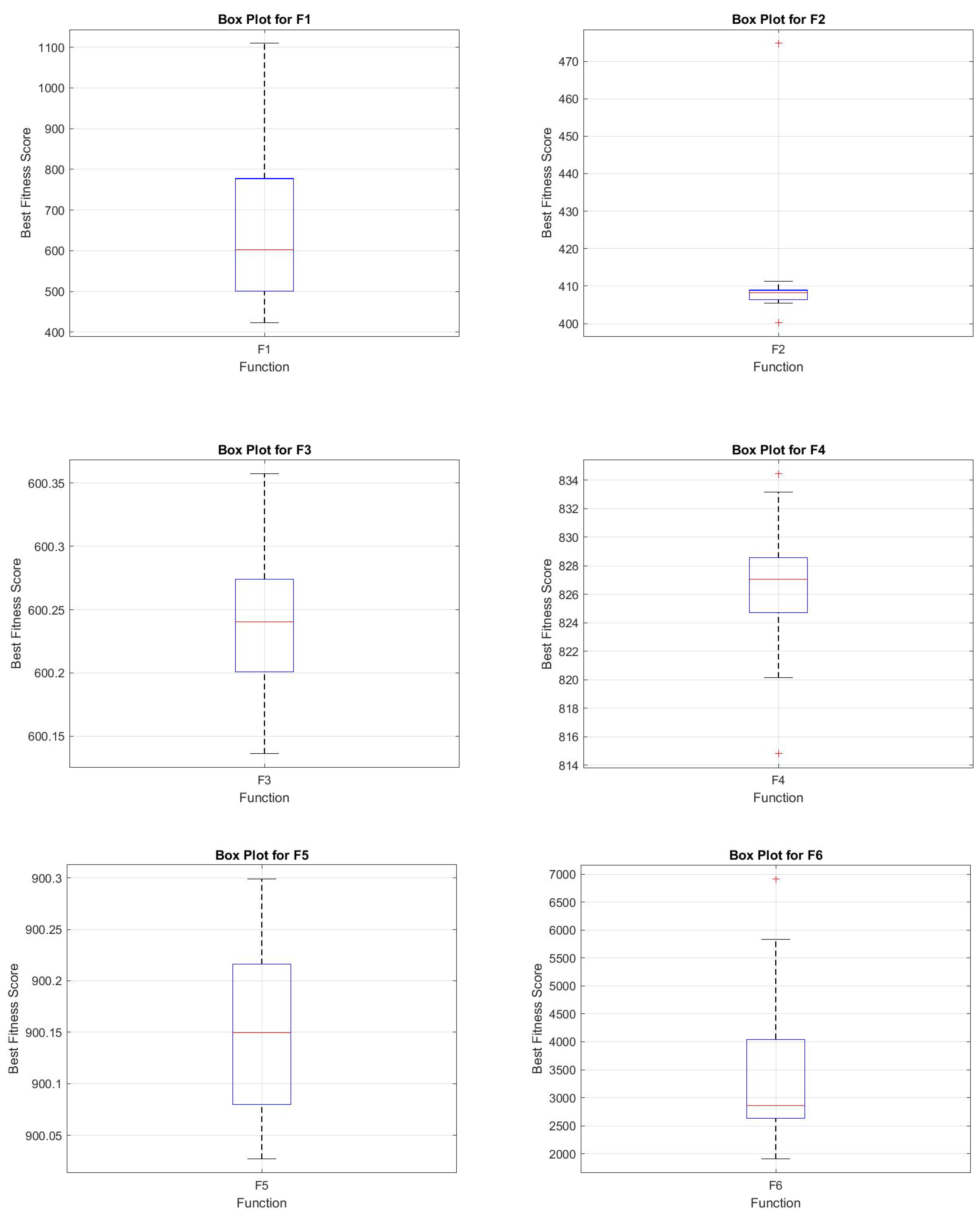
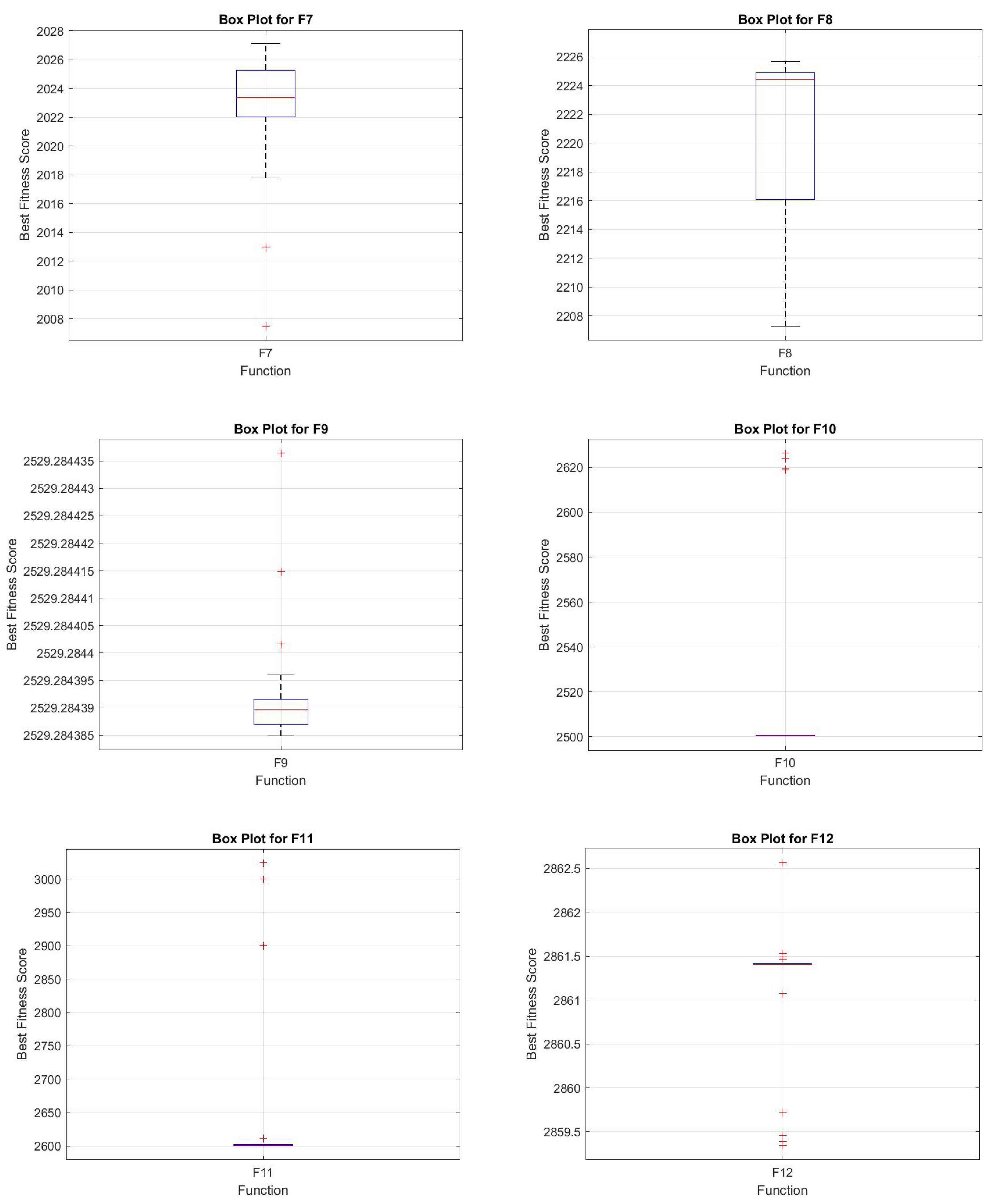
4.8. Box-Plot Analysis
In
Figure 15 and
Figure 16, the box plot analysis of the hybrid JADEGMO algorithm across various benchmark functions (F1 to F12) from the CEC2022 suite demonstrates a consistent performance with varied ranges of fitness scores. For simpler functions like F2 and F3, the box plots reveal tightly grouped fitness scores, indicating a robust optimization capability with minimal deviation among the runs. In contrast, more complex functions such as F6 and F12 display wider interquartile ranges and outliers, suggesting challenges in achieving consistent optima across runs. Functions like F4 and F5 show minimal outliers, implying that the algorithm manages to maintain stability across these problem landscapes.
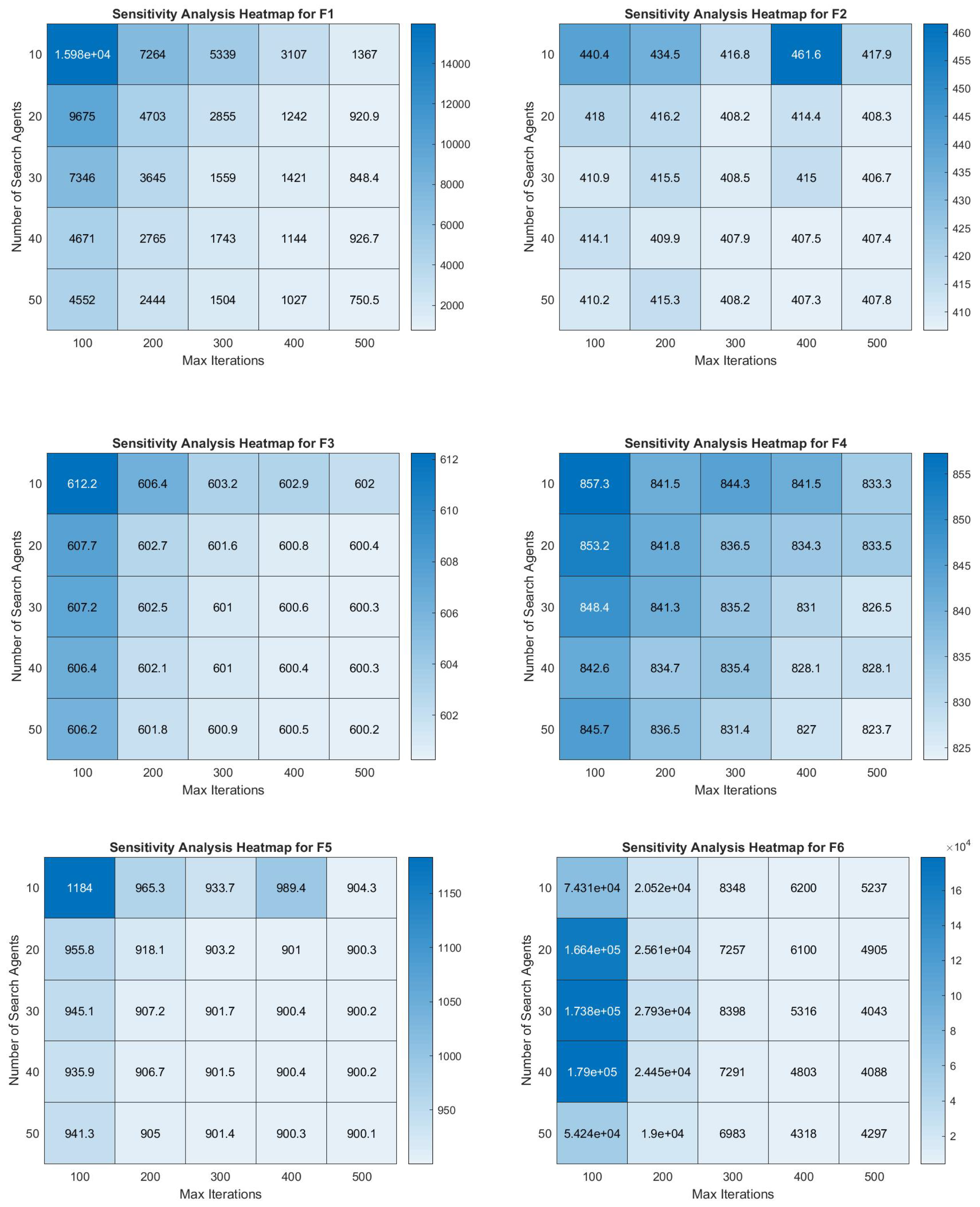
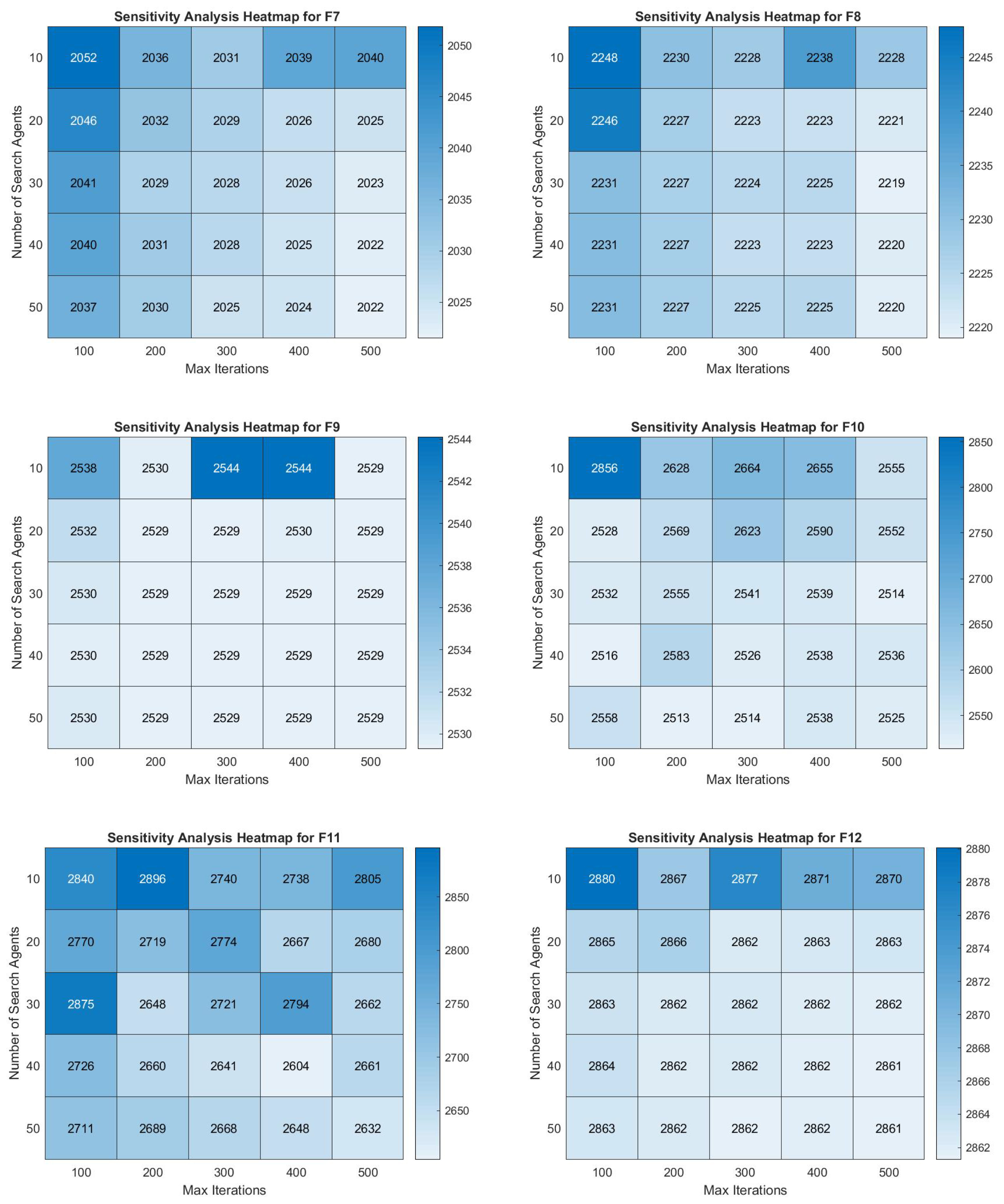
4.9. JADEGMO Heatmap Analysis
In
Figure 17 and
Figure 18, the sensitivity analysis heatmaps for the JADEGMO algorithm foor functions F1 to F12 within the CEC2022 benchmark suite provide insightful revelations into the algorithm’s performance sensitivity relative to the number of search agents and maximum iterations. Notably, the performance tends to stabilize with an increasing number of search agents and iterations, as evidenced by narrower color gradients in the heatmaps for higher values. For example, F1 shows drastic changes at lower search agents but stabilizes as iterations increase. In contrast, functions like F6 display extreme sensitivity across both dimensions, with significant performance variation even at higher numbers of iterations. Functions such as F12 demonstrate minor variations across different setups, indicating robustness against changes in the number of agents and iterations.
4.10. JADEGMO Histogram Analysis
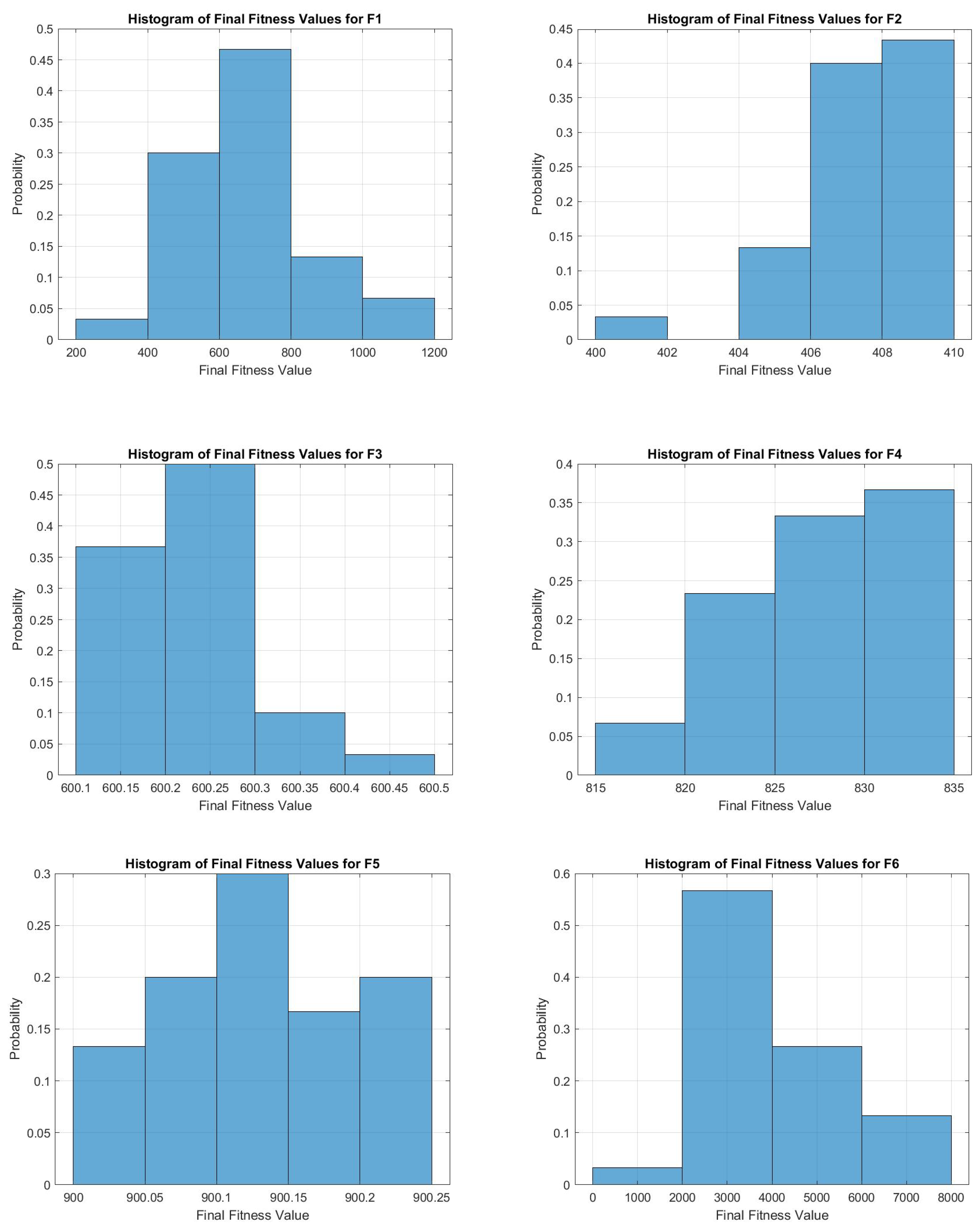
In
Figure 19 and
Figure 20, we can observe that JADEGMO yields consistently favorable outcomes across the 12 benchmark functions (F1–F12) of the CEC2022 suite. In particular, for functions such as F1, F2, F3, and F5, the final fitness values cluster tightly around a relatively low region, suggesting both high solution quality and low variance. This tight clustering indicates that JADEGMO not only converges to promising minima but does so reliably across multiple runs. On the moderately more difficult cases, for example, F4 and F7, the histograms still show a unimodal or near-unimodal pattern around a good fitness level, reinforcing the stability of the algorithm’s performance.
In the more challenging functions (e.g., F6, F9, and F10), the histograms widen somewhat, reflecting a larger spread in the final solutions. Nonetheless, JADEGMO still produces predominantly low fitness values, indicating that while the search space may be more complex, the algorithm consistently locates promising regions. Overall, these histograms underscore JADEGMO’s robustness in handling a variety of CEC2022 functions under constrained function evaluations. Its ability to converge with comparatively small variance highlights the effectiveness of its adaptive strategies in maintaining a balance between exploration and exploitation.
5. Application of JADEGMO in Multi-Cloud Security Configuration
Cloud computing has evolved into a dominant paradigm for delivering scalable and on-demand IT services to organizations of all sizes. With the ability to spin-up virtual machines, containers, serverless functions, and specialized software stacks at will, businesses can adapt much more efficiently to fluctuating computational demands. However, the popularity of cloud environments has also led to increasingly complex security requirements. As organizations embrace hybrid and multi-cloud strategies—where resources are distributed across different providers, such as Amazon Web Services (AWS), Microsoft Azure, and Google Cloud Platform (GCP)—the challenge of managing security configurations grows in scope and difficulty.
Traditionally, security in cloud environments involves configuring firewalls, identity and access management (IAM) policies, encryption schemes, patching routines, and specialized threat detection. Yet, the interplay of these measures can be intricate. For instance, enabling stronger encryption can drastically reduce certain vulnerabilities at the cost of higher computational overhead. Restricting the number of open ports can limit an attack surface but also degrade performance for valid use cases. Adding advanced security subscriptions (e.g., analytics modules or auto-patching) may reduce risk but at an increased financial or performance expense. These push-and-pull relationships motivate the need to systematically find the best compromise between risk mitigation and operational cost.
Metaheuristic algorithms, known for tackling computationally challenging optimization tasks in a wide range of fields, offer a promising approach. They excel in exploring high-dimensional or nonlinear search spaces while avoiding local minima by design. However, no single metaheuristic consistently outperforms all others in every context, as articulated by the “No Free Lunch” [
43]. This reality underscores the importance of algorithmic comparison and problem-specific tuning, further supported by a robust experimental methodology.
We solved a multi-cloud security configuration problem with three major cloud platforms. Each platform had five discrete control parameters, leading to a 15-dimensional decision space. Our goal was to minimize an enhanced security-cost function that merged various risk and cost components. The main contributions are as follows:
Problem formulation: We designed an objective function that models baseline risk, port usage trade-offs, encryption overhead, privilege-level effects, and subscription-based features. The function ensures no trivial zero-cost solution exists, forcing nontrivial exploration.
We compared JADEGMO with six other well-known or newly proposed metaheuristics over 30 runs each. We recorded the standard and advanced statistics, visualized convergence, conducted rank analyses, and held detailed performance discussions.
6. Problem Definition
6.1. Multi-Cloud Configuration Parameters
We consider a scenario involving three primary cloud platforms, each with five parameters that control security-related settings. This results in a 15-dimensional vector representing the entire problem space, as shown in Equation (
11):
where indices 1, 2, and 3 correspond to AWS, Azure, and GCP, respectively. The five parameters for each platform are as follows: encryption level (
, integer), number of open ports (
, integer), privilege level (
, integer), advanced analytics subscription (
, binary), and auto-patching subscription (
, binary). Even when real-coded optimizers generate continuous values, each parameter was rounded and clamped within the function evaluation to ensure validity. Equation (
11) encapsulates the configuration vector for this multi-cloud setup.
6.2. Enhanced Security-Cost Function
One of the contributions of this study is an enhanced cost function that discourages trivial or naive solutions. The cost for each cloud was computed through multiple terms:
6.2.1. Baseline Risk
A minimal level of risk is always present. We chose a baseline of 5 units of risk.
6.2.2. Port Risk
An excessively high number of open ports increases the attack surface, while too few ports may hamper legitimate operations. We thus imposed a penalty for fewer than 2 ports and for more than 5 ports, as shown in Equation (
12):
6.2.3. Privilege-Level Risk
The privilege-level risk was modeled nonlinearly to reflect the steep rise in danger as privileges accumulate. If
p is the privilege level, we use Equation (
13):
6.2.4. Encryption Effects
Encryption can drastically lower risk but at a resource and administrative overhead. If
e is the encryption level (0 to 3), as shown in Equation (
14):
Higher encryption levels decrease residual risk but increase overhead cost.
6.2.5. Subscriptions
Two binary options are available:
If , we reduce the risk by 5 and add a subscription cost of 15. If , we reduce the risk by 3 and add a subscription cost of 8.
6.2.6. Aggregation
Summing these contributions yields a partial risk:
We then impose a residual floor:
The final cost for a single cloud is
Finally, as shown in Equation (
15), the cost across all three clouds is
6.3. Why This Formulation Is Nontrivial
The above cost function has multiple opposing forces. Decreasing open ports beyond a certain threshold triggers a functionality penalty, while opening more than five ports triggers a security penalty. Selecting the highest encryption level eliminates most of the risk but imposes a large overhead. Subscribing to advanced features helps reduce the risk further, yet it inflates costs. Privilege-level risk grows faster than linearly. By carefully balancing these factors, we ensure there is no single, obvious “best” extreme solution (e.g., everything turned off or on), and metaheuristics must explore a nuanced configuration space.
7. Methodology and Experimental Setup
We employed consistent settings across all algorithms: a population size of 20 search agents, a problem dimension of 15 (5 parameters per cloud multiplied by 3 clouds), a maximum of 200 iterations, and 30 independent runs per algorithm. For each run, we recorded the best solution (lowest cost) found by the algorithm, the convergence curve of the best objective value over the iterations, and the execution time. Overall, the dataset comprised a total of runs.
Statistical Analysis
After collecting all runs, extended statistical metrics were computed for each optimizer to evaluate their performance comprehensively. These metrics included the single best cost (minimum) and the worst cost (maximum) found across all runs, as well as the mean and median best costs to represent central tendencies. Dispersion was analyzed using the standard deviation and the interquartile range (IQR), which captures the range between the 75th and 25th percentiles of the best costs. Additionally, the mean and standard deviation of the execution times per run (MeanTime and StdTime) were calculated. To compare algorithms, an average rank was determined by ranking them from 1 to 7 based on the final best cost in each of the 30 runs, with ties assigned an average rank. These ranks were then averaged across runs to provide an overall performance indicator. The average rank is particularly insightful as it highlights an algorithm’s general performance and consistency, with a lower rank indicating stronger or more reliable outcomes.
8. Multi-Cloud Configuration Parameters Results
Table 4 displays the aggregated statistics over 30 runs for each of the seven algorithms. JADEGMO emerges as the top contender, achieving a minimum best cost of 42, a mean best cost near 47.47, and the most favorable average rank (1.40). SCA places second in average rank, while algorithms like HLOA, MVO, and WOA lie in the middle range with slightly higher costs and/or greater variability. FLO and AOA generally yield even higher final costs.
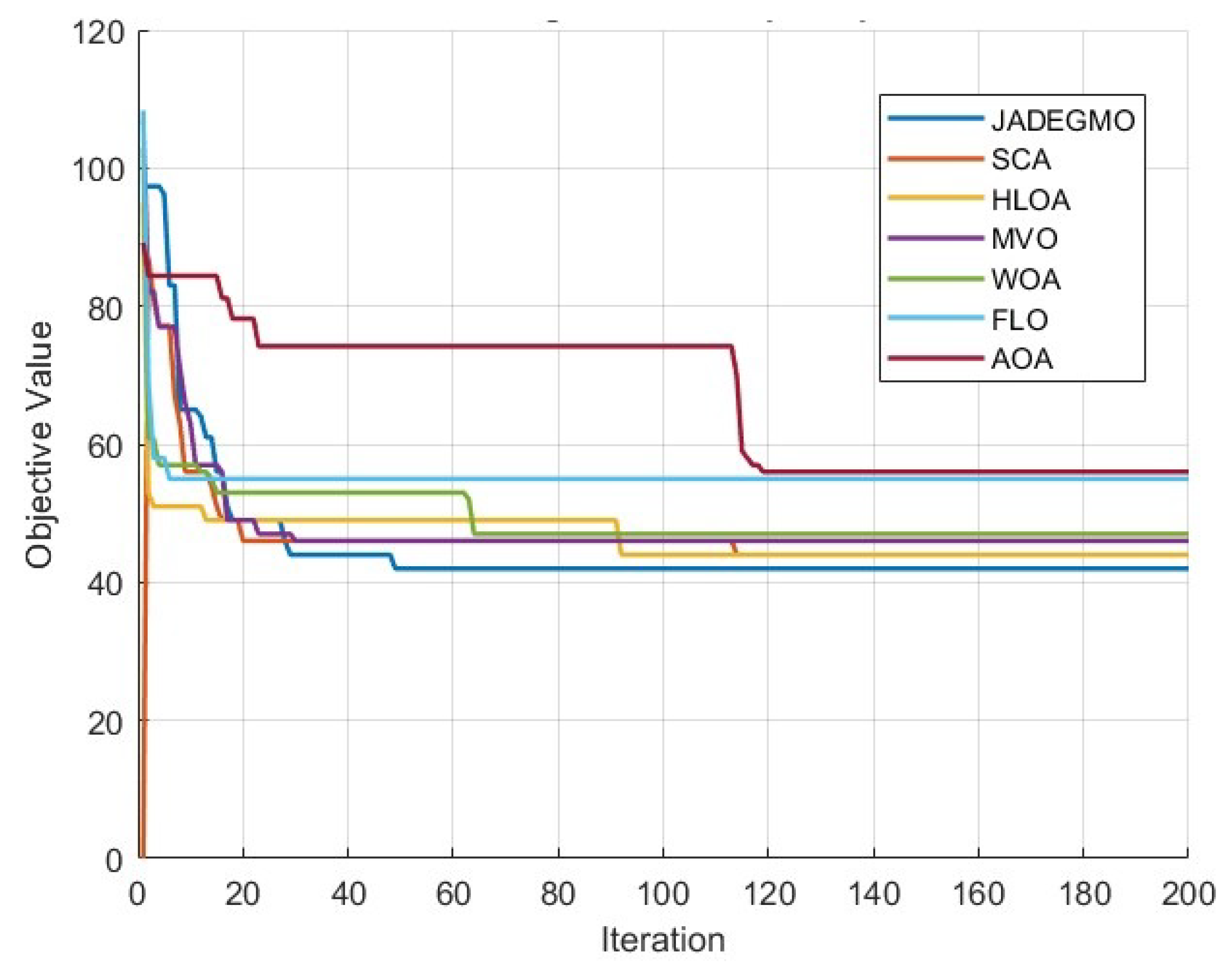
Figure 21 shows the best convergence curves for each algorithm selected from the run that yielded the lowest final cost for that method. JADEGMO converges quickly in the early iterations and continues to refine its solution. Notably, MVO’s best run shows an aggressive improvement early on but eventually levels out at a higher cost. FLO tends to plateau as well, while SCA demonstrates generally smooth and effective convergence to a moderate cost.
Figure 22 presents a box plot of the final best costs across all 30 runs. JADEGMO displays a comparatively lower median and a tight interquartile range. SCA’s distribution is also relatively compact but shifted upward. The others, including HLOA, MVO, WOA, FLO, and AOA, exhibit noticeably wider spreads or higher medians.
In
Figure 23, we show the average ranks for each algorithm across the 30 runs. JADEGMO’s rank is roughly 1.40, indicating that it often achieves the best or near-best result. SCA is next-best ranked at around 2.35. HLOA, MVO, and WOA cluster around ranks of four to five, whereas FLO and AOA near or exceed an average rank of five. The grouped bar chart in
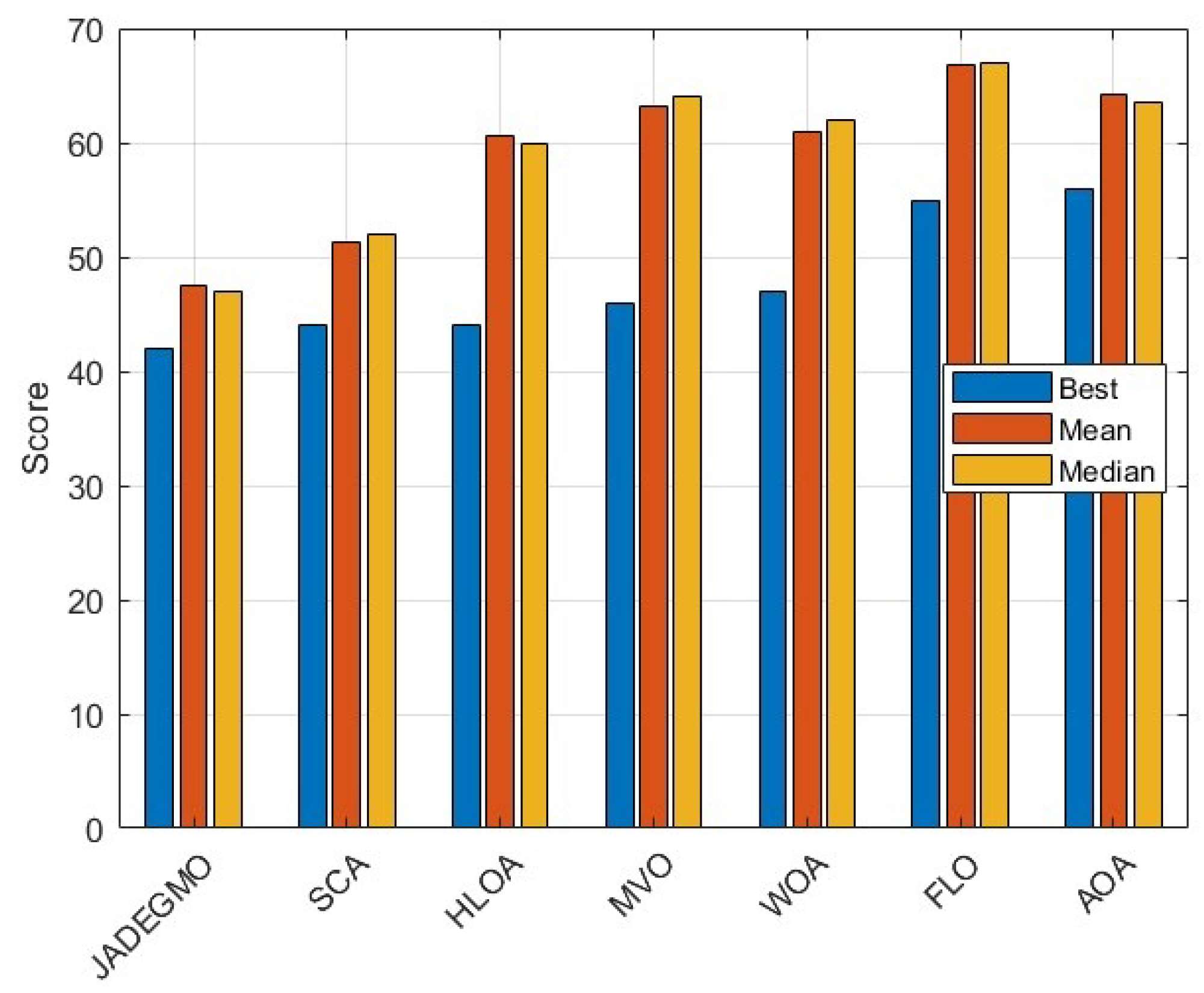
Figure 24 further illustrates the best, mean, and median cost values per optimizer.
As can be seen in
Table 4, our proposed JADEGMO strategy outperforms the other algorithms by a clear margin, whether judged by best solution, mean performance, median performance, or ranking metrics. SCA emerges as the second strongest competitor, though it rarely achieves results on par with JADEGMO.
From a practical viewpoint, in a multi-cloud environment, consistently obtaining lower cost solutions means discovering security configurations that remain robust to a variety of threats while incurring lower subscription costs and overhead. JADEGMO’s hybrid structure—which blends adaptive parameter updates (from JADE) with a genetic operator for diversity—is likely key in achieving these solutions. The early rapid improvements in the convergence curve suggest that the algorithm quickly identifies and locks onto promising configurations, while the subsequent iterations refine it further.
The box plots and standard deviation values reveal important information about stability. Algorithms that have wide cost distributions or large standard deviations (e.g., MVO, HLOA) produce excellent solutions in certain runs but fail to converge in other runs, resulting in worse final costs. JADEGMO’s tight distribution underscores its reliability. In security-critical contexts where consistent results matter more than best-case solutions, such reliability is paramount.
One interesting observation is how the algorithms handle the subscription toggles. Including advanced analytics (−5 risk, cost 15) or auto-patching (−3 risk, cost 8) can drastically change the partial risk. Some solutions with no subscriptions attempt to compensate with high encryption or minimal open ports, but these might raise overhead or functionality penalties. The best approach usually involves a carefully balanced combination, often turning on at least one subscription, selecting moderate encryption, and keeping open ports in a safe yet functional range.
The presence of a minimum risk floor (set to one in our formula) ensures that solutions cannot trivialize the objective by piling on every risk reduction measure for free. The overhead and subscription costs become the limiting factors. In real settings, organizations must weigh the intangible benefits of advanced services or patching automation (e.g., reduced labor). Our cost model performs an approximate job of capturing these aspects, but future expansions could consider a more nuanced subscription synergy.
9. Conclusions
We introduced JADEGMO, a hybrid optimization framework designed to blend JADE’s adaptive memory-driven evolutionary mechanisms with GMO’s elite-guided velocity-based exploration. Through extensive comparisons on the CEC2022 and CEC2017 benchmark problems, JADEGMO demonstrated robust convergence properties, achieving best-in-class performance on many test functions and exhibiting minimal variance across multiple runs. The convergence curves and rank analyses consistently ranked JADEGMO at or near the top, confirming that adaptive parameter tuning plus swarm-inspired guidance yields strong outcomes.
To validate its real-world relevance, we applied JADEGMO to a multi-cloud security configuration problem, constructing a novel cost function that balances security risk, overhead costs, and subscription-based features. The results showed that JADEGMO navigated these conflicting objectives effectively, discovering configurations that lower risk without incurring excessive expenses. This highlights the algorithm’s adaptability and potential as a decision-support tool in modern cloud infrastructures. Future work can extend JADEGMO to higher dimensions, dynamic security scenarios, and multi-objective formulations, broadening its applicability in both industry and research contexts.