Soft-Switching, Duty-Cycle-Extended Two-Phase Interleaved Buck with Positive Inductor Coupling for High-Density Consumer Electronics Power Supplies

Abstract

Against the backdrop of rapid advances in computing, industry, and electric vehicles, DC–DC buck converters—as core point-of-load regulators—are critical for power supplies in applications with stringent voltage-stability requirements. This paper proposes a two-phase interleaved Buck converter based on positively coupled inductor with a high coupling coefficient. The innovation lies in the positively coupled inductor and two-phase interleaved architecture, where two MOSFETs and two diodes form a similar symmetrical full-bridge interleaved structures together achieve a higher conversion ratio and provide $ZCS$ operation for all power devices, thereby effectively reducing switching losses. Relative to traditional topologies, the proposed converter delivers a higher conversion ratio without extreme duty-cycle operation while improving reliability. After detailing the operating mechanism, we derive the input–output voltage relation, outline controller synthesis guidelines, and specify the soft-switching conditions. From the viewpoint of symmetry, the proposed interleaved converter exploits the electrical and magnetic symmetry between phases to achieve current balancing, extended duty-cycle range and soft-switching. Validation is provided by both a $PSIM$ simulation model and a $270W$ hardware prototype using an $STM32F103ZET6$, which achieves 93.3% peak efficiency at a conversion ratio of 0.45, demonstrating the practicality and effectiveness of the approach.

1. Introduction

In recent years, Buck converters have been widely deployed in renewable energy systems, electric vehicles, fuel cells, explosion-proof power supplies, aerospace power units, defense applications, and information-industry (IT) systems. High efficiency, high power density, high reliability, better transient response, and low electromagnetic interference (EMI) remain enduring design goals for Buck converters, such as an inductor Buck converter [1,2,3,4]. Representative approaches include a dual-operating mode control technique introduced to enhance transient response [1]; a peak/valley current mode control method presented to precisely regulate output voltage [2]; an automatic mode switching scheme that ensures robust operation and suppresses EMI in high duty ratios [3]; and a synchronous Buck converter with a coupled inductor that achieves zero voltage switching (ZVS) [4].

For further improving power density and switching frequency while reducing current ripple, the interleaved Buck topology has attracted widespread attention. Interleaved Buck converters are typically implemented as (i) series-capacitor Buck converters, (ii) multiphase Buck converters with discrete inductors, or (iii) multiphase Buck converters employing coupled inductors.

Series capacitor Buck converters (SC Buck) [5,6,7,8] have also been extensively explored to improve operating frequency, improve system dynamics, reduce component stress, and share of current. However, the SC Buck circuit structure is more complicated than that of a discrete inductor multiphase Buck converter. To achieve a high output current, multiphase Buck converters with discrete inductors have been investigated [9,10,11]. For example, in electrical vehicles, the digital control deployed in FPGA used in the bidirectional interleaved Buck converter [9] and the feedback matrix design [10] are given to simplify the design of the controller, and the multiphase Buck converter based on current control of the synchronization of zero-crossing current ripples [11] overcome high-dynamic and high-power issues.

However, interleaved Buck converters that employ discrete inductors require active current-sharing control among phases. In addition, the triangular inductor current also has bad effects, and the control circuit consisting of analog devices will be very complex because its duty cycle is usually between 0 and 1.

Therefore, multiphase Buck converters employing inductors, either inversely or positively coupled, have been widely studied and applied. Positively coupled inductors have also been adopted in other high-efficiency paralleling schemes, where the positive coupling is exploited to redistribute current and shape switching transitions [12]. Positively coupled inductors have also been adopted in other high-efficiency paralleling schemes, where positive coupling is exploited to redistribute current and shape switching transitions [13]. Inversely coupled multiphase Buck converters can effectively improve efficiency and have fast transient responses [14,15,16], but there is an oscillation phenomenon and a larger equivalent coupling inductor when the procedure occurs, which will extend the coupling time. Beyond inversely coupled structures, interleaved buck-type topologies employing coupled inductors have also been explored for voltage balancing in bipolar DC microgrids, where the emphasis is on balancing performance rather than extending duty-cycle range or achieving ZVS/ZCS in DCM/CCM hybrid operation [17]. Furthermore, there is a coupled multiphase Buck converter [18,19,20], whose power devices can operate in zero-voltage switching (ZVS) in continuous conduction mode (CCM), but the resulting second-order dynamics complicates the design of the controller parameter.

Building on previous work on high-gain step-up converters employing coupled inductors, including our earlier design of a non-isolated high-gain step-up DC–DC converter with reduced voltage stresses  [21], this paper focuses on a step-down two-phase interleaved Buck topology with positively coupled inductors.

In this paper, two investigate an interleaved Buck converter employing a positively coupled inductor. The converter is configured so that magnetic coupling occurs during switching transitions, while the phase currents in the individual inductors operate in discontinuous conduction mode (DCM) and their sum remains in continuous conduction mode (CCM). The topology is tailored to meet the stable power supply requirements of modern electronic products. The main contributions of this paper can be summarized as follows.

• A two-phase interleaved Buck converter with positively coupled inductors is proposed, in which the phase currents operate in DCM and their sum remains in CCM. By appropriately timing the magnetic coupling during switching transitions, all main power devices achieve ZVS and ZCS, thereby reducing switching losses without the need for auxiliary switches or resonant networks.
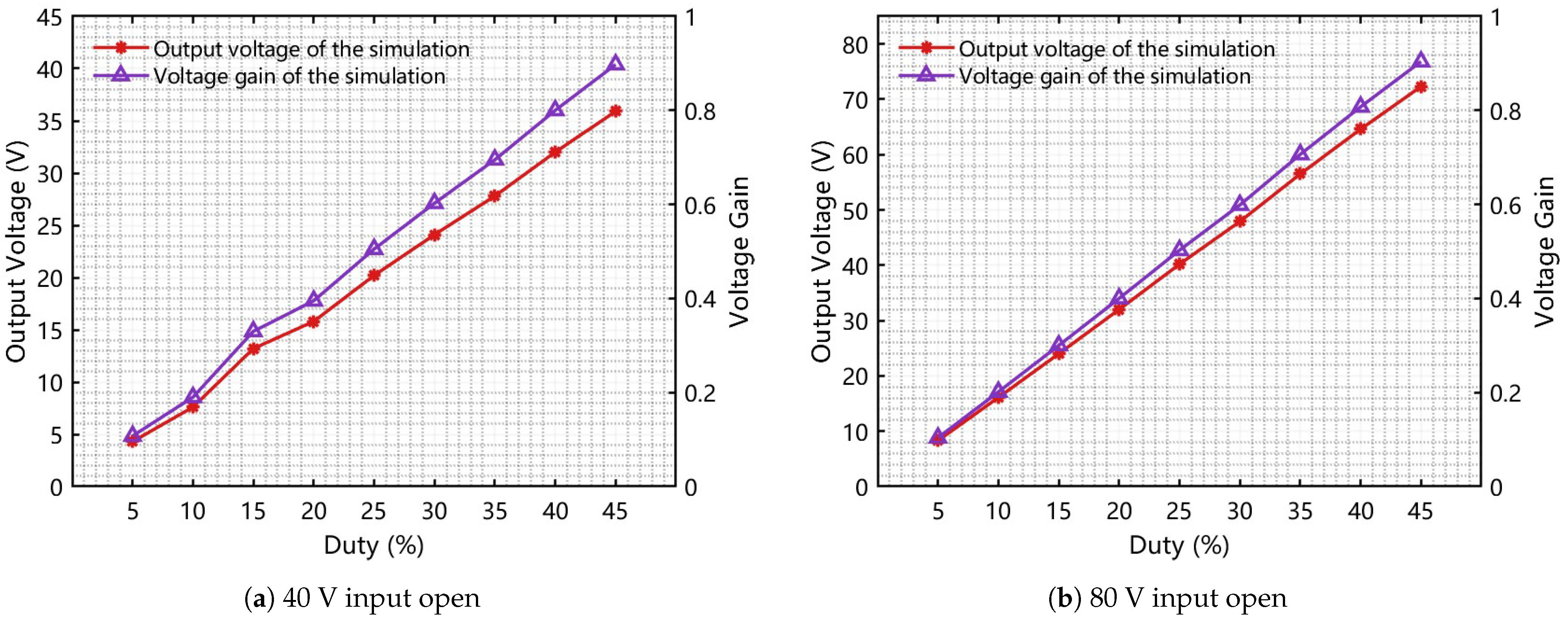
• The proposed architecture extends the effective duty cycle range and achieves a conversion ratio higher than that of conventional interleaved Buck converters, without resorting to extreme duty cycles, facilitating a high conversion ratio and high-power density while maintaining a relatively simple control structure.
• Compared with conventional interleaved Buck converters with discrete inductors, shaped inductor current waveforms exhibit reduced ripple and improved inherent current sharing between phases. The experimental 270W prototype demonstrates a peak efficiency of 93.3% at a conversion ratio of 0.5, confirming that the proposed positively coupled structure provides a significant advance over existing interleaved and coupled-inductor Buck designs.

The remainder of this manuscript is organized as follows. In Section 2, the topology and the control requirement are discussed in detail. In Section 3, the magnetic coupling interval is presented in CCM. In Section 4, the operating principle of CCM is analyzed. In Section 5, the relationship between the output-input voltages and the performances are given. In Section 6 presents the signal model. In Section 7, we summarize the advantages and disadvantages of the mentioned topologies compared to other topologies. Furthermore, Section 8 reports on the simulation results. The experimental results are given in Section 9. Finally, Section 10 concludes this paper.

2. System Configuration of Two-Phase Interleaved Buck Converter

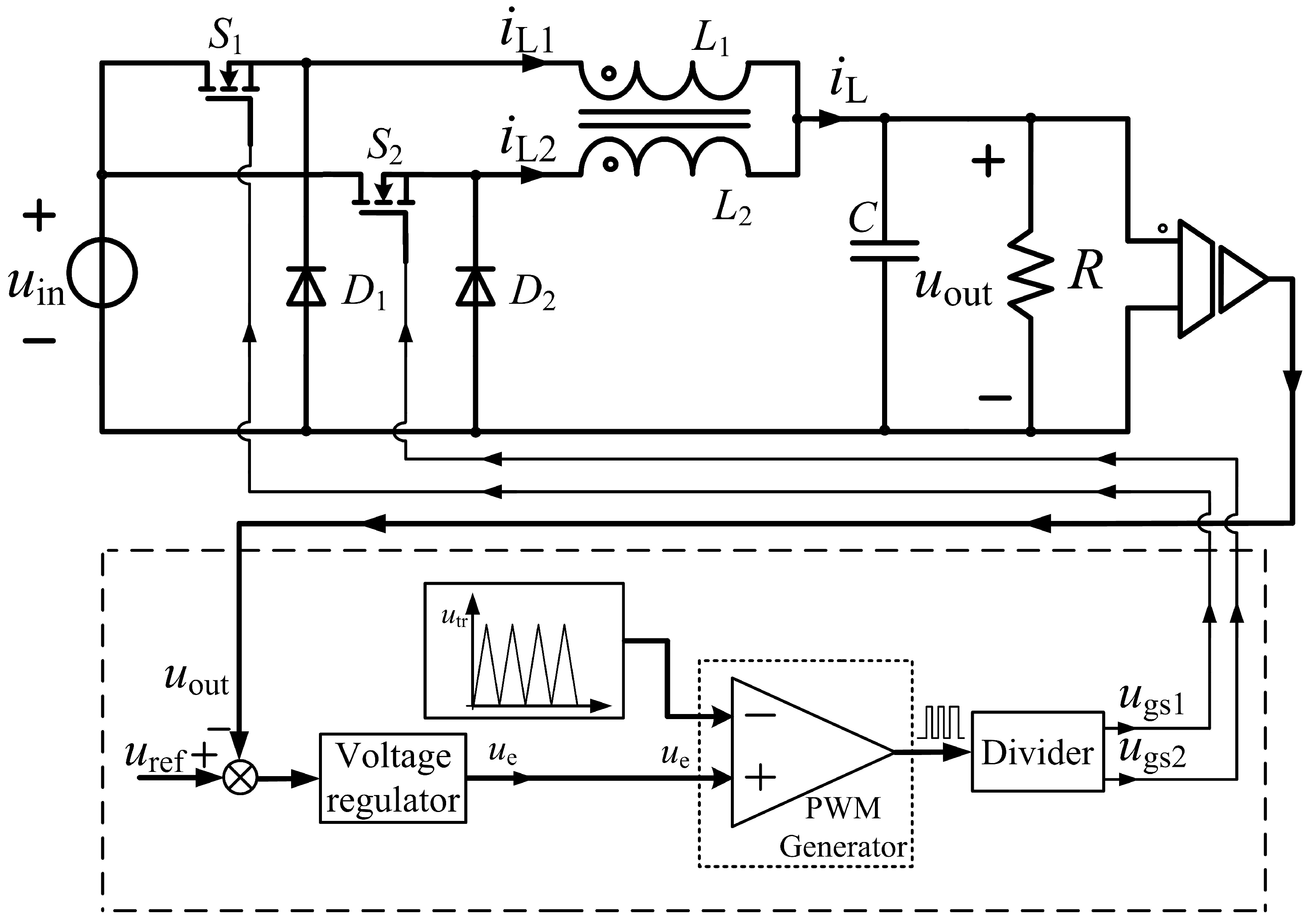
In this paper, a high-conversion ratio Two-Phase Interleaved Buck Converter with a Coupling Inductor topology is proposed, which focuses on the positively coupled inductor and the interleaved parallel connection. Among these, coupled inductors help to improve efficiency. The realization of this efficient energy transfer is closely related to the time-varying interaction of the magnetic and electric fields inside the converter, and the symmetry features inherent in this process are particularly crucial. The two-phase interleaved parallel structure optimizes the current ripple characteristics through the time symmetry in phase (the symmetrical timing of the two-phase interleaved operation), while the symmetrical design of the coupled inductor promotes the symmetrical coupling of the magnetic and electric fields. The two work together to reduce the asymmetric losses in the energy transfer process, providing a symmetrical basis for efficient operation.

The circuit topology adopted in this work is illustrated in Figure 1. The proposed topology may be divided into two functional units: (a) the positively coupled-inductor structure. (b) Interleaved Two-phases. Including coupled inductance (L), two MOSFETs ($S_1$, $S_2$), two diodes ($D_1$, $D_1$), one capacitor (C) and a load R.Where $L_1$, $L_2$, $i_{L1}$, $i_{L2}$ and $i_L$ are the phase inductors, the currents in the phase inductors and the sum of the currents, respectively. $u_{in}$ and $u_{out}$ denote the input and output voltages, respectively. The diodes $D_1$ and $D_2$, together with the MOSFET switching transistors $S_1$ and $S_2$, enable the total inductor current to operate in continuous-conduction mode (CCM). MOSFETs $S_1$ and $S_2$ operate in an interleaved manner.

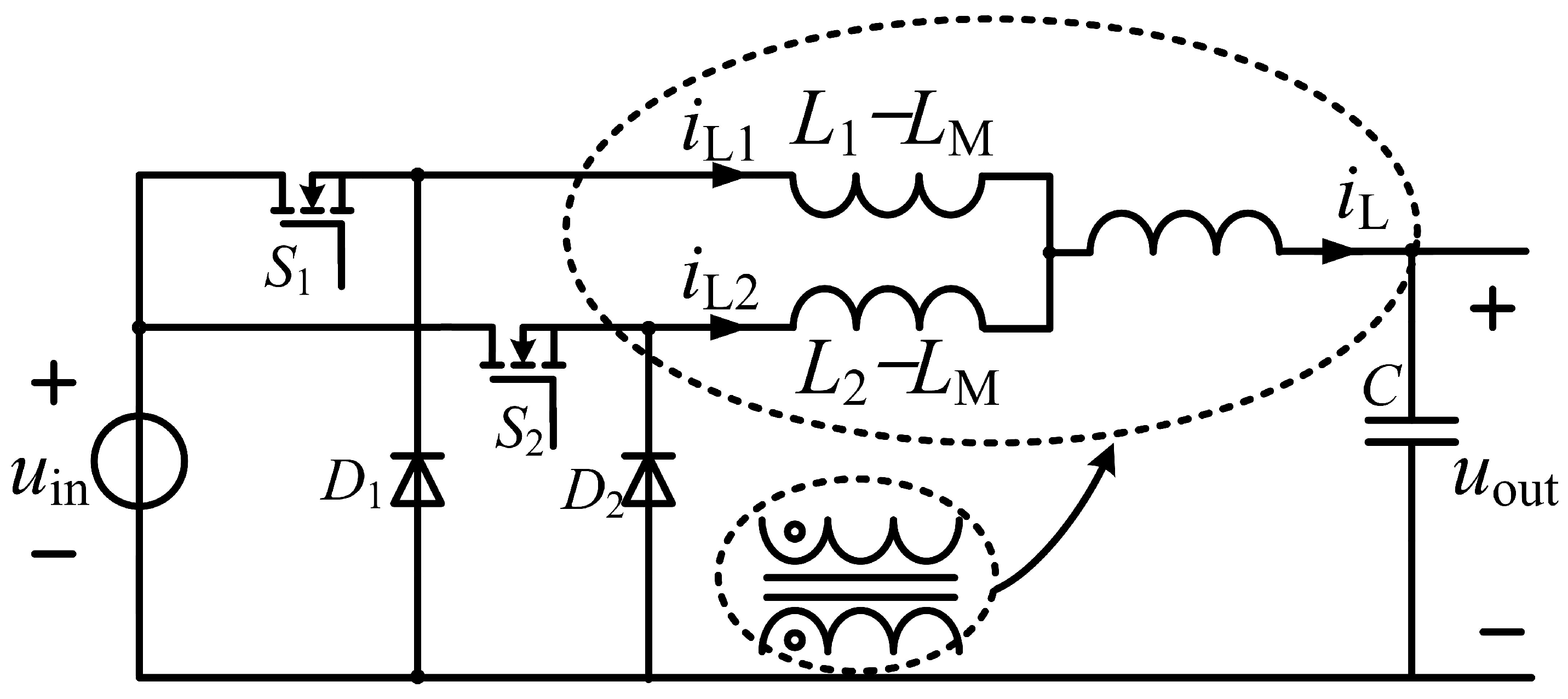
According to the model of a coupling inductor, the equivalent circuit of Figure 1 is given again by Figure 2 when the magnetic coupling interval of currents $i_{L1}$ and $i_{L2}$ occurs. Where $L_M$, $L_1-L_M$ and $L_2-L_M$ are mutual inductance and two leakage inductance, separately. Assuming $L_1=L_2=L_Z$, the relationships of all inductances are demonstrated in detail in Equations (1) and (2), where k is the coupling coefficient. The current $i_L$ is shown in Equation (3) based on Kirchhoff’s Current Law (KCL).

$$L_{\mathrm{M}}=k\sqrt{L_1{L}_2}=k{L}_{\mathrm{Z}}$$

(1)

$$L_1-L_{\mathrm{M}}=L_2-L_{\mathrm{M}}=(1-k)L_{\mathrm{Z}}$$

(2)

$$i_{\mathrm{L}}=i_{\mathrm{L}1}+i_{\mathrm{L}2}$$

(3)

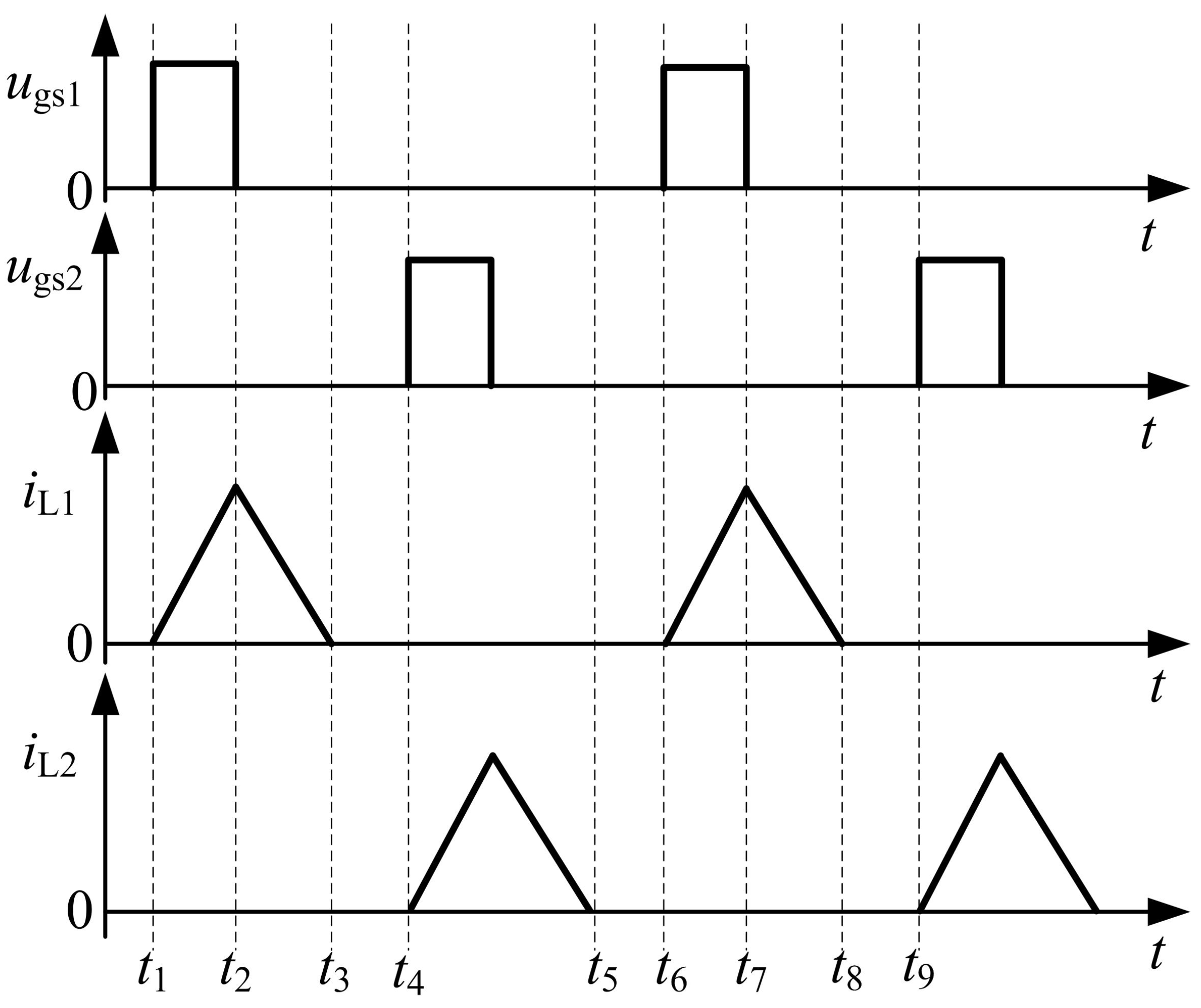
Under steady-state conditions, one switching period is partitioned into six phases, as illustrated in Figure 2. According to the aforementioned content, the main waveforms under CCM of the current $i_L$ are shown in Figure 3. Obviously, the state of the current $i_L$ operates in the CCM under the magnetic coupling interval that occurs, as shown in Figure 3. And at the same time, it is ensured that currents $i_{L1}$ and $i_{L2}$ must work in DCM in any case, where $u_{gs1}$, $u_{gs2}$, $T_s$, and $T_{on}$ are the driving signals of MOSFETs $S_1$ and $S_2$, the switching period, and the conducting time. During the time intervals $t^{\prime }$ ($t^{\prime }=t_1-t_2=t_4-t_5$), the magnetic coupling interval of the currents $i_{L1}$ and $i_{L2}$ will appear.

The coupled inductor is realized on a single core leg, with the two windings wound bifilarly and having the same number of turns. The windings are tightly packed in adjacent layers, with short lead lengths and a single centralized air gap, so that almost all of the main flux is shared and the leakage flux is minimized. Under these conditions, the mutual inductance is very close to the geometric mean of the self-inductances ($L_M=\sqrt{L_1{L}_2}$), and the coupling coefficient $K=L_M/\sqrt{L_1{L}_2}$ is therefore close to 1.

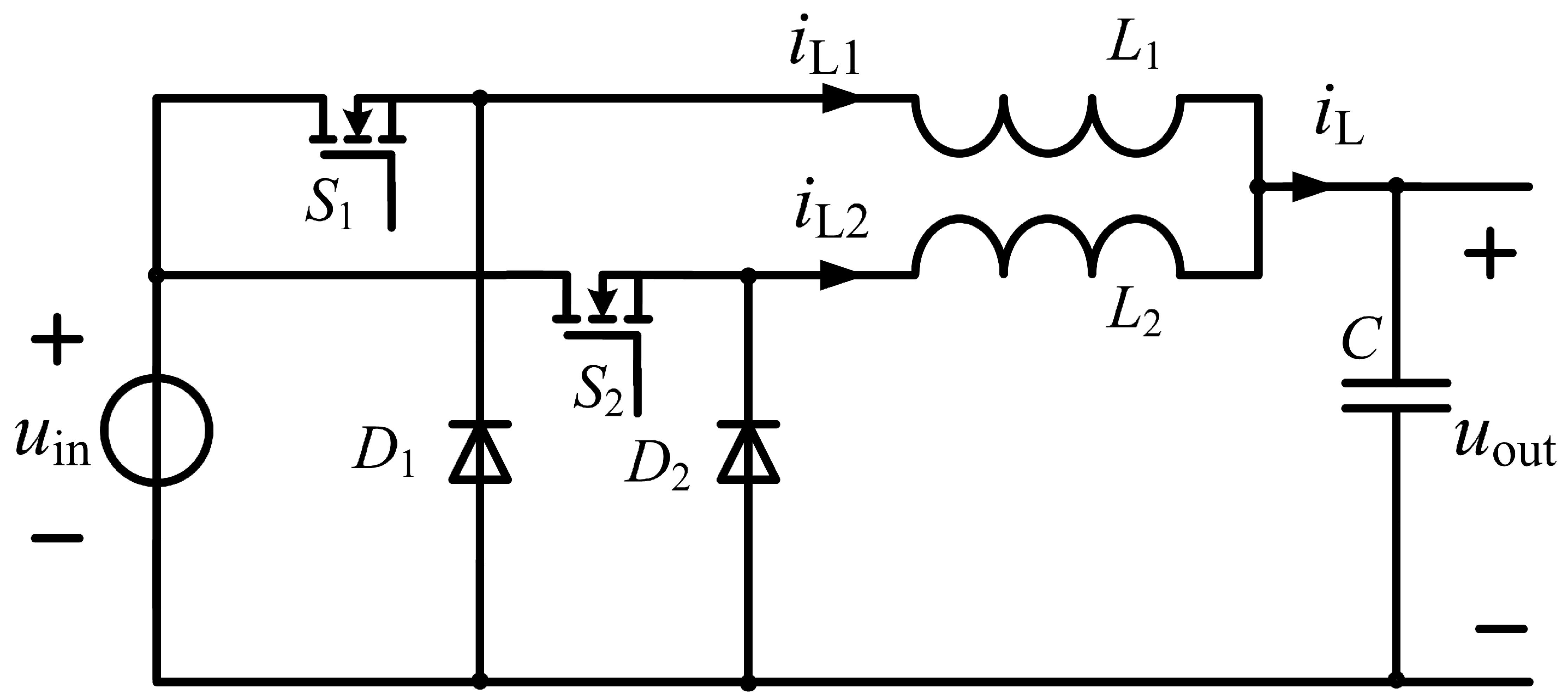
When the magnetically coupled interval is absent—that is, $i_{L1}$ and $i_{L2}$ do not interact—the power stage is reduced to the equivalent circuit in Figure 4, and the representative waveforms are shown in Figure 5. In this case, the operating principle is identical to that of a traditional two-phase interleaved Buck topology operated in DCM. As the underlying dynamics are standard and introduces no additional insight for the proposed topology, a detailed analysis is omitted, and the discussion henceforth focuses on the coupled case.

3. Magnetic Coupling Interval Analysis

At this stage, the switch experiences ZCS; the $D_1$ diode remains reverse-biased and off. According to Figure 3, the coupling procedure appears during the time interval ($t_1-t_2$). The corresponding equivalent circuit for power conversion appears in Figure 6a. The relationships of voltage and current are expressed in Equation (4). Equation (5) is easily obtained by solving (4). In the same way, Equation (6) is also obtained during the time interval ($t_4-t_5$).

$$\left\{\begin{array}{c}{u}_{\mathrm{in}}-u_{\mathrm{out}}=L_1{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}+L_{\mathrm{M}}{\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}=L_{\mathrm{z}}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}+k{L}_{\mathrm{z}}{\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}\hfill \\ -u_{\mathrm{out}}=L_2{\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}+L_{\mathrm{M}}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}=L_{\mathrm{z}}{\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}+k{L}_{\mathrm{z}}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}\hfill \end{array}\right.$$

(4)

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}={\displaystyle \frac{u_{\mathrm{in}}+(k-1)u_{\mathrm{out}}}{\left(1-k^2\right)L_{\mathrm{z}}}}>0\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}={\displaystyle \frac{-\left[k{u}_{\mathrm{in}}+(1-k)u_{\mathrm{out}}\right]}{\left(1-k^2\right)L_{\mathrm{z}}}}<0\hfill \end{array}\right.$$

(5)

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}={\displaystyle \frac{-[k{u}_{\mathrm{in}}+(1-k)u_{\mathrm{out}}]}{(1-k^2)L_{\mathrm{z}}}}<0\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}={\displaystyle \frac{u_{\mathrm{in}}+(k-1)u_{\mathrm{out}}}{(1-k^2)L_{\mathrm{z}}}}>0\hfill \end{array}\right.$$

(6)

When the coefficient k is close to 1, the $u_{out}$ term in Equations (5) and (6) can be approximately equal to 0, that is, it can be further simplified to Equations (7) and (8).

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}\approx {\displaystyle \frac{u_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}\approx {\displaystyle \frac{u_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}>0\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}\approx {\displaystyle \frac{-k{u}_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}={\displaystyle \frac{-u_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}<0\hfill \end{array}\right.$$

(7)

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}\approx {\displaystyle \frac{-k{u}_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}\approx {\displaystyle \frac{-u_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}<0\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}\approx {\displaystyle \frac{u_{\mathrm{in}}}{(1-k^2)L_{\mathrm{z}}}}>0\hfill \end{array}\right.$$

(8)

$${\displaystyle \frac{d{i}_{\mathrm{L}1}}{dt}}\approx -{\displaystyle \frac{d{i}_{\mathrm{L}2}}{dt}}$$

(9)

Thus, it is clear that Equation (9) is established from Equations (7) and (8). That is, current $i_L$ can be regarded as a constant current source as the sum of $i_{L1}$ and $i_{L2}$ is effectively constant and can be modeled as a current source. But the time intervals $t_1-t_2$ and $t_4-t_5$ are very short because the leakage inductance value in Equation 2 is relatively small, which, together with the small equivalent capacitance at the switching node, results in a resonant frequency much higher than the switching frequency. Consequently, the corresponding coupling intervals occupy only a very small fraction of the switching period, and their influence on the average inductor current and conversion ratio can be safely ignored.

4. Operation Principle Under CCM Condition

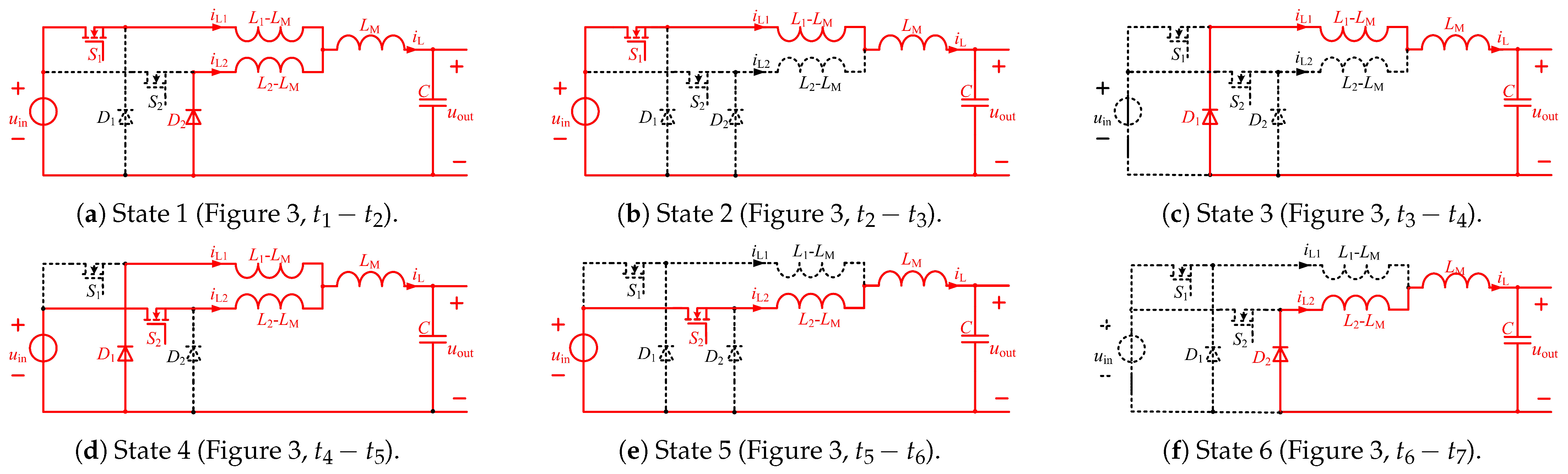
The proposed converter employs two active switches in the power stage. Its operating principle is governed by the dynamic interaction between the gate-drive signals and the current flowing through the coupled inductor winding. Under steady-state conditions, each switching period is divided into six consecutive operating modes, as illustrated in Figure 3, and the corresponding equivalent circuits for these modes are shown in Figure 6.

State 1 ($t_1-t_2$). The switch and the switching diode achieve ZCS in this state, and the diodes $D_1$ are reverse cutoff. The equivalent circuit representing the power conversion path is shown in Figure 6a. Before time $t_1$, the current $i_{L1}$ is zero and the current $i_{L2}$ follows through the diode $D_2$. At $t_1$, the upper MOSFET $S_1$ is switched on with zero current. The current $i_{L1}$ and $i_{L2}$ starts to rise and decrease under voltage $u_{in}$ until the current $i_{L1}$ increases to $i_L$ at time $t_2$. At this time, the current $i_{L2}$ decreases to zero and the diode $D_2$ is automatically turned off without reverse recovery. Because the coefficient k is close to 1, the current changing rate of $i_{L1}$ and $i_{L2}$ is relatively high. The slopes of the currents $i_{L1}$ and $i_{L2}$ can be considered as follows:

$${\displaystyle \frac{d{i}_{L1}}{dt}}=-{\displaystyle \frac{d{i}_{L2}}{dt}}={\displaystyle \frac{u_{in}}{(L_1-L_M)+(L_2-L_M)}}={\displaystyle \frac{u_{in}}{2(1-k)L_z}}$$

(10)

State 2 ($t_2-t_3$). In this state, the $L_1$ self-inductance $L_1-L_M$ network and Mutual induction $L_M$ are charged. The equivalent circuit shown in Figure 6b represents the power conversion path. The current $i_{L1}$ is equal to the current $i_L$. At this instant, $S_2$ is turned off, while the diode remains reverse-biased and, therefore, non-conducting. Apparently, the current rate of change of $i_{L1}$ is smaller than that of Equation (10) when the coefficient k is close to 1. This mode ends at $t_3$. Then, the currents $i_{L1}$ and $i_L$ increase with a slope, which is described as follows:

$${\displaystyle \frac{d{i}_{L1}}{dt}}={\displaystyle \frac{d{i}_L}{dt}}={\displaystyle \frac{u_{in}-u_{out}}{L_1}}={\displaystyle \frac{u_{in}-u_{out}}{L_z}}$$

(11)

State 3 ($t_3-t_4$). In this mode, the inductor discharges its stored energy, and $D_1$ is acted as a freewheeling path. The equivalent circuit for power conversion is shown in Figure 6c. The switches remain on and the diodes $D_2$ are cut off in reverse. Currents $i_{L1}$ and $i_L$ follow through the diode $D_1$ under voltage $u_{out}$. At this time, the slope of the currents $i_{L1}$ and $i_L$ is in the following form:

$${\displaystyle \frac{d{i}_{L1}}{dt}}={\displaystyle \frac{d{i}_L}{dt}}={\displaystyle \frac{-u_{out}}{L_1}}={\displaystyle \frac{-u_{out}}{L_z}}$$

(12)

State 4 ($t_4-t_5$). This state is the stage where coupling occurs. An equivalent schematic for the power stage is provided in Figure 6d. The diode $D_1$ is on, $D_2$ is off. The energy within the system is reallocated through the mutual inductance of the coupled inductors. At this time, the MOSFET $S_2$ starts to work. Obviously, it is on with zero current because the current $i_{L2}$ is zero. Thus, the MOSFET $S_2$ gets ZCS. From $t_4$, the currents $i_{L2}$ and $i_{L1}$ start to increase and decrease separately under voltage $u_{in}$ until the current $i_{L2}$ increases to $i_L$ at time $t_5$. At this moment, the current $i_{L1}$ decreases to zero, hence the diode $D_1$ is automatically turned off without reverse recovery. That is, $D_1$ obtains ZCS. Because the coefficient k is close to 1, the current changing rate of $i_{L1}$ and $i_{L2}$ is also relatively large. The slope of the current functions $i_{L1}$ and $i_L$ is described below.

$${\displaystyle \frac{d{i}_{L2}}{dt}}=-{\displaystyle \frac{d{i}_{L1}}{dt}}={\displaystyle \frac{u_{in}}{(L_1-L_M)+(L_2-L_M)}}={\displaystyle \frac{u_{in}}{2(1-k)L_z}}$$

(13)

State 5 ($t_5-t_6$). In this state, the $L_2$ self-inductance ($L_2-L_M$) network and Mutual induction ($L_M$) are charged. The power conversion equivalent circuit is depicted in Figure 6e. With $S_2$ continuously conducting, the diodes are reverse-biased and block current. During the time interval ($t_5-t_6$), the current changing rate of $i_{L2}$ is calculated using Equation (14). It is clear that the rate of change of $i_{L2}$ is also smaller than that of Equation (13) because the coefficient k is nearly 1. At $t_6$, the MOSFET $S_2$ is turned off. At this time, the slope of the currents $i_{L2}$ and $i_L$ can be given by Equation (14).

$${\displaystyle \frac{d{i}_{L2}}{dt}}={\displaystyle \frac{d{i}_L}{dt}}={\displaystyle \frac{u_{in}-u_{out}}{L_2}}={\displaystyle \frac{u_{in}-u_{out}}{L_z}}$$

(14)

State 6 ($t_6-t_7$). This state sets up the subsequent inductor energy-release phase, during which the current freewheels through $D_1$. The equivalent circuit representing the power conversion path is shown in Figure 6f. All switching devices are off, and a diode $D_{\mathrm{2}}$ is used to move freely. Currents $i_{L2}$ and $i_L$ follow through the diode $D_2$ under voltage $u_{out}$, which is represented in Equation (15). The next operating period will start from time $t_7$.

$${\displaystyle \frac{d{i}_{L2}}{dt}}={\displaystyle \frac{d{i}_L}{dt}}={\displaystyle \frac{-u_{out}}{L_2}}={\displaystyle \frac{-u_{out}}{L_z}}$$

(15)

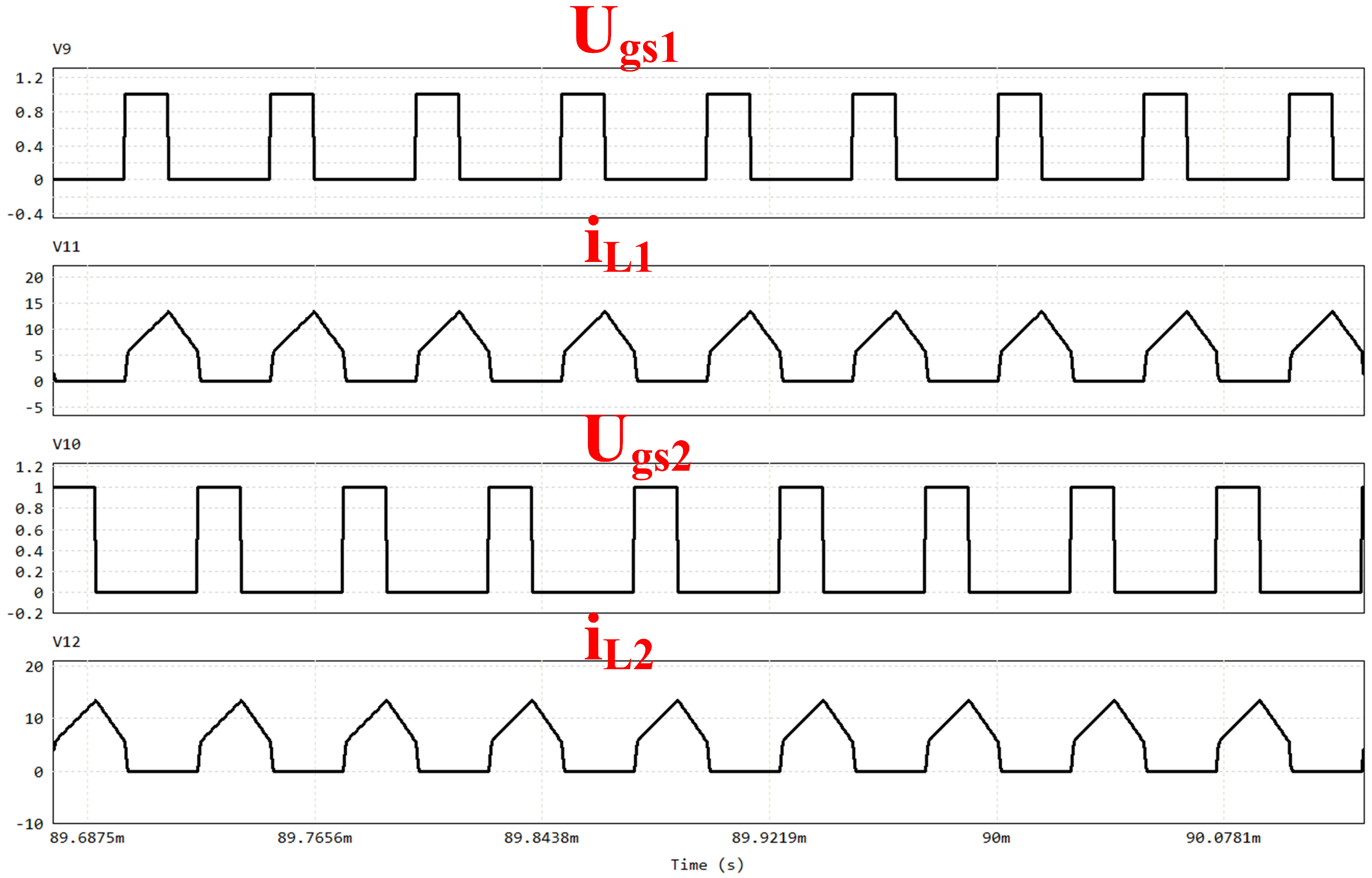
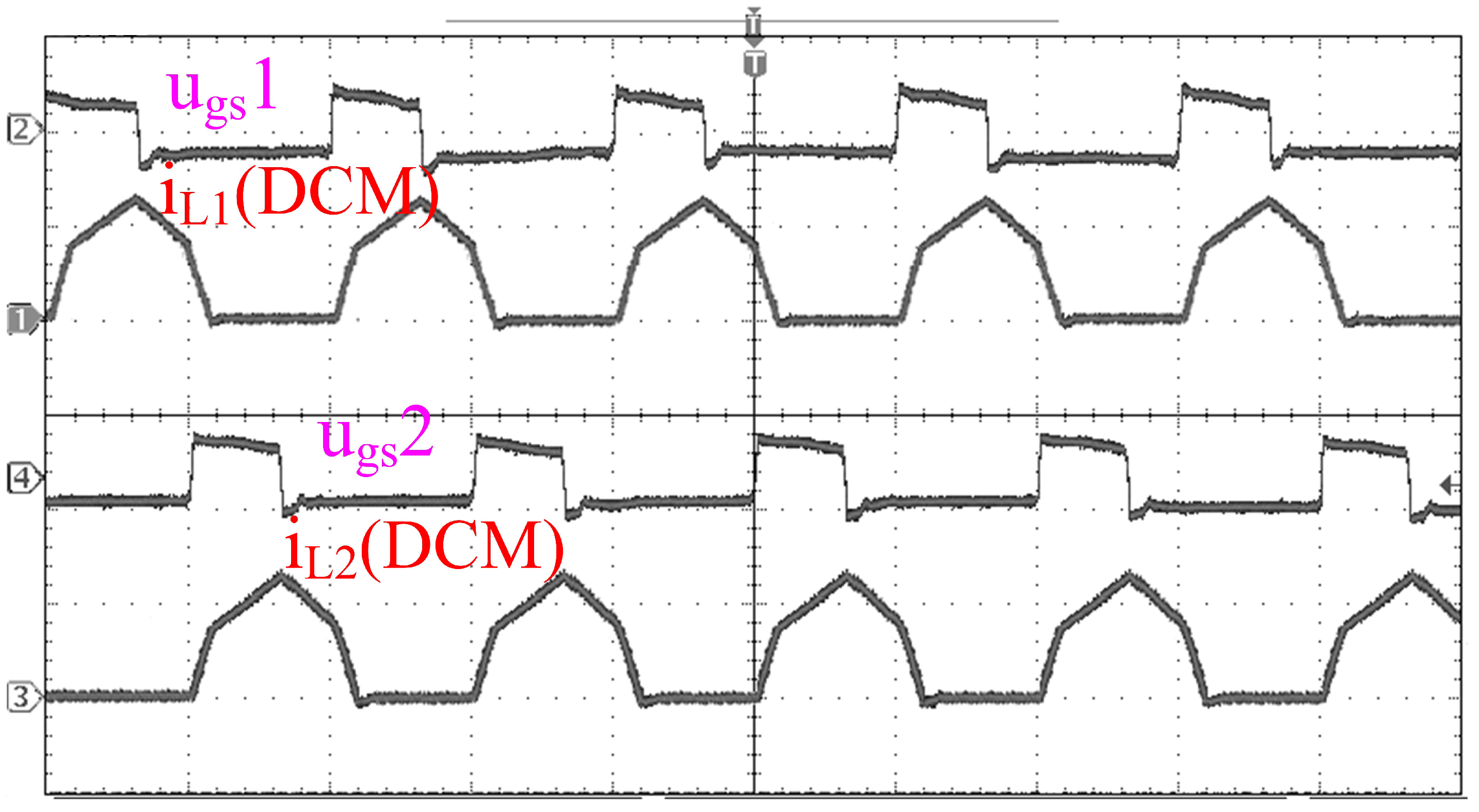
The converter operates through a multi-stage energy-exchange process over each switching period. During each cycle, the inductor current exhibits a periodic piecewise-linear waveform. Within each cycle, it initially maintains zero current, then rapidly rises, linearly rises to a peak, and rapidly falls back to zero current. The overall waveform resembles a cyclical “pulsed triangle wave”, exhibiting distinct piecewise-linear characteristics. The preparation of ZCS is performed by coupled inductance and diode renewal. The phases of the inductor currents $i_{L1}$ and $i_{L2}$ differ, demonstrating a periodic pattern of alternating operation. According to a previous analysis, MOSFETs and freewheeling diodes are found to operate in ZCS.

5. Converter Performance Analysis

For the considered DC–DC converter, the voltage conversion gain exhibits a linear dependence on the duty cycle D. Since the currents of inductors $L_1$ and $L_2$ change periodically, we only analyze the change in inductor current of inductor $L_1$ within one cycle. As shown in Figure 3, the two duty cycles are defined by Equation (16), respectively.

$$\left\{\begin{array}{c}D={\displaystyle \frac{t_{\mathrm{on}}}{T_S}}(0\le D\le 0.5)\hfill \\ D^{\prime }={\displaystyle \frac{t^{\prime }}{T_S}}\hfill \end{array}\right.$$

(16)

Here, D denotes the main duty cycle of the phase switches. In contrast, $D^{\prime }$ denotes the fraction of the switching period occupied by the coupling (commutation) intervals associated with the leakage inductance and the switch-node/device capacitances.

With regard to current $L_1$, only consider $t_1-t_5$. Thus, applying the volt-second balance to $L_{in}$ in this interval gives Equation (17) from Figure 3. Therefore, the relationship between input and output voltages can be easily calculated as in Equation (18). Similarly, for the current $i_{L2}$, the input–output voltage relationship is identical to that given in Equation (18).

$${\displaystyle \frac{u_{\mathrm{in}}{D}^{\prime }{T}_S}{2(1-k)}}+{\displaystyle \frac{(u_{\mathrm{in}}-u_{\mathrm{out}})(D-D^{\prime })T_S}{L_z}}=u_{\mathrm{out}}(0.5-D)T+{\displaystyle \frac{u_{\mathrm{in}}{D}^{\prime }{T}_S}{2{(1-k)}_z}}$$

(17)

$$u_{\mathrm{out}}={\displaystyle \frac{u_{\mathrm{in}}(2D-2D^{\prime })}{1-2D^{\prime }}}$$

(18)

According to Figure 3 and Equation (16), we have $D^{\prime }=T_s/T$. Since $t_1-t_2$ and $t_4-t_5$ are very short, $Ts\ll T$ and hence $D^{\prime }\ll 1$, so $D^{\prime }$ can be neglected in the average model. Hence, the expression for the voltage gain in this mode is obtained by simplifying to Equation (19).

$$u_{\mathrm{out}}=u_{\mathrm{in}}2D$$

(19)

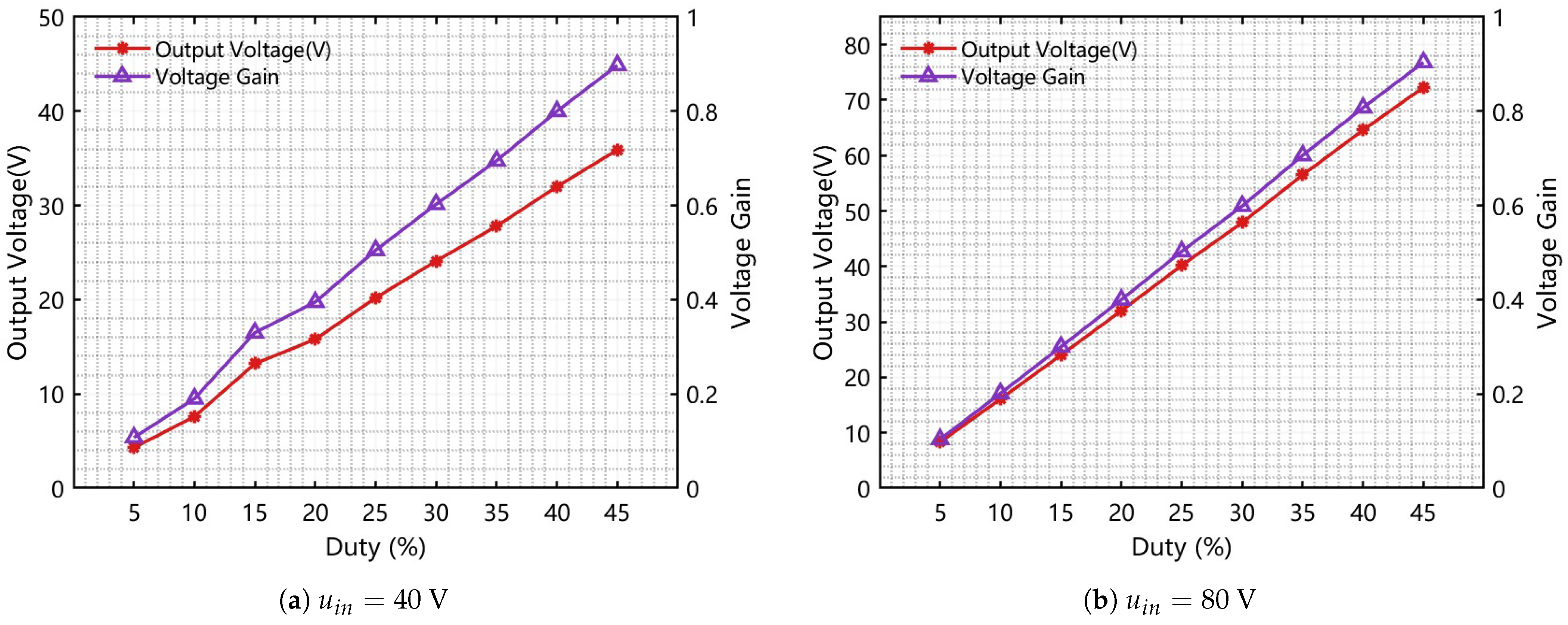
The converter proposed in this paper realizes duty cycle expansion by magnetic coupling and a two-phase interleaved structure. The voltage gain achieves the change of the conventional Buck duty cycle between $(0,1)$ when the duty cycle D changes between $(0,0.5)$. The limitation of conventional high-gain converters, which must operate near extreme duty cycles to cover a wide regulation range, is overcome.

6. Control System Design

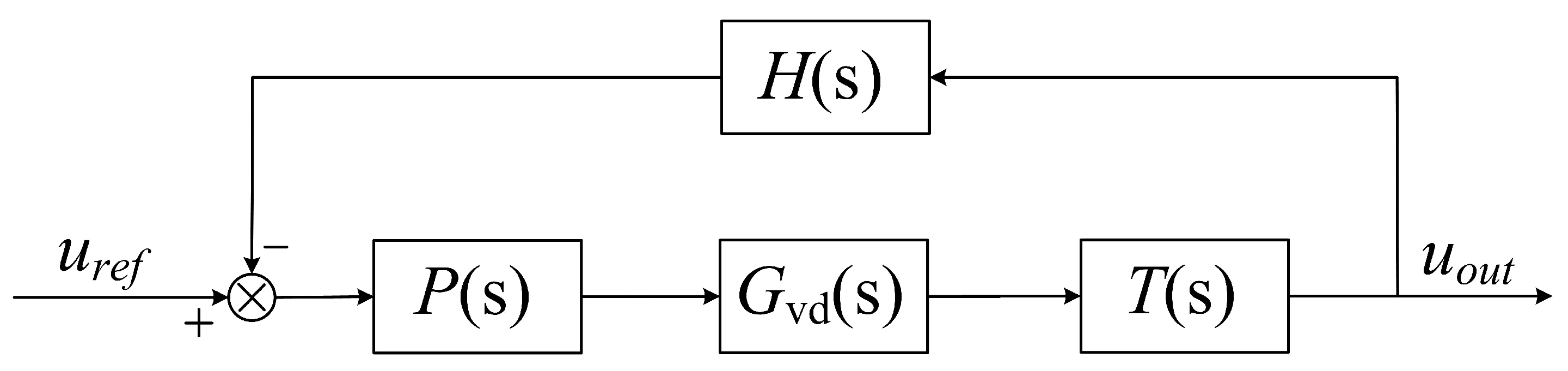
The primary objective of the output voltage control loop is to regulate the output voltage and enhance the dynamic performance of the converter. The corresponding control block diagram is shown in Figure 7. In this diagram, $u_{ref}$ denotes the reference output voltage; $G_{vd}\left(s\right)$ denotes the small-signal transfer function that relates the main switch duty cycle D to the average output voltage; $P\left(s\right)$ denotes the PI compensator; $T\left(s\right)$ represents the transfer function of the voltage detection stage; and $H\left(s\right)$ denotes the transfer function associated with the feedback path.

As shown in Figure 7, $u_{out}$ denotes the actual output voltage. Based on the small-signal model, the control-to-output (duty-to-voltage) transfer function is obtained and expressed in (20) and (21).

$$\left\{\begin{array}{c}{L}_1{\displaystyle \frac{d\left(I_{L1}\right)}{dt}}\left({\displaystyle \frac{1}{2}}-D^{\prime }\right)=u_{in}D+u_{out}{D}^{\prime }-{\displaystyle \frac{1}{2}}{u}_{out}=0\hfill \\ C{\displaystyle \frac{d\left(u_{out}\right)}{dt}}=\left({\displaystyle \frac{1}{2}}-D^{\prime }\right)I_{L1}-{\displaystyle \frac{u_{out}}{R}}\left({\displaystyle \frac{1}{2}}+D^{\prime }\right)+K=0\hfill \end{array}\right.$$

(20)

$$\left\{\begin{array}{c}{L}_1{\widehat{i}}_{L1}S\left({\displaystyle \frac{1}{2}}-D^{\prime }\right)-\widehat{D^{\prime }}{L}_1{I}_{L1}S=u_{in}\widehat{D^{\prime }}+\widehat{u_{in}}D+U_c\widehat{D^{\prime }}\hfill \\ C\widehat{u_{out}}S=-I_{L1}\widehat{D^{\prime }}+{\widehat{i}}_{L1}\left({\displaystyle \frac{1}{2}}-D^{\prime }\right)-{\displaystyle \frac{U_C}{R}}\widehat{D^{\prime }}-{\displaystyle \frac{\widehat{U_C}}{R}}\left({\displaystyle \frac{1}{2}}+D^{\prime }\right)\hfill \end{array}\right.$$

(21)

It is clear that using Equation (20) to obtain that when $D^{\prime }$=0, the output voltage, as a function dependent on the input voltage, satisfies Equation (22). It is equivalent to Equation (19).

$$u_{out}=u_{in}2D$$

(22)

By combining the preceding results with Equation (21), t, the transfer function $G_{vd}\left(s\right)$ is given by Equation (23).

$$G_{vd}\left(s\right)={\displaystyle \frac{2R{u}_{in}}{2C{L}_{1}R{s}^2+\left(2D^{\prime }{L}_1+L_1\right)s+R-2D^{\prime }R}}$$

(23)

Equation (24) is the transfer function of the conventional single-inductor Buck output and duty cycle, which is the same as the new Buck transfer function in form.

$$G_{\mathrm{vd}}\left(s\right)={\displaystyle \frac{u_{\mathrm{in}}}{LC{s}^2+\frac{L}{R}s+1}}$$

(24)

For the voltage control loop, the compensator was designed on the basis of the small-signal control-to-output transfer function of the proposed converter. The plant transfer function $G_{vd}\left(s\right)$ was implemented in MATLAB. A robust PID-type controller was then tuned automatically using the pidtune command with a target phase margin of $60°$, prioritizing phase-margin robustness. This integral controller is adopted in the implementation of the voltage loop to regulate the output voltage and ensure zero steady-state error.

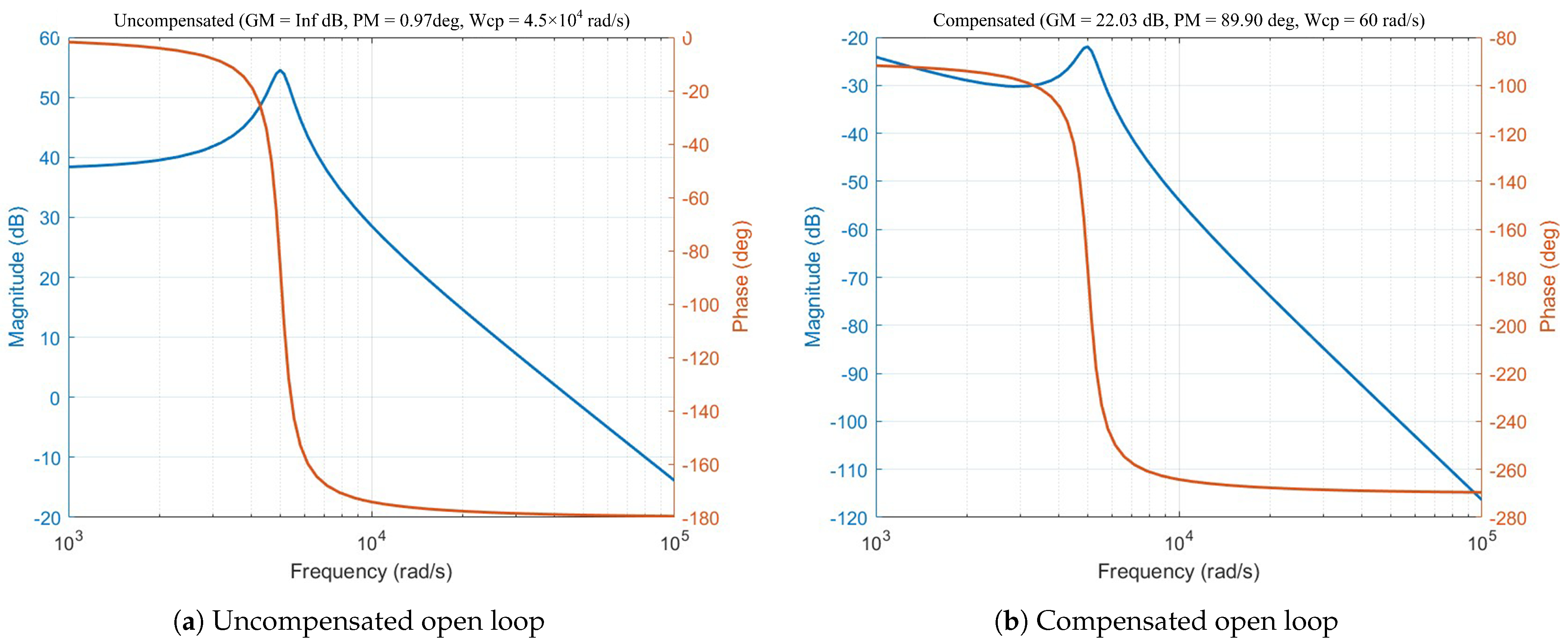
With parameter substitution, the system’s uncompensated open-loop transfer function yields the Bode plot computed in MATLAB R2024b.

As indicated by Figure 8a, the open-loop magnitude response has a shallow slope in the low-frequency range, which leads to a sluggish dynamic response. The phase margin is $1°$, so the system has poor robustness and weak damping. A PI compensator is designed to stabilize the system and enhance its dynamics. The compensated transfer function is defined in Figure 8b, and the corresponding Bode diagram is constructed from it.

With an infinite gain margin and a phase margin of $62.9°$, the compensated system satisfies the classical stability specifications and verifies the validity of the controller design.

7. Comparative Study of the Proposed Converter and Existing Buck Topologies

A compact comparison between representative Buck/interleaved Buck topologies and the proposed converter is given in

Table 1. Compact comparison between existing Buck/interleaved Buck topologies and the proposed converter.

Topology (Representative Works)	Main Limitations in the Literature	Advantages of the Proposed Converter
Conventional inductor Buck with advanced control [1,2,3,4]	Single phase; relatively large inductor and output-voltage ripple; high step-down ratio requires $D\to 1$; no inherent interleaving or current sharing; stringent transient and EMI targets often need complex control schemes.	Two-phase interleaving gives natural ripple cancellation and current sharing; effective duty range limited to $D\in [0,0.5]$ while keeping $V_{\mathrm{o}}/V_{\mathrm{in}}=2D\in [0,1]$, avoiding extreme duty cycles; positively coupled inductor with DCM/CCM hybrid operation enables ZVS/ZCS of the main MOSFETs without auxiliary networks.
Multiphase interleaved Buck with discrete inductors [9,10,11]	Each phase uses a separate inductor ⇒ larger magnetic volume and copper loss; active current-sharing control usually required; triangular inductor currents lead to high RMS currents; control can be complicated because $D\in [0,1]$.	A single positively coupled inductor replaces two independent inductors, reducing magnetic components; 180° phase shift and magnetic coupling provide inherent current sharing; shaped phase inductor currents in DCM reduce RMS current for a given output power; duty range compressed to $D\in [0,0.5]$, simplifying the controller design.
Series-capacitor Buck (SC Buck) [5,6,7,8]	Additional flying capacitors and balancing requirements; more complex power stage and control compared with discrete-inductor interleaved Buck, especially at high frequency.	No flying capacitors are needed; only a positively coupled inductor and output capacitor are used, keeping the hardware simple while still extending the usable duty range and conversion ratio in step-down operation.
Coupled-inductor interleaved/PCI/voltage-balancing topologies [12,13,14,15,16,17,18,19,20]	Often focus on specific aims (e.g., bipolar-bus voltage balancing, full-power-range efficiency) rather than simple step-down regulation; inverse coupling may introduce oscillations and large equivalent inductance; second-order or resonant dynamics complicate small-signal modelling and compensator design; many schemes require extra components or sophisticated control.	Applies positively coupled inductors in a straightforward two-phase step-down Buck; coupling is confined mainly to switching transitions with per-phase DCM and sum-current CCM, giving a simple and well-behaved model; ZVS/ZCS of the main MOSFETs is achieved without resonant tanks or extra active switches, enabling high efficiency (93.3% peak at 270 W) with a simple integral-type voltage controller.
Proposed two-phase interleaved Buck with positively coupled inductors (this work)		Two-phase interleaving + positively coupled inductor; per-phase DCM and sum-current CCM; extended effective duty range ($D\in [0,0.5]$, $V_{\mathrm{o}}/V_{\mathrm{in}}=2D\in [0,1]$); ZVS/ZCS of main MOSFETs without auxiliary networks; reduced ripple and inherent current sharing; experimentally verified 93.3% peak efficiency, about 10 percentage points higher than a conventional Buck prototype using the same devices.

.

8. Simulation Results

The simulation model of the proposed converter was built in a PSIM environment (PSIM Version 2025).

Table 2. Main circuit parameters of experimental prototype.

Mods	Model Number
$u_{in}$	80 $\mathrm{V}/40\mathrm{V}$
f	50 $\mathrm{kHz}$
$S_1/S_2$	IRFP250NPBF
$D_1/D_2$	RHRP3060
C	3 $\times 220\mathrm{\mu }\mathrm{F}$
$L_1$	30 $\mathrm{\mu }\mathrm{H}$
$L_2$	30 $\mathrm{\mu }\mathrm{H}$
k	0.92
Load R	10 $\Omega$

presents the main simulation parameter settings. To verify the accuracy of the voltage gain, the simulation collected data on the voltage gain at various duty cycles. The input voltage $u_{in}$ was set to 40 V and 80 V in the two operating conditions, respectively. The output voltage $u_{out}$ and the output current $I_{out}$ were set to 24 V and 10 A, respectively. The analysis focuses exclusively on the dependence of the voltage conversion gain on the duty cycle.

8.1. Open-Loop Simulation

From Figure 9 and Figure 10, the relationship of the two interleaved driving signals ($u_{gs1}$ and $u_{gs2}$) and the self-inductance currents ($i_{L1}$ and $i_{L2}$) are the same as those in Figure 3. These current waveforms are not triangular waveforms that occur in a conventional Buck converter. The duty cycles ($0.3$ and $0.15$) are clearly smaller than those duty cycles ($0.6$ and $0.3$) of a conventional Buck converter at input voltages are 40 V and 80 V. In the proposed converter topology, a smaller duty cycle corresponds to a higher voltage conversion gain.

From Figure 9 and Figure 10, it can also be seen that MOSFETs $S_1$ and $S_2$ obviously have zero-current turn-on because the currents $i_{L1}$ and $i_{L2}$ have already been zero before the MOSFETs are turned on. The two freewheeling diodes $D_2$ and $D_2$ are also automatically turned off when the currents $i_{L1}$ and $i_{L2}$ decrease to zero, respectively. Thus, the two diodes do not undergo reverse recovery. Therefore, MOSFETs and diodes operate in ZCS.

Theoretical analysis indicates that, for a fixed input voltage, the output voltage increases monotonically with the main-switch duty cycle. Under fixed inputs of 40 V/80 V and a $10\Omega$ load, the output voltage and voltage gain are characterized in open loop as functions of the duty cycle. The open-loop output–voltage and voltage–gain curves in Figure 11a,b share the same monotonic tendency. With the duty ratio fixed at 0.45, the measured open-loop conversion gain is 0.93, thereby corroborating the theoretical result.

8.2. Closed-Loop Simulation

The simulation framework incorporates closed-loop control, with the controller’s effectiveness verified under an abrupt load change scenario. With the input voltage fixed at $40\mathrm{V}$ and the load stepped from $10\Omega$ to $5\Omega$, the output voltage exhibits only a $2\mathrm{V}$ deviation and returns to steady state within approximately $0.01 \mathrm{s}$. Compared to the steady output of 24 V, the voltage fluctuation is only $8.3\%$ of the steady-state value. Figure 12a indicates that a load step from $5\Omega$ to $10\Omega$ at a constant 80 V input causes only a 1 V output fluctuation, with settling achieved in $0.01$ s. Compared to a stable output 24 V, voltage fluctuation is only $4.2\%$ of the steady-state value. The closed-loop simulation results are depicted in Figure 12b. As shown in Figure 12a,b, the controller attains the preset setpoints under both dynamic input–voltage variations and abrupt load changes.

9. Analysis of Experimental Results

To verify the feasibility of the proposed high-gain coupled-inductor converter, a hardware prototype was fabricated using the component values summarized in Table 2. The corresponding experimental setup is illustrated in Figure 13. The control platform is implemented using an STM32F103ZET6 development board as the core controller. The MOSFET is driven by a half-bridge gate-driver circuit to generate the required control pulses. The load stage is formed by the resistor XLGR. The output-voltage node is routed through a parallel voltage sensor board to the STM32 ADC channel, thus closing the feedback control loop.

9.1. Open-Loop Experimental Results

Experiments are performed to confirm the validity of the theoretical analysis and to corroborate the obtained simulation outcomes. From Figure 14 and Figure 15, the relationship of the two interleaved driving signals ($u_{gs1}$ and $u_{gs2}$) and the self-inductance currents ($i_{L1}$ and $i_{L2}$) are the same as those of Figure 9 and Figure 10.

The load resistance is kept at a fixed value of 10 ohms, and the voltage applied to the energy-input port is configured to 40/80 V. The control switch’s duty ratio is adjusted within the range [0.05, 0.45] with a fixed step increment of 0.05. Through open-loop scanning, the curves depicting actual conversion gain and output voltage with respect to switching duty-cycle changes are derived, and the corresponding results are shown in Figure 16a,b.

For duty cycles in the interval $[0.1,0.45]$, the load power is supplied through the output port, with energy flowing from the input port to the output port. When the duty cycle is $0.45$, the open-loop conversion ratio reaches $0.91$.

The converter’s efficiency curve obtained from the open-loop sweep is presented in Figure 17a. Across the entire operating region, the converter maintains a high efficiency level. Under an input of $40\mathrm{V}$, the maximum reaches 93.3% at a switching duty cycle of $0.15$, whereas under $80\mathrm{V}$ input it attains 93.3% at a duty cycle of $0.25$.

Providing an explicit experimental comparison with a conventional buck converter prototype built using the same main power devices and rated power. Under identical operating conditions, the proposed positively coupled two-phase interleaved Buck converter achieves a peak efficiency of 93.3%, which is approximately 10 percentage points higher than that of the conventional buck prototype. This confirms that the proposed topology offers a clear efficiency improvement over a traditional buck implementation.

9.2. Converter Dynamic Response Performance Experiment

Drawing on the preceding analysis, we subsequently validate the feasibility of the closed-loop system. The output-voltage reference is set to $24\mathrm{V}$ (for the respective test cases), and the corresponding results are presented in Figure 18 and Figure 19. The measured output voltage is routed through the distributor to the STM32 for closed-loop PID regulation, and with appropriately tuned parameters a rapid voltage response is achieved. In steady state, the output essentially matches the commanded value and remains stable. After a sudden change in load, the output current settles to a new steady-state level, and the average output voltage returns to a stable value. During this transient, the variation in the load-side voltage is negligible, and the system exhibits a dynamic response time of less than $100\mathrm{ms}$.

At the same time, a closed-loop scan is performed, with the results shown in Figure 20a,b.

10. Conclusions

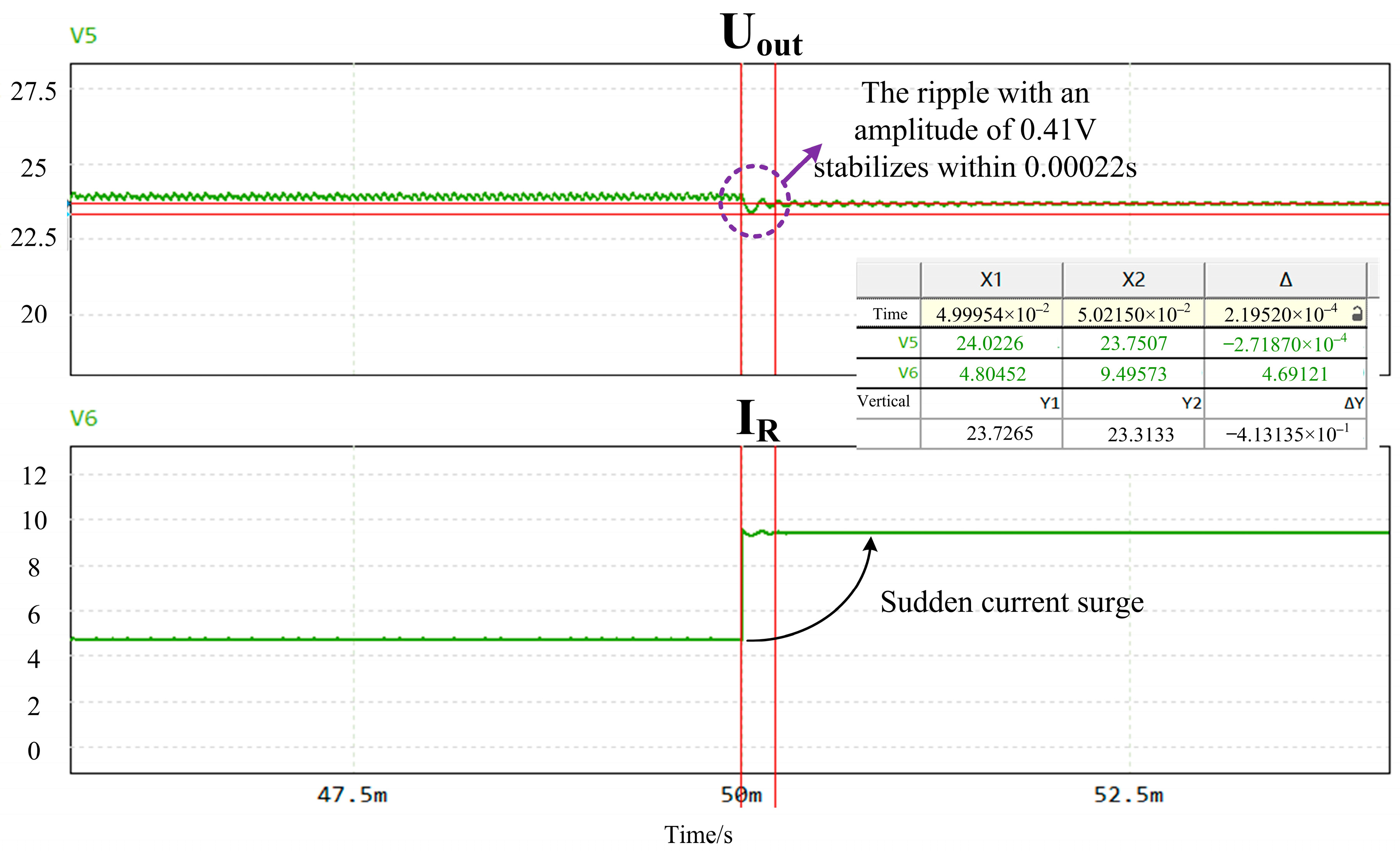
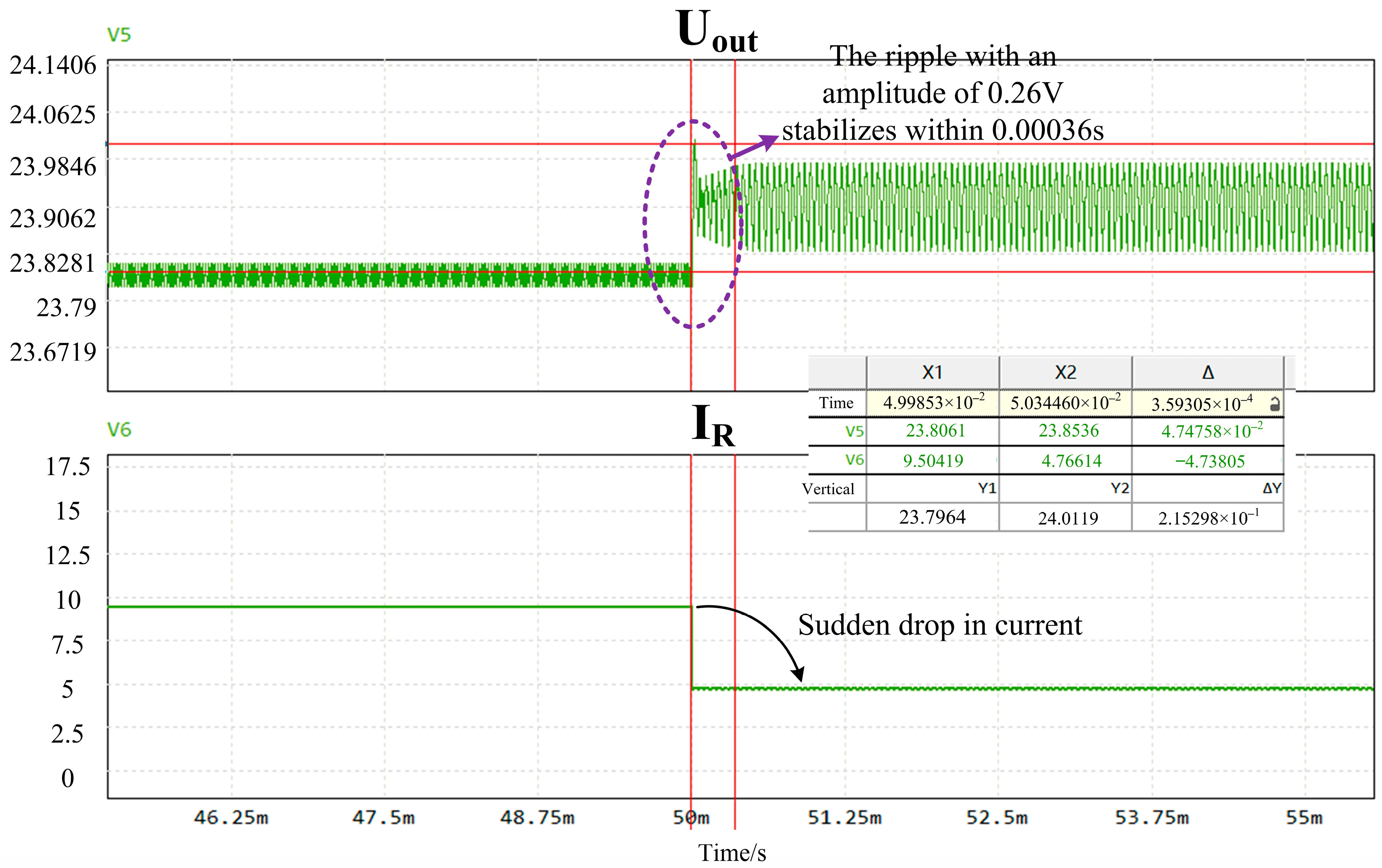
This paper has presented a two-phase interleaved Buck converter employing a positively coupled inductor and operating in a DCM-per-phase but CCM-sum regime. The operating principle, soft-switching conditions, and design guidelines for the magnetic components and control parameters were analyzed in detail. A 270W laboratory prototype was built to validate the theoretical analysis.

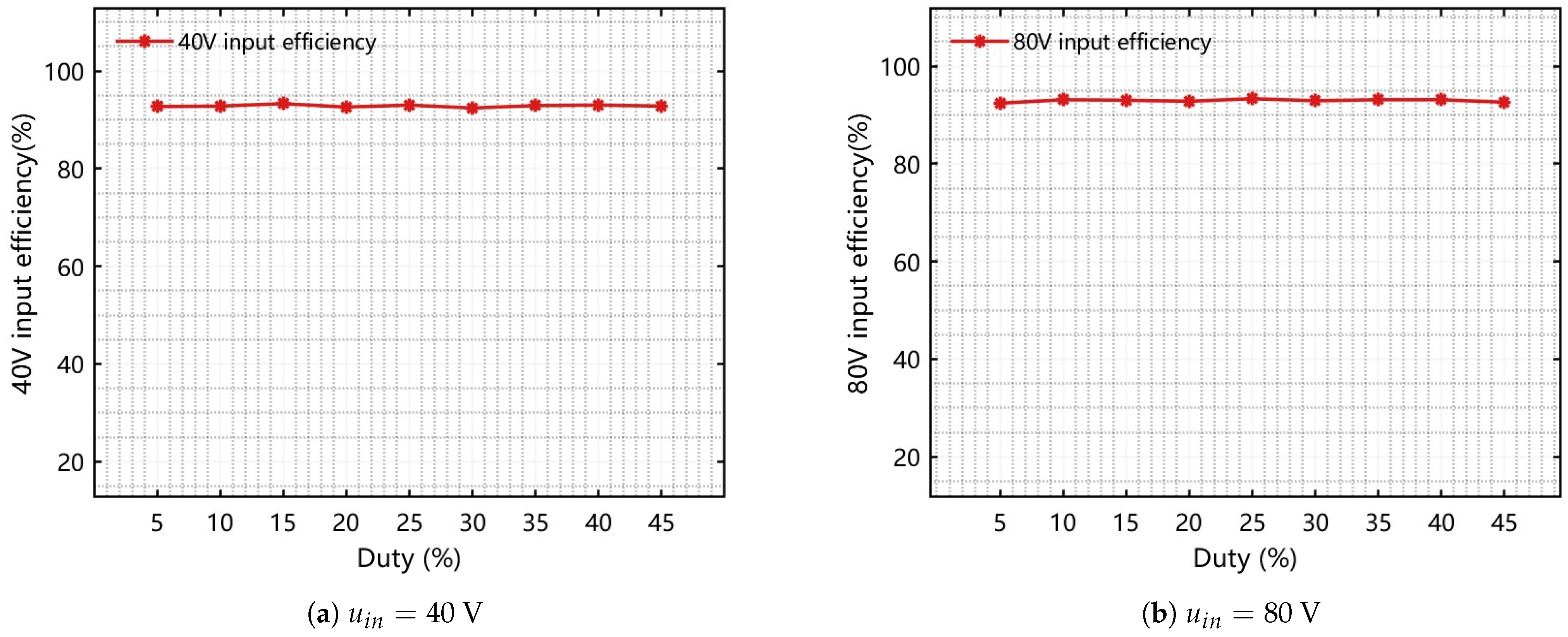
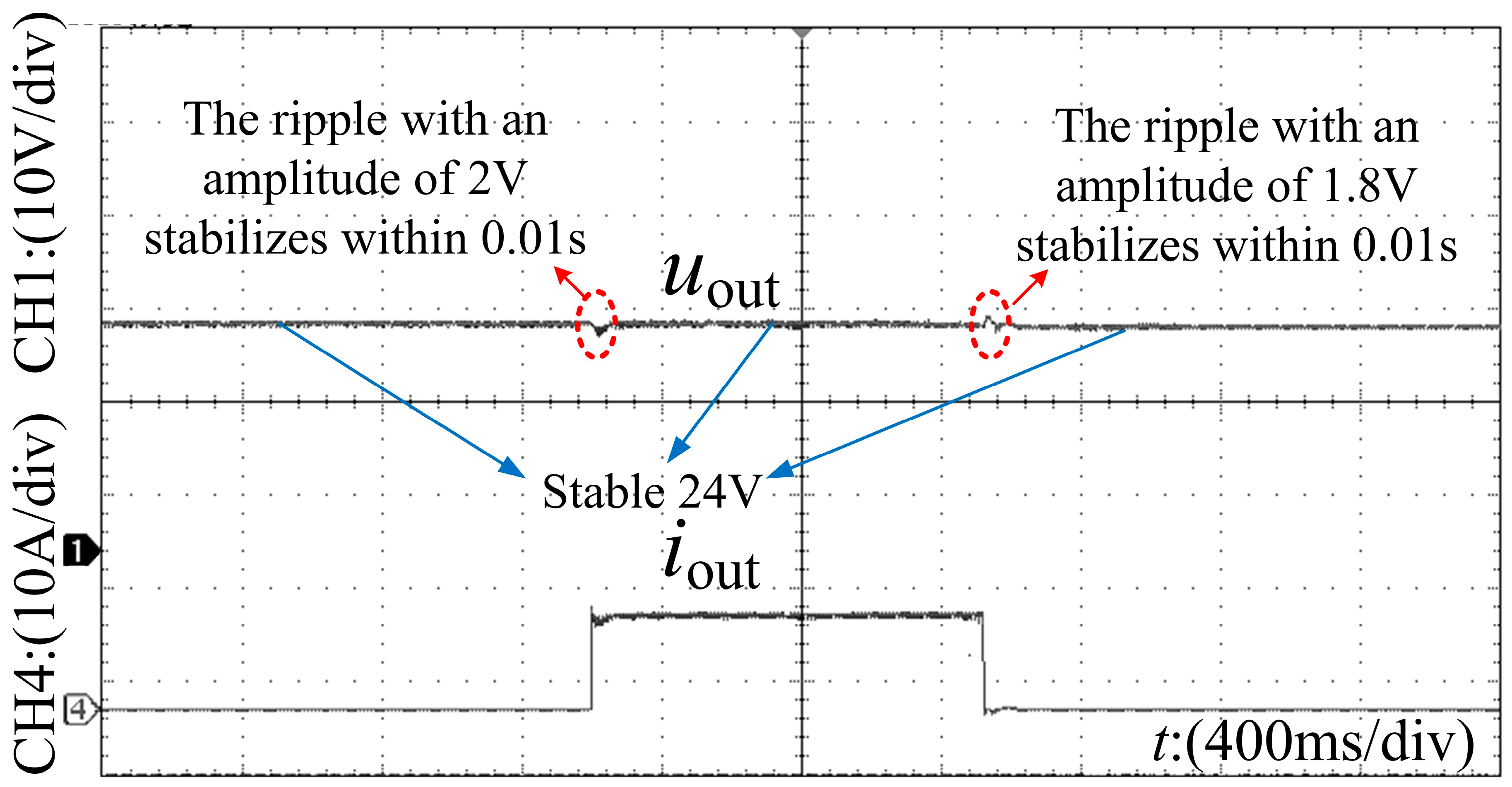
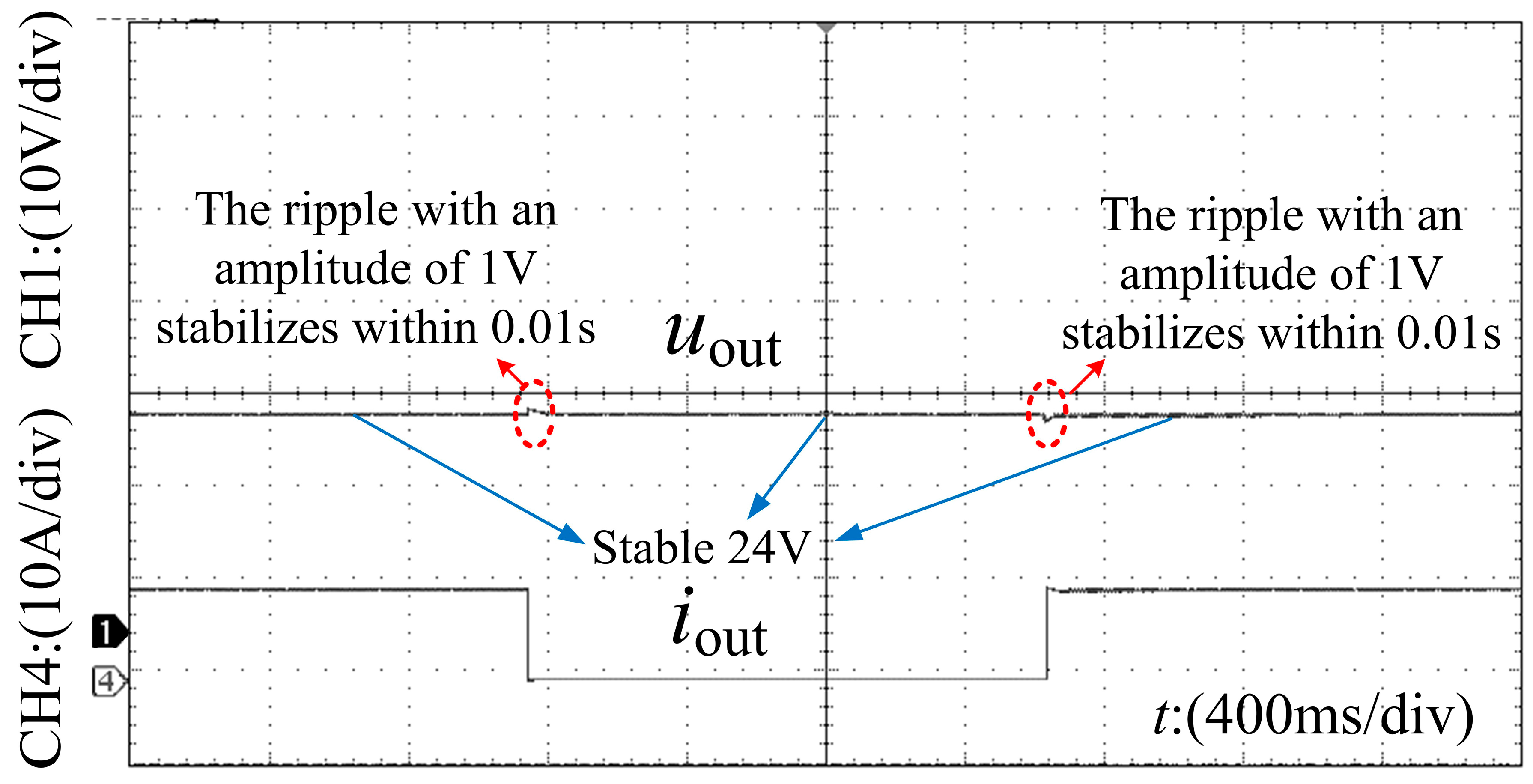
Experimental waveforms confirm that the main power devices can achieve zero-current (and near zero-voltage) switching over the intended operating range, which effectively reduces switching losses. Because of the proposed current-shaping mechanism and positively coupled structure, the effective duty cycle range is extended, and a higher voltage conversion ratio is obtained compared with a conventional interleaved Buck converter at similar duty cycles. The prototype achieves a maximum efficiency of 93.3% with a conversion ratio of 0.5, demonstrating that the proposed topology can simultaneously realize high efficiency and a high conversion ratio with a relatively simple hardware implementation and control scheme.

Future work will focus on a more detailed characterization of electromagnetic interference and grounding effects, as well as investigating how the proposed current-shaping concept can be adapted to other DC-DC converter topologies.