The Circle Group Heuristic to Improve the Efficiency of the Discrete Bacterial Memetic Evolutionary Algorithm Applied for TSP, TRP, and TSPTW

Abstract

The quality of the initial population is a critical factor in the convergence speed and overall performance of an optimization algorithm. A well-structured initial population can significantly enhance the exploration capabilities of the algorithm, allowing it to more efficiently traverse the solution space and converge more quickly and reliably towards optimal or near-optimal solutions. In this paper, we present the Circle Group Heuristic (CGH), a spatially structured initialization method, for generating high-quality initial populations to enhance the convergence speed of the Discrete Bacterial Memetic Evolutionary Algorithm (DBMEA) in solving the Traveling Salesman Problem (TSP) and related combinatorial optimization problems. This work extends the CGH beyond the TSP to a broader class of routing problems. The results show that the integration of CGH into DBMEA demonstrated consistent performance improvements on the TSP, the Traveling Repairman Problem (TRP), and the Traveling Salesman Problem with Time Window (TSPTW) instances of varying sizes. In particular, CGH provided high-quality starting points that accelerated convergence and reduced computational cost. In all tested scenarios, DBMEA enhanced with CGH and consistently preserved the best-known solution quality while reducing execution time.

1. Introduction

The performance of evolutionary and memetic algorithms is determined by many factors, with the selection of the proper initial population as a crucial factor, playing a pivotal role in the performance of population-based optimization algorithms, influencing convergence speed, solution diversity, and the likelihood of escaping local optima [1,2]. Kazimipour et al. [3] presented a comprehensive review of initialization strategies in Evolutionary Algorithms (EAs), classifying them into random, quasi-random, and compositional methods. Their findings indicate that sophisticated initialization techniques, such as low-discrepancy sequences, can significantly enhance performance, particularly in high-dimensional or multimodal problems. Ashraf et al. [4] empirically demonstrated that quasi-random sequences (e.g., Sobol, Torus) improve the exploration capabilities of algorithms like Particle Swarm Optimization (PSO) and Differential Evolution (DE), compared to uniform random seeding. In a broader comparative study, Li, Liu, and Yang [5] evaluated 22 initialization methods across five metaheuristics, Genetic Algorithm (GA), DE, PSO, Cuckoo Search (CS), and Artificial Bee Colony (ABC), and revealed that PSO and CS were particularly sensitive to the choice of initialization, with non-uniform distributions (e.g., Beta, Rayleigh) outperforming uniform strategies. Opposition-based learning, as introduced by Mahdavi et al. [6], was shown to further enhance convergence by generating both a candidate and its opposite, selecting the superior for population seeding. In multi-objective optimization, Friedrich and Wagner [7], and Lu et al. [8] found that incorporating known or approximated Pareto-optimal solutions into the initial population substantially improved convergence behavior. Collectively, these studies underscore that the effectiveness of an optimization algorithm is neither direct nor solely dependent on its operators, but is also critically influenced by the characteristics and distribution of its initial population. In our previous works [9,10], we introduced the Circle Group Heuristic (CGH) as a novel method to generate structured initial populations for solving the Traveling Salesman Problem (TSP) using the Discrete Bacterial Memetic Evolutionary Algorithm (DBMEA) framework. Those studies focused exclusively on the TSP and primarily evaluated the effectiveness of CGH in improving initial solution quality. In the current paper, we extend this approach by integrating CGH into the DBMEA framework and applying it to additional classical NP-hard problems—namely, the Traveling Repairman Problem (TRP) and the Traveling Salesman Problem with Time Window (TSPTW). The main contribution lies not in the proposal of a new heuristic, but in the adaptation and generalization of CGH to a broader class of combinatorial problems. Although CGH was originally introduced for the TSP, this study significantly expands its applicability by (1) generalizing it to TRP and TSPTW, (2) optimizing its radius parameter by dynamically using a Genetic Algorithm, and (3) embedding it as a reusable, modular component within the DBMEA framework. Furthermore, we perform extensive experiments across multiple benchmark sets to evaluate the scalability and robustness of the CGH-augmented DBMEA, analyzing its impact on solution quality and computational efficiency. This integration marks a shift from using CGH merely as a population initializer to treating it as a reusable component embedded into a broader metaheuristic framework. This study aims to assess the extent to which the Circle Group Heuristic can improve convergence speed and solution quality when applied within the DBMEA framework to three NP-hard routing problems.

In Section 2, we describe three NP-hard graph optimization problems within the TSP family. We present the process of the DMBEA algorithm in Section 3. Section 4 emphasizes the importance of initial population strategies in metaheuristic algorithms and introduces the Circle Group Heuristic. In Section 5, we discuss our experimental results and compare them with the previous version of DBMEA. Finally, in Section 6, we draw concluding remarks based on the study’s findings.

2. Various NP-Hard Graph Optimization Problems in the TSP Family

In this section, we present three different problems related to the TSP that are addressed using the proposed algorithm.

2.1. The Traveling Salesman Problem

The TSP is one of the most extensively studied combinatorial optimization problems in operations research and computer science due to its theoretical significance and wide range of practical applications [11,12,13]. The objective of the TSP is to determine the shortest possible route that visits each city in a given graph exactly once and returns to the starting location [14]. Despite its simple formulation, TSP is classified as NP-hard, meaning that no known polynomial-time algorithm can solve all instances of the problem efficiently [15]. TSP has multiple applications in numerous real-world contexts such as vehicle routing, logistics, manufacturing, circuit design, and scheduling, where minimizing travel distance or cost is crucial [16]. Exact algorithms, including branch and bound [17], cutting planes [18], and dynamic programming [19], have been developed to solve small to medium-sized instances of TSP. However, due to the exponential growth of the solution space with problem size, exact methods become computationally infeasible for large instances [20]. As a result, heuristic and metaheuristic approaches such as Genetic Algorithms [21], Ant Colony Optimization (ACO) [22], and Bacterial Foraging Optimization (BFO) [23] have gained significant attention for approximating near-optimal solutions within reasonable time limits [24]. Recent scholarly efforts have focused not only on designing more efficient metaheuristics but also on improving critical components of these algorithms, such as initial population generation, local search mechanisms, and hybridization techniques. A well-constructed initial population can guide the algorithm toward promising regions of the search space and accelerate convergence [9]. In graph theory, the problem is defined on a weighted complete graph, where each vertex represents a city and each edge is assigned a weight corresponding to the cost, distance, or time required to travel between two cities, where the objective is to determine the shortest possible Hamiltonian cycle [25].

$$\begin{array}{c}\hfill G_{TSP}=(V_{cities},E_{conn})\end{array}$$

(1)

$$\begin{array}{c}\hfill V_{cities}=\{v_1,v_2,\dots ,v_n\}\end{array}$$

(2)

$$\begin{array}{c}\hfill E_{conn}\subseteq \left\{(v_i,v_j)\right|i\ne j\}\end{array}$$

(3)

$$\begin{array}{c}\hfill C:V_{cities}\times V_{cities}\to \mathbb{R},C={\left(c_{ij}\right)}_{n\times n}\end{array}$$

(4)

C is the cost matrix, where $c_{ij}$ represents the cost of traveling from city i to city j. The objective is to determine the optimal permutation of vertices $(p_1,p_2,p_3,\dots ,p_n)$ that minimizes the total travel cost $\left(C_{sum}\right)$ [26].

$$C_{sum}=(\sum _{i=1}^{n-1}C{p}_i,p_{i+1})+C{p}_n,p_1$$

(5)

Depending on the characteristics of the cost matrix, the TSP can be classified into two primary categories: symmetric and asymmetric. In the symmetric TSP (STSP), the distance or cost between any two nodes is identical in both directions, i.e., $c_{ij}=c_{ji}$, which implies the underlying graph is undirected. Conversely, in the asymmetric TSP (ATSP), the distance or cost from node i to node j may differ from the distance from node j to node i, i.e., $c_{ij}\ne c_{ji}$ or one of the directions may not exist, reflecting a directed graph structure. This structural difference significantly influences the selection of solution techniques and the associated computational complexity [27].

2.2. Traveling Repairman Problem

Variants of the TSP have been developed to capture more complex and realistic scenarios, such as TRP. Also known as the Minimum Latency Problem or the Deliveryman Problem, TRP is a variant of the classical TSP that focuses on minimizing customer waiting times rather than the total travel distance [28]. In the TRP, a service agent (e.g., a repairman) is required to visit a set of locations starting from a central depot, with the objective of minimizing the total latency, defined as the sum of the arrival times at each location [29].

$$\begin{array}{c}\hfill G_{TRP}=(V_{cities},E_{conn})\end{array}$$

(6)

$$\begin{array}{c}\hfill V_{cities}=v_0\cup \{v_1,v_2,\dots ,v_n\}\end{array}$$

(7)

$$\begin{array}{c}\hfill E_{conn}\subseteq \left\{(v_i,v_j)\right|i\ne j\}\end{array}$$

(8)

$$\begin{array}{c}\hfill C:V_{cities}\times V_{cities}\to \mathbb{R},C={\left(c_{ij}\right)}_{(n+1)\times (n+1)}\end{array}$$

(9)

Formally, the objective is to identify a permutation $(p_1,p_2,p_3,\dots ,p_n)$ of the customer vertices, such that the total latency is minimized:

$$C_{sum}=\sum _{i=1}^{n}C{p}_i$$

(10)

where the arrival time at the customer $p_i$ is defined as the cumulative travel time from the depot to $p_i$ along the given route:

$$C_{p_i}=\sum _{j=1}^{i}C{p}_{j-1},p_j$$

(11)

The TRP has a wide range of real-world applications in domains such as logistics, telecommunications, service scheduling, and healthcare, particularly in contexts where minimizing response time is of greater importance than minimizing distance. For example, in emergency services or on-site maintenance scenarios, a reduction in the average or total waiting time can lead to substantial improvements in service quality and customer satisfaction [30]. Similarly to the TSP, the TRP is also classified as NP-hard, and obtaining optimal solutions for large-scale instances remains computationally intractable [31]. Consequently, traditional optimization methods are generally restricted to small problem sizes, which has motivated the development of heuristic and metaheuristic approaches, including Genetic Algorithms [32].

2.3. Traveling Salesman Problem with Time Windows

In TSPTW, a salesman must visit each customer exactly once within a predefined time window, starting and ending the tour at a central depot. Each customer is associated with a time window, defined by a ready time $a_i$ and a due time $d_i$. The salesman may not begin service at a customer before its ready time; if he arrives earlier, he must wait until service can begin. Conversely, arriving after the due time renders the tour infeasible, as it violates the time window constraints [33]. The objective of TSPTW is to find a feasible Hamiltonian tour of minimum cost (typically measured in total travel distance or time) that satisfies all time window and service time constraints. Formally, the problem can be modeled as a graph search problem on a complete directed graph [34]:

$$\begin{array}{c}\hfill G_{TSPTW}=(V_{customer},E_{conn})\end{array}$$

(12)

$$\begin{array}{c}\hfill V_{customer}=v_0\cup \{v_1,v_2,\dots ,v_n\}\end{array}$$

(13)

$$\begin{array}{c}\hfill E_{conn}\subseteq \left\{(v_i,v_j)\right|i\ne j\}\end{array}$$

(14)

$$\begin{array}{c}\hfill C:V_{customer}\times V_{customer}\to \mathbb{R},C={\left(c_{ij}\right)}_{(n+1)\times (n+1)}\end{array}$$

(15)

where

• Ready time = $\{a_1,a_2,\dots ,a_n\}$;
• Due time = $\{b_1,b_2,\dots ,b_n\}$;
• $V_{customer}$ is the set of customers;
• $v_0$ is the depot.

$c_{ij}$ represents the total cost of traveling from customer i to customer j, including the service time at customer i. The goal is to find a feasible sequence permutation of the vertices $(p_1,p_2,p_3,\dots ,p_n)$ that adheres to the specified time windows at each location and results in the minimum possible tour length.

$$C=C{v}_0,p_1+(\sum _{i=1}^{n-1}C{p}_i,p_{i+1})+C{p}_n,v_0$$

(16)

where

• It is subject to $D_{Pk}\le b_{Pk}$ for all customers;
• $D_{Pk}$ = max $(A_{Pk},a_{Pk})$;
• $A_{Pk}=D_{Pk-1}+C_{Pk-1}{,}_{Pk}$;
• $D_{Pk}$ is departure time at customer _Pk;
• $A_{Pk}$ is arrival time at customer _Pk.

TSPTW, which incorporates time constraints for visiting specific locations, has numerous practical applications in domains such as logistics, transportation planning, postal delivery, and banking services, where time-constrained routing is essential for operational efficiency [35]. The Traveling Salesman Problem with Time Windows is NP-hard, and even verifying the feasibility of a solution is computationally intractable [36]. As a result, exact algorithms are generally limited to small instances. Langevin et al. [37] proposed a two-commodity flow model solving up to 60-node instances, while Dumas et al. [38] extended dynamic programming with elimination tests to handle up to 200 nodes with tight time windows. Focacci et al. [35] integrated constraint programming with optimization techniques to improve efficiency. Due to these limitations, heuristics have been widely used for larger problems, for example, Tabu search by Carlton and Barnes [39], an insertion heuristic by Gendreau et al. [40], and simulated annealing with penalties by Ohlmann and Thomas [41]. Additionally, Variable Neighborhood Search (VNS) by Da Silva and Urrutia [42] achieved competitive results, improving known solutions and reducing computation times.

3. The Discrete Bacterial Memetic Evolutionary Algorithm

The Bacterial Evolutionary Algorithm (BEA) was introduced by Nawa and Furuhashi [43]. It was initially applied to fuzzy system parameter discovery. It has since been adapted for various optimization tasks, including nurse scheduling [44], data clustering [45], three-dimensional bin packing [46], and fuzzy resource allocation [47]. The Discrete Bacterial Memetic Evolutionary Algorithm builds upon the BEA by integrating 2-opt and 3-opt local search techniques, forming a memetic algorithm [27]. Memetic algorithms combine global evolutionary search with local refinement to enhance solution quality and convergence speed, making them well suited for NP-hard problems such as the TSP [26]. This hybrid structure classifies DBMEA as a memetic algorithm, leveraging both global and local search mechanisms for enhanced performance. DBMEA operates through four main stages: initial population creation, bacterial mutation (including coherent segment mutation and loose segment mutation), local search (using 2-opt and 3-opt techniques), and gene transfer, which are cyclically repeated [26].

3.1. Initial Population

Each individual in the DBMEA population represents a potential solution encoded as a permutation. For TSP, A permutation of city indices is used, excluding the starting city (index 0), as it is implicit. The initial population includes both randomly generated individuals and deterministic solutions created using three heuristic approaches [26].

3.1.1. Nearest Neighbor Heuristic

The Nearest Neighbor (NN) heuristic constructs a tour by always selecting, at each step, the nearest unvisited city as the next destination. This method is straightforward to implement and computationally efficient, making it a popular choice for generating initial solutions.

3.1.2. Secondary Nearest Neighbor Heuristic

In the Secondary Nearest Neighbor (SNN) heuristic, the tour is constructed by selecting the second nearest unvisited city at each step. This approach aims to introduce diversity compared to the NN heuristic but may result in longer tours.

3.1.3. Alternating Nearest Neighbor Heuristic

The Alternating Nearest Neighbor (ANN) heuristic combines the NN and SNN methods. It alternates between visiting the nearest and the second nearest unvisited cities during the construction of the tour. This hybrid strategy seeks to balance the strengths of both NN and SNN. Among these three approaches, the NN heuristic generally achieved the best convergence speed and produced higher-quality initial solutions in most cases. For TRP and TSPTW, individuals are random permutations of customer indices (excluding the depot, index 0), which is consistently the starting point of the tour.

3.2. Bacterial Mutation

Bacterial mutation operates individually on each bacterium within the population. For every bacterium, the following procedure is applied: Initially, a number of clones ($N_{clones}$) are generated from the original bacterium. The chromosome of each bacterium is divided into fixed-length segments of size ($I_{seg}$); these segments may be loose segments or coherent segments. In our implementation, both loose segment mutation and coherent segment mutation are applied for solving the TSP, TRP, and TSPTW. Next, a segment is randomly selected from the original bacterium. This segment is randomly modified within each of the clones, while the corresponding segment in the original bacterium remains unchanged. In addition, one of the clones is deterministic and contains the reverse order of the selected segment to encourage structured diversity [26]. The bacterial mutation process is illustrated in Figure 1.

The fitness values of all clones, including the original bacterium, are evaluated: For TSP and TRP, the clone with the minimum tour cost propagates its modified segment back to the original bacterium and to all clones. For TSPTW, if one or more clones yield a feasible solution (i.e., one that satisfies all time window constraints), the clone with the shortest feasible tour length propagates its segment. If no feasible clone exists, the clone with the smallest total delay (the sum of positive differences between arrival times and due times across all customers) propagates its segment to the others. This mutation and replacement process continues sequentially until all segments (genes) of the original bacterium have been subjected to mutation. At the end of this stage, the original bacterium is replaced by the fittest clone, and all other clones are discarded. This ensures that the resulting bacterium is at least as fit as, or fitter than, the original prior to mutation [26].

3.3. Local Search

Local search begins with a candidate solution and iteratively explores its neighborhood in search of an improved solution. At each step, the algorithm moves to a neighboring solution if it offers a better objective value, continuing this process until no further improvements can be found within the local neighborhood. Local search significantly refines individual solutions and accelerates convergence. There are two stages of local searches in DBMEA [26], and they are elucidated below.

3.3.1. A 2-OPT Local Search

A 2-OPT search iteratively replaces two edges in the tour with two others to reduce tour length. Figure 2 shows the 2-OPT local search.

3.3.2. A 3-OPT Local Search

A3-OPT search generalizes this by replacing three edges, allowing more complex improvements. Figure 3 illustrates the potential replacements in the 3-OPT local search.

The local search process begins with 2-OPT and proceeds to 3-OPT only if 2-OPT can no longer improve the solution. To enhance efficiency of the local search, three strategies are added [26]:

• Candidate list: For each vertex, a candidate list is generated containing the indices of its closest neighboring vertices, ordered in ascending distance. During local search, only a predefined number of the nearest vertices (from the candidate list) are considered for edge exchanges. This approach exploits the fact that shorter edges are more likely to be part of high-quality solutions.
• Don’t look back bits: Each vertex is associated with a don’t look back bit. If no improvement is found for a particular vertex during a local search iteration, that vertex is temporarily excluded from consideration (its don’t look back bit is set to 1). The vertex remains inactive until one of its incident edges is modified, at which point its don’t look back bit is reset, and it becomes eligible for further consideration.
• Fixed radius search: For a given vertex $ui$, the new neighbor $uk$ vertex is searched within a fixed radius. The radius is defined as $c(ui,uj)$, which is the distance between the $ui$ vertex and $uj$, one of the two neighboring vertices in the current tour. This strategy restricts the search to spatially proximate vertices, thereby reducing computational overhead. The concept can be extended to 3-OPT local search by performing two fixed-radius searches for each examined vertex pair.

For TSPTW, the local search prioritizes making tours feasible by minimizing delays when necessary and focuses on reducing tour length while preserving feasibility once achieved.

3.4. Gene Transfer

The gene transfer operation facilitates the exchange of information among bacteria within the population, with the aim of improving solution quality through segment sharing. This operation encourages diversity and intensification by allowing superior individuals to influence inferior ones. The process begins by sorting the population in descending order of fitness. The sorted population is then divided into two groups: a superior half and an inferior half. The operator performs $N_{inf}$ gene transfer attempts. One source bacterium is randomly selected from the superior group, and one destination bacterium is randomly selected from the inferior group. Then, a randomly chosen segment of predefined length $I_{transfer}$ is copied from the source bacterium to the destination bacterium. For TSP and TRP, the population is sorted in ascending order of tour cost. While for TSPTW, a two-level sorting is applied: first, individuals are sorted in ascending order of their total delay (the sum of positive differences between arrival times and due times across all customers). Among individuals with equal total delay, secondary sorting is performed based on tour length. During gene transfer, the selected segment is inserted into the destination bacterium’s tour at a randomly chosen position. Duplicate nodes are eliminated to preserve tour feasibility and length [26]. Figure 4 illustrates the segment transfer in the gene transfer stage.

4. Initial Population Strategies in Metaheuristic Algorithms

This section presents the motivation for enhancing the initial population, emphasizing its importance in improving the convergence behavior and overall performance of DBMEA. Building on this motivation, we introduce the concept of the Circle Group Heuristic, which was developed to address the limitations of random initial population generation.

4.1. The Importance of the Initial Population

The selection of the initial population constitutes one of the most critical and influential parameters in metaheuristic optimization algorithms. Optimizing the initial population can serve as a coarse yet effective strategy for improving the performance across a wide range of optimization problems. As discussed in the previous chapter, our earlier work introduced the use of NN, 2NN, and ANN methods within the DBMEA framework, which were evaluated on a diverse set of NP-hard problems. These strategies demonstrated consistent efficiency, often yielding results comparable to the best-known solutions, and in certain cases, surpassing them. Due to their generalizability, these approaches can be effectively applied across a variety of problem domains. Nonetheless, there remains considerable potential to further enhance both the quality and effectiveness of initial population construction.

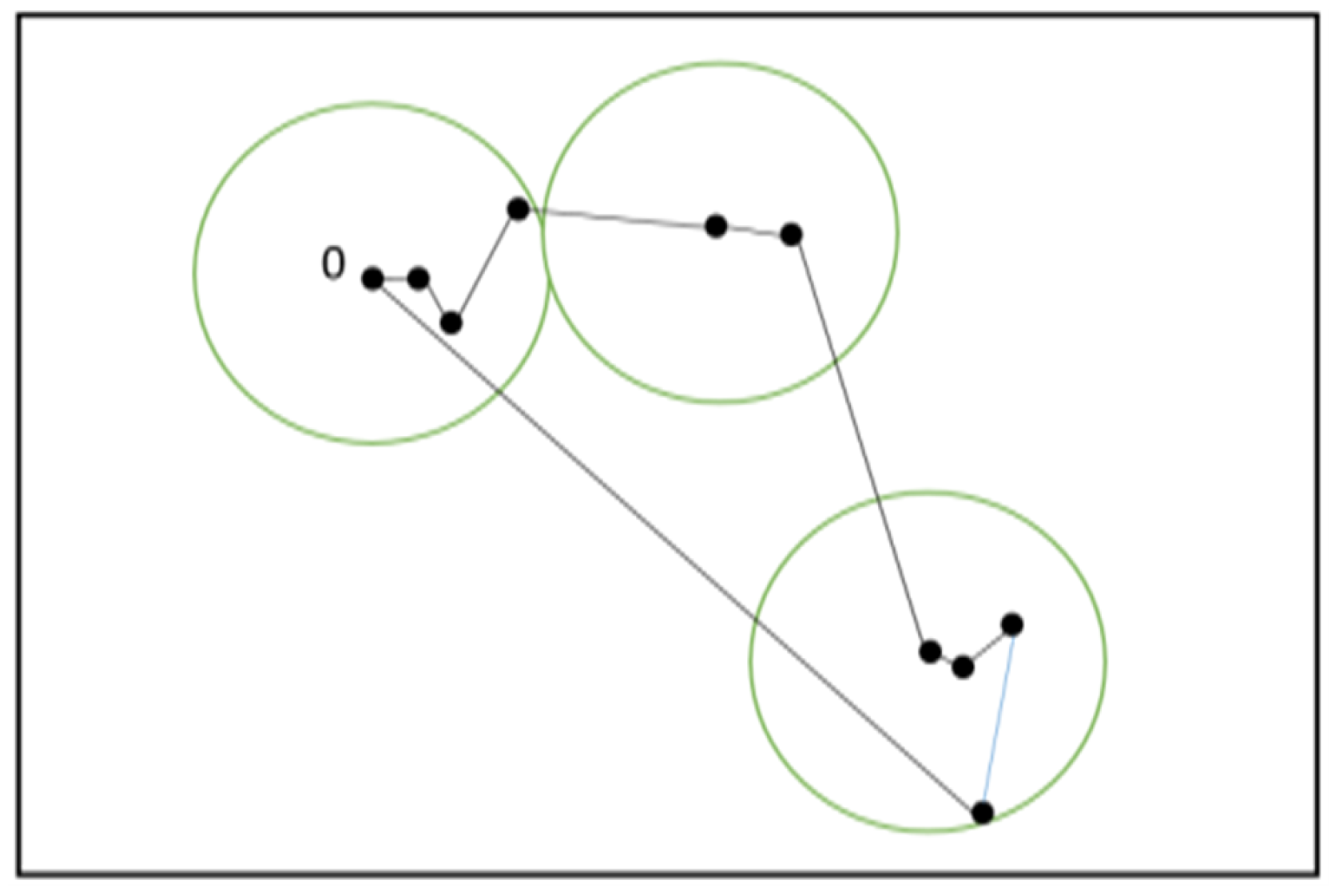
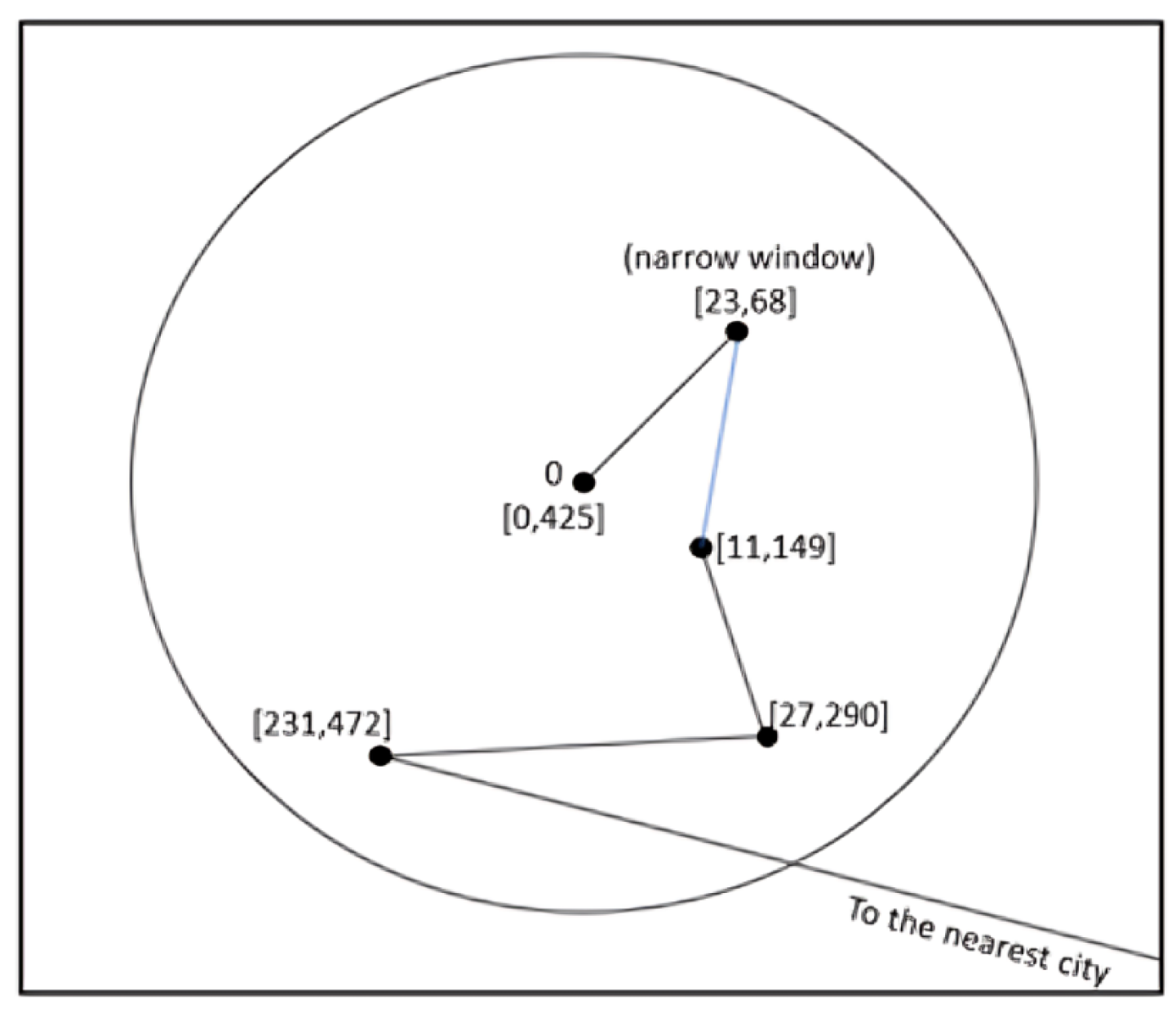
4.2. Circle Group Heuristic Algorithm

In the past, our group was involved in some company-initiated projects that dealt with the quasi-optimization of daily dispatcher decisions concerning the optimal routing of multiple trucks delivering goods to various destinations in Europe—obviously a difficult, and mathematically intractable (NP-hard) problem. Route conditions, regulations, fuel prices, rest area conditions, and other relevant factors vary significantly across European countries and depend on geographic and temporal context. Due to the extreme complexity and heterogeneity of the optimization task in that project, we had proposed a strategy where the overall optimization problem was divided into subtasks, thereby applying the classical and effective algorithmic principle of “Divide and conquer”. Thus, the full optimization task was segmented into smaller components according to countries and geographic regions and conditions, so that each local optimization subtask could be improved independently, and thus influencing the overall cost. When the results of the subtasks were combined, these local solutions of the entire cumulative task showed improvement in the total route length and cost. This approach resulted in financial benefits for the commissioning logistics company. This practical insight supports the notion that local spatial correlations of the conditions can be exploited to improve the efficiency of optimization procedures. Even the computational complexity of such algorithms subdivided into smaller tasks may bring considerable improvement in the total runtime—where it must always be observed that these approaches are heuristic, or so-called metaheuristic solutions, and mathematically, there is never any guarantee that the solution will be close to the real optimum. Motivated by this promising observation, we began formalizing a strategy where spatial locality is preserved during initialization by constraining the search to dynamic neighborhood regions. This strategy was not directly applied to the optimization of the original problem, but to the first and rather crucial step of a more sophisticated and more advanced metaheuristic approach. Specifically, the rather efficient Discrete Bacterial Memetic Evolutionary Algorithm, namely for the first quasi-optimization of the initial population, may be considered as one of the most crucial and rather complex parameters of the DBMEA. A similar idea was explored in our earlier studies [48,49], where optimization was performed within several single countries, allowing multiple alternative routes. There we introduced a novel approach that quasi-optimizes the initial population and ensures consistent improvements for the rather classical and well-researched TSP. In this study, we will further investigate several somewhat related, but mathematically more complex, and obviously also NP-hard problems, namely TRP, and TSPTW. This novel method will be referred to as the Circle Group Heuristic. It applies the simple concept of a Neighborhood Circle (NC) that herein plays the role of a single sub-area within the whole graph under search. As the goal is to structure and guide the generation of high-quality initial solutions, the proper selection of these NCs is the most important element of the heuristic approach. Once the strategy of the subdivision has been determined, the NC is defined by a pre-specified radius (R), which limits and simultaneously accelerates the search for promising initial population candidates. The specification of the value of the R of the NCs is obviously the decisive factor in the efficiency of the whole method. Properly selected neighborhoods will result in the CGH improving the locality selection, and thereby accelerating the local convergence within the subproblems with internal spatial correlations by favoring geographically proximal connections forming clusters or quasi-clusters during early-stage solution construction. The process begins with the starting node (typically City 0) serving as the center of the initial circle. Assuming that the R has somehow been determined, an invisible circle of radius R is drawn. Then, for TSP and TRP, the nearest (less costly) unvisited city within this circle is selected as the next node in the tour, while for the TSPTW, the selection of local subtours within each circle follows a structured two-level sorting procedure. Initially, the candidate cities within the circle are sorted in ascending order based on their time window parameters (the sum of the positive differences between the arrival times and the corresponding due times of all customers). This prioritization favors cities with narrower windows, particularly in cases where the TSP would otherwise arrive after the due time. Such cities are given precedence over others to preserve feasibility. In instances where multiple cities exhibit the same total delay, a secondary sorting criterion based on Euclidean distance is applied. This two-level sorting mechanism ensures that the TSP tour minimizes unnecessary waiting before customer ready times, thereby enhancing temporal feasibility. At the same time, it promotes spatial efficiency by prioritizing nodes that are both geographically proximate and temporally aligned with the current tour progression. Once all cities within the current circle have been visited, the algorithm selects the nearest unvisited city outside the circle as the new center and generates a new circle around it. Figure 5 illustrates the procedure for generating initial tours using CGH for TSP and TRP. The procedure adapted for TSPTW is presented in Figure 6. Moreover, Figure 7 includes an example of a tour generated using CGH for both the TSP and TRP, while Figure 8 depicts a single CGH circle constructed specifically for the TSPTW.

The most effective radius for CGH (which produces superior tours) varies depending on the topology and structure of the graph. Our analysis of benchmark datasets representing different countries, each with its own unique distribution of cities and road networks, revealed that the optimal R is influenced by factors such as the total area of the country, the number of cities, and their spatial distribution. Initially, we employed an exhaustive search strategy to identify the optimal radius for the CGH, testing a discrete range of integer values from 1 to 100 using a brute-force approach. Subsequently, we explored the use of GA to determine the optimal radius, enabling a continuous search over a broader range of rational values within the same interval [1, 100].

5. Results of the DBMEA with CGH Applied for Three NP- Hard Metaheuristics

5.1. Results of Traveling Salesman Problem

The Circle Group Heuristic was evaluated on symmetric national Traveling Salesman Problem benchmark instances [50], with problem sizes reaching up to 10,639 nodes. In these experiments, the initial populations generated by CGH were compared to those produced by previously studied heuristics: NN, SNN, and ANN.

Table 1. Comparison of the initial tours.

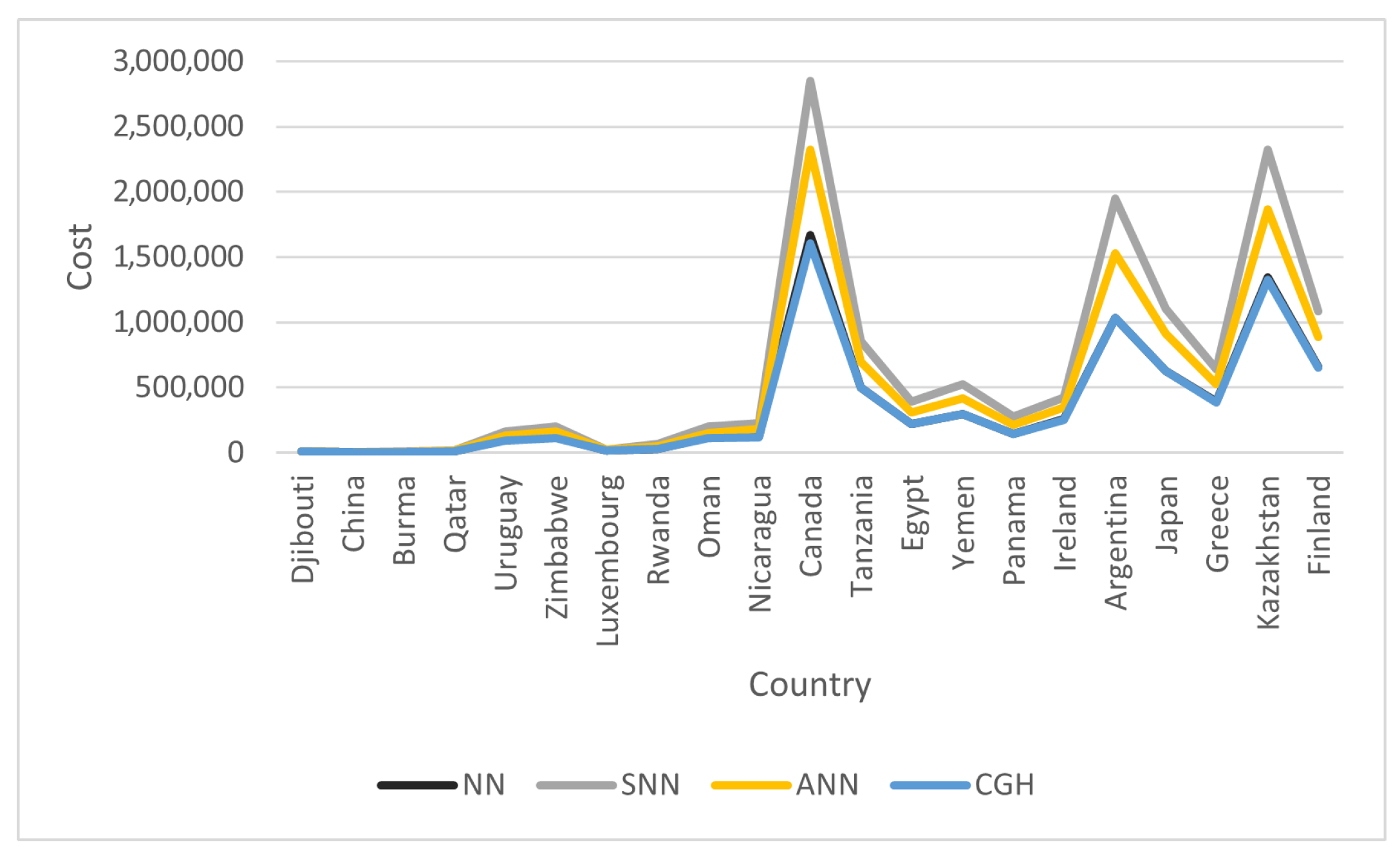
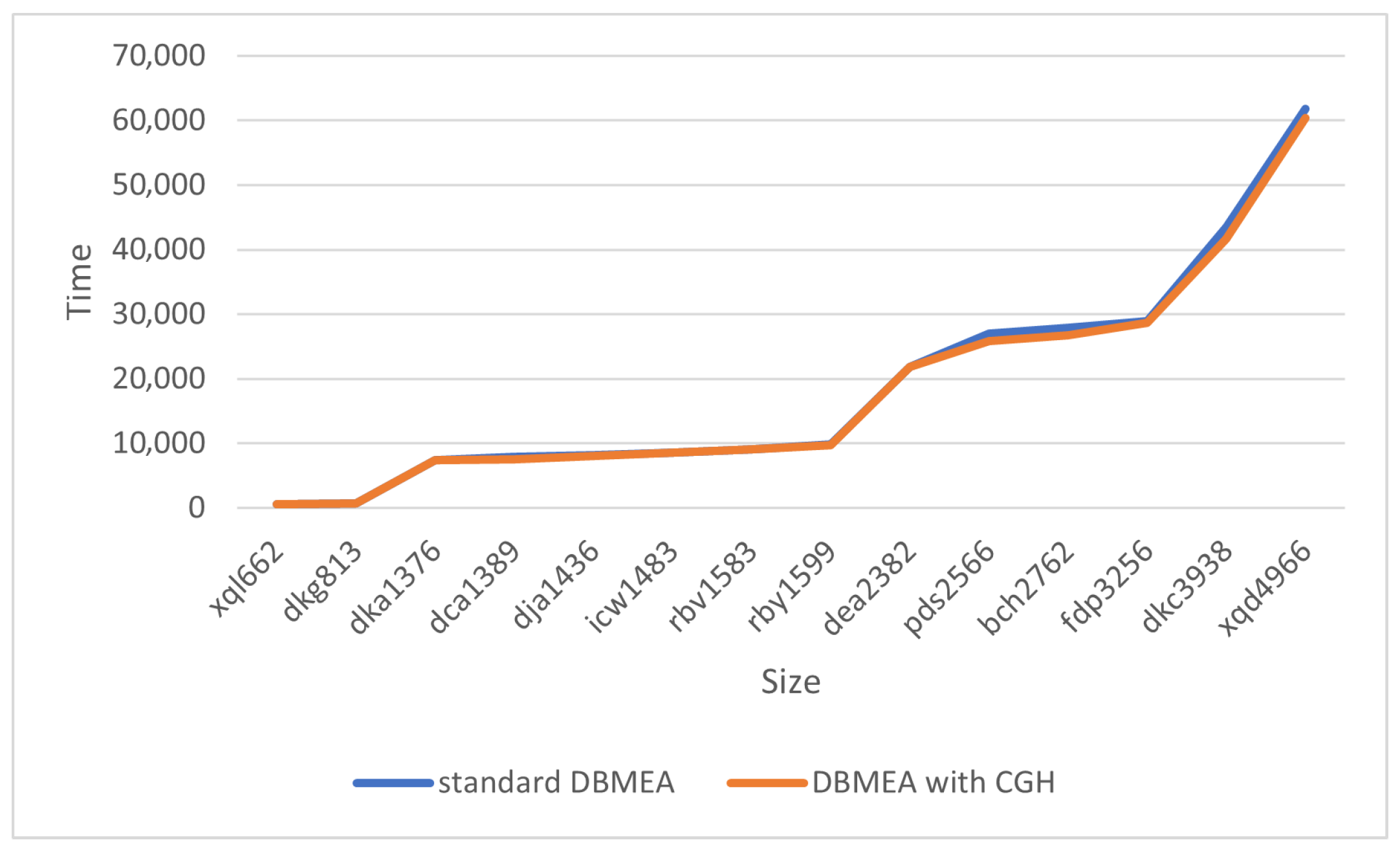
Country	Number of Cities	NN	SNN	ANN	Exhaustive Search		Genetic Algorithm
					R	CGH	R	CGH
Djibouti	38	9748.946	13,509.088	10,474.948	78–100	8306.575	79.834	8306.575
China	70	2570.329	4148.675	3565.305	18	2267.889	21.137	2263.575
Burma	80	5477.026	8674.245	6079.910	98–100	4526.302	98.272	4526.302
Qatar	194	11,892.888	18,980.443	17,199.801	9	11,649.869	56.280	11,255.296
Uruguay	734	102,594.358	165,796.643	130,793.380	57–59	95,536.209	54.832	95,461.998
Zimbabwe	929	117,733.696	200,063.995	160,430.512	10	114,813.039	48.955	114,484.256
Luxembourg	980	14,212.721	26,240.107	20,397.885	8	13,995.032	16.254	13,958.023
Rwanda	1621	32,276.665	68,487.437	45,630.149	10	31,596.476	9.768	31,596.476
Oman	1979	120,542.129	204,249.064	152,503.643	13	110,747.729	12.688	110,029.190
Nicaragua	3496	122,412.147	229,749.240	179,481.992	16	118,141.497	15.935	118,141.497
Canada	4663	1,668,707.230	2,852,242.400	2,320,011.780	71–74	1,603,709.500	73.834	1,603,709.500
Tanzania	6117	501,427.829	852,834.843	696,141.743	16	499,513.302	16.567	499,513.302
Egypt	7146	222,335.231	391,416.939	306,664.393	4	217,487.431	3.981	217,487.431
Yemen	7663	298,953.459	523,144.599	417,814.532	5	298,150.565	5.185	297,972.031
Panama	8079	146,660.520	277,856.032	210,793.510	16	142,277.699	15.984	141,949.651
Ireland	8246	259,165.057	421,610.120	350,446.111	12	255,167.585	11.971	255,167.585
Argentina	9152	1,034,964.600	1,951,034.190	1,527,346.320	16	1,034,084.030	15.635	1,034,084.030
Japan	9847	625,031.710	1,104,954.110	909,941.924	2	624,849.337	2.215	624,849.337
Greece	9882	391,415.926	637,638.279	523,514.157	14	384,948.298	13.158	384,900.881
Kazakhstan	9976	1,346,903.560	2,320,848.050	1,863,893.670	13	1,325,094.710	13.058	1,325,094.710
Finland	10,639	657,774.773	1,081,658.770	889,702.220	20	649,477.672	20.158	649,477.672

presents a comparison of the initial tour costs, highlighting the performance of the initial populations generated by the earlier heuristics and CGH. Figure 9 provides a visual representation of this comparison in the form of a chart.

By comparing the initial tours generated by CGH using different radius values (determined via both the exhaustive search approach and the Genetic Algorithm), the results demonstrated that the GA consistently produced more effective radius values in most cases for constructing initial tours. These values led to higher-quality tours produced by CGH. Based on these findings, the GA-based optimization approach was adopted exclusively for determining the R parameter in all subsequent experiments. The results further indicate that the GA reliably discovers superior radius values within a reasonable computational time, thereby establishing it as the preferred method for tuning this parameter. The Genetic Algorithm was employed using MATLAB R2023b’s Global Optimization Toolbox to optimize the radius parameter R ∈ [1, 100]. The chromosome was encoded as a real-valued vector containing a single gene corresponding to the R. The fitness function evaluates the quality of the solution produced by the core algorithm for a given radius. The GA was configured with a population size of 50, a crossover rate of 0.8 (using intermediate crossover), Gaussian mutation, and a maximum of 100 generations. The optimization aimed to minimize the objective function. No linear or nonlinear constraints were imposed, and the search was conducted within the specified bounds. At the initial population level, the Circle Group Heuristic consistently produced shorter tours compared to the previously investigated heuristics. On average, CGH generated tours that were approximately 4% shorter than those produced by the Nearest Neighbor (NN) heuristic, 44% shorter than the Secondary Nearest Neighbor (SNN) heuristic, and 30% shorter than the Alternating Nearest Neighbor (ANN) heuristic. In specific instances, CGH achieved even greater relative improvements: the best CGH tour was 17% shorter than NN in the Burmese instance (80 cities), 54% shorter than SNN in the Rwandan instance (1621 cities), and 37% shorter than ANN in the Chinese instance (70 cities). Comparisons were also made between the CGH and the known absolute optimum tour for benchmark instances. The CGH generated initial population-produced tours that were approximately 20% longer than the known optimal solutions, demonstrating that CGH provides high-quality starting points suitable for memetic Evolutionary Algorithms.

Table 2. Runtimes of the tour construction heuristics.

Instance	NN	SNN	ANN	CGH
Burma	2 ms	3 ms	2 ms	2 ms
Rwanda	783 ms	1766 ms	1284 ms	673 ms

presents the computational runtimes of the various tour construction heuristics (CGH, NN, SNN, and ANN) on the Burma (80) and Rwanda (1621) instances, showing that CGH not only produces better-quality tours but does so in less time.

We tried other heuristics inside the circle of CGH, such as SNN and ANN, resulting in inferior performance compared to NN, producing less effective initial populations and ultimately leading to poorer overall solution quality. VLSI TSP instances were tested using DBMEA with CGH, and the results were compared against those obtained with the standard DBMEA.

Table 3. Comparison of runtimes for TSP.

Instance	Standard DBMEA		DBMEA with CGH
	Best	Avg	Best	Avg
xql662	2550.84	2550.84	2550.84	2550.84
dkg813	3243.41	3243.41	3243.41	3243.41
dka1376	4738.61	4743.2	4737.86	4738.33
dca1389	5156.43	5158.06	5156.32	5157.8
dja1436	5332.19	5335.93	5328.96	5330.09
icw1483	4467.22	4472.12	4466.68	4469.67
rbv1583	5446.09	5449.99	5445.34	5447.4
rby1599	5589.13	5592.02	5586.59	5591.56
dea2382	8154.34	8160.93	8149.61	8152.12
pds2566	7774.91	7781.57	7772.01	7778.91
bch2762	8376.18	8380.63	8369.98	8372.32
fdp3256	10,104.36	10,108.69	10,102.03	10,105.31
dkc3938	12,715.99	12,723.46	12,707.78	12,711.01
xqd4966	15,554.91	15,560.49	15,553.7	15,558.51

presents the detailed results of this comparison, while Figure 10 illustrates the corresponding runtimes. Various parameter configurations for DBMEA with CGH were evaluated, and the following setup demonstrated the fastest convergence:

• The number of bacteria in the population is $(N_{ind}=100)$;
• The number of clones in the bacterial mutations $(N_{clones}=n_{cities}/15)$;
• The number of infections in the gene transfer is $(N_{inf}=40)$;
• The length of the chromosomes is $(I_{seg}=n_{cities}/20)$;
• The length of the transferred segment is $(I_{trans}=n_{cities}/5)$;
• The length of the candidate lists (square root of the number of cities).

The results of applying the DBMEA with CGH to various TSP benchmark instances demonstrate clear improvements in both computational efficiency and solution quality when compared to the standard DBMEA.

5.2. Results of Traveling Repairman Problem

The enhanced DBMEA with CGH was subjected to testing on a set of benchmarks problems to assess its efficiency and solution quality. Each instance was executed 20 times, and the average results were recorded for analysis. The performance of the new DBMEA variant was compared with that of the standard DBMEA version, which is already recognized for outperforming most the state-of-the-art heuristics [29]. Among the various DBMEA parameter settings tested, the following setup resulted in the most rapid convergence:

• The number of bacteria in the population is $(N_{ind}=100)$;
• The number of clones in the bacterial mutations $(N_{clones}=n_{cities}/15)$;
• The number of infections in the gene transfer is $(N_{inf}=40)$;
• The length of the chromosomes is $(I_{seg}=n_{cities}/20)$;
• The length of the transferred segment is $(I_{trans}=n_{cities}/5)$;
• The length of the candidate lists (square root of the number of cities).

Across all instances, the integration of CGH resulted in faster execution times compared to the standard DBMEA.

Table 4. TRP average runtimes for small instances.

Instance	Standard DBMEA		DBMEA with CGH
	S20	S50	S20	S50
TRP-Sn-R1	0.46620	5.3862	0.46435	4.504
TRP-Sn-R2	1.81035	4.157	1.20820	2.7564
TRP-Sn-R3	0.31860	5.8018	0.26175	4.9896
TRP-Sn-R4	0.64560	10.2186	0.58460	9.6592
TRP-Sn-R5	0.86665	7.1022	0.69775	6.4844
TRP-Sn-R6	0.36460	33.613	0.29005	33.01
TRP-Sn-R7	0.81975	3.9832	0.78280	3.2212
TRP-Sn-R8	0.73525	10.0588	0.72810	8.2512
TRP-Sn-R9	0.62660	9.1434	0.60420	8.1272
TRP-Sn-R10	0.66405	7.851	0.60135	6.7018
TRP-Sn-R11	0.31340	20.6156	0.24940	14.5618
TRP-Sn-R12	0.33315	4.0588	0.27370	3.8696
TRP-Sn-R13	0.46040	11.911	0.38175	10.9524
TRP-Sn-R14	0.25540	36.342	0.24555	34.18
TRP-Sn-R15	0.29265	4.9564	0.22680	4.345
TRP-Sn-R16	0.61670	4.9534	0.59085	4.3752
TRP-Sn-R17	1.41970	22.8882	1.18085	21.4784
TRP-Sn-R18	0.24355	15.444	0.23145	13.415
TRP-Sn-R19	7.2784	8.91	2.9512	6.1426
TRP-Sn-R20	0.83550	2.373	0.62880	1.9478

presents results for smaller instances (with 20 and 50 nodes) originally generated by Salehipour et al. [30], where the new DBMEA with CGH achieved average execution time reductions of 20.45% and 14.29% for the 20-node and 50-node cases, respectively.

For larger, real-city instances comprising up to 226 nodes, as presented in

Table 5. TRP average runtimes for TSPLIB instances.

Instance	Best Known	DBMEA			DBMEA with CGH
		Best Value	Avg. Value	Avg. Sec	Initial CGH	Best Value	Avg. Value	Avg. Sec
eil51	10,178	10,178	10,178	13.1285	10,859.087	10,178	10,178	11.9511
berlin52	143,721	143,721	143,721	3.0569	152,750.51	143,721	143,721	2.5359
st70	20,557	20,557	20,557	12.7221	22,657.996	20,557	20,557	11.3729
eil76	17,976	17,976	17,976	17.6342	19,518.298	17,976	17,976	14.6147
pr76	3,455,242	3,455,242	3,455,242	8.1218	3,696,829.1	3,455,242	3,455,242	7.3098
rat99	57,986	57,986	57,986	54.6843	62,967.779	57,986	57,986	51.8731
kroA100	983,128	983,128	983,128	24.0905	1,103,528.6	983,128	983,128	21.7378
kroD100	976,965	976,965	976,965	19.5177	1,054,638.6	976,965	976,965	18.2528
lin105	603,910	603,910	603,910	57.0368	687,043.79	603,910	603,910	47.8758
pr107	2,026,626	2,026,626	2,026,626	8.23	2,083,980	2,026,626	2,026,626	7.4696
rat195	2,10,191	218,665	218,693.1	157.8004	228,467.18	218,665	218,665	143.2586
pr226	7,100,308	7,196,869	7,196,898.6	208.2368	10,785,832	7,196,869	7,196,869	200.7428

, the benchmark datasets were obtained from TSPLIB [51]. The Circle Group Heuristic generates initial tours that are, on average, about 12% longer than the optimal tour, providing a strong starting point for further optimization. DBMEA with CGH produced an average execution time reduction of 8.69% compared to the standard DBMEA. Moreover, the CGH-enhanced DBMEA yielded superior tour values for the rat195 and pr226 instances, demonstrating both efficiency and solution quality improvements.

5.3. Results of Traveling Salesman Problem with Time Window

The Discrete Bacterial Memetic Evolutionary Algorithm was rigorously evaluated on a comprehensive set of benchmark instances proposed by Gendreau et al. [40]. This benchmark suite consists of 140 individual instances. DBMEA was tested using the following parameter settings:

• The number of bacteria in the population is $(N_{ind}=30)$;
• The number of clones in the bacterial mutations $(N_{clones}=n_{cities}/15)$;
• The number of infections in the gene transfer is $(N_{inf}=20)$;
• The length of the chromosomes is $(I_{seg}=n_{cities}/40)$;
• The length of the transferred segment is $(I_{trans}=n_{cities}/10)$;
• The length of the candidate lists (square root of the number of cities).

Table 6. TSPTW results.

Instance		Best Known	DBMEA			DBMEA with CGH
n	w		Best Value	Avg. Value	Avg. Sec	Best Value	Avg. Value	Avg. Sec
20	120	265.6	265.6	265.6	0.2	265.6	265.6	0.2
	140	232.8	232.8	232.8	0.2	232.8	232.8	1.8
	160	218.2	218.2	218.2	0.2	218.2	218.2	0.2
	180	236.6	236.6	236.6	0.2	236.6	236.6	0.2
	200	241	241	241	0.2	241	241	0.19
40	120	377.8	377.8	377.8	0.6	377.8	377.8	0.53
	140	364.4	364.4	364.4	0.7	364.4	364.4	0.68
	160	326.8	326.8	326.8	0.7	326.8	326.8	0.63
	180	330.4	330.68	330.68	1.1	330.53	330.68	0.98
	200	313.8	314.98	314.98	1.7	313.8	314.98	1.62
60	120	451	451	451	1.3	451	451	1.26
	140	452	452	452	1.4	452	452	1.32
	160	464	464.4	464.58	1.9	464.4	464.4	1.81
	180	421.2	421.2	421.82	3.6	421.2	421.2	3.23
	200	427.4	427.4	427.4	2.7	427.4	427.4	2.61
80	100	578.6	578.6	578.6	1.4	578.6	578.6	1.31
	120	541.4	541.4	542.24	6.9	541.4	542.24	6.84
	140	506	506	506.88	6.4	506	506	6.33
	160	504.8	505.2	506.14	6.7	505.2	505.2	6.7
	180	500.6	502	502.8	7.4	501.27	502	7.34
	200	481.4	481.8	482.86	7.5	481.8	481.8	7.48
100	80	666.4	666.4	667.1	7.4	666.4	666.75	7.37
	100	642	642	642.86	10.4	642	642.63	9.81
	120	597.2	598.2	600.1	15.1	598.2	600.1	14.85
	140	548.4	548.4	548.66	8.8	548.4	548.66	8.13
	160	555	555	556.22	12.8	555	555.86	12.53
	180	561.6	562	562.7	14.1	562	562.45	13.75
	200	550.2	551.2	552.84	15	550.6	551.27	14.64

shows that the integration of the Circle Group Heuristic into the DBMEA framework resulted in an average reduction in execution time of approximately 9% when compared to the previous version of DBMEA. This improvement in computational efficiency reflects the advantage of providing the algorithm with high-quality initial solutions generated by CGH. In addition to faster execution, the CGH-enhanced DBMEA produced superior tour values for several benchmark instances, demonstrating that the approach not only accelerates convergence but also contributes to achieving better solution quality across a range of problem scenarios.

6. Conclusions and Future Work

This paper presents the integration of the Circle Group Heuristic with the Discrete Bacterial Memetic Evolutionary Algorithm (DBMEA) to enhance the performance in solving complex combinatorial optimization problems, including the TSP, TRP, and TSPTW. By constructing a high-quality initial population by grouping cities based on spatial proximity using dynamically optimized neighborhood circles, this quasi-optimized initialization strategy provides the algorithm with promising starting points that accelerate the search process and help avoid premature convergence to local optima. Extensive computational experiments were conducted on a wide range of benchmark instances. The results clearly demonstrated that DBMEA with CGH consistently outperformed the previous version of DBMEA, achieving reductions in execution time while delivering superior or comparable tour values in most cases. The benefits of CGH were particularly pronounced in large-scale and real-world instances, where its ability to provide structured, high-quality initial solutions contributed significantly to faster convergence and better final outcomes. The novelty of this approach lies in combining a spatially driven initialization method with a memetic framework across three distinct NP-hard routing problems. These findings confirm that the use of structured, quasi-optimized initial populations can significantly enhance the efficiency and effectiveness of evolutionary and memetic algorithms in solving NP-hard routing problems. Future research directions include enhancing initial population strategies for other NP-hard graph-based problems, as well as investigating the performance and interactions of hierarchically combined metaheuristics, particularly within layered optimization architectures. Further work will focus on adapting and integrating CGH into alternative metaheuristic frameworks and exploring adaptive radius tuning mechanisms to improve the generalizability and robustness of CGH across a broader range of problem domains.