Distributed Active Support from Photovoltaics via State–Disturbance Observation and Dynamic Surface Consensus for Dynamic Frequency Stability Under Source–Load Asymmetry

Abstract

The power system’s dynamic frequency stability is affected by common-mode ultra-low-frequency oscillation and differential-mode low-frequency oscillation. Traditional frequency control based on generators is facing the problem of capacity reduction. It is urgent to explore new regulation resources such as photovoltaics. To address this issue, this paper proposes a distributed active support method based on photovoltaic systems via state–disturbance observation and dynamic surface consensus control. A three-layer distributed control framework is constructed to suppress low-frequency oscillations and ultra-low-frequency oscillations. To solve the high-order problem of the regional grid model and to obtain its unmeasurable variables, a regional observer estimating both system states and external disturbances is designed. Furthermore, a distributed dynamic frequency stability control method is proposed for wide-area photovoltaic clusters based on the dynamic surface control theory. In addition, the stability of the proposed distributed active support method has been proven. Moreover, a parameter tuning algorithm is proposed based on improved chaos game theory. Finally, simulation results demonstrate that, even under a 0–2.5 s time-varying communication delay, the proposed method can restrict the frequency deviation and the inter-area frequency difference index to 0.17 Hz and 0.014, respectively. Moreover, under weak communication conditions, the controller can also maintain dynamic frequency stability. Compared with centralized control and decentralized control, the proposed method reduces the frequency deviation by 26.1% and 17.1%, respectively, and shortens the settling time by 76.3% and 42.9%, respectively. The proposed method can effectively maintain dynamic frequency stability using photovoltaics, demonstrating excellent application potential in renewable-rich power systems.

1. Introduction

In renewable-rich power systems, dynamic frequency stability is increasingly threatened by common-mode ultra-low-frequency oscillation (ULFO) and differential-mode low-frequency oscillations (LFOs) under source–load asymmetry disturbances [1]. In 2005, inter-area LFOs accompanied by a ULFO (0.015 Hz) occurred in the European power grid, leading to the loss of synchronization of multiple synchronous units, large-scale power outages and economic losses. In 2020, a 0.5 Hz LFO with a 0.02 Hz ULFO were observed in the UK power grid, leading to grid frequency deviation that exceeded ±0.2 Hz.

Currently, LFO control primarily relies on additional damping control, such as power system stabilizers (PSSs). However, their effective bandwidth spans only 0.1–2.5 Hz, and ULFOs remain beyond their reach [2,3]. ULFOs are typically mitigated via long-term power regulation (e.g., GPSS). However, GPSS’s response speed is too slow to match the rapid dynamics of LFOs [4,5]. Moreover, related studies suggest that ULFO and LFO are in fact coupled [6]. Ultra-low-frequency power swings can excite LFO modes, whose fast dynamics in turn disturb ULFO control [7]. In 2021, though ULFOs at the Hami PV plant in Xinjiang were successfully controlled, the 0.8 Hz LFO persisted and drove the frequency deviation beyond ±0.2 Hz. Therefore, coordinated control of both ULFO and LFO is essential, and single-band methods alone cannot solve the problem.

In power systems increasingly dominated by new energy, the decreasing proportion of synchronous machines has led to a rapid deterioration in system regulation capabilities [8,9]. Now photovoltaic (PV) systems, as the leading new energy source, offer millisecond-level power regulation (<100 ms). Thus, PV systems can rapidly inject or absorb power during grid disturbances, providing advantages in suppressing ULFO and LFO. In addition, the China National Energy Administration’s Notice [10] requires centralized PV systems to feature enhanced frequency regulation and real-time operational data reporting. Therefore, a critical technical challenge is how to leverage the active and rapid power support capabilities of PV clusters for dynamic frequency stability.

Currently, there are three main methods for dynamic frequency stability control: centralized, decentralized, and distributed control. Centralized control centralizes decision-making in a single controller to achieve global optimization. Ref. [11] proposed a VSC-HVDC frequency control method by centrally regulating the output of VSC-HVDC. Ref. [12] designed a centralized H∞ controller to suppress ULFO and LFO in hydro–solar complementary systems. Ref. [13] proposes a centralized model predictive controller for frequency stability in microgrids. However, the inherent defects of centralized control are particularly prominent in high-proportion PV power systems: ① A central controller failure will cripple the network’s oscillation suppression, and the large-scale PV plants will further amplify the fault impact. ② Centralized control relies on wide-area communication networks. Since PV plants are widely distributed and numerous, any large communication delay can significantly reduce the control performance. ③ The need for centralized controllers to process real-time status from all grid PV units creates a computational burden that grows exponentially with installed capacity (from GW to TW). This makes real-time control infeasible.

Decentralized control operates by dividing system into multiple locally communicating subsystems, thereby removing reliance on global communication. Ref. [14] proposes decentralized event-triggered load frequency control to address excessive communication burden associated with centralized control. Ref. [15] proposes a decentralized load frequency control based on the differential evolution algorithm for multi-region systems. Despite this advantage, decentralized control still struggles to utilize PV systems to suppress ULFO/LFO: ① Relying solely on local data, photovoltaic controllers struggle to identify and suppress inter-area LFOs. ② Without effective communication and coordination, controllers may conflict and amplify oscillations.

Distributed control can significantly enhance system flexibility and adaptability by assigning tasks to multiple computing nodes that communicate. Addressing those challenges, ref. [16] introduces a leader–follower distributed control strategy for faster voltage control response. Ref. [17] proposes a sliding mode control-based adaptive algorithm for PV primary frequency regulation. However, distributed frequency control still has shortcomings: (1) It focuses on suppressing a single oscillation type without addressing ULFO and LFO concurrently. (2) It requires high-quality communication. (3) It lacks specific applications designed for large-scale PV clusters to provide effective active frequency support.

To address these challenges, this paper proposes a distributed active frequency support method based on photovoltaic systems. A three-layer distributed control framework is constructed to suppress LFOs and ULFOs. To solve the high-order problem of regional grid and to obtain its unmeasurable variables, a regional observer estimating both system states and external disturbances is designed. Furthermore, a distributed dynamic frequency stability control method is proposed for wide-area PV clusters based on the dynamic surface control theory. In addition, the stability of the proposed distributed active support method has been proven. Moreover, a parameter tuning algorithm is proposed based on improved chaos game theory. Finally, simulation results demonstrate that the proposed method can effectively maintain dynamic frequency stability using photovoltaics, demonstrating excellent application potential in renewable-rich power systems.

Main contributions of this paper include the following: ① This paper proposes a regional observer with dual observation for state and disturbance variables. This approach effectively tackles key challenges in wide-area power system with large-scale PVs, including high model order, multiplicity of elements, and the presence of unmeasurable variables.

② To date, the PV-based approach has not yet been established for dynamic frequency stability control in multi-area power systems. We propose a distributed dynamic frequency stability control method for wide-area photovoltaic clusters, which effectively leverages photovoltaics to maintain system frequency stability with high performance.

③ Existing distributed frequency control strategies struggle to simultaneously suppress LFO and ULFO and rely heavily on communication. This paper proposes a new distributed PV frequency control approach by integrating the multi-agent consensus algorithm (MAC) and dynamic surface control (DSC), which can effectively suppress both oscillations even with weak communications and large delays.

④ In contrast to existing control methods for which parameter tuning often relies on ad hoc trial and error, we not only prove the stability of the proposed method but also propose a parameter tuning algorithm based on chaos game optimization (CGO).

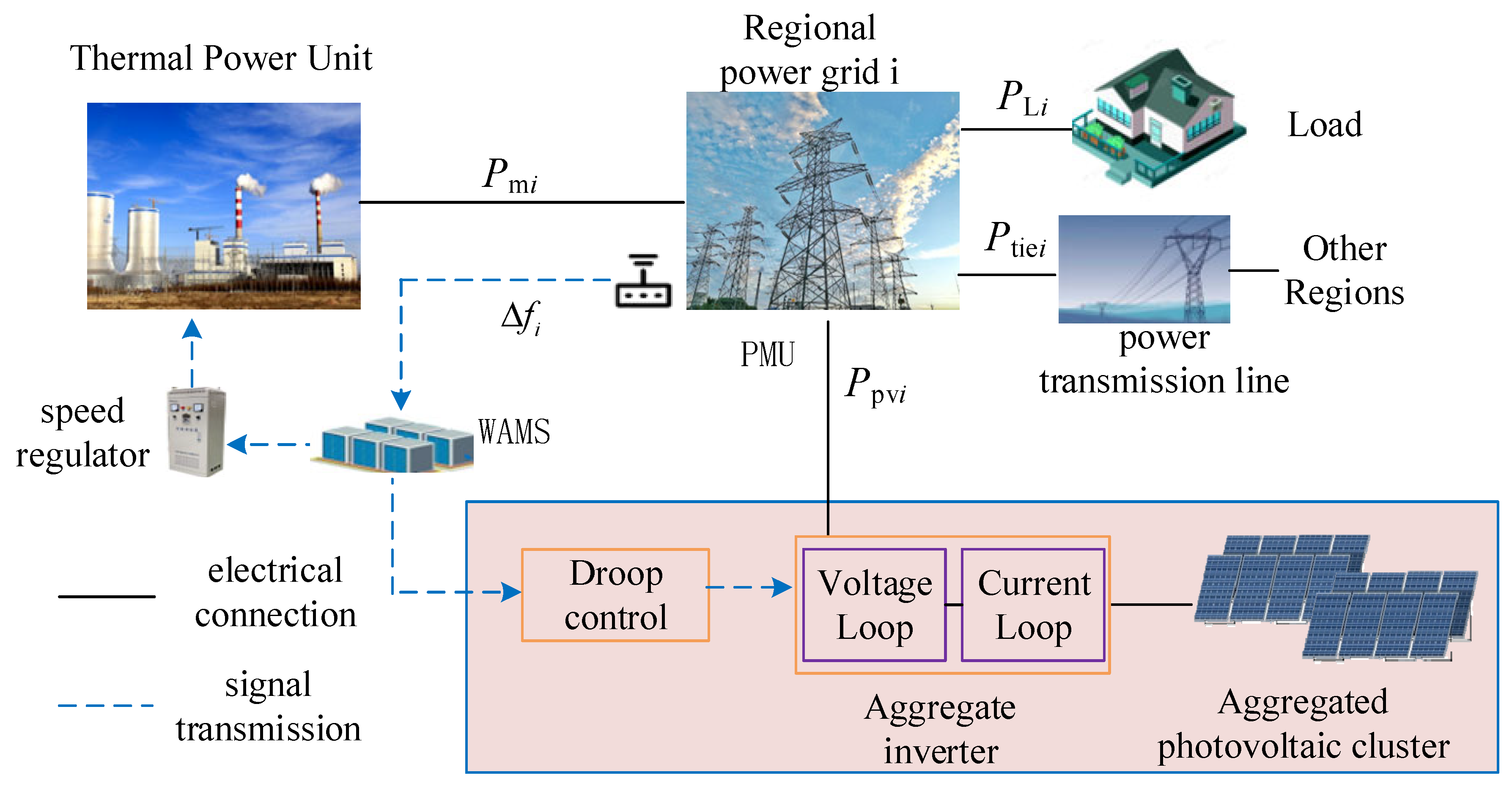
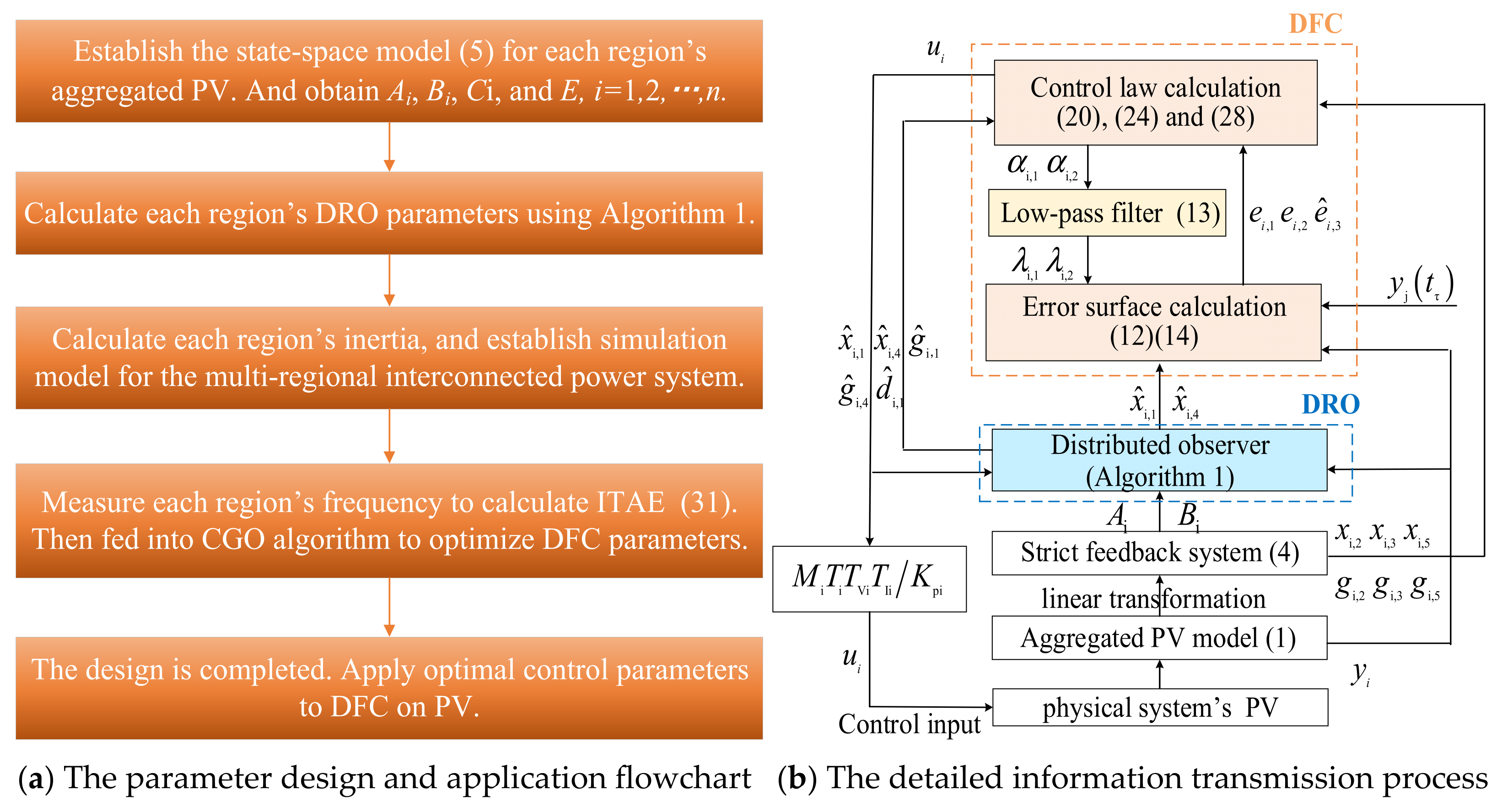
2. Cloud Control Architecture for Dynamic Frequency Active Support of Wide-Area Photovoltaic Clusters

2.1. Cloud-Based Control Architecture for Dynamic Frequency Active Support of Wide-Area Photovoltaic Clusters

(1)

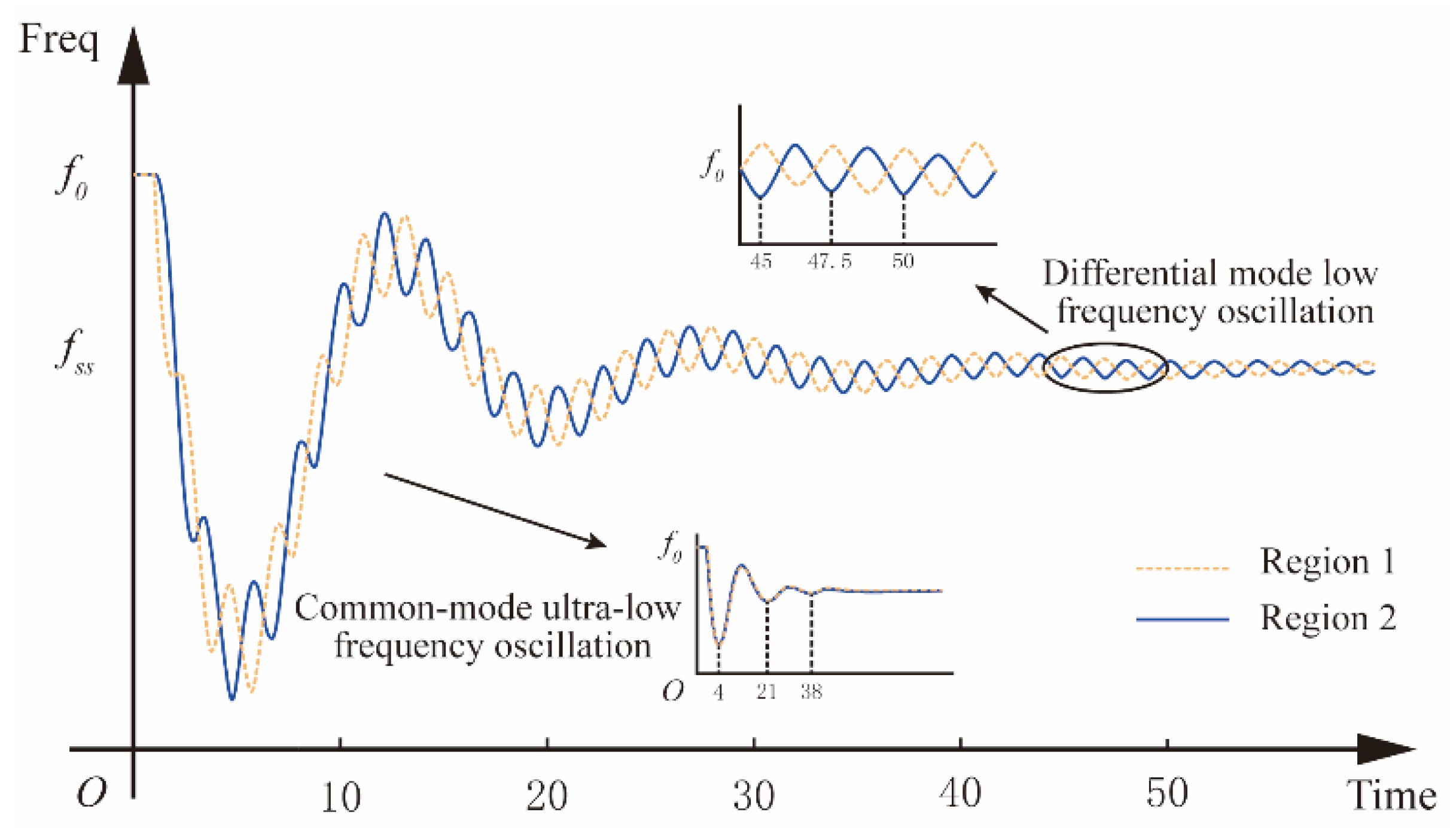
Photovoltaic Participation in Frequency Regulation Structure and Dynamic Frequency Stability Issues

The structure of photovoltaic participation in power system frequency regulation is shown in Figure 1. When a power deficit occurs in the power system, the frequency of the center of inertia (CoI) of region i, calculated using synchronous phasor measurement units (PMUs), will experience a deviation. Based on the WAMS system, the photovoltaic cluster detects $\Delta f_i$ and rapidly adjusts the photovoltaic output power through active frequency droop control at each power station, achieving a rapid response to the frequency deviation and thereby accelerating the power system frequency recovery process.

The above process primarily addresses single-frequency tuning issues and does not consider frequency oscillation issues. Taking a typical two-region interconnected system as an example, the simulation results are shown in Figure 2. When power disturbances occur in the region, the system’s frequency response exhibits significant common-mode ultra-low-frequency and differential-mode low-frequency oscillations, threatening the system’s frequency stability. Therefore, this paper focuses on the issue of dynamic frequency stability and, based on a photovoltaic-participating system frequency regulation structure, further investigates a distributed dynamic frequency stability active support control method for a wide-area photovoltaic cluster.

(2)

Cloud control architecture actively supported by a wide-area photovoltaic cluster

Based on the similarity of frequency changes at various nodes in the power system and the geographical interconnection structure, large power grids can typically be divided into multiple interconnected regional systems. The dynamic frequency active support cloud control architecture for PV clusters in wide-area power systems consists of three layers: terminal, edge, and cooperative control layers, as shown in Figure 3. The relationships among the three layers in each area are as follows.

In terms of the control hierarchy architecture, each area consists of a terminal layer, an edge layer, and a collaborative control layer. The control relationships among the three layers in each area are as follows:

At the terminal layer, each region uses PMUs to measure regional frequency deviations and tie-line power deviations, which are transmitted to the regional phasor data concentrator (PDC) at the edge layer.

At the edge layer, the DRO utilizes the data collected by the PDC from various measurement points to calculate the CoI frequency of the region as input, and outputs the state variables and disturbance variables of the frequency response model for photovoltaic participation in frequency regulation. The observation results are then transmitted to the regional controller.

At the collaborative control layer, the distributed frequency controller (DFC) exchanges frequency information with other regional DFCs via WAMS, and comprehensively considers the state variables and disturbance variables provided by the DROs of each region to formulate control signals through multi-region collaboration. The control signals are then transmitted in reverse through the edge layer to the inverter control chips of photovoltaic power plants at the terminal layer, dynamically adjusting photovoltaic output to suppress frequency oscillations and enhance system frequency dynamic stability.

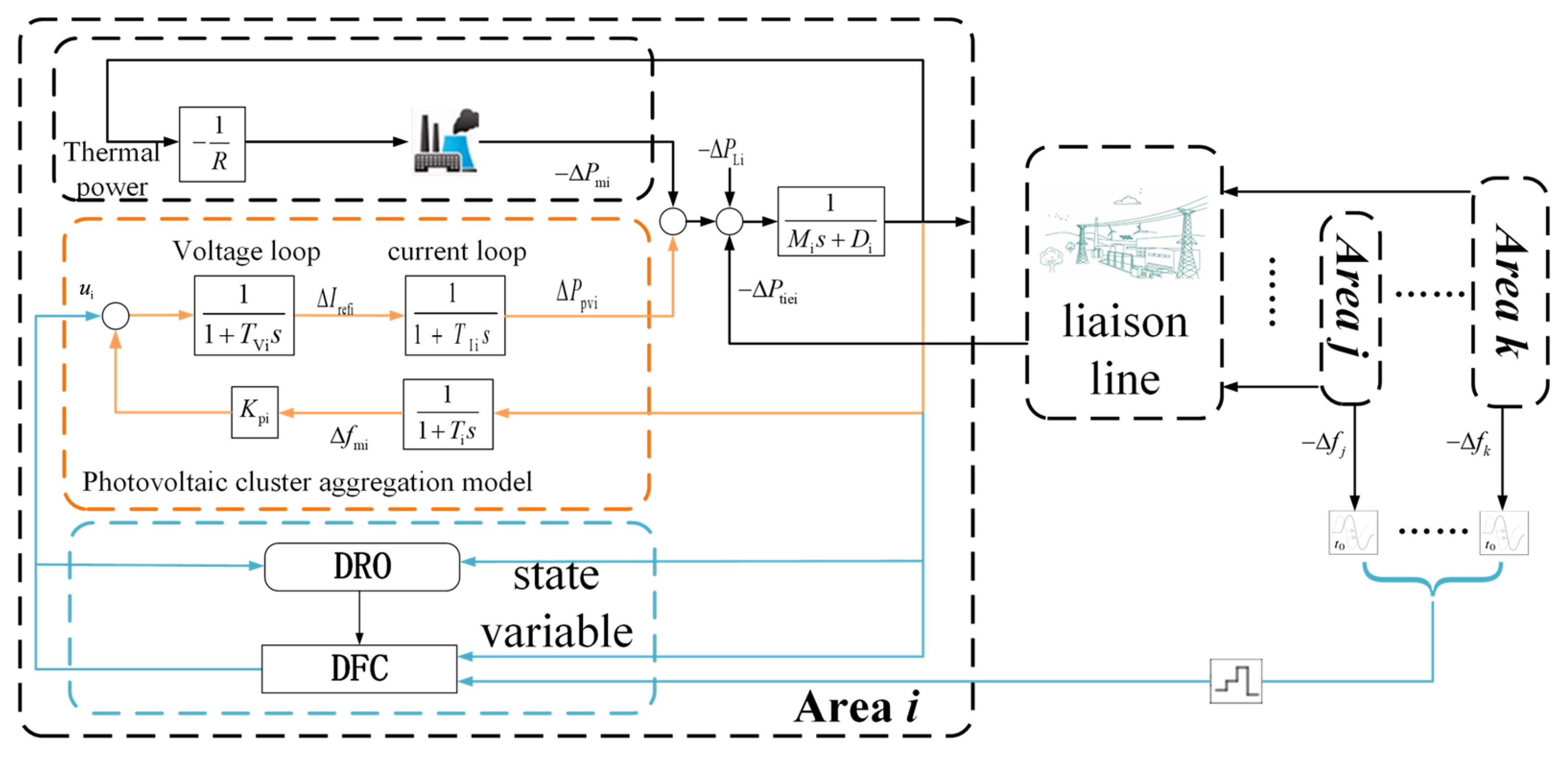
2.2. Fundamental Model for Dynamic Frequency Active Support

(1)

Physical system model

This subsection focuses on PV clusters and establishes their system frequency response (SFR) model for participation in power system frequency regulation. The voltage control and current control modules of the PV cluster are aggregated and modeled as first-order inertial elements, represented by the time constants $T_{\mathrm{Vi}}$ and $T_{\mathrm{Ii}}$ [18], respectively. Considering the time delay in acquiring the aggregated CoI frequency for region i, this delay is modeled as a first-order inertial element with an equivalent time constant $T_{\mathrm{i}}$ [19]. Given that the mechanical power change $\Delta P_{\mathrm{mi}}$ of thermal power units is relatively slow and of small magnitude, it can be collectively treated as an external disturbance along with tie-line power deviation $\Delta P_{\mathrm{tiei}}$ and load power deviation $\Delta P_{\mathrm{Li}}$. $M_{\mathrm{i}}$ denotes the equivalent inertia of region i, and $D_{\mathrm{i}}$ represents its equivalent damping. The equivalent inertia $M_{\mathrm{i}}$ synthesizes the virtual inertia from the rapid power regulation of PV units and the mechanical inertia of conventional thermal units. The equivalent damping $D_{\mathrm{i}}$ integrates the active damping provided by the PV droop control and the natural damping characteristics of thermal units. The overall inertial response and damping effect of the area against frequency disturbances are ultimately characterized by the transfer function $1/M_{i}s+D_i$. Based on this modeling framework, the SFR model for region i is illustrated in Figure 4.

In Figure 4, the SFR model of photovoltaic clusters participating in power system frequency regulation can be established as the state space equation shown in Equation (1):

$$\left\{\begin{array}{l}\Delta {\dot{f}}_{\mathrm{mi}}={\displaystyle \frac{1}{T_{\mathrm{i}}}}(-\Delta f_{\mathrm{mi}}+K_{\mathrm{pi}}\Delta f_{\mathrm{i}})\\ \Delta {\dot{f}}_{\mathrm{i}}={\displaystyle \frac{1}{M_{\mathrm{i}}}}(-D_{\mathrm{i}}\Delta f_{\mathrm{i}}+\Delta P_{\mathrm{pvi}}-\Delta P_{\mathrm{tie},\mathrm{i}}-\Delta P_{\mathrm{Li}}-\Delta P_{\mathrm{mi}})\\ \Delta {\dot{P}}_{\mathrm{pvi}}={\displaystyle \frac{1}{T_{\mathrm{Ii}}}}(-\Delta P_{\mathrm{pvi}}+\Delta I_{\mathrm{refi}})\\ \Delta {\dot{I}}_{\mathrm{refi}}={\displaystyle \frac{1}{T_{\mathrm{Vi}}}}(-\Delta I_{\mathrm{refi}}+\Delta f_{\mathrm{mi}}+u_{\mathrm{i}})\\ y_{\mathrm{i}}=\Delta f_{\mathrm{i}}\\ u_{\mathrm{i}}=f\left(\Delta f_{\mathrm{i}},\Delta f_{\mathrm{dj}}\right)\end{array}\right.$$

(1)

where $\Delta f_{\mathrm{mi}}$ is the aggregated frequency deviation accounting for the CoI frequency. $\Delta f_{\mathrm{dj}}$ is the aggregated frequency deviation that accounts for the inter-area communication delay. $\Delta f_{\mathrm{i}}$, $\Delta P_{\mathrm{pvi}}$, and $\Delta I_{\mathrm{refi}}$ are the aggregated CoI frequency deviation, the aggregated change in PV output active power, and the aggregated current reference value for region i, respectively. $K_{\mathrm{pi}}$ is the equivalent droop coefficient of the PV cluster in region i. $u_{\mathrm{i}}={\displaystyle {\sum }_{j=1}^n\left(S_{\mathrm{i}}/S_{\mathrm{ij}}\right)u_{\mathrm{ij}}}/S_i$ is the aggregated value of the control inputs $u_{cij}$ from all PV plants within region i, where $S_{\mathrm{ij}}$ and $S_{\mathrm{i}}$ are the capacities of PV plant j and region i, respectively.

The dependency relationships among the state variables in Equation (1) are complex, which is inconvenient for control design. Therefore, a linear transformation operator, Equation (2), is employed to convert Equation (1) into the strict-feedback system described by Equation (3). It can be observed that Equation (3) exhibits a cascaded form, where the dynamics of each state variable depend only on the state variables themselves and external inputs, thereby facilitating control design.

$$\begin{array}{c}{x}_{\mathrm{i},1}=\Delta f_{\mathrm{mi}},x_{\mathrm{i},2}={\displaystyle \frac{K_{\mathrm{pi}}}{T_{\mathrm{i}}}}\Delta f_{\mathrm{i}}\\ x_{\mathrm{i},3}={\displaystyle \frac{K_{\mathrm{pi}}}{M_{\mathrm{i}}{T}_{\mathrm{i}}}}\Delta P_{\mathrm{pvi}},x_{\mathrm{i},4}={\displaystyle \frac{K_{\mathrm{pi}}}{M_{\mathrm{i}}{T}_{\mathrm{i}}{T}_{\mathrm{Ii}}}}\Delta I_{\mathrm{ref}}\end{array}$$

(2)

$$\left\{\begin{array}{l}{\dot{x}}_{\mathrm{i},1}=x_{\mathrm{i},2}+g_{\mathrm{i},1}\\ {\dot{x}}_{\mathrm{i},2}=x_{\mathrm{i},3}+g_{\mathrm{i},2}-\left(\Delta P_{\mathrm{tie},\mathrm{i}}+\Delta P_{\mathrm{Li}}+\Delta P_{\mathrm{mi}}\right)/M_{\mathrm{i}}{T}_{\mathrm{i}}\\ {\dot{x}}_{\mathrm{i},3}=x_{\mathrm{i},4}+g_{\mathrm{i},3}\\ {\dot{x}}_{\mathrm{i},4}=g_{\mathrm{i},4}+g_{\mathrm{i},5}+u_{\mathrm{i}}\\ y_{\mathrm{i}}=x_{\mathrm{i},2}\end{array}\right.$$

(3)

where $u_{\mathrm{i}}=u_{\mathrm{i}}{K}_{\mathrm{pi}}/M_{\mathrm{i}}{T}_{\mathrm{i}}{T}_{\mathrm{Ii}}{T}_{\mathrm{Vi}}$, $g_{\mathrm{i},1}=-x_{\mathrm{i},1}/T_{\mathrm{i}}$, $g_{\mathrm{i},2}=-x_{\mathrm{i},2}{D}_{\mathrm{i}}/M_{\mathrm{i}}, g_{i,3}=-x_{\mathrm{i},3}/T_{\mathrm{Ii}},g_{\mathrm{i},4}=-x_{\mathrm{i},4}/T_{\mathrm{Vi}},$ $g_{\mathrm{i},5}=x_{\mathrm{i},1}{K}_{\mathrm{pi}}/M_{\mathrm{i}}{T}_{\mathrm{i}}{T}_{\mathrm{Ii}}{T}_{\mathrm{Vi}}$.

The error in the dynamic equation of the state variable $x_{\mathrm{i},2}$ is further modeled. Compared to the actual frequency, the regional frequency deviation $x_{\mathrm{i},2}$ (i.e., $\Delta f$) inevitably exhibits an error $d_{0,\mathrm{i}}$. The disturbance variable, incorporating this error, is defined as: $d_{\mathrm{i},1}=\left(-\Delta P_{\mathrm{tie},\mathrm{i}}-\Delta P_{\mathrm{Li}}-\Delta P_{\mathrm{mi}}\right)/M_{\mathrm{i}}{T}_{\mathrm{i}}+d_{0,\mathrm{i}}$ Consequently, Equation (3) can be modified as:

$$\left\{\begin{array}{l}{\dot{x}}_{\mathrm{i},1}=x_{\mathrm{i},2}+g_{\mathrm{i},1}\\ {\dot{x}}_{\mathrm{i},2}=x_{\mathrm{i},3}+g_{\mathrm{i},2}+d_{\mathrm{i},1}\\ {\dot{x}}_{\mathrm{i},3}=x_{\mathrm{i},4}+g_{\mathrm{i},3}\\ {\dot{x}}_{\mathrm{i},4}=g_{\mathrm{i},4}+g_{\mathrm{i},5}+u_{\mathrm{i}}\\ y_{\mathrm{i}}=x_{\mathrm{i},2}\end{array}\right.$$

(4)

(2)

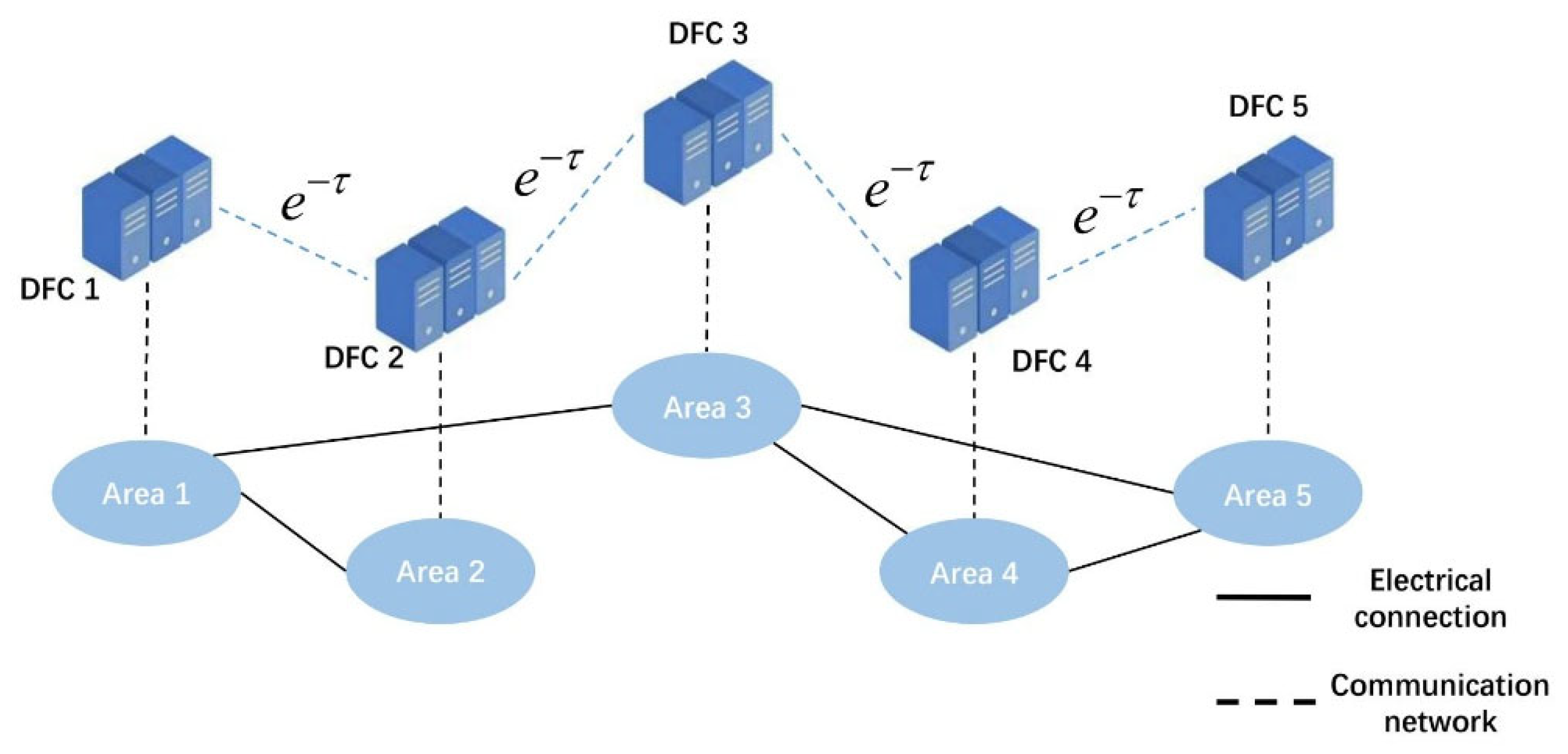
Information Communication Model

In the control framework of this paper, there are mainly two types of time delays in the information system: regional delay and inter-region delay.

Regional delay corresponds to the delay in frequency measurement by PMUi in region i and its transmission to DROi and DFCi, which includes PMU measurement, PMU-to-PDC signal transmission, DRO model calculation, and DRO-to-DFC signal transmission.

The regional delay encompasses the time delay in frequency measurement by PMUi in region i and its subsequent transmission to PDCi, DROi and DFCi, and the calculation time of DRO. Since this delay occurs between PMUs and DFCs within the same region, it is typically small and is therefore ignored in this paper.

The inter-region delay refers to the delay produced during the transmission of the frequency signal Δfj from PMUj to DFCj in Region j and then onward to DFCi in Region i, as illustrated in Figure 5. It shows the inter-region delay is primarily influenced by the longer communication delays between DFCs, making it a significant and non-negligible factor.

The inter-region delay is modeled as follows. Differences in signal delays across different regions can make it difficult for the DFC to perform unified calculations. Therefore, a signal holder is used to retain the signal at time k, ensuring that all necessary regional signals are received before commencing calculations, so that inter-region delay $\tau >0$ can be modeled as an interval delay with an upper bound, i.e., $\tau \in \left(0,{\tau }_{\max }\right]$.

Figure 6 takes DFC4 as an example and specifically demonstrates the synchronization mechanism of the signal holder. At time k, DFC4 caches the input signals from each region via the signal holder until all associated signals arrive. The final delay is determined by the transmission time of the latest arriving signal, thereby eliminating the impact of delay differences.

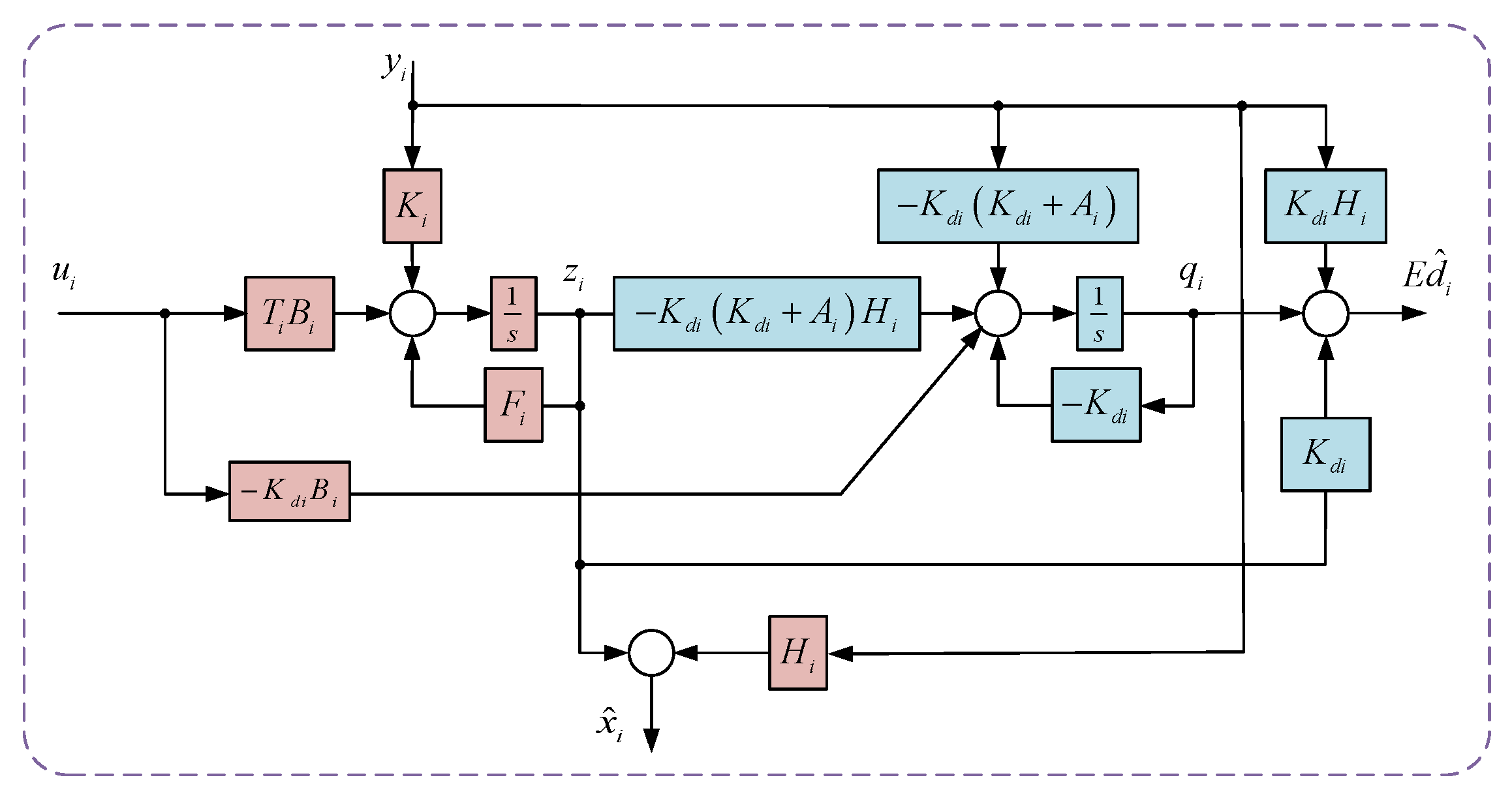
3. Dual Observer for State and Disturbance

The problem of photovoltaic participation in power system frequency control involves the coupled dynamics of photovoltaic and thermal power units. Direct controller design suffers from issues such as multiple elements, high order, and unmeasurable variables. Therefore, this paper focuses on the photovoltaic entities participating in frequency control and uses an observer to construct a frequency response model for photovoltaic participation in frequency control.

Regarding the variables in Equation (1), the regional frequency deviation signal $\Delta f_i$ obtained from WAMS calculations is known, and the PV output power $\Delta P_{\mathrm{p}\mathrm{v}i}$ can be obtained from its own power measurement devices. However, the aggregated values $\Delta f_{\mathrm{mi}}$, $\Delta I_{\mathrm{refi}}$, and $d_{0,\mathrm{i}}$ from each region are difficult to measure, resulting in the inability to directly measure $x_{i,1}$, $x_{i,4}$, $g_{i,1}$, $g_{i,4}$, $g_{i,5}$, and $d_{i,1}$ in Equation (4). Therefore, this section proposes a distributed regional observer (DRO) with dual observation functions for state and disturbance based on the input decoupling approach [20].

The state-space model corresponding to Equation (4) is:

$$\begin{array}{l}{\dot{x}}_i\left(t\right)=A_i{x}_i\left(t\right)+B_i{u}_i\left(t\right)+E{d}_i\left(t\right)\\ y_i\left(t\right)=C_i{x}_i\left(t\right)\end{array}$$

(5)

where $x_i=\left[\begin{array}{c}{x}_{i,1}\\ x_{i,2}\\ x_{i,3}\\ x_{i,4}\end{array}\right]$, $A_i=\left[\begin{array}{cccc}-{\displaystyle \frac{1}{{\tau }_i}}& 1& 0& 0\\ 0& -{\displaystyle \frac{D_i}{M_i}}& 1& 0\\ 0& 0& -{\displaystyle \frac{1}{T_{Ii}}}& 1\\ {\displaystyle \frac{K_{pi}}{M_i{\tau }_i{T}_{Ii}{T}_{Vi}}}& 0& 0& -{\displaystyle \frac{1}{T_{Vi}}}\end{array}\right],\hspace{1em}E=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]$, $B_i=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]$, $C_i=\left[\begin{array}{cccc}0& 1& 0& 0\end{array}\right]$, $d_i=d_{i,1}$.

The dynamic equation of the DRO for the system in (5) is:

$$\left[\begin{array}{c}{\dot{z}}_i(t)\\ {\dot{q}}_i(t)\end{array}\right]=\left[\begin{array}{cc}{F}_i& 0\\ -K_{\mathrm{d}i}\left(K_{\mathrm{d}i}+A_i\right)& -K_{\mathrm{d}i}\end{array}\right]\left[\begin{array}{c}{z}_i(t)\\ q_i(t)\end{array}\right]+\left[\begin{array}{c}{T}_i{B}_{,i}\\ -K_{\mathrm{d}i}{B}_i\end{array}\right]u_i(t)+\left[\begin{array}{c}{K}_i\\ -K_{\mathrm{d}i}(K_{\mathrm{d}i}+A_i)H_i\end{array}\right]y_i(t)$$

(6)

where $z_i\in {\Re }^{4\times 1}$ and $q_i\in {\Re }^{4\times 1}$ are auxiliary variables for the state observation ${\widehat{x}}_i$ and disturbance observation $E{\widehat{d}}_i$, respectively. ${\widehat{x}}_i$ denotes the observed value of state $x_i$. $E{\widehat{d}}_i$ represents the observed value of disturbance $E{d}_i$. Matrices $F_i$, $T_i$, $K_i$, and $H_i$ are parameters to be designed for the state observer. $K_{\mathrm{d}i}$ is the parameter to be designed for the disturbance observer.

The observed state ${\widehat{x}}_i$ and observed disturbance $E{\widehat{d}}_i$ in the actual system can be obtained based on the dynamic model of these auxiliary variables. In the designed DRO, they exhibit the following relationship:

$$\left\{\begin{array}{l}{\widehat{x}}_i=z_i+H_i{y}_i\\ E{\widehat{d}}_i=q_i+K_{\mathrm{d}i}{z}_i+K_{\mathrm{d}i}{H}_i{y}_i\end{array}\right.$$

(7)

Based on Equations (6) and (7), the structure of the DRO designed in this paper can be obtained, as shown in Figure 7. The observer uses the input of the original system, i.e., the control signal $u_i$, and the output of the original system $y_i$, i.e., the regional frequency deviation signal $\Delta f_i$, as the input of the observer, and outputs the unknown state variables and disturbance quantity observation values ${\widehat{x}}_i$ and $E{\widehat{d}}_i$.

Substituting the observed results from Equation (7) into Equation (4) yields the observed values ${\widehat{x}}_{i,1}$, ${\widehat{x}}_{i,4}$, ${\widehat{g}}_{i,1}$, ${\widehat{g}}_{i,4}$, ${\widehat{g}}_{i,5}$ and ${\widehat{d}}_{i,1}$, and the observed error is:

$$\left\{\begin{array}{l}{\tilde{x}}_{i,k}={\widehat{x}}_{i,k}-x_{i,k}\\ {\tilde{g}}_{i,m}={\widehat{g}}_{i,m}-g_{i,m}\\ {\tilde{d}}_{i,1}={\widehat{d}}_{i,1}-d_{i,1}\end{array}\right.$$

(8)

Here ${\tilde{x}}_{i,k}$, ${\tilde{g}}_{i,m}$ and ${\tilde{d}}_{i,1}$ are the observation errors of $x_{i,k}$, $g_{i,k}$ and $d_{i,1}$, respectively, $k\in \left\{1,4\right\}$ and $m\in \left\{1,4,5\right\}$.

Observation errors are significantly affected by relevant parameters, and parameters must be reasonably designed to eliminate the influence of unknown inputs and ensure stable convergence of observations. Therefore, Theorem 1 will be used to ensure the stability of this observer, and a parameter design method will be proposed.

Theorem 1.

By reasonably designing the parameter matrices $F_i$, $T_i$, $K_i$, and $H_i$ to satisfy Equation (9), the state observation error can be guaranteed to converge asymptotically. Additionally, by designing $K_{\mathrm{d}i}$, the disturbance observation error can be guaranteed to be a bounded quantity and arbitrarily small within the closed set ${\mathrm{\Omega }}_{\tilde{d}}$. The larger the value of ${\lambda }_{\min }\left(K_i^{\prime }\right)$, the smaller the disturbance observation error.

$$\begin{array}{l}{F}_i=A_i-H_i{C}_i{A}_i-K_{i1}{C}_i\\ K_{i2}=F_i{H}_i\\ T_i=I_i-H_i{C}_i\\ T_i{E}_i=0\end{array}$$

(9)

Proof. 

The proof is given in Appendix A. □

For the state observer, according to Theorem 1, when the parameters satisfy Equation (9), the state observation part and the input part can be decoupled. Through observability decomposition and the pole placement method, the gain matrix $K_{\mathrm{i}}$ can be set to satisfy the necessary and sufficient conditions for state observation, thereby achieving the asymptotic stability of the state observation error.

For the disturbance observer, it can be seen from Equations (9) and (A7) that the observation error is not only related to the state observer but also mainly related to $K_{\mathrm{d}i}$. Therefore, the coefficient $K_{\mathrm{d}i}$ can be designed as a diagonal matrix with all diagonal elements being positive values, and the larger ${\lambda }_{\min }\left(K_{\mathrm{d}i}\right)$ is, the smaller the disturbance observation error will be.

Based on the above analysis, we propose the following Algorithm 1:

Algorithm 1. Parameter calculation of DRO

Input: System matrix $A,C,E$ Output: Observer gain $F,T,K,H$ 1: if rank(CE) ≠ rank(E) 2:  Output “UIO does not exist” 3: end if 4: H ← E * inv(CE’ * CE) * CE’ 5: T ← I − H * C 6: A1 ← T * A 7: if (C, A1) is observable 8:  Calculate K1 using pole placement and calculate F and K according to Equations (9)–(11) 9: end if 10: Wo ← obsv(C, A1) 11: n1 ← rank(Wo) 12: while True 13: P1 ← the first n1 rows of Wo 14: P2 ← Randomly generate an $(n-n_1)\times n$ matrix 15: P ← [P1; P2] 16: If det(P) ≠ 0 17:      return P 18: PAP_inv ← P * A * inv(P) 19: CP_inv ← C * inv(P) 20: A11 ←The upper-left n1 × n1 submatrix of PAP_inv 21: A12 ←The lower-left n1 × (n − n1) submatrix of PAP_inv 22: A22 ←The lower-right (n − n1) × (n − n1) submatrix of PAP_inv 23: Kp ← place(A11, C(1:n1, :), expected poles) 24: K1 ← inv(P) * Kp 25: K2 ← randomly generate an (n − n1) * m matrix 26: K ← K1 + K2 27: F ← A1 − K1 * C 28: return F, K, T, H

4. Photovoltaic-Based Distributed Frequency Controller

In this section, the distributed DFC is designed based on the strict feedback system observation model provided by DRO for the cooperative control layer for PV. The MAC is employed to construct error surfaces to drive the system to its desired equilibrium. Subsequently, the DSC is utilized to construct the energy function of the error surface in a step-by-step manner, followed by the derivation of the virtual control law. Specifically, an initial error surface $e_{i,1}$ is constructed from the control objective, and the associated energy function $V_{i,1}$ is defined for $e_{i,1}$. To stabilize the derivative of $V_{i,1}$, a virtual control law ${\alpha }_{i,1}$ is designed. Then a second error surface $e_{i,2}$ and a virtual law ${\alpha }_{i,2}$ is derived to stabilize ${\dot{V}}_{i,2}$. This iterative procedure continues until the derivative of $V_{i,3}$ is obtained. At this stage, there is no need to define a new error surface. The final control law $u_i$ is derived directly by stabilizing ${\dot{V}}_{i,3}$ thereby completing the design.

4.1. Error Surface Design Based on MAC

The error surface is designed using the MAC method. The design of the error surface $e_{i,1}$ will simultaneously consider the suppression of low-frequency oscillations and ultra-low-frequency oscillations. Considering that the regional aggregated frequency is observable for ultra-low-frequency oscillations, while the inter-regional aggregated frequency difference $\Delta f_i-\Delta f_j$ is observable for inter-area low-frequency oscillations, $e_{i,1}$ is designed as follows.

$$e_{i,1}={\displaystyle \sum _{j\in N_i}{a}_{i,j}\left(y_i-y_j\left(t-\tau \right)\right)}+a_{i,0}{y}_i$$

(10)

where $t_{\tau }=t-\tau$, $a_{i,j}$ and $a_{i,0}$ are the adjacency weights and reference signal weights, respectively, which must satisfy the condition that the weights of mutually communicating nodes are not zero.

According to the definition of node out-degree in algebraic graph theory: $b_i={\displaystyle {\sum }_{j\in N_i}{a}_{i,j}}$, Equation (10) can be further rearranged as:

$$e_{i,1}=c_{\mathrm{ab}i}{y}_i-{\displaystyle \sum _{j\in N_i}{a}_{ij}{y}_j\left(t_{\tau }\right)}$$

(11)

where $c_{\mathrm{ab}i}=b_i+a_{i,0}$.

In addition, the expected dynamics of state variables $x_{i,3}$ and $x_{i,4}$ are virtual control laws ${\alpha }_{i,1}$ and ${\alpha }_{i,2}$, respectively. In backstepping control, their deviations are typically defined as error surfaces ${\overline{e}}_{i,2}$ and ${\overline{e}}_{i,3}$:

$${\overline{e}}_{i,k-1}=x_{i,k}-{\alpha }_{i,k-2}$$

(12)

where $k=3,4$.

However, defining errors ${\overline{e}}_{i,2}$ and ${\overline{e}}_{i,3}$ using Equation (12) would introduce high-order differentiation in the control law, leading to the “differential explosion” problem. Therefore, the DSC method is adopted, where ${\alpha }_{i,1}$ and ${\alpha }_{i,2}$ are input into the following first-order low-pass filter to obtain ${\lambda }_{i,1}$ and ${\lambda }_{i,2}$:

$$T_{\mathrm{f}i,k-2}{\dot{\lambda }}_{i,k-2}+{\lambda }_{i,k-2}={\alpha }_{i,k-2}$$

(13)

where $T_{\mathrm{f}i,k-2}$ is the filter time constant, ${\lambda }_{i,k-2}\left(0\right)={\alpha }_{i,k-2}\left(0\right)$

By replacing ${\alpha }_{i,1}$ and ${\alpha }_{i,2}$ with ${\lambda }_{i,1}$ and ${\lambda }_{i,2}$, the differential operations in the control law design are transformed into algebraic operations. Consequently, $e_{i,2}$ and $e_{i,3}$ are defined as:

$$e_{i,k-1}=x_{i,k}-{\lambda }_{i,k-2}$$

(14)

Comparing Equations (12) and (14), it follows that the error surface ${\overline{e}}_{i,k-1}$ equals the error surface $e_{i,k-1}$ minus the filtering error ${\eta }_{\mathrm{i},\mathrm{k}-2}={\lambda }_{\mathrm{i},\mathrm{k}-2}-{\alpha }_{\mathrm{i},\mathrm{k}-2}$:

$$e_{i,k-1}={\overline{e}}_{i,k-1}-{\eta }_{i,k-2}=x_{i,k}-{\alpha }_{i,k-2}-{\eta }_{i,k-2}$$

(15)

If we denote ${\psi }_{i,k-2}={\dot{\alpha }}_{i,k-2}$, the dynamics of the filter output error can be expressed as: ${\dot{\eta }}_{i,k-2}=-{\eta }_{i,k-2}/T_{\mathrm{f}i,k-2}-{\psi }_{i,k-2}$

Since $x_{\mathrm{i},\mathrm{k}}$ in Equation (15) must be obtained via the DRO, the observed value of the error surface is:

$${\widehat{e}}_{\mathrm{i},\mathrm{k}-1}={\widehat{x}}_{\mathrm{i},\mathrm{k}}-{\lambda }_{\mathrm{i},\mathrm{k}-2}$$

(16)

Substituting Equation (8) into Equation (16) yields the relationship:

$${\widehat{e}}_{\mathrm{i},\mathrm{k}-1}=e_{\mathrm{i},\mathrm{k}-1}+{\tilde{x}}_{\mathrm{i},\mathrm{k}}$$

(17)

4.2. Control Law Design Based on DSC

Control Law Design

This section designs control laws to ensure that the system state moves according to each virtual control law, guaranteeing stable convergence of the defined error surface and thereby suppressing low-frequency and ultra-low-frequency oscillations. The control laws are designed by constructing the energy function of the error surface and compensating for interference step by step.

(1)

Design virtual control rate ${\alpha }_{\mathrm{i},1}$ for $x_{i,3}$.

For error $e_{i,1}$ in Equation (11), define the Lyapunov function:

$$V_{i,1}={\displaystyle \frac{1}{2}}{e}_{i,1}^2$$

(18)

By taking the derivative of Equation (18) and incorporating Equations (4), (10) and (14), we can obtain:

$${\dot{V}}_{i,1}=e_{i,1}\left(c_{\mathrm{ab}i}\left(e_{i,2}+{\eta }_{i,1}+{\alpha }_{i,1}+g_{i,2}+d_{i,1}\right)\right.-{\displaystyle \sum _{j\in N_i}{a}_{ij}\left(x_{j,3}\left(t_{\tau }\right)+g_{j,2}\left(t_{\tau }\right)+d_{j,1}\left(t_{\tau }\right)\right)}$$

(19)

To stabilize Equation (19), the virtual control law ${\alpha }_{i,1}$ is designed as follows:

$${\alpha }_{i,1}=-g_{i,2}-{\widehat{d}}_{i,1}-(c_{\mathrm{ab}i}+c_{i,1}/c_{\mathrm{ab}i})e_{i,1}+{\displaystyle \frac{1}{c_{\mathrm{ab}i}}}{\displaystyle \sum _{j\in N_i}{a}_{ij}\left[x_{j,3}\left(t_{\tau }\right)+g_{j,2}\left(t_{\tau }\right)+{\widehat{d}}_{j,1}\left(t_{\tau }\right)-e_{i,1}\right]}$$

(20)

where $c_{i,1}$ is a parameter to be designed.

Substituting ${\alpha }_{i,1}$ into Equation (19) and considering Young’s inequality, we obtain:

$${\dot{V}}_{i,1}\le -c_{i,1}{e}_{i,1}^2+{\displaystyle \frac{1}{2}}{\eta }_{i,1}^2+{\displaystyle \frac{1}{2}}{\tilde{d}}_{i,1}^2+{\displaystyle \sum _{j\in N_i}\frac{a_{ij}}{2}{\tilde{g}}_{j,2}^2\left(t_{\tau }\right)}+{\displaystyle \sum _{j\in N_i}\frac{a_{ij}}{2}{\tilde{d}}_{j,1}^2\left(t_{\tau }\right)+c_{\mathrm{ab}i}{e}_{i,1}{e}_{i,2}}$$

(21)

Equation (21) indicates that while $-c_{i,1}{e}_{i,1}^2<0$ contributes to stability, convergence of $e_{i,1}$ is coupled with error surface $e_{i,2}$ and filtering error ${\eta }_{i,1}$, necessitating further energy function construction and design of virtual control rate ${\alpha }_{i,2}$.

(2)

Design virtual control rate ${\alpha }_{\mathrm{i},2}$ for $x_{i,4}$.

Define the Lyapunov function for the first term in Equation (14):

$$V_{i,2}=V_{i,1}+{\displaystyle \frac{1}{2}}{e}_{i,2}^2+{\displaystyle \frac{1}{2}}{\eta }_{i,1}^2$$

(22)

Taking the derivative of Equation (22) and combining Equations (4), (14) and (15) yields:

$${\dot{V}}_{i,2}={\dot{V}}_{i,1}+e_{i,2}\left(e_{i,3}+{\eta }_{i,2}+{\alpha }_{i,2}+g_{i,3}-{\dot{\lambda }}_{i,1}\right)+{\eta }_{i,1}\left(-{\eta }_{i,1}/T_{\mathrm{f}i,1}-{\psi }_{i,1}\right)$$

(23)

To stabilize Equation (23), design the virtual control law ${\alpha }_{i,2}$ as follows:

$${\alpha }_{i,2}=-g_{i,3}+{\dot{\lambda }}_{i,1}-c_{\mathrm{ab}i}{e}_{i,1}-\left(c_{i,2}+1.5\right)e_{i,2}$$

(24)

where $c_{i,2}$ is a parameter to be designed.

Substituting ${\alpha }_{i,2}$ into Equation (23) and considering Young’s inequality, we obtain:

$${\dot{V}}_{i,2}\le {\dot{V}}_{i,1}-c_{\mathrm{ab}i}{e}_{i,1}{e}_{i,2}-c_{i,2}{e}_{i,2}^2+{\displaystyle \frac{1}{2}}{\eta }_{i,2}^2+{\displaystyle \frac{1}{2}}{\psi }_{i,1}^2+\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{T_{\mathrm{f}i,1}}}\right){\eta }_{i,1}^2+e_{i,2}{e}_{i,3}$$

(25)

Equation (25) indicates that the stability of $e_{i,1}$, $e_{i,2}$, and ${\eta }_{i,1}$ is influenced by error surfaces $e_{i,3}$, ${\eta }_{i,2}$, and other factors, necessitating further construction of an energy function and design of control law $u_i$.

(3)

Design Control Law $u_i$

Define the Lyapunov function for the second term in Equation (14):

$$V_{i,3}=V_{i,2}+{\displaystyle \frac{1}{2}}{e}_{i,3}^2+{\displaystyle \frac{1}{2}}{\eta }_{i,2}^2$$

(26)

Taking the derivative of Equation (26) and combining Equations (4) and (14) yields:

$${\dot{V}}_{i,3}={\dot{V}}_{i,2}+e_{i,3}(u_i+{\widehat{g}}_{i,4}+g_{i,5}-{\dot{\lambda }}_{i,2})-{\eta }_{i,2}{\psi }_{i,2}-{\eta }_{i,2}^2/T_{\mathrm{f}i,2}$$

(27)

To stabilize Equation (27), design the control law $u_i$:

$$u_i={\dot{\lambda }}_{i,2}-{\widehat{g}}_{i,4}-g_{i,5}-e_{i,2}-\left(c_{i,3}+2\right){\widehat{e}}_{i,3}$$

(28)

where $c_{i,3}$ is a parameter to be designed.

Substituting $u_i$ into Equation (27) and considering Young’s inequality, we obtain:

$${\dot{V}}_{i,3}\le -c_{i,1}{e}_{i,1}^2-c_{i,2}{e}_{i,2}^2-c_{i,3}{e}_{i,3}^2+{\displaystyle \sum _{\nu =1}^2\left(1/T_{\mathrm{f}i,\nu }-1\right){\eta }_{i,\nu }^2}+{\displaystyle \frac{1}{2}}{\displaystyle \sum _{j\in N_i}{a}_{ij}{\tilde{d}}_{j,1}^2\left(t_{\tau }\right)}+{\displaystyle \frac{1}{2}}{\left(c_{i,3}+2\right)}^2{\tilde{x}}_{i,4}^2+{\displaystyle \frac{1}{2}}\left({\psi }_{i,1}^2+{\psi }_{i,2}^2+{\tilde{g}}_{i,4}^2+{\tilde{d}}_{i,1}^2\right)$$

(29)

The control law design is now complete. Using error surfaces (12), (14) and control laws (20), (24), (28), the photovoltaic-based distributed cooperative frequency controller is realized.

The flowchart of the proposed control method is shown in Figure 8. The overall view of the design and application process are shown in Figure 8a and the detailed information transmission process is given in Figure 8b. And the final control structure of DFC is depicted in Figure 9. In the PV-based distributed cooperative frequency control system, the measurement devices and DROs provide necessary information for DFCs to calculate its outputs. By integrating regional with neighborhood information, control signals for ULFO and LFO can be computed. This approach fully leverages the potential of PV plants to enhance dynamic frequency stability in wide-area power systems.

4.3. Control Law Parameter Design

As evident from the expressions of designed control law, the closed-loop stability performance of the entire system is critically dependent on parameter design. Therefore, this section first derives Theorem 2 on the stability of the distributed photovoltaic DFC, then proposes a parameter design method for the control law based on Theorem 2.

Theorem 2.

For each regional controlled system (1) under the action of DRO-based DFC, if the design parameters $c_{i,k}$ and $T_{\mathrm{f}i,\nu }$ satisfy Equation (30), then for any $P>0$ there exists a bounded compact set ${\mathrm{\Omega }}_i$ such that when $\mu \ge \kappa /P$, all signals in the closed-loop system are semi-globally uniformly ultimately bounded, where $\mu =\min \left[2c_{i,k},2/T_{\mathrm{f}i,\nu }-2\right]$,$\kappa =1/2\cdot {\displaystyle {\sum }_{i=1}^N\left({\displaystyle {\sum }_{\nu =1}^2{A}_{i,\nu }^2}+D_{SF,i}^2+D_{DCO,i}^2\right)}$.

$$c_{i,k}>0,1/T_{\mathrm{f}i,\nu }-1>0,i=1,\dots ,N,\nu =1,2$$

(30)

Proof. 

The proof is given in Appendix B. □

From Theorem 2, it can be seen that the design of distributed observer parameters ensures stable convergence of state observation error and bounded disturbance observation error.

Based on Theorem 2, a parameter optimization model is proposed. Considering that the integral of time multiplied absolute error (ITAE) can evaluate the deviation between the controller and the expected dynamics, the minimization of ITAE of frequency is taken as the objective to suppress the ULFO. At the same time, in order to suppress LFOs, the objective is designed to minimize the absolute frequency deviation between region i and its neighbors. Thus, the final multi-objective optimization problem is established as shown in Equation (31).

$$\begin{array}{l}J=\min ITAE\\ ITAE={\displaystyle {\int }_0^{T}t\left({\displaystyle {\sum }_{i=1}^n\left|f_i-f_{\infty }\right|}+{\displaystyle {\sum }_{i=1}^n\left|\Delta f_i-\Delta f_j\right|}\right)dt}\end{array}$$

(31)

The range of control law parameter values is set to ensure that the values are reasonable, save computation and speed up the optimization search process:

$$\begin{array}{l}{c}_{i\min }\le c_i\le c_{i\max }\left(i=1,\dots ,N\right)\\ T_{\mathrm{f}i\min }\le T_{\mathrm{f}i}\le T_{\mathrm{f}i\max }\left(i=1,\dots ,N\right)\end{array}$$

(32)

Owing to the fact that fixed upper and lower bounds for (32) can slow the convergence speed, we propose an adaptive boundary determination method using Theorem 2. The upper and lower bounds of (32) are updated after each population update. For ${\mathcal{l}}^{\mathrm{th}}$ population with m current candidates, $\kappa$ is estimated to the average value ${\overline{\kappa }}_{\mathcal{l}}$, which is computed by using its definition in Theorem 2. Since a larger value of $\kappa /P$ can accelerate the solution process, $P$ is estimated to be ${\overline{P}}_{\mathcal{l}}$ by the minimum value within the population by utilizing the following expression.

$$P_{\mathcal{l},a}={\displaystyle \frac{1}{2}}\left({\displaystyle \sum _{i=1}^N{\displaystyle \sum _{\beta =1}^3\frac{1}{2}{e}_{a,i,\beta }^2}}+{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{\nu =1}^2\frac{1}{2}{\eta }_{a,i,\nu }^2}}\right)$$

(33)

$${\overline{P}}_{\mathcal{l}}=\min \left[P_{\mathcal{l},1},P_{\mathcal{l},2},\dots ,P_{\mathcal{l},m}\right]$$

(34)

where $a=1,2,\dots ,m$, $e_{a,i,\beta }$ is the minimum value of the time-domain curve for the $\beta$th error surface in region i corresponding to candidate solution $a$. ${\eta }_{a,i,\nu }$ is the minimum value of the time-domain curve for the $v$ filtering error in region i corresponding to candidate solution $a$.

Based on the condition $\mu \ge \kappa /P$ in Theorem 2, $\mu$ is updated by the following equation.

$${\mu }_{\mathcal{l}}={\overline{\kappa }}_{\mathcal{l}}/{\overline{P}}_{\mathcal{l}}$$

(35)

After computing ${\mu }_{\mathcal{l}}$ for the current population, constraint boundaries $c_{i\min }$ and $T_{\mathrm{f}i\max }$ can be updated according to Theorem 2’s definition ${\mu }_x=\min \left[2c_{i,k},2/T_{\mathrm{f}i,\nu }-2\right]$, which serve as constraints for the ${\left(\mathcal{l}+1\right)}^{\mathrm{th}}$ optimization:

$$\left\{\begin{array}{l}{c}_{i\min }={\displaystyle \frac{{\mu }_x}{2}},2c_{i,k}<2/T_{\mathrm{f}i,\nu }-2\\ T_{\mathrm{f}i\max }={\displaystyle \frac{{\mu }_x+2}{2}},2c_{i,k}>2/T_{\mathrm{f}i,\nu }-2\end{array}\right.$$

(36)

To determine the constraint boundaries $c_{i\max }$ and $T_{\mathrm{f}i\min }$ in the ${\left(\mathcal{l}+1\right)}^{\mathrm{th}}$ optimization, the following characteristics are considered. Since larger $c_i$ values (within a certain range) improve system’s dynamics, $c_{i\max }$ can be set moderately high. For $T_{\mathrm{f}i}$, smaller values reduce filtering error. However, excessively small $T_{\mathrm{f}i}$ prolongs simulation time and reduces iteration efficiency. Thus, $T_{\mathrm{f}i\min }$ should satisfy Theorem 2’s requirement $1/T_{\mathrm{f}i,\nu }-1>0$ and avoid being too small.

As to solve the above optimization problem, we adopt the CGO algorithm [21], which employed the Sierpinski triangle algorithm to integrate chaos theory with game theory to improve search efficiency. The main concepts and equations of CGO are as follows.

Assume that in current population, there are m current candidate solutions with expression as follows.

$$W_i=\left[\begin{array}{cccccc}{w}_i^1& w_i^2& \dots & w_i^j& \dots & w_i^d\end{array}\right], \mathrm{with} i=1,2,\dots ,m \mathrm{and} j=1,2,\dots ,d$$

(37)

where d is the number of parameters that need to be optimized, and $W_i$ includes all parameters to be optimized ($c_i$, $T_{\mathrm{f}i}$), which are randomly generated within the search space by Equation (38).

$$w_i^j\left(0\right)=w_{i,\min }^j+rand\left(w_{i,\max }^j-w_{i,\min }^j\right),\left\{\begin{array}{c}i=1,2,\dots ,n\\ j=1,2,\dots ,d\end{array}\right.$$

(38)

where $w_i^j\left(0\right)$ denotes the j-th decision variable of the i-th point in the search space, $w_{i,\max }^j$ and $w_{i,\min }^j$ represent the upper bound and lower bounds of decision variables, respectively, and $rand$ is a random number within the interval [0, 1].

The Sierpinski triangle algorithm is the main approach to update the candidate solutions $W_i$, which is formed by four seeds as follows.

$$S_i^1=W_i+{\rho }_i\times \left({\omega }_i\times GB-{\xi }_i\times M{G}_i\right),i=1,2,\dots ,n$$

(39)

$$S_i^2=GB+{\rho }_i\times \left({\omega }_i\times W_i-{\xi }_i\times M{G}_i\right),i=1,2,\dots ,n$$

(40)

$$S_i^3=M{G}_i+{\rho }_i\times \left({\omega }_i\times W_i-{\zeta }_i\times GB\right),i=1,2,\dots ,n$$

(41)

$$S_i^4=W_i\left(w_i^k=w_i^k+R\right),k=\left[1,2,\dots ,d\right]$$

(42)

where $GB$ stands for the optimal candidate solution in the current state within the search space, $M{G}_i$ is the average value of randomly selected initial qualified points, $W_i$ represents the i-th candidate solution, ${\rho }_i$ denotes a random number generated in a certain manner, ${\omega }_i$ and ${\xi }_i$ are random integers that are either 0 or 1, and R is a random number within the range of [0, 1].

Each candidate solution is regarded as an independent player. These players select the optimal action and update their own states according to their current states and the states of other players. The pseudocode of the optimization process is provided as in Algorithm 2.

Algorithm 2. Optimization process of CGO

Input: $c_{i\min }\le c_i\le c_{i\max }\left(i=1,\dots ,N\right)$, $T_{\mathrm{f}i\min },T_{\mathrm{f}i\max }\left(i=1,\dots ,N\right)$ and Equation (31)  Output: The optimal candidate solution $GB$ (DFC parameters)   ① First, generate random initial points $w_i^j\left(0\right)$ in the search space.   ② Calculate the fitness (degree of proximity to the target) by substituting the initial solutions into the objective function.   ③ Obtain the optimal candidate solution $GB$ in the current state.   ④ Enter the following loop:    While (t < maximum number of iterations)     for i = 1: number of candidate solutions      Generate $M{G}_i$ by randomly selecting initial qualified points      Generate a temporary triangle from $W_i$, $M{G}_i$, and $GB$      Generate new seeds using the calculation formulas for the four seeds      Calculate the fitness of the new seeds       if the fitness value of the new seed is better than that of the worst candidate solution        Replace the worst candidate solution with the new seed       end       If there is a better candidate solution, update $GB$     end      t = t + 1    end   ⑤ Obtain the optimal solution $GB$   So far, the optimization of parameters using CGO has been completed.

5. Case Study and Analysis

In this subsection, the control effect of the proposed method on the dynamic frequency stabilization of the power system is verified by two multi-regional interconnected test systems.

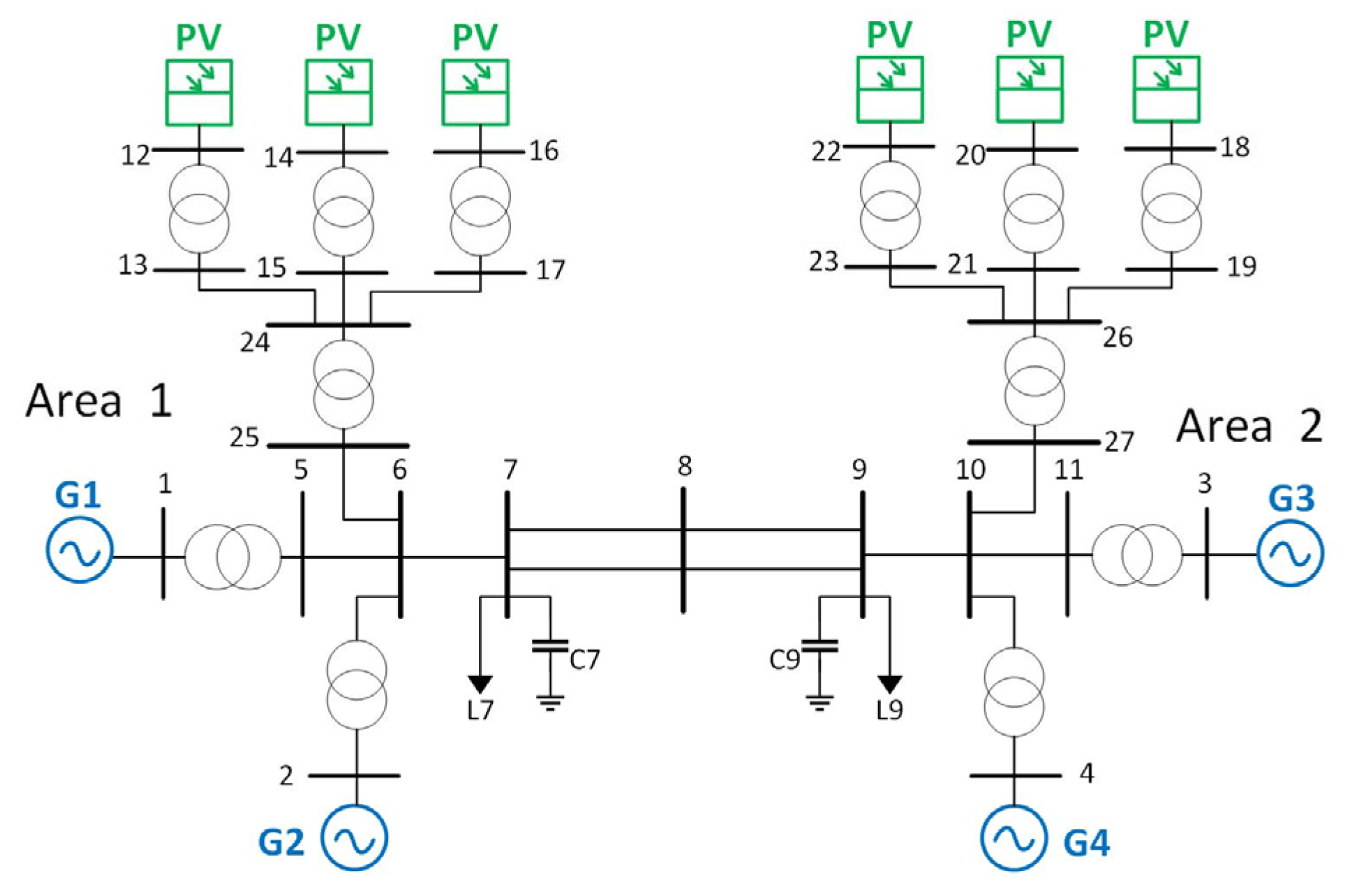
5.1. Case Study and Analysis via a Two-Region Interconnected System

This subsection verifies the effectiveness and superiority of PV DRO and DFC, respectively, based on a two-region interconnected arithmetic system shown in Figure 10. Within each region, four thermal units and six PV units are set up, where each thermal unit has a capacity of 70 MW and each PV unit has a capacity of 20 MW [22,23].The equivalent model parameters are calculated based on [24], and listed in

Table 1. Parameters of six photovoltaic systems.

Number	TV/s	TI/s	Kp/(p.u.)
1	1.1	0.056	−13
2	1.3	0.054	−10
3	1.7	0.051	−20
4	1.2	0.055	−16.67
5	1.3	0.052	−20
6	1.4	0.053	−20

and

Table 2. Parameters of the aggregated photovoltaic system, and the region’s inertia and damping.

TV (s)	TI (s)	Kp/(p.u.)	D/(p.u./Hz)	M (s)
1.363	0.053	−16.5	0.024	19.92

, and the coefficient of tie-line between the two regions is $T_{12}=T_{21}=0.2$ p.u.

At t = 1 s, a step load of 0.06 p.u. is applied to Region 1. The frequency deviation curve of Region 1 without additional dynamic frequency controller is shown in Figure 11a. It can be observed that the system frequency exhibits two oscillatory modes, namely, a low-frequency oscillation at 0.4 Hz and an ultra-low-frequency oscillation at 0.059 Hz. Both oscillations are of weak damping.

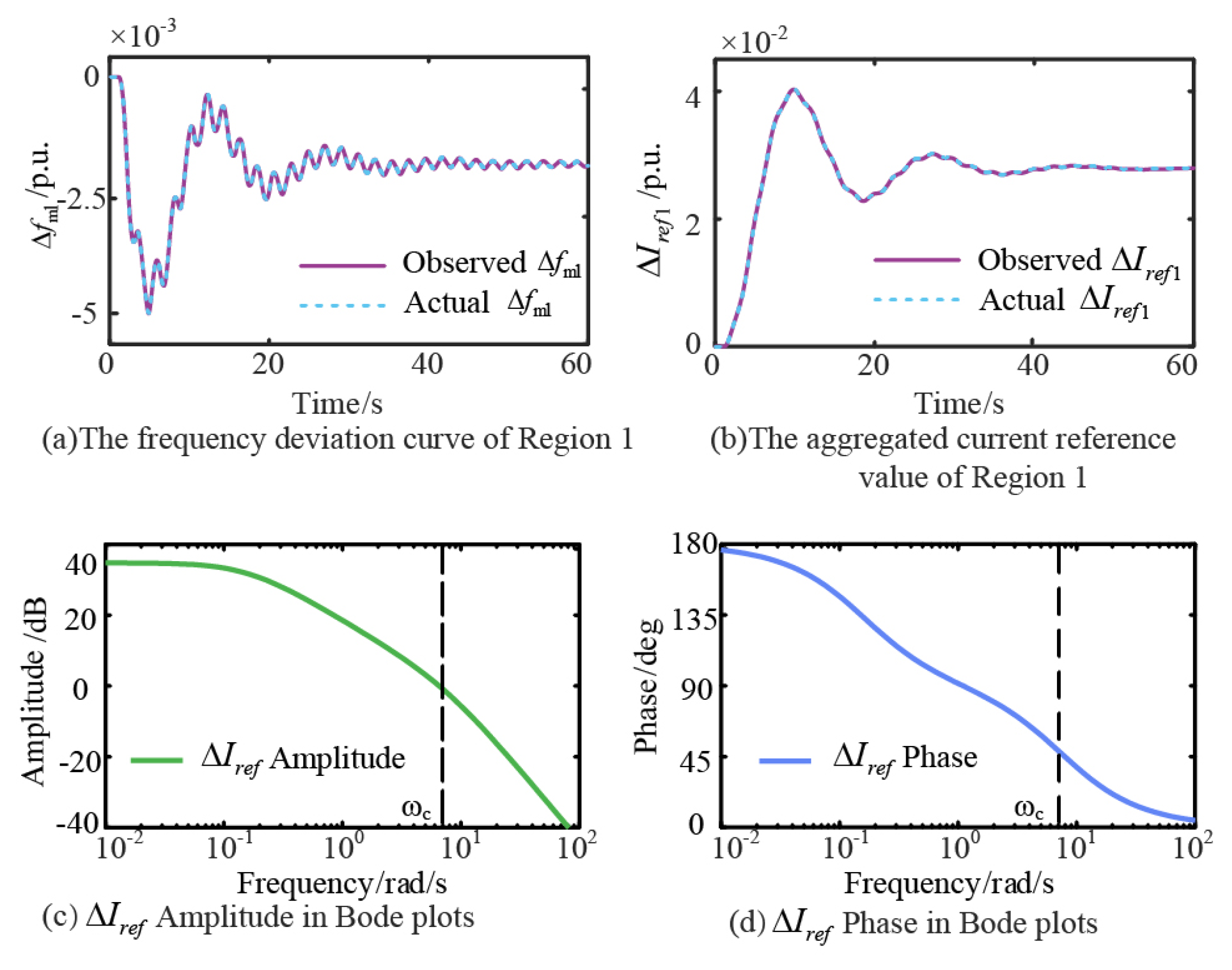
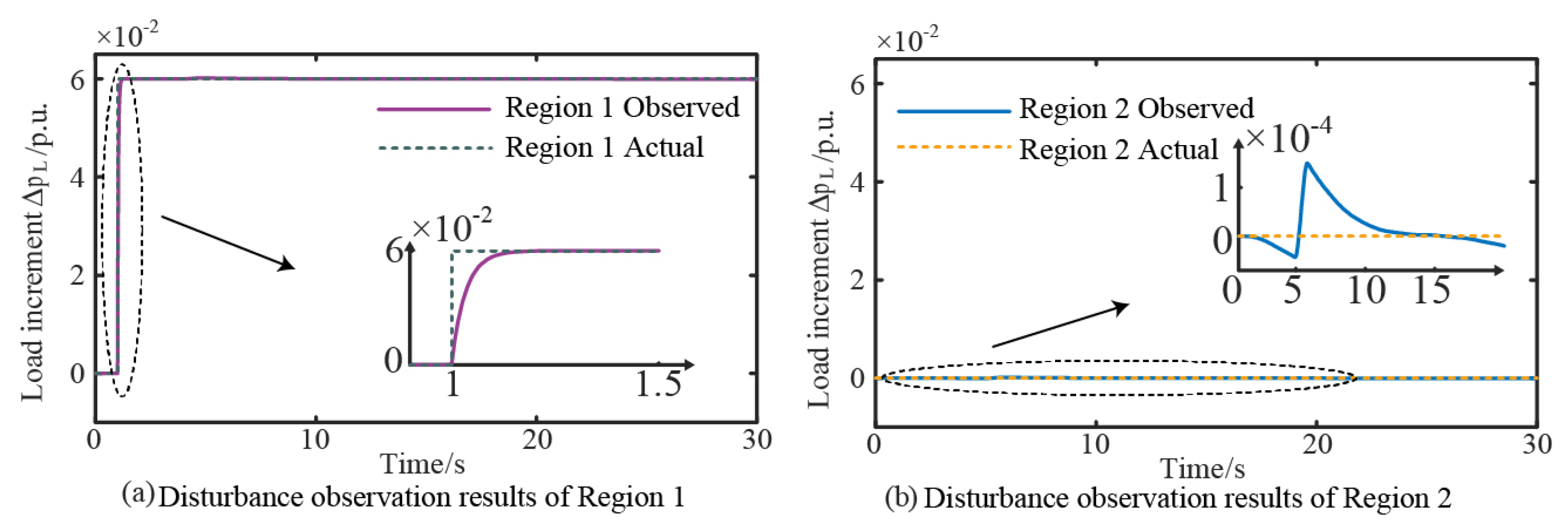
(1)

Observer Performance Analysis

To test the performance of the proposed observer, Figure 11a,b illustrate the comparison between the observed and actual values of the two aggregated states $\Delta f_{\mathrm{m}1}$ and $\Delta I_{\mathrm{ref}1}$ in Region 1. During the observation process, the maximum error of the state observer was 1.6 × 10⁻⁴ p.u., and the steady-state tracking error converged to 6 × 10⁻⁵ p.u. Figure 11c,d show a frequency domain analysis of the observation of signals $\Delta I_{\mathrm{ref}1}$ using Bode plots. The DRO can effectively perform observations in the low-frequency band, and its amplitude gain attenuates at a rate of −40 dB/dec in the high-frequency band, ensuring that the observation results are not affected by high-frequency noise from the sensors.

Figure 12a,b show the comparison between the actual and observed values of disturbances $\Delta p_{\mathrm{L}1}$ and $\Delta p_{\mathrm{L}2}$ in two regions, respectively. As shown in Figure 12a, the observed values rapidly track the actual values in approximately 0.2 s after the disturbance occurs. Figure 12b further demonstrates that the steady-state error converges to 1.5 × 10⁻⁴ p.u through the global time-domain response. The accuracy and speed of the observation results demonstrate the good observation performance of the proposed photovoltaic DRO.

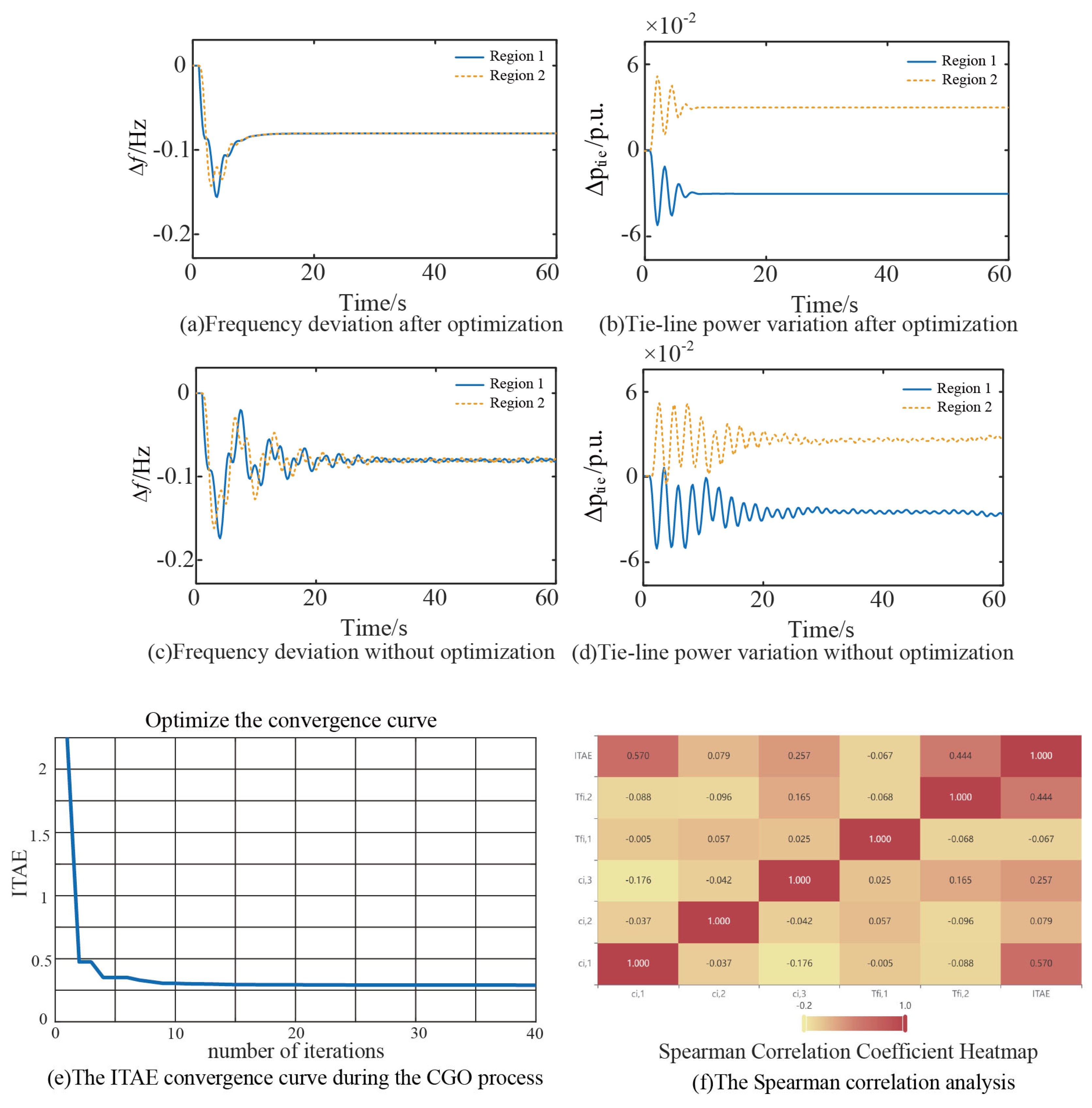
(2)

Dynamic frequency stabilization control effect

To test the performance of the proposed DFC, Figure 13 shows the dynamic frequency response process of the proposed DFC under a 0.06 p.u. step disturbance of load in Region 1. Figure 13a,b show the control effects after optimizing the controller parameters Via CGO. The simulation results indicate that the proposed control method effectively limits the system’s maximum frequency deviation to within 0.17 Hz. And, within 12 s after the disturbance, it effectively suppresses both low-frequency and ultra-low-frequency oscillations. The steady-state frequency deviation ultimately converges to 1 × 10⁻⁸ Hz.

Figure 13c,d present the control effects when the controller parameters are set based on experience. When the controller parameters are not optimized Via the CGO algorithm, neither the frequency nor the tie-line power variations have fully converged at t = 60 s. Through comparison, it is evident that the control effect of the controller without CGO is far inferior to that with CGO.

Figure 13e is the ITAE convergence curve during the CGO process, from which it can be seen that the ITAE value decreases steadily during optimization.

Furthermore, we also randomly selected 100 sets of parameters for Spearman correlation analysis, and the results are presented in Figure 13f. The analysis results indicate that $c_{i,1}$ and $T_{\mathrm{f}i,2}$ are the controller parameters that have a relatively significant impact on the ITAE evaluation. Their correlation coefficients are 0.570 and 0.444, respectively, which are much higher than those of other controller parameters. This finding helps us accurately identify the key parameters and provides data support for the subsequent optimization of control performance.

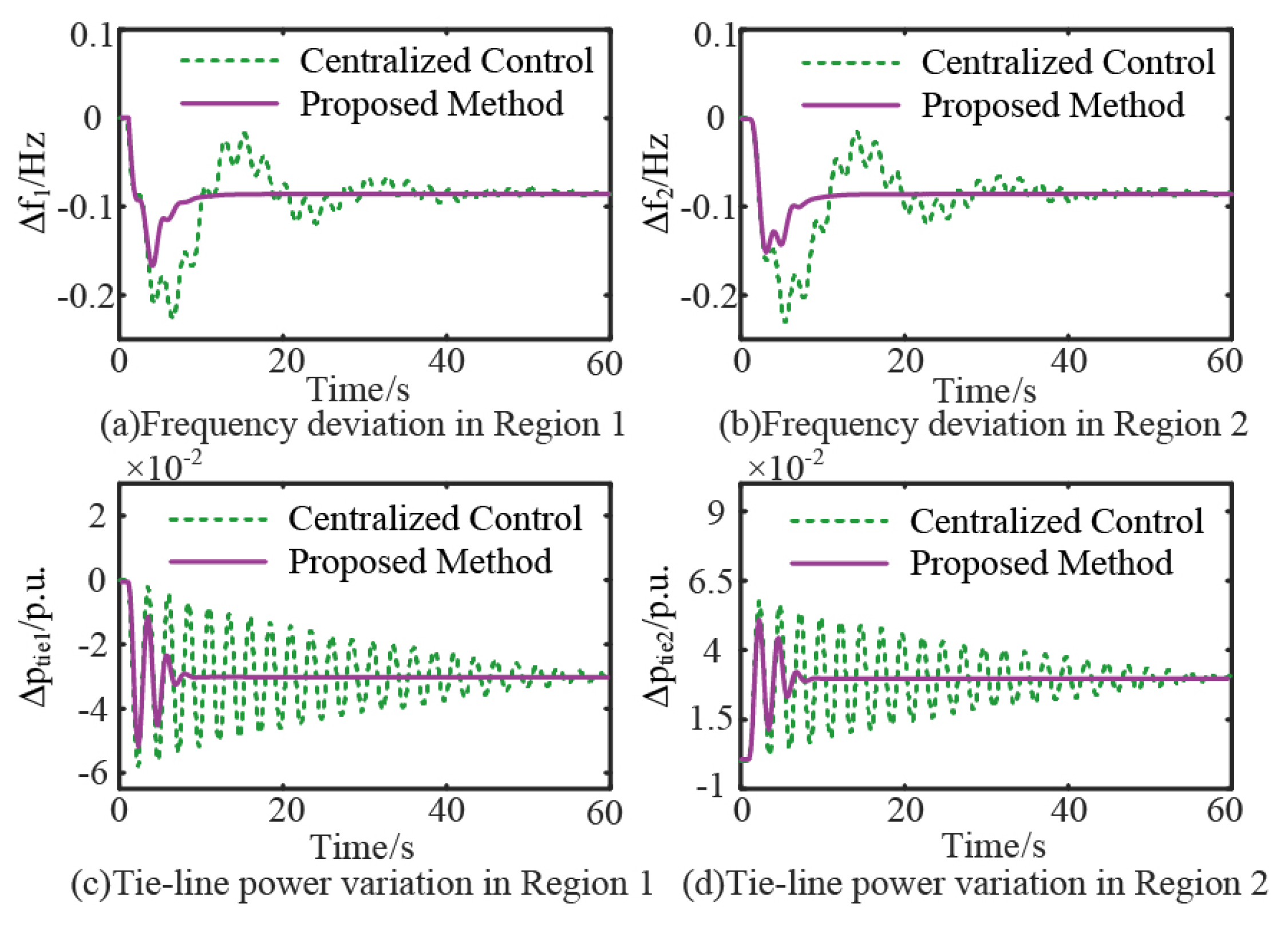
(3)

Comparative analysis with centralized control

Comparative experiments are conducted between the proposed method and the centralized frequency control [23]. A maximum communication time lag ${\tau }_{\max }=2.5 \mathrm{s}$ was set between the two regions. At t = 1 s, a 0.06 p.u. step load is applied to Region 1. Figure 14 shows the resulting frequency response curves of both regions, along with the dynamic variation in the total output power of the tie-line.

As shown in Figure 14a,b, compared with the centralized control, the proposed method reduces the maximum frequency deviation from 0.23 Hz to 0.17 Hz, with a reduction of 26.1%. The settling time is shortened from 50.6 s to 12 s with a reduction of 76.3%.

To quantify the performance of regional coordinated control, the inter-area frequency deviation index is defined as $E_F={\displaystyle {\int }_0^{T}t\left({\displaystyle {\sum }_{i\ne j}\left|\Delta f_i-\Delta f_j\right|}\right)dt}$. The experimental data in Figure 14 show that, during the system’s gradual frequency recovery, the centralized frequency regulation yields a large inter-area frequency cumulative deviation with $E_F=0.222$. Since centralized control requires a double data communication task from the actor and the control center, which amplifies the time delay, which compromises the effect of centralized control.

Under the same communication condition, the proposed controller achieves a significantly smaller $E_F$ of merely 0.014. This indicates the proposed DFC with reduced communication latency can effectively minimize inter-area frequency difference and gain good control performance.

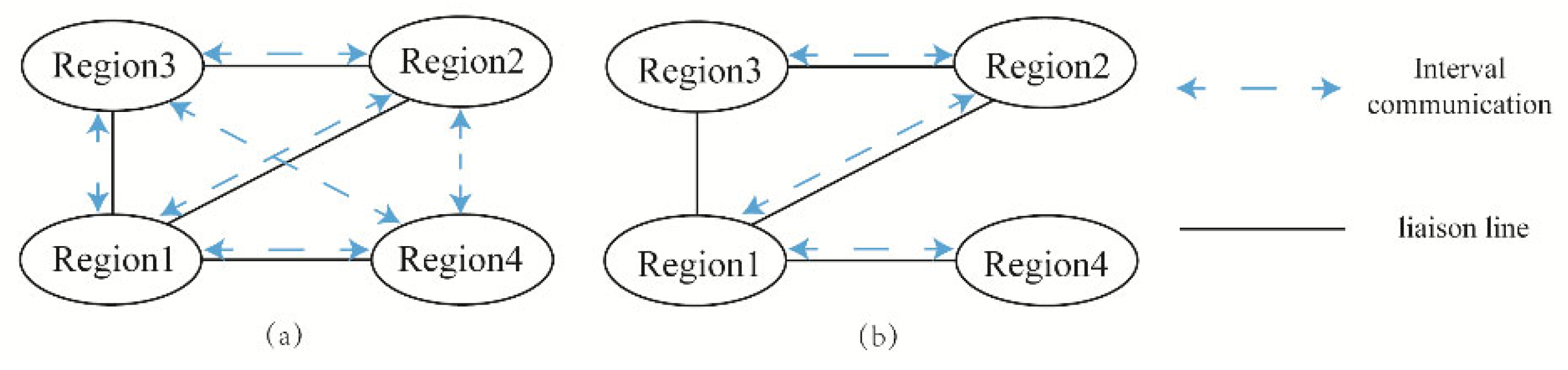
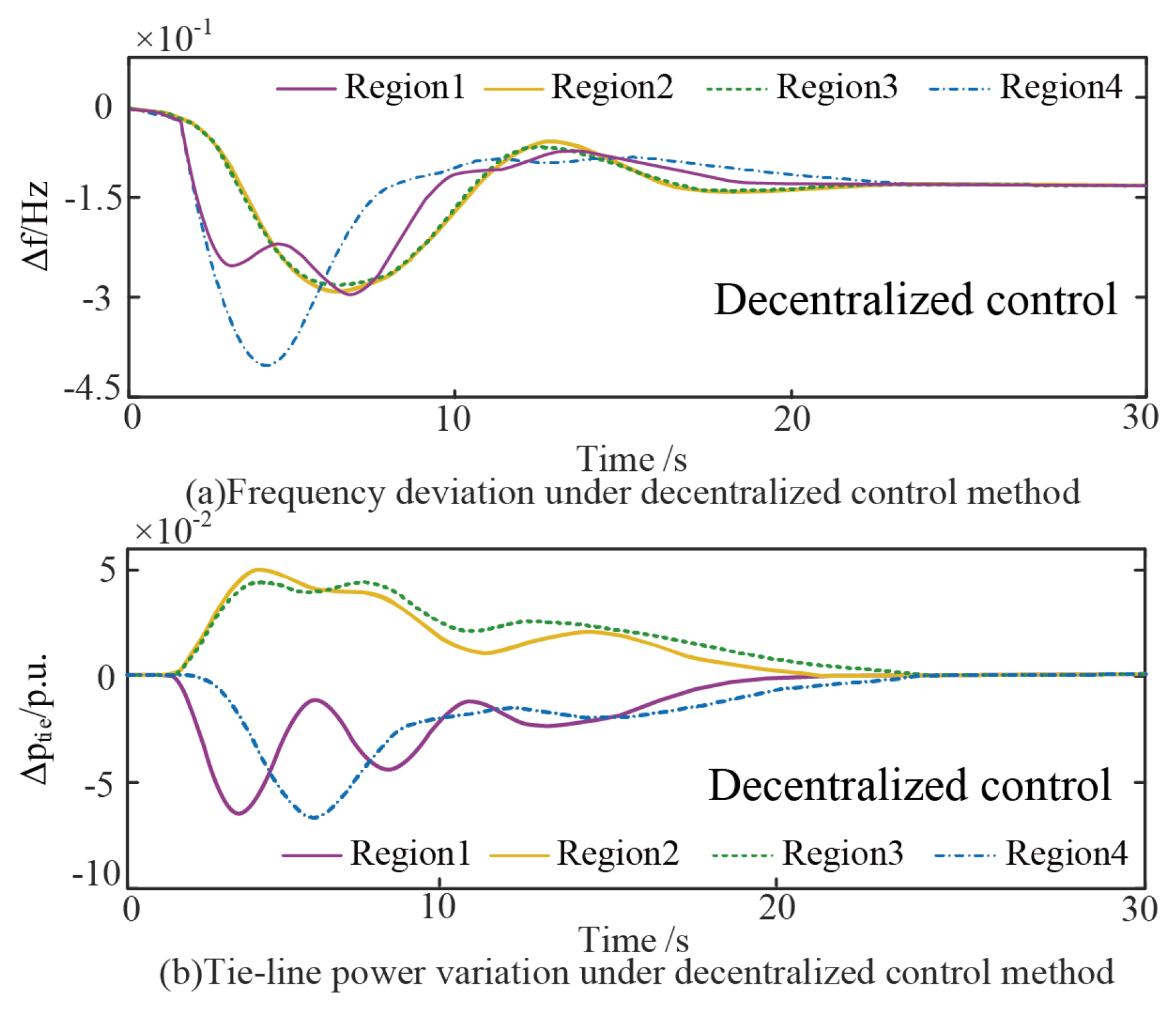
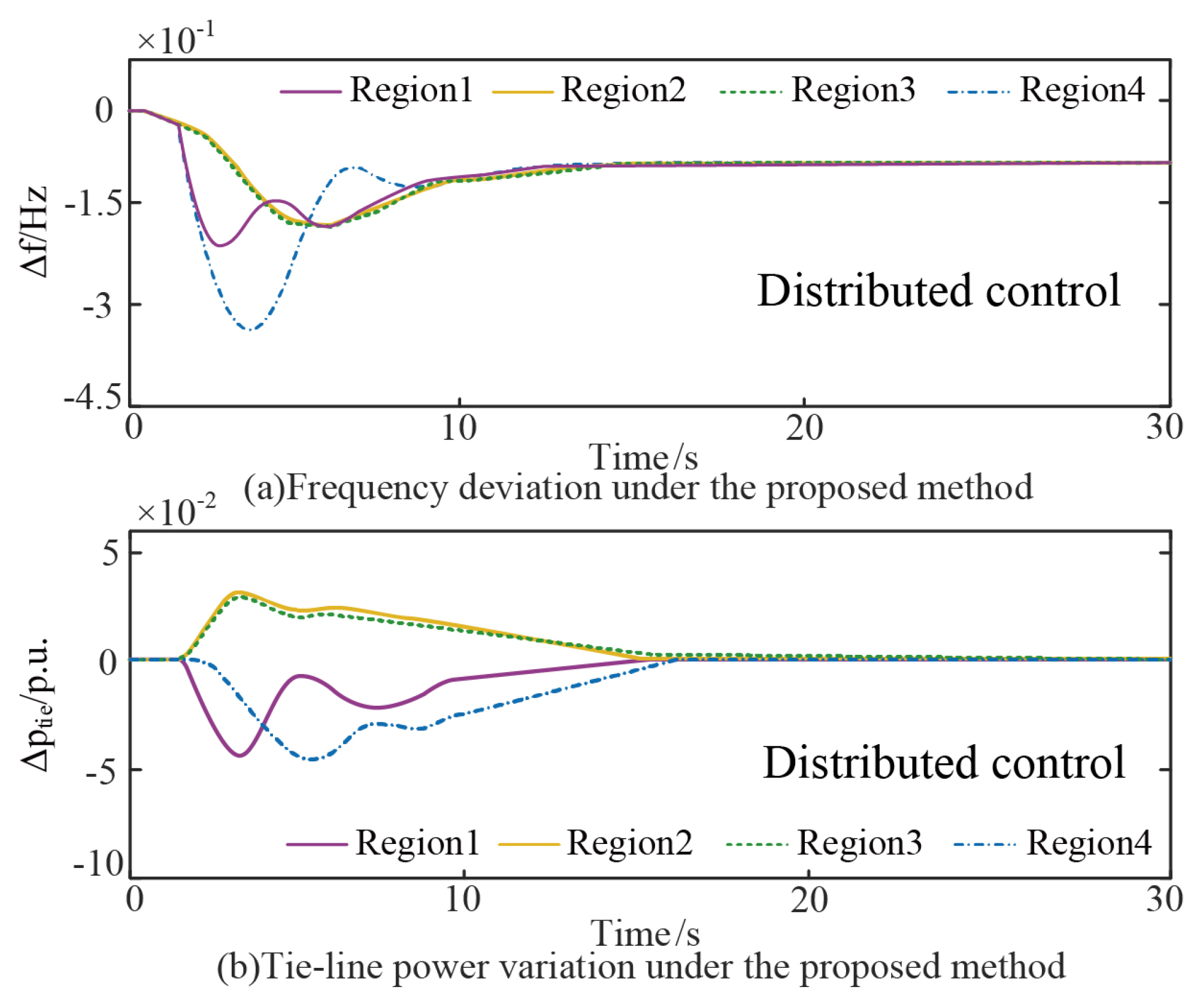
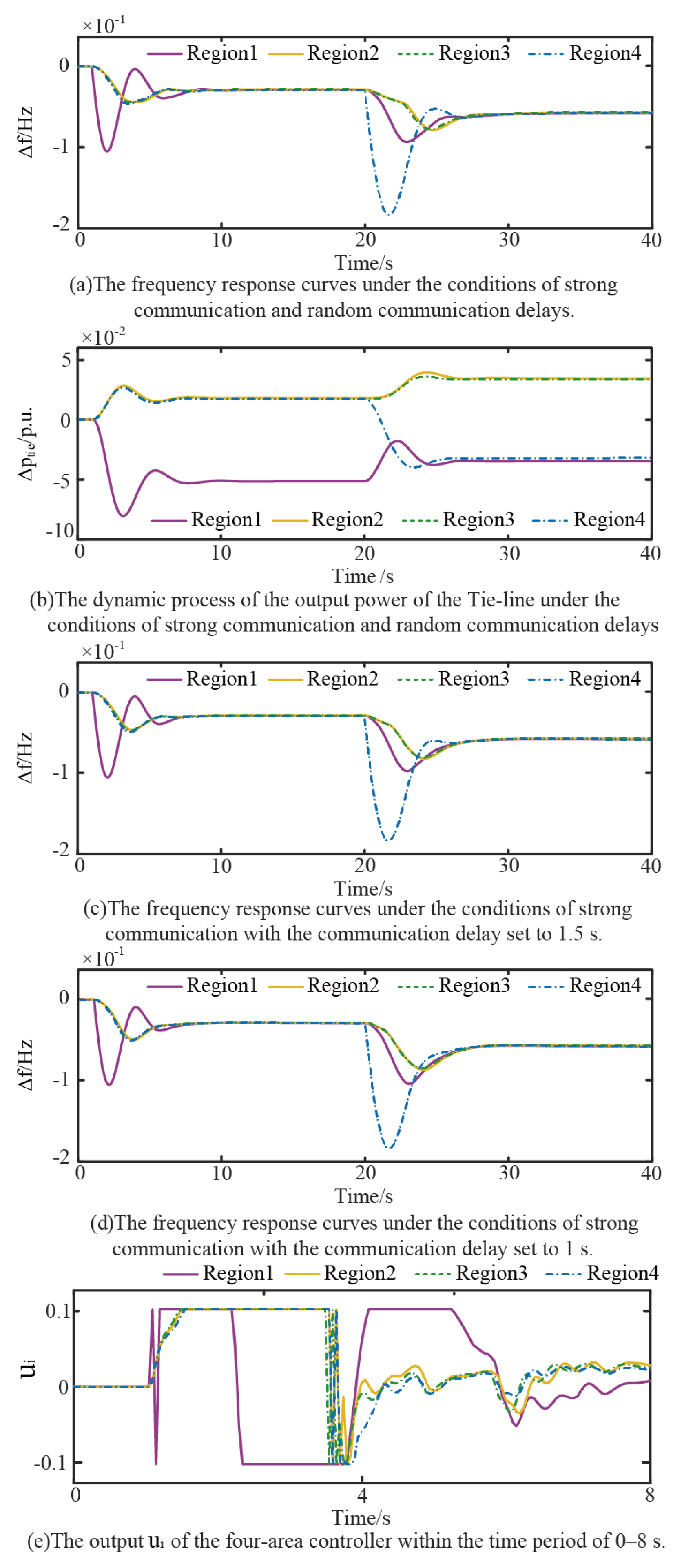
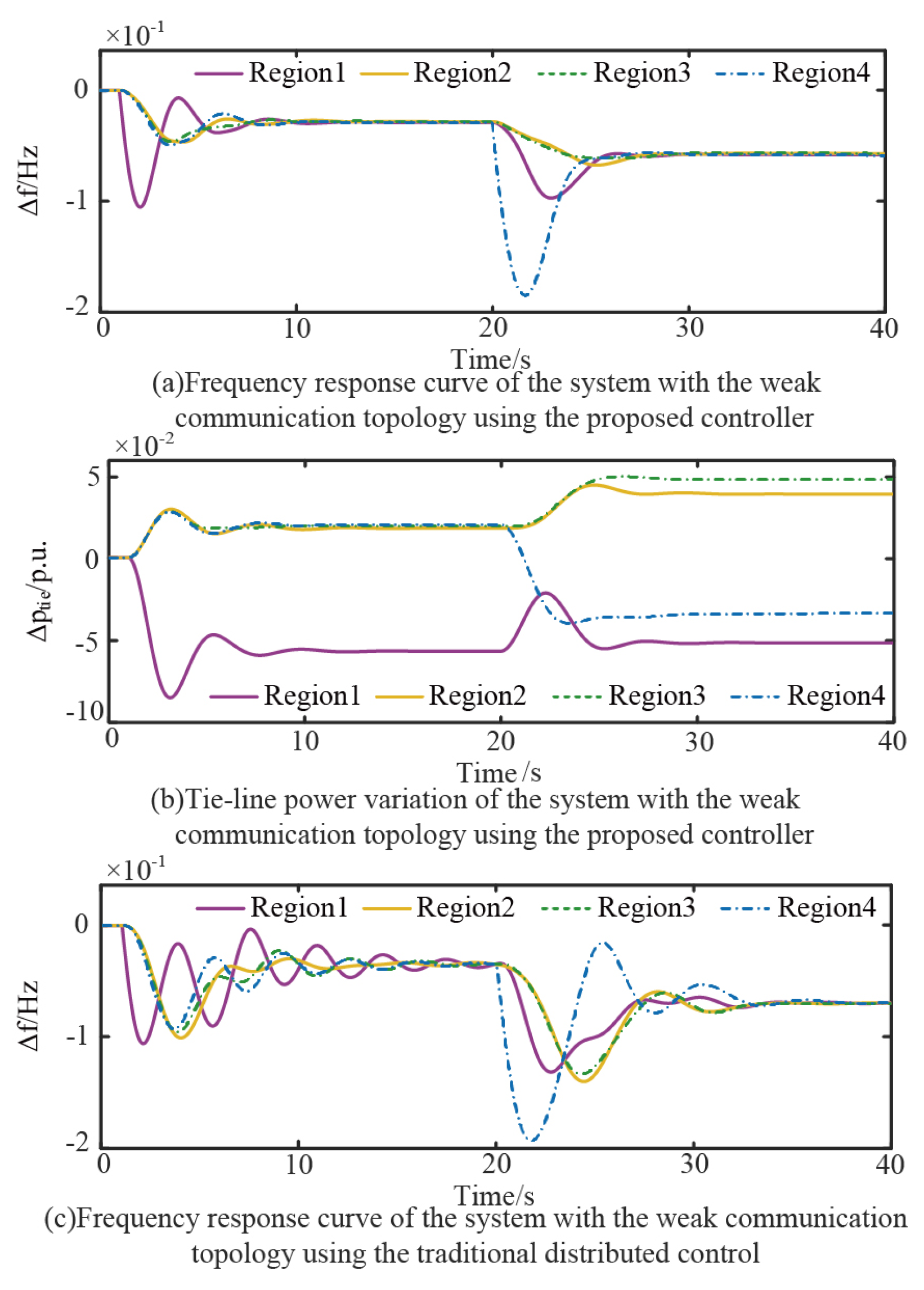
5.2. Case Study of the Four-Region System

This subsection tests the synergy effect of the proposed method using a four-region interconnected system. It also analyzes the impact on the synergy effect under different communication conditions. The corresponding parameter settings are shown in

Table 3. Four region frequency system parameters.

Region	TV/s	TI/s	Kp/(p.u.)	D/(p.u./Hz)	M/s
1	1	0.056	−20	0.0166	16.7
2	1.6	0.054	−18.52	0.0178	22.2
3	2	0.054	−20	0.016	19.3
4	1	0.056	−20	0.0166	16.7

. Among them, $T_{\mathrm{V}}$ is the time constant of the equivalent voltage outer loop of the photovoltaic aggregated PV inverter in the local area, $T_{\mathrm{I}}$ is the time constant of the equivalent current inner loop of the photovoltaic inverter in the local area, $K_{\mathrm{p}}$ is the equivalent droop coefficient of the photovoltaic cluster in the local area, M is the equivalent inertia of the local area, and D is the equivalent damping of the local area.

During the design phase of the observer, matrices $F_i$, $T_i$, $K_i$, and $H_i$ are the to-be-designed parameters of the state observer, and $K_{\mathrm{d}i}$ is the to-be-designed parameter of the disturbance observer

During the design phase of the controller, we have considered parameters as follows.

① The adjacency weight $a_{i,j}$, the reference signal weight $a_{i,0}$: these parameters are the design parameters to build error surface $e_{i,1}$. They are used in the calculation of Equation (10).

② Filter time parameter $T_{\mathrm{f}i}$: they are design parameters to calculate error surfaces $e_{i,2}$ and $e_{i,3}$, which is used in Equation (13).

③ Parameters $c_{i,1}$, $c_{i,2}$ and $c_{i,3}$ (control law design parameters): these parameters enable the system states to evolve in accordance with various virtual control laws and ensure the stable convergence of the defined error surface. They are used in Equations (20), (24) and (28), respectively.

Figure 15 illustrates the communication topology among the interconnected system regions under both strong and weak communication conditions. The dashed line representing inter-area communication with a maximum communication time lag of 2.5 s.

(1)

Comparative Analysis with Decentralized Control

Using the strong interconnection communication topology shown in Figure 15a, the control effects of the traditional decentralized control [14] are compared with the proposed method under good communication environment. At t = 1 s, a step disturbance of load with an amplitude of 0.06 p.u. is synchronously applied to regions 1 and 4. The corresponding frequency response curves of each region are shown in Figure 16, and the dynamic curves of the total output power of the tie-line is illustrated in Figure 17.

As can be seen in Figure 16, after the load disturbance, each region presents independent response characteristics, resulting in significant frequency differences between regions 1 and 4. The maximum instantaneous frequency difference between the two reaches 0.19 Hz. Stability was regained after 23.46 s following the load disturbance. Given that region 4 is only interconnected with region 1 and exhibits the largest frequency deviation, it was selected for observation. Its maximum frequency offset ultimately reached 0.41 Hz. The amplitude of the maximum power fluctuation of the entire tie-line reaches 0.07 p.u.

In contrast, the method in this paper realizes inter-region dynamic synergy through the multi-agent consensus algorithm. The frequency deviation of regions 1–4 converges synchronously, the maximum frequency offset of region 4 is suppressed to 0.34 Hz, and is quickly suppressed within 13.4 s. Compared with decentralized control, this approach resulted in a 17.1% reduction in frequency deviation and a 42.9% shortening of the settling time.

To facilitate the comparison of the performance among centralized control, decentralized control, and the control method proposed in this paper, we have compiled

Table 4. Comparison of key performance metrics.

Metrics	Two-Region Interconnected System		Four-Region Interconnected System
	Centralized Control	The Method in This Paper	Decentralized Control	The Method in This Paper
Settling time/s	50.6	12	23.46	13.4
Maximum frequency offset/Hz	0.23	0.17	0.41	0.34

to compare the key parameters. This table contrasts the three methods in terms of settling time and maximum frequency deviation, allowing for a clear identification of the performance differences between the centralized control, decentralized control, and the method proposed in this paper.

(2)

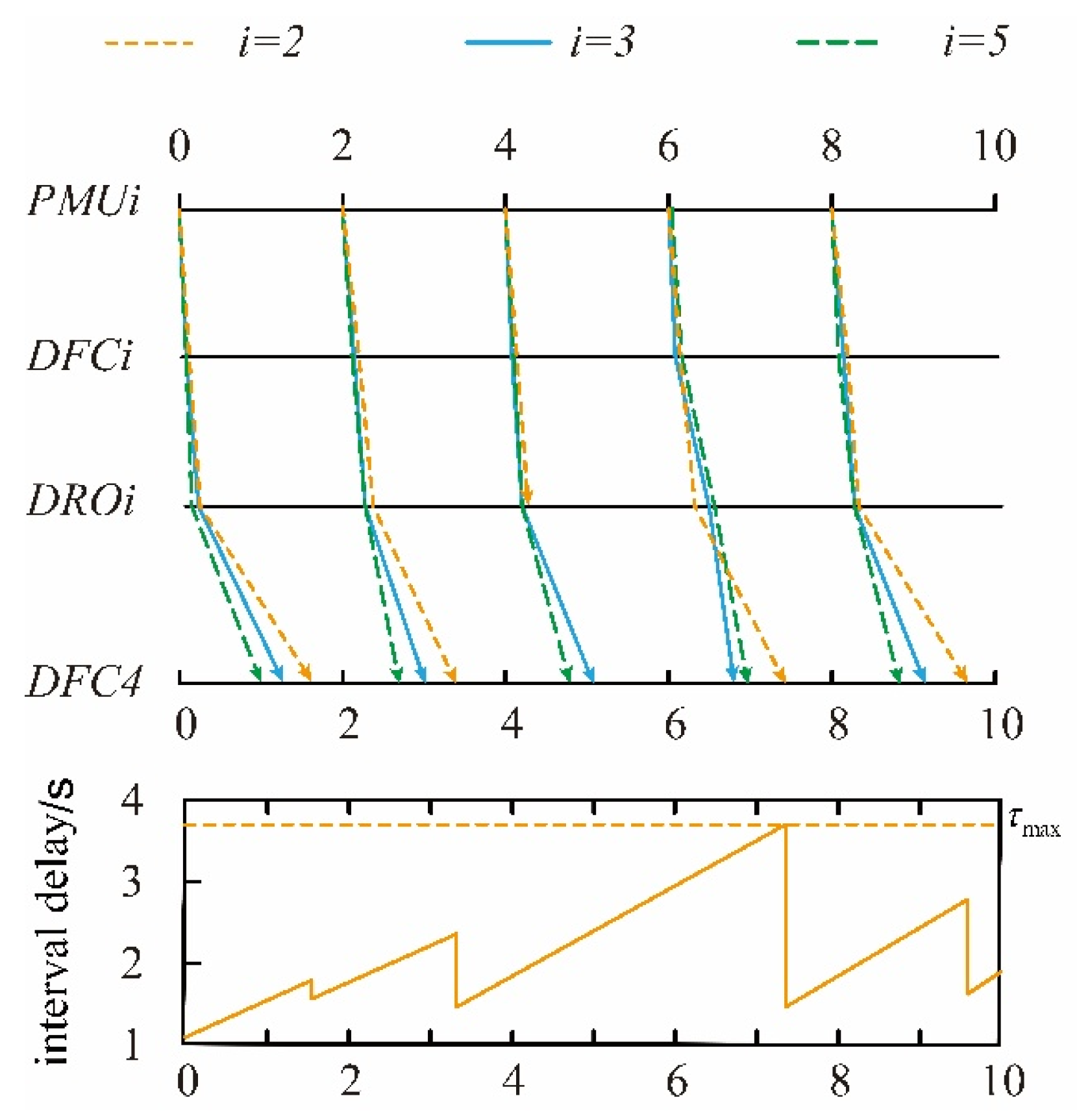
Controller performance analysis under different communication conditions

This subsection evaluates the control performance of the proposed control method under both strong and weak communication topologies. Using the topologies shown in Figure 15a,b as examples, a 0.06 p.u. step load is applied to regions 1 and 4 at t = 1 s and t = 20 s, respectively. Under the conditions of strong communication and random communication delays, the frequency response curves of each region and the dynamic process of the total output power of the contact line are shown in Figure 18a,b. Under the proposed controller, the dynamic process of the system transitions to the steady state rapidly. And, with the inter-region frequency offsets stabilized, the tie-line power fluctuation also tends to stabilize.

Under strong communication conditions, with the communication delay set to fixed values of 1.5 s and 1 s, the frequency response curves of each region are shown in Figure 18c,d. It can be observed that all frequencies can converge quickly and stably. However, the convergence speed and convergence effect under the condition of fixed time delay are better than those under random time delay. Moreover, as the fixed time delay decreases, both the convergence speed and convergence effect improve.

To demonstrate the transient characteristics of the controller, under the condition of strong communication random time delay, we present the output $u_i$ of the four-area controller within the time period of 0–8 s. Figure 18e shows that the controllers responded rapidly to the disturbance. The clipping module effectively suppressed the signal surge in the first two cycles, ensuring stable oscillation control. Subsequently, the control signals fell below the clipping amplitude by the third cycle. This effective response resulted in satisfactory performance by t = 8 s, as further evidenced by the frequency response in Figure 18a.

Figure 19a,b demonstrate the dynamic response curve of the system with the weak communication topology shown in Figure 15b using the proposed controller. It is shown that the frequency oscillation can also be narrowed down and eventually converge to a steady state.

Figure 19c shows the frequency dynamic diagram obtained by using the traditional distributed control method under weak communication conditions. After the first disturbance at t = 1 s, the frequency under the traditional distributed control failed to fully converge even by t = 20 s. After the disturbance at t = 20 s, it took 18 s to reach a stable state. The convergence speed of the traditional distributed control is much slower than that of the control method proposed in this paper. It can be clearly seen that the control effect is far inferior to that of the control method proposed in this paper.

Table 5. Power support by tie-lines.

Test Environment	Region 1 Power Outflow Change/p.u.	Region 4 Power Outflow Change/p.u.
Weak communication	−0.0501	−0.0326
Strong communication	−0.0339	−0.0323

shows the change in outflow power Via the tie-line after the perturbation in regions 1 and 4 under strong and weak communications, respectively. Analysis of the data in Table 5 reveals that under strong communication conditions (Figure 15a), all regions achieve full interconnection. As shown in Table 5, the tie-line power support received by Region 1 and Region 4 is remarkably similar under these conditions (The additional power flowing into Region 4 Via the tie-line is 95.3% of that into Region 1). This indicates that with favorable communication, the proposed coordinated control mechanism can achieve the allocation of cross regional power with the goal of minimizing ITAE in Equation (31), allowing the load disturbance to be shared more evenly across a broader area. Consequently, the overall frequency response performance is further optimized, evidenced by faster recovery and reduced oscillations as depicted in Figure 18a.

In contrast, under weak communication conditions, a significant disparity exists in the power support received by different regions (The additional power flowing into Region 4 via the tie-line is 65.1% of that into Region 1). However, as shown in Figure 19a, the proposed controller can also effectively suppress both low-frequency and ultra-low-frequency oscillations across all four regions. This phenomenon demonstrates that even in extreme situations characterized by non-ideal communication topologies, resulting in information asymmetry and uneven power allocation, and significant max delay conditions of up to 2.5 s, the controller can still maintain dynamic frequency stability, demonstrating the superiority of the distributed control algorithm based on state–disturbance observation and dynamic surface consensus control proposed in this paper.

6. Conclusions

This paper addresses the dynamic frequency stability challenges in wide-area interconnected power systems by proposing a distributed photovoltaic frequency controller based on a multi-agent consensus algorithm and dynamic surface control methodology. The principal conclusions are summarized as follows:

(1)

The PV-based control strategy proposed in this paper can suppress both low-frequency oscillations and ultra-low-frequency oscillations simultaneously and also achieves favorable performance even under weak communication conditions.

(2)

A three-layer distributed cloud control framework of terminal–edge–collaboration is constructed, which realized double high-precision observation of state variables and external perturbations through decentralized regional observer. The maximum error of the state observer is 1.6 × 10⁻⁴ p.u. and the steady state tracking error converges to 6 × 10⁻⁵ p.u.

(3)

A distributed frequency controller (DFC) is proposed using the MAC and DSC method, which can effectively limit the maximum frequency deviation of the system to 0.17 Hz, and the steady state frequency deviation converges to 1 × 10⁻⁸ p.u.

(4)

The parameter adjustment strategy based on CGO is proposed to achieve frequency deviation suppression. Simulation results show that the frequency deviation can be suppressed to ±0.17 Hz under the condition of communication delay of 2.5 s.

(5)

The test results show that compared with that of the traditional centralized control, the proposed dynamic frequency active support method can reduce the frequency deviation by 26.1% and the regulation time by 76.3%. And compared with that of the decentralized control, the proposed method can reduce the frequency deviation by 17.1% and the regulation time by 42.9%.

(6)

The PV-based control method proposed in this study can effectively suppress low-frequency and ultra-low-frequency oscillations, significantly enhancing the power grid’s capacity to accommodate high-proportion clean energy and its stability.

There remains room for further research regarding the finite-time convergence of the control method and we will conduct in-depth studies on this issue in the future. In addition, in our follow-up studies, we will also carry out in-depth research on issues including computational requirements, communication infrastructure needs, and potential integration challenges with existing control systems.