Abstract
Symmetry is a fundamental principle in mathematics, physics, and biology, where it governs structure and invariance. Classical symmetry analysis focuses on exact group-theoretic descriptions, but rarely addresses how robust a symmetric configuration is to perturbations. In this work, we introduce a probabilistic framework for quantifying the stability of finite point-set symmetries under random deletions. Specifically, given a finite set of points with a prescribed nontrivial symmetry group, we define the probability that removing N points reduces the symmetry to the trivial group . The complementary quantity serves as a measure of symmetry stability, providing a robustness profile of the configuration. We calculate explicitly for representative families of symmetric point sets, including linear arrays, polygons, polyhedra, directed necklace of points, and crystallographic unit cells. Our results demonstrate unexpected behaviors: the regular hexagon loses symmetry with a probability of 0.6 under the removal of three vertices, while cubes and tetrahedra exhibit the maximal robustness () for all admissible N. We further introduce a Shannon entropy of symmetry stability, which quantifies the overall uncertainty of symmetry breaking across all deletion sizes. This framework extends classical symmetry studies by incorporating randomness, linking group theory with probabilistic combinatorics, and suggesting applications ranging from crystallography to defect tolerance in physical systems.
1. Introduction
Symmetry plays a central role in biology [1,2,3,4,5,6,7,8,9,10], mathematics [11], physics [12,13], and chemistry [14,15], where it serves as a guiding principle for understanding structure, stability, and invariance. In crystallography, for example, the classification of atomic lattices is determined by symmetry groups [16,17], while, in physics, conservation laws are intimately connected with symmetries through Noether’s theorem [18,19]. Finite sets of points with prescribed symmetries arise naturally in diverse contexts, including molecular geometry [20], cluster formation [21,22,23], coding theory [24], and discrete models of physical systems [25,26,27].
The question of symmetry stability—namely, how resistant a symmetric structure is to perturbations—has received considerable attention in various forms. Most existing approaches investigate deterministic stability, where specific points or components are removed or displaced, and one asks whether symmetry is preserved [28]. Such studies are closely connected to structural rigidity, graph automorphisms, and geometric stability theory [29]. However, in many realistic situations, perturbations occur randomly rather than deterministically. Instead, systems are exposed to random fluctuations, such as thermal noise in physical systems, random deletions in networks, mutations in biological molecules [30], or stochastic failures in engineered structures.
This motivates the development of a probabilistic framework for measuring the robustness of symmetry under random deletions/perturbations. In our recent work, we considered the symmetry stability of Jordan curves [31]. In the present work, we extend the notion of symmetry stability to finite sets of points with nontrivial symmetry groups. Specifically, we consider the following problem: given a finite set of points together with its symmetry group, points are removed randomly and independently. We then ask the following: with what probability does such a removal destroy all nontrivial symmetry, reducing the symmetry group to the trivial group ?
We develop and formalize a probabilistic measure of symmetry stability for such finite point sets, and we provide explicit calculations for representative families of symmetric configurations. The method captures the interplay between local fragility (how easily a given configuration loses its symmetry under single deletions) and global resilience (the persistence of symmetry under multiple deletions).
Beyond its mathematical interest, this probabilistic perspective enriches classical symmetry analysis by incorporating randomness directly into the structural framework. It offers new conceptual insights and potential applications in crystallography, molecular stability, network resilience, coding theory, and other domains where symmetry governs stability but systems are inevitably subject to random perturbations.
2. Results
2.1. Introducing the Probabilistic Measure of the Symmetry Stability
In our recent work, we investigated the following question: given a symmetric Jordan curve, how many points must be removed in order to reduce its symmetry group to the trivial group ? We demonstrated that removing a single point suffices to reduce the symmetry group to , provided that the point does not lie on an axis of symmetry of the curve [31]. The only remarkable exception is the circle, for which this approach fails [31].
However, this method does not extend directly to finite sets of points. For example, consider the vertices of a regular polygon: the removal of a single vertex does not reduce the symmetry group of the set to . In the present paper we extend the proposed approach to sets of points with nontrivial symmetry groups. Specifically, let a finite set of points be given together with its symmetry group, different from the trivial group . We reformulate the problem as follows: points are removed randomly from the set. Let denote the probability that the removal of a single point (chosen randomly) reduces the symmetry group of the set to the trivial group . We define the probabilistic symmetry stability of the set under the removal of one point, denoted , as follows:
where is the probability (over random choice of a single point) that the resulting set has only the trivial symmetry group The value of may be understood, in turn, as the “survival probability” of the symmetry under the random removal of a single point from the set. In other words, , introduced with Equation (1), measures how resistant the symmetry of the set is to the random removal of a single point. If , then almost always at least one symmetry survives when you delete one point. If , then deleting a single point almost always destroys all symmetry. The illustrating examples will be supplied below.
Analogously, let us denote as the probability that the random and independent removal of a pair of points reduces the symmetry group to . The corresponding probabilistic symmetry stability is defined with Equation (2):
where is the probability (over random choice of a pair of points from a given set) that the resulting set has only the trivial symmetry group The introduced measures the robustness of the symmetry under the random removal of two points. In other words, quantifies how resistant the symmetry of a given set is to the random removal of a pair of points. The physical/intuitive interpretation of sounds as follows: imagine a finite structure (for example, the vertices of a regular polygon) as a system possessing geometric symmetry. Randomly removing two points from this structure is analogous to introducing two random “defects” or “damages” into the system, which may be seen as a pair of vacancies (say the Schottky defect) in the crystal lattice. The probability is the chance that these two defects are so disruptive that they completely destroy all symmetry, leaving only the trivial symmetry group . In contrast, represents the probability that some part of the original symmetry survives, even after two points are removed.
More generally, let denote the probability that randomly removing N points from the set containing points reduces the symmetry group to . We then define the probabilistic symmetry stability in this case as follows:
Here is the probability that some nontrivial symmetry still survives after randomly removing N points; in other words, quantifies the probability that at least one nontrivial symmetry remains in the set after the random and independent removal of N points.
In physics language, we can think of as an “order parameter” for symmetry stability, namely, means that symmetry is maximally stable under the random removal of N points. In turn, means that symmetry is fragile under the random removal of N points. So, the sequence provides a profile of the robustness of the symmetry group of the point set against random deletions.
First of all, note that, for the random distribution of points, the sequence is not defined. The symmetry group of randomly distributed points is the trivial group We address a number of examples in which the given location of points is described by the nontrivial symmetry group. Secondly, when , we remain after deletion with a single point, characterized with the symmetry group for the planar configuration of points, whatever their initial symmetry.
2.2. Calculation of the Probabilistic Measure of the Symmetry Stability for 2p Equidistant Points Placed on the Same Straight Line
Consider 2p points placed symmetrically on one straight line (equally spaced and symmetric about the center). The original symmetry of the point set is the two-element group , where is the reflection (or half-turn) that sends each point to its mirror partner. The 2p points form p mirror-pairs; because 2p is even, there is no single point fixed by . Now, we remove The only way the reflection can survive after removing a set R of points is if R is invariant under . For our configuration, this means R must be a set of whole mirror-pairs. Equivalently, if we remove an odd number of points, cannot survive (because mirror-pairs have size 2), so symmetry is certainly destroyed.
If we remove (even) points, survives exactly when the removed set consists of r entire mirror-pairs. Now consider the following particular cases:
- (i)
- . Removing a single point leaves its partner unpaired, so no longer maps the remaining set to itself. Thus, we calculate
- (ii)
- . There are unordered pairs of points that could be removed. Exactly p of those pairs are mirror-pairs (one per mirror-pair). If the removed pair is one of these p pairs, the reflection survives; otherwise, symmetry is lost. So, the probability that the removed pair is a mirror-pair is given by Equation (4):
It is seen from Equation (4) that the probabilistic measure of symmetry may be seen as the function of number p mirror-pairs, Quite expectedly and reasonably, It is intuitively clear that, for a very large (or infinite) symmetric configuration, the chance that a randomly chosen pair is exactly a mirror-pair tends to zero, so a random deletion almost surely destroys the reflection symmetry.
Correspondingly, for the probability , we calculate the following:
It is easily seen that This is also intuitively clear: the probability of the reduction in symmetry to group by deleting a random pair of points from an infinite set of points tends to unity. The initial symmetry group of the set is ; for very large (or infinite) p, a randomly chosen pair is almost certainly not a mirror-pair, so a random deletion almost surely destroys the reflection symmetry.
Now consider the general case. If is odd, then, as already noted, . If N is even, the symmetry survives. If the , the removed points are exactly r whole mirror-pairs. The number of ways to choose r mirror-pairs to remove is The total number of choices of points to remove is Finally, we calculate the following:
Finally, we establish the following:
2.3. Calculation of the Probabilistic Measure of the Symmetry Stability for Symmetrical Triangles
Consider the set of vertices of an equilateral triangle possessing the full dihedral group of symmetry of order six, number of vertices Remove one vertex . The remaining set has two points and nontrivial symmetry, described by the dihedral group . We calculate the following: Let us remove two vertices : the remaining set has one point and nontrivial symmetry, described by the full orthogonal group . Consequently, we establish . Similar results are true for isosceles triangles. We conclude that equilateral and isosceles triangles’ symmetry is maximally stable under the deletion of one or two vertices: we never (with the uniform choice model) end up with only the identity symmetry. Consequently, .
2.4. Calculation of the Probabilistic Measure of the Symmetry Stability for the Sets Built of Four Points
Consider the set of four points, denoted “1”, “2”, “3”, and “4”, belonging to the same plane. Three of them, namely the points labeled “1”, “2”, and “3”, are vertices of an equilateral triangle (see Figure 1). The fourth point, labeled “4”, lays on the side of the equilateral triangle and does not belong to the axis of symmetry of the triangle (see Figure 1).
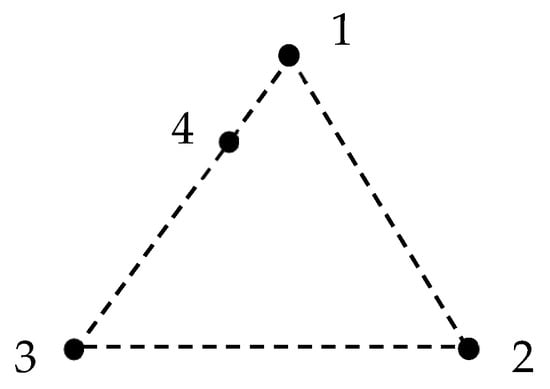
Figure 1.
The set of four points, denoted “1”, “2”, “3”, and “4”, is depicted. Points labeled “1”, “2”, and “3” are vertices of the equilateral triangle. Point “4” lays on the “1,3” of the equilateral triangle and does not belong to the axis of symmetry of the triangle. Dashed lines are supplied for eye guiding only.
We are going to calculate the set of probabilistic measures of the symmetry for the given set of points. Let us remove one point. If we remove point “4” (probability ), the remaining three points are the vertices “1”, “2”, and “3” of an equilateral triangle possessing full nontrivial symmetry (group If we remove any one of 1”, “2”, and “3” (total probability is ), the remaining three points are generically a scalene triple, or a non-symmetric collinear triple (points are collinear but not evenly spaced), when point “2” is removed, and have only the trivial symmetry . The probability that a nontrivial symmetry survives is ; consequently, . After removing two points, we always have exactly two distinct points left. Any unordered set of two distinct points in the plane has a nontrivial symmetry (it is preserved by the half-turn about their midpoint and reflections that swap them), so a nontrivial symmetry always survives. Therefore, When we remove three points, one point survives, characterized by nontrivial symmetry and described by the full orthogonal group O(2); hence, . Eventually, we summarize as follows: Group O(2) appears because a single point is fixed by every isometry of the plane.
The same results remain true for the set of four points, when three of them are vertices of the isosceles triangle. The fourth point lies on the side of the triangle and does not belong to the axis of symmetry of the triangle. The same reasoning yields
Now, let us calculate the probabilistic measures of symmetry for the vertices of a rectangle. When we remove one of its vertices, the emerging triangle is scalene and therefore has no nontrivial symmetry (no reflection or rotation preserving it). Hence, every single-vertex deletion produces a remaining set whose symmetry group is thus, Now, we remove from the rectangle two points. The remaining set has exactly two distinct points. Any two distinct points admit a nontrivial symmetry that swaps them (reflection in the perpendicular bisector, or rotation about the midpoint). So, the symmetry group of a two-point set is nontrivial; hence, we conclude Removing three vertices leaves a single point, described by the full orthogonal group . Eventually, . Consider that, unlike the equilateral triangle/isosceles case depicted in Figure 1, there is no deletion option that preserves a three-point rotational symmetry. The difference emerges from the symmetry group of the initial set of points.
2.5. Calculation of the Probabilistic Measure of the Symmetry Stability for Regular Polygons
This is, perhaps, the most surprising result presented in the paper. It is simple to demonstrate that, for regular quadrangles and pentagons, all of and all of , and the inductive thinking hints that this is true for the vertices of all the regular polygons. However, this conclusion is wrong. Consider the vertices of the regular hexagon depicted in Figure 2A.
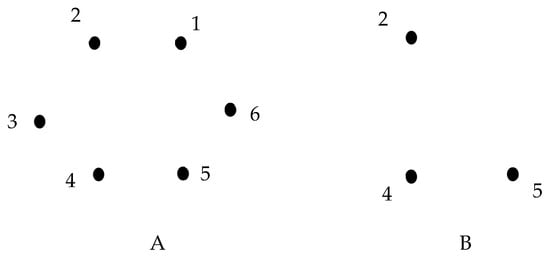
Figure 2.
(A) Vertices of regular hexagon numbered are depicted. (B) Points are removed. The emerging triangle is characterized by the trivial symmetry group .
Let us calculate explicitly. is defined as the probability that, after deleting N vertices (chosen uniformly at random), the remaining set still has a nontrivial symmetry. Equivalently, we re-shape as follows in Equation (9):
where is the number of deleted N-subsets whose complementary has a nontrivial symmetry. We consider ; the cases and are trivial. It is easy to demonstrate that Consequently, In other words removing of points reduces the symmetry of regular hexagon to the symmetry group different from the trivial group . We start from . Delete points labeled “3” and “6”. We obtain the rectangle “1, 2, 4, 5”, and symmetry survives. Deleting the adjacent points “1” and “2”, the reflection symmetry remains untouched. Deleting adjacent points “1” and “4”, the reflection symmetry also remains untouched. The same is true for other pairs points; hence, The same check holds for .
We obtain the nontrivial result for , as illustrated with Figure 2B. Consider the elimination of the triad of points numbered . The emerging scalene triangle denoted and depicted in inset B of Figure 2 possesses the trivial symmetry group .
Now, let us calculate The number of total choices We must count the three-vertex remaining sets (complements) that are symmetric. There are two types of symmetric three-vertex patterns on the hexagon: three consecutive vertices (a block of length 3). There are six such blocks (one starting at each vertex, wrapping around). Each gives a reflection symmetry (axis through the middle of the block). The every-other-vertex triangle (vertices and ) has a 3-fold rotation symmetry. There are two such triples. So, the total symmetric remaining 3-sets = 6 + 2 = 8. Therefore, There are 8 deleted 3-subsets whose complements are symmetric, hence . We conclude that deleting points keeps the symmetry of the hexagon nontrivial, whereas the deleting of points may reduce the symmetry of the hexagon to the trivial group, with
The solution to the general problem for arbitrary regular polygons is complicated and challenging, and it remains unsolved. The calculation of the probabilistic measure of the symmetry stability for a directed necklace of points is supplied in Appendix A.
2.6. Calculation of the Probabilistic Measure of the Symmetry Stability for Tetrahedron and Octahedron
It is instructive to extend the suggested idea to 3D shapes. Let us start from the calculation of the probabilistic measure of symmetry for the set of vertices of a tetrahedron. The total number of vertices is Only are allowed (). Let us start from When we remove one vertex, the remaining set is the three vertices of one face of the tetrahedron. Those three points are the vertices of an equilateral triangle whose point-set symmetry group is nontrivial (dihedral . Therefore, every single-vertex removal leaves a nontrivial symmetry, so the probability that the symmetry is reduced to the trivial group is . Now consider If we remove two vertices, the remaining set is built of two distinct points. Any two-point set has a nontrivial isometry exchanging the two points (reflection in the perpendicular bisector plane, or a half-turn about an appropriate axis), so its symmetry group is nontrivial (contains a swap of the two points). Every pair removal leaves nontrivial symmetry, so . Now address Removing three vertices creates the remaining set, containing a single point. A single point has nontrivial, infinite symmetry group which is in 3D space (the group which includes all rotations/reflections fixing that point), so . We conclude that the set of vertices of a tetrahedron demonstrates a remarkable stability of its symmetry against the random removal of its vertices. Similar calculations lead to the conclusion that for the vertices of an octahedron, another Platonic solid. For the detailed derivation, see Appendix B.
2.7. Calculation of the Probabilistic Measure of the Symmetry Stability for Cubic Crystallographic Cells
Now, we address the structures important for crystallography [16]. Let us start from the simple cubic lattice. It is easy to see that, no matter which vertices we delete from eight vertices, some nontrivial symmetry of the cube still preserves the remaining set. Hence, the whole sequence of probabilistic measures of symmetry equals to unity, namely . The same is true for the BCC and FCC cubic units (consider that the number of vertices will be different for these crystallographic systems). We conclude that the simple cubic FCC and BCC systems demonstrate a remarkable stability/robustness of their symmetry. The calculation of the sequence of probabilistic measures of the symmetry stability for HCP crystallographic cells represents a challenging mathematical task (see Section 2.4).
2.8. Shannon Probabilistic Measure of the Symmetry Stability
The suggested probabilistic measure of the symmetry stability enables the introduction of the Shannon measure of the symmetry stability [32,33]. Consider a given finite set of points (the number of points in the set is ) together with its symmetry group, different from the trivial group . Points are removed randomly and independently from the given set. Let denote the probability that removing a single point reduces the symmetry group of the set to the trivial group . More generally, denotes the probability that randomly removing points from the set containing points reduces the symmetry group to . The Shannon measure of the symmetry stability is defined with Equation (10):
Let us explain Equation (9). Removing points remains in the set a single point possessing the symmetry group , which is different from ; hence, . What is the meaning of the Shannon entropy introduced with Equation (9)?
The Shannon entropy defined in Equation (9) can be interpreted as the average uncertainty associated with destroying the symmetry of the set through the elimination of points of all possible removal sizes. In other words, Sh quantifies the overall information-theoretic uncertainty associated with the full profile of probabilities .
Let us exemplify the introduced Shannon measure of the symmetry stability with its calculation for a regular hexagon, addressed in Section 2.4. It was demonstrated in Section 2.4 that, for the regular hexagon, Consequently, the Shannon measure of the symmetry stability for a hexagon equals . For regular triangles, quadrangles, and pentagons, all of ; hence, Zero Shannon entropy means that the average uncertainty associated with destroying the symmetry of the set through the elimination of points of all possible removal sizes is zero. In other words, the probability that the removal of an arbitrary number of points from the set reduces the symmetry to is zero. Nontrivial symmetry always will survive. For a rectangle, (see Section 2.3); hence, For the configuration of points depicted in Figure 1, we calculate the following:
3. Discussion
Classical symmetry studies (in geometry, crystallography [16,17,34], group theory, graph automorphisms) usually deal with exact symmetries, describing the full symmetry group of a configuration. They rarely ask how fragile that symmetry is under perturbations [35]. Symmetry breaking is a fundamental concept in physics and chemistry (e.g., phase transitions, molecules, crystal defects), but it is typically studied deterministically: you introduce a defect and check whether symmetry survives [31,36,37,38,39]. Symmetry breaking may be continuous [22] or discrete. The discrete breaking of symmetry occurs in crystals, when Schottky, Frenkel, or antisite defects emerge [40]. The idea of quantifying the probability that symmetry survives after random discrete perturbations seems unexplored in the mathematical literature. We introduce the probabilistic measure of the symmetry stability , which may be interpreted as a symmetry robustness metric for finite point-sets (including vertices of polygons, polyhedra, etc.). This makes the introduced approach closer in spirit to “stability” concepts in graph theory and network science, but tailored to geometric symmetry groups. For regular polygons, Platonic solids, and other symmetric point-sets, one can compute explicitly, which leads to new combinatorial results. This has potential connections with probabilistic group theory (probability that a random subset has a trivial stabilizer), Ramsey-type problems (minimal deletions that destroy structure), and symmetry breaking in physics/chemistry (quantitative models of defect-induced asymmetry). The introduced provides a bridge between deterministic symmetry (group theory) and random perturbations (probabilistic combinatorics/statistical physics).
Consider the following example, related to physics. We address the defect stability in crystalline solids, namely crystal lattices with high symmetry (cubic, hexagonal, etc.). Consider random perturbations of the lattice, such as thermal motion, point defects (vacancies, interstitials), or irradiation damage that randomly removes or displaces atoms. The introduced probabilistic measure of symmetry quantifies the probability that, after introducing N random vacancies, the residual point configuration still preserves a nontrivial subgroup of the original space group. For example, a simple cubic lattice with a few vacancies often preserves inversion or rotational symmetry. And the same is true for FCC and BCC lattices. But, in more delicate lattices (like HCP), a single defect may destroy all nontrivial symmetry (see Section 2.4, in which the random breaking of symmetry of a hexagon is treated). The introduced gives a statistical measure of symmetry robustness of a lattice, relevant for understanding defect tolerance, phonon spectra stability, and mechanical properties.
Let us envisage the directions of future investigations. The probabilistic framework for symmetry stability introduced in this work opens several promising avenues for further research, both theoretical and applied:
- (i)
- Extension to higher-dimensional and complex point sets: While we considered 2D polygons and 3D polyhedra, many systems of interest—such as quasicrystals, complex molecular clusters, and high-dimensional lattices—pose challenging combinatorial problems. Extending calculations to these structures could uncover novel symmetry robustness patterns.
- (ii)
- Study of probabilistic symmetry in dynamic systems: In physical and biological systems, perturbations often occur continuously rather than as discrete deletions. Developing a time-dependent or stochastic version of could quantify the resilience of symmetry under fluctuating forces, thermal noise, or dynamic defects. Study of the time evolution of is of particular interest.
- (iii)
- Connection with statistical physics and phase transitions:
The Shannon measure of symmetry stability introduced with Equation (10) suggests a link between symmetry robustness and information-theoretic order parameters. Investigating the relationship between and critical phenomena in disordered systems may provide a new perspective on symmetry breaking and defect-driven phase transitions.
- (iv)
- Systematic computation of for various crystal lattices (including HCP and more complicated structures) can inform defect-tolerance studies, mechanical stability, and design of robust nanostructures. The probabilistic framework could guide the development of materials resistant to random defects.
- (v)
- Integration with network theory and combinatorics looks attractive. Symmetry stability can be generalized to networks with geometric embedding, where nodes or edges are removed randomly. This opens potential connections with probabilistic graph theory, random automorphism groups, and combinatorial optimization.
- (vi)
- Algorithmic and computational development is instructive. Efficient algorithms for the exact or approximate computation of the introduced and the Shannon symmetry entropy Sh for large or high-symmetry point sets will be crucial. Monte Carlo simulations, group-theoretic enumeration, and probabilistic combinatorial techniques can all play a role.
- (vii)
- Experimental validation of the suggested ideas is desirable. Measuring symmetry survival probabilities in real physical systems—such as nanoparticles under random vacancy formation, molecules with isotopic substitutions, or lattice defects under irradiation—could validate and calibrate the theoretical framework, bridging theory with experimental observation.
In summary, the introduced probabilistic approach to symmetry stability provides a versatile framework that can be expanded in multiple directions, linking combinatorial geometry, group theory, statistical physics, and applied materials science. Its future development promises both fundamental insights and practical applications in systems where symmetry is subject to randomness.
4. Conclusions
In this work, we introduced a probabilistic framework for studying the stability of finite point-set symmetries under random perturbations. Instead of addressing symmetry breaking deterministically, as is usually performed in geometry, crystallography, and physics, we defined the probability that the removal of N points reduces the symmetry group of a configuration to the trivial group and the complementary symmetry stability measurement was defined as . The resulting sequence ) characterizes the robustness of a given symmetric configuration to random deletions.
We demonstrated explicit calculations for several representative cases: symmetric linear arrays, equilateral and isosceles triangles, four-point configurations, rectangles, regular polygons, directed necklace of points, tetrahedrons, octahedrons, and cubic crystallographic cells. These examples reveal both expected and surprising behaviors. For instance, cubes, tetrahedrons, and octahedrons exhibit a maximal robustness, with nontrivial symmetry always surviving the removal of any number of vertices, while regular hexagons display partial fragility, losing all symmetry with probability under the deletion of three vertices. Such results illustrate that symmetry stability is highly sensitive to both the geometry and group structure of the given configuration of the points. Our results indicate that the proposed probabilistic symmetry stability captures both local vulnerability (symmetry-breaking caused by specific single deletions) and global persistence (the inevitability of nontrivial symmetry in sufficiently reduced systems). Once the system reduces to two or one points, these configurations inherently admit reflection or rotational invariances.
We also proposed a Shannon entropy measure of symmetry stability, which captures the overall information-theoretic uncertainty of symmetry breaking across all deletion sizes. This connects probabilistic symmetry stability with broader concepts in statistical physics and information theory.
The introduced framework provides a bridge between deterministic group-theoretic symmetry analysis and probabilistic models of random perturbations. It offers a quantitative language for discussing the robustness of symmetry in systems ranging from molecular clusters and nanoparticles to crystallographic lattices and disordered networks. Beyond the explicit examples treated here, the approach suggests new directions for research in probabilistic group theory, combinatorial geometry, and the physics of defect-induced symmetry breaking. We believe that the suggested framework provides both a unifying language and a flexible tool for studying how symmetry persists—or collapses—under the unavoidable randomness present in natural and engineered systems.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author on request.
Acknowledgments
The authors are thankful to Yelena Bormashenko for her kind help in preparing this paper. The author is indebted to anonymous reviewers being extremely helpful in reviewing the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Calculation of the Probabilistic Measure of the Symmetry Stability for the Directed Necklace of Points
Consider p equally spaced points on a circle whose only nontrivial symmetries are the rotations by multiples of . The symmetry group is the cyclic group . Reflections are excluded by hypothesis—e.g., we consider a directed necklace or a configuration where reflections are not allowed. Let and be defined as before, for removing N points at random from the p-point set. The action of the rotation group on the set of p points is transitive: every nontrivial rotation moves every point. A rotation by angle (for ) decomposes the set of points into orbits of length . A removed set R of size N can be invariant under a rotation only if it consists of an integer number of entire orbits of . Equivalently, letting , the remaining points must satisfy the following:
If no such k exists, then every nontrivial rotation is broken by the removal, and the resulting symmetry group is trivial, . Now, the treatment is split as follows:
- (i)
- p is prime. For all nontrivial rotations, . Hence, for , every nontrivial rotation destroys the symmetry, and, consequently, .
- (ii)
- p is composite. Some rotations have orbits. Then, it is possible that is an integer, in which case the removal may leave a nontrivial symmetry intact. The exact probability that the remaining set has a nontrivial rotational symmetry can be computed via the Möbius-function formula:where is the Möbius function. For a directed necklace of six points forming a hexagon, we calculate , and consequently we obtain the following:
Let us estimate the asymptotic behavior of when p goes to infinity and N is fixed, i.e., the number of points goes to infinity under the fixed number of removed points. After removing N points, the orbit-length q of that rotation must divide N, so q is a divisor of N, . Fix N and examine the contributions from each admissible orbit-length . For fixed N and large p (and assuming p is divisible by q), the number of removal-sets that are unions of q-cycles is supplied by Compared to total , and using , we calculate the following:
Summing admissible values of q (and noting overlaps between different rotations give only lower-order corrections) yields the following leading-order asymptotic:
where is 1 when p is divisible by q and 0 otherwise. The decay is polynomial in p. The largest (slowest-decaying) term comes from the divisor q of N that minimizes the exponent . Because increases as q grows, the dominant contribution comes from the smallest nontrivial divisor of N, that also divides p (i.e., the smallest prime divisor of N; if N is prime, then . If no such divisor of N divides p (e.g., p is prime), then there is no surviving nontrivial rotation and . For example when p is even and goes to infinity, and when p is odd; i.e., ; when (N is prime), when p goes to infinity. The general asymptotic of for large values of p is given by Equation (A4).
Appendix B. Calculation of the Probabilistic Measure of the Symmetry Stability for Octahedron
We use the standard coordinate model of the regular octahedron; the coordinates of vertices V are given as follows:
So, the six vertices split into three opposite pairs (, where , and are the unit coordinate vectors in the directions of the x, y, and z-axes, correspondingly.
- (i)
- Let us remove a single vertex , say five vertices remain. The remaining set contains its opposite and the two opposite pairs , . There is at least the reflection in the plane (or rotation about the x-axis composed with other symmetries of the octahedral group) that preserves the remaining five points while not being the identity. Hence, the remaining five-point set has a nontrivial symmetry.
- (ii)
- Remove two vertices (four vertices remain). There are two cases for the two removed vertices:
- (a)
- They are an opposite pair (e.g., removed). The remaining four are the two opposite pairs.that set is a square in the plane , dihedral -type nontrivial symmetry.
- (b)
- They are from different opposite pairs (e.g., , and removed). Then, the remaining set contains the whole opposite pair . rotation about the z-axis (or the reflection in the plane ) preserves the set and is nontrivial. In every subcase, at least one nontrivial isometry of the octahedral group preserves the remaining four points, so
- (iii)
- Remove three vertices three vertices remain.Up to symmetry, the only essentially different possibility is removing one vertex from each opposite pair (if we remove both members of some pair you reduce to the one of the types above). For example, remove , and ; the remaining three points are , and . These vertices are located at the vertices of an equilateral triangle (distances equal) and are permuted cyclically by a —rotation (a coordinate permutation); hence, their point-set symmetry group contains a nontrivial rotation ( subgroup). We conclude that any three-vertex remainder has nontrivial symmetry.
- (iv)
- Remove four vertices ; two vertices remain.Any two-point set has a nontrivial isometry that swaps the two points (reflection in the perpendicular bisector plane or rotation about an appropriate axis). So, the remaining pair always has a nontrivial symmetry.
- (v)
- Remove five vertices ; one vertex remains.A single point has an infinite stabilizer (all rotations/reflections fixing that point), so the symmetry is certainly nontrivial.
Therefore, for every allowed , the remaining vertex set has a nontrivial isometry. We summarize as follows:
References
- Finnerty, J.H. The origins of axial patterning in the metazoa: How old is bilateral symmetry? Int. J. Dev. Biol. 2003, 47, 523–529. [Google Scholar] [PubMed]
- Finnerty, J.H.; Pang, K.; Burton, P.; Paulson, D.; Martindale, M.Q. Origins of Bilateral Symmetry: Hox and Dpp Expression in a Sea Anemone. Science 2004, 304, 1335. [Google Scholar] [CrossRef] [PubMed]
- Longo, G.; Montévil, M. From Physics to Biology by Extending Criticality and Symmetry Breakings. In Perspectives on Organisms; Lecture Notes in Morphogenesis; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Yonekura, T.; Sugiyama, M. Symmetry and its transition in phyllotaxis. J. Plant. Res. 2021, 134, 417–430. [Google Scholar] [CrossRef] [PubMed]
- Dumais, J. Can mechanics control pattern formation in plants? Curr. Opin. Plant Biol. 2007, 10, 58–62. [Google Scholar] [CrossRef]
- Dengler, N.G. Anisophylly and dorsiventral shoot symmetry. Int. J. Plant Sci. 1999, 160, S67–S80. [Google Scholar] [CrossRef]
- Cannon, K.A.; Ochoa, J.M.; Yeates, T.O. High-symmetry protein assemblies: Patterns and emerging applications. Curr. Opin. Struct. Biol. 2019, 55, 77–84. [Google Scholar] [CrossRef]
- Wolynes, P.G. Symmetry and the energy landscapes of biomolecules. Proc. Natl. Acad. Sci. USA 1996, 93, 14249–14255. [Google Scholar] [CrossRef]
- Hollo, G. A new paradigm for animal symmetry. Interface Focus 2015, 5, 20150032. [Google Scholar] [CrossRef]
- Bormashenko, E. Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle. Biophysica 2022, 2, 292–307. [Google Scholar] [CrossRef]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Schwichtenberg, J. Physics from Symmetry, 2nd ed.; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- McGreevy, J. Generalized Symmetries in Condensed Matter. Ann. Rev. Condens. Matter Phys. 2023, 14, 57–82. [Google Scholar] [CrossRef]
- Jaffé, H.H.; Orchin, M. Symmetry in Chemistry; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Hargittai, M.; Hargittai, I. Symmetry in Chemistry. Eur. Rev. 2005, 13 (Suppl. S2), 61–75. [Google Scholar] [CrossRef][Green Version]
- Müller, U.; De La Flor, G. Symmetry Relationships Between Crystal Structures: Applications of Crystallographic Group Theory in Crystal Chemistry; Oxford University Press: Oxford, UK, 2024. [Google Scholar][Green Version]
- Nespolo, M.; Benahsene, A.H. Symmetry and chirality in crystals. J. Appl. Cryst. 2021, 54, 1594–1599. [Google Scholar] [CrossRef]
- Putkaradze, V. Noether’s Theorem and Conservation Laws. In A Concise Introduction to Classical Mechanics. Surveys and Tutorials in the Applied Mathematical Sciences; Springer: Cham, Switzerland, 2025; Volume 16. [Google Scholar]
- Brading, K.; Brown, H.R. Symmetries and Noether’s Theorems. In Symmetries in Physics: Philosophical Reflections; Brading, K., Castellani, E., Eds.; Cambridge University Press: Cambridge, UK, 2003; pp. 89–109. [Google Scholar]
- Atz, K.; Grisoni, F.; Schneider, G. Geometric deep learning on molecular representations. Nat. Mach. Intell. 2021, 3, 1023–1032. [Google Scholar] [CrossRef]
- Zhao, Y.; Siriwardane, E.M.D.; Wu, Z.; Hu, J. Physics guided deep learning for generative design of crystal materials with symmetry constraints. npj Comput. Mater. 2023, 9, 38. [Google Scholar] [CrossRef]
- Frenkel, N.; Fedorets, A.A.; Dombrovsky, L.A.; Nosonovsky, M.; Legchenkova, I.; Bormashenko, E. Continuous Symmetry Measure vs Voronoi Entropy of Droplet Clusters. J. Phys. Chem. C 2021, 125, 2431–2436. [Google Scholar] [CrossRef]
- Kreienkamp, K.L.; Klapp, S.H.L. Nonreciprocal Alignment Induces Asymmetric Clustering in Active Mixtures. Phys. Rev. Lett. 2024, 133, 258303. [Google Scholar] [CrossRef]
- Vermani, L.R. Elements of Algebraic Coding Theory; Routledge: New York, NY, USA, 2022. [Google Scholar]
- Kornyak, V.V. Discrete dynamical systems with symmetries: Computer analysis. Program. Comput. Soft. 2008, 34, 84–94. [Google Scholar] [CrossRef]
- Renner, R. Symmetry of large physical systems implies independence of subsystems. Nat. Phys. 2007, 3, 645–649. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inverse symmetric inflationary attractors. Class. Quantum Grav. 2017, 34, 105009. [Google Scholar] [CrossRef]
- Hellmann, F.; Schultz, P.; Grabow, C.; Heitzig, J.; Kurths, J. Survivability of Deterministic Dynamical Systems. Sci. Rep. 2016, 6, 29654. [Google Scholar] [CrossRef]
- Pillay, A. Geometric Stability Theory; Oxford Academic: Oxford, UK, 1996. [Google Scholar]
- Goodsell, D.S.; Olson, A.J. Structural Symmetry and Protein Function. Ann. Rev. Biophys. 2000, 29, 105–153. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E. Symmetry Breaking: One-Point Theorem. Symmetry 2025, 17, 1395. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ben-Naim, A. Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem. Entropy 2017, 19, 48. [Google Scholar]
- Chatterjee, S.K. Crystallography and the World of Symmetry; Springer: Berlin, Germany, 2008; pp. 47–56. [Google Scholar]
- Albertson, M.; Collins, K. Symmetry breaking in graphs. Electron. J. Combin. 1996, 3, R18. [Google Scholar] [CrossRef]
- Xu, M.; Hu, W.; Han, Z.; Bai, H.; Deng, G.; Zhang, C. Symmetry-breaking dynamics of a flexible hub-beam system rotating around an eccentric axis. Mech. Syst. Signal Process. 2025, 222, 111757. [Google Scholar] [CrossRef]
- Zhu, H.; Han, Z.; Hu, W. Generalized Multi-Symplectic Analysis for Lateral Vibration of Vehicle–Bridge System Subjected to Wind Excitation. J. Vib. Eng. Technol. 2025, 13, 460. [Google Scholar] [CrossRef]
- Strocchi, F. Symmetry Breaking; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 732. [Google Scholar]
- Nambu, Y. Nobel lecture: Spontaneous symmetry breaking in particle physics: A case of cross fertilization. Rev. Mod. Phys. 2009, 81, 1015. [Google Scholar] [CrossRef]
- Carter, C.B.; Norton, M.G. Point Defects, Charge, and Diffusion. In Ceramic Materials; Springer: New York, NY, USA, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).