Abstract
This paper was written in memory of Joao da Providência who passed away in November 2021. It is a pursuit of works developed recently by Joao, Steven and inspired by our many years of discussions. Neutron stars are described within the quark–meson coupling Bogoliubov (QMC Bogoliubov) nuclear model which includes u, d and s quarks. The model is improved by including the - mixing term so that constraints imposed by ab-initio chiral effective field theory pure neutron matter calculations are satisfied. The effects of the symmetry energy slope on the structure and properties of neutron stars are investigated. In particular, the effect on the radius, on the particle fractions, and on the onset of the nuclear direct Urca processes is discussed. It is shown that the improved model is in accordance with GW170817 observations, and that the constrained symmetry energy does not allow for nucleonic direct Urca processes inside neutron stars. Within the present model, no hyperons nucleate inside neutron stars.
Keywords:
nuclear symmetry energy; equation of state; dense nuclear matter; neutron stars; gravitational waves; ab-initio chiral effective field theory; SU(3) symmetry; direct urca process PACS:
26.60.−c; 26.60.+c; 21.65.+f; 97.60.Jd
1. Introduction
In recent decades, the study of the properties of high-density nuclear matter has received a major boost from astronomical observations. Such studies are particularly important in the context of nuclear astrophysics. Thus, neutron stars are considered to be a unique laboratory for nuclear and particle physics, as they are the only systems where high-density baryonic matter exists. In particular, they can provide the conditions for the formation of deconfined quark matter. Observations of neutron stars offer us the opportunity to gain access to an area of nuclear physics that is normally inaccessible. Neutron stars (NS) are systems with several extreme properties, not only very high densities, but also very asymmetric nuclear matter with a very small proton fraction, or very high magnetic fields. The properties of these systems are governed by the equation of state (EOS), which is an essential part of the construction of the stellar mass radius and its tidal deformability. Observations of NS are therefore expected to provide strong constraints on the high-density EOS. Despite its crucial role in our understanding of physics at supranuclear densities, the EOS of nuclear matter deep inside neutron stars remains poorly understood.
The rapid advances in astronomical observational techniques provide many opportunities to study neutron stars using the equation of the state of high-density nuclear matter. Recent neutron star observations include the detection of gravitational waves from neutron star mergers and, where possible, their electromagnetic counterparts [1,2,3,4], the determination of NS masses from radio data, in particular the highly constraining two solar mass pulsars PSR J1614-2230 [5,6], PSR J0348+0432 [7], MSP J0740+6620 [8,9], and the recent simultaneous NS radius and mass measurements by NICER X-ray observations of pulsars PSR J0030-0451 and MSP J0740+6620 [10,11,12,13,14]. These observations place strong constraints on the equation of state of dense matter, but smaller uncertainties are needed to offer a clear indication of the degrees of freedom that make up neutron star matter at high densities. In particular, the two-solar-mass constraint poses some difficulties for the possible appearance of non-nucleonic degrees of freedom, such as hyperons, delta resonances, kaon and pion condensates, or quark deconfined matter [5,15,16]. However, several works have shown that the lack of knowledge about the properties of high-density matter is still large enough to allow the appearance of non-nucleonic degrees of freedom, even considering the two-solar-mass constraint [17,18,19,20,21,22,23]. In [24], the authors used a Bayesian inference approach to determine the conditions under which hyperons could exist inside neutron stars and still explain the occurrence of two-solar-mass stars. They concluded that the presence of hyperons requires the nucleonic EOS to be harder, in particular with greater incompressibility at saturation. Finding the composition of cold dense nuclear matter therefore remains a serious challenge.
In the 1960s, P.N. Bogoliubov [25] proposed a model of baryons, assuming that these baryons are composed of independent quarks bound by a linearly increasing potential, as suggested by gauge theories. Based on this model, the Bogoliubov quark–meson coupling model was developed [26] and applied to the description of neutron star matter including hyperonic degrees of freedom [26,27,28]. Starting from an SU(3) symmetry approach, it was shown in ref. [28] that this symmetry must be broken in order to satisfy the constraints imposed by hypernuclei and neutron stars. The authors were able to describe NS observations, such as two-solar-mass stars or the radius of canonical neutron stars, within the currently accepted uncertainties in a broken SU(3) model. In particular, by constraining the and hyperon potentials to the properties of the hypernuclei, it was shown that no hyperons are produced at densities such as those found inside neutron stars.
The symmetry energy at saturation is still subject to quite a large uncertainty. In [29], the authors constrained the symmetry energy at saturation and its slope to 29.0–32.7 MeV and 40.5–61.9 MeV, respectively, using a set of several experimental nuclear data. A larger interval was obtained for the symmetry energy slope in [30] ( MeV), considering constraints from neutron star properties in addition to experimental nuclear data. PREX-2 [31] and CREX [32] experiments have been performed to measure the lead and calcium neutron skin from the parity-violating asymmetry measurement. However, the uncertainties are still large and the results from PREX-2 and CREX, according to the studies [33,34], seem to be incompatible with each other, although in [35], three models are proposed which are compatible with both measurements within 1. Knowing the symmetry energy is important because it defines the properties of the neutron star, such as its proton fraction. The size of this quantity is directly related to the possibility of nucleonic direct Urca processes occurring, leading to a rapid cooling of the neutron star [36].
In [37,38], within a relativistic mean-field description of nuclear matter, it was shown that it is possible to control the neutron star radius by introducing a term that mixes the and meson fields. This term defines the density dependence of the symmetry energy, in particular its slope [39]. In this paper, we continue our investigation on the Bogoliubov quark–meson coupling model [26,27,28]. The values of the slope of the symmetry energy at saturation of this model, 79 MeV, are above the limits imposed in [29], although still within those obtained in [30]. The aim of the present work is to include a mixing - term in the model and to study the effects of the nuclear symmetry energy on the composition, structure and properties of the neutron star within the Bogoliubov quark–meson coupling model.
In Section 2, we briefly present the model; in Section 3, the description of hadronic matter with strangeness is introduced and the -equilibrium equation of state is built. In Section 4, we obtain the structure and properties of neutron stars described by the present models and discuss the results. In the last section, we draw some concluding remarks.
2. Bogoliubov Quark Meson Coupling Model
Bogoliubov independent quark model of the nucleon is characterized by a linearly rising potential confining the quarks [25]. To describe the QMC Bogoliubov model, we consider the Dirac Hamiltonian written as follows:
where m is the current quark mass, is the external scalar field, denotes the coupling of the quark to the field, is the string tension, and are Dirac matrices. The current quark mass m is taken to be for quarks because their constituent mass is assumed to be determined exclusively by the value of . The constituent mass of the quarks is generated dynamically, while the constituent mass of the s quark arises both dynamically and from its “current” mass. Considering SU(3) symmetry, the coupling is assumed to be the same for quarks . The eigenvalues of are obtained by a scale transformation from
We cannot apply the variational approach to because its eigenvalues are not bounded from below; however, we need the lowest positive eigenvalue of . Thus, the eigenvalues of are determined by considering its square,
using a variational principle and considering the following ansatz:
where are variational parameters, and is a 2-spinor. We look for the eigenvalues as a function of the quantity a which is related to the nucleon radius. From the wave function in Equation (3), it is clear that is a measure of the nucleon radius. Minimizing the expectation value of for the following expression for the quark mass is found:
where , , , , , and are all given in [26,27].
Minimization of Equation (4) with respect to is readily performed, so that
Minimization of the r.h.s. of Equation (5) with respect to b may be easily implemented as detailed in [26,27,28]. However, we found that in the interval that covers the range of densities under consideration, we can express the groundstate energy, of with a very good accuracy, as follows:
Taking for quarks , we obtain, in the vacuum, the constituent mass of these quarks equal to 313 MeV, with and MeV. For quark s, reproduces the vacuum constituent mass 504 MeV of this quark. Consequently, the mass of the baryon B is given as follows:
The -hyperons are not considered, as discussed lately in [28], because experimental data seem to indicate that the potential of the hyperon in nuclear matter is quite repulsive [40]; consequently, their appearance is not expected.
3. Hadronic Matter
In ref. [28], it was shown that the tidal deformability of a 1.36 star is larger than the prediction from GW170817 at a 90% credible interval. Since the symmetry energy in the present model is quite stiff, and it has been shown that the symmetry energy affects the radius of low-mass stars [38,39], a softer symmetry energy produces a smaller tidal deformability. The density dependence of the symmetry energy can be modulated by a term mixing the vector–isoscalar meson and the vector-isovector meson in the Lagrangian as in [39]. In the present work, this term is taken into account and the properties of nuclear matter are used to fix the couplings of these mesons to nucleons.
As indicated in ref. [28], field is interpreted as a vector field of the type, in the spirit of reference [41], with structure , where so that the coupling of –meson to quark s is equal to the coupling to quarks multiplied by factor . This ansatz breaks the SU(3) symmetry and stiffens the EoS. The parameter together with will be fixed to satisfy constraints coming from chEFT calculations for neutron matter and from the astronomical observations.
In the current version of the model, the energy density is written as follows:
and the thermodynamical potential is given by
with , as quark–meson coupling constants. The Lagrange multiplier controls the baryon density and controls the electrical charge. The number density and energy density of the baryons and leptons are written, respectively, as follows:
where is the particle Fermi energy. The field is obtained from the minimization of thermodynamical potential with respect to ,
where
denotes the scalar density of each baryon.
In the spirit of the SU(3) flavor symmetry, the quark–scalar meson coupling that enters in the definition of , Equation (7), is the same for all quarks. The minimization of thermodynamical potential with respect to the field and the field, respectively, offers the relation linking each field to its respective source,
with
where , . Meanwhile, the minimization of with respect to leads to the chemical potential of baryon B, written as follows:
which, explicitly for , Equation (13) reduces to
Finally, the minimization of with respect to leads to the electron Fermi energy, given by
This model predicts a competition between negatively charged hyperons and leptons. This is natural following Bodmer–Witten’s Conjecture [42,43], which stipulates that at high densities, the groundstate of baryonic matter should involve only quarks without leptons.
The model parameters are obtained by fixing the free parameter of the model in order to fit the nucleon mass M = 939 MeV. Once is determined, we can proceed to specify the desired values for various parameters. We take the standard values for the meson masses, namely MeV, MeV, and MeV. Next, the desired values of the neutron effective mass , nuclear matter binding energy MeV, incompressibility K = 315.0 MeV, in agreement with the range of values proposed in [44], and the nucleon radius fm at saturation density fm, are obtained by setting and . The coupling constant is fixed in order to have the symmetry energy coefficient MeV and the symmetry energy slope L = 79.45 MeV at saturation density. Both values are within the ranges obtained in [30], MeV and L = MeV.
4. Results and Discussion
The isovector properties of the QMC Bogoliubov model can provide valuable insights into nuclear physics beyond the properties at saturation density. Before applying the model to the study of stellar matter, we first focus on its properties at saturation and subsaturation densities.
The effect of the symmetry energy on the properties of the neutron star is studied, including the mixing term , which allows variation of the symmetry energy slope. Couplings and are determined such that the symmetry energy is set to 29 MeV at saturation density, and the slope L is defined in the range of values obtained in [30] from a large number of experimental data and astrophysical observations, L = 58.7 ± 28.1 MeV. In Table 1, we list the values of L that will be discussed in the sequel.

Table 1.
Parameters and properties of the model: , , , MeV, K = 315 MeV.
The symmetry energy within the Bogoliubov QMC model exhibits quite a linear behavior with the baryon density. This is a common feature with many NLWM models. The nonlinear mixing - term changes the density dependence of the symmetry energy, and, as a consequence, the symmetry energy of the QMC model becomes softer at higher densities, and harder below saturation density; see Figure 1. In this figure, we plot the symmetry energy in panel (a) and its slope in panel (b) as a function of the baryon density for several values of the mixing term . The effect of the mixing terms is clear: the larger the mixing term coupling, the smaller the slope of the symmetry energy above 0.06 fm and the softer the symmetry energy above the saturation density. The consequences of the isovector properties of the QMC Bogoliubov models are discussed below. Table 1 lists the properties and parameters of the models studied.
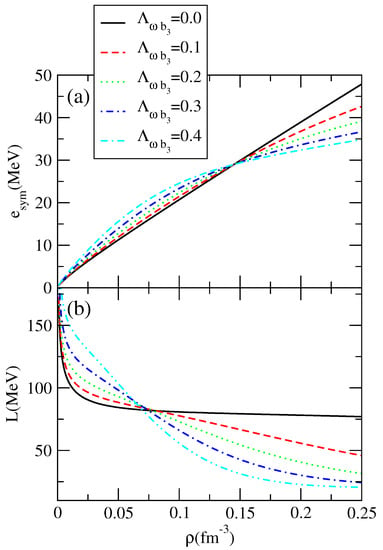
Figure 1.
The symmetry energy (panel (a)) and the symmetry energy slope (panel (b)) as a function of the baryonic density for several values of the mixing term .
It is very instructive to study the behavior of the pressure of pure neutron matter, since it directly reflects the behavior of the symmetry energy. In Figure 2, the pressure of pure neutron matter is plotted as a function of baryon density for several values of mixing term . In this figure, we also include the 1 and 2 constraints obtained from chiral effective field theoretical ab-initio calculations. Decreasing the slope of the symmetry energy at saturation density has a noticeable effect on the EoS, which becomes much softer at a density above fm. Only models with L = 79.5 MeV ( = 0.0) and 67.8 MeV ( = 0.1) miss the chEFT constraints. However, the model with L = 56.2 MeV ( = 0.2) satisfies the 2 constraint and the models with L = 44.6 MeV and 32.9 MeV ( = 0.3 and 0.4) satisfy the 1 constraint.
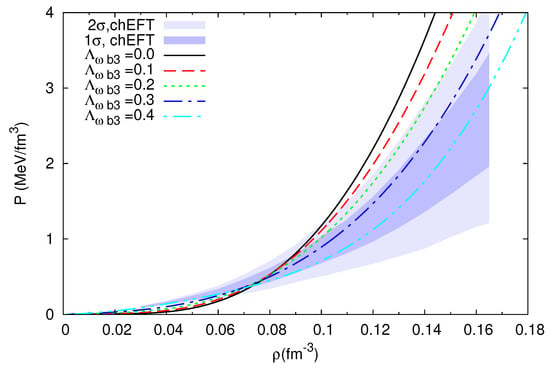
Figure 2.
The pure neutron matter pressure as a function of the baryonic density for several values of mixing term compared with chEFT neutron matter constraints. The dark and the light blue bands represent, respectively, the and the constraint from chEFT calculations [45].
In Figure 3, the fraction of different particles present inside a neutron star for baryonic densities below fm is plotted as a function of density for Bogoliubov QMC models with different values of slope L and . In panel (a), we show the results obtained including hyperons, and in panel (b), the results are restricted to npe matter. In panel (a), for MeV, the onset of hyperons occurs at , and the first hyperon to appear is , at a slightly larger density it is , and at about , it is . An increase in , which corresponds to a decrease in slope L, shifts the onset of these particles to higher densities, and for MeV, the onset of occurs at ∼ and above 6. Moreover, the fraction of -hyperons in the latter case never exceeds 10%, while at L = 79.5 MeV it reaches 20%. Concerning the hyperon onset, a similar behaviour in neutron star matter has been discussed in [21,46]. In panel (b), at subsaturation density, the proton fraction increases as L decreases. However, above saturation density, the proton fraction decreases from 30% for L = 79.5 MeV to 10% for MeV. Notice that a proton fraction below 1/9 does not allow the occurrence of direct Urca processes [47].
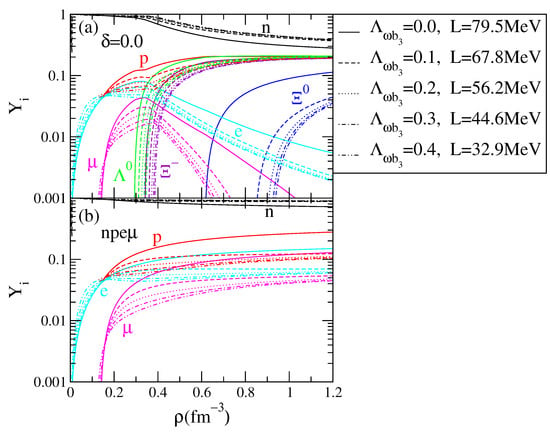
Figure 3.
Baryonic and leptonic particle fractions as a function of the baryonic density for the parameter (panel (a)) and npe matter (panel (b)), and several values of the mixing term : solid line , dashed line 0.1, dotted line 0.2, dash-dotted line 0.3, double-dotted dashed line 0.4.
In Figure 4, the fractions of baryons and leptons for equilibrium matter are represented as a function of density for and for . It was just discussed that for , the onset of hyperons occurs for , and the first hyperon to set in is and, at a slightly larger density, . A finite pushes the onset of these particles to larger densities, and for , the onset of occurs at ∼ and above 8. Besides the fraction of , in this last scenario, it never rises above 4%, while for , it reaches 20%. Above saturation density, the fraction of particles is significantly affected by the decrease in the symmetry energy slope, since the meson field is weaker for a smaller symmetry energy, and, consequently, the chemical potential of the neutrons is also smaller, favouring larger fractions of neutrons.
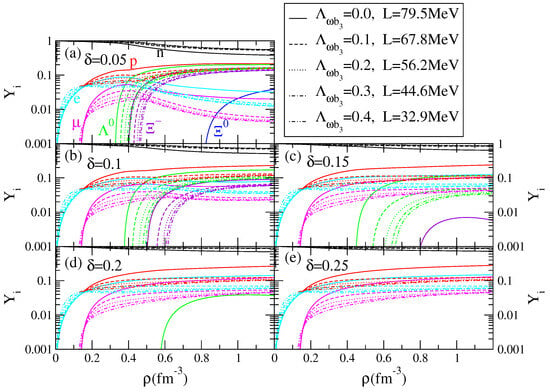
Figure 4.
Baryonic and leptonic particle fractions as a function of the baryonic density, for several values of parameter shown in panels (a–e); and for several values of the mixing term , solid line , dashed line 0.1, dotted line 0.2, dash-dotted line 0.3 double-dot dashed line 0.4. It was shown in ref. [28] that for , the onset of hyperons is shifted to densities above 1.2 fm. The central baryonic density lies between 0.9 and 1.1 fm, depending on hyperonic content.
In Figure 5, we show that different hyperons are affected differently by the symmetry energy. In this figure, the onset baryonic density of , and is plotted as a function of the symmetry energy slope L, where corresponds to L = 79.5 (32.9) MeV. The onset baryonic density increases with the parameter and always increases with the decrease in L, because the baryonic chemical potential decreases. The onset of occurs at quite large densities and, for the range of densities shown, it is present only for . is never the first hyperon to appear due to its large mass, although negatively charged hyperons are favored because they replace electrons keeping neutron star matter neutral. The onset of occurs at larger densities for smaller values of L and are present at baryonic densities below 1.2 fm only for and . Details about the onset density of the hyperons can be seen in Table 2.
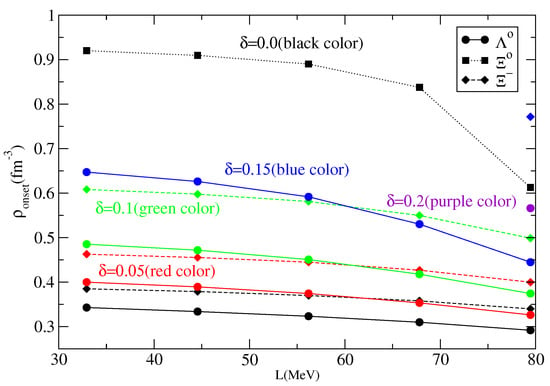
Figure 5.
Onset density of hyperon as a function of the slope L, for several values of parameter .

Table 2.
Onset density of each hyperon.
In order to study the influence of the density dependence of the symmetry energy on nucleonic direct Urca (DU) processes, i.e., processes that involve reactions and , we show, in Figure 6, the DU onset density as a function of the baryon density for several values of L. The DU process starts operating for L = 79.5 MeV at a density around fm for , fm for , and fm for . However, the DU process stops operating when L decreases, e.g., for L = 67.8 MeV; DU processes are allowed only at densities above fm. The symmetry energy is too small at high densities, preventing the nucleonic DU processes to operate; however, hyperonic direct Urca processes operate at densities just above the hyperon onset densities.
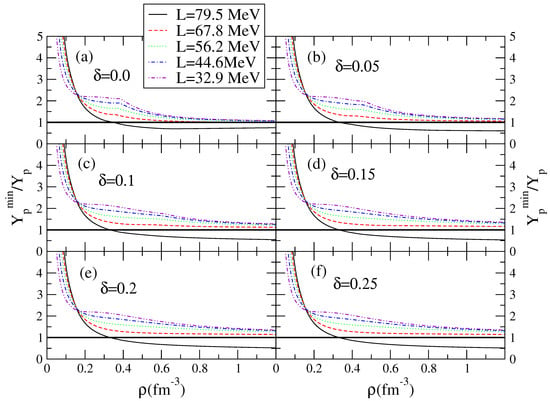
Figure 6.
Direct Urca process condition for several values of parameter and slope L.
In order to complete our study, we explore now the influence of the density dependence of the symmetry energy on the structure of neutron stars as described by the present model. We integrated the Tolman–Oppenheimer–Volkov equations for nonrotating spherical stars in equilibrium [48,49]. We obtained the total EoS by matching the Baym–Pethcik–Sutherland EoS for the outer crust [50], and for the inner crust, we used Thomas–Fermi’s description of nonhomogeneous matter for the NL3 model, with a symmetry energy slope at a saturation of 77 MeV [51], which corresponds to the core EoS. The complete EoS that has been used to integrate the TOV equations is plotted in the left panel of Figure 7. The pressure P obtained for different values of and is shown as a function of the energy density. The inclusion of hyperons softens the EoS as expected. When the parameter is turned on, the EoS becomes stiffer, and the EoS with almost coincides with the nucleonic EoS. However, when the coupling constant is turned on, we notice that the EoS becomes much softer at lower density and stiffer otherwise. Looking at the curve mass versus radius shown in the right panel of Figure 7, some conclusions may be drawn: The different scenarios of EoS considered in our model can describe NS with masses above 1.92 solar masses if parameter . For , the EoS and the M–R curve are almost insensitive to the value of . The onset of hyperons occurs at a density above ∼ fm and the hyperon fraction is too small. Reduction in the symmetry energy slope has a significant influence on the M–R curve. When the slope of symmetry energy L decreases, the maximum gravitational masses increases for and decreases slightly in the other cases, and the corresponding radii decrease; see Table 3. Our model satisfies the constraints coming from the astronomical observation of PSR J0740+6620 and PSR J0030+0451 by NICER [10,11,13,14], except for the case of , when the radii of a 2 are smaller than what the observations indicate within a 68% confidence interval.
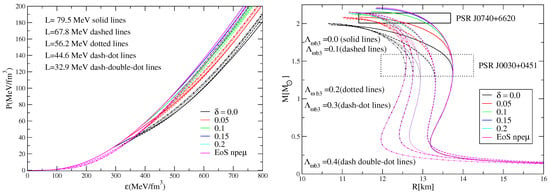
Figure 7.
EoS (left panel) and mass–radius curves obtained from the integration of the TOV equations (right), for different values of the parameter and several values of the mixing term . The curves stop at the maximum mass configuration. The family of stars for nucleonic stars constituted by matter is also represented. Also shown are the constraints from NICER observations of pulsars PSR J0740+6620 and PSR J0030+0451 [10,11,12,13,14].

Table 3.
Properties of the stable neutron star with maximum mass, for several values of and .
In Table 3, several star properties are given, including the maximum gravitational mass and the corresponding baryonic mass , radius R, energy density and baryonic density at the centre , and , the radius and the tidal deformability parameter of 1.4, 1.6 and 2.0 stars, , and , , and .
The canonical star with a mass of 1.4 has a radius of the order ling between 12.5 and 13.7 km, well within the values obtained by NICER [10,11] and other observations [52], and within or just slightly above the prediction obtained from the gravitational wave GW170817 [1,2] detected by LIGO/Virgo from a neutron neutron star merger [53,54,55].
We calculated the tidal deformability of a canonical star with a mass of 1.4 according to [56]. The result obtained was depending on the hyperon content and the slope of the symmetry energy, partially within the prediction of [57], where, depending on the waveform used in the analysis, and ≳ 100.
In Figure 8, we plot the gravitational mass as a function of the tidal deformability parameter for several values of slope L and . At first glance, we can see that QMC Bogoliubov models satisfy the constraint that GW190425 sets on the M- relations, and this for any and L. However, among all models, only the ones with L MeV satisfy the constraint that GW170817 sets on the tidal deformability as indicated by the blue horizontal bar in Figure 8. The QMC Bogoliubov models describe NS as massive as the pulsar MSP J0740+6620 [8], if a correct choice of parameters , which controls the SU(3) symmetry breaking, and , which controls the symmetry energy, is performed.
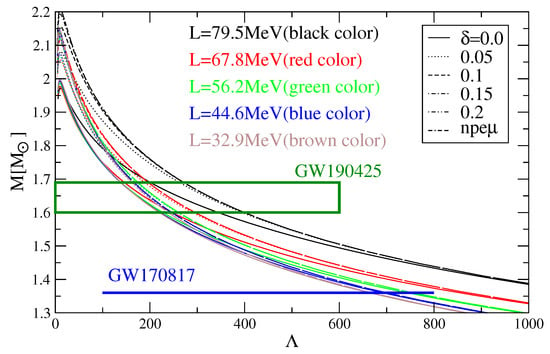
Figure 8.
Mass- curves for different values of and L. Two astronomical observation constraints are also shown, GW190425 and GW170817.
5. Conclusions
In the present study, we investigated the impact of the density dependence of the symmetry energy on the composition and the structure of neutron stars described by the QMC Bogoliubov model. To achieve this, we employed a modified version of the QMC Bogoliubov model which includes a nonlinear – coupling in the same way as it was proposed for the RMF nuclear models [37]. The effects of the medium are taken into account considering the coupling of quarks to meson fields. The mesonic fields are obtained by minimizing the thermodynamical potential. By ensuring that the model’s parameters are set appropriately, the description of saturation nuclear matter properties are in agreement with experimental results.
In the QMC Bogoliubov model, the up, down and strange quarks are considered as fundamental constituents, and baryons are described as composite particles. The interaction between quarks in the vacuum is characterized by a linear interaction and the parameters introduced at the quark level are fixed so that the vacuum constituent quark masses are reproduced. The vector isoscalar meson included to describe hadronic matter also includes s-quark content. Constraints imposed by neutron stars and hypernuclei require that the coupling of the meson to the s-quark must be more repulsive than its coupling to the u- and d-quarks, i.e., the SU(3) flavor symmetry has to be broken.
The additional nonlinear mesonic term between the two vector mesons has allowed the variation in the dependence of the symmetry energy on the baryon density, in particular the softening of the symmetry energy above the saturation density. This was essential to make the model compatible with ab-initio chEFT calculations of pure neutron matter [45]. It has been shown that smaller values of the slope of the symmetry energy at saturation offer rise to stars with smaller radii and tidal deformabilities, and in particular for L MeV, the tidal deformability of a 1.36 star is within the 90% credible interval obtained by the LVC [57]. These are also the models that agree with chEFT calculations. The softening of the symmetry energy further discourages the occurrence of hyperons in the interior of neutron stars. Another important effect is the non-appearance of nucleonic direct Urca processes when the slope is MeV. If parameter is small enough to allow the appearance of hyperons, there could still occur hyperonic direct Urca processes. However, if the parameter is chosen to describe the binding energy in hypernuclei, then no hyperons are allowed to nucleate in neutron stars and only modified Urca processes involving several nucleons are allowed. In conclusion, the QMC Bogoliubov model described here includes strange degrees of freedom, but if properties of nuclear matter and hypernuclei are properly described, hyperons do not nucleate inside neutron stars.
Author Contributions
Conceptualization, O.B. and A.R.; methodology, O.B. and A.R.; software, O.B. and A.R.; validation, O.B. and A.R.; formal analysis, O.B. and A.R.; investigation, O.B. and A.R.; resources, O.B. and A.R.; data curation, A.R.; writing—original draft preparation, A.R.; writing—review and editing, O.B. and A.R.; visualization, A.R.; supervision, O.B.; project administration, O.B. and A.R.; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by national funds from FCT (Fundação para a Ciência e a Tecnologia, I.P, Portugal) under the Projects No. UID/FIS/04564/2019, No. UID/04564/2020.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge Constança Providência for many interesting discussions, for helpful suggestions and carefully reading the manuscript. They are especially grateful for her hospitality at Universidade de Coimbra.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger*. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L.; Greif, S.K.; Morsink, S.M.; Hebeler, K.; Schwenk, A.; Hinderer, T.; Nissanke, S.; Guillot, S.; et al. A NICER view of PSR J0030+0451: Implications for the dense matter equation of state. Astrophys. J. Lett. 2019, 887, L22. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Baldo, M.; Buballa, M.; Burgio, F.; Neumann, F.; Oertel, M.; Schulze, H.J. Neutron stars and the transition to color superconducting quark matter. Phys. Lett. B 2003, 562, 153–160. [Google Scholar] [CrossRef]
- Vidana, I.; Logoteta, D.; Providencia, C.; Polls, A.; Bombaci, I. Estimation of the effect of hyperonic three-body forces on the maximum mass of neutron stars. EPL 2011, 94, 11002. [Google Scholar] [CrossRef]
- Bednarek, I.; Haensel, P.; Zdunik, J.L.; Bejger, M.; Mańka, R. Hyperons in neutron-star cores and a 2 M⊙ pulsar. A&A 2012, 543, A157. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and strangeness. Nucl. Phys. A 2013, 914, 421–426. [Google Scholar] [CrossRef]
- Colucci, G.; Sedrakian, A. Equation of state of hypernuclear matter: Impact of hyperon-scalar-meson couplings. Phys. Rev. C 2013, 87, 055806. [Google Scholar] [CrossRef]
- Providência, C.; Rabhi, A. Interplay between the symmetry energy and the strangeness content of neutron stars. Phys. Rev. C 2013, 87, 055801. [Google Scholar] [CrossRef]
- van Dalen, E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with λ hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef]
- Fortin, M.; Providência, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef]
- Malik, T.; Providência, C. Bayesian inference of signatures of hyperons inside neutron stars. arXiv 2022, arXiv:2205.15843. [Google Scholar] [CrossRef]
- Bogolioubov, P.N. Sur un modèle à quarks quasi-indépendants. Ann. l’IHP Phys. Théorique 1968, 8, 163. [Google Scholar]
- Bohr, H.; Moszkowski, S.A.; Panda, P.K.; Providência, C.; da Providência, J. QMC approach based on the Bogoliubov independent quark model of the nucleon. Int. J. Mod. Phys. E 2016, 25, 1650007. [Google Scholar] [CrossRef]
- Panda, P.K.; Providência, C.; Moszkowski, S.A.; Bohr, H.; da Providência, J. Hyperonic stars within the Bogoliubov quark meson model for nuclear matter. Int. J. Mod. Phys. E 2019, 28, 1950034. [Google Scholar] [CrossRef]
- Rabhi, A.; Providência, C.; Moszkowski, S.A.; da Providência, J.A.; Bohr, H. Neutron stars within the Bogoliubov quark-meson coupling model. Phys. Rev. C 2021, 103, 035811. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Ayerbe Gayoso, C.; Barcus, S.K.; Bellini, V.; Beminiwattha, R.S.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Ayerbe Gayoso, C.; Barcus, S.K.; Bellini, V.; Beminiwattha, R.S.; et al. Precision Determination of the Neutral Weak Form Factor of Ca48. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef]
- Reinhard, P.G.; Roca-Maza, X.; Nazarewicz, W. Combined Theoretical Analysis of the Parity-Violating Asymmetry for Ca48 and Pb208. Phys. Rev. Lett. 2022, 129, 232501. [Google Scholar] [CrossRef] [PubMed]
- Mondal, C.; Gulminelli, F. Nucleonic metamodeling in light of multimessenger, PREX-II, and CREX data. Phys. Rev. C 2023, 107, 015801. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Density Dependence of the Symmetry Energy in the Post PREX-CREX Era. arXiv 2022, arXiv:2305.19376. [Google Scholar]
- Yakovlev, D.G.; Pethick, C.J. Neutron star cooling. Ann. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron star structure and the neutron radius of Pb-208. Phys. Rev. Lett. 2001, 86, 5647. [Google Scholar] [CrossRef] [PubMed]
- Carriere, J.; Horowitz, C.J.; Piekarewicz, J. Low mass neutron stars and the equation of state of dense matter. Astrophys. J. 2003, 593, 463–471. [Google Scholar] [CrossRef]
- Cavagnoli, R.; Menezes, D.P.; Providencia, C. Neutron star properties and the symmetry energy. Phys. Rev. C 2011, 84, 065810. [Google Scholar] [CrossRef]
- Gal, A.; Hungerford, E.V.; Millener, D.J. Strangeness in nuclear physics. Rev. Mod. Phys. 2016, 88, 035004. [Google Scholar] [CrossRef]
- Glashow, S.L. ϕω Mixing. Phys. Rev. Lett. 1963, 11, 48. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Providência, C.; Fortin, M.; Pais, H.; Rabhi, A. Hyperonic stars and the symmetry energy. arXiv 2018, arXiv:1811.00786. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M.; Pethick, C.J.; Haensel, P. Direct URCA process in neutron stars. Phys. Rev. Lett. 1991, 66, 2701–2704. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The ground state of matter at high densities: Equation of state and stellar models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Pais, H.; Providência, C. Vlasov formalism for extended relativistic mean field models: The crust-core transition and the stellar matter equation of state. Phys. Rev. C 2016, 94, 015808. [Google Scholar] [CrossRef]
- Haensel, P.; Bejger, M.; Fortin, M.; Zdunik, L. Rotating neutron stars with exotic cores: Masses, radii, stability. Eur. Phys. J. A 2016, 52, 59. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).