Abstract
Infinite nuclear matter is a suitable laboratory to learn about nuclear forces in many-body systems. In particular, modern theoretical predictions of neutron-rich matter are timely because of recent and planned experiments aimed at constraining the equation of state of isospin-asymmetric matter. For these reasons, we have taken a broad look at the equation of state of neutron-rich matter and the closely related symmetry energy, which is the focal point of this article. Its density dependence is of paramount importance for a number of nuclear and astrophysical systems, ranging from neutron skins to the structure of neutron stars. We review and discuss ab initio predictions in relation to recent empirical constraints. We emphasize and demonstrate that free-space nucleon–nucleon data pose stringent constraints on the density dependence of the neutron matter equation of state, which essentially determines the slope of the symmetry energy at saturation.
1. Introduction
Although infinite nuclear matter is an idealized system, its equation of state (EoS) is a powerful tool for exploring nuclear interactions in the medium. Asymmetric nuclear matter is characterized by the degree of neutron excess, all the way to pure neutron matter. Because neutrons do not form a bound state, the presence of excess neutrons in a nucleus reduces the binding energy; that is, it is a necessary but destabilizing effect that gives rise to the symmetry energy. As a consequence, neutron-rich structures have common features that explain the formation of a neutron skin (in isospin-asymmetric nuclei) or how neutron stars are supported against gravitational collapse by the outward pressure existing in dense systems with high neutron concentrations. Studies of nuclear interactions in systems with high or extreme neutron-to-proton ratios are crucial for understanding the neutron driplines, the location of which is not well known. The new Facility for Rare Isotope Beams (FRIB), operational since May 2022, is expected to increase the number of known rare isotopes from 3000 to about 6000 [1].
For many years, several groups have sought constraints on the density dependence of the symmetry energy. Intense experimental effort has been and continues to be devoted to this question using various measurements, which are typically analyzed with the help of correlations obtained through different parametrizations of phenomenological models. Popular examples are the Skyrme forces (refs. [2,3,4] are only a few of the many review articles on the Skyrme model), and relativistic mean-field models (RMF) [5,6,7]. Papers such as [8,9] are representative examples for applications of Skyrme forces or RMF models, respectively, to the issues confronted in this article. A cross-section of studies where phenomenological and theoretical models or laboratory data were used to extract constraints on the density dependence of the symmetry energy can be found in refs. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Generally, the extracted constraints vary considerably depending on the methods employed.
During the past two decades, there has been remarkable progress in understanding nuclear forces at a fundamental level, through the concept of effective field theories (EFT) [31,32]. Meson theoretic or entirely phenomenological models of the nucleon–nucleon () interaction, augmented with phenomenological few-nucleon forces, were the typical framework used in the past. At the forefront are state-of-the-art ab initio predictions, which generally agree on a relatively soft symmetry energy, in contrast to recent constraints extracted from electroweak scattering experiments [33], as we will discuss later in the paper.
The density dependence of the symmetry energy is also a major component in the physics of neutron stars, in particular, the radius of a medium-mass neutron star. Of course, a very large range of densities can be found in a neutron star, from the density of iron in the outer crust up to several times normal nuclear density in the core, and thus no theory of hadrons can be applicable over the entire region. With that in mind, state-of-the-art ab initio theories of nuclear and neutron matter can be taken as the foundation for any extension method, which will unavoidably involve some degree of phenomenology. Note, though, that the radius of a 1.4 M neutron star is sensitive to the pressure in neutron matter around saturation, and thus it is useful to constrain microscopic theories of the EoS at those densities where the theories are reliable [34]. In fact, the radius of light to medium neutron stars has been found to correlate with the density slope of the symmetry energy at saturation, with correlation coefficient of 0.87 for M = 1.0 M and 0.75 for M = 1.4 M [35].
In this article, we will start with a broad introduction to the symmetry energy and its relevance. To that end, we will briefly review the link between finite nuclei and infinite nuclear matter as it emerges from the liquid drop model. In the process, one defines the energy per nucleon in infinite (isospin-symmetric or asymmetric) matter and the all-important symmetry energy. In Section 3, we describe our theoretical tools, which include high-quality microscopic nuclear forces derived within the framework of chiral EFT. We also take the opportunity to review the foundations and main aspects of chiral EFT. In Section 4, after a brief discussion of symmetric nuclear matter (SNM) in Section 4.1, we focus on the neutron matter (NM) EoS and the symmetry energy (Section 4.2). A focal point of this section is a comparison of ab initio predictions with phenomenological and empirical findings. We include a discussion of the neutron skin (see Section 4.3), and its sensitivity to the density slope of the symmetry energy at saturation. Section 5 reports test calculations designed to underline the sensitivity of the discussed predictions to free-space scattering phases. In Section 6, we reiterate the scope of this article and summarize our conclusions. Also, we wish to reflect on the best way forward to strengthen what should be our most powerful tool—the link between experiment and ab initio theory.
2. Symmetry Energy: General Aspects
We begin with a pedagogical introduction to establish the main concepts and definitions.
The simplest picture of the nucleus goes back to the semi-empirical mass formula (SEMF), also known as the liquid–droplet model. Its ability to capture basic bulk features of nuclei is remarkable in view of its simplicity. The binding energy per nucleon is written in terms of a handful of terms inspired by the dependence of nuclear radii on the cubic root of the mass number A:
where the last term stands for additional, typically smaller, contributions. Note that the second term on the RHS depends on the relative neutron-proton asymmetry, or isospin asymmetry, , and represents the loss of binding energy experienced by a nucleus due to the destabilizing presence of asymmetry in neutron/proton concentrations. Of course, Equation (1) is the simplest picture of a nucleus but can be improved by replacing the number of nucleons A and the number of protons Z with the respective density profiles.
To that end, we introduce the energy per nucleon, , in an infinite system of nucleons at density and isospin asymmetry —namely, the EoS of neutron-rich matter—and expand this quantity with respect to the isospin asymmetry parameter:
Neglecting terms of order , Equation (2) takes the well-known parabolic form:
where = and , the EoS of isospin-symmetric nuclear matter.
With the SEMF as a guideline, one can write the main contributions to the total energy of a given nucleus (Z, A) with proton and neutron density profiles and , respectively, as:
where is a constant typically fitted to -stable nuclei. Note that the second term on the RHS, dependent on the gradient of the density function, is a finite-size contribution: the surface term proportional to the coefficient in Equation (1). The last term on the RHS stands for the Coulomb interaction among protons. The link to Equation (1) is apparent. In particular, the first integral on the RHS of Equation (4) comprises the first two terms on the RHS of Equation (1).
Within the parabolic approximation (Equation (3)), the symmetry energy becomes the difference between the energy per neutron in NM and the energy per nucleon in SNM:
where , the energy per neutron in pure neutron matter.
The minimum of at a density approximately equal to the average central density of nuclei, , is a reflection of the saturating nature of the nuclear force. Next, we expand the symmetry energy about the saturation point:
which helps identify several useful parameters. L is known as the slope parameter, as it is a measure of the slope of the symmetry energy at saturation:
Furthermore, it is clear from Equations (5) and (7), recalling that the SNM EoS has vanishing derivative at that point, that L measures the degree of “stiffness” of the NM EoS at saturation density.
The parameter characterizes the curvature of the symmetry energy at saturation density:
Note that a similar expansion of the energy per particle in SNM identifies the quantity
as a measure of the curvature of the EoS in SNM.
Using the standard thermodynamic relation,
where P is the pressure and e is the energy per particle, we define the symmetry pressure as
If the derivative is evaluated at or very near , the symmetry pressure is essentially the pressure in NM because the pressure in SNM vanishes at saturation. Then:
From Equations (7) and (12), it is clear that the slope parameter L is a measure of the pressure in NM around saturation density:
showing that the pressure in NM is proportional to the slope of the symmetry energy at normal density. The value of L is then a measure of the pressure gradient acting on excess neutrons and pushing them outward from the neutron-enriched core of the nucleus to the outer region, thus determining the formation and size of the neutron skin.
3. Theoretical Tools
3.1. Energy per Nucleon in Infinite Matter
To calculate the energy per nucleon in nuclear or neutron matter, we use the nonperturbative particle–particle ladder approximation, which generates the leading-order terms in the hole–line expansion of the energy per particle. Next in the expansion are the three hole–line contributions, which include the third-order particle–hole (ph) diagram studied in ref. [36]. Those were found to bring in an uncertainty of about 1 MeV on the potential energy per particle at normal density. The third-order hole–hole (hh) diagram has a very small effect on the energy per particle at normal density (see Tables II and III of ref. [36]).
We compute the single-particle spectrum self-consistently. The Bethe–Goldstone (or Brueckner) equation for two particles having center-of-mass momentum , initial relative momentum , and starting energy in nuclear matter with Fermi momentum is
where the Pauli operator, Q, has been angle-averaged, and V is the potential augmented with effective three-nucleon forces (3NFs) as density dependent potentials, to be discussed in Section 3.4. When calculating the single-particle potential, U, one must recall that, in order to avoid double-counting, a factor of must be applied to the density-dependent part of V at the Hartree–Fock level [37]:
where, again, the first term on the right-hand side is the actual potential and the second one is a density-dependent effective 3NF.
Using partial wave decomposition, Equation (14) can be solved for each partial wave using standard matrix inversion techniques. Note that the single-particle energy, , contains the single-particle potential, U, yet to be determined. Because the G-matrix depends on U and U depends on G, an iteration scheme is applied to obtain a self-consistent solution for U and G, which are related as
where are single-particle momenta. Starting from some initial values and a suitable parametrization of the single-particle potential, a first solution is obtained for the G-matrix, which is then used in Equation (16). The procedure continues until convergence to the desired accuracy. A diagrammatic representation of the G-matrix equation in the ladder approximation is shown in Figure 1.
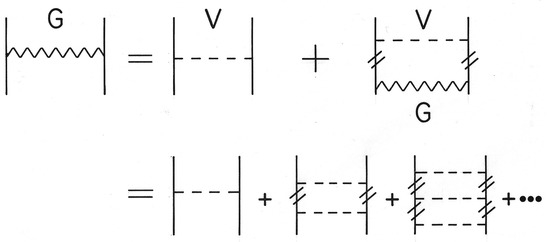
Figure 1.
Diagrammatic representation of the Brueckner integral equation. Intermediate nucleon lines with the double slash represent in-medium particle states.
The energy per nucleon is then evaluated as
where the averages of the single-nucleon kinetic () and potential () energies are taken over the Fermi sea.
Next, we give a short review of the main principles and advantages of chiral effective field theory (EFT) and describe the input two-nucleon forces (2NFs) and 3NFs which we employ.
3.2. Chiral Effective Field Theory
Chiral EFT [31,32] allows for the development of nuclear interactions as an expansion where theoretical uncertainties can be assessed at each order. The organizational scheme that controls the expansion is known as “power counting”.
Chiral EFT is linked to the underlying fundamental theory of strong interactions, quantum chromodynamics (QCD), via the symmetries and symmetry-breaking mechanisms of the low-energy QCD Lagrangian. The development of an EFT starts with the identification of a “soft scale” and a “hard scale”. For this purpose, guidance can be found in the hadron spectrum, observing the large separation between the mass of the pion and the mass of the vector meson . It is therefore natural to identify the pion mass and the mass (approximately 1 GeV) with the soft and the hard scale, respectively. Moreover, since quarks and gluons are ineffective degrees of freedom in the low-energy regime, pions and nucleons can be taken as the appropriate degrees of freedom of the EFT.
The link between QCD and the EFT is established through the symmetries of low-energy QCD. Following the prescriptions of the theory as thoroughly reviewed in ref. [38], we begin with the QCD Lagrangian:
where q is the quark field, the gauge covariant derivative, the quark mass matrix, and the gluon strength field tensor, with a the color index. Note that quark indices (for spin, color, and flavor) have been suppressed.
Chiral symmetry is conservation of “handedness,” an exact symmetry for massless particles. Thus, the presence of the quark mass matrix term in the above Lagrangian breaks chiral symmetry; this is the mechanism of explicit symmetry breaking. The quark mass matrix in flavor space,
can be written in terms of the identity matrix and the Pauli spin matrix :
showing that the first term respects isospin symmetry, while the second term vanishes if the masses of the “up” (u) and “down” (d) quarks are equal. We recall that, for massless quarks, the right- and left-handed components do not mix: the symmetry or chiral symmetry. As noted above, the expression in Equation (20) breaks chiral symmetry explicitly as a result of the non-zero quark masses. Thus, the small difference in the quark masses breaks isospin symmetry. However, since the masses of the u and d quarks are very small compared to typical hadronic masses, explicit breaking of chiral symmetry is a small effect. We will remain in the lightest quark sector, u and d, as appropriate in a theory of pions and nucleons. QCD with three flavors of light quarks, u, d, s, displays global flavor symmetry in the limit of massless quarks. The masses of the heavier quarks are much larger than the QCD spontaneus chiral symmetry breaking scale and thus cannot be treated as a small perturbation around the symmetry limit.
Next, we need to address the spontaneous breaking of chiral symmetry, for which there is clear evidence in the hadron spectrum. The spontaneous breaking of a global symmetry is accompanied by the appearance of a massless boson, referred to as a “Goldstone Boson”. The particle that fulfills these requirements is the pion, an isospin triplet pseudoscalar boson. The pion is light relative to the other mesons in the hadron spectrum but not massless, which is due to the explicit chiral symmetry breaking from the non-vanishing quark masses.
A quick review of the spontaneous symmetry breaking (SSB) mechanism may be useful to the reader. The main point is that the state of a system (say, the ground state) does not necessarily have the symmetries of the theory from which the state is derived. In the QCD case, a conserved quantity with negative parity (the axial charge, ) would lead to the expectation that a hadron of positive parity exists for every hadron of negative parity. Inspection of the hadron spectrum reveals that such symmetry—the existance of degenerate doublets of opposite parity—is indeed violated. The vector meson with negative parity, , cannot be the “chiral partner” of the meson, which has a mass of 1230 MeV. We recall, however, that the meson exists in three charge (isospin) states, with masses differing by only a few MeV. Therefore, isospin symmetry () is observed in the hadron spectrum, whereas axial symmetry, , is broken. The spontaneous breaking of a global symmetry generates massless Goldstone bosons, which must have the quantum numbers of the broken symmetry generators, the pseudoscalar , and are therefore identified with the isospin triplet of the pseudoscalar pions.
Having identified pions and nucleons as the effective degrees of freedom of the EFT, one can proceed to construct the Lagrangian of the effective theory:
which is then expanded in terms of a natural parameter, the ratio of the “soft scale” over the “hard scale”, , where p is of the order of the soft scale, whereas is the energy scale of chiral symmetry breaking, approximately 1 GeV. See, however, Section 3.2.1 below for additional comments on the meaning of the chiral symmetry breaking scale, the breakdown scale, and the ultraviolet cutoff applied in calculations with nucleons. The contributions to the effective Lagrangian are arranged according to the power counting scheme, with increasing order resulting in smaller terms. While the expansion itself is, of course, infinite, at each order we are assured that the number of terms is finite and the contributions well defined.
Each order of the chiral expansion is identified with the maximum power of the expansion parameter, , denoted by . Note that p in the chiral perturbation expansion stands for the typical value of the momentum in the system under consideration. The first order is dubbed the Leading Order, or “LO,” being equivalent to the power = 0. Terms with = 1 vanish, as they would violate conservation of parity. The next power in the expansion ( = 2) generates the Next-to-Leading-Order (NLO) terms; = 3 gives the Next-to-Next-to-Leading-Order (NLO), and so on. At the first two orders of the chiral expansion, only 2NFs are generated, while 3NFs appear for the first time at NLO.
To summarize, symmetries relevant to low-energy QCD, in particular chiral symmetry, are incorporated in the EFT, which is therefore a low-energy realization of the strong interaction having the global symmetries of QCD. Thus, there is a solid connection with the fundamental theory of strong interactions, even though the degrees of freedom are pions and nucleons instead of quarks and gluons. Following a power counting scheme in which the progression of 2NFs and 3NFs is constructed in a systematic and internally consistent manner, the inconsistencies inherent to meson-theoretic or phenomenological forces are eliminated. Next, we discuss how chiral EFT allows for control of truncation error on an order-by-order basis.
3.2.1. Quantifying Errors in Chiral EFT
A reliable determination of the truncation error is a crucial aspect of chiral EFT. If observable X has been calculated at order and at order , a simple estimate of the truncation error at order is
which is a measure for what is neglected at order . A suitable prescription is needed to estimate the uncertainty at the highest (included) order. For that purpose, we follow the prescription of ref. [39]. If p is of the order of the typical momentum involved in the system, the dimensionless parameter Q is defined as the largest between and , where is the breakdown scale, taken to be about 600 MeV [39]. Before proceeding, some comments are in place to avoid confusion. In the pion–nucleon sector, it is natural to set the scale to the chiral symmetry breaking scale, , about 4 1 GeV, where is the pion decay constant, equal to 92 MeV (see ref. [21] of ref. [39]). However, in the nucleon sector, it is common practice to apply a so-called breakdown scale, , chosen around 600 MeV. This scale is smaller than because the non-perturbative resummation, necessary for nucleons, fails for momenta larger than approximately 600 MeV.
The uncertainty in the value of observable X at NLO as derived in ref. [39] can be understood with the following arguments. If NLO ( = 4) is the highest included order, the expression
is a reasonable estimate for in absence of the value , because Q to the power of 1 takes the error up by one order, the desired fourth order. To avoid accidental underestimations, a more robust prescription is to proceed in the same way for all the lower orders ( = 0, 2, 3) and define, at NLO,
In infinite matter, p can be identified with the Fermi momentum at the density being considered.
Cutoff variations have sometimes been used to estimate contributions beyond truncation. However, they do not allow for estimation of the impact of neglected long-range contributions. Also, due to the intrinsic limitations of the EFT, a meaningful cutoff range is hard to estimate precisely, and often very limited. The method of Equation (24) allows us to determine truncation errors from predictions at all lower orders, without the need to use cutoff variations.
3.3. The Two-Nucleon Force
The 2NFs we employ are part of a set of potentials from leading order (LO) to fifth order (NLO) [40]. The long-range contributions are fixed by the low-energy constants (LECs) determined very accurately in the analysis of ref. [41,42]. Those carry very small uncertainties, as seen from Table II of ref. [40], rendering variations in the LECs unnecessary when estimating the overall uncertainty in applications of the potential. At the fifth order, the data below pion production threshold are reproduced with high precision (/datum = 1.15).
Our G-matrix calculation requires iteration of the potential in the non-perturbative Lippmann–Schwinger equation, and thus high-momentum components must be suppressed. To that end, we apply a regulator function for which we take the non-local form
where and are the final and initial nucleon relative momenta, respectively. The integer n is the exponent of the regulator and is given in Table 1. We use = 450 MeV throughout this work, which is reasonable, since it is smaller than the breakdown scale, 600 MeV. The potentials we use are relatively soft, which was confirmed by a Weinberg eigenvalue analysis [43] and perturbative calculations of infinite matter [44]. In NM, we use the neutron–neutron versions of these potentials.

Table 1.
The LECs used in our calculations. n is the exponent of the regulator, Equation (25). The LECs are given in units of GeV, and and are in units of GeV.
3.4. The Three-Nucleon Force
Three-nucleon forces appear at the third order (NLO) of the -less EFT. The leading 3NF includes [45]: the long-range two-pion-exchange (2PE), the medium-range one-pion-exchange (1PE), and a short-range contact interaction. In infinite matter, the 3NF can be approximately expressed as density-dependent effective potentials [46,47] which can be incorporated in the usual partial wave formalism.
The effective 3NF at NLO consist of six one-loop topologies. Of those, three originate from the 2PE part of the chiral 3NF and depend on the LECs , already present in the 2PE part of the potential. Two one-loop topologies originate from the 1PE diagram of the chiral 3NF and depend on . The one-loop contribution arising from the 3NF contact diagram depends on the LEC . Figure 2 shows the diagrams of the leading 3NF. The contributions depending on the LECs and are absent in neutron matter [48].
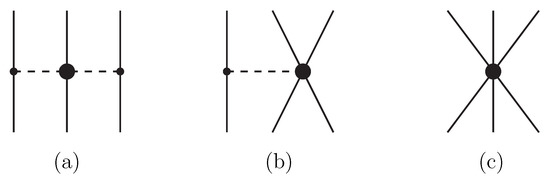
Figure 2.
Diagrams of the leading 3NF: (a) the long-range 2PE, depending on the ; (b) the medium-range 1PE, involving ; and (c) the short-range contact, proportional to .
The 3NF at NLO was derived in refs. [49,50]. The long-range part includes: the 2PE topology (Figure 3a), the two-pion–one-pion exchange (2P1PE) topology (Figure 3b), and the ring topology (Figure 3c), representing a pion absorbed and re-emitted from each of the three nucleons. The 2PE component is the longest-range part of the subleading 3NF. The in-medium potentials representing the long-range subleading 3NFs were derived in Ref. [51] for SNM and in ref. [52] for NM. The short-range subleading 3NF includes the following topologies: the one-pion–exchange-contact (1P-contact), Figure 3d, which gives a vanishing net contribution, the two-pion–exchange-contact (2P-contact), Figure 3e, and relativistic corrections, proportional to , where M is the nucleon mass. The relativistic corrections depend on the and the LECs present in the 2NF. We include those contributions and find them to be very small: a fraction of 1 MeV in the energy per nucleon. The in-medium potentials representing the short-range subleading 3NFs can be found in ref. [53] for SNM and in ref. [54] for NM.
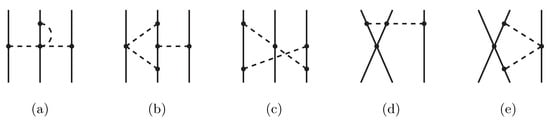
Figure 3.
Selected diagrams of the subleading 3NF, each representative of a specific topology: (a) 2PE; (b) 2P1PE; (c) ring; (d) 1P-contact; (e) 2P-contact.
The LECs we use, which appear already in the 2NF, are displayed in Table 1. We recall the and are determined through the fit of the contact terms in the potential [40]. The and LECs vanish in NM. Their values for SNM are taken from ref. [55].
Note that when the subleading 3NFs are included, the and LECs are shifted to −1.20 GeV and −4.43 GeV, respectively. The reason is that most of the subleading 2PE 3NF can be taken into account by shifting the LECs in the leading 3NF to −0.13 GeV and 0.89 GeV, for and , respectively [49], plus additional terms resulting from Equation (1) of ref. [52].
4. Ab Initio Predictions in Infinite Matter
We perform order-by-order calculations, including all subleading 3NFs up to NLO and with uncertainty quantification as from Equation (24). Our calculations being complete at each order, we can draw reliable conclusions regarding the convergence pattern of the chiral perturbation series up to NLO.
4.1. Symmetric Nuclear Matter
Although this article is mostly about isospin-asymmetric systems, for completeness, we include a short section about SNM, an important laboratory for testing many-body theories. Recently, challenges with simultaneous description of masses and radii of medium-mass nuclei has brought SNM saturation properties to the forefront of contemporary ab initio nuclear structure [56].
To evaluate the truncation error for the saturation parameters using Equation (24), one could take the standard value, say = 0.16 fm, for all orders. Because the EoS at LO and NLO do not exhibit a saturating behavior, it may be more appropriate to use the actual saturation densities for the EoS that include 3NFs, namely, those that do saturate. It would not be very meaningful to evaluate, for instance, the incompressibility, which measures the curvature of the EoS at the minimum, if such minimum is absent. Estimating, pessimistically, the truncation error at NLO as , we obtain the values displayed in Table 2 [57]. Adopting, instead, the prescription , where p is the Fermi momentum at saturation density, the errors would be reduced by about 44%. In Figure 4, we show the predictions at NLO with the uncertainty band calculated from Equation (24). The LECs and are equal to 0.50 and −1.25, respectively, and are taken from ref. [44]. For comparison, we display saturation properties for the final posterior predictive distribution (PPD) from ref. [58] (see Table 2).

Table 2.
Predictions for the saturation properties of SNM from the final PPD of ref. [58]. Shown are the medians, 68% credible regions (CR), and 90% CR. The last column contains our predictions [57]. The energy per nucleon, E/A, and the incompressibility, K, are in units of MeV. The saturation density, , is in units of fm.
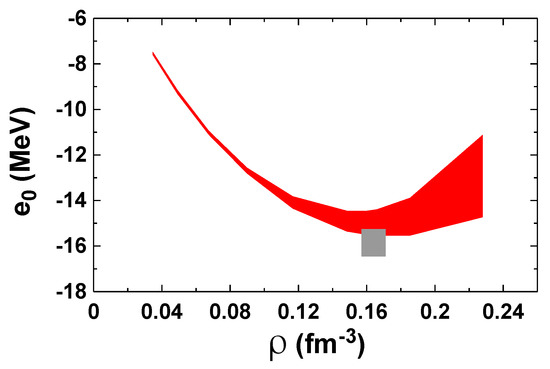
Figure 4.
Energy per nucleon in SNM vs. density at the fourth order of chiral perturbation theory. The band signifies the uncertainty calculated from Equation (24). The grey box marks the empirical saturation point, consistent with refs. [22,48] in ref. [44].
4.2. Neutron Matter and the Symmetry Energy
As mentioned earlier, the formation of the neutron skin in neutron-rich nuclei is a fascinating phenomenon. It is the result of excess neutrons forced outward by the neutron-rich core of the nucleus, which effectively amounts to a pressure gradient that moves some of the excess neutrons to the outskirts of the nucleus. Although it is a small contribution relative to the size of the nuclear radius, the neutron skin contains important information about nucleon interactions in a strongly isospin-asymmetric environment.
The EoS of neutron-rich matter plays a major role in nuclear astrophysics. Neutron stars are natural laboratories for constraining theories of the EoS in neutron-rich matter, to which the star mass–radius relationship is sensitive. Interest in these compact stars has grown with the onset of the “multi-messenger era” for astrophysical observations. We will start with discussing predictions based on chiral EFT [59].
In Figure 5, we show our predictions for the energy per neutron in NM over four chiral orders. The large variations between NLO and NLO are in large part due to the first appearance of 3NFs at NLO. The predictions at NLO show a slight increase in attraction with respect to those at NLO, in agreement with other calculations [60]. Our NM EoS is on the soft side of the large spectrum of EoS found in the literature, with a correspondingly soft density dependence of the symmetry energy, as can be seen from Figure 6. This feature is generally true for predictions based on chiral EFT.
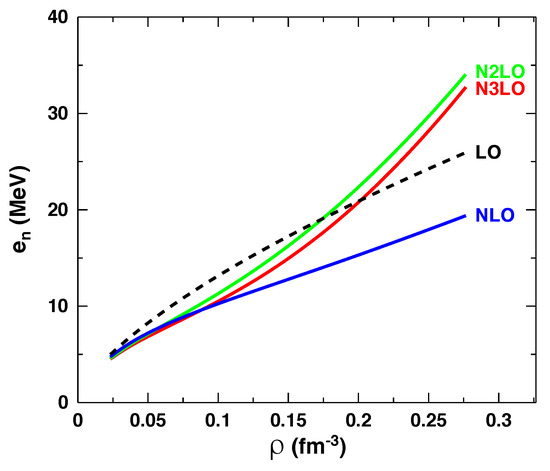
Figure 5.
(Color online) Energy per neutron in NM vs. density, from leading (black dashes) to fourth order (solid red).
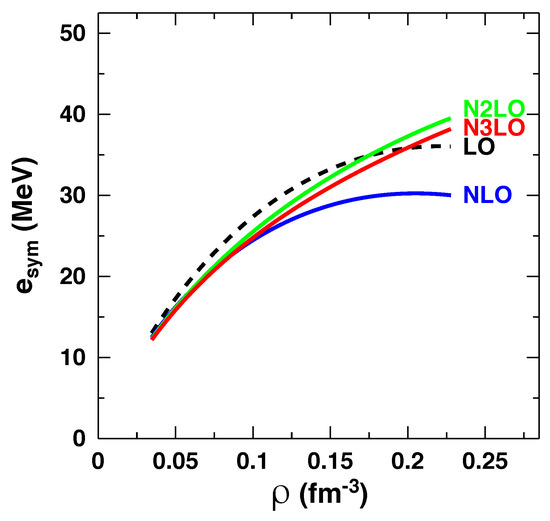
Figure 6.
(Color online) The symmmetry energy vs. density, from leading (black dashes) to fourth order (solid red).
For the purpose of the present discussion, we replace the EoS of SNM with an empirical parametrization [61] that produces values for the energy per nucleon (−16.0 MeV) and the saturation density ( = 0.155 fm) consistent with the traditionally cited empirical saturation point. We emphasize that our motivation is to spotlight the energy and pressure in neutron matter and their impact on the symmetry energy while the isoscalar properties do not change. Semi-empirical constraints for the symmetry energy are typically obtained by constructing sets of parametrized model EoS which differ, sometimes quite broadly, in their values of L while remaining otherwise equivalent. Under these circumstances, the linear relation between L and the neutron skin thickness is observed. Therefore, the comparisons we explore in this section are more meaningful if we remove additional uncertainties arising, for instance, from the sensitivity of the theoretical SNM EoS to the , LECs. Varying simultaneously isoscalar properties would mask what we wish to highlight.
A large spectrum of phenomenological analyses suggest that typical values for L fall within 70 ± 15 MeV [20,62,63,64,65,66]. This is not in agreement with the findings from the recent PREX-II experiment [33]: = (38.29 ± 4.66) MeV and L = (109.56 ± 36.41) MeV, for the symmetry energy and its slope at saturation, respectively, also at variance with a large number of results based on experimental measurements.
In Table 3 we show some of our predictions at NLO with their truncation errors: the energy per neutron and the symmetry energy at saturation, the slope parameter as defined in Equation (7), and the pressure in NM. As already observed, the softer nature is common to most chiral predictions. A comparison with phenomenological interactions of the past, such as Argonne V18 augmented the UIX 3NF [67], can be found in ref. [68]. A more recent analysis [69] reports values for and L of (31.7 ± 1.1) MeV and (59.8 ± 4.1) MeV, respectively.

Table 3.
The energy per neutron, the symmetry energy, the L parameter, and the pressure at NLO at selected densities, , in units of = 0.155 fm. L is defined in Equation (7) and calculated at the specified density. The values in parentheses are from ref. [66]. The constraint for L in the third row () applies to = 0.1 fm. The constraint at is from ref. [70].
We observe that the values in the first row of Table 3—approximately L = (50 ± 10) MeV, and pressure at in the order of 2–3 MeV/fm—differ considerably from those resulting from the PREX-II experiment. The PREX-II value of the pressure at is approximately between 3.66 MeV/fm and 7.30 MeV/fm. Such a stiff symmetry energy would allow rapid cooling of the star through direct Urca processes to proceed at atypically low values of the neutron star mass and central density [33], which seems unlikely [71]. On the other hand, the proton fraction we obtain is close to 6% at 0.2 fm, still considerably smaller than the direct Urca threshold, about 1/9 [72].
Before we take a short detour towards neutron stars, we wish to emphasize that no theory of hadrons can describe neutron star matter from outer crust to inner core. However, the normal density region is relevant for the physics of neutron stars, given the sensitivity of the radius to the slope parameter L for star masses around 1.4 solar masses.
We recall that the direct Urca process is the fastest cooling mechanism for neutron stars. It is due to thermally excited neutrons undergoing -decay,
while thermally excited protons undergo inverse -decay,
The neutrinos carry away energy as they escape, and the star cools very rapidly to temperatures below 10 K, at which point a minimum proton fraction (the Urca threshold mentioned above) must be present in order to preserve conservation of momentum. The proton fraction in a cold neutron star (temperature below 10 K) is determined by the symmetry energy, which is a measure of the energy change associated with variations in relative proton and neutron concentrations. The proton fractions we obtain in -stable stellar matter are shown in Figure 7 as a function of density. The similarity of pattern with Figure 6 is noticeable. At typical nuclear densities, our predicted proton fraction at NLO is about 1/25.
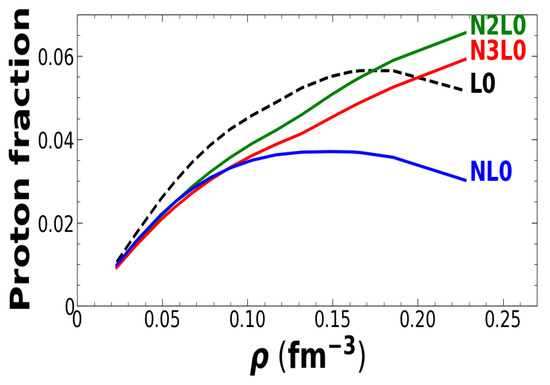
Figure 7.
(Color online) The proton fraction in -stable matter vs. density, from leading (black dashes) to fourth order (solid red).
Within the mean-field philosophy, on the other hand, one proceeds in the opposite direction. We take note, for instance, of ref. [73], where the authors construct equations of state using covariant density functional theory and explore the coupling parameter space of the isovector meson to generate a variety of models. Not surprisingly, when the constraint on L from PREX-II is included, all models allow direct Urca cooling at densities as low as 1.5 and within neutron stars with mass as low as one solar mass.
Returning to our discussion of Table 3, we also report predictions at some selected densities less than , which were found to be sensitive to specific observations in ref. [66]. This was determined from the slope of the correlation in the plane of vs. L, noticing that a particular slope identifies the density at which that observable is most sensitive to the symmetry energy. Our ab initio predictions agree within uncertainties with the values from ref. [66]. We recall that, at = (2/3) 0.1 fm (an approximate average between central and peripheral densities in a nucleus), reliable constraints to the symmetry energy can be obtained through the binding energy of heavy, neutron-rich nuclei [33]. Therefore, this density region is important when exploring correlations between L and the neutron skin of Pb.
In summary, a range for L between 45 and 65 MeV can be taken as typical for state-of-the-art nuclear theory predictions.
We close this section with a few comments on the symmetry energy at higher densities. Heavy-ion collisions are typical experiments used to probe higher densities. For instance, the reaction Au + Au at an incident energy of 400 MeV/nucleon was used in the ASY–EOS experiment at the GSI laboratory [29] to measure directed and elliptic flows of neutrons and charged particles. The densities probed by the experiment reach beyond twice the saturation density. For both low and high density, one must be cautious with the interpretation of constraints extracted from the measured observables, which may be model dependent.
Moving to even higher densities, the composition of a neutron star core will remain largely unknown unless reliable constraints on the symmetry energy at high densities become available. The minimum mass for direct Urca cooling may be a suitable constraint for the density dependence of the symmetry energy [74] above approximately 3, which is found to be strongly correlated with the neutron star mass at which the onset of direct Urca neutrino cooling takes place in the core. The analysis from ref. [75] finds that the values of tidal deformability and radius for a 1.4 neutron star are correlated with the pressure in -equilibrated matter at about 2.
From a theoretical standpoint, densities around twice the saturation density or higher are outside the reach of current ab initio calculations. Nevertheless, the normal density regime is of far-reaching importance for higher density features.
4.3. Impact on the Neutron Skin
Relating the spatial extension of a nucleus directly to the microscopic EoS can be done by employing the droplet model. Recently, we calculated the neutron skin [76],
of Pb using expressions that contain explicitly the symmetry energy and its density slope at saturation [76] (see Table 4). We emphasize that the simple droplet model is being used because we can directly input the values of J and L; the table entries relative to one another should be the focal point.

Table 4.
The neutron skin of Pb, S, calculated as described in ref. [76] using the given symmetry energy, J, and its slope at , L.
The first three entries in Table 4 are obtained from EoS based on chiral EFT and including two- and three-nucleon interactions at NLO. We note that they are relatively soft, cover a narrow range, and are consistent with one another. As to be expected from earlier discussions, the corresponding neutron skins are relatively small. Recently, ab initio predictions for the neutron skin of Pb have been found [58] to lie between 0.14 and 0.20 fm, in disagreement with the values extracted from electroweak (EW) scattering. The values on the fourth line are taken from an analysis of current constraints from nuclear theory and experiment [78], where the authors utilized 48 phenomenological models, relativistic mean field, and Skyrme Hartree–Fock. Finally (last line), the values of J and L from the recent PREX II experiment are shown. The reported value for the skin of Pb in ref. [33] is (0.283 ± 0.071) fm, corresponding to a range between 0.21 and 0.35 fm.
Clearly, phenomenological interactions can generate a much larger range for the neutron skins, including values consistent with the findings of PREX II. Of course, this is a reflection of the larger range for L that can be generated through parametrizations of mean-field models. On the other hand, the realistic nature of few-nucleon forces should be preserved in heavier systems, which is the essence of the ab initio philosophy. For these reasons, while an important tool to explore sensitivities and correlations, mean-field models lack the predictive power needed to answer the open questions in ab initio nuclear structure.
We conclude this section pointing to the interesting discussion in ref. [79], where the authors extended their previous analysis of the PREX experiment to recent measurements of parity-violating asymmetry in Ca (CREX experiment). The study included the static electric dipole polarizability, an observable that is expected to correlate with the neutron skin. We fully agree that a critical search is needed for the limitations of interactions currently used in ab initio calculations and other sources of experimental error. Figure 8, generated from information extracted from the figure in ref. [80], shows the discrepancy between CREX and PREX measurements and current theoretical predictions. The lines mark the mean values of the measured asymmetry in lead and calcium, respectively, and the bands represent the errors. Theoretical predictions should be, but are not, at the intersection of CREX and PREX results, marked by the red dot.
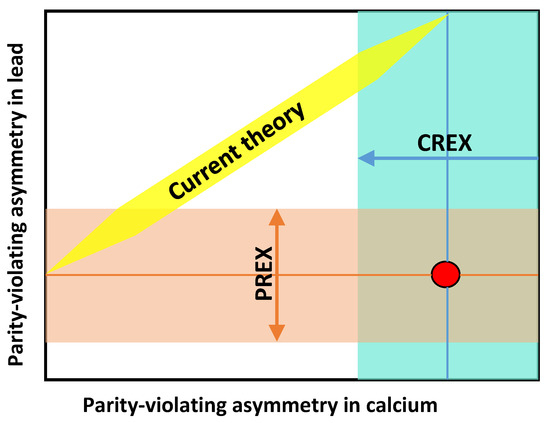
Figure 8.
(Color online) Discrepancy between the CREX and PREX measurements and theoretical predictions. See text and ref. [80] for more details.
5. Impact of the Isovector Part of the Free-Space Force
In the impressive analysis in ref. [58], 10 nuclear force parametrizations consistent with chiral EFT are examined. Employing state-of-the-art statistical methods and computational technology, the authors are able to make quantitative predictions for bulk properties and skin thickness of Pb. In the process, they find a strong correlation between L and the phase shift at laboratory energies around 50 MeV.
Here, we perform a single-shot calculation which serves as a simple and transparent test of the impact of the isovector part of the free-space force in neutron matter. We consider 2NFs only.
For the purpose of this test, we made a version of the NLO(450) potential where the fit of isospin-1 partial waves is deteriorated as compared to the original potential (see Figure 9). This is accomplished by adjusting two LECs in channel and one LEC for each of the P-waves (all changes are on average between 2 and 10%), while keeping the scattering length at its correct value. Although not dramatic, the impact on the phase shifts is considerable, especially above 100 MeV.
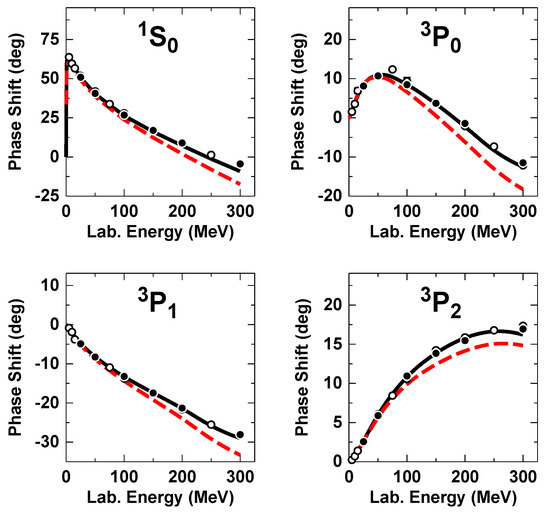
Figure 9.
(Color online) Phase shifts for selected isospin-1 partial waves as a function of the laboratory energy. Solid black: original potential; Red dashes: modified potential.
We then calculate the EoS of NM with the modified potential, shown in Figure 10 along with the original NLO predictions (2NF only). As we do not include 3NFs, these values are not realistic, but we are interested in highlighting differences due to the 2NF. Around saturation, the energy moves up by about 25%, while the (very sensitive) slope and closely related pressure increase by a factor of 1.75. This comparison is shown in Table 5. In other words, the “modified” phase shifts are not disastrous, but the slope of the NM EoS changes dramatically. Notice that our modified interaction is only very little different from the original interaction below 100, confirming extreme sensitivity of the neutron matter slope (and thus the slope of the symmetry energy) to the description of the isovector component of the interaction. Of course, a more “quantitative” test would require the inclusion of 3NFs, readjusted for consistency with the 2NF modifications. On the other hand, this simple exercise suffices to demonstrate that relaxing or abandoning the constraint of free-space data can produce dramatic changes in L (and thus the neutron skin).
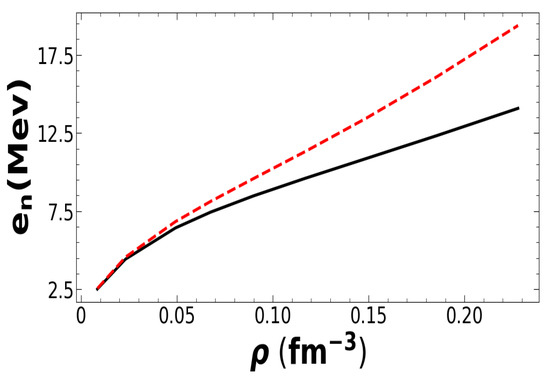
Figure 10.
(Color online) Energy per neutron as a function of NM density. Solid black: original potential; Red dashes: modified potential.

Table 5.
The energy per neutron, its slope, and the pressure at a density of 0.155 fm with the originl and the modified potentials. Only the 2NF is included.
The freedom to modify a model in such a way that isovector properties (such as the slope of the NM EoS) vary while retaining good fits to nuclei and nuclear matter is the mechanism that generates the popular correlations from mean-field models. However, free-space data do not enter into this picture, contrary to the basic principle of ab initio predictions. Also, variations within the model parameter space are generally applied to predefined analytical expressions, such as power laws of the density.
6. Conclusions and Future Perspective: Where Do We Go from Here?
We performed an analysis of existing literature addressing the nuclear symmetry energy, with the objective of identifying and discussing current gaps or problems and providing recommendations for future research.
There has been enormous progress in nuclear theory since the days of one-boson-exchange or phenomenological potentials and phenomenological 3NFs, selected with no clear scheme or guidance. One is now able to construct nuclear forces in a systematic manner, as they naturally emerge order by order. This allows us to perform calculations that are complete at each order.
To advance our understanding of intriguing systems such as neutron skins and neutron stars, it is important to build on that progress. Predictions from state-of-the-art nuclear theory favor a softer density dependence of the symmetry energy on the low-to-medium end of the spectrum found in the literature and, naturally, smaller neutron skins and radii of canonical mass neutron stars.
On the other hand, mean-field models, while a very useful tool to provide insight into the phenomenology of the system, cannot, by their very nature, provide answers to the open questions in ab initio nuclear structure.
On the experimental side, it is important to keep in mind that the symmetry energy parameters that control the neutron skin (and more) are extracted from measurements of suitable observables rather than being measured directly. While EW methods avoid the uncertainty and model dependence that come with the use of hadronic probes, the weakness of the signal seems to generate large errors: the measured observable is the very small left–right asymmetry in weak electron scattering off nuclei. This may hinder the ability of the experiment to provide a benchmark.
It can be demonstrated, and should be expected on fundamental grounds, that accurate reproduction of low-energy data is an important requirement for realistic predictions of many-body systems. Ignoring or weakening that constraint takes us back to mean-field approaches and thus is not progress.
Whether one chooses to call it “tension” [58] or “irreconcilable differences” [76], large pressure in neutron matter at saturation and large neutron skins are inconsistent with essentially all state-of-the-art predictions. We suggest that the way forward is for the low-energy experimental and theory communities to work together closely. Theorists should continue to identify and confront systematic problems in nuclear structure, critically examining the interactions used in up-to-date ab initio calculations. Claims that most recent results from EW scattering represent a benchmark are premature.
Funding
This research was funded by the U.S. Department of Energy under grant number DE-FG02-03ER41270. The APC was funded by the author.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The equations of state used in this study are available on request from the author.
Acknowledgments
This research was funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, grant number DE-FG02-03ER41270. The APC was funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, grant number DE-FG02-03ER41270.
Conflicts of Interest
The author declares no conflict of interest.
References
- Available online: https://frib.msu.edu (accessed on 3 December 2022).
- Zahed, I.; Broen, G.E. The Skyrme model. Phys. Rept. 1986, 142, 1. [Google Scholar] [CrossRef]
- Li, G. Skyrme forces and their Applications in Low Energy Nuclear Physics. Commun. Theor. Phys. 1990, 13, 457. [Google Scholar]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar] [CrossRef]
- Waletcka, J.D. A Theory of highly condensed matter. Annals Phys. 1974, 83, 491. [Google Scholar] [CrossRef]
- Serot, B.D.; Waletcka, J.D. The Relativistic Nuclear Many Body Problem. Adv. Nucl. Phys. 1986, 16, 1. [Google Scholar]
- Serot, B.D.; Waletcka, J.D. Recent Progress in Quantum Hadrodynamics. Int. J. Mod. Phys. 1997, E6, 515. [Google Scholar] [CrossRef]
- Brown, B.A. Neutron Radii in Nuclei and the Neutron Equation of State. Phys. Rev. Lett. 2000, 85, 5296. [Google Scholar] [CrossRef]
- Piekarewicz, J.; Fattoyev, F. Neutron-rich matter in heaven and on Earth. Phys. Today 2019, 72, 30. [Google Scholar] [CrossRef]
- Santos, B.M.; Dutra, M.; Lourenco, O.; Delfino, A. Correlations between the nuclear matter symmetry energy, its slope, and curvature. J. Phys. Conf. Ser. 2015, 630, 012033. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Shen, G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C 2010, 82, 055803. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Centelles, M.; Vinas, X.; Warda, M. Neutron Skin of 208Pb, Nuclear Symmetry Energy, and the Parity Radius Experiment. Phys. Rev. Lett. 2011, 106, 252501. [Google Scholar] [CrossRef]
- Mondal, C.; Agrawal, B.K.; De, J.N.; Samaddar, S.K.; Centelles, M.; Vinas, X. Searching for a universal correlation among symmetry energy parameters. Proc. DAE Symp. Nucl. Phys. 2017, 62, 72. [Google Scholar]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Mondal, C.; Agrawal, B.K.; De, J.N.; Samaddar, S.K. Correlations among symmetry energy elements in Skyrme models. Int. J. Mod. Phys. E 2018, 27, 1850078. [Google Scholar] [CrossRef]
- Tong, H.; Ren, X.-L.; Ring, P.; Shen, S.-H.; Wang, S.-B.; Meng, J. Relativistic Brueckner-Hartree-Fock theory in nuclear matter without the average momentum approximation. Phys. Rev. C 2018, 98, 054302. [Google Scholar] [CrossRef]
- Holt, J.W.; Lim, Y. Universal correlations in the nuclear symmetry energy, slope parameter, and curvature. Phys. Lett. B 2018, 784, 77. [Google Scholar] [CrossRef]
- Agrawal, B.K.; De, J.N.; Samaddar, S.K.; Colo, G.; Sulaksono, A. Constraining the density dependence of symmetry energy from nuclear masses. Phys. Rev. C 2013, 87, 051306. [Google Scholar] [CrossRef]
- Vinas, X.; Centelles, M.; Roca-Maza, X.; Warda, M. Density dependence of the nuclear symmetry energy from measurements of neutron radii in nuclei. AIP Conf. Proc. 2014, 1606, 256. [Google Scholar]
- Agrawal, B.K.; De, J.N.; Samaddar, S.K. Determining the density content of symmetry energy and neutron skin: An empirical approach. Phys. Rev. Lett. 2012, 109, 262501. [Google Scholar] [CrossRef]
- Tsang, M.B.; Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Lynch, W.G.; Steiner, A.W. Constraints on the density dependence of the symmetry energy. Phys. Rev. Lett. 2009, 102, 122701. [Google Scholar] [CrossRef]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Jenny, L.; Lynch, Z.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Kortelainen, M.; Lesinski, T.; Moré, J.; Nazarewicz, W.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S. Nuclear energy density optimization. Phys. Rev. C 2010, 82, 024313. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colò, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
- Tamii, A.; Poltoratska, I.; von Neumann-Cosel, P.; Fujita, Y.; Adachi, T.; Bertulani, C.A.; Carter, J.; Dozono, M.; Fujita, H.; Fujita, K.; et al. Complete Electric Dipole Response and the Neutron Skin in 208Pb. Phys. Rev. Lett. 2011, 107, 062502. [Google Scholar] [CrossRef]
- Brown, B.A. Constraints on the Skyrme Equations of State from Properties of Doubly Magic Nuclei. Phys. Rev. Lett. 2013, 111, 232502. [Google Scholar] [CrossRef]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F.; et al. Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Russotto, P.; Wu, P.Z.; Zoric, M.; Chartier, M.; Leifels, Y.; Lemmon, R.C.; Li, Q.; Łukasik, J.; Pagano, A.; Pawłowski, P.; et al. Symmetry energy from elliptic flow in 197Au + 197Au. Phys. Lett. B 2011, 697, 471. [Google Scholar] [CrossRef]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288. [Google Scholar] [CrossRef]
- Weinberg, S. Three-body interactions among nucleons and pions. Phys. Lett. B 1992, 295, 114. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-II on the equation of state of neutron-rich matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star. Universe 2022, 8, 133. [Google Scholar] [CrossRef]
- Alam, N.; Agrawal, B.K.; Fortin, M.; Pais, H.; Providencia, C.; Raduta, A.R.; Sulaksono, A. Strong correlations of neutron star radii with the slopes of nuclear matter incompressibility and symmetry energy at saturation. Phys. Rev. C 2016, 94, 052801. [Google Scholar] [CrossRef]
- Coraggio, L.; Holt, J.W.; Itaco, N.; Machleidt, R.; Marcucci, L.E.; Sammarruca, F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys. Rev. C 2014, 89, 044321. [Google Scholar] [CrossRef]
- Carbone, A.; Cipollone, A.; Barbieri, C.; Rios, A.; Polls, A. Self-consistent Green’s functions formalism with three-body interactions. Phys. Rev. C 2013, 88, 054326. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Chiral Effective Field Theory and Nuclear Forces. Phys. Rep. 2011, 503, 1. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Meißner, U.-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur. Phys. J. A 2015, 51, 53. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R.; Nosyk, Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys. Rev. C 2017, 96, 024004. [Google Scholar] [CrossRef]
- Hoferichter, M.; Ruiz de Elvira, J.; Kubis, B.; Meissner, U.-G. Matching Pion-Nucleon Roy-Steiner Equations to Chiral Perturbation Theory. Phys. Rev. Lett. 2015, 115, 192301. [Google Scholar] [CrossRef]
- Hoferichter, M.; Ruiz de Elvira, J.; Kubis, B.; Meissner, U.-G. Roy-Steiner-equation analysis of pion-nucleon scattering. Phys. Rep. 2016, 625, 1. [Google Scholar] [CrossRef]
- Hoppe, J.; Drischler, C.; Furnstahl, R.J.; Hebeler, K.; Schwenk, A. Weinberg eigenvalues for chiral nucleon-nucleon interactions. Phys. Rev. C 2017, 96, 054002. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef] [PubMed]
- Epelbaum, E.; Nogga, A.; Glöckle, W.; Kamada, H.; Meißner, U.-G.; Witala, H. Three nucleon forces from chiral effective field theory. Phys. Rev. C 2002, 66, 064001. [Google Scholar] [CrossRef]
- Holt, J.W.; Kaiser, N.; Weise, W. Chiral three-nucleon interaction and the 14C-dating β decay. Phys. Rev. C 2009, 79, 054331. [Google Scholar] [CrossRef]
- Holt, J.W.; Kaiser, N.; Weise, W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 2010, 81, 024002. [Google Scholar] [CrossRef]
- Hebeler, K.; Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.-G. Subleading contributions to the chiral three-nucleon force: Long-range terms. Phys. Rev. C 2008, 77, 064004. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.-G. Subleading contributions to the chiral three-nucleon force. II. Short-range terms and relativistic corrections. Phys. Rev. C 2011, 84, 054001. [Google Scholar] [CrossRef]
- Kaiser, N.; Singh, B. Density-dependent NN interaction from subleading chiral three-nucleon forces: Long-range terms. Phys. Rev. C 2019, 100, 014002. [Google Scholar] [CrossRef]
- Kaiser, N. Density-dependent nn-potential from subleading chiral three-neutron forces: Long-range terms. arXiv 2020, arXiv:2010.02739v4. [Google Scholar]
- Kaiser, N.; Niessner, V. Density-dependent NN interaction from subleading chiral 3N forces: Short-range terms and relativistic corrections. Phys. Rev. C 2018, 98, 054002. [Google Scholar] [CrossRef]
- Treuer, L. Density-Dependent Neutron-Neutron Interaction from Subleading Chiral Three-Neutron Forces. arXiv 2020, arXiv:2009.11104. [Google Scholar]
- Drischler, C.; Hebeler, K.; Schwenk, A. Supplemental Material for “Chiral Interactions up to Next-to-Next-to-Next-to-Leading Order and Nuclear Saturation”. Available online: https://journals-aps-org.uidaho.idm.oclc.org/prl/supplemental/10.1103/PhysRevLett.122.042501/MC_MBPT_short_supp.pdf (accessed on 2 February 2023).
- Nosyk, Y.; Entem, D.R.; Machleidt, R. Nucleon-nucleon potentials from Δ-full chiral effective-field-theory and implications. Phys. Rev. C 2021, 104, 054001. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. Overview of symmetric nuclear matter properties from chiral interactions up to fourth order of the chiral expansion. Phys. Rev. C 2021, 104, 064312. [Google Scholar] [CrossRef]
- Hu, B.; Jiang, W.; Miyagi, T.; Sun, Z.; Ekström, A.; Forssen, C.; Hagen, G.; Holt, J.D.; Papenbrock, T.; Stroberg, S.R.; et al. Ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nat. Phys. 2022, 18, 1196–1200. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. Analysis of the neutron matter equation of state and the symmetry energy up to fourth order of chiral effective field theory. Phys. Rev. C 2021, 104, 034308. [Google Scholar] [CrossRef]
- Drischler, C.; Carbone, A.; Hebeler, K.; Schwenk, A. Neutron matter from chiral two- and three-nucleon calculations up to N3LO. Phys. Rev. C 2016, 94, 054307. [Google Scholar] [CrossRef]
- Oyamatsu, K.; lida, K.; Koura, H. Neutron drip line and the equation of state of nuclear matter. Phys. Rev. C 2010, 82, 027301. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F. The Nuclear Symmetry Energy. Prog. Part. Nucl. Phys. 2016, 91, 203. [Google Scholar] [CrossRef]
- Burrello, S.; Colonna, M.; Zheng, H. The Symmetry Energy of the Nuclear EoS: A Study of Collective Motion and Low-Energy Reaction Dynamics in Semiclassical Approaches. Front. Phys. 2019, 7, 53. [Google Scholar] [CrossRef]
- Moeller, P.; Myers, W.D.; Sagawa, H.; Yoshida, S. New Finite-Range Droplet Mass Model and Equation-of-State Parameters. Phys. Rev. Lett. 2012, 108, 052501. [Google Scholar] [CrossRef] [PubMed]
- Moeller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations (FRDM) 2012. At. Data Nucl. Tables 2016, 109, 1. [Google Scholar] [CrossRef]
- Lynch, W.G.; Tsang, M.B. Decoding the density dependence of the nuclear symmetry energy. Phys. Lett. B 2022, 830, 137098. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Drischler, C.; Soma, V.; Schwenk, A. Microscopic calculations and energy expansions for neutron-rich matter. Phys. Rev. C 2014, 89, 025806. [Google Scholar] [CrossRef]
- Drischler, C.; Furnstahl, R.J.; Melendez, J.A.; Phillips, D.R. How Well Do We Know the Neutron-Matter Equation of State at the Densities Inside Neutron Stars? A Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 2020, 125, 202702. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.-W. Electric dipole polarizability in 208Pb as a probe of the symmetry energy and neutron matter around ρ0/3. Phys. Rev. C 2015, 92, 031301. [Google Scholar] [CrossRef]
- Page, D.; Lattimer, J.M.; Prakash, M.; Steiner, A.W. Neutrino Emission from Cooper Pairs and Minimal Cooling of Neutron Stars. Astrophys. J. 2009, 707, 1131. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Pethick, C.J.; Prakash, M.; Haensel, P. Direct URCA Process in Neutron Stars. Phys. Rev. Lett. 1991, 66, 2701. [Google Scholar] [CrossRef]
- Thapa, V.B.; Sinah, M. Direct URCA process in light of PREX-2. arXiv 2022, arXiv:2203.02272. [Google Scholar]
- Malik, T.; Agrawal, B.K.; Providencia, C. Inferring the nuclear symmetry energy at supra saturation density from neutrino cooling. Phys. Rev. C 2022, 106, L042801. [Google Scholar] [CrossRef]
- Patra, N.K.; Iman, S.k.M.d.A.; Agrawal, B.K.; Mukherjee, A.; Malik, T. Nearly model-independent constraints on dense matter equation of state. Phys. Rev. D 2022, 106, 043024. [Google Scholar] [CrossRef]
- Sammarruca, F. Neutron skin systematics from microscopic equations of state. Phys. Rev. C 2022, 105, 064303. [Google Scholar] [CrossRef]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral Effective Field Theory and the High-Density Nuclear Equation of State. Annu. Rev. Nucl. Part. Sci. 2021, 71, 403. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J. Bayesian modeling of the nuclear equation of state for neutron star tidal deformabilities and GW170817. Eur. Phys. J. A 2019, 55, 209. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Roca-Maza, X.; Nazarewicz, W. Combined Theoretical Analysis of the Parity-Violating Asymmetry for 48Ca and 208Pb. Phys. Lett. 2022, 129, 232501. [Google Scholar] [CrossRef]
- PREX, CREX, and Nuclear Models: The Plot Thickens. Available online: https://frib.msu.edu/news/2022/prl-paper.html (accessed on 3 December 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).