Abstract
The matroid concept is an important model in real life applications. Determining the existence of mutations of DNA and RNA plays an essential role in biological studies. The matroidal structures of matrices are used for determining the existence of mutations of DNA; graph theory and matroid theory can be used to identify important mutations in genetic data. We construct an algorithm to determine the existence of a mutation. Finally, we study the similarity and dissimilarity between genes using matroids.
MSC:
54A05; 54C10; 05B25; 92D20
1. Introduction
Matroidal structures have been an area of active research in mathematics for several decades which abstracts the notion of independence in linear algebra to more general settings. Matroids have applications in diverse fields such as computer science, combinatorics and optimization [1,2,3,4]. Matroidal structures are mathematical structures that capture the essential properties of independence and spanning in a variety of mathematical contexts including graph theory, geometry, combinatorics and algebra. Matroid theory was first introduced in the 1935s by Whitney [5] and has since become an important area of research in mathematics and computer science. Matroids can be found in many algebraic and combinatorial contexts. Both cycles in graphs and linear independence in vector spaces can be reduced to the same matroidal structure. Matroids are a subject of considerable interest due to their diverse fields, as noted in [6].
El Atik [7] describes the construction of new types of matroids called simplicial matroids using matrices and rough sets on simplicial complexes, explores the properties of these matroids including circuit and base axioms, rank functions and closure operators and provides examples of their applications.
El Atik [8,9] investigates topological structures in pre-approximation spaces including new lower types of pre-approximation spaces. Mutations can arise spontaneously, as a result of exposure to environmental factors such as radiation or carcinogens, or through errors in DNA replication or repair. The consequences of these mutations can range from single nucleotide changes to large-scale chromosomal aberrations and they can have significant effects on gene expression, protein function and cellular processes. Mutations in nucleic acids have been linked to a variety of diseases and disorders including cancer, genetic disorders and neurodegenerative diseases [10].
The omics technologies refer to a more comprehensive way of looking at the molecules that build up a cell, tissue and organism. The main role of genomics, transcriptomics and proteomics is to find all genes, messenger RNA (mRNA) and proteins in a specific biological sample without bias. It could also be used for something called ”high-dimensional biology”. The combination of all these techniques is known as systems biology. The fundamental aspect of these methods is a complicated system that, when looked at as a whole, is capable of eliciting a more in-depth comprehension than it would otherwise [11,12,13]. The application of computer technology to the management of biological data is bioinformatics. Gene-based medication discovery and development is aided using computers for data collection, storage, analysis and integration of biological and genetic data. The explosion of genomic information that has been made available to the public as a direct result of the genome project has prompted an increased need for capabilities in the field of bioinformatics.
We demonstrate the idea of a mutation space via an example involving genotypes [14]. Nucleotides are smaller molecules that combine to make DNA and RNA strands. These smaller molecules are called nucleotides. In DNA, the nucleotides are guanine (G), thymine (T) (or uracil (U) for RNA), adenine (A) and cytosine (C). The most important pairings for folding are guanine with cytosine and adenine with thymine (uracil). However, guanine and uracil can also pair. In theory, a nucleotide chain can fold and bond in many ways. Here, we use the nucleotide chain to illustrate the structure and the topological model from the graph; see [14,15,16,17]. Many topologists looked at topological models in biology [18,19] and medicine [20,21] to ascertain how DNA and RNA change from the point of view of multisets and topological structures.
Gioan [22] presents a study of complete graphs and their drawings with a focus on triangle mutations. The authors define triangle mutations as transformations of a complete graph drawing that preserve its planarity and connectivity while changing its embedding. They explore the properties of triangle mutations and provide examples of complete graph drawings that are equivalent to triangle mutations. Nieto et al. [23] suggest that a link between mathematics and the DNA structure may provide a better understanding of the DNA structure and its properties.
The study of mutations in nucleic acids is a fundamental area of research in genetics and molecular biology. Nucleic acids, such as DNA and RNA, carry the genetic information that determines the traits and characteristics of living organisms. Mutations in nucleic acids can have a variety of effects, ranging from benign to life-threatening and understanding the mechanisms behind these mutations is an important area of research.
This paper discusses the importance of the matroid concept in real-life applications and how it can be used to determine the existence of mutations in DNA and RNA. It also compares the validity of these mathematical results to the validity of these biological solutions. In particular, the use of matroidal structures in matrices is highlighted as a tool for identifying mutations, which is crucial in biological applications. This article starts off with a brief overview of the many notations and results of matroids. We approach DNA sequences as matrices and induce from them a matroid structure. The content continues to describe an algorithm that can be used to determine the existence of mutations. Finally, the content mentions that matroids can also be used to study the similarity and dissimilarity between genes. Determining the structure of matroids helps with solving important problems concerning DNA mutation in order to detect diseases and aid biologists in disease treatment.
2. Basic Concepts on Matroid Theory
2.1. Matroid Theory
Definition 1 ([6,24,25]).
A matroid structure M is an ordered pair composed of a finite set E that is known as a ground set and a collection T of subsets of E that meets the characteristics listed below:
()
() If and , then .
() and (where denotes the cardinality of A) then where
Remark 1.
In Definition 1, the condition can be written as: let and (or with , then such that
The matriod M is typically represented by the notation . Each component of T is represented an indepentent set of M. Dependent sets are subsets of E that are not independent. Because of the criterion , it is guaranteed that T is not empty; more specifically, it is guaranteed that it contains at least one subset of E. It is not possible to conclude this from or , which indicates that each two maximally independent sets in matroid have the same cardinal number. As an illustration, consider the following examples.
Example 1.
If E = {a,b,c}, therefore is a matroid, but is not a matroid.
Definition 2 ([26]).
Let . We have the following:
- (i)
- The members of T are called the independent sets of M and symbolised by IND (M).
- (ii)
- For any is said to be dependent if and is symbolised by D(M)
- (iii)
- A set in T that is maximal in the sense of inclusion is called a base of the matroid M and is symbolised by B(M)
- (iv)
- A minimal, in the sense of inclusion, dependent subset of E is called a circuit of the matroid M and is symbolised by C(M). The singleton circuit is called a loop. If {a,b} is a circuit, then a and b are said to be parallel.
- (v)
- The rank function of the matroid is a function , for .
- (vi)
- For each , the closure operator of a matrix M is defined as (A) = and (A) is called the closure of A in M. When there is confusion, we use the symbol . A is called a closed set if
2.2. Matroid and Matrices
Definition 3 ([27]).
A basis of any subsets each of the columns of matrix A may be defined as a maximal linear independent set . Maximal here means that there are no linear independent subsets of S that properly contain J.
Now, we present some examples to show that the independent set in matroids is an extension of the linearly independent set of vector spaces.
Example 2.
Assume that A is a matrix of which the columns are indexed by . and a circuit
Example 3.
Suppose a matrix of which the columns are indexed by . Consider linear independence among column vectors. Then: T = is a matroid. For A = {1, 2} and B = {2, 3, 4}, B-A = {3, 4}, for instance, we can take a = 3 to obtain , whereas a = 4 leads to .
The family β of the maximal members of T is given by in which the members of T and only of the maximal members of T (maximal with the respect inclusion) are called a base of M. Note that the family β satisfies: for , and for where (). For , , = 4 to obtain (). Additionally, the circuit is
Example 4.
Let matrix Then one can deduce that T = , , is a matroid. The family of circuit is C = {{4}, {6, 7}, {1, 2, 6}, {1, 2, 7}, {2, 3, 5}, {1, 2, 5, 6}, {1, 3, 5, 7}}.
In the following example, we can simply write the matroid and its circuit in other forms.
Example 5.
Let matrix Then: and and any subsets containing {5, 6}.
The matrix can also define a field which is similar to vector spaces.
2.3. Matroids and Graph Theory
Graph G can be thought of as a zero-one matrix A, mod 2, where each column contains exactly two ones. The rows of A represent the nodes and the columns represent the edges in a graph. If there is one in a given row and column, then there is a connection between that node and the adjacent edge. Given that the graph is connected, which means that the row of A cannot be partitioned into two non-empty sets in such a way that every column has both of its ones in the same set, the column bases of A are identical to the edge sets of the spanning-trees of G and the linearly independent sets of columns are identical to the edge sets of forests in G. To define a matroid from a graph, we will set the ground set E to be the set of edges. Then the independent sets will be those sets of edges that do not contain a cycle [4]. By Definitions 1, 2 and basic definitions in graph theory, one can easily deduce Proposition 1.
Proposition 1.
- (i)
- if A does not contain a cycle of G.
- (ii)
- B is a circuit of if B is a cycle of G.
- (iii)
- B is a base of if B is a spanning forest of G.
The following two examples are of a graphic matroid.
Example 6.
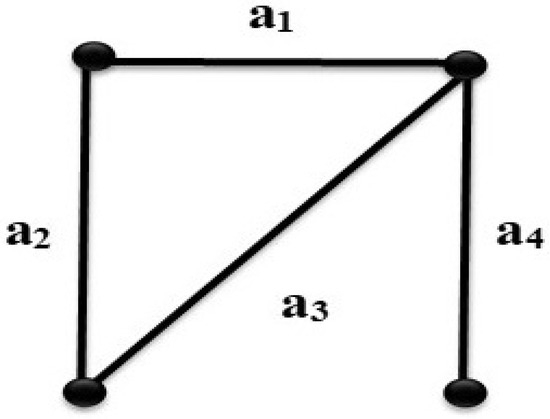
Suppose that G is a graph as shown in Figure 1, then the edge set from the ground set of a matroid whose independent sets are T = , and the base will be . The dependent set . Hence,

Figure 1.
A matroid for a simple graph G.
Example 7.
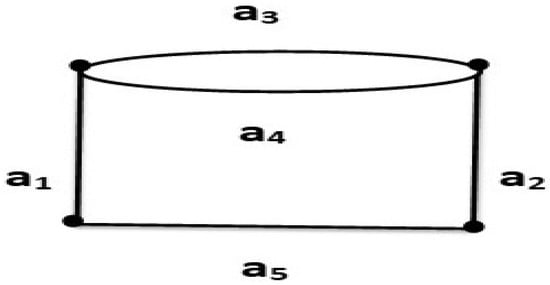
Assume that G is a graph as shown in Figure 2, then the edges from the ground set of a matroid whose independent sets are } and a set of circuits of is and the base will be . The dependent sets are . It is clear that

Figure 2.
A matroid for a nonsimple graph G.
Definition 4 ([6]).
Let be two isomorphic matroid structures if there exist a bijection since , set of if A is an independent set in
Remark 2.
By comparing the dependent sets which are with in Example 7, we see that, under the bijection is defined as , a set is a circuit in if ) is a circuit in . In the same way, a set B is an independent set in if ) is an independent set in
Example 8.
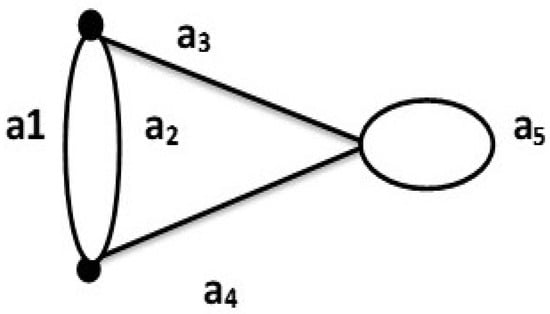
Consider G be a graph as shown in Figure 3. Then the T = , and the base will be . The dependent sets are . It is obvious that In this case, if G has a loop, then

Figure 3.
A graph G with multiedges and loops.
Proposition 2.
In a matroid structure , the following statements hold:
- (i)
- if and only if , equivalently, if and only if .
- (ii)
- if and only if
Proof.
According to Definition 1 and Remark 1, the proof is straightforward. □
3. Matroidal Structure Induced by Topological Operators
We define a matroidal structure in terms of topological operators in this section.
Let X be a non-empty finite set and let F be a family of subsets of that is .
Definition 5 ([28]).
Let a family F on X be a preclosure system (PCS) when it satisfies these conditions:
- (i)
- .
- (ii)
- .
Proposition 3.
Let F be a preclosure system. If , is preclosed. Let then it is simple to verify that for all the next properties hold:
- (PCL1)
- (PCL2)
- If , then ;
- (PCL3)
- (PCL4)
- ;
- (PCL5)
- ;
- (PCL6)
- (PCL7)
- For any
Proof.
The properties from PCL1 to PCL5 are obvious. It is sufficient to prove (PCL6). Since and then . So and so PCL7 is directly proven by PCL6. □
Definition 6.
A map is named a preclosure operator (PCO) on X if pCl satisfies the above conditions (PCL1), (PCL2) and (PCL3).
- (i)
- By Definition 5, it is simple to verify this. = is a preclosure system on X.
- (ii)
- A preclosure operator that satisfies (PCL4) and (PCL5) is called a Kuratowski preclosure operator (KPO), which determines a supra topology on X.
- (iii)
- A matroid structure is defined by a preclosure operator that satisfies (PCL6), which we refer to as a matroidal preclosure operator (MPO) and is defined by
Proposition 4.
The structure () is a matroid.
Proof.
- (i)
- That is obvious
- (ii)
- If and and for every then Therefore, there exists a preopen set G where and so . By , since and for Therefore, and
- (iii)
- By the fact that for any subset A, we have that if since , therefore there exists where .
□
Rough set theory states that a preclosure operator pCl is an upper approximation operator (UPO) if pCl satisfies (PCL5) and (PCl7).
Let MPS and UPS be the preclosure system corresponding to the preclosure operator respectively. We will now discuss the relation between these three types of preclosure operators (system).
Theorem 1.
A UPO is a .
Proof.
Consider As is known, a , so we simply prove that pCl is a MPO. For , and by (PCL5), . To prove , we need merely to show , by (PCL2). If , then )= . That is . It follows (PCL3) and (PCL7) that ) = this contradicts with Hence, (PCL6) holds and MPO. □
Remark 3.
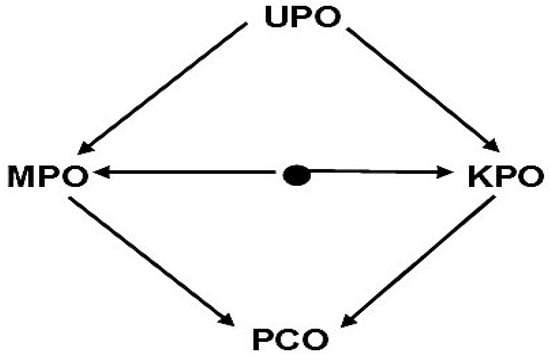
The following is the preclosure systems diagram that corresponds to Figure 4, which is as follows:

Figure 4.
The relation between four kinds of preclosure operators.
Proposition 5.
IF is a MPS and KPS, then is a UPS.
Proof.
Assuming that is the preclosure operator caused by (V, J), we will show that is a UPO. To prove this, we just need to prove a partition on V since (. Such that is a KPO, . That is, . is a MPS, so D includes the following: , if is the family of preclosed sets that cover J, therefore partition . Suppose that is the family of preclosed sets that cover , then is a partition of V. , we show that J is the union of some elements of . , where is a partition of V, there is since . We claim that , or else, and , contradicts that is a preclosed set covering . Hence we have . Now we show (.
Let , we let and find a contradiction. and , following from that and . therefore , in contrast to . Then and . That is .
We now point in a new direction. Let . Since is a partition of U and . For each satisfying , it follows that J contains . Thus, J contains , and . □
Graph theory is a mathematical framework used to study the properties and relationships of objects represented as nodes or vertices connected by edges. In the context of genetics, graph theory can be applied to analyze the relationships between genes and their mutations. Using graph theory, researchers can analyze the properties of this network of genes and mutations, and such analysis can help identify key mutations that play important roles in disease development and progression. Graph theory and matroid theory are two mathematical frameworks that can be used to analyze the structure of mutations and their relationships in genetic data. Both graph theory and matroid theory can be used to identify important mutations in genetic data. Additionally, these frameworks can be used to identify mutations, which can provide insights into the molecular mechanisms underlying disease.
4. Mutations via Their Graph and Matroidal Structures
In this section, we study a substitution mutation, an insertion mutation and a deletion mutation with a new procedure using matroids with graphs.
DNA Structure and Mutations
Figure 5 depicts the transcription process in which an RNA polymerase creates an RNA copy from a section of DNA. Translation is the process by which polypeptide sequences are created using the translated mRNA as a template. The type of the RNA’s coding that is actually read during the production of polypeptides is messenger RNA (mRNA), which is coded in stacks of RNA [29,30]. The majority of genes are now discovered at the DNA level before they are discovered as mRNA or as a portion product. The fundamental tenet of molecular biology is the explanation of how genetic information is transferred from one component of a biological system to another. It is well known that DNA leads to RNA and RNA, in turn, leads to protein. Every C is linked with G and vice versa. On the other side, A is linked with and vice versa. Otherwise, a mutation will occur. There are different types of mutations including substitution, insertion, deletion.
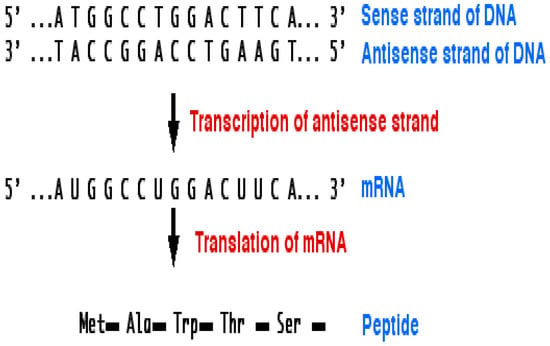
Figure 5.
Central dogma of biology [29,30].
- (i)
- A mutation that exchanges one base for another is called substitution as in Figure 6.
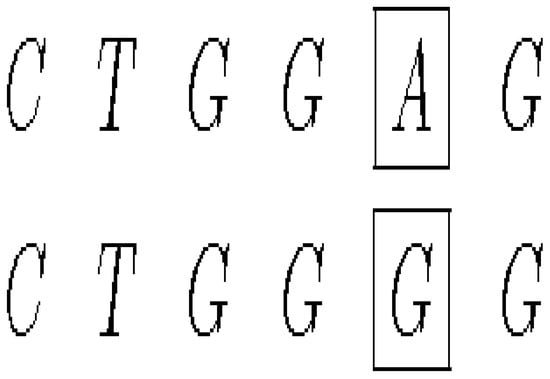 Figure 6. Mutation by substitution.
Figure 6. Mutation by substitution. - (ii)
- Insertion mutation occurs when extra base pairs are inserted as in Figure 7.
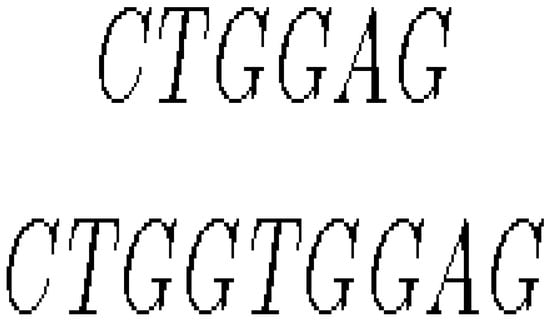 Figure 7. Mutation by insertion.
Figure 7. Mutation by insertion. - (iii)
- If a section of DNA is lost or deleted, then the mutation is called a deletion as in Figure 8.
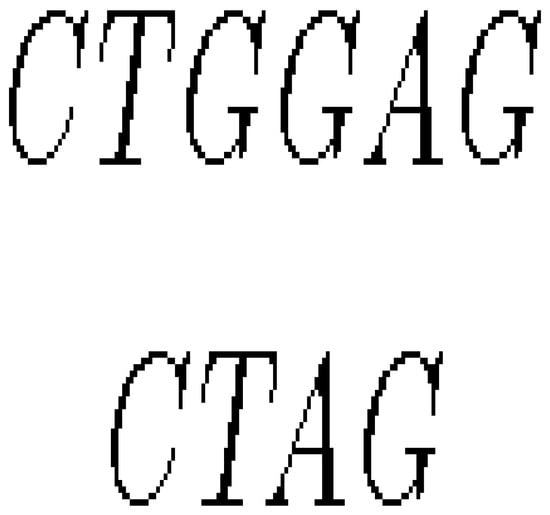 Figure 8. Mutation by deletion.
Figure 8. Mutation by deletion.
Matroids have many applications in computer science, combinatorial optimization and algorithm design. For example, matroids are used in graph theory to model the structure of graphs and in optimization theory to model various optimization problems, such as the minimum spanning tree problem and the maximum flow problem. Matroids are also used in coding theory to construct error-correcting codes and in machine learning to model complex data structures [31,32]. In graph theory [16], the set of vertices will be denoted by V of a finite set. The set of edges had the form s. t. . In other words, are called adjacent vertices.
Recent studies have determined the existence of the mutation by the distance function, relations and topology. In the following, we will use graph theory to determine the mutation of genes which do not require a certain length.
One of the challenges in genetic research is the handling of gene sequences, including converting these sequences into numerical data, identifying relationships between them and organizing them in tables, as in Table 1 (analysis); for more information, see [19]. In this regard, the application of graph and matrix theory provides a promising approach for analyzing genetic data. By representing genes as graphs and matrices, researchers can more effectively visualize and analyze genetic information, potentially leading to new insights into the fundamental nature of genetic structures.
Definition 7.
A graph on genes is defined as a set of nucleotide from the sequence of DNA. In other words, it is the set of all vertices V and the edges between the vertices such that such that , where will denote the set of vertices incident with x.
In the following, we discuss the existence of mutations via graph and matroidal structures. This can be considered throughout the discussion of the following examples and results.
Example 9.
Let . Then, the induced graph through the relation is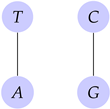

Proposition 6.
Let the types be strings of bits, vectors and DNA or RNA sequences such that a mutation has not occurred. Then, its graph structure will be undirected.
Proof.
Consider the types that do not have a mutation. Then the relation between types ( and ) will be only a symmetric relation. So, the type of graph will be undirected. □
Example 10.
Let . Then its graph structure is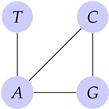

Corollary 1.
If the types contain a mutation, then its graph structure is directed.
Corollary 2.
If the types do not contain a mutation, then its graph structure in terms of multiset relation is directed.
Now, we state an Algorithm 1 which determines whether a DNA sequence has a mutation by using a graph representation of the sequence. It examines each edge in the graph and connects it with non-cyclic edges. It then constructs a matroid from the resulting graph to represent the independence structure of the edge set. Algorithm 1 checks if any subset of the edge set belongs to the matroid. If it does, there is no mutation and if it does not, there is a mutation. However, Algorithm 1 assumes that the input graph is a valid representation of the DNA sequence and that the mutation alters the graph structure.
| Algorithm 1: Mutation via matroids and graphs. |
Input: A graph G = (V,E) from DNA stand. Output: The existence of mutation in DNA or not
|
Example 11.
Arabidopsis Thaliana Gamma-Glutamylcysteine Synthetase Gene (abbreviated as CAD2) [33]
| Tair Accession: | 1005028114. |
| GenBank Accession: | AF068299. |
| Sequence Length | 5277. |
AT CGATATGTAACACAAT ⋯ TGTATGTTTTT ;
;
By using MSC-code [19], we obtain the data in Table 1.


Table 1.
Bonding between nucleotide.
Table 1.
Bonding between nucleotide.
| A | T | C | G | |
|---|---|---|---|---|
| A | 0 | 1859 | 0 | 0 |
| T | 1543 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1019 |
| G | 0 | 0 | 856 | 0 |
Then its graph structure is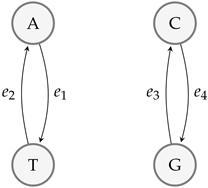

By Algorithm 1 it is evident that there is no mutation.
Example 12.

If we locate a mutation in CAD2 [33], then by MSC-code, we obtain the data in Table 2.

Table 2.
Bonding between nucleotides.
The graph structure induced by Table 2: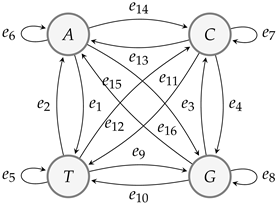

Since , , , , , , , , , , , , , , , . By Algorithm 1, there exists a mutation. The number of mutations can be calculated with —the same result as obtained from code MSC-code [19].
We would like to clarify that our focus in this section was to introduce a novel approach to modelling the mutations of nucleic acids using matroidal structures. While the basic concepts of matroidal structures may be known to some mathematicians, we believe that the application of this theory to the study of nucleic acid mutations is a novel contribution to the field, we also acknowledge that simply naming mathematical expressions does not produce new knowledge. However, our work goes beyond a mere description of matroidal structures and demonstrates their potential application to the study of nucleic acid mutations, we provide examples of how matroidal structures can be used to model the behavior of nucleic acids and predict the occurrence of mutations. We believe that these applications demonstrate the potential value of matroidal structures in the context of nucleic acid research. We also believe that this section provides a valuable contribution to the field by introducing a new approach to modelling the mutations of nucleic acids. By using matroidal structures, we are able to capture the underlying combinatorial structure of nucleic acids and provide insights into their behavior.
5. Matroidal Structure of DNA via Matrices
Previous studies [18,19,34,35] to identify mutations depend on establishing a function and proving that it is a measurement function and require many calculations. The matroid method is easier and depends on the bonding between the nucleotides. In this section, we study a mutation with new procedure using matroids with a matrix. We created Algorithm 1 to determine the existence (or absence) of a mutation. Algorithm 1 indicates how many (A, T, G and C) elements there are; through Algorithm 1, the gene sequence was converted into a matrix.
Definition 8.
Let be a sense strand of DNA (the first tape in wild type) and be an antisense strand of DNA (the second tape in wild type).
As shown in Figure 9, after finding the relationship between the gene sequence by [19] and converting it into a table as in Table 1 and Table 2, the table can be converted into a matrix by Algorithm 2.
| Algorithm 2: Mutation via matroids and matrices. |
Input: A matrix (aij) from DNA stand, where i indicates to row and j indicates to column. Output: the existence of mutation in DNA or not.
|
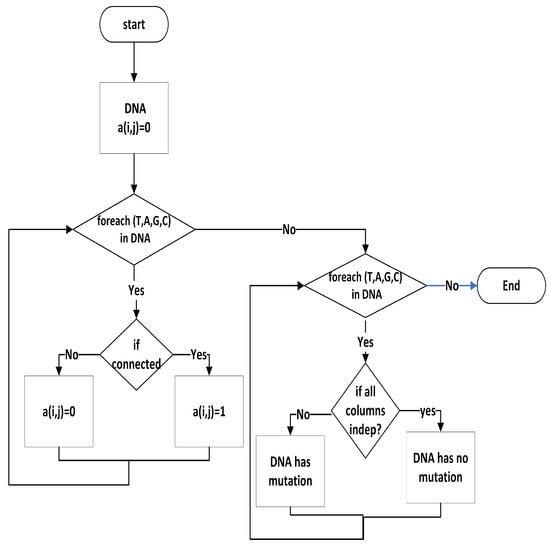
Figure 9.
Mutation via matroids and matrices.
Example 13.
- (i)
- Consider the following DNA strand, and . By Algorithm 2, the matrix , where the row represents the first tape in wild type and the column represents the second tape in wild type , if , the structure for the matrix We observe that which means that all vectors of matroid are independent. Then there is no mutation in this DNA sequence.
- (ii)
- Consider the following DNA strand, and By Algorithm 2, the matrix if the structure for the matrix M2 is = . We observe that C() = which means that not all vectors of the matroid are independent. There is substitution mutation in this DNA strand.
Example 14.


Continue for Example 11;

Table 3.
Bonding between nucleotide.

Table 4.
Relation between nucleotides.
Then the matrix , if , the structure for the matrix We observe that which means that all vectors of matroid are independent. There is no mutation in this DNA sequence. These results correspond to the National Center for Biotechnology Information (NCBI) [33].
6. A Similarity and Dissimilarity between the Sequences of DNA
We can define a similarity and dissimilarity in matrorid M = M(E, T) as
A similarity =;
dissimilarity=.
Since DNA sequences consist of 4 nucleotides {A,T,C,G} = E, then we define a similarity and dissimilarity between the sequences of DNA as:
A similarity =;
Dissimilarity = .
Example 15.
(Continue for Example 9)
- (i)
- A similarity = = 1; dissimilarity=.
- (ii)
- A similarity =; dissimilarity=.
7. Conclusions and Future Work
Matroids are one of the most important branches of modern mathematics, which play an important role in various applications. Determining the existence of mutations of DNA and RNA is an essential issue in biological applications. We created Algorithm 1 to determine the existence (or absence) of a mutation and through Algorithm 1, the gene sequence was converted into a matrix. The mutation of DNA and RNA can be determined by the matrix. The matroidal structures of matrices are used for determining the existence of mutations which is an essential issue in biological applications. In the future, these results can be applied to develop new mutations that are useful in agriculture and industry, as well as the pharmaceutical industry and the treatment of diseases. We will study how matroidal structures can be used to model mutations in RNA secondary structures and predict the effects of these mutations on RNA function, how matroidal optimization can be used to model and predict the evolution and fitness of RNA viruses, how matroidal structures can be used to model DNA recombination and repair processes and predict the effects of mutations on these processes and how matroidal structures can be used to model genome rearrangements and predict the effects of mutations on these processes.
Author Contributions
Methodology, M.B.; formal analysis, A.A.N.; investigation, R.A.-G.; resources, M.B.; writing—original draft preparation, M.B.; writing—review and editing, R.A.-G.; supervision, A.A.N. The contributions of authors to this research article are equal. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available from the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, W.; Wang, S. Matroidal approaches to generalized rough sets based on relations. Int. J. Mach. Learn. Cybern. 2011, 2, 273–279. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, W. Matroidal structure of covering-based rough sets through the upper approximation number. Int. J. Granular Comput. Rough Sets Intell. Syst. 2011, 2, 141–148. [Google Scholar] [CrossRef]
- Tang, J.; She, K.; Min, F.; Zhu, W. A matroidal approach to rough set theory. Theory Comput. Sci. 2013, 471, 1–11. [Google Scholar] [CrossRef]
- Oxley, J. Matroid Theory, 2nd ed.; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Whitney, H. On the abstract properties of linear dependence. Am. J. Math. 1935, 57, 509–533. [Google Scholar] [CrossRef]
- Oxley, J.G. Matroid Theory; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Atik, A.E. Approximation of simplicial complexes using matroids and rough sets. Soft Comput. 2023, 27, 2217–2229. [Google Scholar] [CrossRef]
- Atik, A.E.; Ali, M.E. Matroidal and Lattices Structures of Rough Sets and Some of Their Topological Characterizations. Inf. Sci. Lett. 2022, 11, 331–341. [Google Scholar]
- Atik, A.E.; Haroun, S. A topological representation of matroids using graphs. Int. J. Math. Comput. Sci. 2022, 17, 1079–1086. [Google Scholar]
- Bone, M.; Vernizzi, G.; Orland, H.; Zee, A. Topological classification of RNA structures. J. Mol. 2008, 379, 900–911. [Google Scholar] [CrossRef]
- Pervouchine, D.D. Circular exonic RNAs: When RNA structure meets topology. BBA Gene Regul. Mech. 2019, 1862, 194384. [Google Scholar] [CrossRef]
- Qiu, W.; Xin, H. Topological structure of closed circular DNA. J. Mol. Struct. Theochem 1998, 428, 35–39. [Google Scholar] [CrossRef]
- Silva-Santiago, E.; Pardo, J.P.; Hernandes-Munoz, R.; Aranda-Anzaldo, A. The nuclear higher-order structure defined by the set of topological relationships between DNA and the nuclear matrix is species-specific in hepatocytes. Gene 2017, 597, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Adams, C.C.; Robert, D.F. Introduction to Topology: Pure and Applied; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan: London, UK, 1976; Volume 290. [Google Scholar]
- Diestel, R. Graph Theory, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Nada, S.I.; El-Atik, A.A.; Atef, M. New types of topological structure via graphes. Math. Methods Appl. Sci. 2018, 41, 5801–5810. [Google Scholar] [CrossRef]
- El-Sharkasy, M.M.; Badr, M.S. Modeling DNA and RNA mutation using mset and topology. Int. J. Biomath. 2018, 11, 18500584. [Google Scholar] [CrossRef]
- El-Atik, A.; Tashkandy, Y.; Jafari, S.; Nasef, A.A.; Emam, W.; Badr, M. Mutation of DNA and RNA sequences through the application of topological spaces. AIMS Math. 2023, 8, 19275–19296. [Google Scholar] [CrossRef]
- El-Bably, M.K.; Abu-Gdairi, R.; El-Gayar, M.A. Medical diagnosis for the problem of Chikungunya disease using soft rough sets. AIMS Math. 2023, 8, 9082–9105. [Google Scholar] [CrossRef]
- Hosny, A.R.; Abu-Gdairi, R.; El-Bably, M.K. Approximations by Ideal Minimal Structure with Chemical Application. Intell. Autom. Soft Comput. 2023, 36, 3073–3085. [Google Scholar] [CrossRef]
- Gioan, E. Complete graph drawings up to triangle mutations. Discret. Comput. Geom. 2022, 67, 985–1022. [Google Scholar] [CrossRef]
- Nieto, J.A.; Nieto-Marín, C.C.; Nieto-Marín, N.; Nieto-Marín, I. New mathematical tools for the study of the DNA structure. J. Appl. Math. Phys. 2021, 9, 1896–1903. [Google Scholar] [CrossRef]
- Bonin, J.; Oxley, J.G. Matroid Theory. Grad. Texts Math. 1996, 197, 234–260. [Google Scholar]
- Lai, H. Matroidal Theory; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Li, X.; Liu, S. Matroidal approaches to rough set theory via closure operator. Int. J. Approx. Reason. 2012, 53, 513–527. [Google Scholar] [CrossRef]
- Wang, Z.; Yanping, L. The relationships between degree rough sets and matroids. Anals Fuzzy Math. Inform. 2012, 12, 139–153. [Google Scholar]
- Nasef, A.A.; Jafari, S.; Caldas, M.; Latif, R.M.; Azzam, A.A. preclosure operator and its applications in general topology. J. Linear Topol. Algebra 2018, 7, 1–9. [Google Scholar]
- Crick, F.; Anderson, P.W. What mad pursuit: A personal view of scientific discovery. Phys. Today 1989, 17, 42–68. [Google Scholar] [CrossRef]
- Nirenberg, M.W.; Matthaei, J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Nat. Acad. Sci. USA 1961, 47, 1588–1602. [Google Scholar] [CrossRef]
- Blikstad, J.; Mukhopadhyay, S.; Nanongkai, D.; Tu, T.W. Fast Algorithms via Dynamic-Oracle Matroids. In Proceedings of the 55th Annual ACM Symposium on Theory of Computing, Orlando, FL, USA, 20–23 June 2023; pp. 1229–1242. [Google Scholar]
- Baiou, M.; Barahona, F. On some algorithmic aspects of hypergraphic matroids. Discret. Math. 2023, 346, 113222. [Google Scholar] [CrossRef]
- Available online: https://www.ncbi.nlm.nih.gov (accessed on 1 January 2023).
- Nieto, J.J.; Torres, A.; Georgiou, D.N.; Karakasidis, T.E. Fuzzy polynucleotide spaces and metrics. Bull. Math. Biol. 2006, 68, 703–725. [Google Scholar] [CrossRef]
- Georgiou, D.N.; Karakasidis, T.E.; Nieto, J.J.; Torres, A. A study of entropy clarity of genetic sequences using metric spaces and fuzzy sets. J. Theory Biol. 2010, 267, 95–105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).