Nonextensive Footprints in Dissipative and Conservative Dynamical Systems
Abstract
1. Introduction
2. Few Degrees of Freedom
2.1. Dissipative Models
2.1.1. Sensitivity to Initial Conditions
2.1.2. Relaxation Dynamics
2.1.3. Central Limit Behavior
2.2. Conservative Models
3. Many Degrees of Freedom
3.1. Coupled Pendula Models
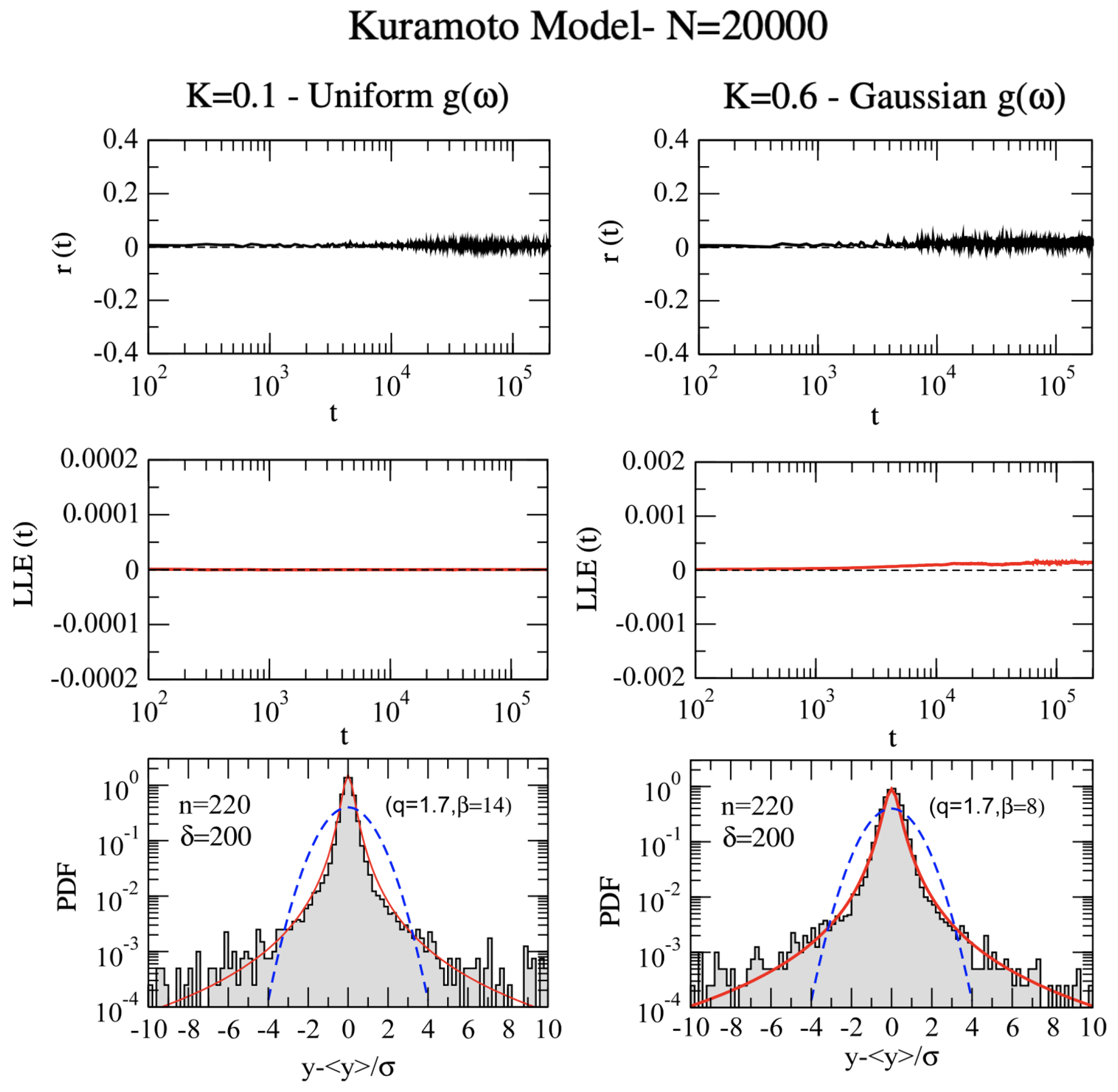
3.2. The Kuramoto Model
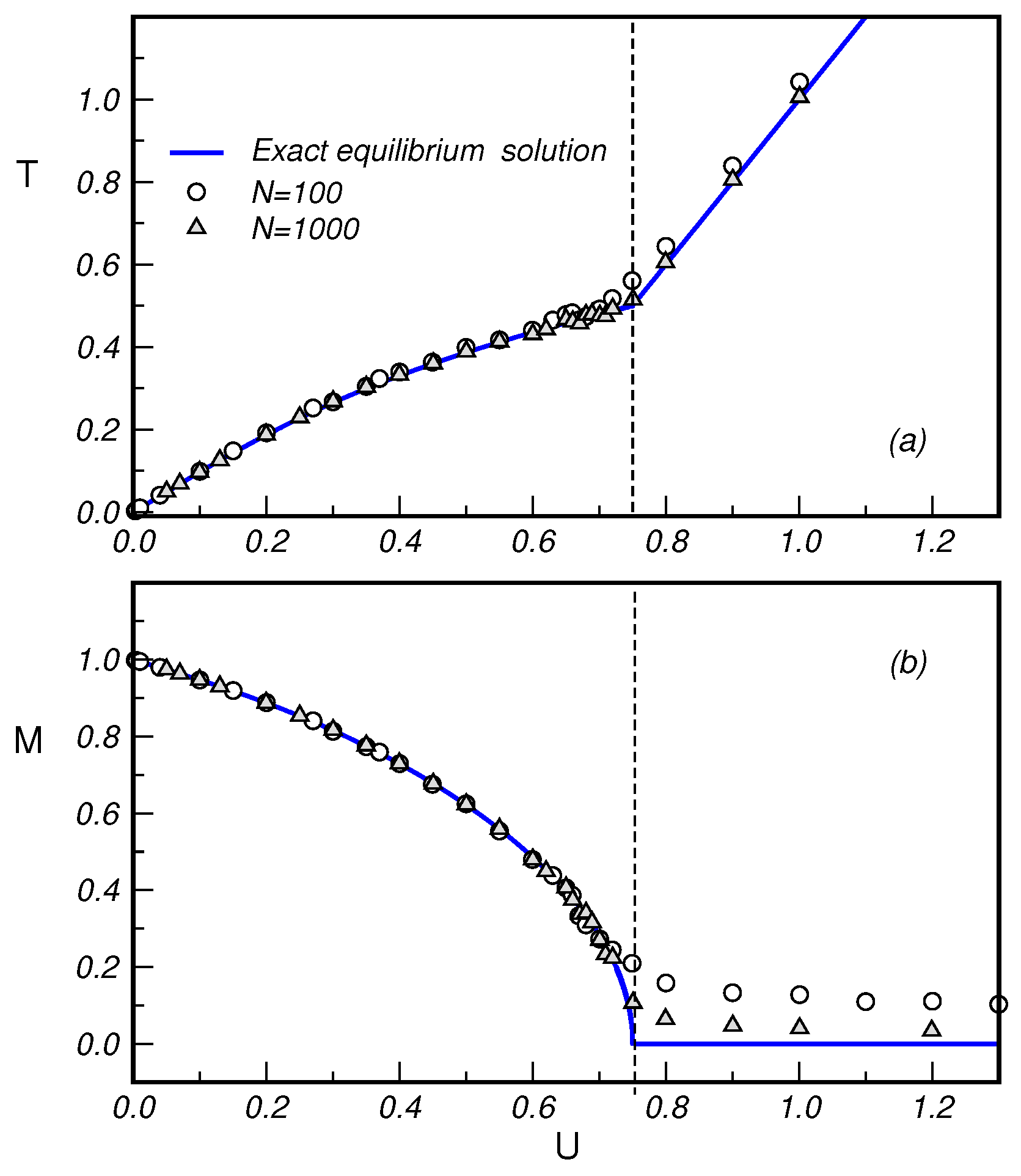
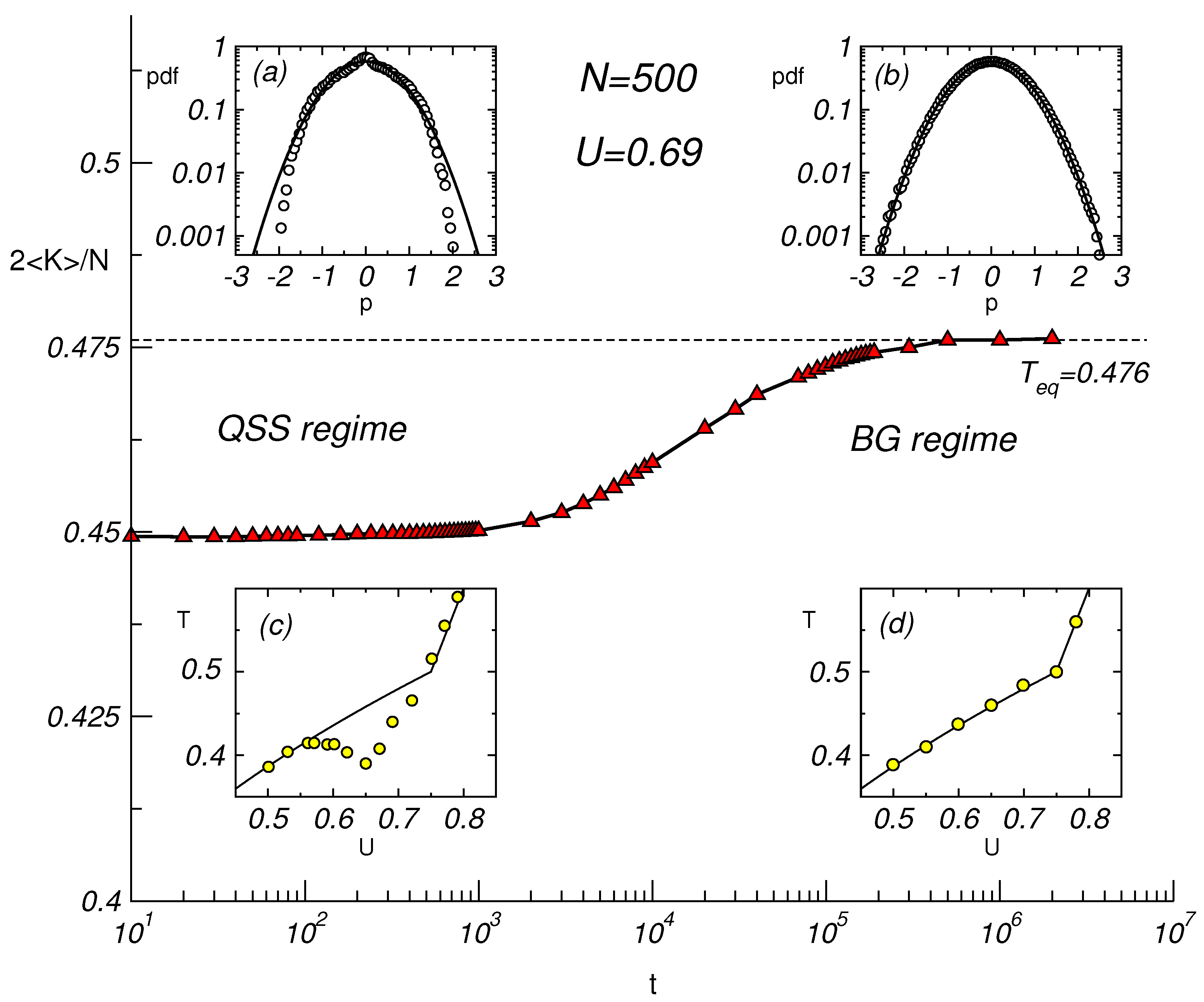
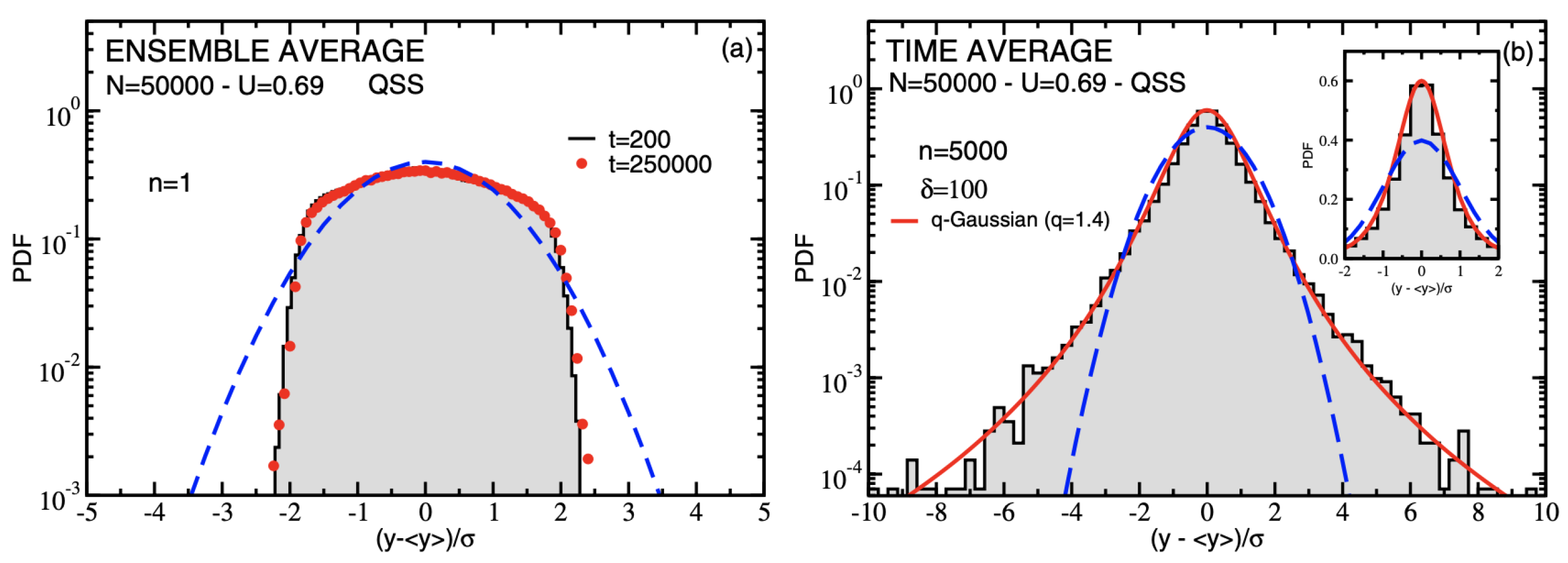
3.3. The HMF Model
3.4. Classical Inertial Rotors in d Dimensions
4. Asymptotically Scale-Free Networks
5. Clues Concerning the Domains of Validity of BG and q-Statistics
5.1. Clue I—Asymptotically Scale-Free Networks
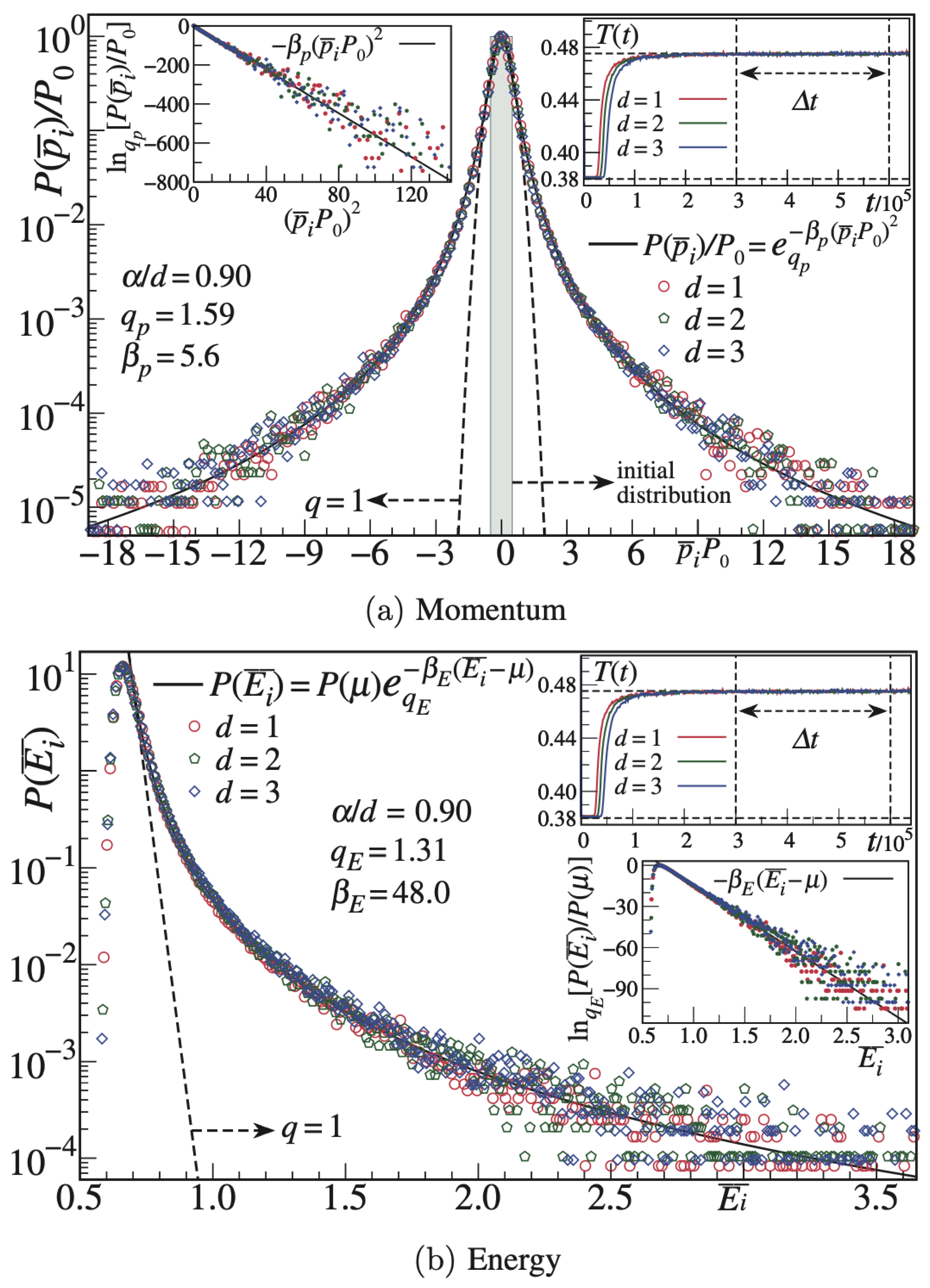
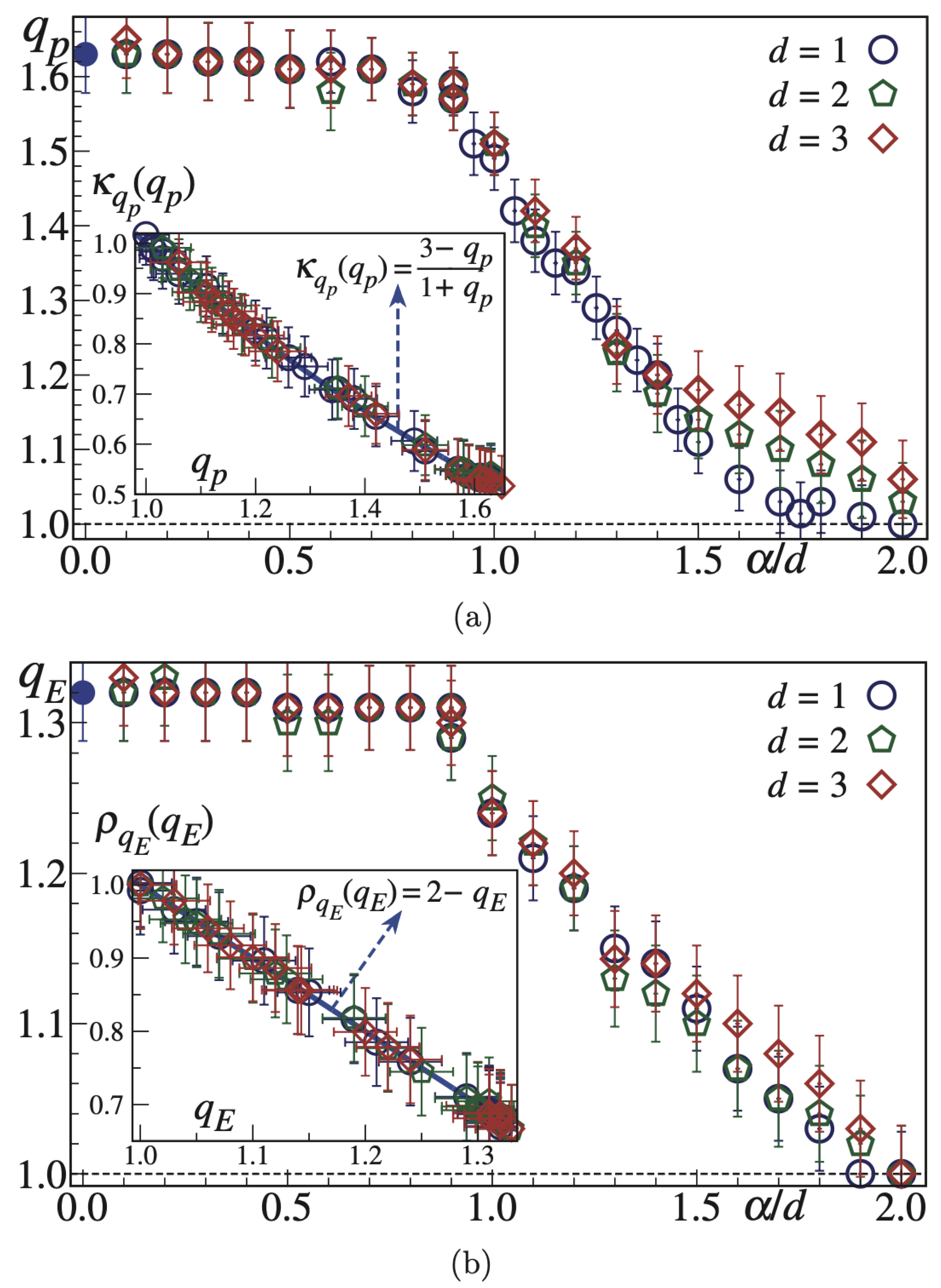
5.2. Clue II—Momenta and Energy Distributions of Classical Many-Body Hamiltonians
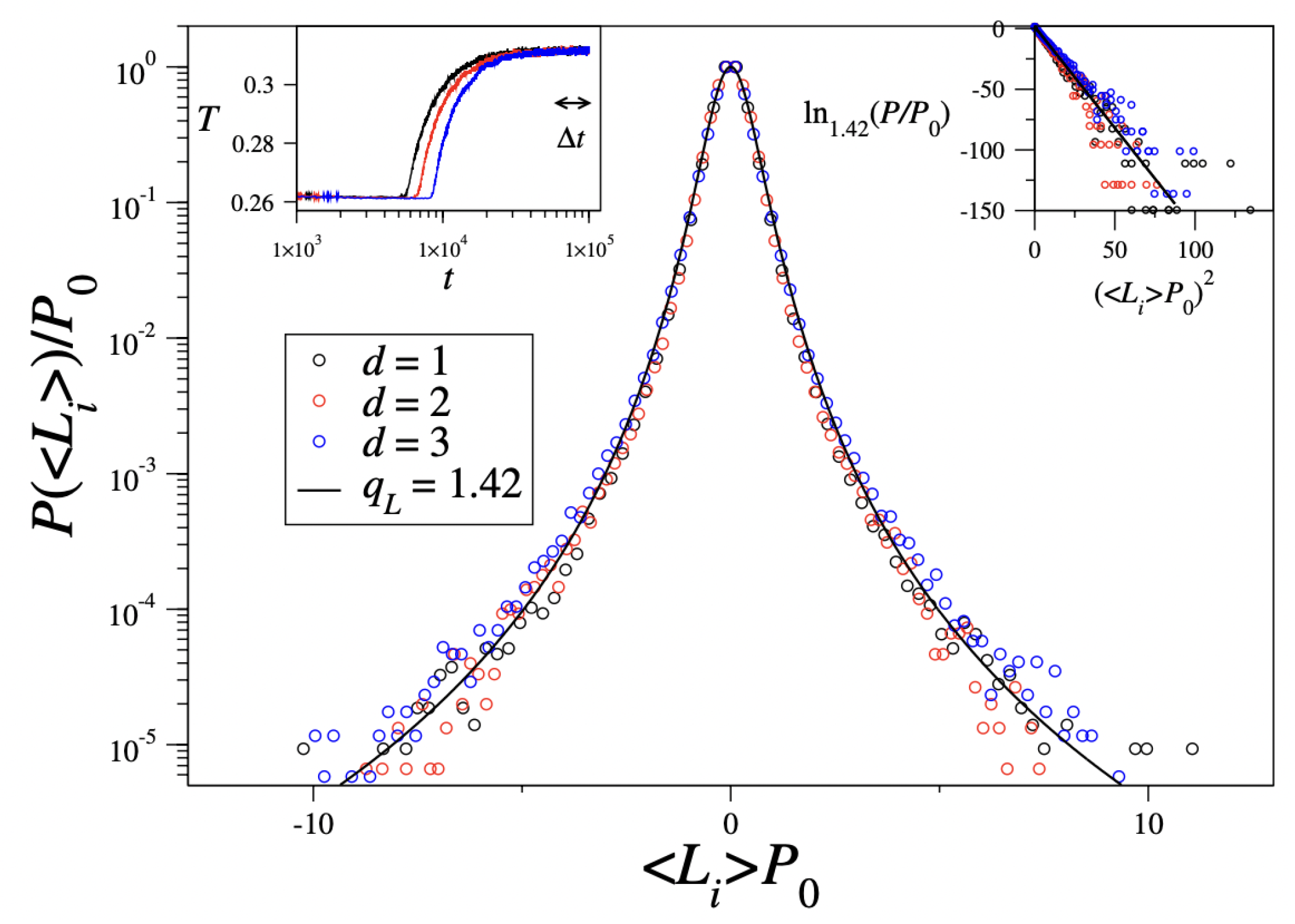
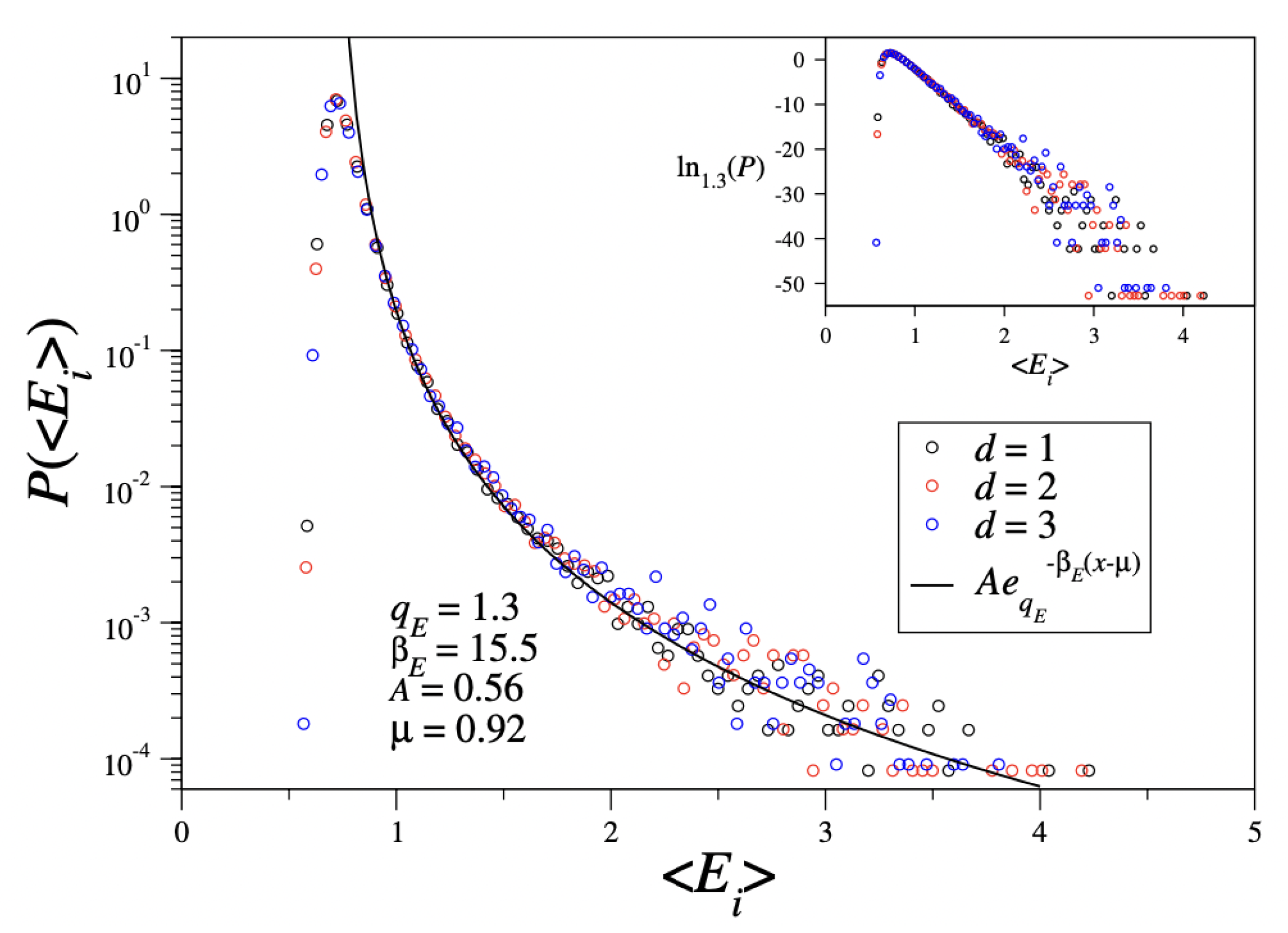
5.3. Clue III—Maximal Lyapunov Exponent of the Classical -Heisenberg Inertial Ferromagnet
5.4. Clue IV—Viscous-Fluid Spherical Capacitor
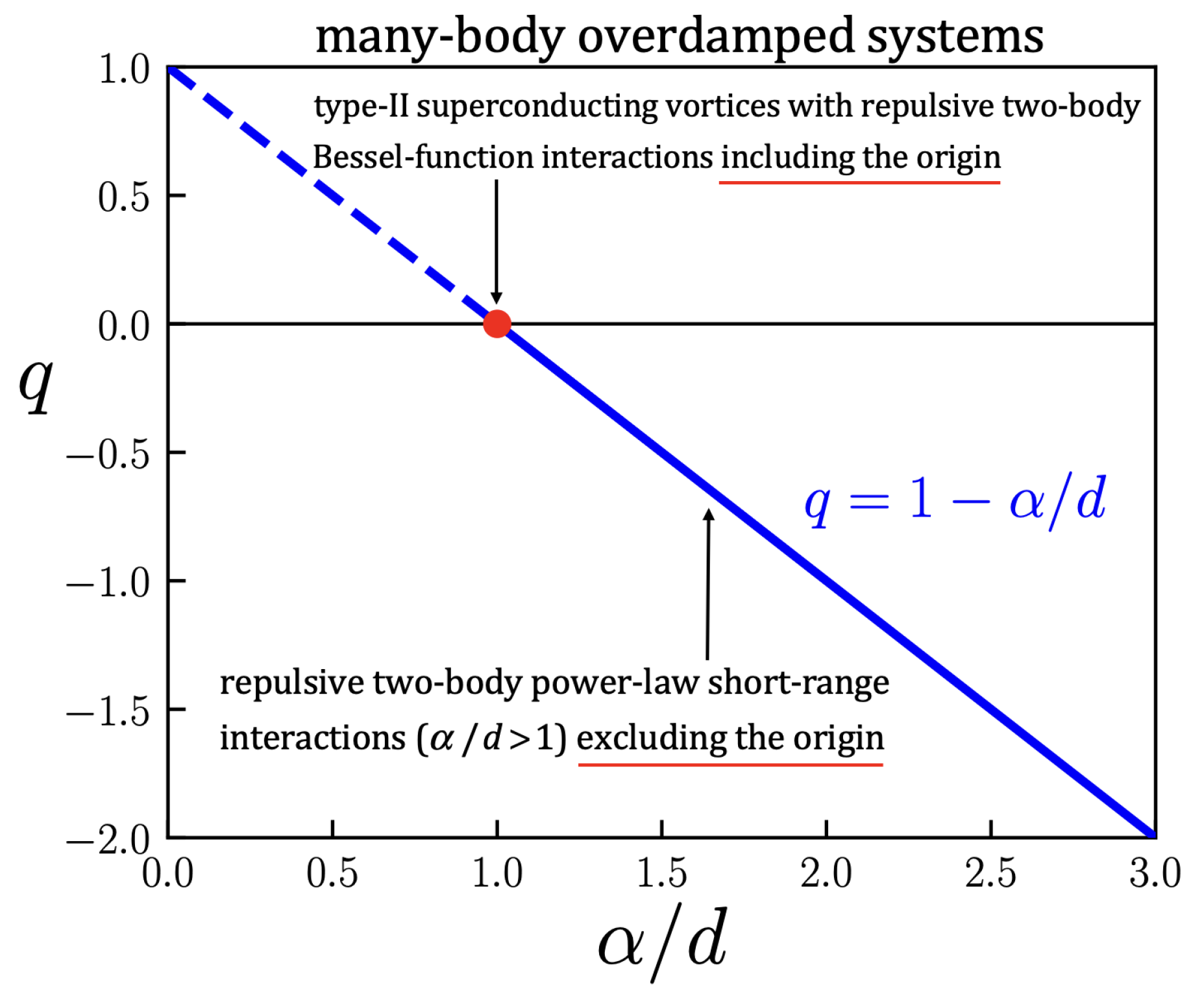
5.5. Clue V—Overdamped Many-Body Systems
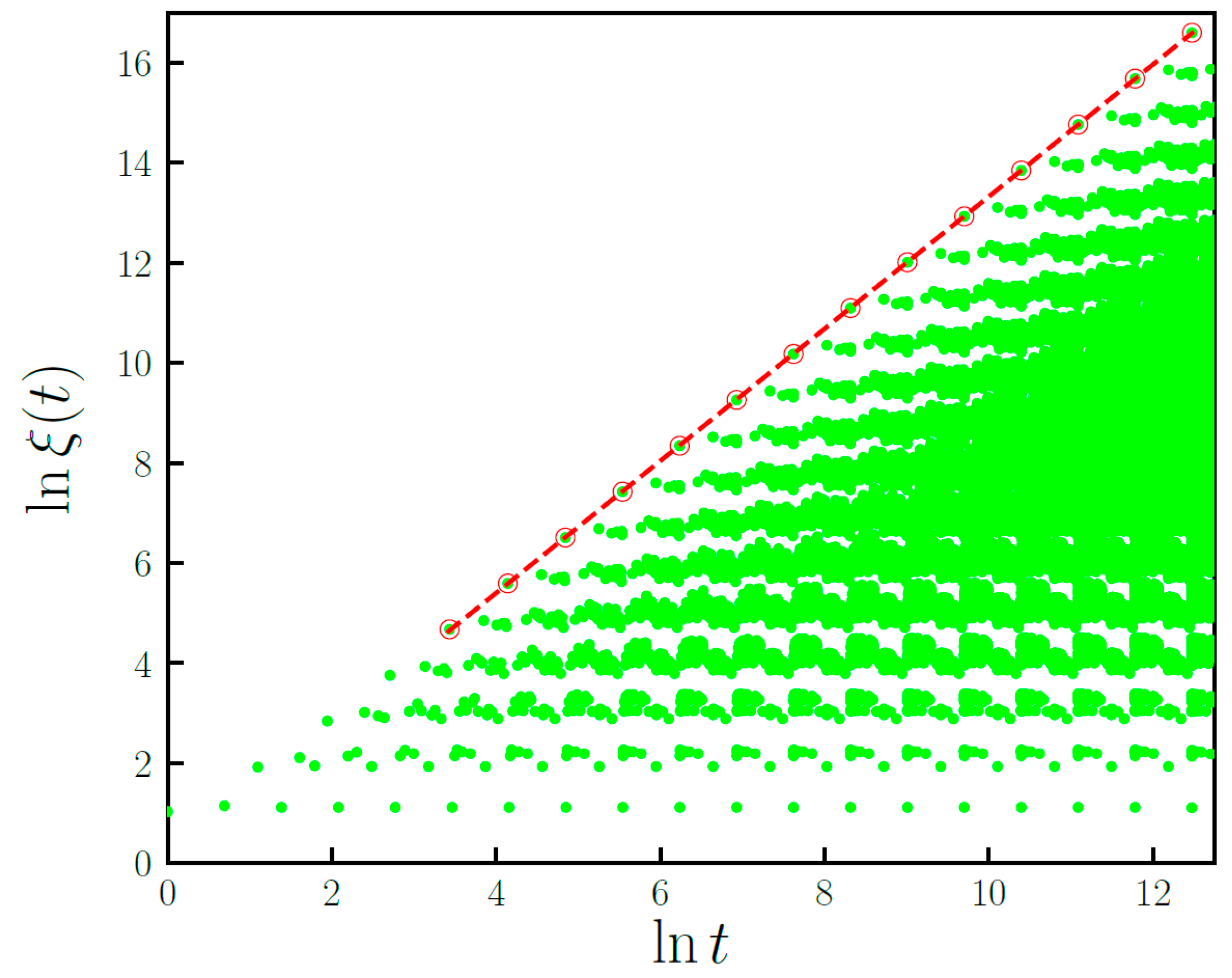
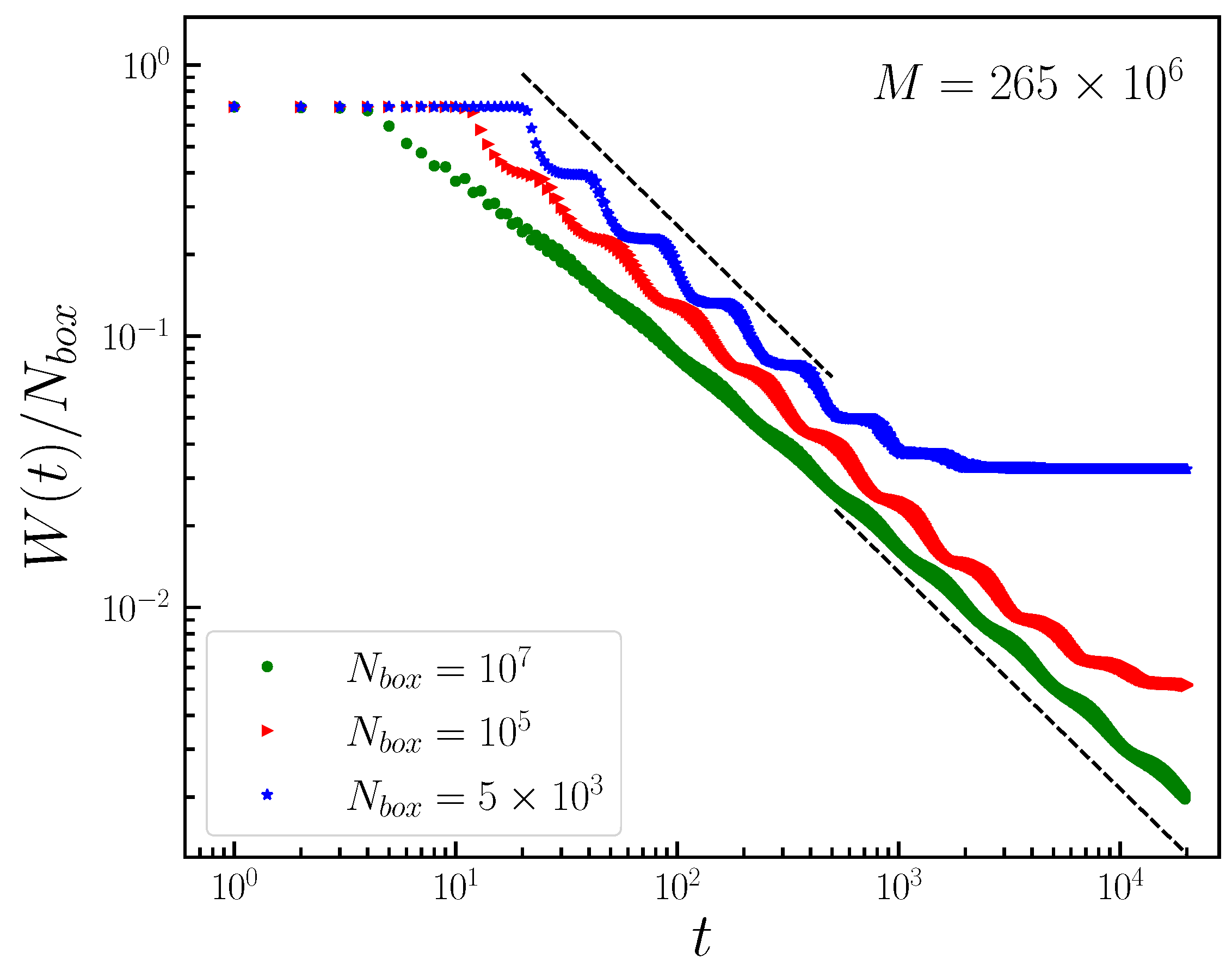
5.6. Clue VI—Kinetics of Point Defects in Short-Range-Interacting Hamiltonians
5.7. The Intriguing Case Of The Lennard–Jones’ Two-Body Potentials For Modeling Real Gases
6. Final Remarks and Conclusions
- -
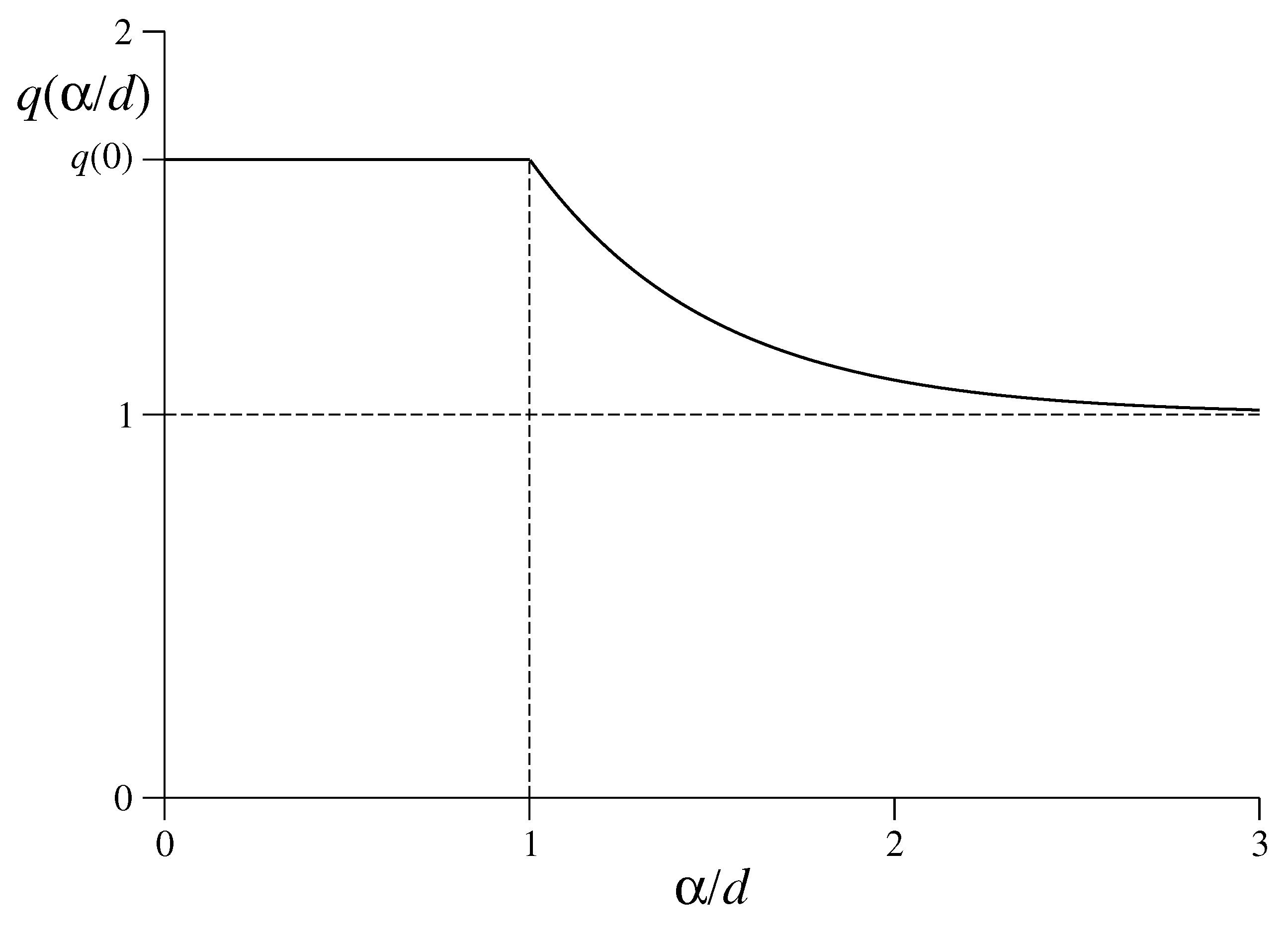
- The spatially averaged two-body potential is finite for , and diverges for . Such finiteness is necessary but not sufficient for all the BG thermostatistical quantities to be finite. Consistently, the total internal energy is thermodynamically extensive for , and superextensive for .
- -
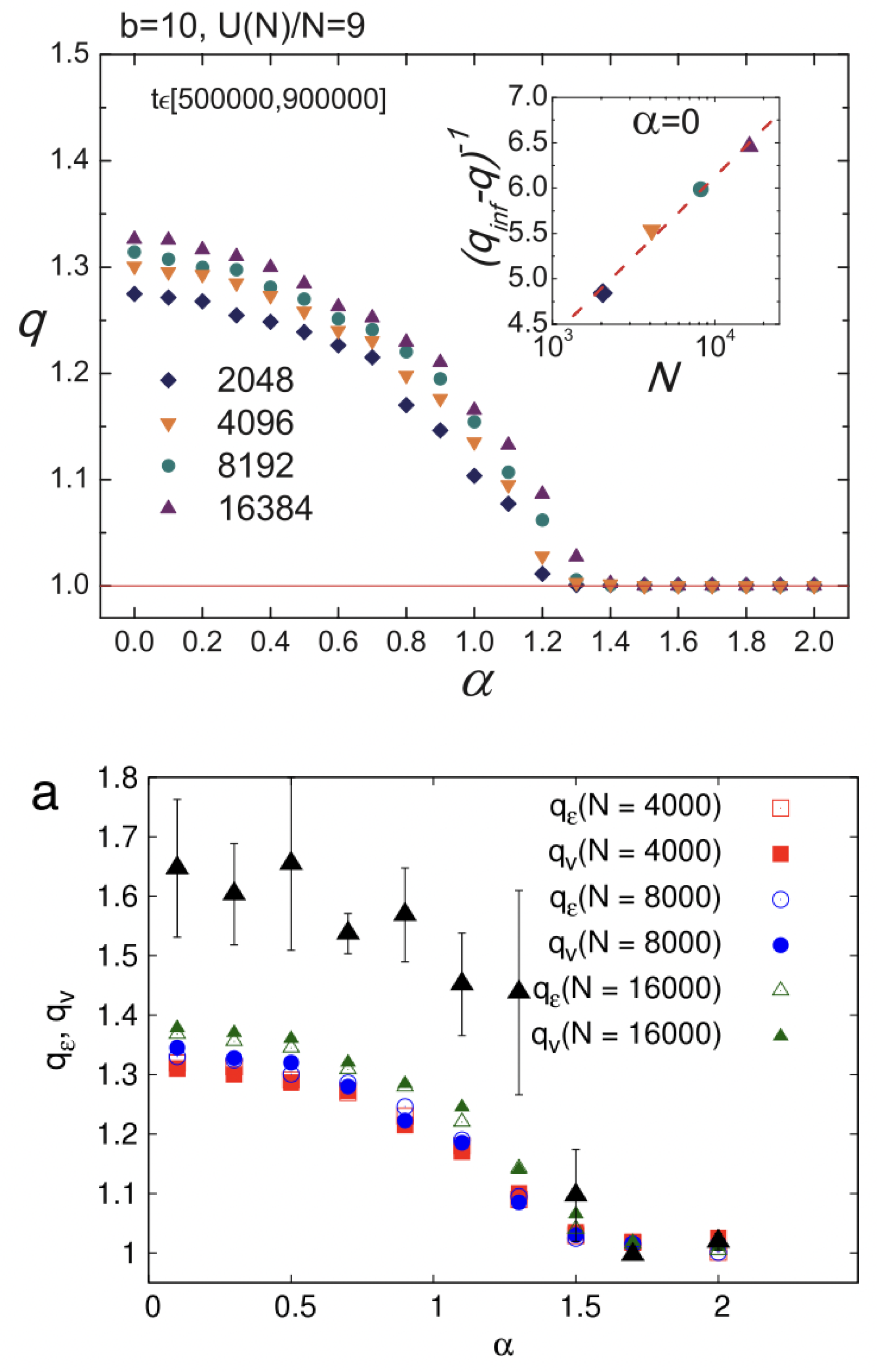
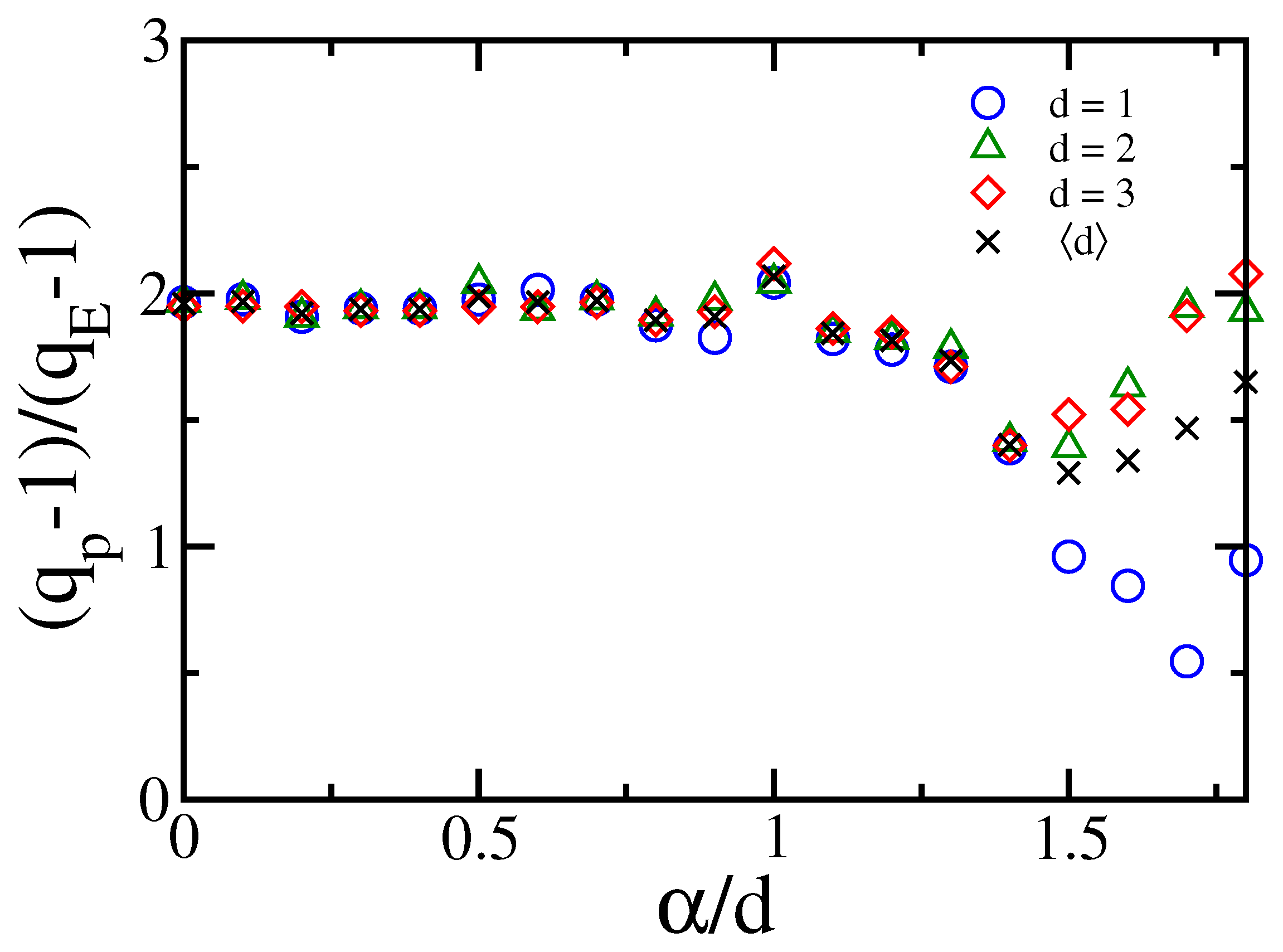
- The finiteness of the spatially averaged two-body potential is necessary for BG statistical mechanics to be applicable but it is not sufficient. Its full applicability requires also the finiteness of all the associated momenta, i.e., must also be finite for . Such a strong requirement is satisfied only in the limit of the present power-law models, or for Hamiltonians involving interactions only among relatively close neighbors (first, second, and third neighbors, for instance).
- -
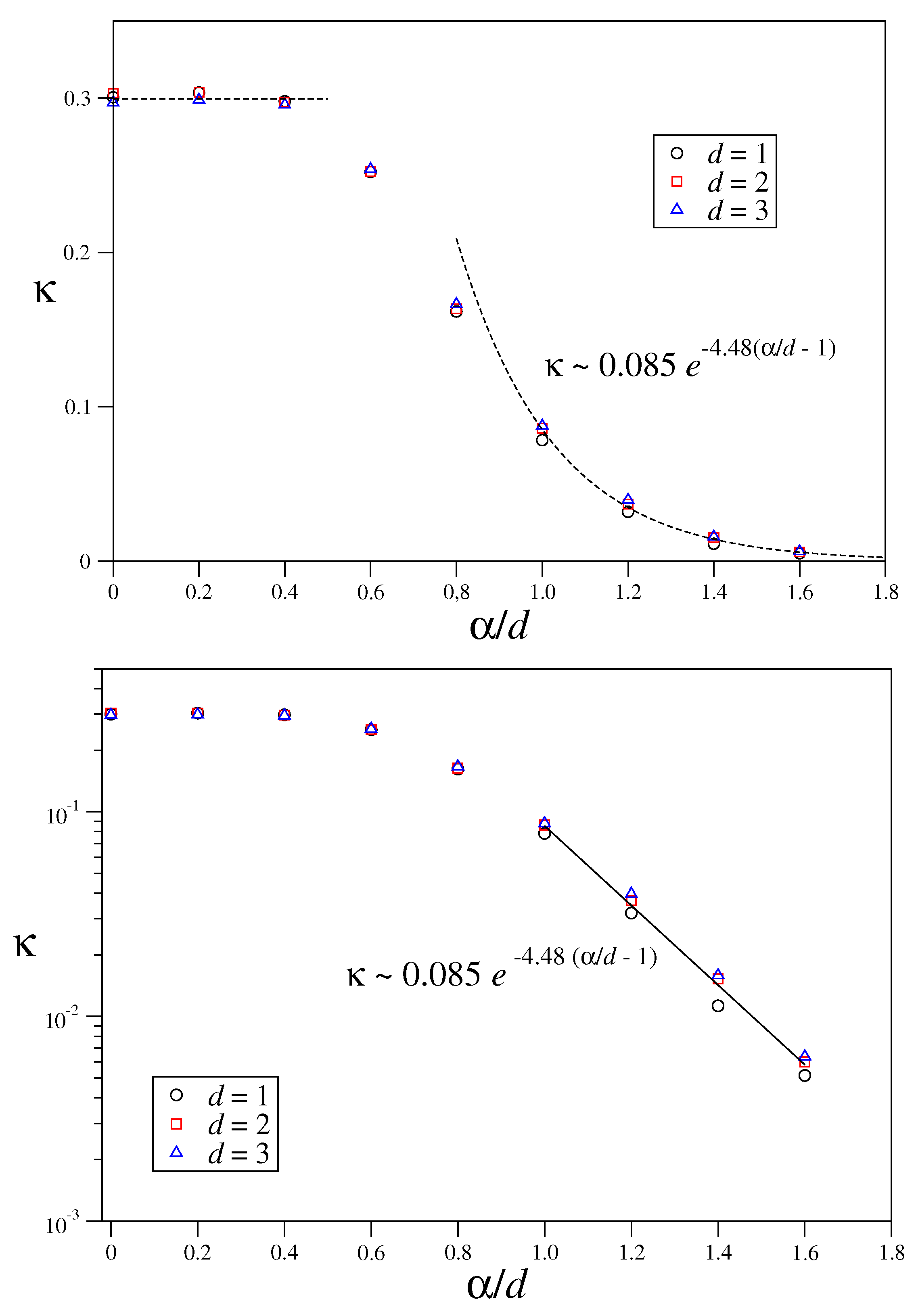
- The maximal Lyapunov exponent appears to decay with the number N of elements as with . It is possible that roughly , for all values of . If so, we can guarantee strong chaos (hence, mixing in phase-space, hence ergodicity) in the limit only for . In all other cases, i.e., , we would have, in the , weak chaos, and therefore ergodicity and mixing will not be guaranteed. This is consistent with the failure of the BG theory which is observed (nonexponential energy distribution, and non-Gaussian momenta distribution).
- -
- The fact that a BG partition function, as well as other thermostatistically relevant quantities (e.g., equations of states, energy and velocity distributions) are computable (within analytical mean-field methods, for example) is necessary but not sufficient for the BG theory to satisfactorily describe the system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Penrose, O. Foundations of Statistical Mechanics: A Deductive Treatment; Pergamon: Oxford, UK, 1970; p. 167. [Google Scholar]
- Tsallis, C. Entropy. Encyclopedia 2022, 2, 264–300. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- See This Website for a Regularly Updated Bibliography. Available online: http://tsallis.cat.cbpf.br/biblio.htm (accessed on 10 January 2023).
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and pp¯ collisions. Phys. Rev. D 2015, 91, 114027. [Google Scholar] [CrossRef]
- Deppman, A.; Megias, E.; Menezes, D.P. Fractals, non-extensive statistics, and QCD. Phys. Rev. D 2020, 101, 034019. [Google Scholar] [CrossRef]
- Yalcin, G.C.; Beck, C. Generalized statistical mechanics of cosmic rays: Application to positron-electron spectral indices. Sci. Rep. 2018, 8, 1764. [Google Scholar] [CrossRef]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis distributions in dissipative optical lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar] [CrossRef]
- Lutz, E.; Renzoni, F. Beyond Boltzmann-Gibbs statistical mechanics in optical lattices. Nat. Phys. 2013, 9, 615–619. [Google Scholar] [CrossRef]
- Combe, G.; Richefeu, V.; Stasiak, M.; Atman, A.P.F. Experimental validation of nonextensive scaling law in confined granular media. Phys. Rev. Lett. 2015, 115, 238301. [Google Scholar] [CrossRef]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Soc. USA 2005, 102, 15377. [Google Scholar] [CrossRef]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1996, 261, 459. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 1978, 19, 25. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. The Universal Metric Properties of Nonlinear Transformations. J. Stat. Phys. 1979, 21, 669. [Google Scholar] [CrossRef]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems: An Introduction; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263. [Google Scholar] [CrossRef]
- Tsallis, C.; Plastino, A.R.; Zheng, W.-M. Power-law sensitivity to initial conditions—New entropic representation. Chaos Solitons Fractals 1997, 8, 885. [Google Scholar] [CrossRef]
- Costa, U.M.S.; Lyra, M.L.; Plastino, A.R.; Tsallis, C. Power-law sensitivity to initial conditions within a logisticlike family of maps: Fractality and nonextensivity. Phys. Rev. E 1997, 56, 245. [Google Scholar] [CrossRef]
- Lyra, M.L.; Tsallis, C. Nonextensivity and Multifractality in Low-Dimensional Dissipative Systems. Phys. Rev. Lett. 1998, 80, 53. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Lyra, M.L. Circular-like maps: Sensitivity to the initial conditions, multifractality and nonextensivity. Eur. Phys. J. B 1999, 11, 309. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Lyra, M.L. Asymmetric unimodal maps at the edge of chaos. Phys. Rev. E 2002, 65, 036207. [Google Scholar] [CrossRef] [PubMed]
- Tirnakli, U. Dissipative maps at the chaos threshold: Numerical results for the single-site map. Phys. A 2002, 305, 119. [Google Scholar] [CrossRef]
- Beck, C.; Schlogl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Molteni, A. An Efficient Method for the Computation of the Feigenbaum Constants to High Precision. arXiv 2015, arXiv:1602.02357v1. Available online: https://arxiv.org/pdf/1602.02357.pdf (accessed on 10 January 2023).
- Latora, V.; Baranger, M.; Rapisarda, A.; Tsallis, C. The rate of entropy increase at the edge of chaos. Phys. Lett. A 2002, 273, 97. [Google Scholar] [CrossRef]
- Baranger, M.; Latora, V.; Rapisarda, A.A. Time evolution of thermodynamic entropy for conservative and dissipative chaotic maps. Chaos Solitons Fractals 2002, 13, 471–478. [Google Scholar] [CrossRef]
- Tirnakli, U.; Ananos, G.F.J.; Tsallis, C. Generalization of the Kolmogorov–Sinai entropy: Logistic-like and generalized cosine maps at the chaos threshold. Phys. Lett. A 2001, 289, 51. [Google Scholar] [CrossRef]
- de Moura, F.A.B.F.; Tirnakli, U.; Lyra, M.L. Convergence to the critical attractor of dissipative maps: Log-periodic oscillations, fractality, and nonextensivity. Phys. Rev. E 2000, 62, 6361. [Google Scholar] [CrossRef] [PubMed]
- Tonelli, R.; Coraddu, M. Numerical study of the oscillatory convergence to the attractor at the edge of chaos. Eur. Phys. J. B 2006, 2006 50, 355. [Google Scholar] [CrossRef]
- Grassberger, P. Temporal Scaling at Feigenbaum Points and Nonextensive Thermodynamics. Phys. Rev. Lett. 2005, 95, 140601. [Google Scholar] [CrossRef]
- Robledo, A. Incidence of nonextensive thermodynamics in temporal scaling at Feigenbaum points. Physica A 2006, 370, 449. [Google Scholar] [CrossRef]
- Robledo, A.; Moyano, L.G. q-deformed statistical-mechanical property in the dynamics of trajectories en route to the Feigenbaum attractor. Phys. Rev. E 2008, 77, 032613. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of Probability Measures; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Beck, C. Brownian motion from deterministic dynamics. Phys. A 1990, 169, 324. [Google Scholar] [CrossRef]
- Tirnakli, U.; Beck, C.; Tsallis, C. Central limit behavior of deterministic dynamical systems. Phys. Rev. E 2007, 75, 040106. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Beck, C. Closer look at time averages of the logistic map at the edge of chaos. Phys. Rev. E 2009, 79, 056209. [Google Scholar] [CrossRef] [PubMed]
- Ozgur, A.; Tirnakli, U. Generalized Huberman-Rudnick scaling law and robustness of q-Gaussian probability distributions. EPL 2013, 101, 20003. [Google Scholar]
- Huberman, B.A.; Rudnick, J. Scaling Behavior of Chaotic Flows. Phys. Rev. Lett. 1980, 45, 154. [Google Scholar] [CrossRef]
- Lichtenberg, A.J.; Lieberman, M.A. Regular and Chaotic Dynamics; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef]
- Bountis, A.; Veerman, J.J.P.; Vivaldi, F. Cauchy distributions for the integrable standard map. Phys. Lett. A 2020, 384, 126659. [Google Scholar] [CrossRef]
- Ruiz, G.; Tirnakli, U.; Borges, E.P.; Tsallis, C. Statistical characterization of the standard map. J. Stat. Mech. 2017, 063403. [Google Scholar] [CrossRef]
- Ruiz, G.; Tirnakli, U.; Borges, E.P.; Tsallis, C. Statistical characterization of discrete conservative systems: The web map. Phys. Rev. E 2017, 96, 042158. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Cetin, K. Dynamical robustness of discrete conservative systems: Harper and generalized standard maps. J. Stat. Mech. 2020, 063206. [Google Scholar] [CrossRef]
- Cetin, K.; Tirnakli, U.; Boghosian, B.M. A generalization of the standard map and its statistical characterization. Sci. Rep. 2022, 12, 8575. [Google Scholar] [CrossRef]
- Dauxois, T.; Ruffo, S.; Arimondo, E.; Wilkens, M. Dynamics and Thermodynamics of Systems with Long Range Interactions; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Dauxois, T.; Latora, V.; Rapisarda, A.; Ruffo, S.; Torcini, A. The Hamiltonian Mean Field Model: From Dynamics to Statistical Mechanics and Back; Lectures Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2002; p. 458. [Google Scholar]
- Pluchino, A.; Latora, V.; Rapisarda, A. Dynamics and thermodynamics of a model with long-range interactions. Contin. Mech. Thermodyn. 2004, 16, 245–255. [Google Scholar]
- Pluchino, A.; Latora, V.; Rapisarda, A. Metastable states, anomalous distributions and correlations in the HMF model. Phys. D Nonlinear Phenom. 2004, 193, 315–328. [Google Scholar] [CrossRef]
- Rapisarda, A.; Pluchino, A. Nonextensive thermodynamics and glassy behaviour. Europhys. News 2005, 36, 202. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Strogatz, S.H.; Mirollo, R.E.; Matthews, P.C. Coupled nonlinear oscillators below the synchronization threshold: Relaxation by generalized Landau damping. Phys. Rev. Lett. 1992, 68, 2730. [Google Scholar] [CrossRef]
- Pluchino, A.; Rapisarda, A. Metastability in the Hamiltonian Mean Field model and Kuramoto model. Phys. A 2006, 365, 184–189. [Google Scholar] [CrossRef]
- Miritello, G.; Pluchino, A.; Rapisarda, A. Phase Transitions and Chaos in Long-Range Models of Coupled Oscillators. Europhys. Lett. 2009, 85, 10007. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.P.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef]
- Panaggio, M.J.; Abrams, D.M. Chimera states: Coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity 2015, 28, R67. [Google Scholar] [CrossRef]
- Belykh, I.V.; Brister, B.N.; Belykh, V.N. Bistability of patterns of synchrony in Kuramoto oscillators with inertia. Chaos Interdisc. J. Nonlinear Sci. 2016, 26, 094822. [Google Scholar] [CrossRef] [PubMed]
- Odor, G.; Kelling, J. Critical synchronization dynamics of the Kuramoto model on connectome and small world graphs. Sci. Rep. 2019, 9, 19621. [Google Scholar] [CrossRef] [PubMed]
- Vandermeer, J.; Hajian-Forooshani, Z.; Medina, N.; Perfecto, I. New forms of structure in ecosystems revealed with the Kuramoto model. R. Soc. Open Sci. 2021, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Miritello, G.; Pluchino, A.; Rapisarda, A. Central limit behavior in the Kuramoto model at the ‘edge of chaos’. Phys. A 2009, 388, 4818–4826. [Google Scholar] [CrossRef]
- Ruffo, S. Transport, Plasma Physics; Benkadda, S., Elskens, Y., Doveil, F., Eds.; World Scientific: Singapore, 1994; p. 114. [Google Scholar]
- Antoni, M.; Ruffo, S. Clustering and relaxation in Hamiltonian long-range dynamics. Phys. Rev. E 1995, 52, 2361. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Rapisarda, A.; Ruffo, S. Lyapunov instability and finite size effects in a system with long-range forces. Phy. Rev. Lett. 1998, 80, 692. [Google Scholar] [CrossRef]
- Latora, V.; Rapisarda, A.; Ruffo, S. Superdiffusion and out-of-equilibrium chaotic dynamics with many degrees of freedom. Phys. Rev. Lett. 1999, 83, 2104. [Google Scholar] [CrossRef]
- Latora, V.; Rapisarda, A.; Tsallis, C. Non-Gaussian equilibrium in a long-range Hamiltonian system. Phys. Rev. E 2001, 64, 056134. [Google Scholar] [CrossRef] [PubMed]
- Pluchino, A.; Rapisarda, A.; Tsallis, C. Nonergodicity and central-limit behavior for long-range Hamiltonians. EPL 2007, 80, 26002. [Google Scholar] [CrossRef]
- Pluchino, A.; Latora, V.; Rapisarda, A. Glassy phase in the Hamiltonian mean-field model. Phys. Rev. E 2004, 69, 056113. [Google Scholar] [CrossRef]
- Anteneodo, C.; Tsallis, C. Breakdown of Exponential Sensitivity to Initial Conditions: Role of the Range of Interactions. Phys. Rev. Lett. 1998, 80, 5313–5316. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators, Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Campa, A.; Giansanti, A.; Moroni, D.; Tsallis, C. Classical spin systems with long-range interactions: Universal reduction of mixing. Phys. Lett. A 2001, 286, 251–256. [Google Scholar] [CrossRef]
- Firpo, M.C. Analytic estimation of the Lyapunov exponent in a mean-field model undergoing a phase transition. Phys. Rev. E 1998, 57, 6599–6603. [Google Scholar] [CrossRef]
- Cirto, L.J.L.; Rodríguez, A.; Nobre, F.D.; Tsallis, C. Validity and failure of the Boltzmann weight. EPL 2018, 123, 30003. [Google Scholar] [CrossRef]
- Rodríguez, A.; Nobre, F.D.; Tsallis, C. Quasi-stationary-state duration in the classical d-dimensional long-range inertial XY ferromagnet. Phys. Rev. E 2021, 103, 042110. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, A.; Nobre, F.D.; Tsallis, C. Criticality in the duration of quasistationary state. Phys. Rev. E 2021, 104, 014144. [Google Scholar] [CrossRef] [PubMed]
- Cirto, L.J.L.; Lima, L.S.; Nobre, F.D. Controlling the range of interactions in the classical inertial ferromagnetic Heisenberg model: Analysis of metastable states. J. Stat. Mech. Theory Exp. 2015, P04012. [Google Scholar] [CrossRef]
- Rodriguez, A.; Nobre, F.D.; Tsallis, C. d-dimensional classical Heisenberg model with arbitrarily-ranged interactions: Lyapunov exponents and distributions of momenta and energies. Entropy 2019, 21, 31. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, A.; Nobre, F.D.; Tsallis, C. Quasi-stationary-state duration in d-dimensional long-range model. Phys. Rev. Res. 2020, 2, 023153. [Google Scholar] [CrossRef]
- Soares, D.J.B.; Tsallis, C.; Mariz, A.M.; da Silva, L.R. Preferential attachment growth model and nonextensive statistical mechanics. Europhys. Lett. 2005, 70, 70. [Google Scholar] [CrossRef]
- Thurner, S.; Tsallis, C. Nonextensive aspects of self-organized scale-free gas-like networks. Europhys. Lett. 2005, 72, 197–203. [Google Scholar] [CrossRef]
- Brito, S.G.A.; da Silva, L.R.; Tsallis, C. Role of dimensionality in complex networks. Sci. Rep. 2016, 6, 27992. [Google Scholar] [CrossRef]
- Nunes, T.C.; Brito, S.; da Silva, L.R.; Tsallis, C. Role of dimensionality in preferential attachment growth in the Bianconi-Barabasi model. J. Stat. Mech. 2017, 093402. [Google Scholar] [CrossRef]
- Brito, S.; Nunes, T.C.; da Silva, L.R.; Tsallis, C. Scaling properties of d-dimensional complex networks. Phys. Rev. E 2019, 99, 012305. [Google Scholar] [CrossRef]
- Cinardi, N.; Rapisarda, A.; Tsallis, C. A generalised model for asymptotically-scale-free geographical networks. J. Stat. Mech. 2020, 2020, 043404. [Google Scholar] [CrossRef]
- de Oliveira, R.M.; Brito, S.; da Silva, L.R.; Tsallis, C. Connecting complex networks to nonadditive entropies. Sci. Rep. 2021, 11, 1130. [Google Scholar] [CrossRef]
- de Oliveira, R.M.; Brito, S.; da Silva, L.R.; Tsallis, C. Statistical mechanical approach of complex networks with weighted links. JSTAT 2022, 063402. [Google Scholar] [CrossRef]
- Tsallis, C.; de Oliveira, R.M. Complex network growth model: Possible isomorphism between nonextensive statistical mechanics and random geometry. Chaos 2022, 32, 053126. [Google Scholar] [CrossRef]
- Christodoulidi, H.; Tsallis, C.; Bountis, T. Fermi-Pasta-Ulam model with long-range interactions: Dynamics and thermostatistics. EPL 2014, 108, 40006. [Google Scholar] [CrossRef]
- Bagchi, D.; Tsallis, D. Fermi-Pasta-Ulam-Tsingou problems: Passage from Boltzmann to q-statistics. Phys. A 2018, 491, 869–873. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Casas, G.A.; Nobre, F.D.; Curado, E.M.F. New type of equilibrium distribution for a system of charges In a spherically-symmetric electric field. EPL 2019, 126, 10005. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar] [CrossRef]
- Moreira, A.A.; Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Tsallis, C. Overdamped dynamics of particles with repulsive power-law interactions. Phys. Rev. E 2018, 98, 032138. [Google Scholar] [CrossRef]
- Mazenko, G.F. Vortex velocities in the O(n) symmetric time-dependent Ginzburg-Landau model. Phys. Rev. Lett. 1997, 78, 401–404. [Google Scholar] [CrossRef]
- Qian, H.; Mazenko, G.F. Vortex dynamics in a coarsening two-dimensional XY model. Phys. Rev. E 2003, 68, 021109. [Google Scholar] [CrossRef] [PubMed]
- Mie, G. Zur kinetischen Theorie der einatomigen Korper. Ann. Phys. 1903, 316, 657–697. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. Ser. A 1924, 106, 441–462. [Google Scholar]
- Jones, J.E. On the determination of molecular fields. —II. From the equation of state of a gas. Proc. R. Soc. Lond. Ser. A 1924, 106, 463–477. [Google Scholar]
- Lennard-Jones, J.E. Cohesion. Proc. Phys. Soc. 1931, 43, 461–482. [Google Scholar] [CrossRef]

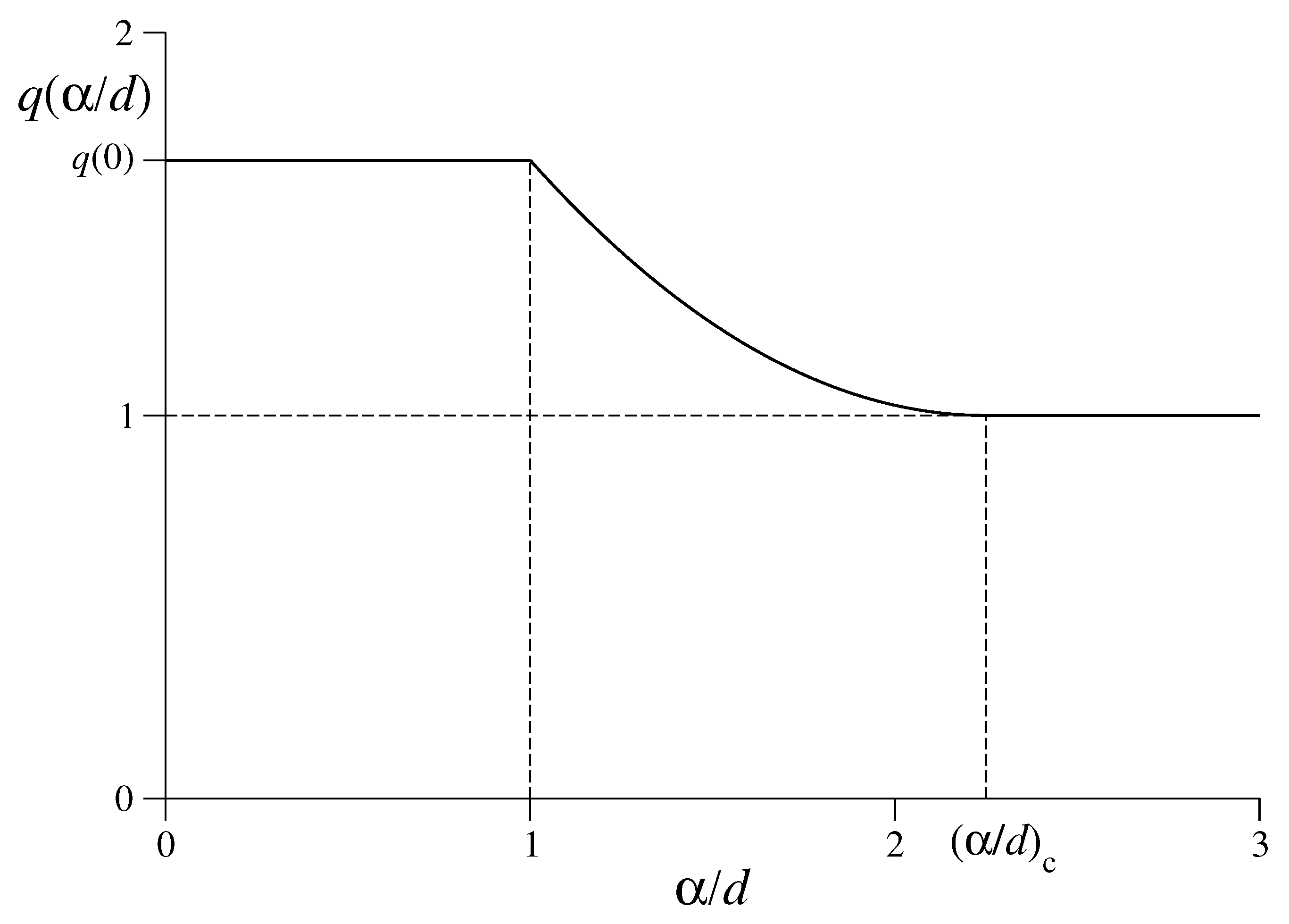
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, A.; Pluchino, A.; Tirnakli, U.; Rapisarda, A.; Tsallis, C. Nonextensive Footprints in Dissipative and Conservative Dynamical Systems. Symmetry 2023, 15, 444. https://doi.org/10.3390/sym15020444
Rodríguez A, Pluchino A, Tirnakli U, Rapisarda A, Tsallis C. Nonextensive Footprints in Dissipative and Conservative Dynamical Systems. Symmetry. 2023; 15(2):444. https://doi.org/10.3390/sym15020444
Chicago/Turabian StyleRodríguez, Antonio, Alessandro Pluchino, Ugur Tirnakli, Andrea Rapisarda, and Constantino Tsallis. 2023. "Nonextensive Footprints in Dissipative and Conservative Dynamical Systems" Symmetry 15, no. 2: 444. https://doi.org/10.3390/sym15020444
APA StyleRodríguez, A., Pluchino, A., Tirnakli, U., Rapisarda, A., & Tsallis, C. (2023). Nonextensive Footprints in Dissipative and Conservative Dynamical Systems. Symmetry, 15(2), 444. https://doi.org/10.3390/sym15020444