Numerical Analysis of Fractional-Order Camassa–Holm and Degasperis–Procesi Models

Abstract

This study proposes innovative methods for the time-fractional modified Degasperis–Procesi (mDP) and Camassa–Holm (mCH) models of solitary wave solutions. To formulate the concepts of the homotopy perturbation transform method (HPTM) and Elzaki transform decomposition method (ETDM), we mix the Elzaki transform (ET), homotopy perturbation method (HPM), and Adomian decomposition method (ADM). The Caputo sense is applied to this work. The solutions to a few numerical examples of the modified Degasperis–Procesi (mDP) and Camassa–Holm (mCH) are shown for integer and fractional orders of the issues. The derived and precise solutions are compared using two-dimensional and three-dimensional plots of the solutions, confirming the suggested method’s improved accuracy. Tables are created for each problem to display the suggested approach’s results, precise solutions, and absolute error. These methods provide the iterations as a series of solutions. To show the proposed techniques’ efficiency, we compute the absolute error. It is evident from the estimated values that the approaches are precise and simple and that they can therefore be further extended to linear and nonlinear issues.

1. Introduction

Fractional calculus (FC) is an easy and useful method for obtaining precise data for various equation forms. This dynamic field of mathematics, which generalizes the integer order to its fractional order and gives rise to a broad class of mathematical modeling [1,2,3] generates the most significant fractional differential equations (FDEs). Numerous physical phenomena utilizing fractional differential equations have recently been the focus of significant research for various scientific and engineering applications. Caputo–Fabrizio, Atangana–Baleanu, Riemann–Liouville, Liouville–Caputo, and Hadamard, among others, presented various fundamental fractional derivative principles [4,5,6,7]. To generate a fractional derivative in the desired order, the Caputo fractional derivative calculates first an ordinary derivative and then a fractional integral. The fractional Riemann–Liouville derivative is calculated in reverse order. The fractional Riemann–Liouville derivative permits initial sources to be stated as fractional derivatives and their integrals. In contrast, the fractional Caputo derivative only permits the inclusion of conventional initial and boundary sources [8]. Nonlinear models have been utilized to describe various industrial and scientific applications, including astrophysics, hydrology, nuclear engineering, meteorology, and astrobiology [9,10].

Fractional partial differential equations (FPDEs) have gained popularity among mathematicians in recent years due to their numerous applications, particularly in applied sciences, engineering, mathematical physics, biology, neural materials, strong state material science, plasma physics, geo-optical filaments, electrode’s electrolyte, allometric scaling laws in ecology and biology, the quantum evolution of complex systems, chemical physics, dielectric polarization, fractional dynamics, quantitative finance, astrophysics, electromagnetic waves, nonlinear optics and stochastic dynamical systems. A few other applications of FPDEs can be found in viscoelastic and viscoplastic flow [11], continuum mechanics [12], spherical flames [13], wave propagation [14], image processing [15], anomalous diffusion [16], entropy [17], turbulent flow [18], groundwater containment transport [19] and so on.

Due of the above-mentioned useful applications of FC in real-world challenges, the study of this area has become attractive to academics. Mathematicians realized it was required to investigate the numerical or analytical solutions of FPDEs and their systems to further the topic’s investigation [20,21,22]. Using analytical and numerical methods, numerous significant mathematical models that mirror some of the physical processes in nature are routinely solved [23,24,25]. To resolve FPDEs and similar systems, mathematicians have developed a variety of approaches. This is a well-known field of inquiry since the outputs of the given challenges support the dynamics of natural systems as they occur [26,27,28]. Scholars have put their best efforts into this subject and have regularly developed useful approaches. In this regard, significant and effective procedures have been put into place to address FPDEs and associated systems, such as the Sine–Gordon expansion method [29], Elzaki transform decomposition method [30], variational iteration method [31,32], finite element method [33], first integral method [34], natural transform decomposition method [35,36], generalized Kudryashov method [37], finite volume methods [38], and many other techniques.

In this work, we consider a family of significant physical equations known as a modified $\beta$-equation, which has the following form [39]:

$$\frac{{\partial }^{\varsigma }\zeta (\varrho ,\lambda )}{\partial {\lambda }^{\varsigma }}-\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+(\beta +1){\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }-\beta \frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}=0,0<\varsigma \le 1.$$

(1)

Choosing $\beta =3$ results in the mDP model

$$\frac{{\partial }^{\varsigma }\zeta (\varrho ,\lambda )}{\partial {\lambda }^{\varsigma }}-\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }-3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}=0,0<\varsigma \le 1.$$

(2)

Choosing $\beta =2$ in Equation (1) results in the mCH model

$$\frac{{\partial }^{\varsigma }\zeta (\varrho ,\lambda )}{\partial {\lambda }^{\varsigma }}-\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }-2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}=0,0<\varsigma \le 1.$$

(3)

Here, $\zeta$ denotes a horizontal component of the fluid velocity and $\varrho$ and $\lambda$ denote the spatial and temporal components. The mCH and mDP models resemble the incompressible Euler equation, which was revealed to be fully integrable with a Lax pair and emerges in shallow water [40]. Liu and Ouyang [41] employed numerical simulations to develop new solitary wave solutions for this model. To acquire significant results for the time-fractional mCH and mDP models, Dubey et al. [42] proposed a q-homotopy analysis approach coupled with a novel approach. Behera and Mehra created a wavelet-optimized finite difference approach to research the approximations of the mCH and mDP models’ solutions [43]. To give a few different bright and dark soliton results of the mCH and mDP models in the form of Weierstrass elliptic functions and Jacobi elliptic functions, Kader and Latif [44] employed a Lie symmetry technique. To solve the mCH and mDP models, Yousif et al. developed two methods, namely, HPM and VIM, and established the results in good agreement [45]. In the present study, we develop a concept for novel schemes that allow us to approximately solve the fractional mCH and mDP models in the Caputo sense. The homotopy perturbation transform technique (HPTM) and Elzaki transform decomposition method (ETDM) were both combined with Elzaki’s transform (ET). It is essential to remember that the proposed procedures can perform better overall since they can need less computing work than the other techniques while maintaining a high accuracy of the numerical result. This work’s structure is as follows: We give a few basic aspects of calculus theory in Section 2. Section 3 and Section 4 provide the HPTM and ETDM formulations for obtaining the general solution. In Section 5, using a few numerical examples and comparisons to the exact solution, we show the viability and effectiveness of both approaches. Finally, Section 6 contains the conclusion.

2. Preliminaries Concepts

Definition 1.

The Abel–Riemann derivative of fractional operator $D^{\varsigma }$ of order ς is given as [46,47,48]

$$D^{\varsigma }\zeta \left(\varrho \right)=\left\{\begin{array}{c}\frac{d^j}{d{\varrho }^j}\zeta \left(\varrho \right),\varsigma =j,\hfill \\ \frac{1}{\Gamma (j-\varsigma )}\frac{d}{d{\varrho }^j}{\int }_0^{\varrho }\frac{\zeta \left(\varrho \right)}{{(\varrho -\psi )}^{\varsigma -j+1}}d\psi ,j-1<\varsigma <j,\hfill \end{array}\right.$$

where $j\in Z^{+}$, $\varsigma \in R^{+}$ and

$$D^{-\varsigma }\zeta \left(\varrho \right)=\frac{1}{\Gamma \left(\varsigma \right)}{\int }_0^{\varrho }{(\varrho -\psi )}^{\varsigma -1}\zeta \left(\psi \right)d\psi ,0<\varsigma \le 1.$$

Definition 2.

The fractional-order Abel-Riemann integration operator $J^{\psi }$ is defined as [46,47,48]

$$J^{\varsigma }\zeta \left(\varrho \right)=\frac{1}{\Gamma \left(\varsigma \right)}{\int }_0^{\varrho }{(\varrho -\psi )}^{\varsigma -1}\zeta \left(\varrho \right)d\varrho ,\varrho >0,\varsigma >0.$$

The operator has the basic properties:

$$\begin{array}{c}\hfill J^{\varsigma }{\varrho }^j=\frac{\Gamma (j+1)}{\Gamma (j+\varsigma +1)}{\varrho }^{j+\psi },\\ \hfill D^{\varsigma }{\varrho }^j=\frac{\Gamma (j+1)}{\Gamma (j-\varsigma +1)}{\varrho }^{j-\psi }.\end{array}$$

Definition 3.

The Caputo fractional operator $D^{\varsigma }$ of ς is defined as [46,47,48]

$${}^C{D}^{\varsigma }\zeta \left(\varrho \right)=\left\{\begin{array}{c}\frac{1}{\Gamma (j-\varsigma )}{\int }_0^{\varrho }\frac{{\zeta }^j\left(\psi \right)}{{(\varrho -\psi )}^{\varsigma -j+1}}d\psi ,j-1<\varsigma <j,\hfill \\ \frac{d^j}{d{\varrho }^j}\zeta \left(\varrho \right),j=\varsigma .\hfill \end{array}\right.$$

(4)

Definition 4.

$$\begin{array}{cc}\hfill J_{\varrho }^{\varsigma }{D}_{\varrho }^{\varsigma }\zeta \left(\varrho \right)& =g\left(\varrho \right)-\sum _{k=0}^m{g}^k\left(0^{+}\right)\frac{{\varrho }^k}{k!},for\varrho >0,andj-1<\varsigma \le j,j\in N.\hfill \\ \hfill D_{\varrho }^{\varsigma }{J}_{\varrho }^{\varsigma }\zeta \left(\varrho \right)& =g\left(\varrho \right).\hfill \end{array}$$

(5)

Definition 5.

The fractional-order Caputo operator of Elzaki’s transform is given by:

$$\mathtt{E}\left[D_{\varrho }^{\varsigma }\zeta \left(\varrho \right)\right]=s^{-\varsigma }\mathtt{E}\left[\zeta \left(\varrho \right)\right]-\sum _{k=0}^{j-1}{s}^{2-\varsigma +k}{\zeta }^{\left(k\right)}\left(0\right),wherej-1<\varsigma <j.$$

3. Procedure of HPTM

Here, the HPTM procedure is given to solve the FPDEs:

$$D_{\lambda }^{\varsigma }\zeta (\varrho ,\lambda )={\mathcal{P}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )+{\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda ),0<\varsigma \le 1,$$

(6)

having initial source

$$\zeta (\varrho ,0)=\xi \left(\varrho \right).$$

Here, $D_{\lambda }^{\varsigma }=\frac{{\partial }^{\varsigma }}{\partial {\lambda }^{\varsigma }}$ is the Caputo type derivative of order $\varsigma$, and ${\mathcal{P}}_1\left[\varrho \right],$${\mathcal{R}}_1\left[\varrho \right]$ are linear and nonlinear functions.

Operating the ET, we have

$$\mathtt{E}\left[D_{\lambda }^{\varsigma }\zeta (\varrho ,\lambda )\right]=\mathtt{E}[{\mathcal{P}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )+{\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )],$$

(7)

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}[{\mathcal{P}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )+{\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )].$$

(8)

Using the differential property of the ET, we get

$$M\left(u\right)=u^2\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}[{\mathcal{P}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )+{\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )].$$

(9)

Using the inverse ET, we have

$$\zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}[{\mathcal{P}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )+{\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )]\right].$$

(10)

Now, by implementing HPM on Equation (12),

$$\zeta (\varrho ,\lambda )=\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda ).$$

(11)

where $ϵ\in [0,1]$ is a homotopy parameter.

The nonlinear term in Equation (8) can be represented as

$${\mathcal{R}}_1\left[\varrho \right]\zeta (\varrho ,\lambda )=\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\zeta \right),$$

(12)

We can get the polynomials utilizing the following method [49]:

$$H_k({\zeta }_0,{\zeta }_1,\dots ,{\zeta }_n)=\frac{1}{\Gamma (n+1)}{D}_{ϵ}^k{\left[{\mathcal{R}}_1\left(\sum _{k=0}^{\infty }{ϵ}^i{\zeta }_i\right)\right]}_{ϵ=0},$$

(13)

where $D_{ϵ}^k=\frac{{\partial }^k}{\partial {ϵ}^k}.$

By utilizing (14) and (15) in (12), we have

$$\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )=\zeta (\varrho ,0)+ϵ\times \left({\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}\{{\mathcal{P}}_1\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )+\sum _{k=0}^{\infty }{ϵ}^k{H}_k\left(\zeta \right)\}\right]\right).$$

(14)

Correlating the coefficient of $ϵ$, we obtain

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\varrho ,\lambda )=\zeta (\varrho ,0),\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\varrho ,\lambda )={\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}({\mathcal{P}}_1\left[\varrho \right]{\zeta }_0(\varrho ,\lambda )+H_0\left(\zeta \right))\right],\hfill \\ \hfill & {ϵ}^2:{\zeta }_2(\varrho ,\lambda )={\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}({\mathcal{P}}_1\left[\varrho \right]{\zeta }_1(\varrho ,\lambda )+H_1\left(\zeta \right))\right],\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & {ϵ}^k:{\zeta }_k(\varrho ,\lambda )={\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}({\mathcal{P}}_1\left[\varrho \right]{\zeta }_{k-1}(\varrho ,\lambda )+H_{k-1}\left(\zeta \right))\right],k>0,k\in N.\hfill \end{array}$$

(15)

Thus, the series form approximation Equation (8) is

$$\zeta (\varrho ,\lambda )=\underset{M\to \infty }{\lim }\sum _{k=1}^M{\zeta }_k(\varrho ,\lambda ).$$

(16)

4. Procedure of ETDM

Here, the ETDM procedure is presented to solve the FPDEs:

$$D_{\lambda }^{\varsigma }\zeta (\varrho ,\lambda )={\mathcal{P}}_1(\varrho ,\lambda )+{\mathcal{R}}_1(\varrho ,\lambda ),0<\varsigma \le 1,$$

(17)

having initial source

$$\zeta (\varrho ,0)=\xi \left(\varrho \right).$$

Here, $D_{\lambda }^{\varsigma }=\frac{{\partial }^{\varsigma }}{\partial {\lambda }^{\varsigma }}$ is the Caputo type derivative of order $\varsigma$, and ${\mathcal{P}}_1$ and ${\mathcal{R}}_1$ are linear and non-linear functions.

Operating the ET, we have

$$\begin{array}{cc}\hfill & \mathtt{E}\left[D_{\lambda }^{\varsigma }\zeta (\varrho ,\lambda )\right]=\mathtt{E}[{\mathcal{P}}_1(\varrho ,\lambda )+{\mathcal{R}}_1(\varrho ,\lambda )],\hfill \\ \hfill & \frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}[{\mathcal{P}}_1(\varrho ,\lambda )+{\mathcal{R}}_1(\varrho ,\lambda )].\hfill \end{array}$$

(18)

Using the differential property of the ET, we get

$$M\left(u\right)=u\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}[{\mathcal{P}}_1(\varrho ,\lambda )+{\mathcal{R}}_1(\varrho ,\lambda )],$$

(19)

Using the inverse ET, we have

$$\zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}[u^{\varsigma }\mathtt{E}[{\mathcal{P}}_1(\varrho ,\lambda )+{\mathcal{R}}_1(\varrho ,\lambda )].$$

(20)

The decomposition solution of $\zeta (\varrho ,\lambda )$ is as follows:

$$\zeta (\varrho ,\lambda )=\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda ).$$

(21)

The nonlinear term in Equation (19) can be represented as

$${\mathcal{R}}_1(\varrho ,\lambda )=\sum _{m=0}^{\infty }{\mathcal{A}}_m\left(\zeta \right).$$

(22)

with

$${\mathcal{A}}_m\left({\zeta }_0,{\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_m\right)=\frac{1}{m!}{\left[\frac{{\partial }^m}{\partial {\ell }^m}\left\{{\mathcal{R}}_1\left(\sum _{m=0}^{\infty }{\ell }^m{\zeta }_m\right)\right\}\right]}_{\ell =0},m=0,1,2,\cdots$$

(23)

By utilizing (24) and (26) in (23), we have

$$\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}{u}^{\varsigma }\left[\mathtt{E}\left\{{\mathcal{P}}_1\left(\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )\right)+\sum _{m=0}^{\infty }{\mathcal{A}}_m\left(\zeta \right)\right\}\right].$$

(24)

Thus, we get

$${\zeta }_0(\varrho ,\lambda )=\zeta (\varrho ,0),$$

(25)

$${\zeta }_1(\varrho ,\lambda )={\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}\{{\mathcal{P}}_1\left({\zeta }_0\right)+{\mathcal{A}}_0\}\right],$$

In general, for $m\ge 1$, we have

$${\zeta }_{m+1}(\varrho ,\lambda )={\mathtt{E}}^{-1}\left[u^{\varsigma }\mathtt{E}\{{\mathcal{P}}_1\left({\zeta }_m\right)+{\mathcal{A}}_m\}\right].$$

5. Numerical Problem

Example 1.

Let us assume the following fractional mDP model

$$\frac{{\partial }^{\varsigma }\zeta (\varrho ,\lambda )}{\partial {\lambda }^{\varsigma }}-\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }-3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}=0$$

(26)

with initial source

$$\zeta (\varrho ,0)=-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)$$

Operating the ET, we have

$$\mathtt{E}\left(\frac{{\partial }^{\varsigma }\zeta }{\partial {\lambda }^{\varsigma }}\right)=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(27)

Using the differential property of the ET, we get

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(28)

$$M\left(u\right)=u\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right].$$

(29)

Using the inverse ET, we have

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}],\hfill \\ \hfill & \zeta (\varrho ,\lambda )=(-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right))+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}].\hfill \end{array}$$

(30)

Now, by means of the HPM procedure, we have

$$\begin{array}{cc}\hfill & \sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )=\left(-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)\right)+\left({\mathtt{E}}^{-1}\right[u^{\varsigma }\mathtt{E}[\left(\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k^2(\varrho ,\lambda )\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial {\zeta }_k(\varrho ,\lambda )}{\partial \varrho }\right)\hfill \\ \hfill & +3\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial {\zeta }_k(\varrho ,\lambda )}{\partial \varrho }\sum _{k=0}^{\infty }{ϵ}^k\frac{{\partial }^2{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^2}+\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )\sum _{k=0}^{\infty }{ϵ}^k\frac{{\partial }^3{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right]).\hfill \end{array}$$

(31)

Correlating the coefficient of ϵ, we obtain

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\varrho ,\lambda )=-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right),\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\varrho ,\lambda )={\mathtt{E}}^{-1}\left(u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }_0^2(\varrho ,\lambda )\frac{\partial {\zeta }_0(\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial {\zeta }_0(\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^2}\right)+{\zeta }_0(\varrho ,\lambda )\frac{{\partial }^3{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^3}\right]\right)\hfill \\ \hfill & =-450{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}\hfill \\ \hfill ⋮\end{array}$$

Finally, the series form result is stated as

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )={\zeta }_0(\varrho ,\lambda )+{\zeta }_1(\varrho ,\lambda )+\cdots \hfill \\ \hfill & \zeta (\varrho ,\lambda )=-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)-450{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}+\cdots \hfill \end{array}$$

Utilizing the ETDM

Operating the ET, we have

$$\mathtt{E}\left\{\frac{{\partial }^{\varsigma }\zeta }{\partial {\lambda }^{\varsigma }}\right\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(32)

Using the differential property of the ET, we get

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(33)

$$M\left(u\right)=u^2\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right].$$

(34)

Using the inverse ET, we have

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}],\hfill \\ \hfill & \zeta (\varrho ,\lambda )=(-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right))+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+3\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}].\hfill \end{array}$$

(35)

The series form approximation is

$$\zeta (\varrho ,\lambda )=\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )$$

(36)

with ${\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$, $\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)={\sum }_{m=0}^{\infty }{\mathcal{B}}_m$ and $\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}={\sum }_{m=0}^{\infty }{\mathcal{C}}_m$ are the Adomian polynomials which show the nonlinear terms, and

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )=\zeta (\varrho ,0)-{\mathtt{E}}^{-1}\left[u^{\varsigma }\left\{\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4\sum _{m=0}^{\infty }{\mathcal{A}}_m+3\sum _{m=0}^{\infty }{\mathcal{B}}_m+\sum _{m=0}^{\infty }{\mathcal{C}}_m\right]\right\}\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )=(-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right))-{\mathtt{E}}^{-1}\left[u^{\varsigma }\left\{\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-4\sum _{m=0}^{\infty }{\mathcal{A}}_m+3\sum _{m=0}^{\infty }{\mathcal{B}}_m+\sum _{m=0}^{\infty }{\mathcal{C}}_m\right]\right\}\right].\hfill \end{array}$$

(37)

The comparison of both sides gives the recursive algorithm:

$${\zeta }_0(\varrho ,\lambda )=-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right).$$

On $m=0$,

$${\zeta }_1(\varrho ,\lambda )=-450{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}.$$

Finally, the series form result is stated as

$$\zeta (\varrho ,\lambda )=\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )={\zeta }_0(\varrho ,\lambda )+{\zeta }_1(\varrho ,\lambda )+\cdots$$

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=-\frac{15}{8}{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)-450{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}+\cdots \hfill \end{array}$$

Hence, we get the exact result at $\varsigma =1$ as

$$\zeta (\varrho ,\lambda )=-\frac{15}{8}\left[{\mathrm{sech}}^2\frac{1}{2}\left(\varrho -\frac{5}{2}\lambda \right)\right]$$

(38)

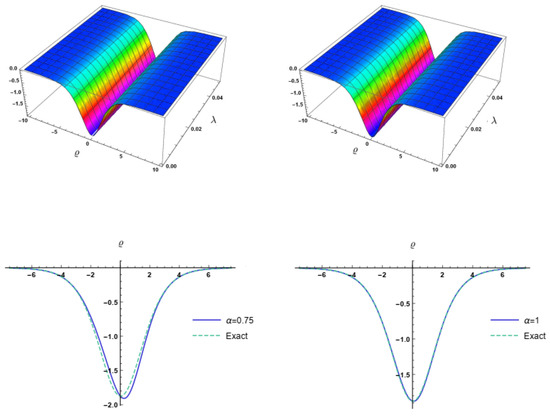
In Figure 1, graphical layout of the suggested methods and exact solution at $\varsigma =1$ for $\zeta (\varrho ,\lambda )$. Graphical layout of the suggested methods solution for $\zeta (\varrho ,\lambda )$ at various ς values. In Table 1, comparison of our methods and exact solution at $\varsigma =1$ with the absolute error (AE).

Figure 1. Graphical layout of the suggested methods and exact solution at $\varsigma =1$ for $\zeta (\varrho ,\lambda )$. Graphical layout of the suggested methods solution for $\zeta (\varrho ,\lambda )$ at various $\varsigma$ values.

Table 1. Comparison of our methods and exact solution at $\varsigma =1$ with the absolute error (AE).

$\mathit{\lambda }=0.01$	Exact Solution	Our Methods’ Solution	AE of Our Methods
$\varrho$	$\varsigma =1$	$\varsigma =1$	$\varsigma =1$
1	−1.49154	−1.50142	2.324274 $\times {10}^{-3}$
2	−0.80253	−0.80532	3.806376 $\times {10}^{-4}$
3	−0.34656	−0.34432	3.588191 $\times {10}^{-4}$
4	−0.13570	−0.13432	2.553213 $\times {10}^{-4}$
5	−0.05110	−0.05070	1.146792 $\times {10}^{-4}$
6	−0.01896	−0.01872	4.523050 $\times {10}^{-5}$
7	−0.00699	−0.00690	1.706341 $\times {10}^{-5}$
8	−0.00257	−0.00255	6.335290 $\times {10}^{-6}$
9	−0.00094	−0.00089	2.338505 $\times {10}^{-6}$
10	−0.00034	−0.00034	8.613563 $\times {10}^{-7}$

Example 2.

Let us assume the following fractional mCH model

$$\frac{{\partial }^{\varsigma }\zeta (\varrho ,\lambda )}{\partial {\lambda }^{\varsigma }}-\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }-2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}=0$$

(39)

with initial source

$$\zeta (\varrho ,0)=-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)$$

Operating the ET, we have

$$\mathtt{E}\left(\frac{{\partial }^{\varsigma }\zeta }{\partial {\lambda }^{\varsigma }}\right)=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(40)

Using the differential property of the ET, we get

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(41)

$$M\left(u\right)=u^2\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right].$$

(42)

Using the inverse ET, we have

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}],\hfill \\ \hfill & \zeta (\varrho ,\lambda )=\left(-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)\right)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}].\hfill \end{array}$$

(43)

Now, by means of the HPM procedure, we have

$$\begin{array}{cc}\hfill & \sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )=\left(-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)\right)+\left({\mathtt{E}}^{-1}\right[u^{\varsigma }\mathtt{E}[\left(\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k^2(\varrho ,\lambda )\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial {\zeta }_k(\varrho ,\lambda )}{\partial \varrho }\right)\hfill \\ \hfill & +2\sum _{k=0}^{\infty }{ϵ}^k\frac{\partial {\zeta }_k(\varrho ,\lambda )}{\partial \varrho }\sum _{k=0}^{\infty }{ϵ}^k\frac{{\partial }^2{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^2}+\sum _{k=0}^{\infty }{ϵ}^k{\zeta }_k(\varrho ,\lambda )\sum _{k=0}^{\infty }{ϵ}^k\frac{{\partial }^3{\zeta }_k(\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right]).\hfill \end{array}$$

(44)

Correlating the coefficient of ϵ, we obtain

$$\begin{array}{cc}\hfill & {ϵ}^0:{\zeta }_0(\varrho ,\lambda )=-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right),\hfill \\ \hfill & {ϵ}^1:{\zeta }_1(\varrho ,\lambda )={\mathtt{E}}^{-1}\left(u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }_0^2(\varrho ,\lambda )\frac{\partial {\zeta }_0(\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial {\zeta }_0(\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^2}\right)+{\zeta }_0(\varrho ,\lambda )\frac{{\partial }^3{\zeta }_0(\varrho ,\lambda )}{\partial {\varrho }^3}\right]\right)\hfill \\ \hfill & =-384{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}\hfill \\ \hfill ⋮\end{array}$$

Finally, the series form result is stated as

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )={\zeta }_0(\varrho ,\lambda )+{\zeta }_1(\varrho ,\lambda )+\cdots \hfill \\ \hfill & \zeta (\varrho ,\lambda )=-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)-384{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}+\cdots \hfill \end{array}$$

Utilizing the ETDM

Operating the ET, we have

$$\mathtt{E}\left\{\frac{{\partial }^{\varsigma }\zeta }{\partial {\lambda }^{\varsigma }}\right\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(45)

Using the differential property of the ET, we get

$$\frac{1}{u^{\varsigma }}\{M\left(u\right)-u^2\zeta (\varrho ,0)\}=\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right],$$

(46)

$$M\left(u\right)=u^2\zeta (\varrho ,0)+u^{\varsigma }\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\right].$$

(47)

Using the inverse ET, we have

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=\zeta (\varrho ,0)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}],\hfill \\ \hfill & \zeta (\varrho ,\lambda )=\left(-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)\right)+{\mathtt{E}}^{-1}\left[u^{\varsigma }\right\{\mathtt{E}[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3{\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }+2\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)+\hfill \\ \hfill & \zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}\left]\right\}].\hfill \end{array}$$

(48)

The series form approximation is

$$\zeta (\varrho ,\lambda )=\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )$$

(49)

with ${\zeta }^2(\varrho ,\lambda )\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }={\sum }_{m=0}^{\infty }{\mathcal{A}}_m$, $\frac{\partial \zeta (\varrho ,\lambda )}{\partial \varrho }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)={\sum }_{m=0}^{\infty }{\mathcal{B}}_m$ and $\zeta (\varrho ,\lambda )\frac{{\partial }^3\zeta (\varrho ,\lambda )}{\partial {\varrho }^3}={\sum }_{m=0}^{\infty }{\mathcal{C}}_m$ are the Adomian polynomials which show the nonlinear terms, and

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )=\zeta (\varrho ,0)-{\mathtt{E}}^{-1}\left[u^{\varsigma }\left\{\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3\sum _{m=0}^{\infty }{\mathcal{A}}_m+2\sum _{m=0}^{\infty }{\mathcal{B}}_m+\sum _{m=0}^{\infty }{\mathcal{C}}_m\right]\right\}\right],\hfill \\ \hfill & \sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )=\left(-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)\right)-{\mathtt{E}}^{-1}\left[u^{\varsigma }\left\{\mathtt{E}\left[\frac{\partial }{\partial \lambda }\left(\frac{{\partial }^2\zeta (\varrho ,\lambda )}{\partial {\varrho }^2}\right)-3\sum _{m=0}^{\infty }{\mathcal{A}}_m+2\sum _{m=0}^{\infty }{\mathcal{B}}_m+\sum _{m=0}^{\infty }{\mathcal{C}}_m\right]\right\}\right].\hfill \end{array}$$

(50)

The comparison of both sides gives the recursive algorithm:

$${\zeta }_0(\varrho ,\lambda )=-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right).$$

On $m=0$,

$${\zeta }_1(\varrho ,\lambda )=-384{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}.$$

Finally, the series form result is stated as

$$\zeta (\varrho ,\lambda )=\sum _{m=0}^{\infty }{\zeta }_m(\varrho ,\lambda )={\zeta }_0(\varrho ,\lambda )+{\zeta }_1(\varrho ,\lambda )+\cdots$$

$$\begin{array}{cc}\hfill & \zeta (\varrho ,\lambda )=-2{\mathrm{sech}}^2\left(\frac{\varrho }{2}\right)-384{\mathrm{csch}}^5\left(\varrho \right){\mathrm{sinhh}}^6\left(\frac{\varrho }{2}\right)\frac{{\lambda }^{\varsigma }}{\Gamma (\varsigma +1)}+\cdots \hfill \end{array}$$

Hence, we get the exact result at $\varsigma =1$ as

$$\zeta (\varrho ,\lambda )=-2{\mathrm{sech}}^2\left(\frac{\varrho -\lambda }{2}\right)$$

(51)

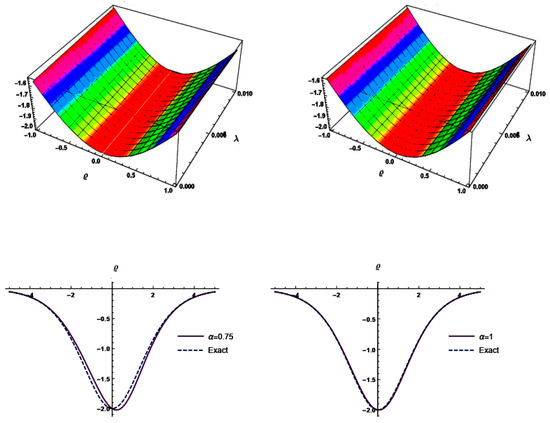
In Figure 2, graphical layout of the suggested methods and exact solution at $\varsigma =1$ for $\zeta (\varrho ,\lambda )$. Graphical layout of the suggested methods solution for $\zeta (\varrho ,\lambda )$ at various ς values. In Table 2, comparison of our methods and exact solution at $\varsigma =1$ with the absolute error (AE).

Figure 2. Graphical layout of the suggested methods and exact solution at $\varsigma =1$ for $\zeta (\varrho ,\lambda )$. Graphical layout of the suggested methods solution for $\zeta (\varrho ,\lambda )$ at various $\varsigma$ values.

Table 2. Comparison of our methods and exact solution at $\varsigma =1$ with the absolute error (AE).

$\mathit{\lambda }=0.01$	Exact Solution	Our Methods’ Solution	AE of Our Methods
$\varrho$	$\varsigma =1$	$\varsigma =1$	$\varsigma =1$
1	−1.58014	−1.59532	2.703113 $\times {10}^{-4}$
2	−0.84636	−0.85142	9.720903 $\times {10}^{-5}$
3	−0.36469	−0.36484	2.742579 $\times {10}^{-6}$
4	−0.14267	−0.14192	7.853812 $\times {10}^{-6}$
5	−0.05371	−0.05351	4.412590 $\times {10}^{-6}$
6	−0.01992	−0.01983	1.848193 $\times {10}^{-6}$
7	−0.00735	−0.00730	7.113341 $\times {10}^{-7}$
8	−0.00270	−0.00269	2.659878 $\times {10}^{-7}$
9	−0.00099	−0.00099	9.843626 $\times {10}^{-7}$
10	−0.00036	−0.00036	3.629193 $\times {10}^{-7}$

6. Conclusions

In this paper, we described a method using HPTM and ETDM to get the fractional order solitary wave solutions for the mDP and mCH models. These schemes’ main benefit was that it delivered meaningful results in the calculation of consecutive iterations. It is clear that all of the terms could be found as series solutions. Two steps were taken to achieve the numerical solutions. The targeted issues were first simplified using the Elzaki transformation, and the solutions were then obtained by applying the decomposition method and homotopy perturbation method. The tables and figures showed that the current techniques were better able to evaluate the results of the targeted issues. The solutions were provided at various fractional orders, and a very quick convergence of fractional solutions toward an integer-order solution was demonstrated. The relationship between the fractional and integer-order solutions was very clearly demonstrated by the graphical representation. Both approaches can be expanded to tackle highly nonlinear FPDEs and associated systems because both of them are simple and easy to understand.