Author Contributions
Data curation, J.R.; formal analysis, J.R., M.A.R., P.L.C. and J.A.; investigation, J.R., M.A.R. and P.L.C.; methodology, J.R., M.A.R., P.L.C. and J.A.; writing—original draft, J.R., M.A.R., P.L.C. and J.A.; writing—review and editing, M.A.R., P.L.C. and J.A.; Funding Acquisition, J.R., M.A.R. and J.A. All authors have read and agreed to the published version of the manuscript.
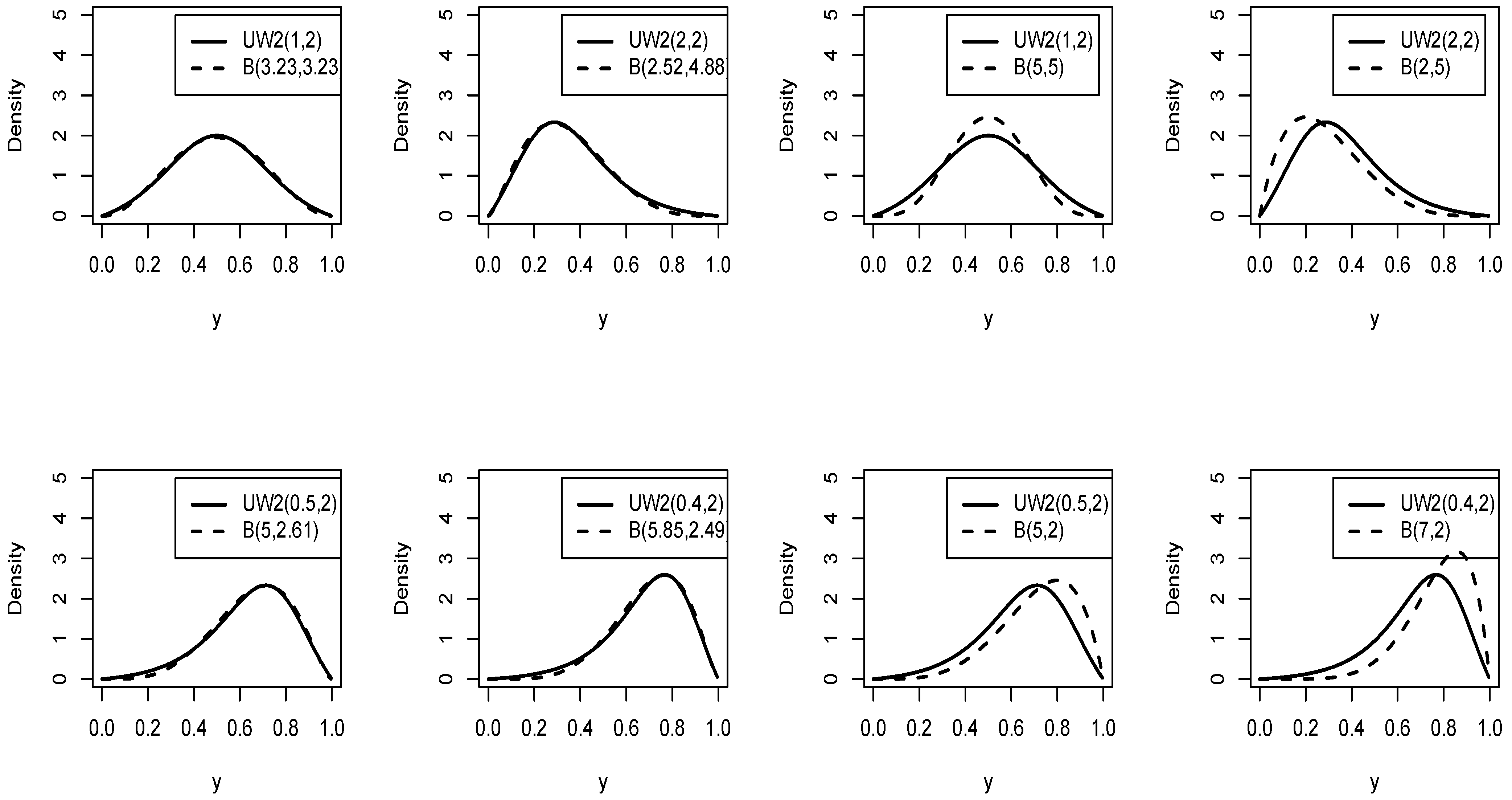
Figure 1.
pdf for and different values of .
Figure 1.
pdf for and different values of .
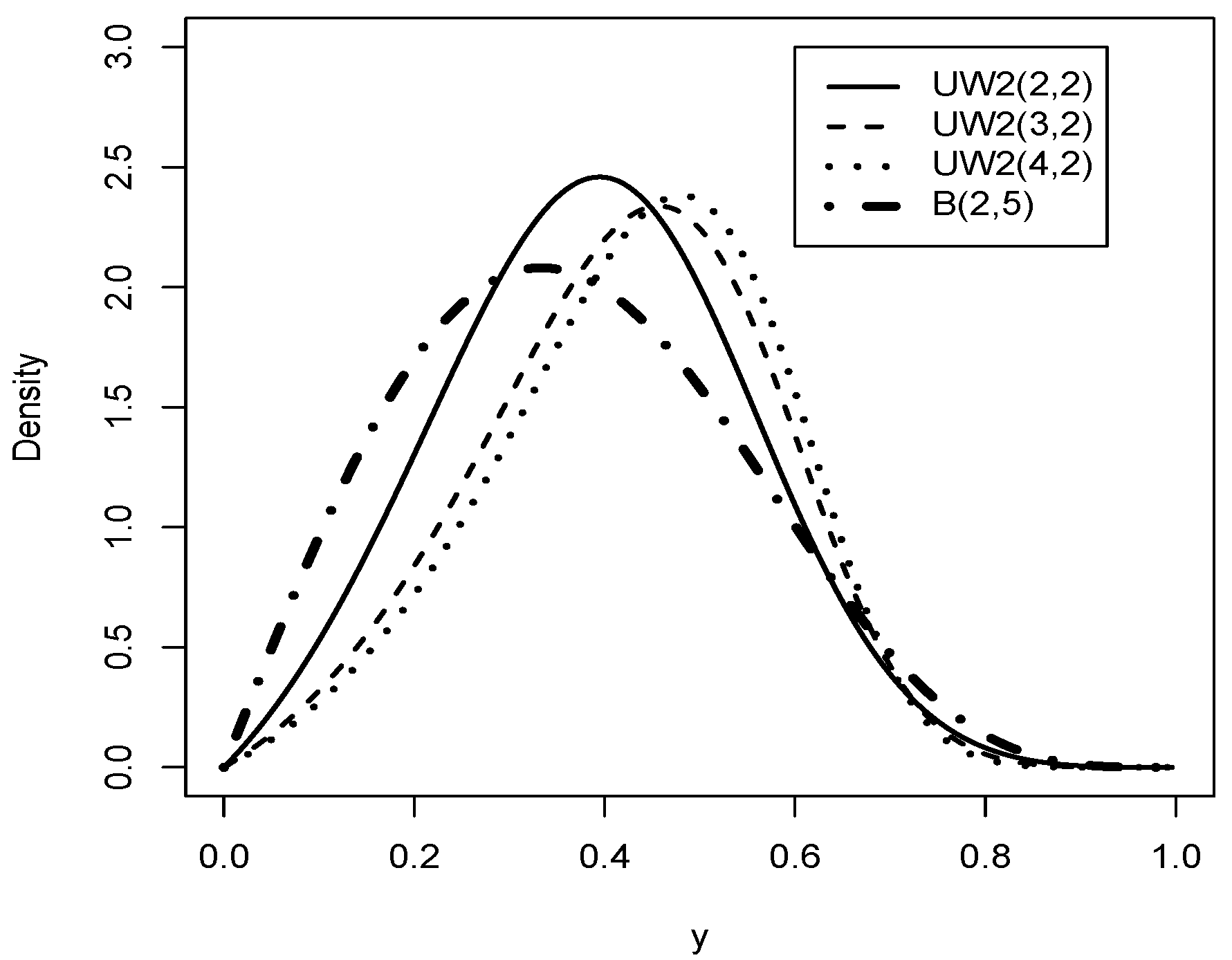
Figure 2.
pdf for and different values of .
Figure 2.
pdf for and different values of .
Figure 3.
Cdf of for different values and .
Figure 3.
Cdf of for different values and .
Figure 4.
The hazard rate functions for the distribution.
Figure 4.
The hazard rate functions for the distribution.
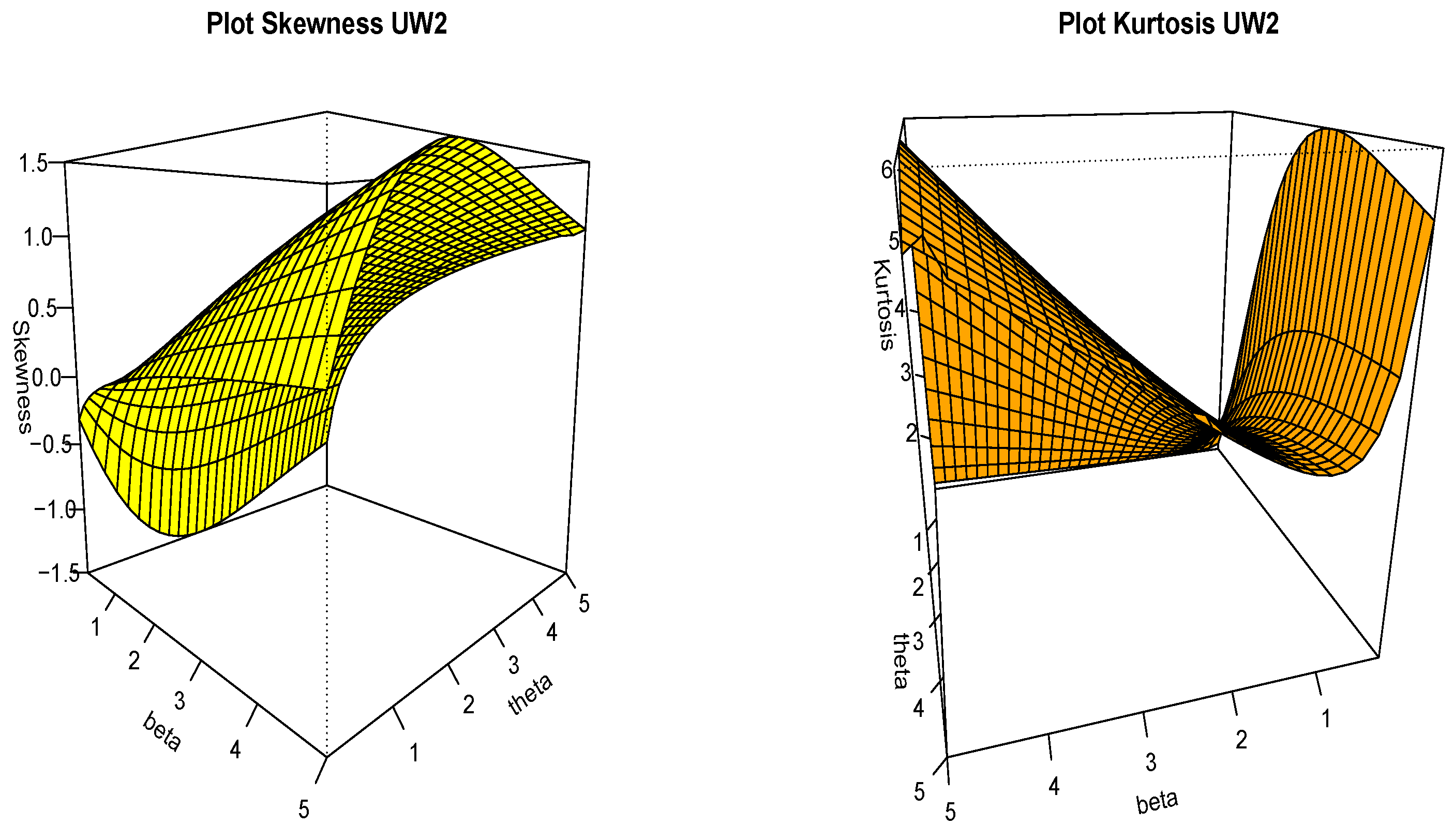
Figure 5.
Plots of the skewness (left) and kurtosis of the distribution (right).
Figure 5.
Plots of the skewness (left) and kurtosis of the distribution (right).
Figure 6.
Lorenz Curve for different values of and .
Figure 6.
Lorenz Curve for different values of and .
Figure 7.
canonical kurtosis for different values of .
Figure 7.
canonical kurtosis for different values of .
Figure 8.
Lorenz curve and Gini index of the canonical distribution for different values of .
Figure 8.
Lorenz curve and Gini index of the canonical distribution for different values of .
Figure 9.
Graph of the entropy of the canonical distribution for different values of .
Figure 9.
Graph of the entropy of the canonical distribution for different values of .
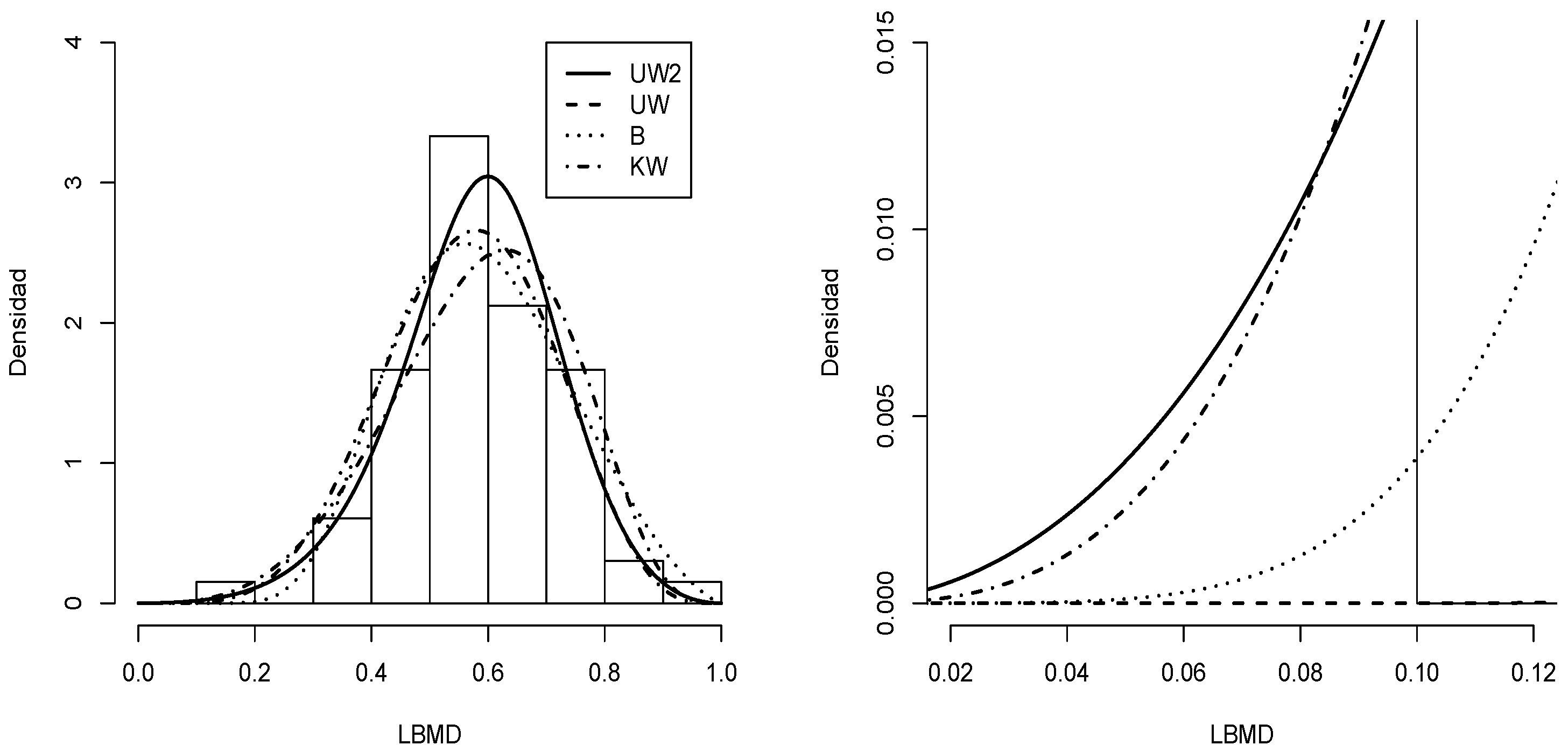
Figure 10.
Histogram for LBMD data with Densities (solid line), (dashed line), (dotted line), and (dashed dotted line) (left) and tails (right).
Figure 10.
Histogram for LBMD data with Densities (solid line), (dashed line), (dotted line), and (dashed dotted line) (left) and tails (right).
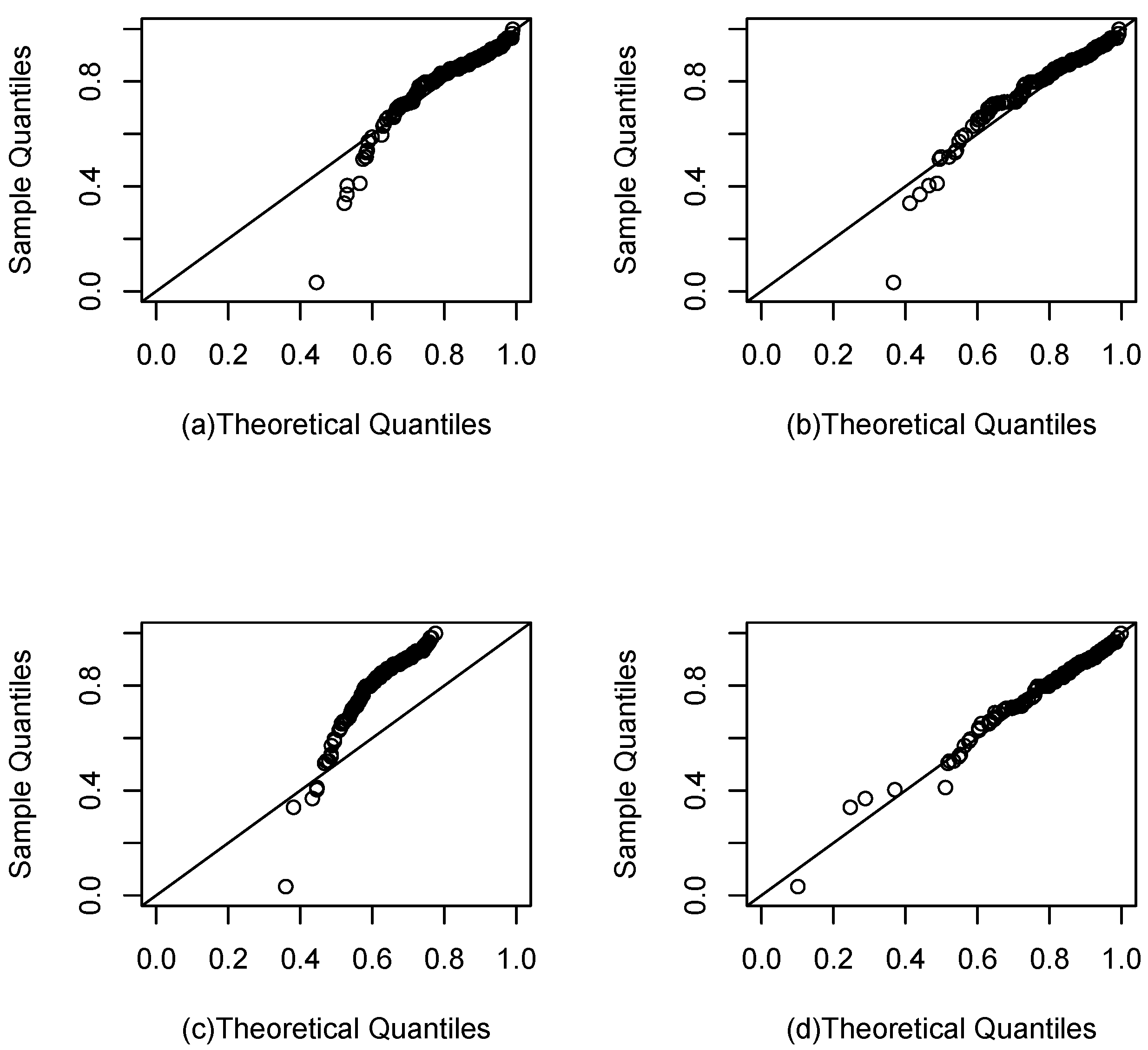
Figure 11.
QQ plots for the LBMD data set: (a), (b), (c), and (d).
Figure 11.
QQ plots for the LBMD data set: (a), (b), (c), and (d).
Figure 12.
Comparison of cumulative distributions for the LBMD data set for (blue line), (red line), (green line), and (orange line).
Figure 12.
Comparison of cumulative distributions for the LBMD data set for (blue line), (red line), (green line), and (orange line).
Figure 13.
Histogram for percent dissolved oxygen data (left) with densities of (solid line), (dashed line), (dotted line), and (dashed line) and tails (right).
Figure 13.
Histogram for percent dissolved oxygen data (left) with densities of (solid line), (dashed line), (dotted line), and (dashed line) and tails (right).
Figure 14.
QQ plots for the data set: (a), (b), (c), and (d).
Figure 14.
QQ plots for the data set: (a), (b), (c), and (d).
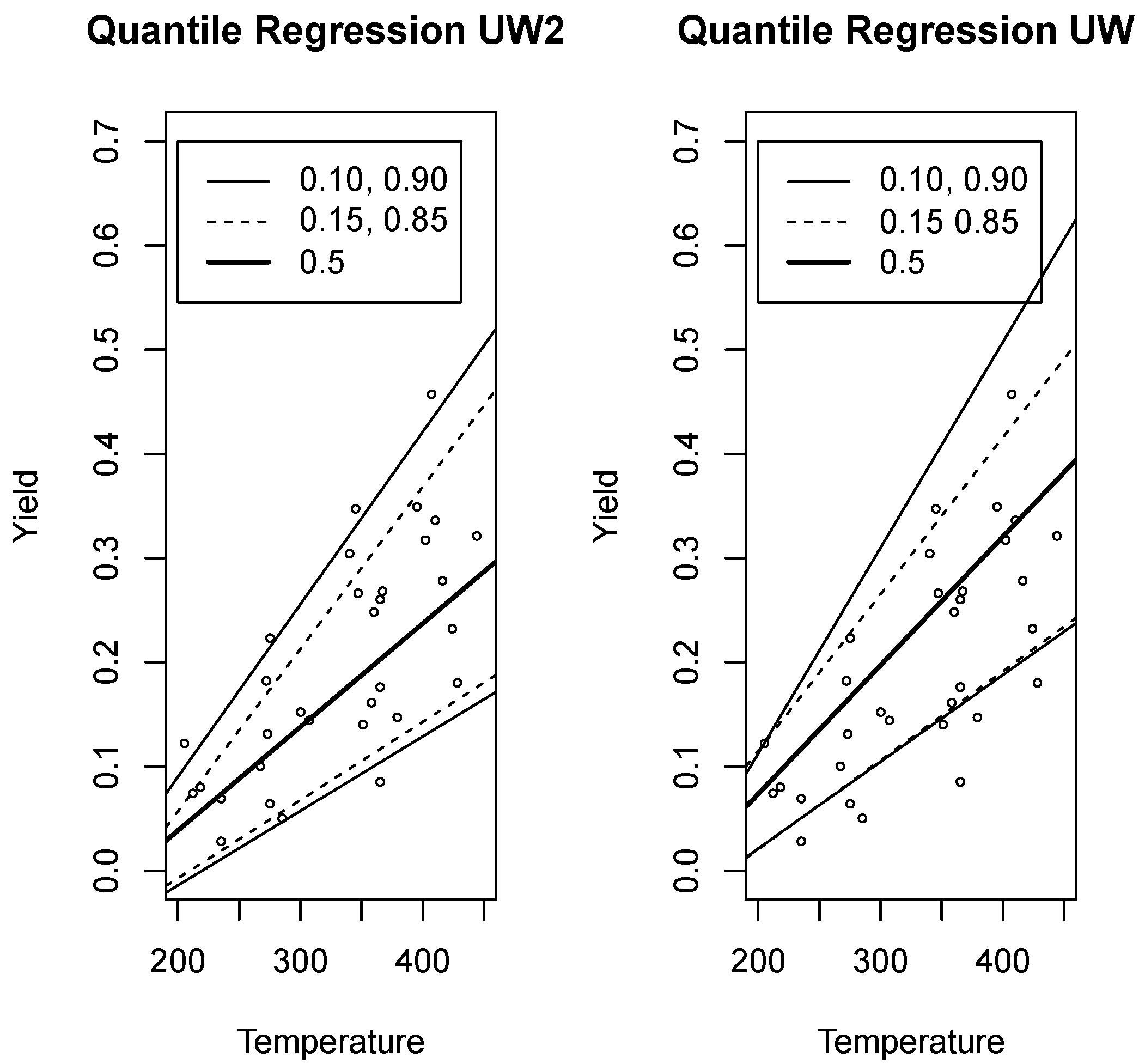
Figure 15.
Quantile regression for Yield and Temperature data with density (left) and density (right).
Figure 15.
Quantile regression for Yield and Temperature data with density (left) and density (right).
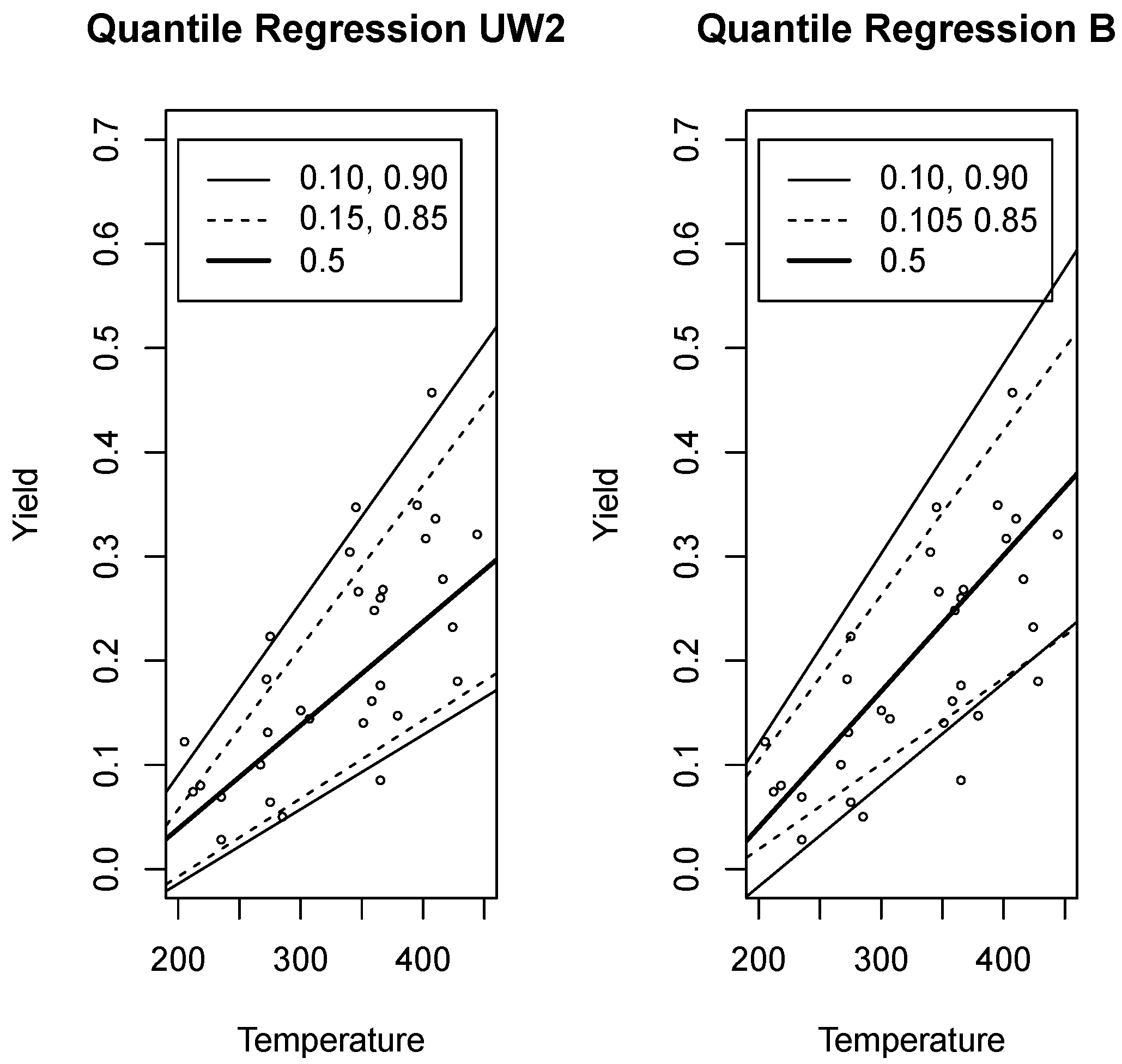
Figure 16.
Quantile regression for Yield and Temperature data with density (left) and density (right).
Figure 16.
Quantile regression for Yield and Temperature data with density (left) and density (right).
Table 1.
Reliability function comparisond for distributions of , , , and .
Table 1.
Reliability function comparisond for distributions of , , , and .
| | |
|---|
| | | | |
| 0.70 | 0.0789474 | 0.0057559 | 0.0024300 | 0.0024300 |
| 0.75 | 0.0625000 | 0.0019685 | 0.0009766 | 0.0009766 |
| 0.80 | 0.0476191 | 0.0005531 | 0.0003200 | 0.0003200 |
| 0.85 | 0.0340909 | 0.0001134 | 0.0000759 | 0.0000759 |
| 0.90 | 0.0217391 | 0.0000130 | 0.0000100 | 0.0000100 |
| 0.95 | 0.0104167 | 0.0000004 | 0.0000003 | 0.0000003 |
Table 2.
Skewness and kurtosis values of the model with different values of and .
Table 2.
Skewness and kurtosis values of the model with different values of and .
| | | |
|---|
| | | | | | | | | | |
| 1 | −0.4861 | −0.7849 | 0 | 0.4861 | 0.7849 | 2.0928 | 2.5644 | 1.8000 | 2.0928 | 2.5644 |
| 2 | −0.5980 | −0.9739 | 0 | 0.5980 | 0.9739 | 3.0459 | 3.9578 | 2.5013 | 3.0459 | 3.9578 |
| 3 | −0.5744 | −0.9279 | 0 | 0.5744 | 0.9279 | 3.5809 | 4.5497 | 2.9939 | 3.5809 | 4.5497 |
| 4 | −0.5176 | −0.8255 | 0 | 0.5176 | 0.8255 | 3.8564 | 4.7050 | 3.3240 | 3.8564 | 4.7050 |
| 5 | −0.4592 | −0.7237 | 0 | 0.4592 | 0.7237 | 3.9995 | 4.6954 | 3.5460 | 3.9994 | 4.6954 |
| 6 | −0.4077 | −0.6363 | 0 | 0.4077 | 0.6363 | 4.0765 | 4.6377 | 3.6984 | 4.0765 | 4.6377 |
| 7 | −0.3642 | −0.5641 | 0 | 0.3642 | 0.5641 | 4.1201 | 4.5736 | 3.8058 | 4.1201 | 4.5736 |
| 8 | −0.3278 | −0.5048 | 0 | 0.3278 | 0.5048 | 4.1460 | 4.5161 | 3.8836 | 4.1460 | 4.5161 |
| 9 | −0.2972 | −0.4557 | 0 | 0.2972 | 0.4557 | 4.1620 | 4.4678 | 3.9412 | 4.1620 | 4.4678 |
| 10 | −0.2715 | −0.4148 | 0 | 0.2715 | 0.4148 | 4.1723 | 4.4281 | 3.9848 | 4.1723 | 4.4281 |
| 11 | −0.2496 | −0.3802 | 0 | 0.2496 | 0.3802 | 4.1793 | 4.3957 | 4.0186 | 4.1793 | 4.3957 |
| 12 | −0.2307 | −0.3508 | 0 | 0.2307 | 0.3508 | 4.1840 | 4.3692 | 4.0472 | 4.1840 | 4.3693 |
| 13 | −0.2144 | −0.3254 | 0 | 0.2144 | 0.3254 | 4.1874 | 4.3475 | 4.0665 | 4.1874 | 4.3475 |
| 14 | −0.2002 | −0.3033 | 0 | 0.2002 | 0.3033 | 4.1899 | 4.3295 | 4.0765 | 4.1899 | 4.3295 |
| 15 | −0.1877 | −0.2840 | 0 | 0.1877 | 0.2840 | 4.1917 | 4.3144 | 4.0979 | 4.1917 | 4.3145 |
| 16 | −0.1766 | −0.2670 | 0 | 0.1766 | 0.2670 | 4.1932 | 4.3018 | 4.1096 | 4.1931 | 4.3018 |
| 17 | −0.1667 | −0.2518 | 0 | 0.1667 | 0.2518 | 4.1942 | 4.2911 | 4.1194 | 4.1942 | 4.2908 |
| 18 | −0.1578 | −0.2393 | 0 | 0.1578 | 0.2382 | 4.1951 | 4.4034 | 4.1278 | 4.1951 | 4.2837 |
| 19 | −0.1498 | −0.2261 | 0 | 0.1498 | 0.2263 | 4.1958 | 4.2741 | 4.1350 | 4.1958 | 4.2692 |
| 20 | −0.1426 | −0.2405 | 0 | 0.1426 | 0.2149 | 4.1963 | 5.7680 | 4.1411 | 4.1963 | 4.2746 |
Table 3.
Entropy values for the distribution () for different values of and .
Table 3.
Entropy values for the distribution () for different values of and .
| | | | | |
|---|
| 1 | −0.1976 | −0.0798 | 0.0000 | −0.0781 | −0.1939 |
| 2 | −0.5145 | −0.3657 | −0.2640 | −0.3657 | −0.5146 |
| 3 | −0.8398 | −0.6808 | −0.5714 | −0.6808 | −0.8398 |
| 4 | −1.0984 | −0.9350 | −0.8223 | −0.9350 | −1.0984 |
| 5 | −1.3079 | −1.1423 | −1.0279 | −1.1423 | −1.3079 |
| 6 | −1.4828 | −1.3159 | −1.2006 | −1.3159 | −1.4828 |
| 7 | −1.6324 | −1.4648 | −1.3488 | −1.4648 | −1.6324 |
| 8 | −1.7630 | −1.5949 | −1.4785 | −1.5949 | −1.7630 |
| 9 | −1.8788 | −1.7103 | −1.5936 | −1.7103 | −1.8788 |
| 10 | −1.9827 | −1.8139 | −1.6971 | −1.8139 | −1.9827 |
| 11 | −2.0770 | −1.9080 | −1.7910 | −1.9080 | −2.0770 |
| 12 | −2.1632 | −1.9940 | −1.8769 | −1.9940 | −2.1632 |
| 13 | −2.2426 | −2.0733 | −1.9561 | −2.0733 | −2.2426 |
| 14 | −2.3162 | −2.1469 | −2.0295 | −2.1469 | −2.3162 |
| 15 | −2.3848 | −2.2154 | −2.0980 | −2.2154 | −2.3848 |
| 16 | −2.4490 | −2.2795 | −2.1621 | −2.2795 | −2.4490 |
| 17 | −2.5093 | −2.3398 | −2.2223 | −2.3398 | −2.5093 |
| 18 | −2.5663 | −2.3967 | −2.2792 | −2.3967 | −2.5663 |
| 19 | −2.6201 | −2.4505 | −2.3330 | −2.4505 | −2.6201 |
| 20 | −2.6713 | −2.5016 | −2.3841 | −2.5016 | −2.6713 |
Table 4.
Simulation of 1000 iterations of the model ).
Table 4.
Simulation of 1000 iterations of the model ).
| n | | | | | | | | |
|---|
| 50 | 2 | 0.5 | 2.2512 | 1.1014 | 90.6 | 0.5105 | 0.0603 | 94.6 |
| 100 | 2 | 0.5 | 2.1292 | 0.7380 | 94.3 | 0.5043 | 0.0422 | 94.0 |
| 200 | 2 | 0.5 | 2.0346 | 0.4975 | 94.2 | 0.5022 | 0.0297 | 94.5 |
| 50 | 2 | 1 | 2.0559 | 0.5021 | 92.8 | 1.0209 | 0.1207 | 94.6 |
| 100 | 2 | 1 | 2.0340 | 0.3523 | 95.1 | 1.0086 | 0.0844 | 94.0 |
| 200 | 2 | 1 | 2.0029 | 0.2450 | 95.0 | 1.0043 | 0.0594 | 94.5 |
| 50 | 2 | 2 | 2.0118 | 0.2455 | 94.3 | 2.0419 | 0.2413 | 94.6 |
| 100 | 2 | 2 | 2.0097 | 0.1740 | 95.4 | 2.0172 | 0.1687 | 94.0 |
| 200 | 2 | 2 | 1.9979 | 0.1222 | 95.2 | 2.0087 | 0.1188 | 94.4 |
| 50 | 2 | 4 | 2.0020 | 0.1221 | 94.1 | 4.0837 | 0.4826 | 94.6 |
| 100 | 2 | 4 | 2.0031 | 0.0867 | 95.8 | 4.0344 | 0.3374 | 94.0 |
| 200 | 2 | 4 | 1.9981 | 0.0611 | 95.3 | 4.0173 | 0.2376 | 94.5 |
| 50 | 0.5 | 4 | 0.5005 | 0.0305 | 94.2 | 4.0837 | 0.4826 | 94.6 |
| 100 | 0.5 | 4 | 0.5008 | 0.0217 | 95.8 | 4.0344 | 0.3374 | 94.0 |
| 200 | 0.5 | 4 | 0.4995 | 0.0153 | 95.3 | 4.0173 | 0.2376 | 94.5 |
| 50 | 0.5 | 2 | 0.5030 | 0.0614 | 94.2 | 2.0419 | 0.2413 | 94.6 |
| 100 | 0.5 | 2 | 0.5024 | 0.0435 | 95.4 | 2.0172 | 0.1687 | 94.0 |
| 200 | 0.5 | 2 | 0.4995 | 0.0306 | 95.2 | 2.0086 | 0.1188 | 94.5 |
| 50 | 1 | 2 | 1.0059 | 0.1228 | 94.3 | 2.0419 | 0.2413 | 94.6 |
| 100 | 1 | 2 | 1.0049 | 0.0870 | 95.4 | 2.0172 | 0.1687 | 94.0 |
| 200 | 1 | 2 | 0.9989 | 0.0611 | 95.2 | 2.0087 | 0.1188 | 94.5 |
Table 5.
Summary statistics for ant data set of the LBMD.
Table 5.
Summary statistics for ant data set of the LBMD.
| n | | | | |
|---|
| 66 | 0.5864 | 0.1339 | 0.04085 | 3.5395 |
Table 6.
Parameters estimates for , , , and distributions.
Table 6.
Parameters estimates for , , , and distributions.
| Parameter Estimates | | | | |
|---|
| 5.0241 (1.0507) | 4.4717 (0.7554) | 2.3068 (0.2055) | - |
| 3.8972 (0.4386) | 6.4115 (1.1016) | 2.8807 (0.3867) | 0.6992 (0.0513) |
| - | - | - | 2.9370 (0.3041) |
| Log-likelihood | 33.9586 | 35.5639 | 36.333 | 38.0463 |
| AIC | −61.712 | −67.1278 | −68.666 | −72.0926 |
| BIC | −59.333 | −62.748 | −64.281 | −67.713 |
| KS Statistic | 0.1212 | 0.1515 | 0.1212 | 0.0909 |
| W* | 0.1380 | 0.1029 | 0.08197 | 0.06354 |
| A* | 0.9276 | 0.7149 | 0.6091 | 0.4204 |
Table 7.
Summary statistics for environment data set of the percentage of dissolved oxygen.
Table 7.
Summary statistics for environment data set of the percentage of dissolved oxygen.
| n | | | | |
|---|
| 210 | 0.8294 | 0.1283 | −2.3702 | 11.3423 |
Table 8.
Parameter estimates for the distributions , , , and .
Table 8.
Parameter estimates for the distributions , , , and .
| Parameter Estimates | | | | |
|---|
| 7.3538 (0.7436) | 6.9905 (0.5687) | 5.4931 (0.4721) | - |
| 1.6043 (0.1435) | 1.8721 (0.0.2003) | 1.1210 (0.0504) | 0.1616 (0.0089) |
| - | - | - | 2.1259 (0.1740) |
| AIC | −344.234 | −352.005 | −326.509 | −394.225 |
| BIC | −337.540 | −345.311 | −319.814 | −387.530 |
Table 9.
Summary statistics for data set of the temperature and yield.
Table 9.
Summary statistics for data set of the temperature and yield.
| n | | | | |
|---|
| Yield | 52 | 332.0938 | 69.7559 | −0.2657 | 1.3058 |
| Temp | 52 | 0.1965 | 0.1070 | 0.3687 | 2.1997 |
Table 10.
Parameters estimates and standard error for the quantile regression coefficients , , and models for the dataset and the quantile of 0.5.
Table 10.
Parameters estimates and standard error for the quantile regression coefficients , , and models for the dataset and the quantile of 0.5.
| | | | | | | | | | | | | |
|---|
| | | t-Value | p-Value | | | t-Value | p-Value | | | t-Value | p-Value |
| −0.1702 | 0.0800 | −2.1256 | 0.0418 | −0.1733 | 0.0963 | −1.7992 | 0.0820 | −0.1339 | 0.0528 | −2.5333 | 0.0167 |
| 0.0011 | 0.0002 | 4.1976 | 0.0002 | 0.0012 | 0.0003 | 3.6745 | 0.0009 | 0.0009 | 0.0001 | 5.1823 | 0.0000 |
Table 11.
AIC and BIC values for the models , , and of the Temperature and Yield.
Table 11.
AIC and BIC values for the models , , and of the Temperature and Yield.
| Model | AIC | BIC |
|---|
| −58.07373 | −53.67652 |
| −53.75805 | −49.36084 |
| −43.69310 | −39.29589 |