Abstract
This study addresses a nonlinear fractional Drinfeld–Sokolov–Wilson problem in dispersive water waves, which requires appropriate numerical techniques to obtain an approximative solution. The Adomian decomposition approach, the homotopy perturbation method, and Sumudu transform are combined to tackle the problem. The Caputo manner is used to describe fractional derivative, and He’s polynomials and Adomian polynomials are employed to address nonlinearity. By following these approaches, we obtain solutions in the form of convergent series. We verify and demonstrate the effectiveness of our suggested strategies by examining the assumed model in terms of fractional order. We use plots for various fractional orders to represent the physical behavior of the suggested technique solutions, and show a numerical simulation. The results demonstrate that the suggested algorithms are systematic, simple to use, effective, and accurate in analyzing the behavior of coupled nonlinear differential equations of fractional order in related scientific and engineering fields.
1. Introduction
Fractional partial differential equations (FPDEs) are a powerful mathematical tool used to model a wide range of complex physical phenomena. These equations involve partial derivatives of fractional order, which provide a means of describing the behavior of systems with long-range interactions or non-local effects. FPDEs have found applications in various fields, such as fluid mechanics, electromagnetism, finance, and biology, among others. Unlike classical partial differential equations, FPDEs have a non-local character, which makes their solutions more challenging to find. Nevertheless, the development of numerical methods, such as fractional finite differences, fractional calculus, and fractional Laplacians, has allowed researchers to study and simulate these equations in a more efficient way [1,2,3,4].
One of the advantages of using FPDEs is their ability to capture the memory effects and non-local interactions that are often observed in real-world systems. This feature makes FPDEs particularly useful in modeling complex systems, such as biological networks, financial markets, and porous media, where the interactions between the components can span over long distances [5,6,7]. In this context, understanding the properties and behavior of FPDEs has become a critical topic in applied mathematics and physics. Researchers continue to develop new techniques and methods to solve these equations and gain insights into the complex phenomena they describe [8,9,10,11,12,13,14,15,16].
Partial differential equations (PDEs) play a crucial role in describing many physical and mathematical phenomena. One important class of PDEs is the fractional partial differential equations (FPDEs), which involve derivatives of non-integer order. FPDEs have recently gained much attention due to their ability to accurately model anomalous diffusion, viscoelasticity, and other phenomena that cannot be captured by traditional integer-order PDEs [17,18,19]. FPDEs have a wide range of applications in various fields such as physics, engineering, finance, and biology. For example, in physics, FPDEs are used to describe the behavior of particles in fractal media, where the traditional diffusion equation fails to capture the true behavior of the particles [20,21]. In engineering, FPDEs are used to model the transport of fluids in porous media and to describe the viscoelastic properties of materials. In finance, FPDEs are used to model the dynamics of financial derivatives and to estimate the risk associated with financial investments. In biology, FPDEs are used to model the movement of molecules in biological systems and the spread of diseases [22,23,24,25,26].
The interaction of various long waves with various dispersion relations is illustrated by linked KdV equation systems which Hirota and Satsum convincingly establish in [27,28] and present as follows.
The expression for the forcing term in the KdV system is , and according to Drinfeld and Sokolov, this equation is a specific case of the Kadomtsev–Petviashvili (KP) hierarchy with four reductions [29]. Moreover, in [30], Wilson established a relationship between Equation (1) and affine Lie algebras, showing how it can be obtained as a general Drinfeld and Sokolov construction. Wilson also associated this equation with the affine Lie algebra . Later, Wilson introduced and provided an example of the remarkable equation known as the Drinfeld–Sokolov–Wilson (DSW) equation, which is given by:
In the present framework, we consider a system of equations in which non-zero parameters and represent the amplitude of wave modes. The functions and represent the amplitude of wave modes with respect to time ℜ and space , respectively. This system is especially significant for modeling dispersive water waves when and . In this context, we consider the fractional DSW (FDSW) equation in the following form.
The use of the Caputo fractional operator allows us to define the fractional order of the system, which incorporates memory effects and genetic consequences. This feature enables us to identify crucial physical characteristics of complex problems. The shallow water wave models were initially proposed by Drinfeld and Sokolov [31] and later refined by Wilson [30] to develop the classical DSW equations. The diffusive wave approximations of the shallow water equations (DSW) have been effectively used to model gravitational water flow dominated by shear stress, such as overland flows, dam breaks, flows through vegetation, and floods. These equations have significant importance in physics and engineering, and many researchers have made concerted efforts to find solutions for them. For example, Santillana [32] investigated the features of approximate DSW equation solutions using the Galerkin finite element method. Inc [33] employed the Adomian decomposition approach to obtain approximate doubly periodic wave solutions of the traditional DSW equations. Truncated Painlev’e and Mobius invariant forms were used [34] to find explicit solutions to the classical DSW equations with nonlocal symmetry. Zhao et al. [35] utilized the F-expansion technique to locate solutions to common DSW equations.
Although the precise solutions of fractional DSW equations are less frequently reported, Sahoo [36] derived double-periodic solutions using the Jacobi elliptical function approach. Misirli and Gurefe used the exp-function approach to study common DSW equations [37]. However, finding the exact solutions of the time-fractional DSW system is more challenging than for the classical DSW equations. Most studies focus on the classical DSW equations, and the research on fractional DSW equations is still in its nascent stage. Moreover, in addition to the approximate and periodic solutions, more solutions to the fractional DSW equations need to be determined [38,39,40].
In this study, we have used the Sumudu Transform Decomposition method (STDM) and the Homotopy Perturbation Transform method (HPTM) to derive an analytical solution for time-fractional coupled DSW equations. It is worth noting that these methods offer a superior performance, requiring less computational work while maintaining a high level of numerical precision. The paper is organized as follows: Section 2 provides fundamental definitions for fractional calculus, while Section 3 and Section 4 thoroughly explain the steps of the suggested methods. In Section 5, we apply the suggested methods to obtain approximate solutions for the time-fractional Drinfeld–Sokolov–Wilson system. Finally, the last section includes our observations and conclusions.
2. Basic Definitions
Definition 1.
A function defined for belongs to the space , where , if there is a real number such that , where . Similarly, is said to be in the space , where , if , meaning that the mth derivative of belongs to .
Definition 2.
The definition of the Riemann-Liouville fractional integral operator of order for a function , is as follows:
Properties of the operator mentions only the following. For , and
Lemma 1.
If and , and , then
Definition 3.
Let us consider a function of n variables, denoted as for , and assume that it belongs to the class C on a domain .
We denote the standard partial derivative of integer order m with respect to as .
Definition 4.
The definition of the Sumudu transform for the Caputo fractional derivative can be stated as follows:
3. Fundamental Idea of HPTM
In this part, we take the arbitrary order differential equation to show the basic solution procedure.
subject to the initial guess
Here, is the Caputo fractional derivative, is representing the linear operator, and is depicting the nonlinear differential operator.
On using ST operator
We have after simplification
By operating inverse ST
Now, in terms of HPM,
we express the nonlinear operator as
with He’s polynomials as
Equating in terms of identical powers p, we get
Finally, we obtain the analytical solution by the truncated series as
4. Fundamental Idea of STDM
In this part, we take the arbitrary order differential equation to show the basic solution procedure.
subject to the initial guess
Here, is the Caputo fractional derivative, is representing the linear operator, and is depicting the nonlinear differential operator.
On using ST operator,
We have, after simplification,
By operating inverse ST,
Now, in terms of STDM,
We express the nonlinear operator as
with Adomian polynomials as
The following terms are obtained.
Thus the analytical solution by the truncated series for is as
5. Applications
We obtain the analytical solutions for fractional coupled DSW equation by implementing the proposed techniques as follow.
Example
Consider the DSW equation having a fractional order as
subjected to the initial guesses,
By setting , we get an exact solution as
On using the ST operator,
We have, after simplification,
By operating inverse ST,
Now, in terms of HPM,
we express the nonlinear first few terms as
Equating in terms of identical powers p, we get
At we get
Implementation of STDM
On using the ST operator,
We have, after simplification,
By operating inverse ST,
Now, in terms of STDM,
where the nonlinear terms , and are expressed in terms of Adomian polynomials as
The Adomian polynomials’ first few terms are given by
The following terms are obtained:
For ,
For ,
Thus, the analytical solution by the truncated series for is calculated in the same manner.
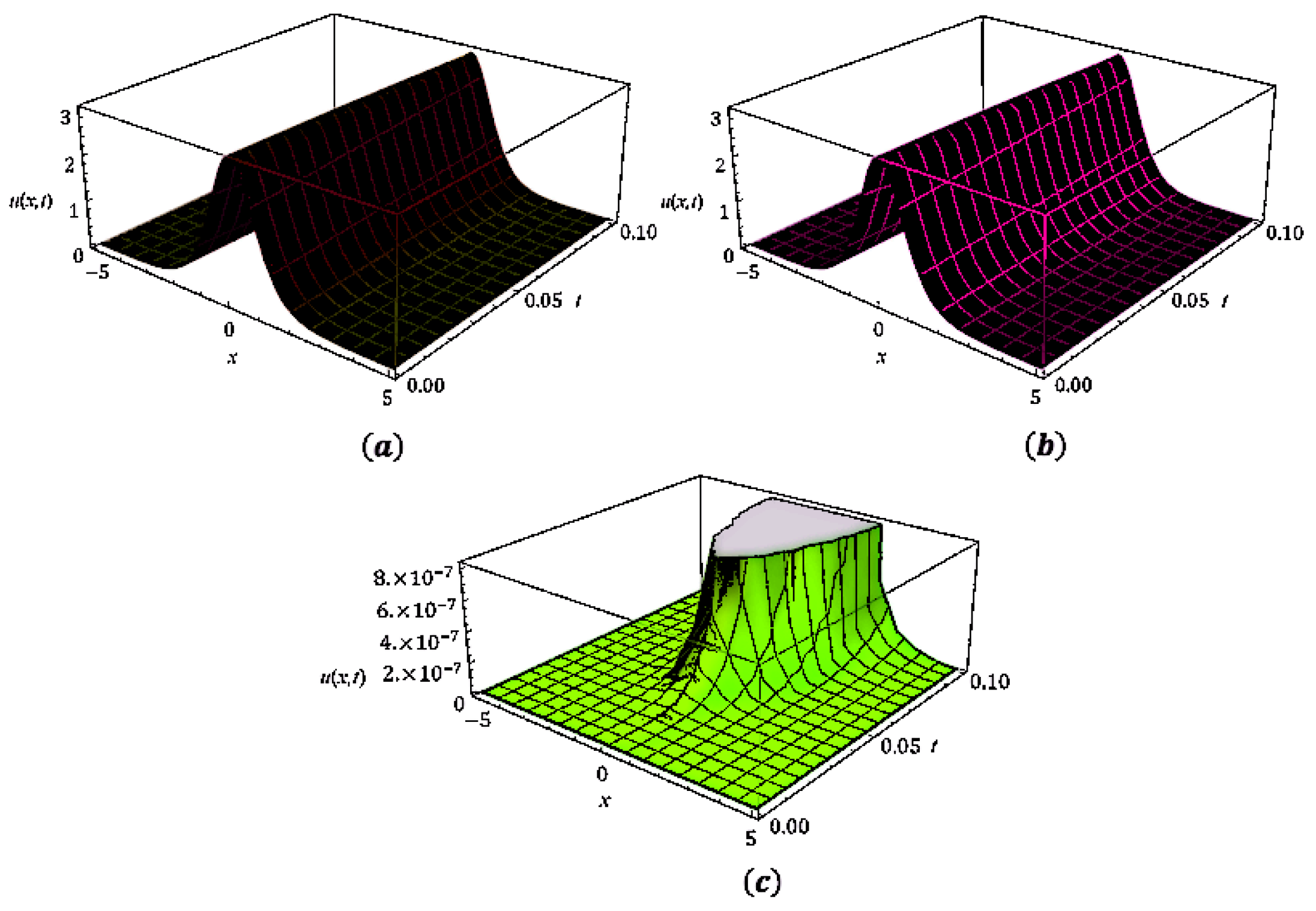
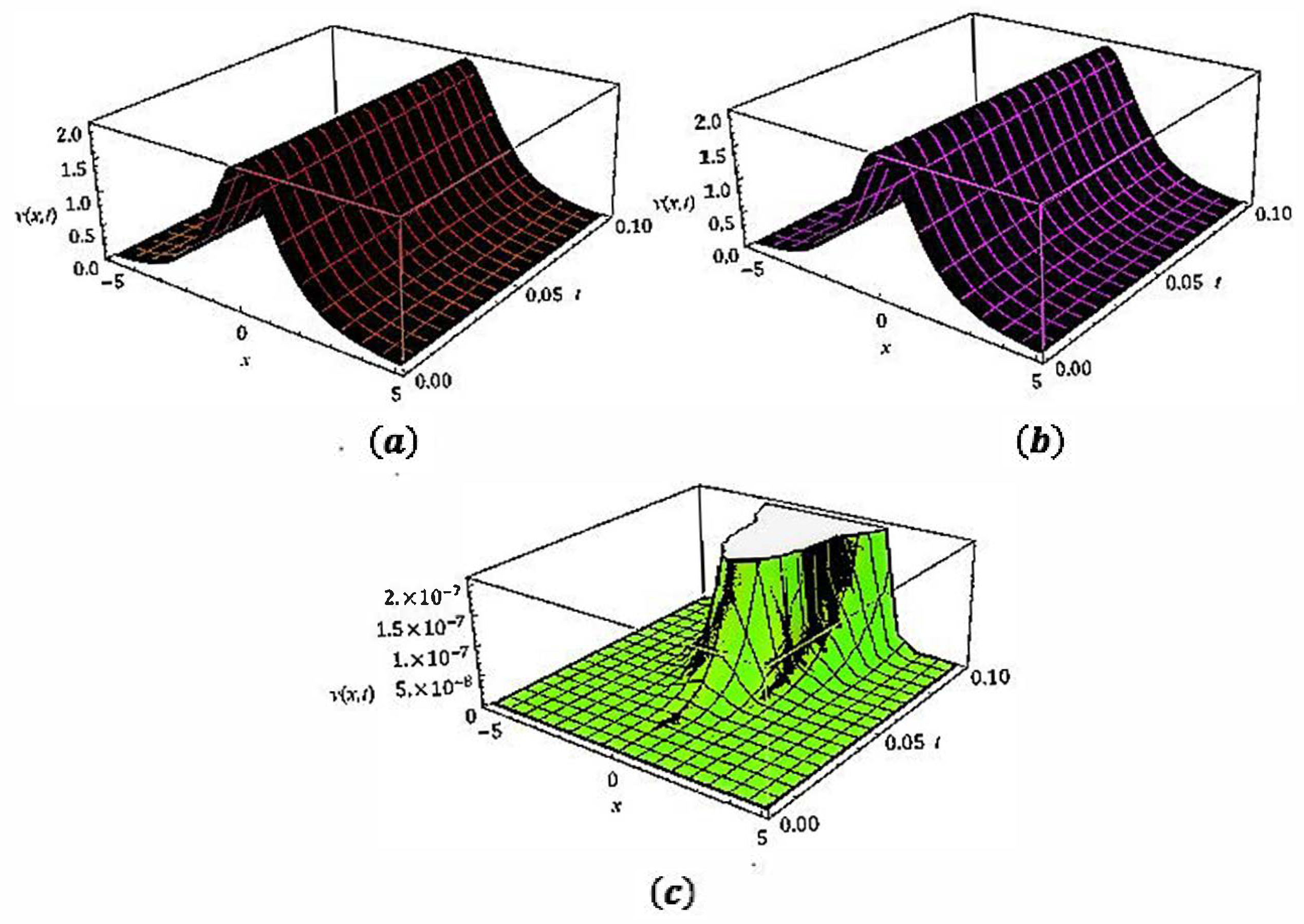
In Figure 1, (a) show that the exact, (b) represent the analytical solutions and (c) the error plot of . In Figure 2, (a) show that the exact, (b) represent the analytical solutions and (c) the error plot of .
Figure 1.
In figure (a) show that the exact, (b) represent the analytical solutions and (c) the error plot of .
Figure 2.
In figure (a) show that the exact, (b) represent the analytical solutions and (c) the error plot of .
6. Conclusions
In conclusion, the nonlinear fractional Drinfeld–Sokolov–Wilson problem encountered in dispersive water waves requires a combination of appropriate numerical techniques, including the Adomian decomposition approach, the homotopy perturbation method, and Yang transform, to obtain an approximative solution. The use of the Caputo manner to describe the fractional derivative and the employment of He’s polynomials and Adomian polynomials help to address the nonlinearity of the problem. By following the steps of these approaches, we can obtain solutions in the form of a convergent series. Our investigation of the assumed model in terms of the fractional order demonstrates the effectiveness of these suggested strategies. We have represented the physical behavior of the suggested technique solutions through plots for various fractional orders and have provided a numerical simulation. The results obtained show that the suggested algorithms are extremely systematic, simple to use, effective, and accurate for analyzing the behavior of coupled nonlinear differential equations of fractional order in related scientific and engineering fields.
Author Contributions
Conceptualization, S.N. and A.S.A.; methodology, R.S. and H.M.D.; software, R.N.; validation, S.N.; formal analysis, R.S.; investigation, A.K.; resources, H.M.D.; data curation S.N.; writing—original draft preparation, R.S.; writing—review and editing, S.N.; visualization, A.S.A.; supervision, A.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R183), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 3051).
Data Availability Statement
The numerical data used to support the findings of this study are included within the article.
Acknowledgments
This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R183), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 3051).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Ciani, S.; Vespri, V. On Holder continuity and equivalent formulation of intrinsic Harnack estimates for an anisotropic parabolic degenerate prototype equation. Constr. Math. Anal. 2021, 4, 93–103. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Xie, Z.; Feng, X.; Chen, X. Partial Least Trimmed Squares Regression. Chem. Intell. Lab. Syst. 2022, 221, 104486. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Meng, L.; Chen, X.; Yuan, L.; Cai, Q.; Huang, G. Non-Parametric Partial Least Squares-Discriminant Analysis Model Based on Sum of Ranking Difference Algorithm for Tea Grade Identification Using Electronic Tongue Data. Sens. Actuators B Chem. 2020, 311, 127924. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.; Wang, L.; Niu, X.; Yamaguchi, H.; Li, D.; Yu, P. A Magnetic Field Coupling Fractional Step Lattice Boltzmann Model for the Complex Interfacial Behavior in Magnetic Multiphase Flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Cao, Y.; Nikan, O.; Avazzadeh, Z. A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Appl. Numer. Math. 2023, 183, 140–156. [Google Scholar] [CrossRef]
- Ma, J.; Hu, J. Safe Consensus Control of Cooperative-Competitive Multi-Agent Systems via Differential Privacy. Kybernetika 2022, 58, 426–439. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Sun, L.; Hou, J.; Xing, C.; Fang, Z. A Robust Hammerstein-Wiener Model Identification Method for Highly Nonlinear Systems. Processes 2022, 10, 2664. [Google Scholar] [CrossRef]
- Oderinu, R.A.; Owolabi, J.A.; Taiwo, M. Approximate solutions of linear time-fractional differential equations. J. Math. Comput. Sci. 2023, 29, 60–72. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.; Liu, Y.; Deng, X.; Chen, Q.; Ma, Z. 60-GHz Compact Dual-Mode On-Chip Bandpass Filter Using GaAs Technology. IEEE Electron Device Lett. 2021, 42, 1120–1123. [Google Scholar] [CrossRef]
- Wang, X.; Lyu, X. Experimental Study on Vertical Water Entry of Twin Spheres Side-by-Side. Ocean. Eng. 2021, 221, 108508. [Google Scholar] [CrossRef]
- Kalimbetov, B.; Abylkasymova, E.; Beissenova, G. On the asymptotic solutions of singulary perturbed differential systems of fractional order. J. Math. Comput. Sci. 2022, 24, 165–172. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive Control of Time Delay Teleoperation System with Uncertain Dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Wang, T.; Zhang, W. Existence of Solutions for the (p,q)-Laplacian Equation with Nonlocal Choquard Reaction. Appl. Math. Lett. 2023, 135, 108418. [Google Scholar] [CrossRef]
- Zhong, T.; Wang, W.; Lu, S.; Dong, X.; Yang, B. RMCHN: A Residual Modular Cascaded Heterogeneous Network for Noise Suppression in DAS-VSP Records. IEEE Geosci. Remote Sens. Lett. 2022, 20. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Y.; Li, T.; Ghosh, B.K. Consensus Control of General Linear Multiagent Systems with Antagonistic Interactions and Communication Noises. IEEE Trans. Autom. Control 2019, 64, 2122–2127. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, Y.; Hu, J. On the Role of Community Structure in Evolution of Opinion Formation: A New Bounded Confidence Opinion Dynamics. Inf. Sci. 2023, 621, 672–690. [Google Scholar] [CrossRef]
- Fan, X.; Wei, G.; Lin, X.; Wang, X.; Si, Z.; Zhang, X.; Shao, Q.; Mangin, S.; Fullerton, E.; Jiang, L.; et al. Reversible Switching of Interlayer Exchange Coupling through Atomically Thin VO2 via Electronic State Modulation. Matter 2020, 2, 1582–1593. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Tanwar, K.; Baleanu, D. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler laws. Int. J. Heat Mass Transf. 2019, 138, 1222–1227. [Google Scholar] [CrossRef]
- Liu, M.; Gu, Q.; Yang, B.; Yin, Z.; Liu, S.; Yin, L.; Zheng, W. Kinematics Model Optimization Algorithm for Six Degrees of Freedom Parallel Platform. Appl. Sci. 2023, 13, 3082. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math. Methods Appl. Sci. 2019, 43, 443–457. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Zhang, L.; Pan, G.; Yu, J. Multi-UUV Maneuvering Counter-Game for Dynamic Target Scenario Based on Fractional-Order Recurrent Neural Network. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef]
- Luo, Z.-Z.; Cai, S.; Hao, S.; Bailey, T.P.; Luo, Y.; Luo, W.; Yu, Y.; Uher, C.; Wolverton, C.; Dravid, V.P.; et al. Extraordinary role of Zn in enhancing thermoelectric performance of Ga-doped n-type PbTe. Energy Environ. Sci. 2021, 15, 368–375. [Google Scholar] [CrossRef]
- Satsuma, J.; Hirota, R. A coupled KdV equation is one case of the four-reduction of the KP hierarchy. J. Phys. Soc. Jpn. 1982, 51, 3390–3397. [Google Scholar] [CrossRef]
- Hirota, R.; Grammaticos, B.; Ramani, A. Soliton structure of the Drinfel’d-Sokolov-Wilson equation. J. Math. Phys. 1986, 27, 1499–1505. [Google Scholar] [CrossRef]
- Drinfeld, V.G.; Sokolov, V.V. Equations of Korteweg-de Vries type and simple Lie algebras. Sov. Math. Dokl. 1981, 23, 457–546. [Google Scholar]
- Wilson, G. The affine lie algebra C 21 and an equation of Hirota and Satsuma. Phys. Lett. A 1982, 89, 332–334. [Google Scholar] [CrossRef]
- Drinfel’d, V.G.; Sokolov, V.V. Lie algebras and equations of Korteweg-de Vries type. J. Sov. Math. 1985, 30, 1975–2036. [Google Scholar] [CrossRef]
- Santillana, M.; Dawson, C. A numerical approach to study the properties of solutions of the diffusive wave approximation of the shallow water equations. Comput. Geosci. 2009, 14, 31–53. [Google Scholar] [CrossRef]
- Inc, M. On numerical doubly periodic wave solutions of the coupled Drinfel’d-Sokolov-Wilson equation by the decomposition method. Appl. Math. Comput. 2006, 172, 421–430. [Google Scholar] [CrossRef]
- Ren, B.; Lou, Z.M.; Liang, Z.F.; Tang, X.Y. Nonlocal symmetry and explicit solutions for Drinfel’d-Sokolov-Wilson system. Eur. Phys. J. Plus 2016, 131, 441. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Zhi, H.Y. An improved F-expansion method and its application to coupled Drinfel’d-Sokolov-Wilson equation. Commun. Theor. Phys. 2008, 50, 309–314. [Google Scholar]
- Sahoo, S.; Ray, S.S. New double-periodic solutions of fractional Drinfeld–Sokolov–Wilson equation in shallow water waves. Nonlinear Dynam. 2017, 88, 1869–1882. [Google Scholar] [CrossRef]
- Misirli, E.; Gurefe, Y. Exp-function method for solving nonlinear evolution equations. Math. Comput. Appl. 2011, 16, 258–266. [Google Scholar] [CrossRef]
- Yan, A.; Li, Z.; Cui, J.; Huang, Z.; Ni, T.; Girard, P.; Wen, X. Designs of Two Quadruple-Node-Upset Self-Recoverable Latches for Highly Robust Computing in Harsh Radiation Environments. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Yan, A.; Xiang, J.; Cao, A.; He, Z.; Cui, J.; Ni, T.; Huang, Z.; Wen, X.; Girard, P. Quadruple and Sextuple Cross-Coupled SRAM Cell Designs with Optimized Overhead for Reliable Applications. IEEE Trans. Device Mater. Reliab. 2022, 22, 282–295. [Google Scholar] [CrossRef]
- Yan, A.; Xu, Z.; Yang, K.; Cui, J.; Huang, Z.; Girard, P.; Wen, X. A Novel Low-Cost TMR-Without-Voter Based HIS-Insensitive and MNU-Tolerant Latch Design for Aerospace Applications. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2666–2676. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).