Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions †
Abstract
1. Introduction
- 1.
- Scattering data The minimal sets of scattering data are determined by the asymptotics ofHere, and are the factors of the Gauss decompositions of the scattering matrix .
- 2.
- Resolvent The FAS determine the kernel of the resolvent of L. Applying the contour integration method on , one can derive the spectral expansions for L, i.e., the completeness relation of the FAS.
- 3.
- Dressing method Zakharov–Shabat dressing method is a very effective and convenient method to construct the class of reflectionless potentials of L and to derive the soliton solutions of the NLEE. The simplest dressing factor has pole singularities at , which determine the new discrete eigenvalues that are added to the spectrum of the initial Lax operator.
- 4.
- Generalized Fourier transforms (GFTs) Here, we start with a GZS system related to a simple Lie algebra with Cartan-Weyl basis , [21] and construct the so-called ‘squared solutions’where is the projector onto the image of the operator . It is known that the ‘squared solution‘ are complete set of functions in the space of allowed potentials [22]. In particular, if we expand the potential over the ‘squared solutions’ the expansion coefficients will provide the minimal set of scattering data. Similarly, the expansion coefficients of are the variations of the minimal set of scattering data. Therefore, the ‘squared solutions’ can be viewed as FAS in the adjoint representation of , see [11,22,23,24,25,26,27,28,29,30,31,32,33,34].
- 5.
- Hierarchies of Hamiltonian structures The GFTs described above allow one to prove that each of the NLEE related to L allows a hierarchy of Hamiltonian structures. More precisely, each NLEE allows a hierarchy of Hamiltonians and a hierarchy of symplectic forms (or a hierarchy of Poisson brackets) such that for any n they produce the relevant NLEE [22,35,36].
- 6.
- Complete integrability and action-angle variables Starting from the famous paper by Zakharov and Faddeev [1] it is known that some of the NLEE allow action-angle variables. The difficulty here is that these NLEE are Hamiltonian systems with infinitely many degrees of freedom. Therefore, the strict derivation of the proof must be based on the completeness relation for the ‘squared solutions’. In fact, V. Gerdjikov and E. Khristov [27,28] (see also [30]) proposed the so-called ‘symplectic basis’ of squared solutions, which maps the variation of the potential of the AKNS system to the variation of the action-variables. Unfortunately, for many multi-component systems such bases are not yet known.
2. From the Lax Representation to the RHP
2.1. N-Waves According to Manakov and Zakharov
- C.1
- By we mean that possesses smooth derivatives of all orders and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding operator L has only a finite number of simple discrete eigenvalues.
2.2. MNLS Equations According to Manakov, Fordy and Kulish
2.3. Generic Lax Representation
3. Jost Solutions and FAS of
3.1. Jost Solutions and Scattering Matrix
3.2. Construction of the FAS
3.3. The Time-Dependence of
4. RHP and Integrable NLEE
4.1. Uniqueness of the Regular Solution of RHP
4.2. Zakharov–Shabat Theorem
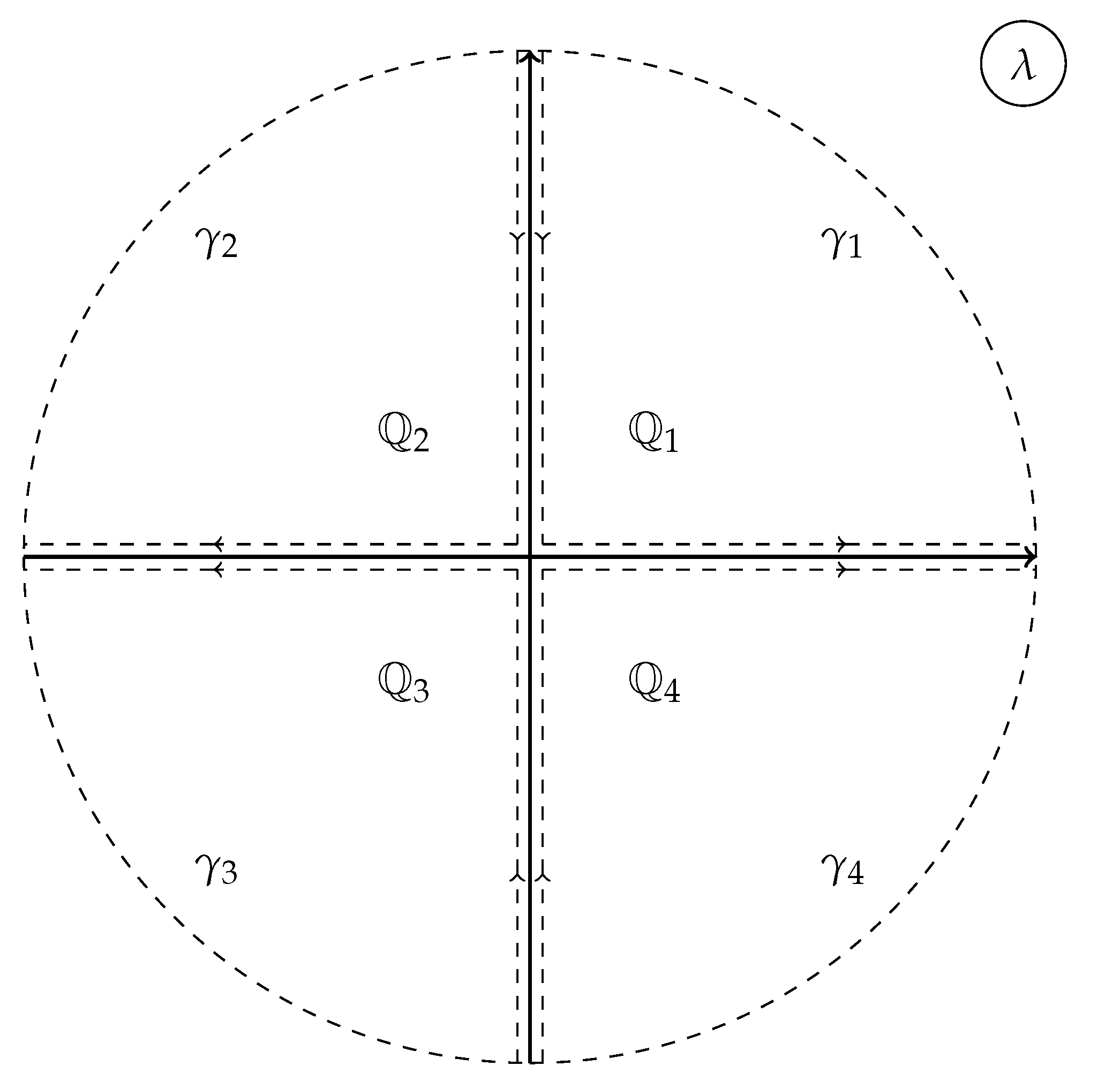
5. Mikhailov’s Reduction Groups and the Contours of RHP
5.1. General Theory
5.2. Involutive Reductions
5.3. Reduction Groups
5.4. Reduction Groups
6. Parametrizing the RHP with Canonical Normalization
6.1. Generic Parametrization of the RHP with Canonical Normalization
6.2. The Family of N-Wave Equations with Cubic Non-linearities
6.3. The Main Idea of the Dressing Method
6.4. Dressing of N-Wave Equations: Two Involutions
6.5. Dressing of N-Wave Equations: Three Involutions
7. MNLS Family and Symmetric Spaces
7.1. Lax Pairs on Symmetric Spaces. Generic Case
7.2. NLEE on Symmetric Spaces: A.III
7.3. MNLS Equations Related to D.III and C.I Symmetric Spaces
7.4. MNLS Related to BD.I-Type Symmetric Spaces
8. Soliton Solutions of the MNLS Equations
8.1. Dressing for NLEE on Symmetric Spaces: A.III Case
8.2. Dressing for NLEE on Symmetric Spaces: C.I and D.III Cases
8.3. Dressing for NLEE on Symmetric Spaces: BD.I Cases
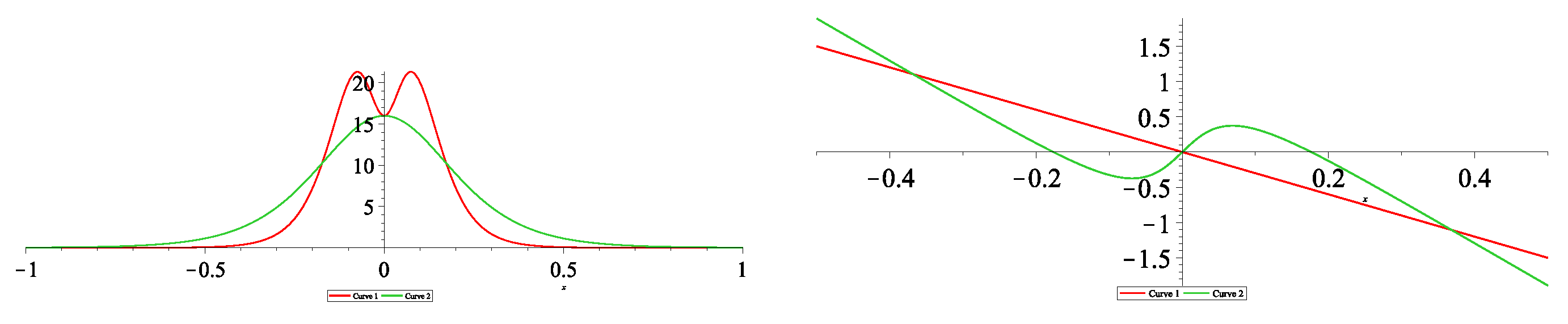
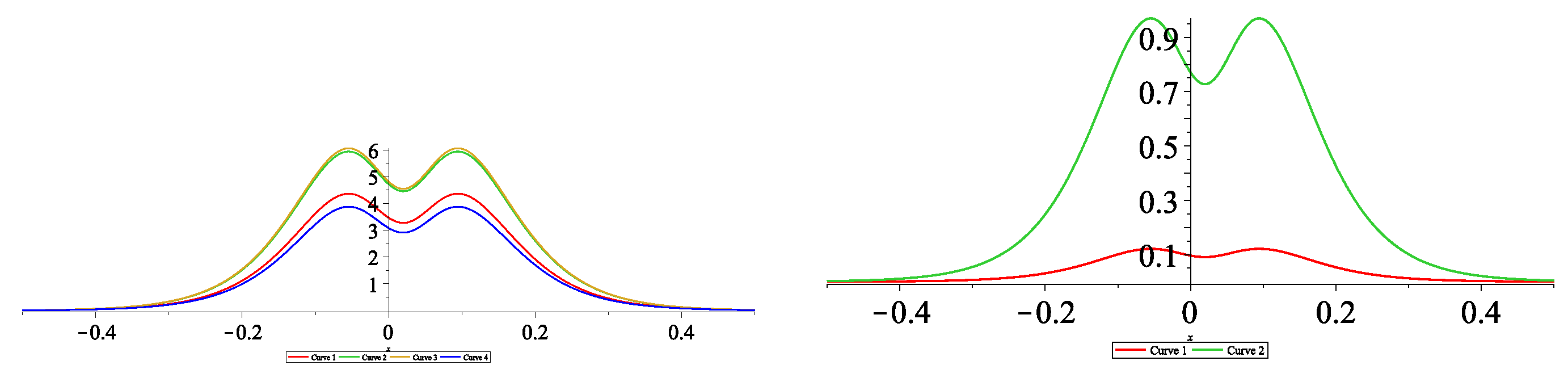
9. Multi-Soliton Solutions
10. The Resolvent and Spectral Properties of Lax Operators
- C.1
- possesses smooth derivatives of all orders with respect to x and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding RHP has finite index. For the class of RHP that we have been dealing with this means that the solution of the RHP must have finite number of simple zeroes and pole singularities.
- 1.
- if is a zero or pole of , then there must exist , which is also a zero or pole of ;
- 2.
- if is a zero or pole of , then there must exist , which is also zero or pole of .
- 3.
- if is a zero or pole of , then there must exist which is a zero or pole of .
- (i) the continuous spectrum of consists of all points for which is an unbounded integral operator;
- (ii) the discrete spectrum of consists of all points for which develops pole singularities.
- 1.
- is obvious from the fact that are the FAS of (86). It is also easy to see that if satisfies conditions (C.1) and (C.2) then and will also satisfy condition C1. In addition obviously will satisfy condition C2 and will have poles and zeroes at the points , see Remark 10.
- 2.
- Assume that and consider the asymptotic behavior of for . From Equation (86) we find that
- 3.
- For the arguments of (2) can not be applied because the exponentials in the right-hand side of (276) only oscillate. Thus, we conclude that for is only a bounded function of x and thus the corresponding operator is an unbounded integral operator.
- 4.
- The proof of Equation (275) follows from the fact that and
11. Natural Generalizations
11.1. Cubic Pencils as Lax Operators
11.2. Cubic Pencils with Dihedral Reduction Group
12. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
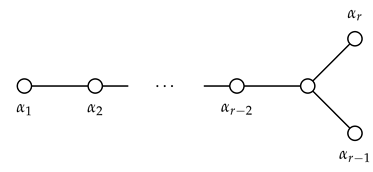
Appendix A. Root Systems of Simple Lie Algebras
- The Cartan subalgebras of all simple Lie algebras can be represented by diagonal matrices;
- There is a one-to-one mapping between the elements of and the vectors in r-dimensional Euclidean space ;
- The Weil generators are defined as eigenvectors of all the elements of , i.e.,where . Here, is the vector corresponding to H, and is a root of the algebra belonging to its system of roots .
- Root systems
- Dynkin diagrams
- Cartan-Weyl basis
- Automorphisms of finite order
- If then is also a root, .
- Each root system is split into positive and negative roots:
- In each root system, one can introduce a basis, known as system of simple roots. By definition , are simple roots if: (i) they are linearly independent and form a basis in ; (ii) they are positive roots such that ;
- Each positive root can be expressed as sum of simple roots where all are integers;
- There is a maximal (resp. minimal) root (resp ) such that (resp. ) is not a root;
- Symmetry properties of and Weyl group. Introduce the Weyl reflections by:The Weyl reflections form a finite group, which preserves , i.e., .
Appendix A.1. The Root System of Algebras

Appendix A.2. The Root System of Algebras

Appendix A.3. The Root System of Algebras

Appendix A.4. The Root System of Algebras
Appendix B. Gauss Decompositions
References
- Zakharov, V.E.; Faddeev, L.D. Korteweg-de Vries equation: A completely integrable Hamiltonian system. Funct. Anal. Appl. 1971, 5, 280–287. [Google Scholar] [CrossRef]
- Zabusky, N.J. Fermi–Pasta–Ulam, solitons and the fabric of nonlinear and computational science: History, synergetics, and visiometrics. Chaos 2005, 15, 015102. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. Interaction between solitons in a stable medium. Sov. Phys. JETP 1973, 37, 823–828. [Google Scholar]
- Wadati, M. The exact solution of the modified Korteweg de Vries equation. J. Phys. Soc. Jpn. 1972, 32, 1681. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Manakov, S.V. On the theory of resonance interactions of wave packets in nonlinear media. Zh. Exp. Teor. Fiz 1975, 69, 1654–1673. [Google Scholar]
- Manakov, S.V. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP 1974, 38, 248. [Google Scholar]
- Ablowitz, A.; Clarkson, A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Calogero, F.; Degasperis, A. Spectral transform and solitons. I. In Studies in Mathematics and its Applications; Elsevier: Haarlem, The Netherlands, 1982; Volume 13. [Google Scholar]
- Faddeev, L.D.; Takhtadjan, L.A. Hamiltonian Methods in the Theory of Solitons; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Gerdjikov, V.S.; Yanovski, A.B. Completeness of the eigenfunctions for the Caudrey–Beals–Coifman system. J. Math. Phys. 1994, 35, 3687–3725. [Google Scholar] [CrossRef]
- Novikov, S.; Manakov, S.; Pitaevskii, L.; Zakharov, V. Theory of Solitons: The Inverse Scattering Method; Plenum, Consultants Bureau: New York, NY, USA, 1984. [Google Scholar]
- Shabat, A.B. A one-dimensional scattering theory. I. Differ. Uravn. 1972, 8, 164–178. [Google Scholar]
- Shabat, A.B. The inverse scattering problem for a system of differential equations. Funkts. Anal. Prilozhen 1975, 9, 75–78. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. Algebraic and analytic aspects of n-wave type equations. Contemp. Math. 2002, 301, 35–68. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. A scheme for integrating nonlinear evolution equations of mathematical physics by the inverse scattering method. I. Funkts. Anal. Prilozhen 1974, 8, 43–53. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. Integration of the nonlinear equations of mathematical physics by the inverse scattering method. Funkts. Anal. Prilozhen 1979, 13, 13–22. [Google Scholar] [CrossRef]
- Mikhailov, A.V. The reduction problem and the inverse scattering problem. Phys. D 1981, 3D, 73–117. [Google Scholar] [CrossRef]
- Beals, R.; Coifman, R.R. Scattering and inverse scattering for first order systems. Commun. Pure Appl. Math. 1984, 37, 39. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Yanovski, A.B. CBC systems with Mikhailov reductions by Coxeter automorphism. I. Spectral theory of the recursion operators. Stud. Appl. Math. 2015, 134, 145–180. [Google Scholar] [CrossRef]
- Helgasson, S. Differential Geometry, Lie Groups and Symmetric Spaces; Graduate Studies in Mathematics; AMS: Providence, RI, USA, 2012; Volume 34. [Google Scholar]
- Gerdjikov, V.S. Generalised Fourier transforms for the soliton equations. gauge covariant formulation. Inverse Probl. 1986, 2, 51–74. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform—Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Constantin, A.; Gerdjikov, V.S.; Ivanov, R.I. Generalized Fourier transform for the Camassa–Holm equation. Inverse Probl. 2007, 23, 1565–1597. [Google Scholar] [CrossRef]
- Gaiarin, S.; Perego, A.M.; da Silva, E.P.; Da Ros, F.; Zibar, D. Dual-polarization nonlinear Fourier transform-based optical communication system. Optica 2018, 5, 263–270. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. On nonlocal models of Kulish–Sklyanin type and generalized Fourier transforms. In Advanced Computing in Industrial Mathematics. Studies in Computational Intelligence; Georgiev, K., Todorov, M., Georgiev, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 681, pp. 37–52. [Google Scholar]
- Gerdjikov, V.S.; Khristov, E.K. On the evolution equations solvable through the inverse scattering problem. I. The spectral theory. Bulg. J. Phys. 1979, 7, 28–41. [Google Scholar]
- Gerdjikov, V.S.; Khristov, E.K. On the evolution equations solvable through the inverse scattering problem. II. Hamiltonian structures and Backlund transformations. Bulg. J. Phys. 1979, 7, 119–133. [Google Scholar]
- Gerdjikov, V.S.; Smirnov, A.O.; Matveev, V.B. From generalized Fourier transforms to spectral curves for the Manakov hierarchy. I. Generalized Fourier transforms. Eur. Phys. J. Plus 2020, 135, 659. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Vilasi, G.; Yanovski, A.B. Integrable Hamiltonian Hierarchies: Spectral and Geometric Methods; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 748. [Google Scholar]
- Goossens, J.V.; Yousefi, M.; Jaou, Y.; Haffermann, H. Polarization-division multiplexing based on the nonlinear Fourier transform. Opt. Express 2017, 25, 437–462. [Google Scholar] [CrossRef]
- Kaup, D.J. Closure of the squared Zakharov–Shabat eigenstates. J. Math. Annal. Appl. 1976, 54, 849–864. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Gerdjikov, V.S.; Matveev, V.B. From generalized fourier transforms to spectral curves for the Manakov hierarchy. II. Spectral curves for the Manakov hierarchy. Eur. Phys. J. Plus 2020, 135, 561. [Google Scholar] [CrossRef]
- Gerdzhikov, M.I.I.V.S.; Kulish, P.P. Quadratic bundle and nonlinear equations. Theor. Math. Phys. 1980, 44, 784–795. [Google Scholar] [CrossRef]
- Kaup, D.J.; Newell, A.C. An exact solution for a derivative nonlinear Schrödinger equation. J. Math. Phys. 1978, 19, 798–801. [Google Scholar] [CrossRef]
- Kulish, P.P.; Reiman, A.G. Hamiltonian structure of polynomial bundles. J. Sov. Math. 1985, 28, 505–513. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. Riemann–Hilbert problems with canonical normalization and families of commuting operators. Pliska Stud. Math. Bulgar. 2012, 21, 201–216. [Google Scholar]
- Gerdjikov, V.S.; Stefanov, A.A. New types of two component NLS-type equations. Pliska Stud. Math. 2016, 26, 53–66. [Google Scholar]
- Gerdjikov, V.S.; Stefanov, A.A. On an example of derivative nonlinear Schrödinger equation with D2 reduction. Pliska Stud. Math. 2019, 30, 99–108. [Google Scholar]
- Gerdjikov, V.S.; Yanovski, A.B. Riemann–Hilbert problems, families of commuting operators and soliton equations. J. Phys. Conf. Ser. 2014, 482, 012017. [Google Scholar] [CrossRef]
- Ivanov, R. On the dressing method for the generalised Zakharov–Shabat system. Nucl. Phys. B 2004, 694, 509–524. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Zakharov, V.E. On the integrability of classical spinor models in two-dimensional space–time. Commun. Math. Phys. 1980, 74, 21–40. [Google Scholar]
- Zakharov, V.E. The inverse scattering method. In Solitons; Bullough, R.K., Caudrey, P.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; pp. 243–286. [Google Scholar]
- Zakharov, V.E. Exact solutions of the problem of parametric interaction of wave packets. Dokl. Akad. Nauk SSSR 1976, 228, 1314–1316. [Google Scholar]
- Fordy, A.P.; Kulish, P.P. Nonlinear Schrödinger equations and simple lie algebras. Commun. Math. Phys. 1983, 89, 427–443. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Grahovski, G.G. Multi-component NLS models on symmetric spaces: Spectral properties versus representations theory. Symmetry Integr. Geom. Methods Appl. 2010, 6, 44–73. [Google Scholar] [CrossRef]
- Matveev, V.B.; Smirnov, A.O. AKNS hierarchy, MRW solutions, Pn breathers, and beyond. J. Math. Phys. 2018, 59, 091419. [Google Scholar] [CrossRef]
- Gerdjikov, R.I.V.; Grahovski, G. On integrable wave interactions and Lax pairs on symmetric spaces. Wave Motion 2017, 71, 53–70. [Google Scholar] [CrossRef]
- Gerdjikov, R.I.V.; Stefanov, A. Riemann–Hilbert problem, integrability and reductions. J. Geom. Mech. 2019, 11, 167–185. [Google Scholar] [CrossRef]
- Valchev, T.I. On certain reductions of integrable equations on symmetric spaces. AIP Conf. Proc. 2011, 1340, 154–164. [Google Scholar]
- Warren, O.H.; Elgin, J.N. The vector nonlinear Schrödinger hierarchy. Phys. D 2007, 228, 166–171. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Ivanov, M.I. The quadratic bundle of general form and the nonlinear evolution equations. I. Expansions over the “squared” solutions are generalized Fourier transforms. Bulg. J. Phys. 1983, 10, 13–26. [Google Scholar]
- Gerdjikov, V.S.; Ivanov, M.I. The quadratic bundle of general form and the nonlinear evolution equations. II. Hierarchies of Hamiltonian structures. Bulg. J. Phys. 1983, 10, 130–143. [Google Scholar]
- Dai, H.H.; Fan, E.G. Variable separation and algebro-geometric solutions of the Gerdjikov–Ivanov equation. Chaos Solitons Fractals 2004, 22, 93–101. [Google Scholar] [CrossRef]
- Fan, E.G. Darboux transformation and solion-like solutions for the Gerdjikov–Ivanov equation. J. Phys. A 2000, 33, 6925–6933. [Google Scholar] [CrossRef]
- Fan, E.G. A family of completely integrable multi-hamiltonian systems explicitly related to some celebrated equations. J. Math. Phys. 2001, 42, 4327–4344. [Google Scholar] [CrossRef]
- Luo, J.; Fan, E. -dressing method for the coupled Gerdjikov–Ivanov equation. Appl. Math. Lett. 2020, 110, 106589. [Google Scholar] [CrossRef]
- Dickey, L.A. Soliton Equations and Hamiltonian Systems; World Scientific: Singapore, 2003. [Google Scholar]
- Gel, I.M.; Dikii, L.A. Fractional powers of operators and hamiltonian systems. Funct. Anal. Appl. 1976, 10, 259–273. [Google Scholar]
- Gel, I.M.; Dikii, L.A. The resolvent and hamiltonian systems. Funct. Anal. Appl. 1977, 11, 93–105. [Google Scholar]
- IGel, M.; Dikii, L.A. The calculus of jets and nonlinear Hamiltonian systems. Funct. Anal. Appl. 1978, 12, 81–94. [Google Scholar]
- Gel, I.M.; Dikii, L.A. Integrable nonlinear equations and the Liouville theorem. Funct. Anal. Appl. 1979, 13, 6–15. [Google Scholar]
- Bury, R.T. Automorphic Lie Algebras, Corresponding Integrable Systems and Their Soliton Solutions. Ph.D. Thesis, University of Leeds, Leeds, UK, 2010. [Google Scholar]
- Berkeley, A.V.M.G.; Xenitidis, P. Darboux transformations with tetrahedral reduction group and related integrable systems. J. Math. Phys. 2016, 57, 092701. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. zn—reductions and new integrable versions of derivative nonlinear Schrödinger equations. In Nonlinear Evolution Equations: Integrability and Spectral Methods; Lakshmanan, M., Fordy, A.P., Degasperis, A., Eds.; Manchester University Press: Manchester, UK, 1991; pp. 367–379. [Google Scholar]
- Gerdjikov, V.S. Derivative nonlinear Schrödinger equations with Zn and Dn–reductions. Rom. J. Phys. 2013, 58, 573–582. [Google Scholar]
- Lombardo, S.; Mikhailov, A.V. Reductions of integrable equations: Dihedral group. J. Phys. A 2004, 37, 7727–7742. [Google Scholar] [CrossRef]
- Lombardo, S.; Mikhailov, A.V. Reduction groups and automorphic Lie algebras. Commun. Math. Phys. 2005, 258, 179–202. [Google Scholar] [CrossRef]
- Gerdjikov, G.G.G.V.S.; Mikhailov, A.V.; Valchev, T.I. On soliton interactions for the hierarchy of a generalised Heisenberg ferromagnetic model on SU(3)/S(U(1)× U(2)) symmetric space. J. Geom. Symmetry Phys. 2012, 25, 23–55. [Google Scholar]
- Yanovski, A.B.; Valchev, T.I. Pseudo-hermitian reduction of a generalized Heisenberg ferromagnet equation. I. Auxiliary system and fundamental properties. J. Nonlinear Math. Phys. 2018, 25, 324–350. [Google Scholar] [CrossRef]
- Drinfel, V.G.; Sokolov, V.V. Lie algebras and equations of Korteweg-de Vries type. Sov. J. Math. 1985, 30, 1975–2036. [Google Scholar] [CrossRef]
- Bourbaki, N. Elements of Mathematics. Lie Groups and Lie Algebras; Springer: Berlin/Heidelberg, Germany, 2002; Chapters 4–6. [Google Scholar]
- Coxeter, H.; Moser, W. Generators and Relations for Discrete Groups, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Knibbeler, V.; Lombardo, S.; Sanders, J.A. Higher-dimensional automorphic Lie algebras. Found. Comput. Math. 2017, 17, 987–1035. [Google Scholar] [CrossRef]
- Mikhailov, A.V. Reductions in integrable systems. The reduction group. JETP Lett. 1980, 32, 187–192. [Google Scholar]
- Leznov, A.N.; Saveliev, M.V. Two-dimensional nonlinear equations of the string type and their complete integration. Theor. Math. Phys. 1983, 54, 323–337. [Google Scholar] [CrossRef]
- Valchev, T.I. Dressing method and quadratic bundles related to symmetric spaces. Vanishing boundary conditions. J. Math. Phys. 2016, 57, 021508. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. Kulish-Sklyanin type models: Integrability and reductions. Theor. Math. Phys. 2017, 192, 1097–1114. [Google Scholar] [CrossRef]
- NAkhiezer, I.; Glazman, I.M. Theory of Linear Operators in Hilbert Space; Dover Publications: New York, NY, USA, 1963. (In Russian) [Google Scholar]
- Dunford, N.; Schwartz, J.T. Spectral Theory: Self-Adjoint Operators in Hilbert Space; Linear Operators; Interscience Publishers, Inc.: New York, NY, USA, 1963; Volume 2. [Google Scholar]
- Gerdjikov, V.S.; Kulish, P.P. Complete integrable Hamiltonian systems related to the non–self–adjoint Dirac operator. Bulg. J. Phys. 1978, 5, 337–349. [Google Scholar]
- Gerdjikov, V.S.; Kulish, P.P. The generating operator for the n × n linear system. Phys. D 1981, 3D, 549–564. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. On the spectral theory of the integro-differential operator λ, generating nonlinear evolution equations. Lett. Math. Phys. 1982, 6, 315–324. [Google Scholar] [CrossRef]
- Gerdjikov, V.S. Basic aspects of soliton theory. In Geometry, Integrability and Quantization; Hirshfeld, A.C., Mladenov, I.M., Eds.; Sortex: Sofia, Bulgaria, 2005; pp. 78–125. [Google Scholar]
- Holm, D.D. Geometric Mechanics Part I: Dynamics and Symmetry; Imperial College Press: London, UK, 2011. [Google Scholar]
- Holm, D.D. Geometric Mechanics Part II: Rotating, Translating and Rolling; Imperial College Press: London, UK, 2011. [Google Scholar]
- Ablowitz, B.P.M.J.; Trubach, A.D. Discrete and Continuous Nonlinear Schrödinger Systems; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Mikhailov, A.V.; Shabat, A.B.; Sokolov, V.V. The symmetry approach to classification of integrable equations. In What is Integrability? Springer Series in Nonlinear Dynamics; Zakharov, V.E., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 115–184. [Google Scholar]
- Zakharov, V.E. Integrable systems in multidimensional spaces. In Mathematical Problems in Theoretical Physics; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1982; Volume 153, pp. 190–216. [Google Scholar]
- Ablowitz, M.J.; Ladik, J.F. Nonlinear differential–difference equations and Fourier analysis. J. Math. Phys. 1976, 17, 1011–1018. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Ivanov, M.I.; Kulish, P.P. Expansions over the “squared” solutions and difference evolution equations. J. Math. Phys. 1984, 25, 25–34. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Shabat, A.B.; Yamilov, R.I. The symmetry approach to the classification of non-linear equations. Complete lists of integrable systems. Russ. Math. Surv. 1987, 42, 3–53. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Shabat, A.B.; Yamilov, R.I. Extension of the module of invertible transformations. classification of integrable systems. Commun. Math. Phys. 1988, 115, 1–19. [Google Scholar] [CrossRef]
- Zhao, G. Integrability of Two-Component Systems of Partial Differential Equations. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2020. [Google Scholar]
- Gerdjikov, V.S.; Stefanov, A.A.; Iliev, I.D.; Boyadjiev, G.P.; Smirnov, A.O.; Pavlov, M.V. Recursion operators and the hierarchies of MKdV equations related to , and Kac-Moody algebras. Theor. Math. Phys. 2020, 204, 1110–1129. [Google Scholar] [CrossRef]
- Adler, M. On a trace functional for pseudo-differential operators and the symplectic structure of the Korteweg-de Vries equation. Invent. Math. 1979, 50, 219–248. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Mladenov, D.M.; Stefanov, A.A.; Varbev, S.K. Mkdv-type of equations related to and . In Nonlinear Mathematical Physics and Natural Hazards; Springer Proceedings in Physics; Aneva, B., Kouteva-Guentcheva, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 163, pp. 59–69. [Google Scholar]
- Gerdjikov, V.S.; Mladenov, D.M.; Stefanov, A.A.; Varbev, S.K. On mKdV equations related to the affine Kac-Moody algebra . J. Geom. Symmetry Phys. 2015, 39, 17–31. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Mladenov, D.M.; Stefanov, A.A.; Varbev, S.K. Soliton equations related to the affine Kac-Moody algebra . Eur. Phys. J. Plus 2015, 130, 106–123. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Yanovski, A.B. On soliton equations with and reductions: Conservation laws and generating operators. J. Geom. Symmetry Phys. 2013, 31, 57–92. [Google Scholar]
- Kaup, D.J. The three-wave interaction—A nondispersive phenomenon. Stud. Appl. Math. 1976, 55, 9–44. [Google Scholar] [CrossRef]
- Kaup, D.J. On the inverse scattering problem for cubic eigenvalue problems of the class ψxxx + 6qψx + 6rψ = λψ. Stud. Appl. Math. 1980, 62, 189–216. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Olshanetsky, M.A.; Perelomov, A.M. Two-dimensional generalized Toda lattice. Comm. Math. Phys. 1981, 79, 473–488. [Google Scholar] [CrossRef]
- Babalic, R.C.N.C.; Gerdjikov, V. On the solutions of a family of Tzitzeica equations. J. Geom. Symmetry Phys. 2015, 37, 1–24. [Google Scholar]
- Babalic, R.C.N.C.; Gerdjikov, V.S. On Tzitzeica equation and spectral properties of related Lax operators. Balk. J. Geom. Appl. 2014, 19, 11–22. [Google Scholar]
- Changzheng, Q.U.; Song, J.; Yao, R. Multi-component integrable systems and invariant curve flows in certain geometries. Symmetry Integr. Geom. Methods Appl. 2013, 9, 1–20. [Google Scholar]
- Gerdjikov, V.S.; Ivanov, R.I. Multicomponent Fokas-Lenells equations on Hermitian symmetric spaces. Nonlinearity 2021, 34, 939. [Google Scholar] [CrossRef]
- Haberlin, J.; Lyons, T. Solitons of shallow-water models from energy-dependent spectral problems. Eur. Phys. J. Plus 2018, 133, 16. [Google Scholar] [CrossRef]
- Holm, D.; Ivanov, R. Smooth and peaked solitons of the CH equation. J. Phys. A Math. Theor. 2010, 43, 434003. [Google Scholar] [CrossRef]
- Holm, D.; Ivanov, R. Two-component CH system: Inverse scattering, peakons and geometry. Inverse Probl. 2011, 27, 045013–045032. [Google Scholar] [CrossRef]
- Ivanov, R.; Lyons, T. Integrable models for shallow water with energy dependent spectral problems. J. Nonlinear Math. Phys. 2012, 19, 1240008–12400025. [Google Scholar] [CrossRef]
- Ivanov, R.I. Nls-type equations from quadratic pencil of Lax operators: Negative flows. Chaos Solitons Fractals 2022, 161, 112299. [Google Scholar] [CrossRef]
- Gaiarin, S.; Perego, A.M.; da Silva, E.P.; Da Ros, F.; Zibar, D. Experimental demonstration of dual polarization nonlinear frequency division multiplexed optical transmission system. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar]
- Gerdjikov, V.S. Bose-Einstein condensates and spectral properties of multicomponent nonlinear Schrödinger equations. Discret. Contin. Dyn. Syst. 2011, 4, 1181–1197. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Grahovski, G.G. Two soliton interactions of BD.I multicomponent NLS equations and their gauge equivalent. AIP Conf. Proc. 2010, 1301, 561–572. [Google Scholar]
- Gerdjikov, V.S.; Kostov, N.A.; Valchev, T.I. Bose-Einstein condensates with F = 1 and F = 2. Reductions and soliton interactions of multi-component NLS models. In Proceedings of the Ultrafast Nonlinear Optics 2009, Bourgas, Bulgaria, 14–18 September 2009; Volume 7501. [Google Scholar]
- Gerdjikov, V.S.; Kostov, N.A.; Valchev, T.I. Solutions of multi-component NLS models and spinor Bose-Einstein condensates. Phys. D 2009, 238, 1306–1310. [Google Scholar] [CrossRef]
- Ieda, J.; Miyakawa, T.; Wadati, M. Exact analysis of soliton dynamics in spinor Bose-Einstein condensates. Phys. Rev. Lett. 2004, 93, 194102. [Google Scholar] [CrossRef] [PubMed]
- Ieda, J.; Miyakawa, T.; Wadati, M. Matter-wave solitons in an F = 1 spinor Bose-Einstein condensate. J. Phys. Soc. Jpn. 2004, 73, 2996. [Google Scholar] [CrossRef]
- Kostov, N.A.; Atanasov, V.A.; Gerdjikov, V.S.; Grahovski, G.G. On the soliton solutions of the spinor Bose-Einstein condensate. In Proceedings of the 14th International School on Quantum Electronics: Laser Physics and Applications, Sunny Beach, Bulgaria, 18–22 September 2006. [Google Scholar]
- Kulish, P.P.; Sklyanin, E.K. O(N)-invariant nonlinear Schrodinger equation—A new completely integrable system. Phys. Lett. A 1981, 84, 349–352. [Google Scholar] [CrossRef]
- Ohmi, T.; Machida, K. Bose–Einstein condensation with internal degrees of freedom in alkali atom gases. J. Phys. Soc. Jpn. 1998, 67, 1822. [Google Scholar] [CrossRef]
- Streche-Pauna, A.; Florian, A.; Gerdjikov, V.S. On generalized Kulish-Sklyanin models. Phys. AUC 2020, 30, 175–195. [Google Scholar]
- Uchiyama, M.; Ieda, J.; Wadati, M. Dark solitons in F = 1 spinor Bose–Einstein condensate. J. Phys. Soc. Jpn. 2006, 75, 064002. [Google Scholar] [CrossRef]
- Uchiyama, M.; Ieda, J.; Wadati, M. Multicomponent bright solitons in f = 2 spinor Bose–Einstein condensates. J. Phys. Soc. Jpn. 2007, 76, 74005. [Google Scholar] [CrossRef]
- Ueda, M.; Koashi, M. Theory of spin-2 Bose–Einstein condensates: Spin correlations, magnetic response, and excitation spectra. Phys. Rev. A 2002, 65, 063602. [Google Scholar] [CrossRef]
- Atanasov, V.A.; Gerdjikov, V.S.; Grahovski, G.G.; Kostov, N.A. Fordy-kulish models and spinor Bose–Einstein condensates. J. Nonlinear Math. Phys. 2008, 15, 291–298. [Google Scholar] [CrossRef][Green Version]
- Gerdjikov, V.S. On soliton interactions of vector nonlinear Schrödinger equations. AIP Conf. Proc. 2011, 1404, 57–67. [Google Scholar]
- Gerdjikov, V.S.; Li, N.; Matveev, V.B.; Smirnov, A.O. On soliton solutions and soliton interactions of Kulish–Sklyanin and Hirota–Ohta systems. Theor. Math. Phys. 2022, 213, 1331–1347. [Google Scholar] [CrossRef]
- Konopelchenko, B.G. Solitons in Multidimensions. Inverse Spectral Transform Method; World Scientific: Singapore, 1993. [Google Scholar]
- Manakov, S.V.; Zakharov, V.E. Soliton Theory. In Soviet Scientific Reviews A; Khalatnikov, I.M., Ed.; IMSc Library: London, UK, 1979; Volume 1, pp. 133–190. [Google Scholar]
- Dubrovin, B.A. Matrix finite-zone operators. J. Sov. Math. 1985, 28, 20–50. [Google Scholar] [CrossRef]
- Enol, V.Z.; Kostov, N.A. Quasiperiodic and periodic solutions for vector nonlinear Schrödinger equations. J. Math. Phys. 2000, 41, 8236. [Google Scholar]
- Smirnov, A.O. Spectral curves for the derivative nonlinear Schrodinger equations. Symmetry 2021, 13, 1203. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Frolov, E.A.; Gerdjikov, V.S. Spectral curves for the multi-phase solutions of Manakov system. IOP Conf. Ser. Mater. Sci. Eng. 2020, 862, 052041. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Gerdjikov, V.S.; Aman, E.E. The Kulish–Sklyanin type hierarchy and spectral curves. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1047, 012114. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Kolesnikov, A.S. Dubrovin’s method and Ablowitz-Kaup-Newell-Segur hierarchy. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1181, 012028. [Google Scholar] [CrossRef]


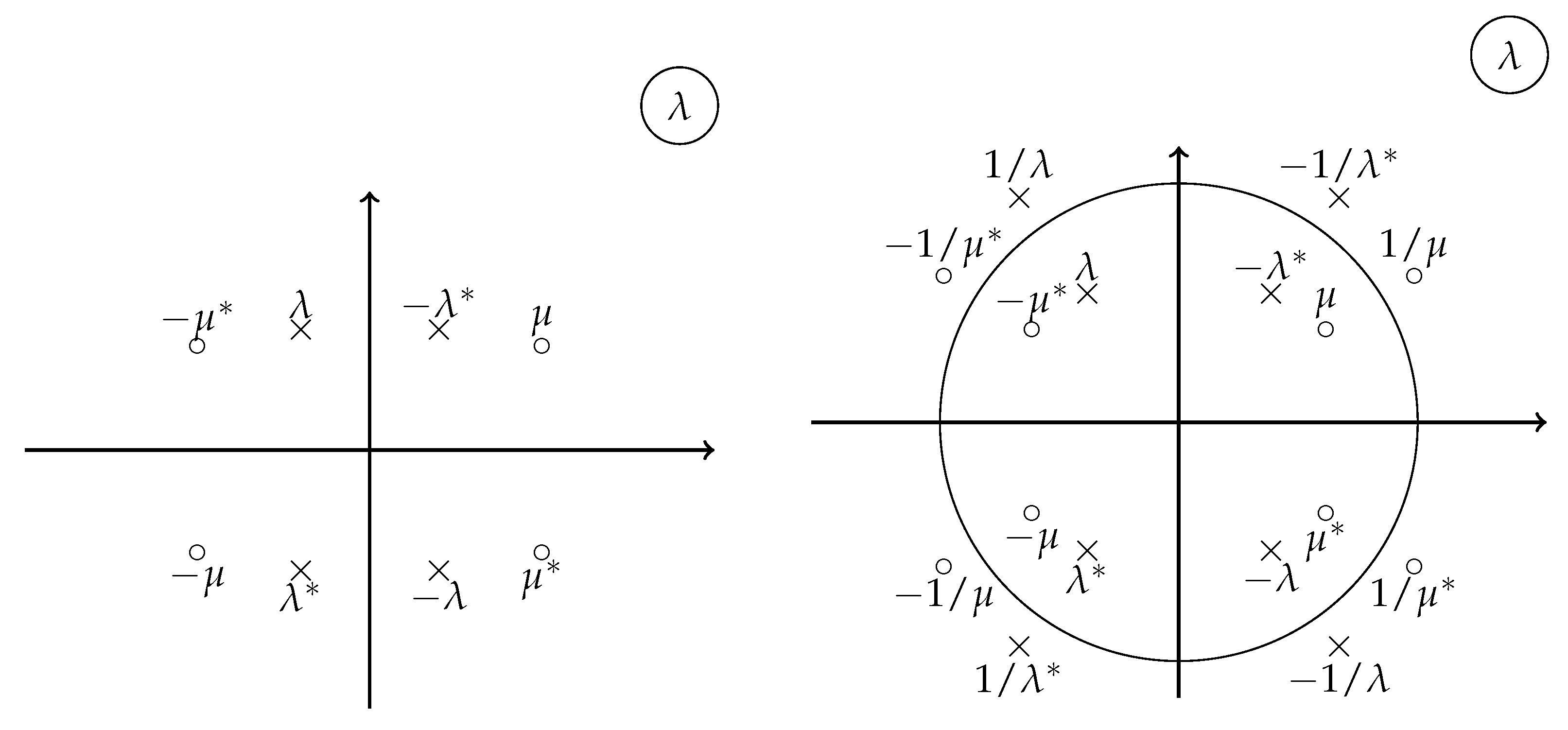



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerdjikov, V.S.; Stefanov, A.A. Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions. Symmetry 2023, 15, 1933. https://doi.org/10.3390/sym15101933
Gerdjikov VS, Stefanov AA. Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions. Symmetry. 2023; 15(10):1933. https://doi.org/10.3390/sym15101933
Chicago/Turabian StyleGerdjikov, Vladimir Stefanov, and Aleksander Aleksiev Stefanov. 2023. "Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions" Symmetry 15, no. 10: 1933. https://doi.org/10.3390/sym15101933
APA StyleGerdjikov, V. S., & Stefanov, A. A. (2023). Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions. Symmetry, 15(10), 1933. https://doi.org/10.3390/sym15101933




