Abstract
By using Gronwall’s inequality and coincidence degree theory, the sufficient conditions of the globally exponential stability and existence are given for a Hebbian-type network with time-varying delays. The periodic behavior phenomenon is one of the hot topics in network systems research, from which we can discover the symmetric characteristics of certain neurons. The main theorems in the present paper are illustrated using a numerical example.
1. Introduction
In the past few decades, Hopfield-type neural networks has been investigated by engineers, physicists, computer scientists and mathematicians. Gopalsamy [1] considered a second-order Hopfield-type neural network with constant lags and an unsupervised Hebbian-type learning algorithm as follows:
All coefficients of system (1) are constants. However, in nature, dynamic systems are inevitably influenced by external environments, and variable coefficient systems are more capable of depicting real-world situations. Hence, we study a neural networks with variable coefficients and lags as follows:
where is the state of the system; is the feedback rate of the system; represents the synaptic vector; represents the acceptance rate of the input signals; and are synaptic weights; and are disposable; is learning the signal vector; is the time-varying lag with ; is the external input signal vector; and is the neuronal activation function. Let
We rewrite (2) into
where . The initial conditions of system (3) are given by
where and are continuous and bounded functions on , and is defined by (5).
From the models proposed by Amari [2,3], we obtain system (3) which belongs to a higher-order network system. A high-order neural network system can simulate complex neuronal changes, and many scholars have been dedicated to this research. A method for defining an unknown nonlinear system was presented by Gonzalez, Basin and Vargas [4]. Huang and Cao [5] studied bifurcation problems regarding different lags of high-order fractional networks. Liu et al. [6] obtained fixed-time combined control for high-order multi-agent networks with variable failures. For more results regarding high-order neural networks, please see, e.g., references [7,8,9,10,11].
The periodic phenomenon widely exists in nature, and its research can deepen the understanding of the changing patterns of neurons, promoting the development and utilization of network systems. Over the past decades, there are many profound results for the periodic solution research of high-order network systems. A stochastic Cohen–Grossberg neural network with variable lags has been studied by Wu, Yang and Ren [12]. Zhang and Liu [13] dealt with global exponential stability and the existence of a periodic solution for a BAM neural network with multiple lags on time scales. From the Lyapunov functional method and some inequality techniques, Luo, Jiang and Wang [14] studied the anti-periodic solutions of a Clifford-valued high-order neural network with proportional lags. The almost periodic solution problem for a quaternion-valued neural networks has been investigated by Li and Xiang [15]. For more results for high-dimensional dynamic systems and networks systems, please see, e.g., references [16,17,18,19,20] and related references.
Affected by the existing research results, in the present paper, we will study the periodic solution for a Hebbian-type network with time-varying lags. The main contributions of this paper are as follows:
- (1)
- There is not much research on the periodic solution research of system (3), and this study expands its research scope.
- (2)
- On the basis of fully considering the variable delays and coefficients, this article constructs a new function, which can conveniently obtain the stability of system (3).
The remaining parts of this article are arranged as follows. Section 2 gives some preparations. Section 3 gives some existence results of a periodic solution for the system (3). Section 4 gives the stability results of a periodic solution for system (3). In Section 5, we give an example to illustrate the correctness of Theorems 1 and 2. The conclusions are given in Section 6.
In the whole paper, the following notations are listed:
Furthermore, the following assumptions hold.
- (H1) In system (3), for , are —periodic continuous functions.
- (H2) There is constant such that
- (H3) There is constant such that
2. Preliminaries
Let and be two Banach spaces. Let be a Fredholm operator with index zero, which means that is closed in and . Let projectors such that . Furthermore, is invertible. Denote using the inverse of .
Let be an open bounded subset of . Let the operator be -compact in which means that is bounded and the operator is relatively compact. The following lemma is the famous Mawhin’s continuation theorem.
Lemma 1
([21]). Assume that Δ and Π are two Banach spaces, and is a Fredholm operator with index zero. Furthermore, is an open bounded set and is L-compact on . If all the following conditions hold:
- (1)
- (2)
- (3)
- .
Then equation has a solution on
Definition 1.
Let be a periodic solution of (3) with initial conditions . and be a solution of (3) with initial conditions . The periodic solution is called globally exponentially stable, if there are and such that
where .
3. Existence of Periodic Solution
Theorem 1.
Suppose that (H1)–(H3) satisfy. There exists for system (3) at least one periodic solution, provided that
Proof.
Let
where . Define the norm of by for . Obviously, is a Banach space. Define projectors P and Q by, respectively,
and
Set
and
where
Obviously, the operator is a Fredholm operator with index zero. Consider the following operator equation:
and can be found in (7) and (8), respectively. We first prove that the solution of the operator system (9) is bounded. Using (9), we obtain
From (11), (H1) and (H2), we obtain
and
From (10), (12), (H1) and (H2), we have
and
Obviously, and do not depend on . Let
Here, we select that is sufficiently large such that
where is defined by (6). Let
where . It is easy to see that condition (1) in Lemma 1 satisfies. For , then and are constants with . From (6), (H2), and (H3), we obtain
and
Consequently,
which means that condition (2) in Lemma 1 satifies. Define by
For , is a -dimensional constant vector. Thus,
and
Hence,
Therefore, all conditions of Lemma 1 satisfy and there exists a periodic solution for system (3). □
Remark 1.
Usually, the Lyapunov–Kravsovskii functional method is the main method for studying the stability of equations, and a large number of stability results are obtained using this method. But constructing a suitable Lyapunov function is very difficult. In this article, we use the basic theory of differential equations and Gronwall’s inequality to obtain the dynamical behaviors of system (3). The method presented in this article is easier to understand and the proof process is not complicated.
4. Globally Exponential Stability
Theorem 2.
Assume that all conditions of Theorem 1 satisfy. Then, the periodic solution of system (3) is globally exponentially stable, if
where
Proof.
Using Theorem 1, (3) has a periodic solution , where . Let be any solution of (3). Let
Obviously satisfies (H3). System (3) can be rewritten as follows:
For , using (14) we obtain
Furthermore, for , using (15) we obtain
Using (14), (H2), and (H3), we have
From (15) and (H3), we have
From (18) and (19), we obtain
where
is defined by (13). Using Gronwall’s inequality, we obtain
Due to Definition 1, there exists a globally exponentially stable periodic solution for system (3). □
Remark 2.
Usually, the Lyapunov–Kravsovskii functional method is the main method for studying the stability of equations, and a large number of stability results are obtained using this method. But constructing a suitable Lyapunov function is very difficult. In this article, we use the basic theory of differential equations and Gronwall’s inequality to obtain the dynamical behaviors of system (3). The method presented in this article is easier to understand and the proof process is not complicated.
5. Example
Consider the following Hebbian-type networks:
where
After simple calculations, we have
We obtain and . From selections of and , it is obvious that there exists a periodic solution for system (20) . Furthermore, using the above calculations, we confirm that all conditions of Theorem 1 and Theorem 2 satisfy. Hence, there exists a globally asymptotically periodic solution for system (20) . Figure 1 and Figure 2 show the evolution of the solution of system (20).
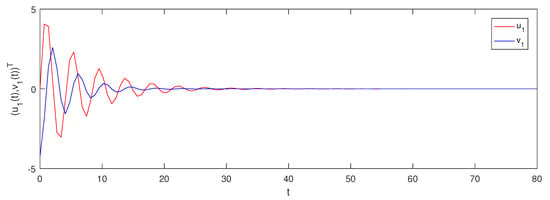
Figure 1.
Evolution for the solution of system (20).
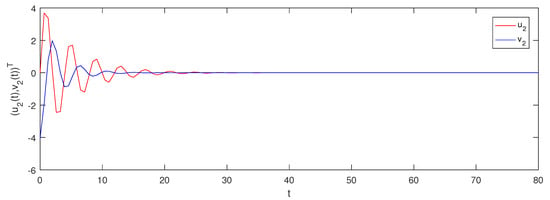
Figure 2.
Evolution for the solution of system (20).
6. Conclusions and Discussions
We study a class of Hebbian-type networks with variable lags. More precisely, we obtain some criteria for the existence of a periodic solution. Also, we examine the globally exponential stability analysis of system (3). Finally, we provided an example to show the analytical results. We can further investigate the dynamic behavior of system (3) under different environmental interference factors. One aspect future research is the stochastic Hebbian-type networks.
Author Contributions
Methodology, M.X. and H.Y.; Writing—original draft, B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank the editor and the referees for their valuable comments and suggestions that improved the quality of our paper.
Conflicts of Interest
The author declares that there are no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Gopalsamy, K. Learning dynamics in second order networks. Nonlinear Anal. Real World Appl. 2007, 8, 688–698. [Google Scholar] [CrossRef]
- Amari, S. Competitive and cooperative aspects in dynamics of neural excitation and self-organization. In Competition and Cooperation in Neural Nets; Lecture Notes in Biomathematics; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Amari, S. Mathematical theory of neural learning. New Gener. Comput. 1991, 8, 281–294. [Google Scholar] [CrossRef]
- Gonzalez, M.; Basin, M.; Vargas, E. Discrete-time high-order neural network identifier trained with high-order sliding mode observer and unscented Kalman filter. Neurocomputing 2021, 424, 172–178. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J. Bifurcations due to different delays of high-order fractional neural networks. Int. J. Biomath. 2022, 15, 2150075. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Zhang, Y.; Chen, C. Neural network-based smooth fixed-time cooperative control of high-Order multi-agent systems with time-varying failures. J. Frankl. Inst. 2022, 359, 152–177. [Google Scholar] [CrossRef]
- Huang, Z.; Raffoul, Y.; Cheng, C. Scale-limited activating sets and multiperiodicity for threshold-linear networks on time scales. IEEE Trans. Cybern. 2014, 44, 488–499. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Liang, J.; Lam, J. Exponential stability of high order bidirectional associative memory neural networks with time delays. Physica D 2004, 199, 425–436. [Google Scholar] [CrossRef]
- Kosmatopoulos, E.; Polycarpou, M.; Christodoulou, M.; Ioannou, P. High order neural network structures for identification of dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 422–431. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liu, X. An LMI approach to stability analysis of stochastic high-order Markovian jumping neural networks with mixed time delays. Nonlinear Anal. Hybrid Syst. 2008, 2, 110–120. [Google Scholar] [CrossRef]
- Xing, J.; Peng, C.; Cao, Z. Event-triggered adaptive fuzzy tracking control for high-order stochastic nonlinear systems. J. Frankl. Inst. 2022, 359, 6893–6914. [Google Scholar] [CrossRef]
- Wu, W.; Yang, L.; Ren, Y. Periodic solutions for stochastic Cohen—CGrossberg neural networks with time-varying delays. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 13–21. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, K. Existence and global exponential stability of a periodic solution to interval general bidirectional associative memory (BAM) neural networks with multiple delays on time scales. Neural Netw. 2011, 24, 427–439. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Jiang, Q.; Wang, Q. Anti-periodic solutions on Clifford-valued high-order Hopfield neural networks with multi-proportional delays. Neurocomputing 2022, 472, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Xiang, J. Existence and global exponential stability of almost periodic solution for quaternion-valued high-order Hopfield neural networks with delays via a direct method. Math. Methods Appl. Sci. 2020, 43, 6165–6180. [Google Scholar] [CrossRef]
- Guo, X.; Huang, C.; Cao, J. Nonnegative periodicity on high-order proportional delayed cellular neural networks involving D operator. AIMS Math. 2021, 6, 2228–2243. [Google Scholar] [CrossRef]
- Cao, Q.; Guo, X. Anti-periodic dynamics on high-order inertial Hopfield neural networks involving time-varying delays. AIMS Math. 2020, 5, 5402–5421. [Google Scholar] [CrossRef]
- Gao, J.; Dai, L. Anti-periodic synchronization of quaternion-valued high-order Hopfield neural networks with delays. AIMS Math. 2022, 7, 14051–14075. [Google Scholar] [CrossRef]
- Huang, C.; Liu, B.; Qian, C.; Cao, J. Stability on positive pseudo almost periodic solutions of HPDCNNs incorporating D operator. Math. Comput. Simul. 2021, 190, 1150–1163. [Google Scholar] [CrossRef]
- Duan, L.; Huang, L.; Guo, Z.; Fang, X. Periodic attractor for reaction—Cdiffusion high-order hopfield neural networks with time-varying delays. Comput. Math. Appl. 2017, 73, 233–245. [Google Scholar] [CrossRef]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Differential Equations; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).