Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations
Abstract
1. Introduction
2. n-Fold DT for the Fractional CNLS Equation (1)
3. GDT for the Fractional CNLS Equation (1)
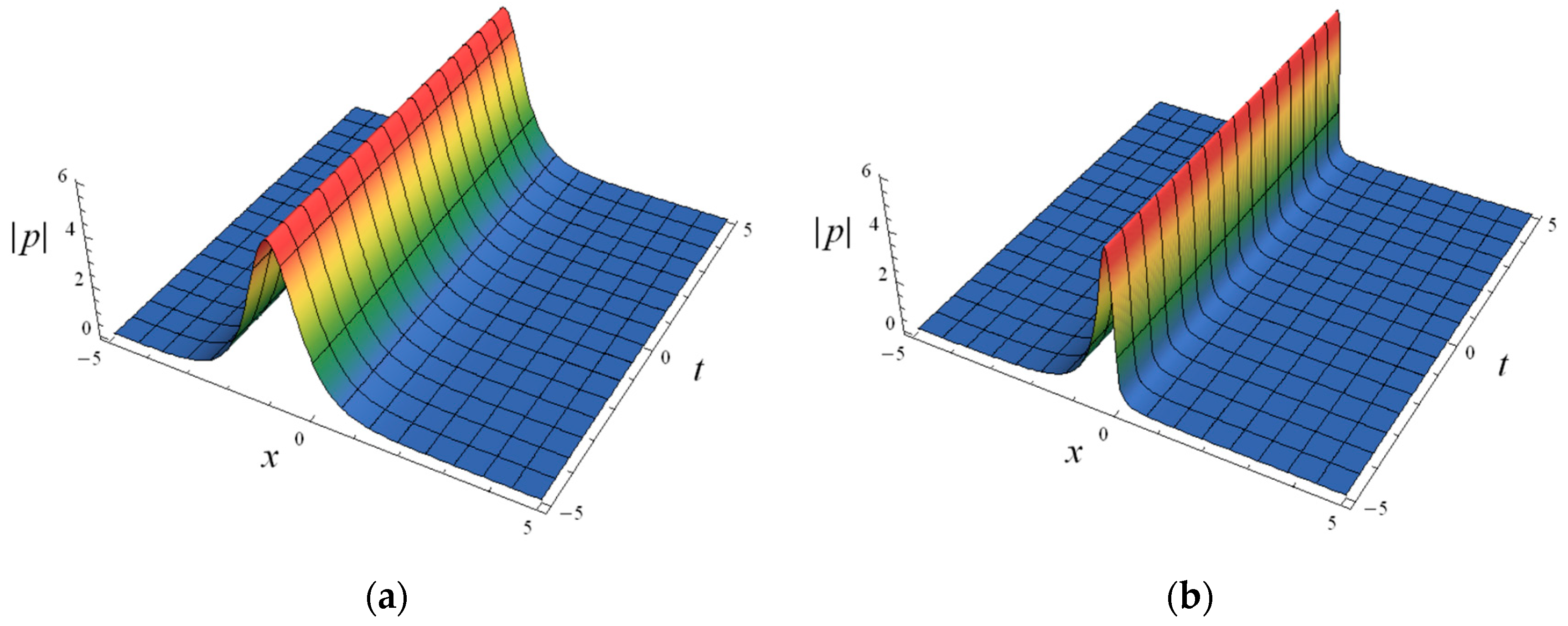
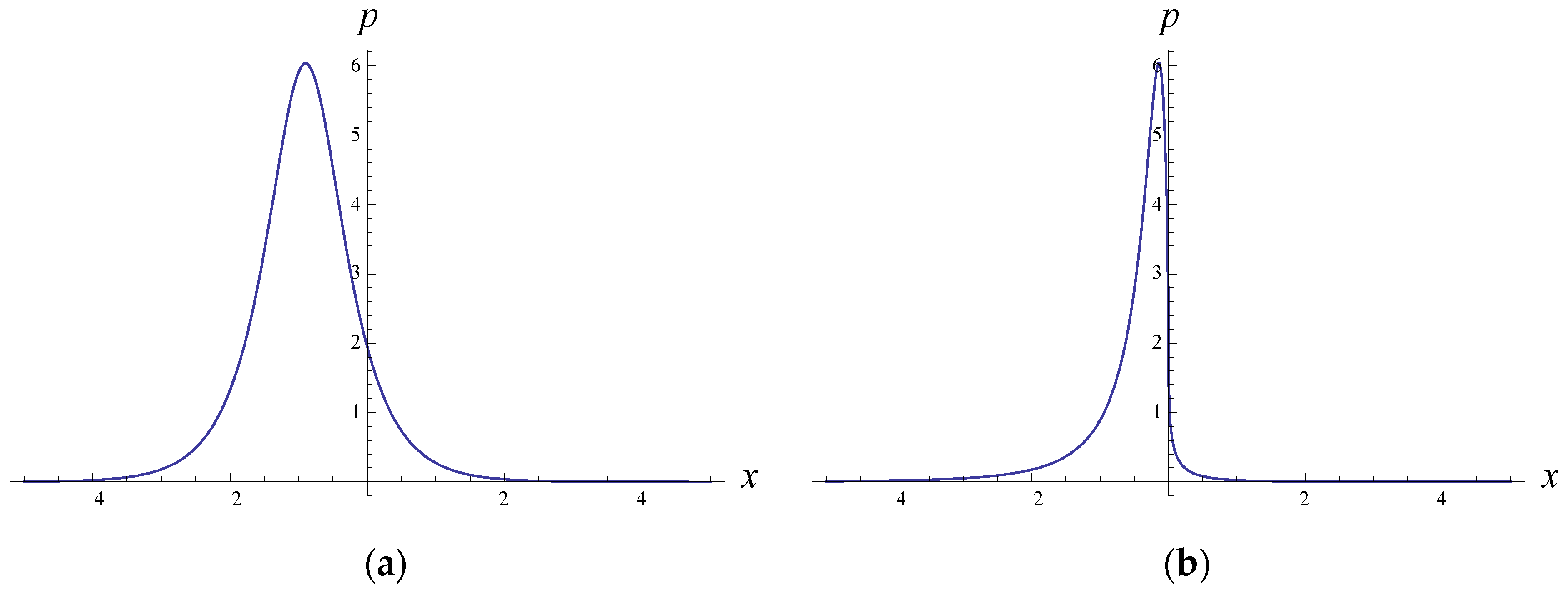
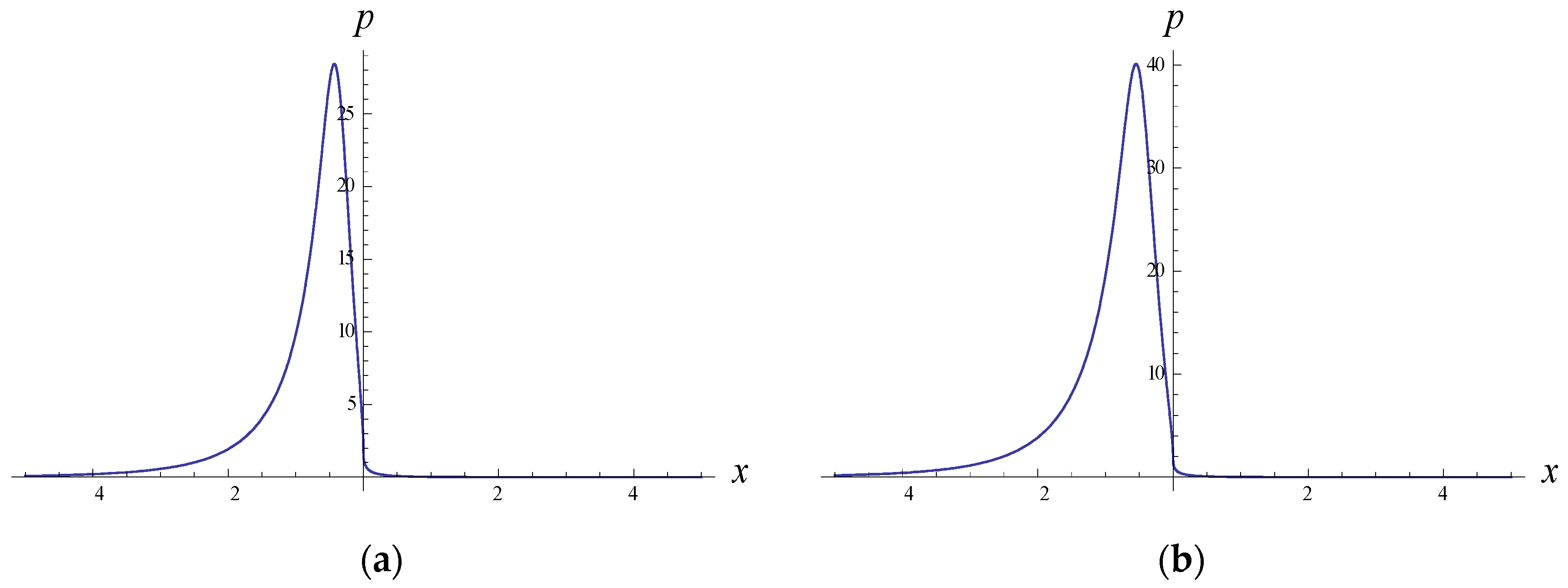
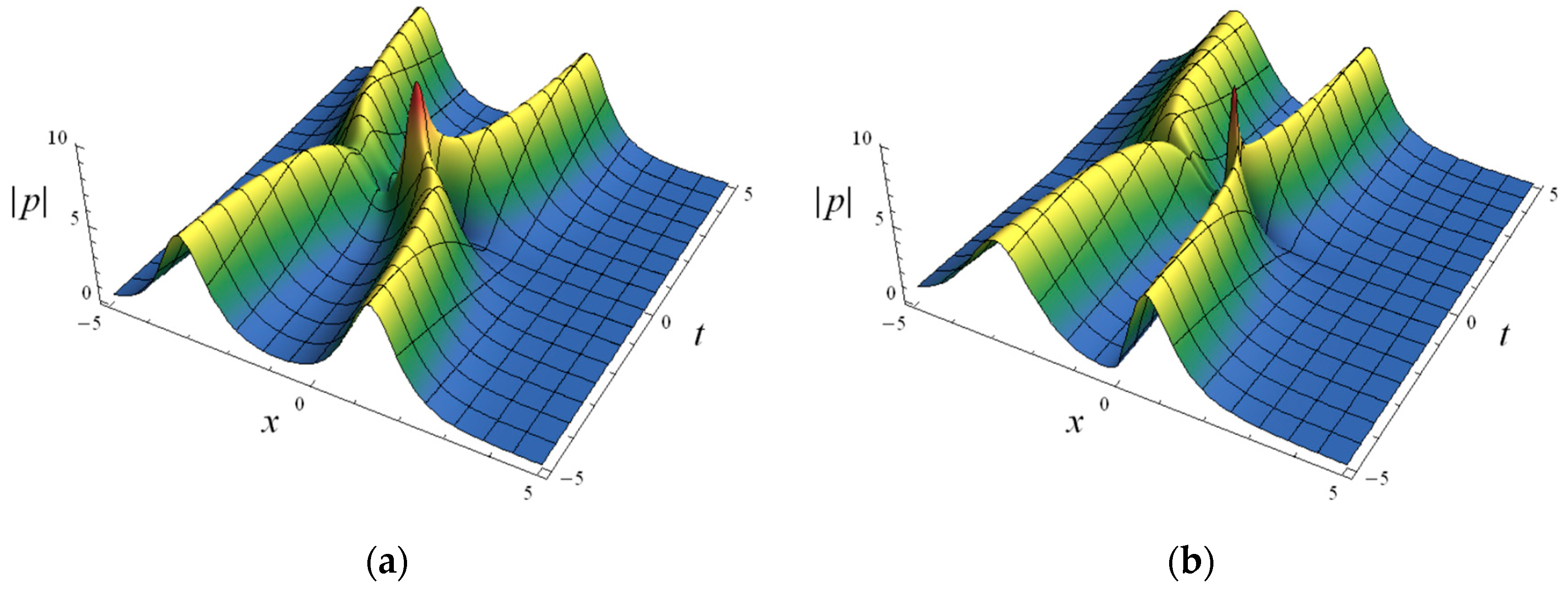
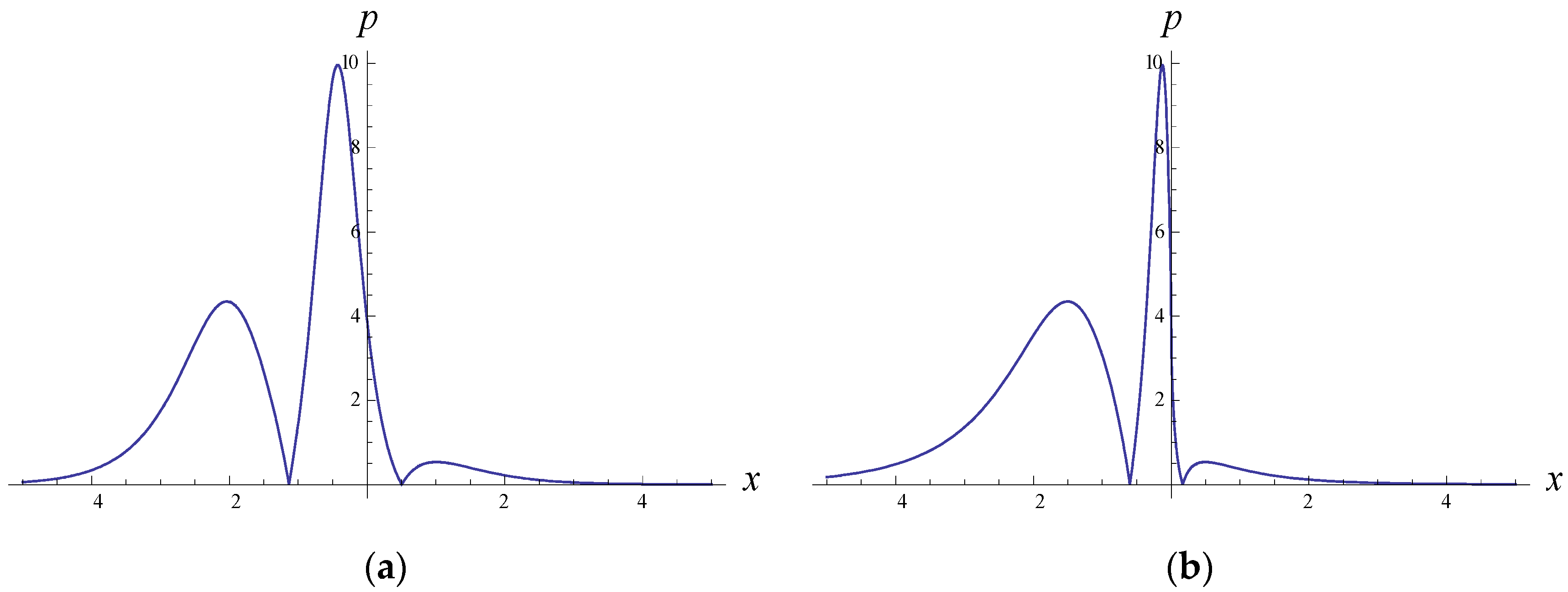
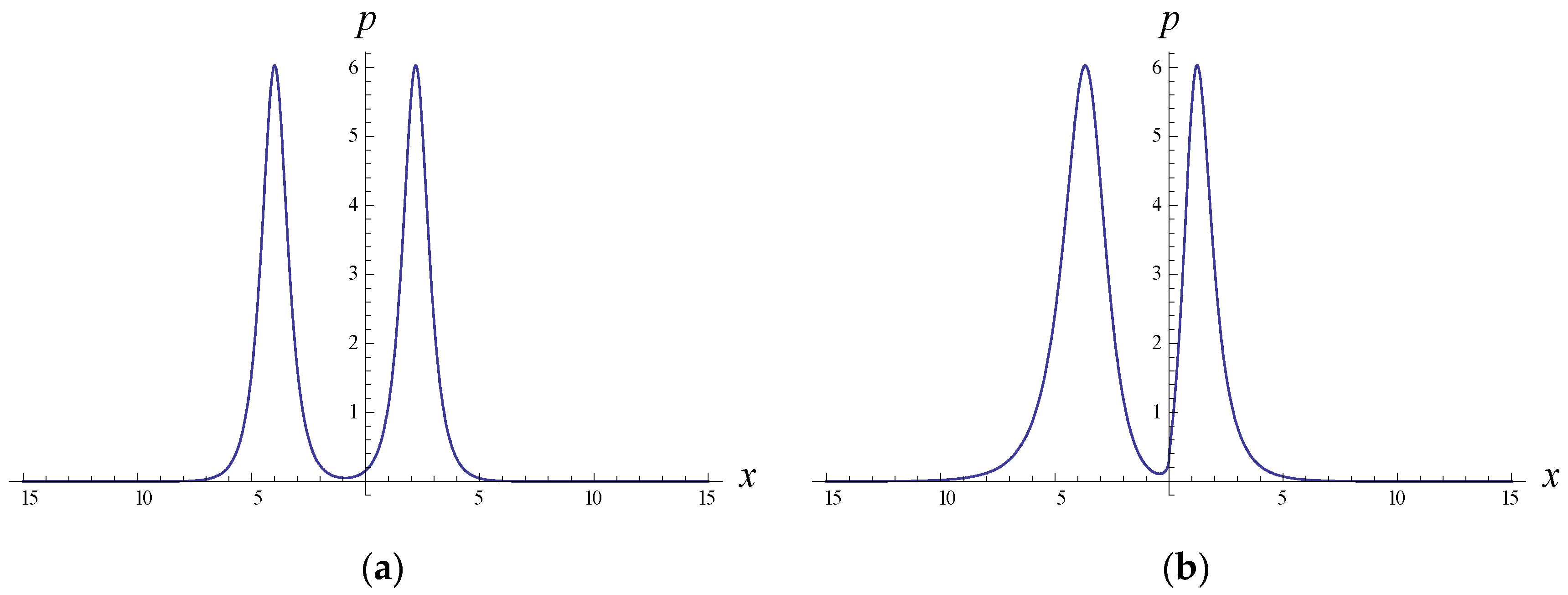
4. Symmetric and Asymmetric Solitary Wave Solutions of the Fractional NLS Equation (1)
5. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, USA, 1991. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Soliton; Springer: Berlin, Germany, 1991. [Google Scholar]
- Hirota, R. Exact envelope-soliton solutions of a nonlinear wave equation. J. Math. Phys. 1973, 14, 805–809. [Google Scholar] [CrossRef]
- Wang, M.L. Exact solutions for a compound KdV-Burgers equation. Phys. Lett. A 1996, 213, 279–287. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Soliton. Fract. 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T.C. A generalized auxiliary equation method and its application to (2+1)-dimensional asymmetric Nizhnik-Novikov-Vesselov equations. J. Phys. A Math. Theor. 2007, 40, 227–248. [Google Scholar] [CrossRef]
- Zeng, X.H.; Wu, X.L.; Lang, C.Z.; Yuan, C.P.; Cai, J.P. Exact solutions for coupled variable coefficient KdV equation via quadratic Jacobi’s elliptic function expansion. Symmetry 2023, 15, 1021. [Google Scholar] [CrossRef]
- Fan, E.G. Darboux transformation and soliton-like solutions for the Gerdjikov-Ivanov equation. J. Phys. A Gen. Phys. 2000, 33, 6925–6934. [Google Scholar] [CrossRef]
- Fan, E.G. Explicit N-Fold Darboux transformations and soliton solutions for nonlinear derivative Schrödinger equations. Commun. Theor. Phys. 2001, 35, 650–656. [Google Scholar]
- Huang, D.J.; Li, D.S.; Zhang, H.Q. Explicit N-fold Darboux transformation and multi-soliton solutions for the (1+1)-dimensional higher-order Broer-Kaup system. Chaos Soliton. Fract. 2007, 33, 1677–1685. [Google Scholar] [CrossRef]
- Wen, X.Y. N-fold Darboux transformation and soliton solutions for Toda lattice equation. Rep. Math. Phys. 2011, 68, 211–223. [Google Scholar] [CrossRef]
- Ling, L.M.; Zhao, L.C.; Guo, B.L. Darboux transformation and multi-dark soliton for N-component nonlinear Schrödinger equations. Nonlinearity 2015, 28, 3243–3261. [Google Scholar] [CrossRef]
- Sun, H.Q.; Zhu, Z.N. Darboux transformation and soliton solution of the nonlocal generalized Sasa–Satsuma equation. Mathematics 2023, 11, 865. [Google Scholar] [CrossRef]
- Guo, B.L.; Ling, L.M.; Liu, Q.P. Nonlinear Schrödinger equation: Generalized Darboux transformation and rogue wave solutions. Phys. Rev. E 2012, 85, 026607. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.L.; Ling, L.M.; Liu, Q.P. High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Stud. Appl. Math. 2013, 130, 317–344. [Google Scholar] [CrossRef]
- Guo, B.L.; Tian, L.X.; Yan, Z.Y.; Lin, L.M. Rogue Wave and Its Mathematical Theory; Zhejiang Science and Technology Press: Zhejiang, China, 2015. [Google Scholar]
- Zhang, G.Q.; Yan, Z.Y. Three-component nonlinear Schrodinger equations: Modulational instability, Nth-order vector rational and semi-rational rogue waves, and dynamics. Commun. Nonlinear Sci. Numer. Simula. 2018, 62, 403–413. [Google Scholar] [CrossRef]
- Jiang, Y.; Qu, Q.X. Some semirational solutions and their interactions on the zero-intensity background for the coupled nonlinear Schrdinger equations. Commun. Nonlinear Sci. Numer. Simula. 2019, 67, 403–413. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Zhang, Y.F. Generalized Darboux transformation, semi-rational solutions and novel degenerate soliton solutions for a coupled nonlinear Schrdinger equation. Eur. Phys. J. Plus 2021, 136, 459. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Xu, B. Solitons, rogon-solitons and their propagations and reflections in three-component coupled nonlinear Schrödinger equation. Optik 2023, 272, 170338. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D. Exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 2003, 90, 113902. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A.; Belyaeva, T.L. Nonautonomous solitons in external potentials. Phys. Rev. Lett. 2007, 98, 074102. [Google Scholar] [CrossRef]
- Yang, J.K. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Liu, W.M.; Kengne, E. Schrödinger Equations in Nonlinear Systems; Springer Nature Singapore Pte Ltd.: Singapore, 2019. [Google Scholar]
- Ma, W.X. Matrix integrable fourth-order nonlinear Schrödinger equations and their exact soliton solutions. Chin. Phys. Lett. 2022, 39, 100201. [Google Scholar] [CrossRef]
- Ma, W.X. Matrix integrable fifth-order mKdV equations and their soliton solutions. Chin. Phys. B 2023, 32, 020201. [Google Scholar] [CrossRef]
- Ma, W.X.; Batwa, S. A binary Darboux transformation for multicomponent NLS equations and their reductions. Anal. Math. Phys. 2021, 11, 44. [Google Scholar] [CrossRef]
- Ma, W.X. Binary Darboux transformation for general matrix mKdV equations and reduced counterparts. Chaos Soliton. Fract. 2021, 146, 110824. [Google Scholar] [CrossRef]
- Ma, W.X. Soliton hierarchies and soliton solutions of type (−λ*, −λ) reduced nonlocal nonlinear Schrödinger equations of arbitrary even order. Partial Differ. Equ. Appl. Math. 2023, 7, 100515. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Fujioka, J.; Espinosa, A.; Rodríguez, R.F. Fractional optical solitons. Phys. Lett. A 2010, 374, 1126–1134. [Google Scholar] [CrossRef]
- He, J.H. A new fractal derivation. Therm. Sci. 2011, 15, S145–S147. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- He, J.H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: London, UK, 2015. [Google Scholar]
- Xu, B.; Zhang, S. Riemann-Hilbert approach for constructing analytical solutions and conservation laws of a local time-fractional nonlinear Schrödinger equation. Symmetry 2021, 13, 1593. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable nonlinear soliton equation. Phys. Rev. Lett. 2022, 128, 184101. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.L.; Ling, L.M. Rogue wave, breathers and bright-dark-rogue solutions for the coupled Schrödinger equations. Chin. Phys. Lett. 2011, 28, 110202. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, A.M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.F.; Zhang, S. Line soliton interactions for shallow ocean-waves and novel solutions with peakon, ring, conical, columnar and lump structures based on fractional KP equation. Adv. Math. Phys. 2021, 2021, 6664039. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhu, F.; Xu, B. Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations. Symmetry 2023, 15, 1211. https://doi.org/10.3390/sym15061211
Zhang S, Zhu F, Xu B. Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations. Symmetry. 2023; 15(6):1211. https://doi.org/10.3390/sym15061211
Chicago/Turabian StyleZhang, Sheng, Feng Zhu, and Bo Xu. 2023. "Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations" Symmetry 15, no. 6: 1211. https://doi.org/10.3390/sym15061211
APA StyleZhang, S., Zhu, F., & Xu, B. (2023). Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations. Symmetry, 15(6), 1211. https://doi.org/10.3390/sym15061211




