New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations
Abstract
1. Introduction
2. Preliminaries of Fractional Calculus
3. Fractional Novel Analytical Method for Fifth-Order Fractional Korteweg–De Vries Equations
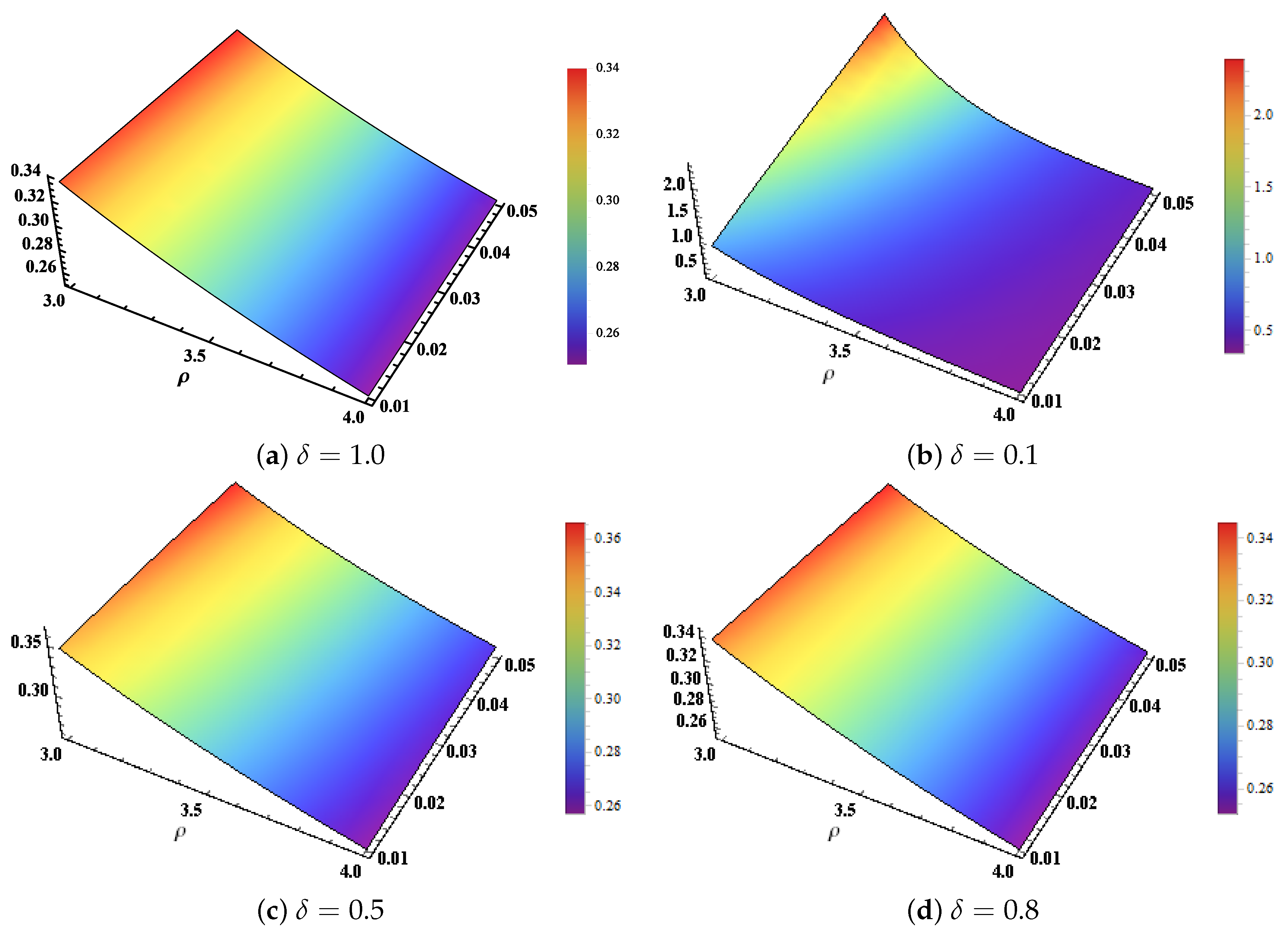
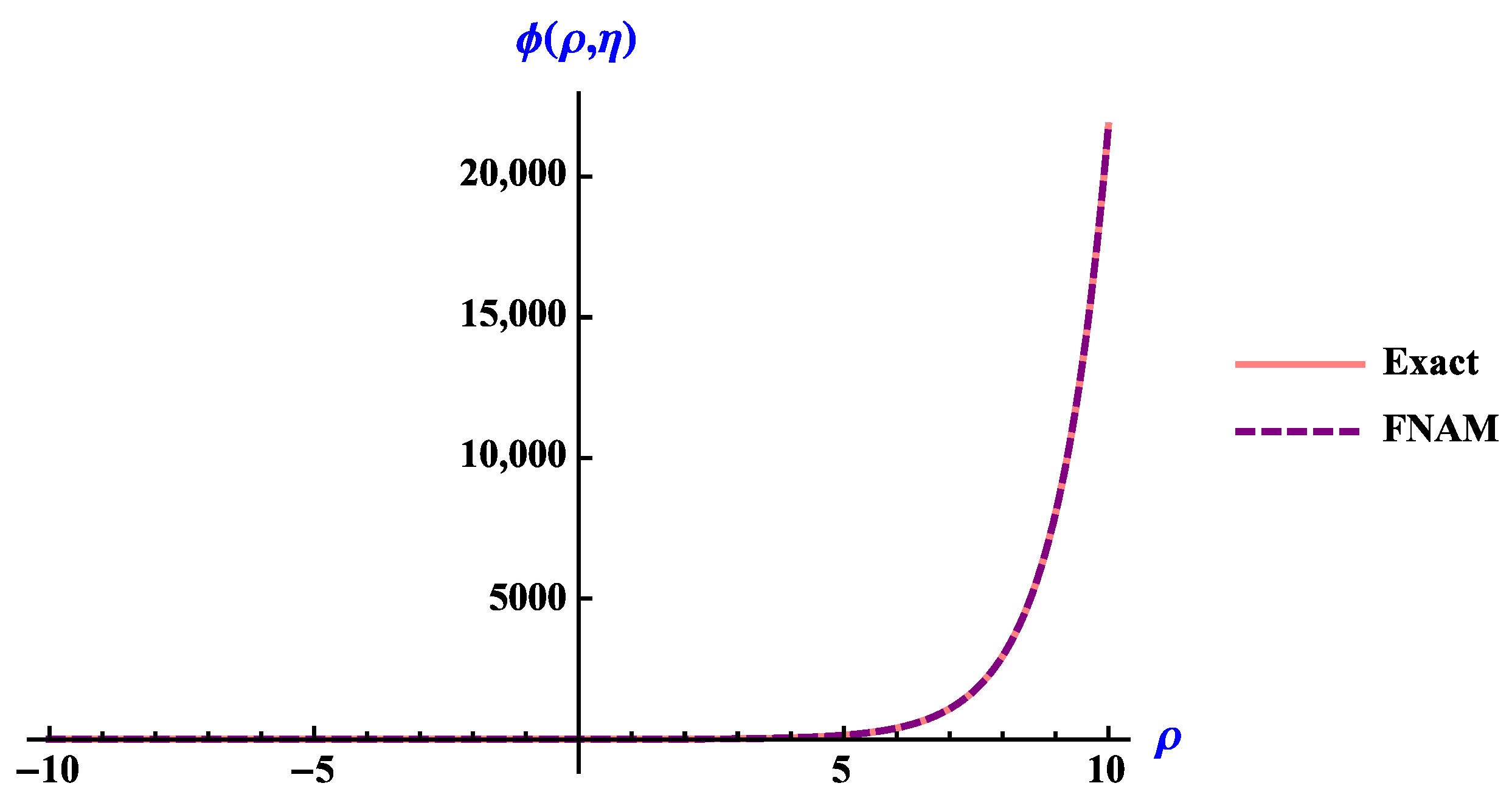
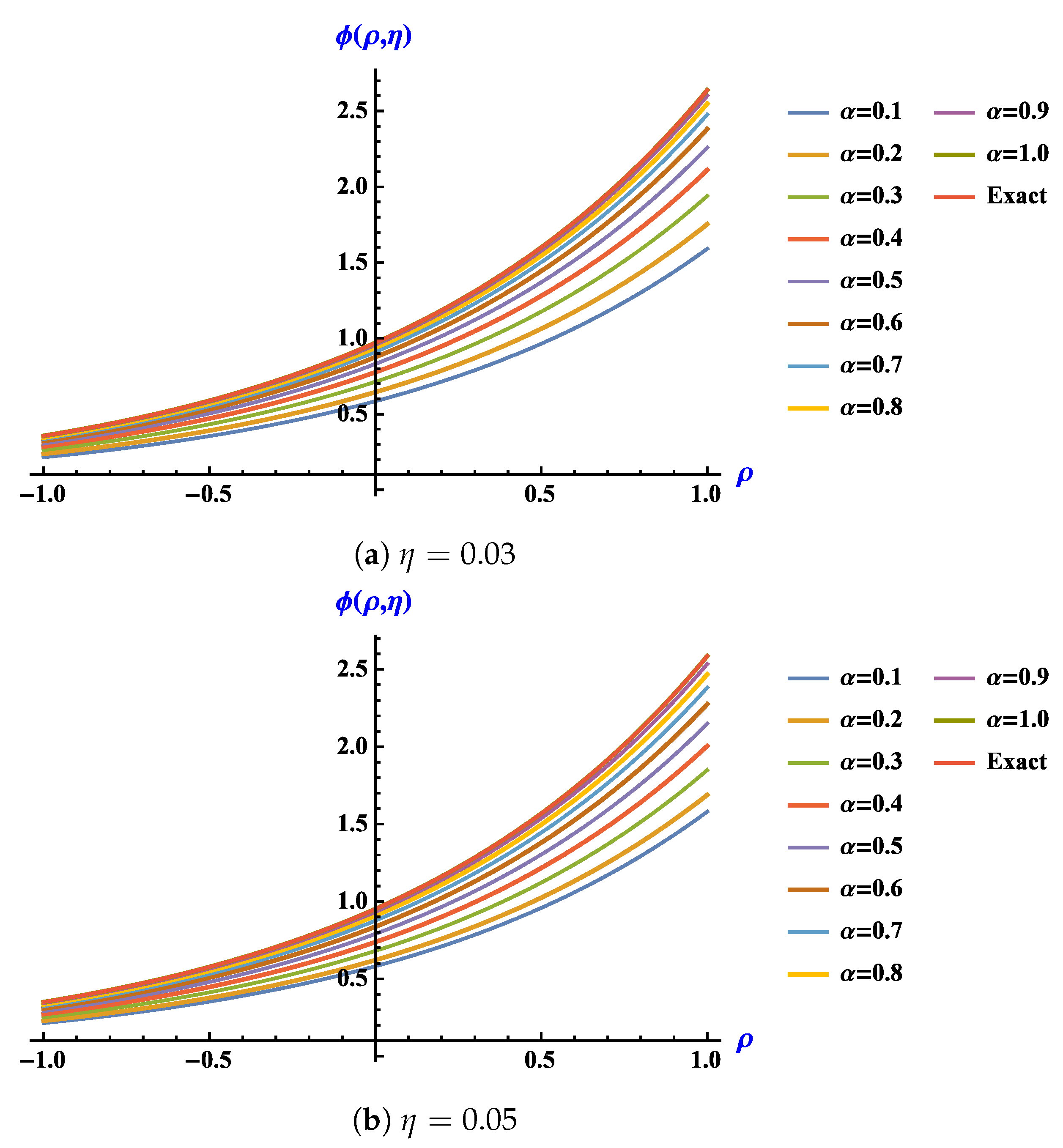
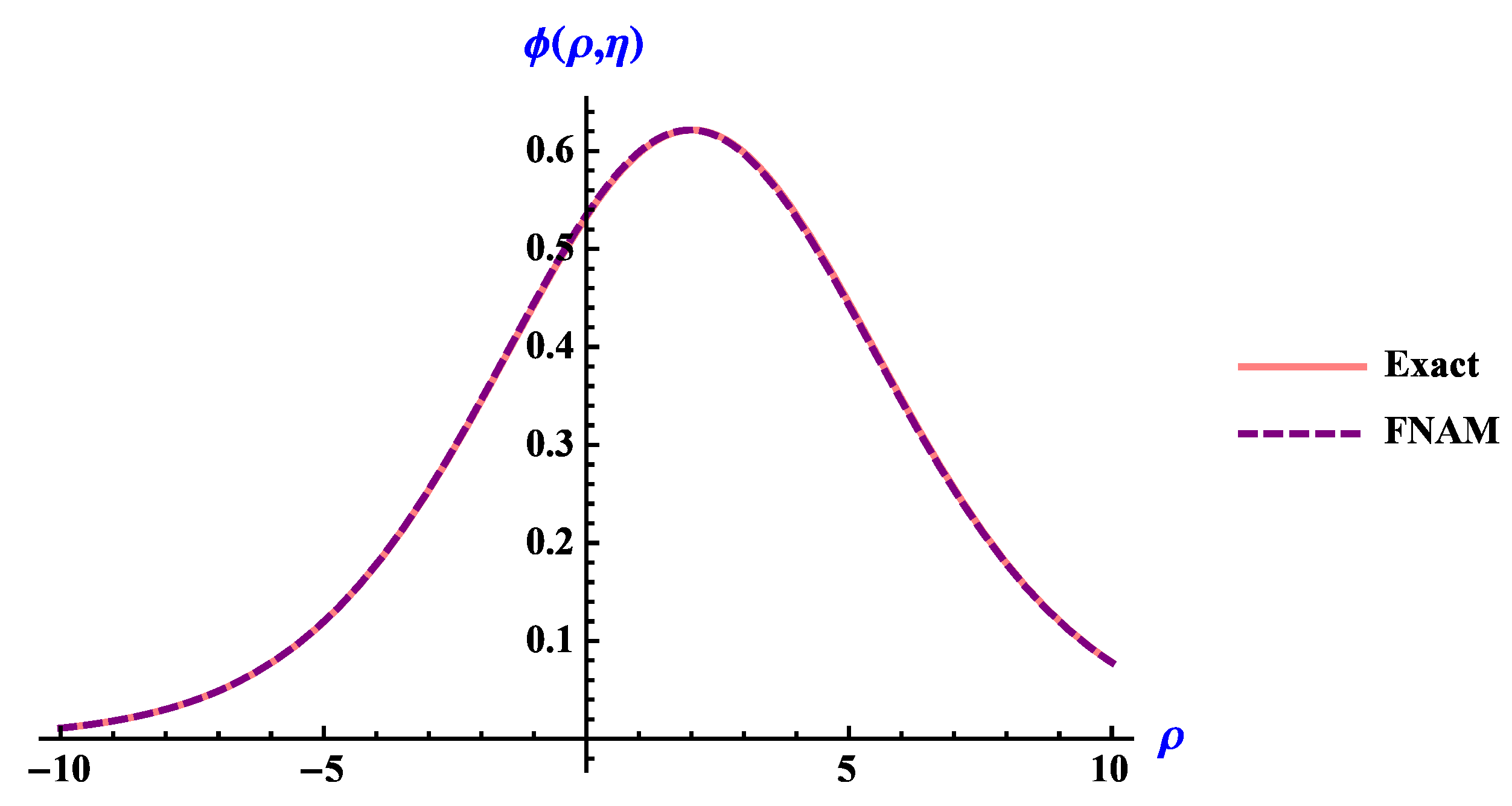
4. Numerical Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moghaddam, B.P.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. In Volume 7, Applications in Engineering, Life and Social Sciences, Part A; Dumitru, B., António, M.L., Eds.; De Gruyter: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Jesus, I.S.; Machado, J.A.T. Application of integer and fractional models in electrochemical systems. Math. Probl. Eng. 2012, 2012, 248175. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J. Comput. Appl. Math. 2017, 309, 493–510. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. New spectral solutions of multi-term fractional order initial value problems with error analysis. Comput. Model. Eng. Sci. 2015, 105, 375–398. [Google Scholar] [CrossRef]
- Youssri, Y.H. Two Fibonacci operational matrix pseudo-spectral schemes for nonlinear fractional Klein-Gordon equation. Int. J. Mod. Phys. C 2022, 33, 2250049. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Spectral solutions for fractional differential equations via a novel Lucas operational matrix of fractional derivatives. Rom. J. Phys. 2016, 61, 795–813. [Google Scholar]
- Maleknejad, K.; Rashidinia, J.; Eftekhari, T. A new and efficient numerical method based on shifted fractional-order Jacobi operational matrices for solving some classes of two-dimensional nonlinear fractional integral equations. Numer. Methods Partial Differ. Equ. 2021, 37, 2687–2713. [Google Scholar] [CrossRef]
- Zaky, M.A.; Machado, J.A.T. Multi-dimensional spectral tau methods for distributedorder fractional diffusion equations. Comput. Math. Appl. 2020, 79, 476–488. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. Numerical approximations to the nonlinear fractional-order logistic population model with fractional-order Bessel and Legendre bases. Chaos Soliton Fract. 2021, 145, 110779. [Google Scholar] [CrossRef]
- Ganji, R.M.; Jafari, H.; Kgarose, M.; Mohammadi, A. Numerical solutions of time-fractional Klein-Gordon equations by clique polynomials. Alex. Eng. J. 2021, 60, 4563–4571. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Melville, W.K. Long Nonlinear Internal Waves. Annu. Rev. Fluid Mech. 2006, 38, 395–425. [Google Scholar] [CrossRef]
- Ostrovsky, Y.; Stepanyants, A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos 2005, 15, 037111. [Google Scholar] [CrossRef] [PubMed]
- Rottman, J.W.; Grimshaw, R. Atmospheric Internal Solitary Waves. In Environmental Stratified Flows; Topics in Environmental Fluid Mechanics, Volume 3; Grimshaw, R., Ed.; Springer: Boston, MA, USA, 2003. [Google Scholar] [CrossRef]
- Korteweg, D.J.; de Vries, G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Benney, D.J. Long Non-Linear Waves in Fluid Flows. J. Math. Phys. 1966, 45, 52–63. [Google Scholar] [CrossRef]
- Marchant, T.R.; Smyth, N.F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J. Fluid Mech. 1990, 221, 263–288. [Google Scholar] [CrossRef]
- Marchant, T.R.; Smyth, N.F. Soliton interaction for the extended Korteweg-de Vries equation. IMA J. Appl. Math. 1996, 56, 157–176. [Google Scholar] [CrossRef]
- Marchant, T.R. High-Order Interaction of Solitary Waves on Shallow Water. Stud. Appl. Math. 2002, 109, 1–17. [Google Scholar] [CrossRef]
- Chow, K.W. A second-order solution for the solitary wave in a rotational flow. Phys. Fluids Fluid Dyn. 1989, 1, 12–35. [Google Scholar] [CrossRef]
- Koop, C.G.; Butler, G. An investigation of internal solitary waves in a two-fluid system. J. Fluid Mech. 1981, 112, 225–251. [Google Scholar] [CrossRef]
- Lamb, K.; Yan, L. The evolution of internal wave undular bores: Comparisons of a fully nonlinear numerical model with weakly nonlinear theory. J. Phys. Oceanogr. 1996, 26, 2712–2734. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Poloukhina, O.E.; Lamb, K. Nonlinear internal waves in the ocean stratified on density and current. Oceanology 2000, 40, 805–815. [Google Scholar]
- Elinovsky, E.; Polukhina, O.; Slunyaev, A.; Talipova, T. Internal solitary waves. In Solitary Waves in Fluids; WIT Press: Southampton, UK, 2007; pp. 85–110. [Google Scholar]
- Canıvar, A.; Sari, M.; Dag, I. A Taylor-Galerkin finite element method for the KdV equation using cubic B-splines. Phys. B Condens. Matter 2010, 405, 3376–3383. [Google Scholar] [CrossRef]
- Shen, J. A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation. SIAM J. Numer. Anal. 2003, 41, 1595–1619. [Google Scholar] [CrossRef]
- Aka, T.; Karakocb, S.B.G.; Biswas, A. Application of Petrov-Galerkin finite element method to shallow water waves model: Modified Korteweg-de Vries equation. Sci. Iran. B 2017, 24, 1148–1159. Available online: http://hdl.handle.net/20.500.11787/5241 (accessed on 1 June 2017). [CrossRef]
- Ahmad, H.; Khan, T.A.; Yao, S.W. An efficient approach for the numerical solution of fifth-order KdV equations. Open Math. 2020, 18, 738–748. [Google Scholar] [CrossRef]
- Kaya, D. An explicit and numerical solutions of some fifth-order KdV equation by decomposition method. Appl. Math. Comput. 2003, 144, 353–363. [Google Scholar] [CrossRef]
- Soliman, A.A. A numerical simulation and explicit solutions of KdV-Burgers’and Lax’s seventh-order KdV equations. Chaos Soliton Fract. 2006, 29, 294–302. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Singh, J. Solution for fractional forced KdV equation using fractional natural decomposition method. AIMS Math. 2020, 5, 798–810. [Google Scholar] [CrossRef]
- Le, U.; Pelinovsky, D.E. Green’s function for the fractional KdV equation on the periodic domain via Mittag-Leffler function. Fract. Calc. Appl. Anal. 2021, 24, 1507–1534. [Google Scholar] [CrossRef]
- An, N.; Huang, C.; Yu, X. Error analysis of discontinuous Galerkin method for the time fractional KdV equation with weak singularity solution. Discret. Contin. Dyn. Syst. B 2020, 25, 321–334. [Google Scholar] [CrossRef]
- Ford, N.J.; Xiao, J.; Yan, Y. A finite element method for time fractional partial differential equations. Fract. Calc. Appl. Anal. 2011, 14, 454–474. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Chen, H.; Sun, T. A Petrov-Galerkin spectral method for the linearized time fractional KdVequation. Int. J. Comput. Math. 2018, 95, 1292–1307. [Google Scholar] [CrossRef]
- Zhang, Y. Formulation and solution to time-fractional generalized Korteweg-de Vries equation via variational methods. Adv. Differ. Equ. 2014, 2014, 65. [Google Scholar] [CrossRef]
- Wang, Q. Homotopy perturbation method for fractional KdV equation. Appl. Math. Comput. 2007, 190, 1795–1802. [Google Scholar] [CrossRef]
- Wiwatwanich, A. A Novel Technique for Solving Nonlinear Differential Equations. Ph.D. Dissertation, Faculty of Science, Burapha University, Chon Buri, Thailand, 2016. [Google Scholar]
- Qaraad, B.; Bazighifan, O.; Nofal, T.A.; Ali, A.H. Neutral differential equations with distribution deviating arguments: Oscillation conditions. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Sultana, M.; Arshad, U.; Alam, M.N.; Bazighifan, O.; Askar, S.; Awrejcewicz, J. New Results of the Time-Space Fractional Derivatives of Kortewege-de Vries Equations via Novel Analytic Method. Symmetry 2021, 13, 2296. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Handibag, S.; Karande, B.D. Existence the Solutions of Some Fifth-Order Kdv Equation by Laplace Decomposition Method. Am. J. Comput. Math. 2013, 3, 80–85. [Google Scholar] [CrossRef][Green Version]
- Almarri, B.; Ali, A.H.; Al-Ghafri, K.S.; Almutairi, A.; Bazighifan, O.; Awrejcewicz, J. Symmetric and Non-Oscillatory Characteristics of the Neutral Differential Equations Solutions Related to p-Laplacian Operators. Symmetry 2022, 14, 566. [Google Scholar] [CrossRef]
- Almarri, B.; Ali, A.H.; Lopes, A.M.; Bazighifan, O. Nonlinear Differential Equations with Distributed Delay: Some New Oscillatory Solutions. Mathematics 2022, 10, 995. [Google Scholar] [CrossRef]
- Almarri, B.; Janaki, S.; Ganesan, V.; Ali, A.H.; Nonlaopon, K.; Bazighifan, O. Novel Oscillation Theorems and Symmetric Properties of Nonlinear Delay Differential Equations of Fourth-Order with a Middle Term. Symmetry 2022, 14, 585. [Google Scholar] [CrossRef]
- Bazighifan, O.; Ali, A.H.; Mofarreh, F.; Raffoul, Y.N. Extended Approach to the Asymptotic Behavior and Symmetric Solutions of Advanced Differential Equations. Symmetry 2022, 14, 686. [Google Scholar] [CrossRef]
- Ali, A.H.; Meften, G.; Bazighifan, O.; Iqbal, M.; Elaskar, S.; Awrejcewicz, J. A Study of Continuous Dependence and Symmetric Properties of Double Diffusive Convection: Forchheimer Model. Symmetry 2022, 14, 682. [Google Scholar] [CrossRef]
- Abed Meften, G.; Ali, A.H.; Al-Ghafri, K.; Awrejcewicz, J.; Bazighifan, O. Nonlinear Stability and Linear Instability of Double-Diffusive Convection in a Rotating with LTNE Effects and Symmetric Properties: Brinkmann-Forchheimer Model. Symmetry 2022, 14, 565. [Google Scholar] [CrossRef]
- Bazighifan, O. An Approach for Studying Asymptotic Properties of Solutions of Neutral Differential Equations. Symmetry 2020, 12, 555. [Google Scholar] [CrossRef]
- Santra, S.S.; Ghosh, T.; Bazighifan, O. Explicit criteria for the oscillation of second-order differential equations with several sub-linear neutral coefficients. Adv. Differ. Equ. 2020, 2020, 643. [Google Scholar] [CrossRef]
- Bazighifan, O.; Kumam, P. Oscillation Theorems for Advanced Differential Equations with p-Laplacian Like Operators. Mathematics 2020, 8, 821. [Google Scholar] [CrossRef]
- Bazighifan, O.; Alotaibi, H.; Mousa, A.A.A. Neutral Delay Differential Equations: Oscillation Conditions for the Solutions. Symmetry 2021, 13, 101. [Google Scholar] [CrossRef]
- Moaaz, O.; El-Nabulsi, R.A.; Bazighifan, O. Oscillatory Behavior of Fourth-Order Differential Equations with Neutral Delay. Symmetry 2020, 12, 371. [Google Scholar] [CrossRef]
- Moaaz, O.; Elabbasy, E.M.; Shaaban, E. Oscillation Criteria for a Class of Third Order Damped Differential Equations. Arab J. Math. Sci. 2018, 24, 16–30. [Google Scholar] [CrossRef]





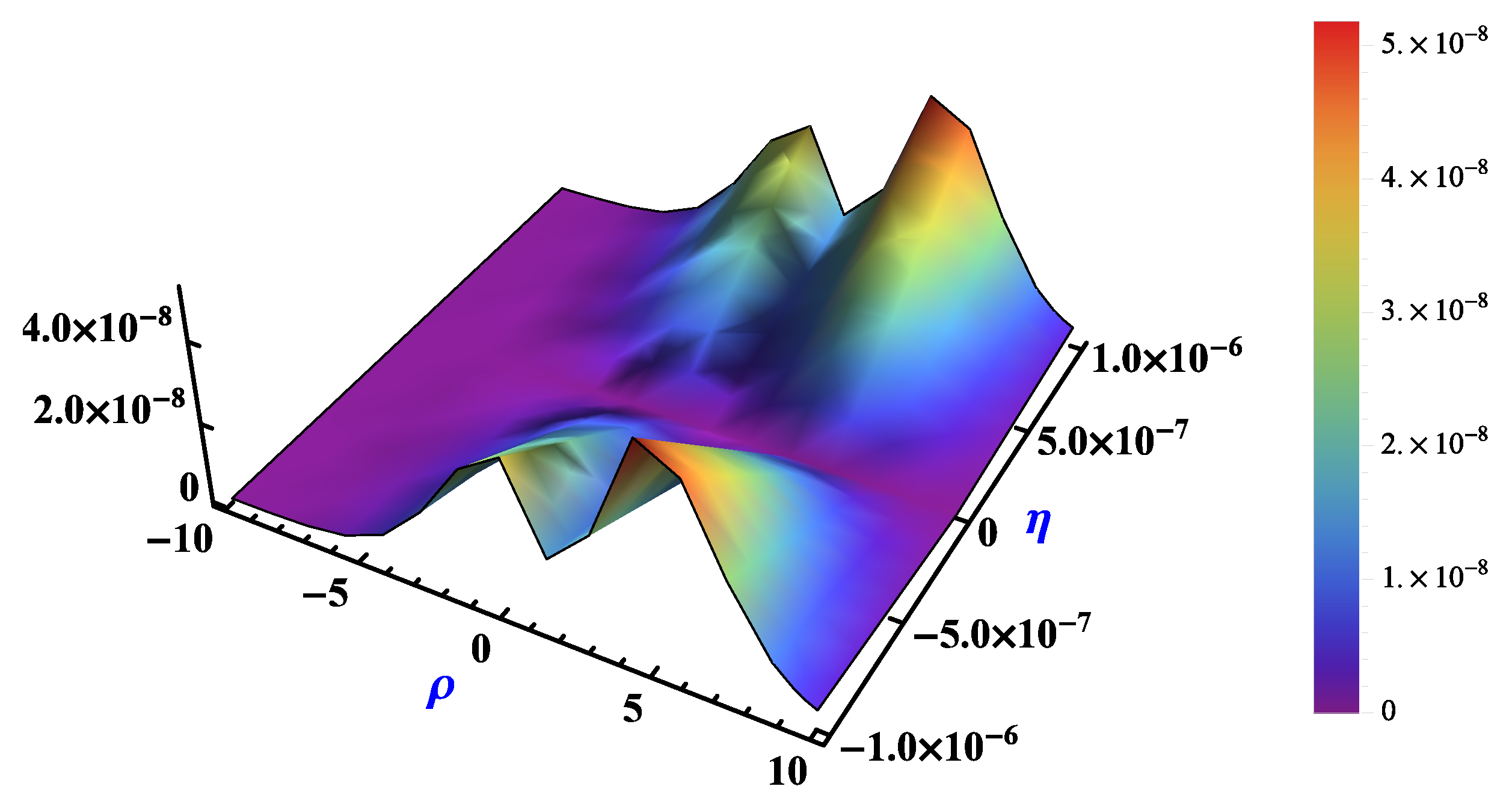



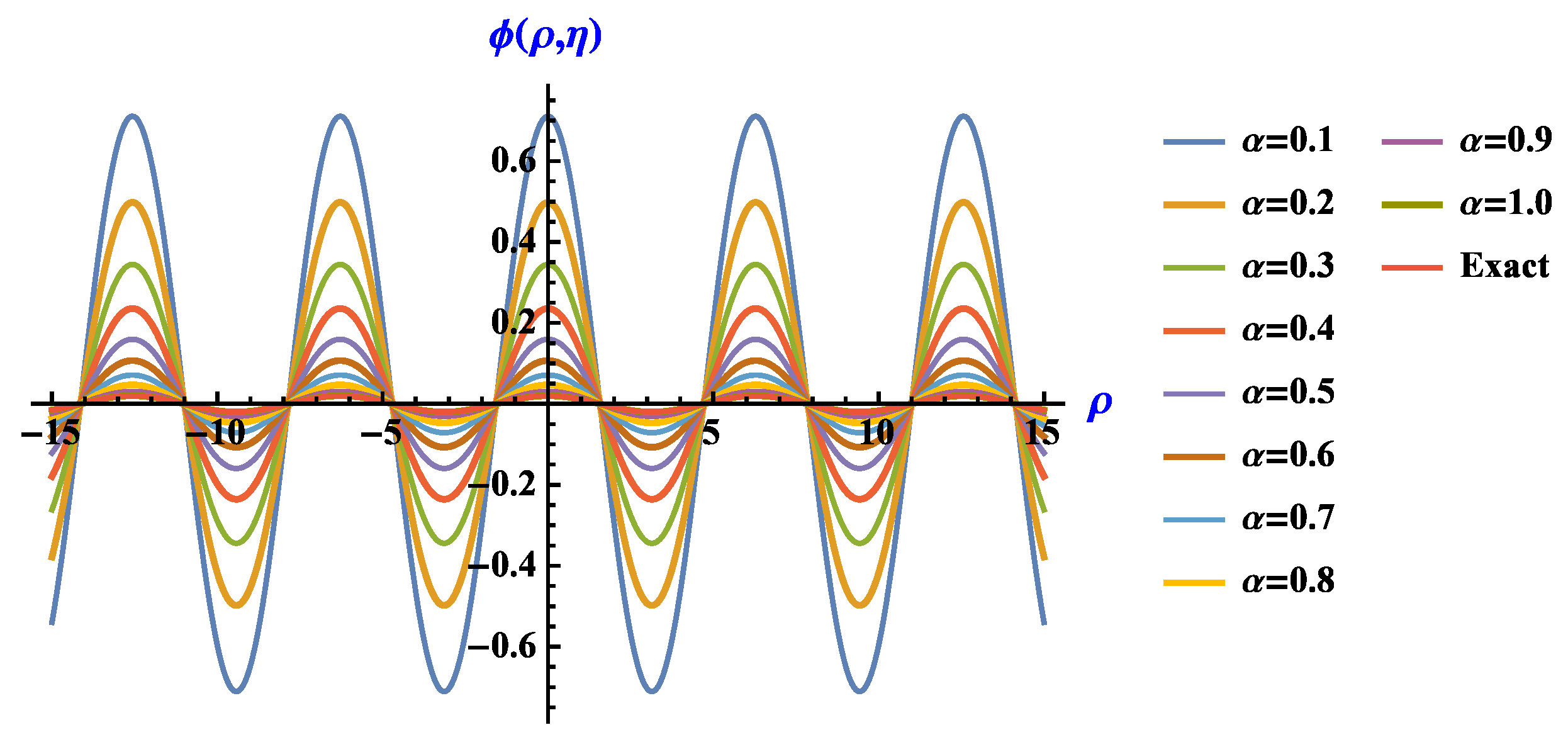
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | |
| 0.01 | 0.00 | 6.53 | 0.00 | 2.13 | 1.11 | 1.65 | 0.00 | 7.12 | 5.55 | 2.22 |
| 0.02 | 8.88 | 1.01 | 0.00 | 3.26 | 0.00 | 2.50 | 0.00 | 1.06 | 0.00 | 3.28 |
| 0.03 | 7.72 | 8.83 | 2.22 | 2.84 | 0.00 | 2.17 | 0.00 | 9.23 | 5.55 | 2.83 |
| 0.04 | 1.86 | 1.57 | 4.44 | 5.05 | 0.00 | 13.85 | 0.00 | 1.63 | 5.55 | 5.00 |
| 0.05 | 2.22 | 4.11 | 5.10 | 1.32 | 1.11 | 1.00 | 1.11 | 4.26 | 5.55 | 1.30 |
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | |
| 0.01 | 2.22 | 1.37 | 0.00 | 4.38 | 0.00 | 3.32 | 0.00 | 1.39 | 3.55 | 4.25 |
| 0.02 | 0.00 | 2.26 | 0.00 | 7.22 | 8.88 | 5.47 | 0.00 | 2.30 | 0.00 | 7.02 |
| 0.03 | 0.00 | 3.72 | 0.00 | 1.19 | 8.88 | 9.03 | 0.00 | 3.79 | 3.55 | 1.15 |
| 0.04 | 0.00 | 6.14 | 4.44 | 1.96 | 8.88 | 1.48 | 0 | 6.26 | 0.00 | 1.90 |
| 0.05 | 0.00 | 1.01 | 0.00 | 3.23 | 0.00 | 2.45 | 8.88 | 1.03 | 3.55 | 3.14 |
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | FNAM | LDM | |
| 0.01 | 1.11 | 1.11 | 3.33 | 0.00 | 2.22 | 8.88 | 0.00 | 2.66 | 1.11 | 8.44 |
| 0.02 | 0.00 | 3.33 | 0.00 | 0.00 | 0.00 | 7.77 | 1.11 | 2.55 | 5.55 | 6.66 |
| 0.03 | 0.00 | 2.22 | 3.33 | 0.00 | 1.11 | 2.22 | 1.11 | 7.77 | 2.22 | 3.89 |
| 0.04 | 0.00 | 0.00 | 3.33 | 1.11 | 4.44 | 1.11 | 3.33 | 2.22 | 2.22 | 2.22 |
| 0.05 | 0.00 | 0.00 | 1.11 | 5.55 | 1.11 | 4.44 | 2.22 | 1.44 | 1.11 | 3.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, M.; Arshad, U.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry 2022, 14, 1653. https://doi.org/10.3390/sym14081653
Sultana M, Arshad U, Ali AH, Bazighifan O, Al-Moneef AA, Nonlaopon K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry. 2022; 14(8):1653. https://doi.org/10.3390/sym14081653
Chicago/Turabian StyleSultana, Mariam, Uroosa Arshad, Ali Hasan Ali, Omar Bazighifan, Areej A. Al-Moneef, and Kamsing Nonlaopon. 2022. "New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations" Symmetry 14, no. 8: 1653. https://doi.org/10.3390/sym14081653
APA StyleSultana, M., Arshad, U., Ali, A. H., Bazighifan, O., Al-Moneef, A. A., & Nonlaopon, K. (2022). New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry, 14(8), 1653. https://doi.org/10.3390/sym14081653









