Multi-Label Attribute Reduction Based on Neighborhood Multi-Target Rough Sets
Abstract
:1. Introduction
- A neighborhood rough set model considering the label correlation is proposed for multi-label learning.
- The properties of the proposed models are investigated.
- An algorithm for calculating the approximations in the proposed rough set model is designed.
- Attribute significance measure is given based on the rough set model we proposed.
- Experiments are conducted to validate the efficiency and effectiveness of the proposed algorithms.
2. Neighborhood Multi-Target Rough Sets
2.1. Definitions
2.2. Properties
2.3. Approximation Computation of NMTRS
| Algorithm 1: Computing approximations of NMTRS | |
| Input: | |
| Output: | |
| 1: | |
| 2: | for |
| 3: | for |
| 4: | if then |
| 5: | |
| 6: | else |
| 7: | |
| 8: | end if |
| 9: | if then |
| 10: | |
| 11: | else |
| 12: | |
| 13: | end if |
| 14: | end for |
| 15: | end for |
| 16: | |
| 17: | |
| 18: | Return |
3. Attribute Reduction Based on NMTRS
3.1. Attribute Significance Measure Based on NMTRS
3.2. Multi-Granulation Discrimination Analysis Based on NMTRS
3.3. Attribute Reduction Algorithm Based on NMTRS
| Algorithm 2: Attribute reduction algorithm based on NMTRS | |
| Input: | |
| Output:Reduction of the attribute set | |
| 1: | |
| 2: | while |
| 3: | for all |
| 4: | Calculate with Algorithm 1 |
| 5: | end for |
| 6: | ifthen |
| 7: | break |
| 8: | end if |
| 9: | |
| 10: | Return |
4. Experimental Evaluations
4.1. Comparison of Performance Measures Using ML-kNN
4.1.1. Experimental Settings
4.1.2. Discussions of the Experimental Results
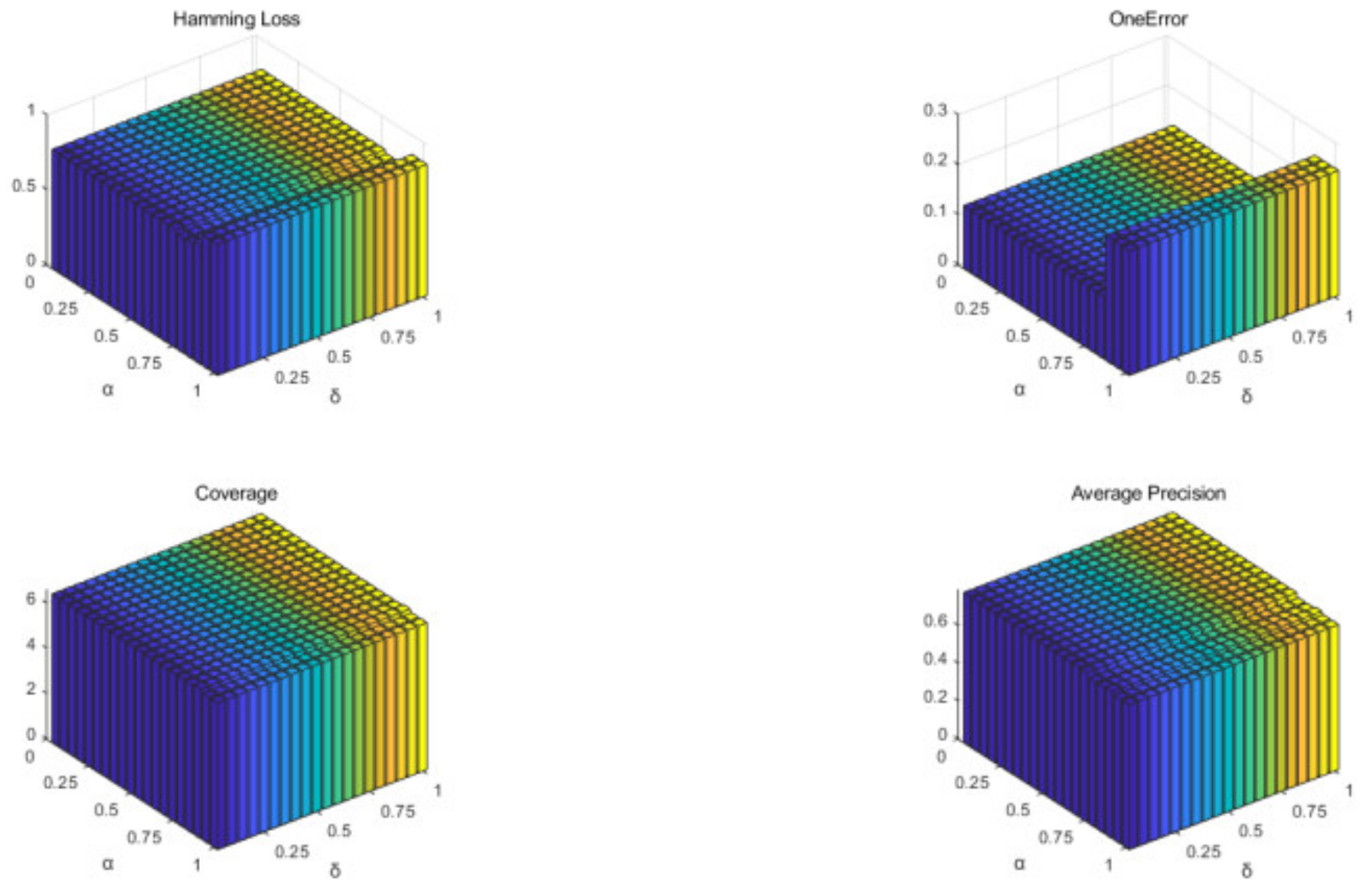
4.2. Effectiveness of Parameters α and δ
4.2.1. Experimental Settings
4.2.2. Discussions of the Experimental Results
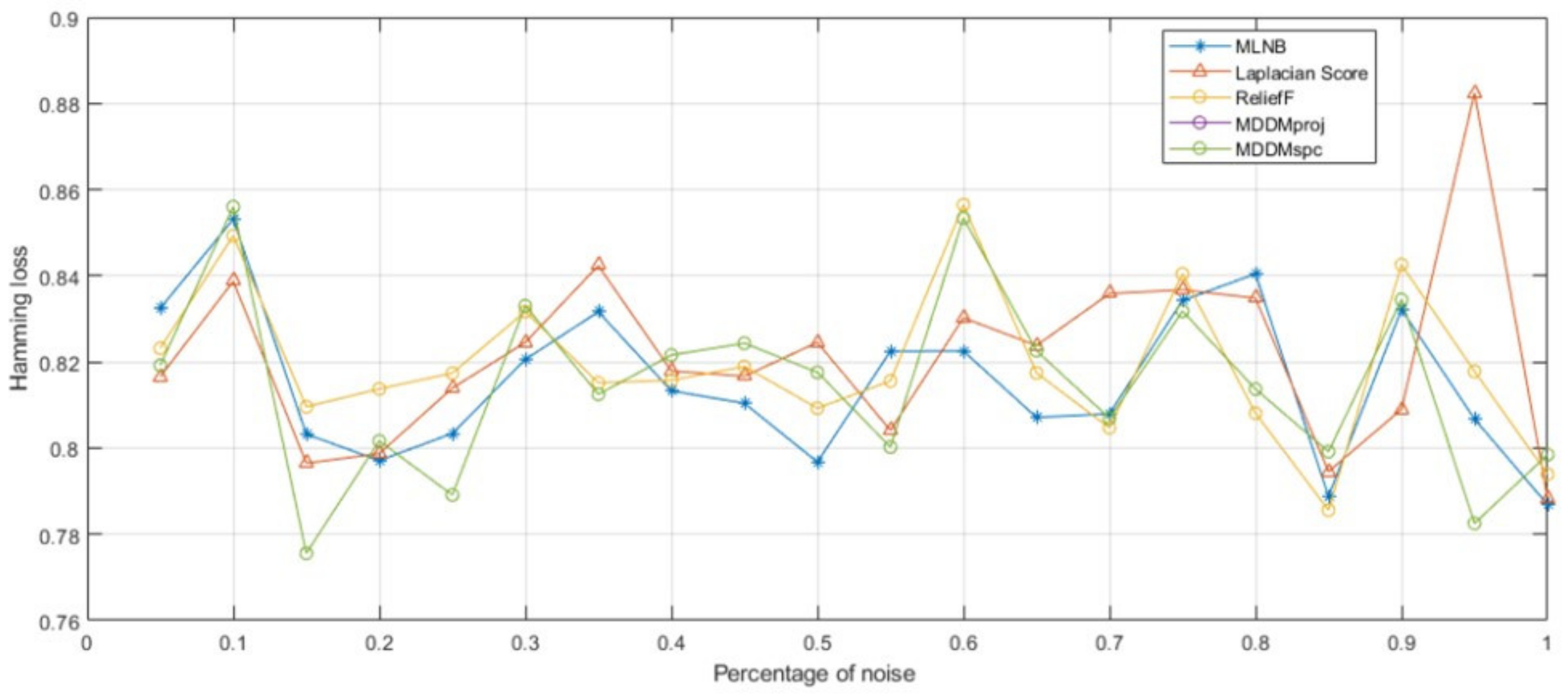
4.3. Effectiveness of Noise
4.3.1. Experimental Settings
4.3.2. Discussions of the Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pawlak, Z. Rough set. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Ziarko, W. Probabilistic approach to rough sets. Int. J. Approx. Reason. 2008, 49, 272–284. [Google Scholar] [CrossRef]
- Bazan, J.G.; Nguyen, H.S.; Nguyen, S.H.; Synak, P.; Wróblewski, J. Rough set algorithms in classification problem. In Rough Set Methods and Applications Physical; Springer: Heidelberg, Germany, 2000. [Google Scholar]
- Lingras, P. Unsupervised Rough Set Classification Using Gas. J. Intell. Inf. Syst. 2001, 16, 215–228. [Google Scholar] [CrossRef]
- Miao, D.; Duan, Q.; Zhang, H.; Jiao, N. Rough set based hybrid algorithm for text classification. Expert Syst. Appl. 2009, 36, 9168–9174. [Google Scholar] [CrossRef]
- Sharma, H.K.; Majumder, S.; Biswas, A.; Prentkovskis, O.; Kar, S.; Skačkauskas, P. A Study on Decision-Making of the Indian Railways Reservation System during COVID-19. J. Adv. Transp. 2022, 2022, 7685375. Available online: https://www.hindawi.com/journals/jat/2022/7685375/ (accessed on 7 July 2022). [CrossRef]
- Lingras, P. Rough set clustering for web mining. In Proceedings of the 2002 IEEE World Congress on Computational Intelligence, 2002 IEEE International Conference on Fuzzy Systems, FUZZ-IEEE’02. Proceedings (Cat. No. 02CH37291), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Lingras, P.; Peters, G. Applying rough set concepts to clustering. In Rough Sets: Selected Methods and Applications in Management and Engineering; Springer: London, UK, 2012; pp. 23–37. [Google Scholar]
- Parmar, D.; Wu, T.; Blackhurst, J. MMR: An algorithm for clustering categorical data using Rough Set Theory. Data Knowl. Eng. 2007, 63, 879–893. [Google Scholar] [CrossRef]
- Vidhya, K.A.; Geetha, T.V. Rough set theory for document clustering: A review. J. Intell. Fuzzy Syst. 2017, 32, 2165–2185. [Google Scholar] [CrossRef]
- Hedar, A.R.; Ibrahim, A.M.M.; Abdel-Hakim, A.E.; Sewisy, A.A. Modulated clustering using integrated rough sets and scatter search attribute reduction. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 1394–1401. [Google Scholar]
- Xia, S.; Zhang, H.; Li, W.; Wang, G.; Giem, E.; Chen, Z. GBNRS: A Novel Rough Set Algorithm for Fast Adaptive Attribute Reduction in Classification. IEEE Trans. Knowl. Data Eng. 2022, 34, 1231–1242. [Google Scholar] [CrossRef]
- Qian, Y.; Liang, J.; Yao, Y.; Dang, C. MGRS: A multi-granulation rough set. Inf. Sci. 2010, 180, 949–970. [Google Scholar] [CrossRef]
- Yao, Y.; Yao, B. Covering based rough set approximations. Inf. Sci. 2012, 200, 91–107. [Google Scholar] [CrossRef]
- Kumar, S.U.; Inbarani, H.H. A Novel Neighborhood Rough Set Based Classification Approach for Medical Diagnosis. Procedia Comput. Sci. 2015, 47, 351–359. [Google Scholar] [CrossRef]
- Zhang, J.; Li, T.; Ruan, D.; Liu, D. Neighborhood rough sets for dynamic data mining. Int. J. Intell. Syst. 2012, 27, 317–342. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, D.; Liu, J.; Wu, C. Neighborhood rough set based heterogeneous feature subset selection. Inf. Sci. 2008, 178, 3577–3594. [Google Scholar] [CrossRef]
- Yong, L.; Wenliang, H.; Yunliang, J.; Zeng, Z. Quick attribute reduce algorithm for neighborhood rough set model. Inf. Sci. 2014, 271, 65–81. [Google Scholar] [CrossRef]
- Chen, H.; Li, T.; Cai, Y.; Luo, C.; Fujita, H. Parallel attribute reduction in dominance-based neighborhood rough set. Inf. Sci. 2016, 373, 351–368. [Google Scholar] [CrossRef]
- Zhou, P.; Hu, X.; Li, P.; Wu, X. Online streaming feature selection using adapted Neighborhood Rough Set. Inf. Sci. 2018, 481, 258–279. [Google Scholar] [CrossRef]
- Sun, L.; Ji, S.; Ye, J. Multi-Label Dimensionality Reduction; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Wold, H. Estimation of principal components and related models by iterative least squares. In Multivariate Analysis; Academic Press: Cambridge, MA, USA, 1966; pp. 391–420. [Google Scholar]
- Zhang, Y.; Zhou, Z.H. Multilabel dimensionality reduction via dependence maximization. ACM Trans. Knowl. Discov. Data 2010, 4, 1–21. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Peña, J.M.; Robles, V. Feature selection for multi-label naïve Bayes classification. Inf. Sci. 2009, 179, 3218–3229. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Liu, J.; Chen, J.; Duan, J. Multi-label feature selection based on neighborhood mutual information. Appl. Soft Comput. 2016, 38, 244–256. [Google Scholar] [CrossRef]
- Liu, J.; Lin, Y.; Li, Y.; Weng, W.; Wu, S. Online multi-label streaming feature selection based on neighborhood rough set. Pattern Recognit. 2018, 84, 273–287. [Google Scholar] [CrossRef]
- Deng, Z.; Zheng, Z.; Deng, D.; Wang, T.; He, Y.; Zhang, D. Feature Selection for Multi-Label Learning Based on F-Neighborhood Rough Sets. IEEE Access 2020, 8, 39678–39688. [Google Scholar] [CrossRef]
- Al-Shami, T.M.; Ciucci, D. Subset neighborhood rough sets. Knowl. Based Syst. 2021, 237, 107868. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, Y.; Ma, Y.; Xu, F. Measures of uncertainty for neighborhood rough sets. Knowl. Based Syst. 2017, 120, 226–235. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Y.; Fan, X.; Shao, M. Attribute reduction based on k-nearest neighborhood rough sets. Int. J. Approx. Reason. 2018, 106, 18–31. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Y.; Liu, J.; Weng, W.; Shi, Z.; Wu, S. Feature selection for multi-label learning based on kernelized fuzzy rough sets. Neurocomputing 2018, 318, 271–286. [Google Scholar] [CrossRef]
- Xu, J.; Shen, K.; Sun, L. Multi-label feature selection based on fuzzy neighborhood rough sets. Complex Intell. Syst. 2022, 8, 2105–2129. [Google Scholar] [CrossRef]
- Wang, Q.; Qian, Y.; Liang, X.; Guo, Q.; Liang, J. Local neighborhood rough set. Knowl. Based Syst. 2018, 153, 53–64. [Google Scholar] [CrossRef]
- Lin, G.; Qian, Y.; Li, J. NMGRS: Neighborhood-based multi-granulation rough sets. Int. J. Approx. Reason. 2012, 53, 1080–1093. [Google Scholar] [CrossRef]
- Ziarko, W. Variable precision rough set model. J. Comput. Syst. Sci. 1993, 46, 39–59. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. Adv. Neural Inf. Process. Syst. 2005, 18, 1–8. Available online: https://proceedings.neurips.cc/paper/2005/file/b5b03f06271f8917685d14cea7c6c50a-Paper.pdf (accessed on 7 July 2022).
- Spolaôr, N.; Cherman, E.A.; Monard, M.C.; Lee, H.D. Relief for multi-label feature selection. In Proceedings of the 2013 Brazilian Conference on Intelligent Systems, Fortaleza, Brazil, 20–24 October 2013; IEEE: Manhattan, NY, USA, 2013; pp. 6–11. [Google Scholar]
- Liu, G.L. Axiomatic systems for rough sets and fuzzy rough sets. Int. J. Approx. Reason. 2008, 48, 857–867. [Google Scholar] [CrossRef]
| 1.5 | M | 1 | 0 | 1 | |
| 2 | F | 2 | 1 | 1 | |
| 2 | M | 2 | 1 | 0 | |
| 1.5 | M | 2 | 0 | 0 | |
| 2 | F | 2 | 1 | 1 |
| No. | Datasets | Samples | Attributes | Labels |
|---|---|---|---|---|
| 1 | Bird Song | 4998 | 38 | 13 |
| 2 | CAL-500 | 502 | 68 | 174 |
| 3 | Emotions | 593 | 72 | 6 |
| 4 | Flags | 194 | 14 | 12 |
| 5 | FGNET | 1002 | 262 | 78 |
| 6 | Water Quality Nom | 1060 | 16 | 14 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 1 | 0.60024 | 1.3229 | 0.61599 | |
| MLNB | |||||
| Laplacian Score | 1 | 0.60024 | 1.3229 | 0.61599 | |
| ReliefF | 1 | 0.60024 | 1.3229 | 0.61599 | |
| MDDMproj | 0.94641 | 0.22601 | 0.41394 | 0.86440 | |
| MDDMspc | 0.94641 | 0.22601 | 0.41394 | 0.86440 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 0.96755 | 0.18771 | 0.13001 | 132.03 | 0.48148 |
| MLNB | 0.96806 | 0.18763 | 0.12386 | 131.26 | 0.48137 |
| Laplacian Score | 0.96880 | 0.18701 | 0.11717 | 131.22 | 0.48484 |
| RelieF | 0.96870 | 0.18593 | 0.1208 | 131 | 0.48684 |
| MDDMproj | 0.96755 | 0.18771 | 0.13001 | 132.03 | 0.48148 |
| MDDMspc | 0.96806 | 0.18763 | 0.12386 | 131.26 | 0.48137 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 0.95468 | 0.51255 | 2.7671 | 0.62310 | 0.95468 |
| MLNB | |||||
| Laplacian Score | 0.95033 | 0.56044 | 2.9738 | 0.59137 | 0.95033 |
| RelieF | 0.89657 | 0.40958 | 2.4069 | 0.69350 | 0.89657 |
| MDDMproj | 0.89657 | 0.40958 | 2.4069 | 0.69350 | 0.89657 |
| MDDMspc | 0.88908 | 0.42924 | 2.3618 | 0.68983 | 0.88908 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 0.81977 | 0.24048 | 6.1901 | 0.75653 | 0.81977 |
| MLNB | |||||
| Laplacian Score | 0.80916 | 0.23298 | 5.8892 | 0.76737 | 0.80916 |
| RelieF | 0.81433 | 0.23269 | 6.2364 | 0.75832 | 0.81433 |
| MDDMproj | 0.81416 | 0.21904 | 6.1963 | 0.76229 | 0.81416 |
| MDDMspc | 0.81416 | 0.21904 | 6.1963 | 0.76229 | 0.81416 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 1 | 0.93427 | 21.477 | 0.15097 | |
| MLNB | |||||
| Laplacian Score | 1 | 0.93427 | 21.477 | 0.15097 | |
| RelieF | 1 | 0.93427 | 21.477 | 0.15097 | |
| MDDMproj | 1 | 0.95291 | 21.475 | 0.13413 | |
| MDDMspc | 1 | 0.95291 | 21.475 | 0.13413 |
| Algorithms | Hamming Loss (↓) | Ranking Loss (↓) | One-Error (↓) | Coverage (↓) | Average Precision (↑) |
|---|---|---|---|---|---|
| Ours | 0.88209 | 0.33826 | 9.3556 | ||
| MLNB | |||||
| Laplacian Score | 0.8825 | 0.35662 | 9.2995 | ||
| RelieF | 0.85437 | 0.32326 | 9.2675 | ||
| MDDMproj | 0.85437 | 0.32326 | 9.2675 | ||
| MDDMspc | 0.88296 | 0.36373 | 9.5964 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Li, J.; Liao, S.; Lin, Y. Multi-Label Attribute Reduction Based on Neighborhood Multi-Target Rough Sets. Symmetry 2022, 14, 1652. https://doi.org/10.3390/sym14081652
Zheng W, Li J, Liao S, Lin Y. Multi-Label Attribute Reduction Based on Neighborhood Multi-Target Rough Sets. Symmetry. 2022; 14(8):1652. https://doi.org/10.3390/sym14081652
Chicago/Turabian StyleZheng, Wenbin, Jinjin Li, Shujiao Liao, and Yidong Lin. 2022. "Multi-Label Attribute Reduction Based on Neighborhood Multi-Target Rough Sets" Symmetry 14, no. 8: 1652. https://doi.org/10.3390/sym14081652
APA StyleZheng, W., Li, J., Liao, S., & Lin, Y. (2022). Multi-Label Attribute Reduction Based on Neighborhood Multi-Target Rough Sets. Symmetry, 14(8), 1652. https://doi.org/10.3390/sym14081652







