Capture in Regime of a Trapped Motion with Further Inelastic Collision for Finite-Sized Asteroid in ER3BP

Abstract

The application of a modern solving algorithm or method of resolving dynamical equations for small projectile of finite sizes orbiting to be captured in a trapped zigzaging oscillations on orbit around the another large asteroid and in a further inelastic colliding scenario with him (using a formulation of the elliptic restricted three-body problem, ER3BP) is studied semi-analytically. Herein, two primaries M_Sun and m_p (m_p < M_Sun) revolve around their barycenter on Keplerian orbits with low eccentricities. A smaller body (projectile for attacking a large asteroid) is supposed to be a solid, almost symmetric ellipsoid, having the gravitational potential of the MacCullagh type. Our aim is to develop a previously introduced solving procedure and to investigate the updated dynamics of the projectile captured to a trapped dynamical resonance, thereby having the inelastic collision of a small projectile orbiting on quasi-stable elliptic orbits around the large asteroid, m_p.

1. Introduction

A lot of meaningful attempts have been made during the last 60 years in the field of celestial mechanics for the theoretical description or prediction of the orbital, rotational, resonance and collision dynamics of asteroids or other small celestial bodies with respect to the Earth, other planets, natural satellites and other large celestial bodies in the Solar System [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Having looked upon the search results of scientific databases (e.g., Scopus) regarding the request “inelastic collision of asteroids”, one can find a wide variety of approaches such as: modelling the after-impact dynamics of asteroids as a collisions inside the flows of rubble-pile [1,2] fragments of asteroids; large-scale stochastic models for the collision dynamics of asteroids within the Oort cloud; and various perturbations of classical two-body problem which consider the relations stemming from conserving the angular momentum or the orbital angular momentum (we should especially note here that the spatial ER3BP, elliptical restricted three-body problem is not conservative, and no integrals of motion are known [3,4,5,6]). For example, in the profound abovementioned work [1], the moniker approach is applied to investigate wide-ranging population of rubble-pile asteroids on near-Earth orbits with induced self-gravity (whereas they have significant void space or bulk porosity inside) by direct or indirect methods of observations depending on their shape and spin. Such rubble-pile asteroids are likely by-products of the continued collisional evolution of the Main Asteroid Belt.

Significant findings have been illuminated in seminal works [7,8] which should be especially outlined. In [7], complex program computing-based algorithms (including the Asteroid Redirection Demonstration System) are proposed as a demonstration mission to redirect a small asteroid less than 10 m in diameter to collide with a larger asteroid hundreds of meters in diameter, near the Earth. This collision will aim to disrupt the larger asteroid or alter its trajectory, thereby demonstrating a capability to prevent such an asteroid from colliding with Earth. In work [8], the authors proposed a new hazard scale that would describe the risk posed by a particular potential impact in both absolute and relative terms in order to conveniently compare and categorize the numerous potential impact solutions being discovered.

As we can see, the aforementioned research investigated possible collision or approach scenario near the Earth, in contrary to our approach suggested in the current semi-analytical investigation with numerical findings, where we concentrate our efforts on small projectile approaching large asteroid far from Earth, still using the formulation of the elliptical restricted three-body problem, ER3BP (which is the main feature of our research direction). In addition, we should note with respect to methodological basement that previous studies were purely numerical (in the mainstream way of other research in this direction), which is distinct from our research which is based on a semi-analytical algorithm with further numerical findings.

In references [7,8,9], one can find empirically useful celestial mechanics applications and data and formula (see (1) in [7]) on how to estimate the size of an asteroid via its absolute magnitude H (a measure of the luminosity of an asteroid on an inverse logarithmic magnitude scale) and geometric albedo, p. In [10], the authors come to the conclusion that when a large asteroid suffers a catastrophic impact with only a fraction of the initial mass re-accumulating into a “rubble pile,” a significant amount of angular momentum is carried away by the escaping material. Important conclusions are made by the authors in [11] where they outline, regarding the long timescale orbital dynamics of small celestial bodies (which are suffering from repeatedly close approaches to large celestial bodies, and should be in highly chaotic motion), that on two different computers—taking the same dynamical model, the same initial conditions and the same numerical integrator—the outcome of long-term integration would be different already after several close approaches. In [12], the authors investigate the rotational dynamics of various types of asteroids depending on their structure and size. In addition, the authors mention the interesting fact (referencing work [13] in their rationale) that >15% of projectile kinetic energy survives as the kinetic energy of the survived parts of the projectile (here, a small asteroid) following cratering events, with the rest being absorbed internally by the target (a large asteroid).

The main idea of the current research is to suggest the use of a semi-analytical algorithm for calculating the orbit of small projectile critically approaching other large asteroid (or minor planet in the Asteroid Belt), assuming the phenomenon of cosmic billiard for correcting the orbit of the large asteroid, which has a potential risk of further close approach to Earth in the future. This motivates us to develop research previously illuminated in work [43], solve an algorithm or method of resolving the dynamical equations for small satellite m of finite sizes (orbiting around minor planet), and semi-analytically study the updated type of dynamics of finite-sized asteroid m (small satellite in the terminology of the problem formulated in [43]) correlated implicitly to a kind of trapped motion governed by primaries (in the synodic co-rotating Cartesian coordinate system)—here, Sun M_Sun and large asteroid m_p (or minor planet)—in such a way that small asteroid m will be captured into further inelastic collision with the bigger ones, m_p, both moving on quasi-stable elliptic orbits.

In most optimistic scenario (excluding the direct impact of an asteroid to the minor planet’s surface), small asteroid will pass very close to the surface of such a celestial body or large asteroid at a negligible distance of the Roche limit [6] for this chosen celestial body. As for the complete introduction to the problem under consideration, we recommend seminal articles [14,15], especially [14], where significant theoretical explanations have been made in detail regarding planar dynamics of small celestial body of finite sizes, presented previously in a case of the elliptical restricted three-body problem ER3BP (where the satellite was assumed as a small celestial body—here, small asteroid—which is moving under the influence of gravitational forces of two primaries M_Sun and m_p, m_p < M_Sun, which are orbiting around their barycenter in mutual Keplerian motion) with the help of clear mathematical formulae by the system of two coupled ordinary differential equations of the second order. We restrict our current study by using the final form of the approximated scaled equations derived in work [43].

2. Convenient form of Equations of Motion for Further Solving Procedure

According to [43], we present equations of motion in the scaled, pulsating, planar coordinate system $\overrightarrow{r}$ = {x, y} (in the elliptical restricted three-body problem, ER3BP) for the following chosen set of initial conditions:

$$\begin{array}{l}\frac{d^{2}x}{d{f}^2}{(1+e·\cos f)}^4-2e{(1+e·\cos f)}^3(\sin f)\frac{dx}{df}-2{(1+e·\cos f)}^4\frac{dy}{df}=\\ ={(1+e·\cos f)}^{4}x-2e{(1+e·\cos f)}^3(\sin f)y-\frac{(x-\mu +1)}{{\left({(x-\mu +1)}^2+y^2\right)}^{\frac{3}{2}}}+\\ +\frac{3hx\left[2\left({(x-\mu +1)}^2+y^2\right)-5(x-\mu +1)x\right]}{10{\left({(x-\mu +1)}^2+y^2\right)}^{\frac{7}{2}}},\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \\ \frac{d^{2}y}{d{f}^2}{(1+e·\cos f)}^4-2e{(1+e·\cos f)}^3(\sin f)\frac{dy}{df}+2{(1+e·\cos f)}^4\frac{dx}{df}=\\ ={(1+e·\cos f)}^{4}y+2e{(1+e·\cos f)}^3(\sin f)x-\frac{y}{{\left({(x-\mu +1)}^2+y^2\right)}^{\frac{3}{2}}}-\frac{3hy{x}^2}{2{\left({(x-\mu +1)}^2+y^2\right)}^{\frac{7}{2}}}.\end{array}$$

(1)

where e is the eccentricity, f is the true anomaly, μ is the ratio of the mass (mass parameter in denotations chosen in [43]), and h is the extent of deviation of the projectile from the symmetrical form of the ellipsoid of rotation (also in denotations given in work [43]).

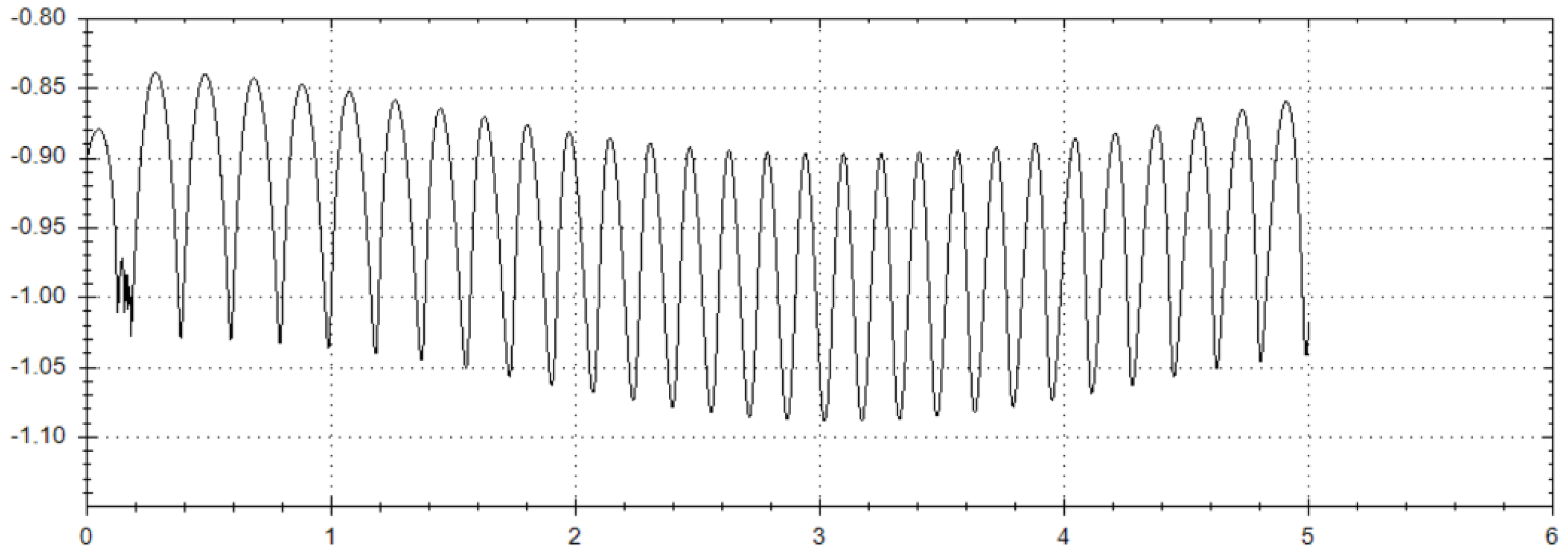
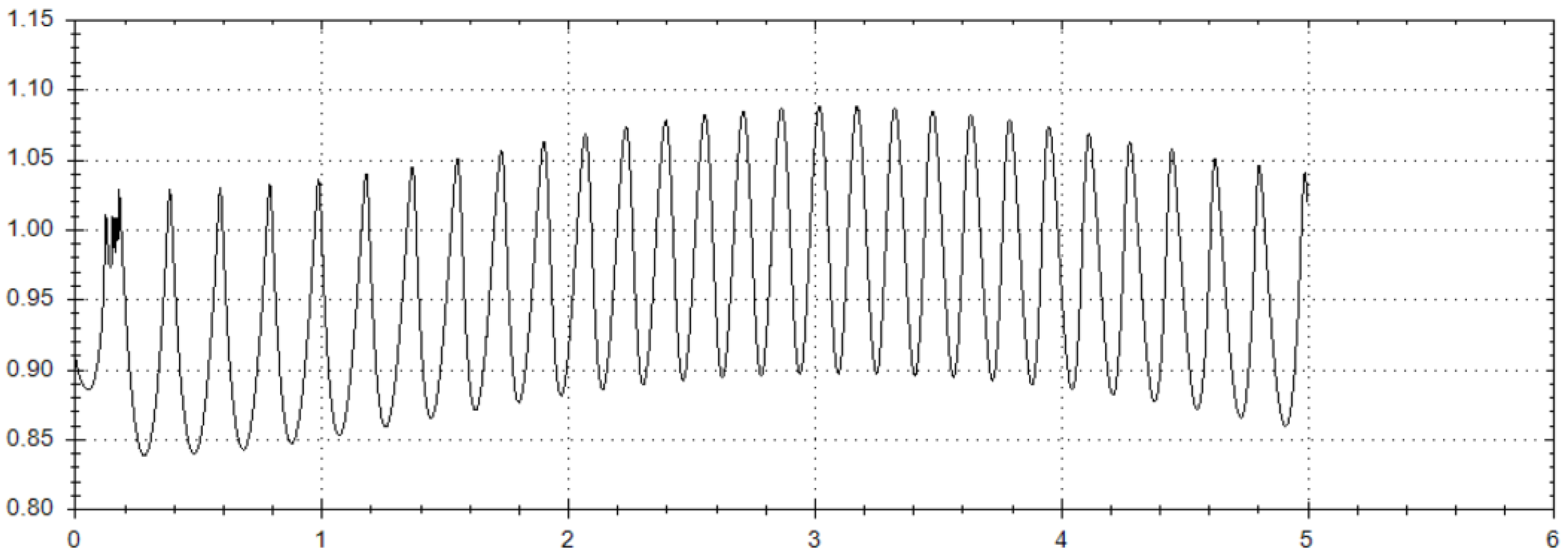
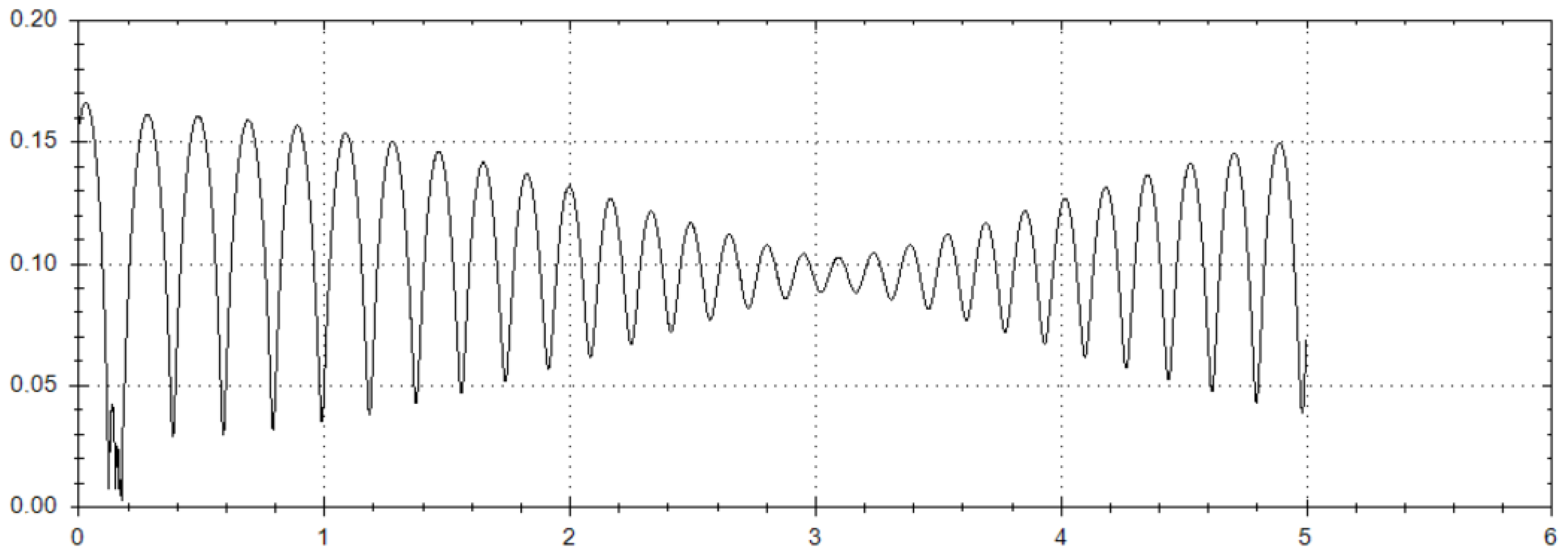
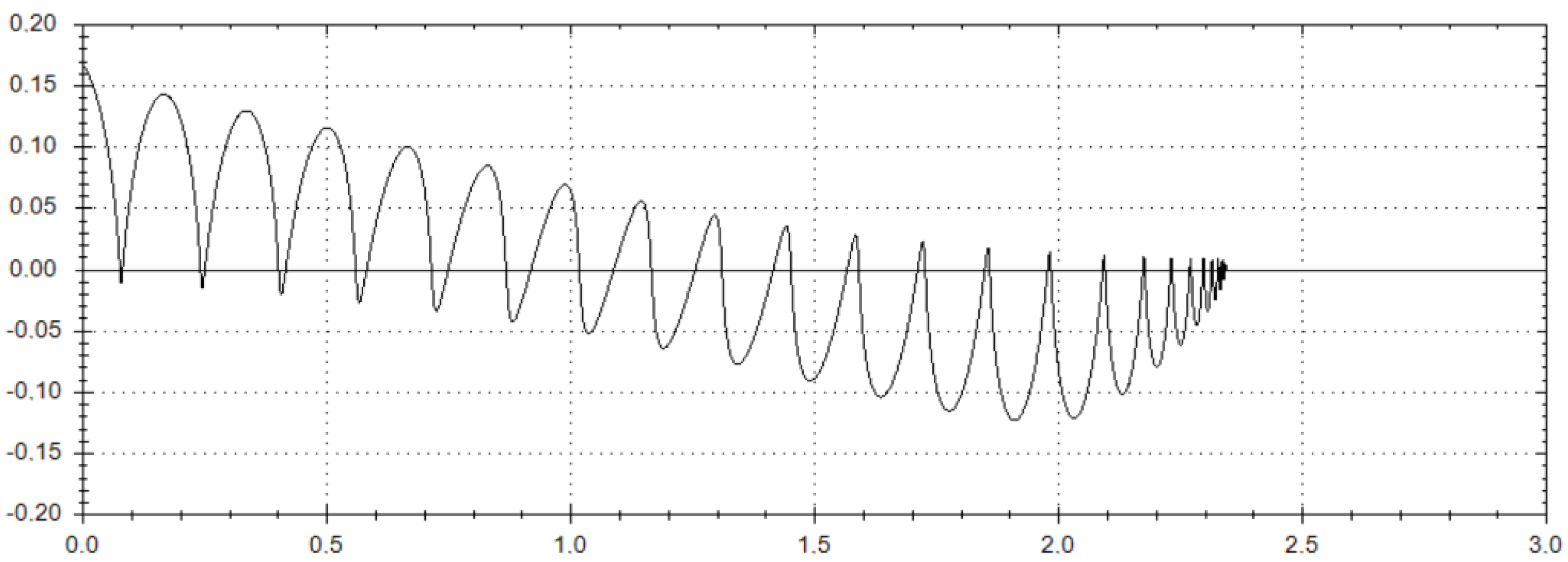
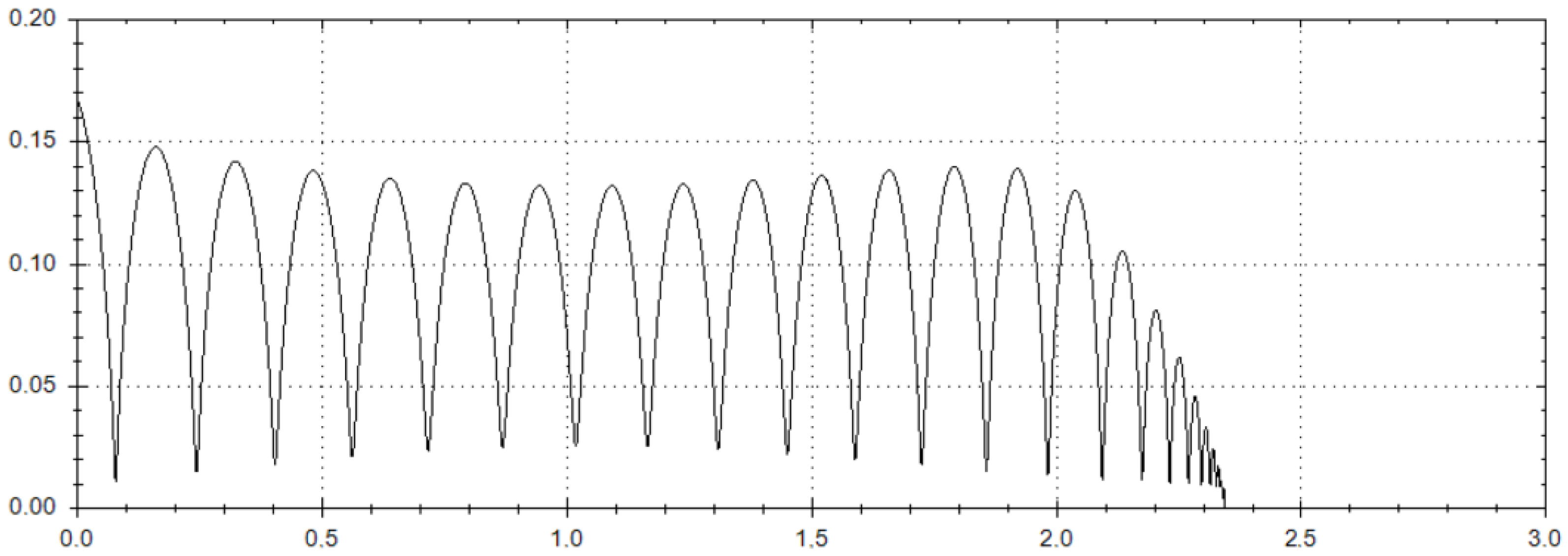
3. Graphical Plots for Numerical Solutions

Furthermore, let us present hereby the schematic imaging for numerical solutions of Equation (1) (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). It is worthy to note that dynamical trends of numerical solutions and their quasi-periodicity (depending on the true anomaly f) are dependent on parameter h in (1), which stems from the deviation of the form of the projectile from an ellipsoid of rotation.

The required clarifications should be given regarding an essential brief explanation vis-à-vis the text with a total research flowchart or framework diagram for the proposed algorithm in order to indicate how this employed model is working to receive the experimental results (for an easy understanding of how the proposed approach is working for common readers of the journal). Namely, the aforementioned total research flowchart is as follows:

• First, we choose from the very beginning the set of initial data with zero values;
• Then, we initiate the numerical solving of system (1) using the Runge–Kutta fourth-order method with step 0.001 starting from the abovementioned set of initial conditions;
• In the case where we obtain the required positive result (which is associated with recognizing the dynamical features of the projectile’s trapped motion when approaching the large asteroid during such celestial motion in ER3PB), the algorithm will be stopped;
• In the case where we obtain a negative result, initial data should be shifted by step (+/−) 0.001 with respect to the absolute magnitudes of the initial conditions. Hereafter, the algorithm should work during the next cycles of numerical calculating up to reaching the positive result.

It is of keen interest to consider the case of two primaries for the system “Ceres (dwarf planet, large asteroid)—Sun” where eccentricity is chosen to be e = 0.0785, $\mu \cong 4.7·{10}^{-10}$ in the series of numerical solutions illuminated by Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. We obtain the numerical solutions by the Runge–Kutta fourth-order method with step 0.001 starting for the case of Ceres (Figure 1, Figure 2, Figure 3 and Figure 4) with the initial conditions chosen as:

$$x_0=-0.9, {(\dot{x})}_0=0.9, y_0=-0.12, {(\dot{y})}_0=-0.2.$$

We can make the obvious conclusion from Figure 3 and Figure 4 that the projectile experiences strong oscillations during forced trapped orbiting when approaching the large asteroid. Such a regime of fast zigzagging oscillations stems from having been capturing into a resonance with Ceres at the final part of the trajectory of the projectile’s motion in ER3PB (case of two primaries “Ceres-Sun” for system “projectile-Ceres-Sun”).

In addition, let us consider the additional case of initial values for system “Ceres-Sun” with respect to the numerical solutions illuminated by Figure 5, Figure 6, Figure 7 and Figure 8. We will obtain the help of Runge–Kutta fourth-order ansatz (step 0.001 starting from initial conditions): x₀ = −1, ${(\dot{x})}_0$ = −0.53, y₀ = 0.167, ${(\dot{y})}_0$ = −0.57.

As we can obviously see from Figure 7 and Figure 8, the projectile also experiences strong zigzagging oscillations during its trapped motion when approaching the large asteroid (here, the minor planet Ceres) for the reason of having been captured into a resonance during such celestial motion in ER3PB (here, the case of two primaries “Ceres-Sun” for the system “projectile-Ceres-Sun”).

4. Discussion and Conclusions

A sufficient volume of profound scientific research has been made in celestial mechanics when discussing the superposing gravity fields obviously influencing the dynamics of satellite of finite sizes (here, projectile), consisting of the combined central fields of primaries in the elliptic restricted three-body problem (ER3BP).

An elegant application of modern solving algorithms or methods of resolving dynamical equations for small finite-sized projectile’s orbiting to be captured in trapped zigzagging oscillations in orbit around another large asteroid and in a further inelastic colliding scenario with him (using the formulation of the elliptic restricted three-body problem, ER3BP) is studied here by semi-analytical methods along with numerical findings. In such a formulation, two primaries, M_Sun and m_p (m_p < M_Sun), are revolving around their barycenter on Kepler orbits with low eccentricities. A smaller body (a projectile attacking a large asteroid) is supposed to be a solid, almost symmetric ellipsoid, having the gravitational potential of the MacCullagh type.

Our aim is to develop previously introduced solving procedure [43] and to investigate the updated dynamics of projectile captured in a trapped dynamical resonance, thereby having the inelastic collision of that small projectile orbiting on quasi-stable elliptic orbits around the large asteroid, m_p.

It is worthy to note that the distance of the projectile from the large asteroid should exceed Roche distance for this minor primary [6] (e.g., equal to $5R_p\cong 1.55·{10}^{-5}$ in units of a_p or circa 6.4 km, in the case of Ceres) if we wish to exclude the direct impact of the projectile to the minor primary’s surface. In any case, our calculations are valid for a restricted part of the projectile’s trajectory, where such a small mass m (projectile) will be moving inside the sphere of effective attraction, approaching the minor primary m_p inside the so-called Hill sphere [6] (but beyond Hill spheres of other planets of the Solar system):

$$r_H\cong a_p·(1-e^2)·{\left(\frac{m_p}{3(M_{Sun}+m_p)}\right)}^{\frac{1}{3}}$$

where we have chosen in [43] {a_p (1 − e²)} = 1. Thus, we have for the case of Ceres, $r_H\cong {\left(\frac{\mu }{3}\right)}^{\frac{1}{3}},\mu \cong 4.7·{10}^{-10}\to r_2<r_H\cong 5.38·{10}^{-4}$; this means that in the case of Ceres, the distance from the small asteroid to this minor planet should be less than $r_2<r_H\cong 5.38·{10}^{-4}(2.7653·1a.e.)$ ≅ 222.6⋅10³ km. Taking into account that the average velocity of a small asteroid (projectile) is circa 12–15 km/s, this means that such a projectile will be moving more than 4 h in the Hill sphere of a minor planet before reaching the minor primary (as the final target of the projectile’s trajectory). Despite the fact that the aforementioned distance within the Hill sphere is located sufficiently close to the secondary planet (minor planet), it is very important to describe correctly the final approaching motion of the small asteroid (projectile) to the target minor planet or large asteroid using the approximation of ER3BP (elliptic restricted three-body problem).

If we consider the case of Apophis as a large asteroid system “small asteroid-Apophis-Sun”, $r_H\cong {\left(\frac{\mu }{3}\right)}^{\frac{1}{3}},\mu \cong 1.358·{10}^{-20}\to r_2<r_H\cong 1.59·{10}^{-7}$; this means that in the case of Apophis, the distance from the small asteroid to this large asteroid should be less than $r_2<r_H\cong 1.59·{10}^{-7}(0.9223·1a.e.)$ ≅ 21.9 km. Taking into account that the average velocity of a small asteroid is circa 12–15 km/s, this means that the small asteroid will be moving less than 2 s in a Hill sphere of Apophis before reaching the large asteroid as a target. Thus, we conclude that it is sufficient for the calculation of the orbit of small asteroid approaching Apophis to use the equations of ER2BP (two-body problem, “small asteroid—Sun”), taking into account the Yarkovsky effect [25] for the proper correction of the orbit of Apophis (“Apophis-Sun”). It is also worth noting that we have succeeded in the numerical solving of system (1) (bearing estimation for h or restriction in Appendix A1 in mind) for the system “projectile-Ceres-Sun” where the eccentricity is chosen to be e = 0.0785, $\mu \cong 4.7·{10}^{-10}$ in the scheme of our numerical experiments presented by Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 (with the estimation of h as reported in [43]). For obtaining numerical solutions we used the Runge–Kutta fourth-order method with step 0.001 starting from various sets of initial conditions for the case of Ceres.

Last but not least, we should clarify properly which problems still need to be solved and why the proposed approach is suitable to be used to solve this critical problem. We have succeded in ajusting the initial data for numerical solving of system (1) as mentioned above for system “projectile-Ceres-Sun”, but the cases of other large asteroids (

Table 1. Asteroids with nominal mass >10 × 10¹⁸ kg.

Name	Approx. Mass (×1018 kg)	Approx. Proportion of All Asteroids
1. Ceres	938.4	31%
2. Vesta	259.1	8.6%
3. Pallas	204	6.7%
4. Hygiea	87	3.7%
5. Interamnia	35	1.3%
6. Eunomia	30	1.1%

, referring to hierarchy by their masses) should be investigated additionally.

The proposed approach is adjustable to be used to solve the aforementioned critical problem with help of adjusting the optimal set of initial data for each case.

As for a convincing literature review to indicate clearly the state-of-the-art development, we have given in the Introduction (according to our understanding) an up-to-date mentioning of scientific results in the field under consideration. We also should note that the approach proposed in the current research quite differs from that one in [45] for investigating the approach of asteroid 2006 RH120 to Earth. Moreover, the remarkable articles [46,47,48,49,50] should be cited which detail the problem under consideration.

To the best of our knowledge, there are no alternative models (which could be used as benchmark models) which use similar methods or approaches, or present such results. This proves the novelty and originality both in the solving of the algorithm and in the results presented by our model, with respect to the dynamics of the celestial motion of projectile approaching a large asteroid in the problem formulated as ER3BP (with further capturing into a resonance motion of projectile around a large asteroid resulting in inelastic collision as a reliable scenario).