Abstract
This article is focused on investigating the convective magneto-hydrodynamic single-phase flow for comparative analysis of two different base fluids above an exponentially stretchable porous surface under the effect of the chemical reaction. The Buongiorno fluid model is incorporated to observe the Thermophoresis and Brownian diffusion in this study. Boussinesq approximation for temperature and concentration are accounted for flow to be naturally convective. In this study, water and ethanol are assumed for comparative analysis. Additionally, to achieve the outcomes of the designed three-dimensional flow boundary value, problem technique is employed to simulate the problem in MATLAB. Increase in the magnetic field, thermophoresis diffusion, temperature exponent, and Prandtl number expand thermal boundary, whereas contraction is observed with an increase in porosity. Shear stress rates in respective directions have decreased with an increase in the stretching ratio of the surface. Moreover, through comparison, reasonably enhanced Nusselt number is observed for water under influence of study parameters while the Nusselt number abruptly decreases for ethanol. High mass coefficients are observed for both examined fluids.
1. Introduction
The study of fluid flow and thermal transmission encouraged many researchers due to its frequent application in the engineering field during the last few decades. First of all, Crane [1] gave the boundary layer flow over the stretchable sheet. Later on, researchers proceeded with his idea for further investigations in different fields of science and engineering including the manufacturing process, preparation of rubber and plastic sheets, biological science, material processing, etc. Later on, Takhar et al. [2] explored the 3D magneto-hydrodynamic boundary layer flow over the stretching sheet. Sajid and Hayat [3] investigated the thermal radiation effect on boundary layer flow above an exponentially stretching sheet. Researchers further examined this model for nanofluids studies. Fang et al. [4] scrutinized the boundary layer flow with variable thickness over the stretching surface. Hussain et al. [5,6] exposed the engine oil-based nanofluid flow above the stretching surface with different nanoparticles. Makinde et al. [7] inspected the turbulent MHD flow across a slippery stretching surface contained in a porous medium. Arshad et al. [8] explored nanostructured material flow above exponentially stretching surfaces, whereas Hamid et al. [9] inspected the impact of nanoparticle shape on rotating flow.
The effect of an oblique magnetic strength on the convective movement of Newtonian and non-Newtonian fluids across different kinds of stretchable surfaces has been discussed by several researchers. Shyam et al. [10] discussed the single isolated ferrofluid in the presence of applied magnetic field. Kumar and Mondal [11], including the thermal and radiation effect, made an irreversibility analysis for hybrid nanofluid in a rotating geometry. Arshad et al. [12] investigated the thermal energy transfer rate for water base nanofluid above a stretchable surface. Farooq et al. [13] explored the magneto hydrodynamic Maxwell fluid flow over the exponentially stretching surface. Similarly, many researchers [14,15,16,17,18] investigated the heat transfer phenomenon with different geometries and considerations. Hayat et al. [19] inspected the unsteady MHD flow with slippery settings above the stretching sheet. Hassan et al. [20] used the Rosseland radiation to investigate the heat transport for hybrid nanofluid flow. Chamkha et al. [21] investigated similarity solutions for Hiemenz flow in porous medium using hydro-magnetic mixed convection heat and mass transmission.
The porous medium is a solid medium containing holes (voids) that are linked and full of fluid, allowing the fluid to flow through them. The interaction surface area between the fluid and the solid surface increases when a porous medium is introduced, and as a result, they may be utilized as insulations and heat transmission supporters in various systems. Porous medium with boundary layer flow has many applications in cooling the nuclear reactor, oil production, dissident discarding of nuclear waste resources, cooling of electronic systems, temperature exchangers, geothermal engineering, and energy conservation because of the above advantages. Bahiraei and Hangi [22] examined and summarized recent research on magnetic-nanofluids (MNFs), including studies on thermophysical characteristics such as natural convection, forced convection, boiling, and their industrial applications. Arshad et al. [23] used the chemical reaction effect to elaborate the heat and mass transmission above an exponentially stretching surface and husssain et al. [24] made a computational analysis [24] for nanofluid flow. Pramanik [25] explored the Casson fluid flow and heat transmission past above the exponentially porous stretching surface.
Due to the wide range of applications, like nuclear power plants and fossil fuel burning, thermal radiation and chemical reaction effect, heat and mass transport over a stretching surface play essential part in engineering and physics. Mukhopadhyay and Gorla [26] presented the partial slip influence over the porous exponential stretching surface. Several scholars [27,28,29,30] have examined the impact of heat contamination on a stretched sheet under different flow conditions. Misra and Sinha [31] described the influence on magneto hydrodynamic flow of blood. Mukhopadhyay [32] investigated the Stefan blowing effect above an exponentially stretching surface. Gorthi et al. [33] used the electric and magnetic field effect for numerical investigation of the two dynamically immiscible nanofluids.
Thermophoresis and Brownian motion are the two most important phenomena of particle movement in nanofluid due to having a major influence on thermo-physical characteristics of nanofluid. Many industrial uses, such as filters, ignition, and turbine blades, rely on this phenomenon. Several types of research involve this special phenomenon with other important effects. Irfan and Farooq [34] investigated thermophoresis MHD free stream flow in a porous medium above a radiative exponentially stretching surface. Nanoparticle thermophoretic diffusion across a porous exponential stretching surface in viscoelastic flow is examined by Etwire et al. [35]. Arshad et al. [36] used the exponentially stretching surface to analyze the thermophoretic and Brownian effects for MHD flow. The joined impact of thermo-diffusion and thermal radiation on non-Newtonian nanofluid across a porous stretching sheet was computationally examined by Bhatti and Rashidi [37], who found that the temperature field enhances as the thermo-diffusion and thermal radiation constraint increase.
Chemical reaction effect on heat and mass transport above a stretched sheet has a wide variety of uses in numerous industries, including nuclear power plants, fossil fuel combustion, geophysics, and different propulsion technologies for missiles, airplanes, space vehicles, and satellites MHD nanofluid flow with bio-convection, and quartic autocatalysis chemical reaction over an upper surface of a paraboloid of revolution was inspected by Makinde and Animasaun [38]. Chamkha, Aly and Mansour [39] presented the unsteady mass and heat transfer from the stretching surface with chemical reaction and suction/injection parameter. Chaudhary and Jain [40] explored the combined effect of heat and mass transfer for MHD flow past. Abouelregal and Marin [41] utilized the thermoplastic model, which determines the vibrations of nanobeams. Bhatti et al. [42] presented the recent trends in fluid dynamics. A numerical investigation of radiation assimilation and chemical effects on turbulent MHD free convection from a permeable media was carried out by Hernández and Zueco [43]. Pal and Mondal [44] examined the mixed convection mass and heat transmission above a non-linear stretching sheet using the chemical reaction.
The novelty of this article is to scrutinize the flow of a single-phase fluid using the Buongiorno model above a porous exponentially stretchable surface with variable permeability, magnetic field, and chemical reaction. Keeping in view the aforementioned assumptions, no convective conditions are assigned on boundaries. The problem-governing flow equations are derived with the help of constitutive relations and are then transformed into a set of non-dimensional forms utilizing suitable similarity transform. In this study, a more appropriate numerical technique boundary value problem technique is employed to obtain the results. Moreover, a comparative analysis is conducted for selected base fluids to determine and analyze the effect of different externally applied effects, specifically on shear stress rates, coefficient of heat transfer, and Sherwood number.
2. Problem Formulation
Consider the laminar 3D electrically conductive MHD flow with constant density above a stretchable sheet. The Cartesian coordinates -axis are taken alongside the stretchable surface in the direction of motion and the -axis is perpendicular to it. The configuration of the problem is shown in Figure 1. Also, the following assumptions are considered for this study:
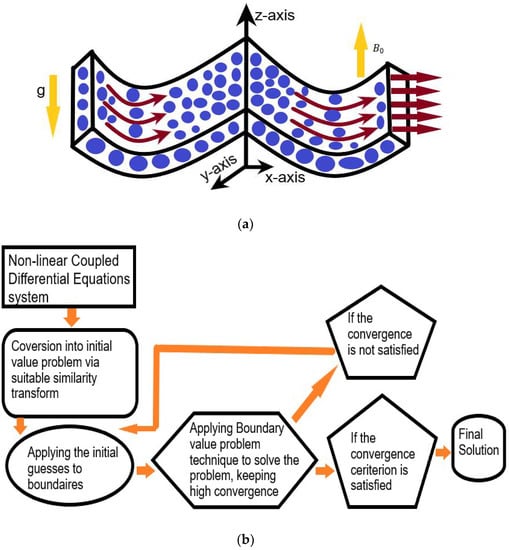
Figure 1.
(a)The geometry of the problem; (b) Algorithm of the solution.
- (1)
- The negligible effect of gravitation is considered.
- (2)
- Thermal conductivity and specific heat are not depending on temperature.
- (3)
- A uniform magnetic field is applied normally on the stretching sheet.
- (4)
- The flow is laminar and has constant density.
- (5)
- The adjustable chemical reaction is considered, and the sheet is permeable.
- (6)
- The induced electric and magnetic fields are neglected.
Applying boundary layer approximation with these assumptions, the governing equations [45] of continuity, velocity, temperature, and concentration takes the following form:
The boundary conditions are:
Here, are constants, is reference length, and are temperature and concentration exponents. The following similarity transformation is employed to convert the boundary layer equations into the dimensionless form:
Applying the above-mentioned similarity transformation in Equation (1) to Equation (5), the continuity equation is satisfied. The velocity, temperature, and concentration equations take the following form:
The transformed boundary conditions after employing the similarity transformation are:
Here
Here are Magnetic parameter, thermophoresis and Brownian motion parameter, stretching velocity ratio parameter, Prandtl number, thermal and mass Grass Number, Schmidt number, temperature and mass convective parameter, chemical reaction, and porosity parameter respectively. The local Reynolds number in the x and y-direction is defined as and respectively. Skin frictions in x and y-direction are defined as:
Here and are wall shear stresses in and directions and are defined as follows:
By using Equations (8) and (17), the non-dimensional forms of Equations (15) and (16) can be written as:
The Nusselt and Sherwood [45,46] coefficients are expressed as:
where is wall heat flux and is mass flux from stretchable surface respectively. The non-dimensional form of Equations (19) and (20) is written as:
3. Numerical Scheme
The boundary value problem technique is used in MATLAB to solve a coupled system of ordinary differential Equations (9)–(12) with boundary conditions (13). Figure 1b shows the complete algorithm of the solution.
For this purpose, a new set of variables is defined as:
A new set of variables defined above is used in the following way in MATLAB to tackle the problem numerically.
Transformed boundary conditions are:
Similarly, the skin frictions, Nusselt number, and Sherwood are inserted in MATLAB as follows:
4. Results and Discussion
This section contains the results of a 3D stretchable natural convection flow of viscous fluid through porous medium. The impact of the variable magnetic field, non-uniform permeability, and variable chemical reaction is investigated. The Buongiorno model is employed to examine the effect of Brownian motion and thermophoretic distribution. Similarity transformation is used to transform the governing equations. The boundary value problem technique is used to tackle the problem. The outcomes are presented through graphs and tables.
4.1. Velocity Profiles
The impact of flow limitations on non-dimensional velocity profiles is shown in the graphs below for water and ethanol. The influence of porosity constraint on velocity profiles and is shown in Figure 2a,b. Both velocity profiles decay by increasing the porosity parameter. This outcome is consistent with phenomena. As medium porosity always acts as a resistive force, a rise in signifies a higher resistive force, which has the effect of slowing down the fluid motion. A high decay in boundary layer thickness is noted for velocity profile as compared to the velocity profile. Mass convection is defined as the ratio of movement of material to flow of fluid. This is an important phenomenon due to its application. The effect of magnetic field strength is displayed in Figure 2c,d for both primary and secondary profiles. It is clear that as the magnetic strength parameter rises both velocity profiles decay. This is because the magnetic field provides a resistive force that confines the fluid flow.
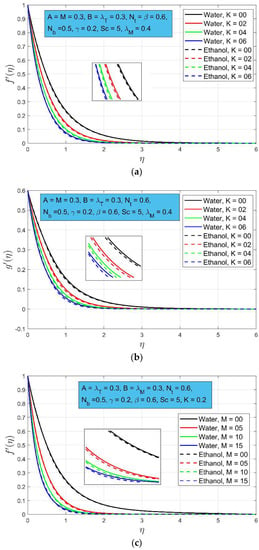
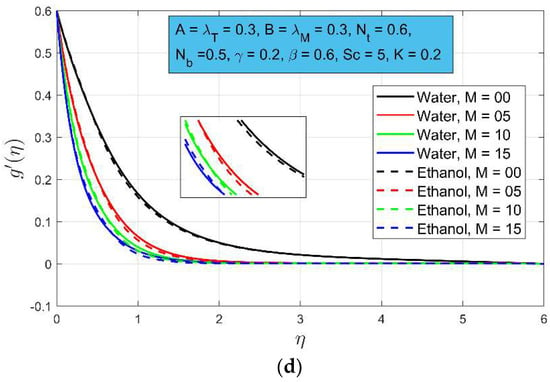
Figure 2.
(a): The influence of on the velocity profile ; (b): The influence of on the velocity profile (c): The influence of on velocity profile ; (d): The influence of on velocity profile .
4.2. Temperature Profile
The effect of different parameters such as on temperature profile is shown in the following Figure 3a–d. It is observed that increases in and increase fluid temperature and hence thermal resistance, resulting in a larger thermal boundary layer, although increases in and temperature exponent appear to have the opposite effect. As a result, the thermal boundary layer becomes thinner. As the Lorentz increases because of magnetic field strength, restricts the fluid flow resulting rise in the temperature profile. Stronger thermophoretic distribution sweeps the nanoparticles away from the surface, but the heated surface prevents the nano-sized particles. Figure 3c demonstrates how upsurging the porosity constraint increases the temperature and thickness of the thermal boundary layer. The permeability of the porous medium determines the porosity parameter. The bigger the permeability value, the lower the permeability of the porous media. So, the temperature profile upsurges when increases. Temperature exponent and Prandtl number have opposite behavior on the temperature profile. Figure 3d shows that higher Prandtl fluids with lower thermal diffusivity reduce fluid temperature, resulting in a shrinking thermal boundary layer. Molecular bond energy and temperature have an inverse relation between them. Figure 3b shows that upsurge in temperature exponent results in lessening the temperature profile.
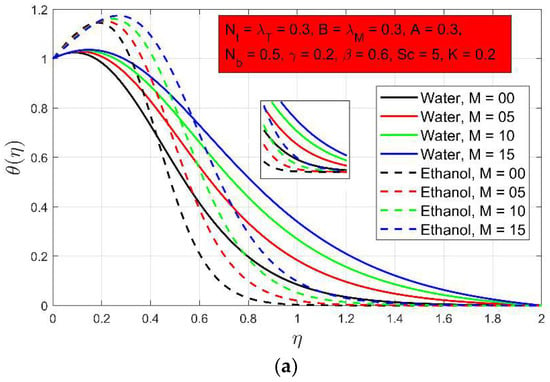
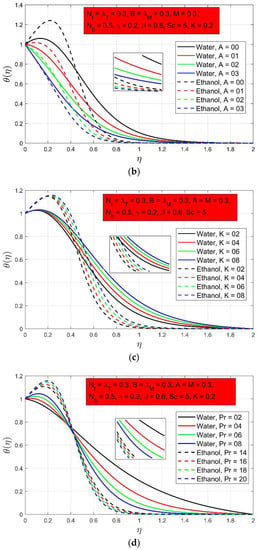
Figure 3.
(a) The influence of on temperature profile ; (b) The influence of on temperature profile ; (c) The influence of on temperature profile ; (d) The influence of on temperature profile .
4.3. Concentration Profile
The following Figure 4a–c shows the different parameters such as and on concentration profiles. Figure 4a,b show the influence of Schmidt number and chemical reaction constraint on concentration profile . It is self-evident that when increases, the concentration profile decreases. is the ratio of velocity and mass diffusivity, which is mostly responsible for this. As a result, a rise in suggests more momentum diffusivity, resulting in lower concentrations of chemically reactive species. The chemical reaction parameter is a decreasing function of the concentration profile, a increase in chemical reaction parameter decays the concentration profile. Figure 4c illustrates the influence of concentration exponent on the concentration profile. The concentration exponent has an inverse relation with the concentration profile. This figure shows that an increase in concentration exponent decreases the concentration profile and vice versa.
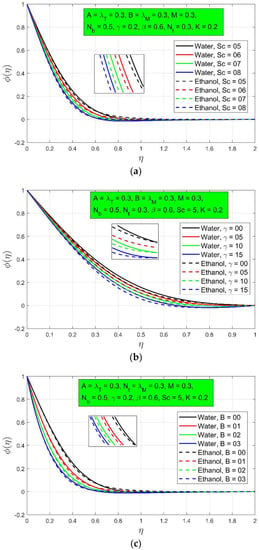
Figure 4.
(a) The influence of on concentration profile ; (b) The influence of on concentration profile ; (c) The influence of on concentration profile .
4.4. Skin Frictions, Nusselt and Sherwood Numbers
The following figures show the influence of magnetic parameter and porosity on skin frictions, Nusselt number, and Sherwood number, respectively. It can be noted in Figure 5a–c that skin friction, Nusselt number, and Sherwood number decay when the porosity parameter increases. High skin friction along the axial direction is noted for Ethanol, whereas high Nusselt and Sherwood numbers are noted for water. Additionally, Table 1 and Table 2 show the effect of different study parameters on skin frictions, Nusselt number, and Sherwood number for water and ethanol, respectively.
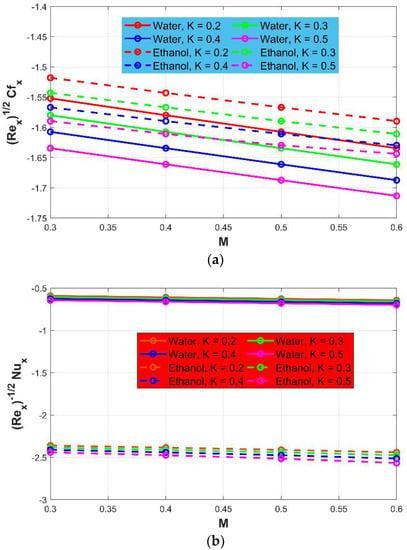
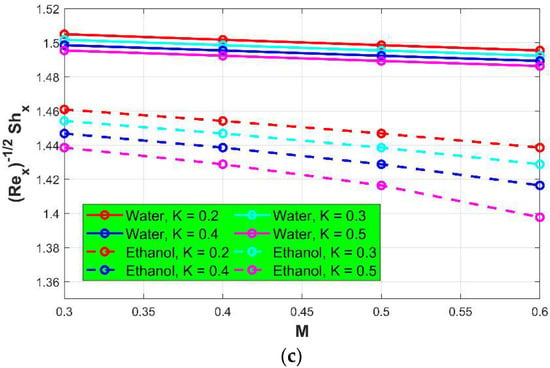
Figure 5.
(a) Skin friction versus porosity and magnetic field ; (b) Nusselt number versus porosity and magnetic field ; (c) Sherwood number versus porosity and magnetic field .

Table 1.
Comparison of present outcomes for skin friction along x-axis for pure fluid with with literature.

Table 2.
Influence of different study parameters on and for Water.
Furthermore, Table 1 shows the validation of current outcomes with the literature. This comparison shows our outcome maintains a good agreement with the literature. Table 2 and Table 3 show the numerical outcomes of different study parameters on skin frictions, Nusselt number, and Sherwood number for water and ethanol, respectively. It can be noted from Table 2 and Table 3 that skin frictions and decrease by rising in , and parameters but there are insignificant change due to . While these skin frictions increase by a rise in parameters. The Nusselt number increases by a rise in , and parameters while it decreases for all other parameters. Similarly, Sherwood number decreases only for the rise in , and while it increases for all other parameters.

Table 3.
Influence of different study parameters on and for Ethanol.
5. Conclusions
A numerical analysis is attempted to investigate the influence of chemical reaction and magnetic field for viscous fluid flow above a 3D permeable exponentially stretching surface. Similarity transformation is used to convert the governing equations of momentum, energy, and concentrations into ordinary differential equations. The boundary value technique is used to tackle these equations in MATLAB. The influence of different study parameters on different profiles is presented through graphs and tables. The main key conclusions of this study are listed below.
- The velocity profile increases by a rise in mass and temperature convective parameter while it decays with a rise in porosity and magnetic parameter.
- The temperature profile decays by a rise in temperature exponent and Prandtl number while it increases by a rise in porosity, thermophoresis, and magnetic parameter.
- The concentration profile increases by rising in porosity while it decays by rising in concentration exponent, chemical reaction, and Schmidt number.
- Skin frictions, Nusselt number, and Sherwood number decay by an increase in porosity and magnetic parameter.
- Chemical reaction and thermophoresis parameters increase the Sherwood number.
- Nusselt number increases by rising in mass and temperature convective parameter, temperature exponent, thermophoresis parameter, and concentration exponent.
- Low skin friction and Nusselt and Sherwood number are observed for water as compared to ethanol.
Author Contributions
Conceptualization, M.A. and A.H.; methodology, A.E.; software, M.A.; validation, J.A., W.P. and M.A.E.; formal analysis, S.G. and F.M.A.; investigation, M.A.; resources, A.E.; data curation, M.A.E.; writing—original draft preparation, M.A.; writing—review and editing, M.A.; visualization, S.G.; supervision, M.A.; project administration, M.A. and F.M.A.; funding acquisition, M.A.E., A.E. and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Program under grant no. RGP. 2/19/43. This research is supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R184), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, this work was supported by Taif University Researchers Supporting Project number (TURSP-2020/40), Taif University, Taif, Saudi Arabia.
Conflicts of Interest
Authors declare no conflict of interest.
Nomenclature
| Brownian and Thermophoresis diffusion | |
| Constants | |
| Magnetic parameter | |
| Temperature and concentration | |
| Nusselt and Sherwood number | |
| Chemical reaction, porous medium parameter | |
| Prandtl and Schmidt number | |
| Stretching ratio parameter | |
| Heat and mass flux | |
| Temperature diffusivity | |
| MHD | Magneto-hydrodynamic |
| Temperature and mass Grashof number | |
| Skin friction coefficients | |
| Thermal conductivity | |
| Wall shear stress | |
| Dimensionless velocity | |
| Temperature, and concentration | |
| Temperature and mass convective parameter | |
| Temperature exponent | |
| Brownian diffusion and Thermophoresis parameter | |
| Kinematic viscosity | |
| Reference length | |
| 3D | Three dimensional |
| Concentration exponent |
References
- Crane, L.J. Flow past a stretching plate. Z. Für Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Unsteady three-dimensional MHD-boundary-layer flow due to the impulsive motion of a stretching surface. Acta Mech. 2001, 146, 59–71. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Zhong, Y. Boundary layer flow over a stretching sheet with variable thickness. Appl. Math. Comput. 2012, 218, 7241–7252. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Hassan, A.; Rehman, A.; Ahmad, H.; Baili, J.; Gia, T.N. Heat transport investigation of engine oil based rotating nanomaterial liquid flow in the existence of partial slip effect. Case Stud. Therm. Eng. 2021, 28, 101500. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Alshehri, N.A. Heat transmission of engine-oil-based rotating nanofluids flow with influence of partial slip condition: A Computational model. Energies 2021, 14, 3859. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, Z.H.; Ahmad, R.; Khan, W.A. Numerical study of unsteady hydromagnetic radiating fluid flow past a slippery stretching sheet embedded in a porous medium. Phys. Fluids 2018, 30, 083601. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Khan, I.; Badran, M.; Mehrez, S.; Elfasakhany, A.; Abdeljawad, T.; Galal, A.M. Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study. Nanomaterials 2022, 12, 1204. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Zubair, T.; Haq, R.U.; Wang, W. Shape effects of MoS2 nanoparticles on rotating flow of nanofluid along a stretching surface with variable thermal conductivity: A Galerkin approach. Int. J. Heat Mass Transf. 2018, 124, 706–714. [Google Scholar] [CrossRef]
- Shyam, S.; Yadav, A.; Gawade, Y.; Mehta, B.; Mondal, P.K.; Asfer, M. Dynamics of a single isolated ferrofluid plug inside a micro-capillary in the presence of externally applied magnetic field. Exp. Fluids 2020, 61, 210. [Google Scholar] [CrossRef]
- Kumar, M.; Mondal, P.K. Irreversibility analysis of hybrid nanofluid flow over a rotating disk: Effect of thermal radiation and magnetic field. Colloids Surf. A Physicochem. Eng. Asp. 2022, 635, 128077. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Shah, S.A.G.A.; Wróblewski, P.; Elkotb, M.A.; Abdelmohimen, M.A.; Hassan, A. Thermal energy investigation of magneto-hydrodynamic nano-material liquid flow over a stretching sheet: Comparison of single and composite particles. Alex. Eng. J. 2022, 61, 10453–10462. [Google Scholar] [CrossRef]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 7312. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transportation enrichment and elliptic cylindrical solution of time-dependent flow. Case Stud. Therm. Eng. 2021, 27, 101248. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Alanazi, M.M.; Zahran, H.Y. Numerical and Thermal Investigation of Magneto-Hydrodynamic Hybrid Nanoparticles (SWCNT-Ag) under Rosseland Radiation: A Prescribed Wall Temperature Case. Nanomaterials 2022, 12, 891. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Arshad, M.; Rehman, A.; Matoog, R.T.; Abdeljawad, T. Numerical simulation and thermal enhancement of multi-based nanofluid over an embrittled cone. Case Stud. Therm. Eng. 2021, 28, 101614. [Google Scholar] [CrossRef]
- Ahmad, F.; Tang, X.W.; Qiu, J.N.; Wróblewski, P.; Ahmad, M.; Jamil, I. Prediction of slope stability using Tree Augmented Naive-Bayes classifier: Modeling and performance evaluation. Math. Biosci. Eng. 2022, 19, 4526–4546. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud. Therm. Eng. 2021, 27, 101244. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A.; Shahzad, S.A. Unsteady MHD flow over exponentially stretching sheet with slip conditions. Appl. Math. Mech. 2016, 37, 193–208. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Haider, Q.; Althobaiti, A.; Elagan, S.K.; Alqurashi, M.S.; Abdelmohimen, M.A. Heat transport investigation of hybrid nanofluid (Ag-CuO) porous medium flow: Under magnetic field and Rosseland radiation. Ain Shams Eng. J. 2022, 13, 101667. [Google Scholar] [CrossRef]
- Chakhma, A.J.; Khaled, A.R.A. Similarity solutions for hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through porous media. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 94–115. [Google Scholar]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Shah, S.A.G.A.; Elkotb, M.A.; Gouadria, S.; Alsehli, M.; Galal, A.M. Heat and mass transfer analysis above an unsteady infinite porous surface with chemical reaction. Case Stud. Therm. Eng. 2022, 36, 102140. [Google Scholar] [CrossRef]
- Hussain, A.; Elkotb, M.A.; Arshad, M.; Rehman, A.; Sooppy Nisar, K.; Hassan, A.; Saleel, C.A. Computational investigation of the combined impact of nonlinear radiation and magnetic field on three-dimensional rotational nanofluid flow across a stretchy surface. Processes 2021, 9, 1453. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Gorla, R.S.R. Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presence of thermal radiation. Heat Mass Transf. 2012, 48, 1773–1781. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Rehman, K.; Wróblewski, P.; Lewicki, W.; Kavin, B.P. Exploiting the Moth–Flame Optimization Algorithm for Optimal Load Management of the University Campus: A Viable Approach in the Academia Sector. Energies 2022, 15, 3741. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Mdallal, Q.A.; Ahmad, H.; Sherif, E.S.M.; Rehman, A.; Arshad, M. Comsolic solution of an elliptic cylindrical compressible fluid flow. Sci. Rep. 2021, 11, 20030. [Google Scholar] [CrossRef]
- Wróblewski, P.; Niekurzak, M. Assessment of the Possibility of Using Various Types of Renewable Energy Sources Installations in Single-Family Buildings as Part of Saving Final Energy Consumption in Polish Conditions. Energies 2022, 15, 1329. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Ahmad, H.; Ishan, A. Three-dimensional water-based magneto-hydrodynamic rotating nanofluid flow over a linear extending sheet and heat transport analysis: A numerical approach. Energies 2021, 14, 5133. [Google Scholar] [CrossRef]
- Misra, J.C.; Sinha, A. Effect of thermal radiation on MHD flow of blood and heat transfer in a permeable capillary in stretching motion. Heat Mass Transf. 2013, 49, 617–628. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng. J. 2013, 4, 485–491. [Google Scholar] [CrossRef]
- Gorthi, S.R.; Mondal, P.K.; Biswas, G.; Sahu, K.C. Electro-capillary filling in a microchannel under the influence of magnetic and electric fields. Can. J. Chem. Eng. 2021, 99, 725–741. [Google Scholar] [CrossRef]
- Irfan, M.; Farooq, M.A. Thermophoretic MHD free stream flow with variable internal heat generation/absorption and variable liquid characteristics in a permeable medium over a radiative exponentially stretching sheet. J. Mater. Res. Technol. 2020, 9, 4855–4866. [Google Scholar] [CrossRef]
- Etwire, C.J.; Seini, I.Y.; RABIU, M.; Makinde, O.D. Impact of thermophoretic transport of Al2O3 nanoparticles on viscoelastic flow of oil-based nanofluid over a porous exponentially stretching surface with activation energy. Eng. Trans. 2019, 67, 387–410. [Google Scholar]
- Arshad, M.; Hussain, A.; Hassan, A.; Haider, Q.; Ibrahim, A.H.; Alqurashi, M.S.; Almaliki, A.H.; Abdussattar, A. Thermophoresis and brownian effect for chemically reacting magneto-hydrodynamic nanofluid flow across an exponentially stretching sheet. Energies 2021, 15, 143. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liq. 2016, 221, 567–573. [Google Scholar] [CrossRef]
- Makinde, O.D.; Animasaun, I.L. Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. Int. J. Therm. Sci. 2016, 109, 159–171. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Aly, A.M.; Mansour, M.A. Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects. Chem. Eng. Commun. 2010, 197, 846–858. [Google Scholar] [CrossRef]
- Chaudhary, R.C.; Jain, A. Combined heat and mass transfer effects on MHD free convection flow past an oscillating plate embedded in porous medium. Rom. J. Phys. 2007, 52, 505–524. [Google Scholar]
- Abouelregal, A.E.; Marin, M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Recent trends in computational fluid dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
- Hernández, V.R.; Zueco, J. Network numerical analysis of radiation absorption and chemical effects on unsteady MHD free convection through a porous medium. Int. J. Heat Mass Transf. 2013, 64, 375–383. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. MHD non-Darcian mixed convection heat and mass transfer over a non-linear stretching sheet with Soret–Dufour effects and chemical reaction. Int. Commun. Heat Mass Transf. 2011, 38, 463–467. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Pandey, V.S. MHD 3D free convective flow of nanofluid over an exponentially stretching sheet with chemical reaction. Adv. Powder Technol. 2017, 28, 2159–2166. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Zulfiqar, M.; Bilal, M.; Shafee, A.; Chung, J.D.; Lu, D.; Farooq, U. Entropy analysis of 3D non-Newtonian MHD nanofluid flow with nonlinear thermal radiation past over exponential stretched surface. Entropy 2018, 20, 930. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet. Alex. Eng. J. 2014, 53, 219–224. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).