1. Introduction
Sophus Lie proposed the symmetry theory of differential equations in the late 19th century. Lie symmetry theory unifies and extends existing techniques for constructing explicit solutions to differential equations. The basic idea of lie groups is to find symmetry groups of given equations. It is an effective method to analyze differential equations. It is usually used to reduce the order of ordinary differential equations (ODEs). We can obtain its explicit solution of the first order ODE.
As an important branch of ODEs, impulsive differential equations (IDEs) are regarded as a vital mathematical tool in some areas of research. IDEs are related to mechanical systems, theoretical physics, chemistry, control theory and so on. Hence, they are regarded as an effective mathematical tool to solve some real-world problems in the applied sciences (see, for instance, [
1,
2,
3,
4]). Many authors are devoted to the existence of solutions to IDEs.
Recently, boundary value problems (BVPs) in IDEs have been extensively studied. Correspondingly, some basic results for BVPs of second-order IDEs have been obtained by many authors. For example, W. Ding and M. Han studied the existence of solutions to the periodic BVPs for second-order IDEs in [
5]. Ref. [
6] was concerned with multiple non-negative solutions to periodic BVPs for second-order IDEs. Additionally, refs. [
7,
8,
9,
10] researched some BVPs for various types of differential equations, such as fourth-order differential systems with parameters, nonlinear fourth-order differential equations,
-Caputo fractional differential equations and fractional (p, q)-difference equations, respectively.
As we know, continuity is a clear limitation to its applicability in degree theory. The existence of BVP solutions is usually established by transformation into fixed-point problems of integral operators. However, there many differential equations are discontinuous in many fields, such as mechanical engineering, mechanics, automatic control, neural network, biology and so on. As the corresponding operators are not continuous, most discontinuous differential equations, see [
11,
12], fall outside that scope. To overcome this problem, R. Figueroa et al. define a new topological degree for discontinuous operators and derived some fixed-point theorems for these operators in [
13], such as discontinuous operators’ Schauder and Krasnoselskii fixed point theorem.
Moreover, R. Figueroa and G. Infante in [
14] considered a class of BVPs of second-order discontinuous differential equation using Schauder fixed point theorem. In [
15], J. R. Lopez studied a class of discontinuous one-dimensional beam equations involving BVP. By using Krasnoselskii’s fixed point theorem on cones, the existence of non-negative solutions is obtained. However, there are few studies on multiple solutions for integral BVPs of second-order discontinuous differential equations with impulse effects. The purpose of the present paper is to fill this gap.
This paper is strongly motivated by the above discussions. It studies multiple solutions for the following BVP:
where
,
a.e. on
,
and
,
.
is an impulsive function,
. And
,
denotes the jump of
and
at
, respectively. This paper has the following features. Firstly, compared with [
16,
17], BVP (
1) is a second-order discontinuous differential equation with impulse effects. The nonlinear term
f here is discontinuous over countable curve families. Secondly, the integral boundary value conditions we consider are more extensive. Thirdly, the method adopted in this paper has some advantages compared to some of the reference methods listed above. The tool used here is multivalued analysis. A special cone is constructed by studying the properties of Green’s function. Therefore, the existence of positive solutions can be established by Krasnoselskii’s fixed point theorem for discontinuous operators.
The remainder of this paper is organized as follows.
Section 2 gives some basic definitions and some preliminary results. The existence results are given and proved in
Section 3. Finally,
Section 4 indicate an example to illustrate the main results.
2. Preliminaries
In this section, we first present some preliminary facts.
They are Banach spaces with the norm
and
respectively.
For convenience, we denote and
Lemma 1. Suppose that . Then, for , the following boundary value problemhas a positive solutionwhereand Proof. First, by integrating both sides of Equation (
2), we have
where
Then,
From Equation (
2), we know
and
From (
4), (
6) and (
7), one can easily see that
and
Therefore, for
, (8) and (9) imply that
Now, by (
10) and (
3), for
, we obtain
Hence,
and
which together with (6) implies that
Similar to the above process, by substituting (
10) into (
3), for
, one can obtain that
□
Assume that the following condition is satisfied throughout this paper:
Hypothesis 1 (H1). .
Lemma 2. The functions and have the following properties:
(1) for all
(2) for all ;
(3) for all , whereand , . Proof. First, it is obvious that
,
for all
. For a given
,
is increasing with
t for
. Then,
Now, we are in a position to prove (3).
Firstly, for
, one can easily obtain that
Secondly, for
, we get
Therefore, for all . □
Lemma 3 ([
18]).
The set is relatively compact if, and only if,(1) F is bounded, that is, for each and some ;
(2) F is quasi-equicontinuous in . That is to say, for any , there exists such that, if and , we have .
In the following, let be a Banach space. is a nonempty open subset of . is an operator which is not necessarily continuous.
Definition 1 ([
19]).
The closed-convex Krasovskij envelope (cc-envelope) of an operator is the multivalued mapping given by where denotes the closed ball centered at x and radius ε, and means closed convex hull. Lemma 4 ([
13,
19]).
if, for every and every , there exist and a finite family of vectors and coefficients , such that and Next, we introduce Krasnoselskii’s fixed-point theorems for discontinuous operators on cones. Denote for .
Lemma 5 ([
13]).
Let , be relatively open subsets of . is a mapping such that is relatively compact and it fulfills condition in .(a) If for all with and all , then .
(b) If there exists with such that for every and all with then .
Lemma 6 ([
13]).
Condition (a) in Lemma 5 is satisfied if one of the following two conditions holds:(i) ![Symmetry 14 01549 i001 Symmetry 14 01549 i001]() for all with and .
for all with and . (ii) for all and all with .
Analogously, assumption (b) in Lemma 5 holds if one of the following two conditions holds:
(i) ![Symmetry 14 01549 i002 Symmetry 14 01549 i002]() for all with and .
for all with and . (ii) If for all and all with .
Now, we define the admissible discontinuities curves where we allow the nonlinearities f to be discontinuous.
Definition 2. We say that , is an admissible discontinuity curve for the differential system (1) if γ satisfies the boundary value conditions of (1), , and one of the following conditions holds: (ii) there exist , a.e. for , , , , and such that (iii) there exist such that (iv) there exist , a.e. for , , , and , , such that If (i) holds, then we say that γ is viable for the BVP (1); if one of (ii)-(iv) holds, we say that γ is inviable. 3. Existence Results
Let , and
Then,
is a real Banach space and
P is a cone on
E. We can recall that
is a BVP solution (
1) if (and only if )
u is a solution of the following integral equation:
Define operator
as follows:
For any , by , the continuity of and the assumption of f, is well-defined. Next, we will find the positive fixed point of T in the following work.
Now, let us list the following assumptions.
Hypothesis 2 (H2). is such that:
(a) For any , the mapping is measurable;
(b) For each there exists , such that for a.e. and all .
Hypothesis 3 (H3). g is measurable and a.e. for .
Hypothesis 4 (H4). There are admissible discontinuity curves , such that the function is continuous in for .
Hypothesis 5 (H5).
; .
Hypothesis 6 (H6).
; .
Hypothesis 7 (H7).
.
Hypothesis 8 (H8).
.
Lemma 7. The operator is well-defined and maps bounded sets into relatively compact sets.
Proof of Lemma 7. First, we shall show that
is well-defined. It is obvious that
From the expression of
T, we have
and
Next, we are in the position to prove that T maps bounded sets into relatively compact sets by Lemma 3. Indeed, it is enough to show that, from each , is a relatively compact set, where .
In fact, from
, there exists
such that
for
(
). By (H2),
is bounded. Moreover, for a.e.
and any
, we have
which implies that
where
with
. Hence,
T is quasi-equicontinuous. □
Lemma 8. Assume that (H4) is valid and let be the cc-envelope of an operator . Then, Proof of Lemma 8. Fix and let .
Case 1: for all .
Using (H4), we obtain
for a.e.
if
in
. From (H2) and (H3), it is easy to see that
converges to
in
. Hence,
T is continuous at
x. By Proposition 2.2 in [
19], we have
.
Case 2: There exists such that is inviable and . Let . Case 2 will be divided into three subcases to prove.
Case 2.1: The above
satisfies (ii) in Definition 2. Then, there exist
,
,
, and
such that
(I) for all .
We will prove that if , then By , for a.e. , we have , which implies Therefore, for a.e.
Next, we will prove that a.e. in , which shows if .
Since
, for each
, by Lemma 4 with
, we can find functions
and coefficients
such that
and
Let
We have that
uniformly when
in
J and
for all
,
.
Moreover,
is continuous at
for a.e.
. Hence, there is some
such that
for any
, where
,
. Therefore,
Hence,
for a.e.
. Then, by Corollary 3.10 in [
19], we have
for a.e.
(II) There exists such that .
Without loss of generality, suppose . In this case, we will show that .
First, by (H2), for a.e.
, there exists
such that
. Set
and
. Then there exists at least one interval
such that
. Let
. Noticing that
, by Lemma 3.8 in [
19], there is a measurable set
with
such that, for all
, we have
Moreover, by Corollary 3.9 in [
19], there exists
with
such that, for all
, we have
Fix a point
. From (
20) and (
21); the following inequalities are satisfied:
where
and
and
sufficiently close to
.
Now we prove that .
Claim: There exists
, for every finite family
and
with
such that
Let
and
be as in the claim and denote
. Then, for a.e.
, one can get
Moreover, for every
and
, we have
and
Hence, , if
By replacing with , and a similar calculation, one can obtain that if .
Case 2.2: The above
satisfies (iii) in Definition 2. Then, there exists
such that
From the continuity of , we suppose that there exist such that .
(I) or .
From (
29), we have
for
. Without loss of generality, similar to the proof process of (I) in Case 2.1, one can obtain that
or
if
. Hence,
for all
(II) and . In this case, we will show that .
Claim: Let
and
, for every finite family
and
with
, we have
Let
and
be as in the claim and denote
. In view of
, one can see that
which implies that
The claim is proven.
Case 2.3: The above
satisfies (iv) in Definition 2. By a similar process to that proving Case 2.1 and Case 2.2, one can also obtain that
Case 3: for such that is viable.
Let . We will show that, in this case, implies .
For each
and a.e.
,
Hence, a.e. in Now, by process of proving (I) in Case 2.1, one can obtain that a.e. in if . Hence, . □
Theorem 1. Assume that (H1)–(H6) hold. Then, BVP (1) admits at least one positive solution. Proof of Theorem 1. We need only to prove T has at least one positive fixed point in .
Claim 1: There exists
, such that
![Symmetry 14 01549 i002 Symmetry 14 01549 i002]()
for all
and all
with
.
(H5) implies that
and
, such that
Supposing that
with
, for every finite family
and
, with
, and
, we have
Hence,
![Symmetry 14 01549 i002 Symmetry 14 01549 i002]()
for all
with
and
. And by Lemma 6, one can obtain that
Claim 2: There exists such that for all and all with .
(H6) implies that there exists
such that
Choosing
, for
, one can see that
Supposing that
with
, then, for every finite family
and
, with
, and
we have
Therefore, if
, then this is the limit of a sequence of functions
v as above, so
, for all
and all
with
. Using Lemma 6, we get
Together with (
31), we have
In sum, BVP (
1) admits at least one positive solution. □
Theorem 2. Under the assumptions (H1)–(H4), (H7) and (H8), suppose
Hypothesis 9 (H9): There exist such that and , where Then, BVP (1) admits at least two positive solutions. Proof of Theorem 2. We only need to prove that T has at least two positive fixed points in and respectively.
First, by (H7), there exist
and
such that
We claim that for
In fact, suppose that there exist
,
such that
for some
i.e.,
Taking the supremum for
,
which is a contradiction.
Now, given , we can similarly prove that for any and with . Hence,
Second, the assumption (H8) implies that there exist
,
such that
Choosing
, for any
, one can obtain that
We claim that, for all
and
,
where
In fact, that there exist
,
such that
for some
This, together with the definition of
, guarantees that
which is a contradiction because
.
Given , we prove similarly that for any and with . Therefore,
Now, we can see that
. By Lemma 5, one can obtain that
and
. Hence,
Third, by (H9), there exist and such that and .
Similar to the process above, we have
Together with (
37), BVP (
1) admits at least two positive solutions in
and
, respectively. □
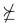 for all with and .
for all with and .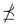 for all with and .
for all with and .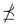 for all and all with .
for all and all with .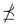 for all with and . And by Lemma 6, one can obtain that
for all with and . And by Lemma 6, one can obtain that





