Data-Driven Model Predictive Control for Wave Energy Converters Using Gaussian Process
Abstract
:1. Introduction
- A novel data-driven WEC model using machine learning techniques and targeting the control perspective is proposed, promising to advance state-of-the-art WEC modelling. The PAWEC system dynamics are learned by the Gaussian Process model, which aims to capture the nonlinear system characteristics with mean value and uncertainties.
- Developing a new data-driven MPC scheme based on the GP model for efficient and real-time implementation in the actual operation of WEC. The cross-entropy technique is introduced to deal with the trajectory optimization for fast, sample-efficient and high performance.
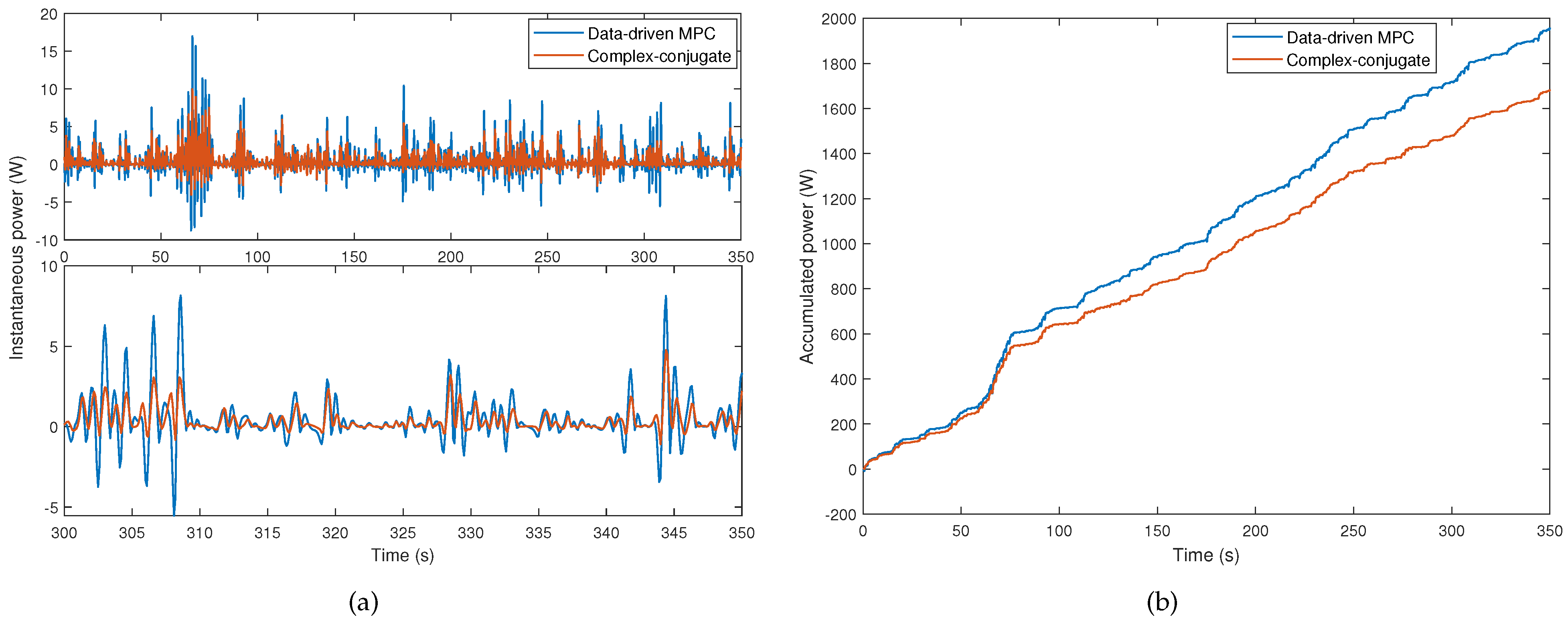
- The investigation of the performance of the data-driven MPC compared with the classical complex-conjugate controller is expected to fill the gap in the literature.
- The developed GP-based MPC scheme is validated in a small-sized and single-type WEC in this study, which can generally be applied to any WECs across different deployment prototypes (e.g., sizes, shapes) and other energy-maximizing control problems.
2. Classical WaveStar PAWEC Modelling and Gaussian Process Regression
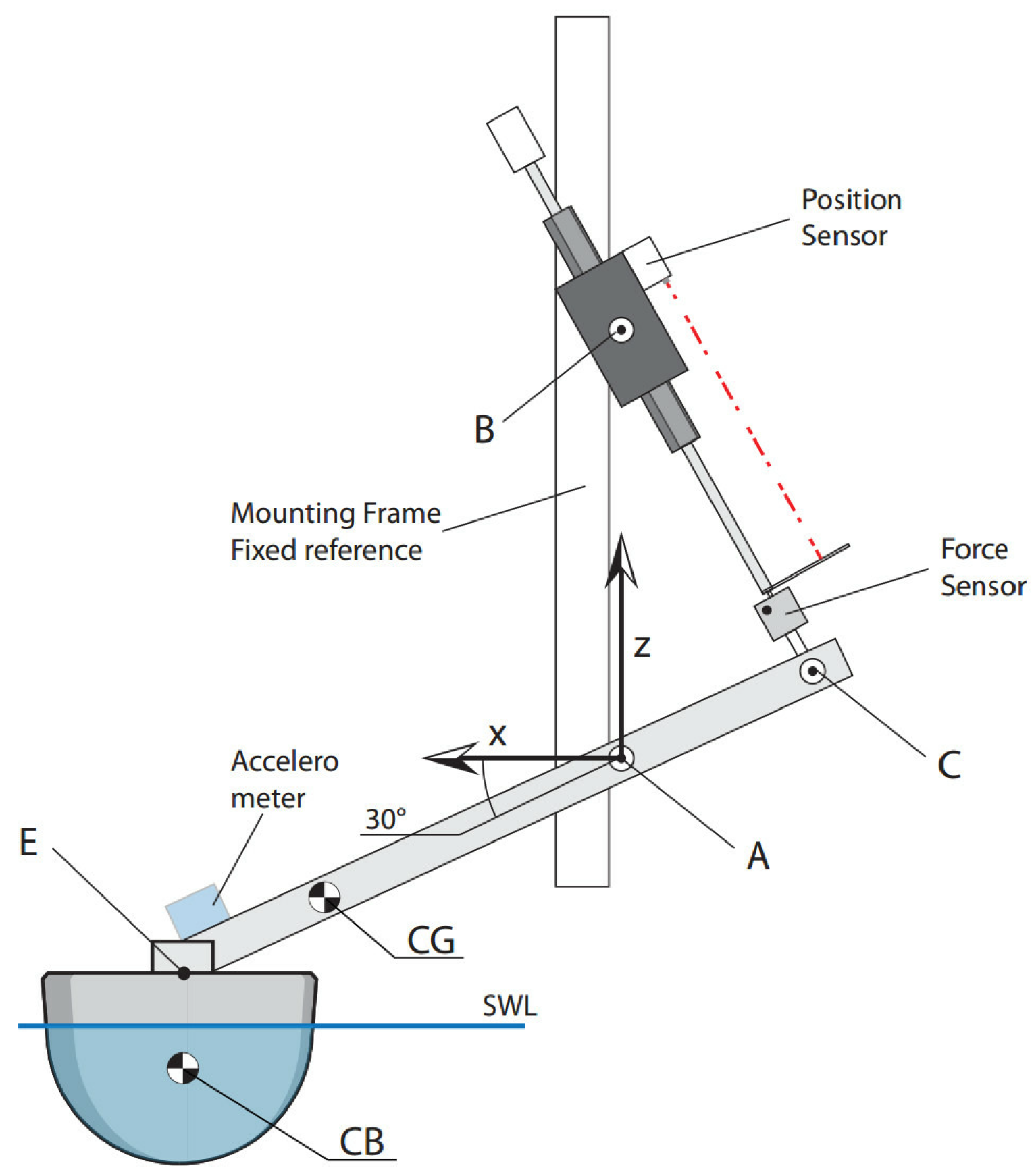
2.1. Classical WaveStar PAWEC Modelling
2.2. Gaussian-Process-Based Modeling Method
3. Control for Optimal Power Extraction from WEC
3.1. Complex-Conjugate Control
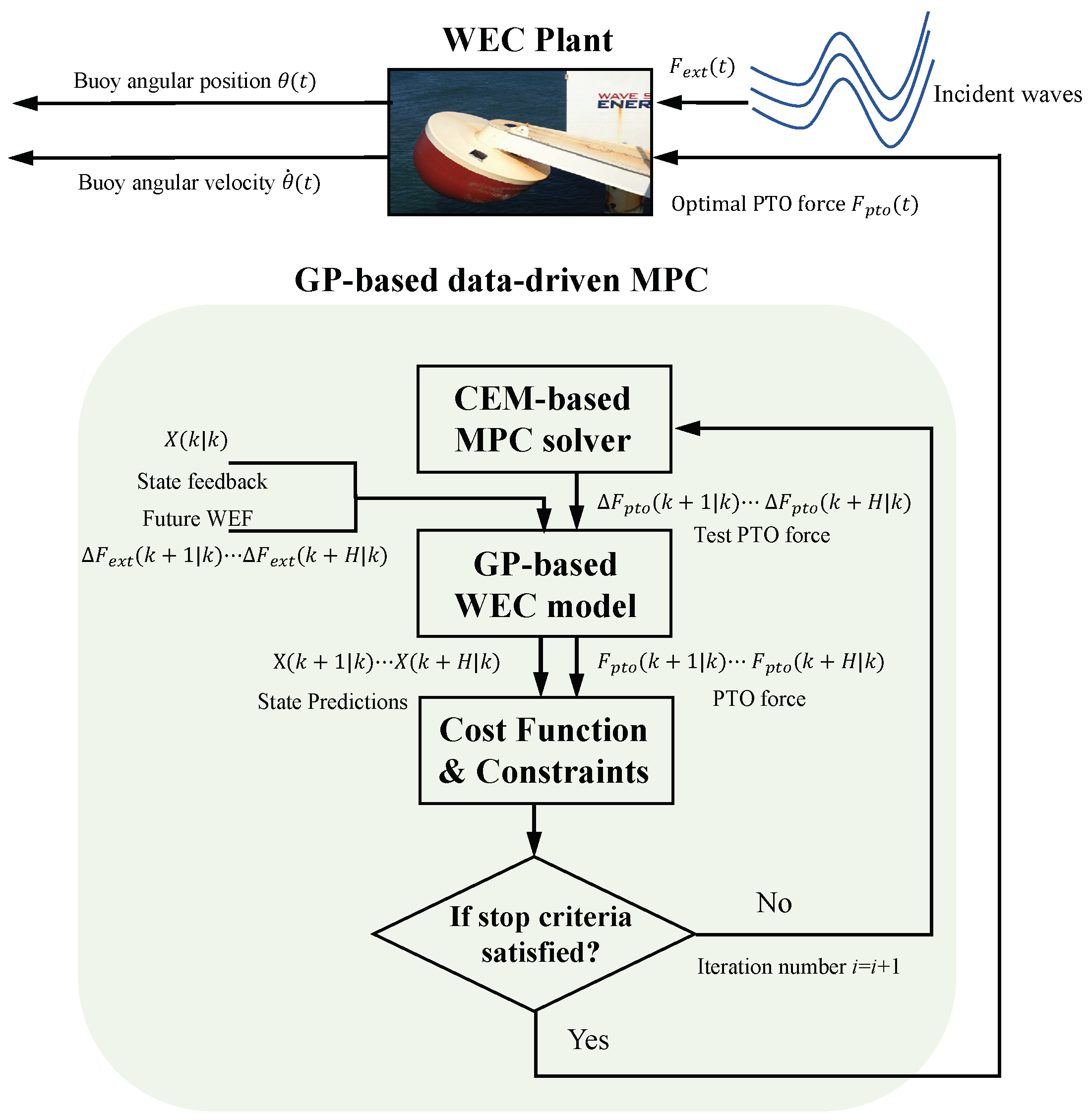
3.2. Data-Driven MPC Design with Cross-Entropy Optimization
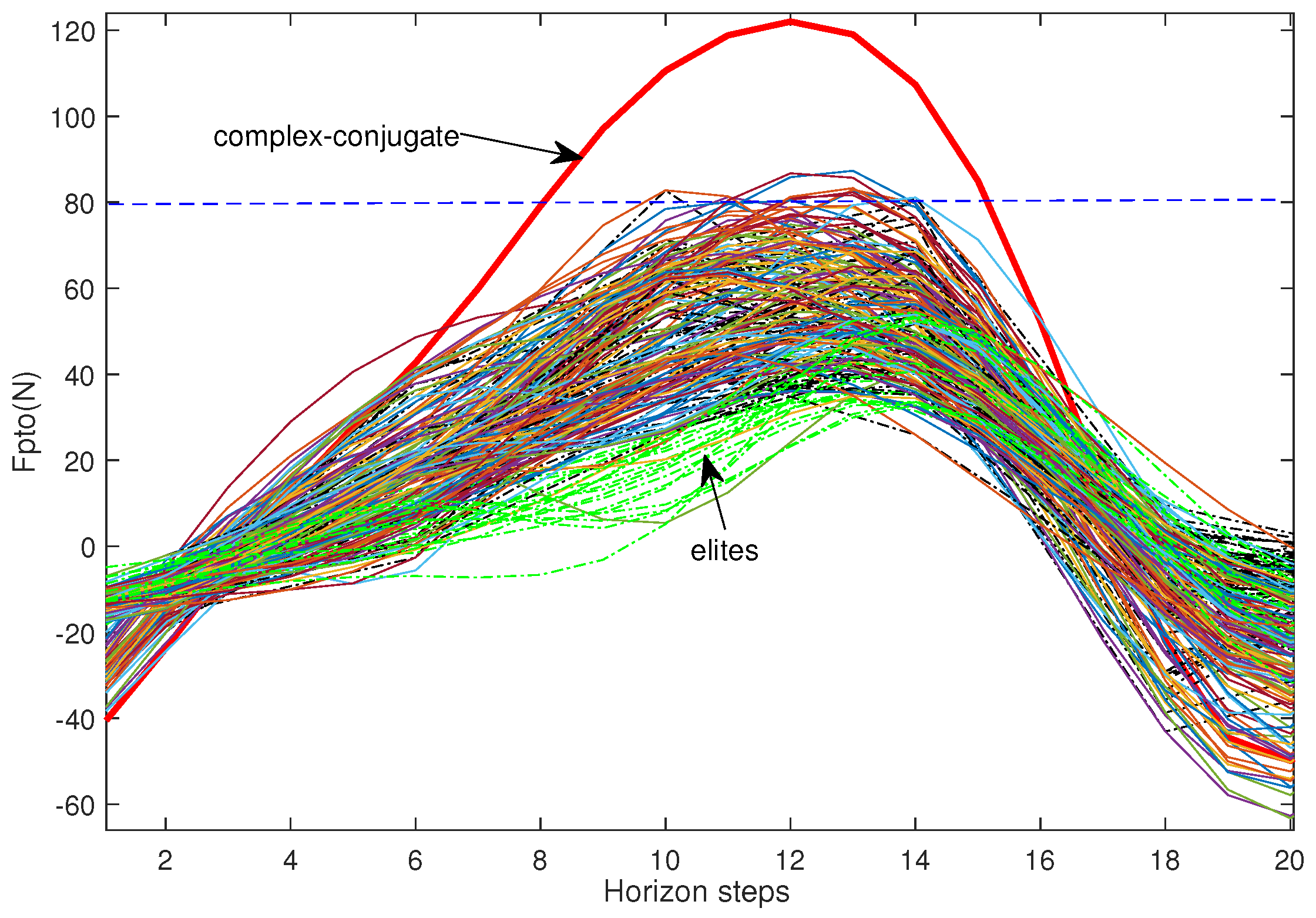
3.2.1. Cross-Entropy Optimization
| Algorithm 1: The CEM optimization algorithm. |
 |
3.2.2. Data-Driven MPC Formulation
4. Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020; Volume 8. [Google Scholar]
- Nolan, G.; Ringwood, J.; Butler, S.; Leithead, W. Optimal damping profiles for a heaving buoy wave energy converter. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, OnePetro, Seoul, Korea, 19–24 June 2005. [Google Scholar]
- Fusco, F.; Ringwood, J. Suboptimal causal reactive control of wave energy converters using a second order system model. In Proceedings of the 21st (2011) International Offshore and Polar Engineering Conference—International Society of Offshore and Polar Engineers (ISOPE), Maui, HI, USA, 19–24 June 2011; pp. 687–694. [Google Scholar]
- Babarit, A.; Clément, A.H. Optimal latching control of a wave energy device in regular and irregular waves. Appl. Ocean. Res. 2006, 28, 77–91. [Google Scholar] [CrossRef]
- Babarit, A.; Guglielmi, M.; Clément, A.H. Declutching control of a wave energy converter. Ocean. Eng. 2009, 36, 1015–1024. [Google Scholar] [CrossRef] [Green Version]
- Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-maximizing control of wave-energy converters: The development of control system technology to optimize their operation. IEEE Control. Syst. Mag. 2014, 34, 30–55. [Google Scholar]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control. 2017, 1, 37–56. [Google Scholar] [CrossRef] [Green Version]
- Cummins, W. The Impulse Response Function and Ship Motions; Technical Report; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Davidson, J.; Genest, R.; Ringwood, J. Adaptive control of a wave energy converter simulated in a numerical wave tank. In Proceedings of the 12th European Wave and Tidal Energy Conference, European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; number 747. pp. 1–10. [Google Scholar]
- O’Sullivan, A.C.; Lightbody, G. Co-design of a wave energy converter using constrained predictive control. Renew. Energy 2017, 102, 142–156. [Google Scholar] [CrossRef]
- Li, G. Nonlinear model predictive control of a wave energy converter based on differential flatness parameterisation. Int. J. Control. 2017, 90, 68–77. [Google Scholar] [CrossRef]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K. Nonlinear model predictive control of a point absorber wave energy converter. IEEE Trans. Sustain. Energy 2012, 4, 118–126. [Google Scholar] [CrossRef]
- Ma, Y. Machine Learning in Ocean Applications: Wave Prediction for Advanced Controls of Renewable Energy and Modeling Nonlinear Viscous Hydrodynamics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2020. [Google Scholar]
- Li, L.; Yuan, Z.; Gao, Y. Maximization of energy absorption for a wave energy converter using the deep machine learning. Energy 2018, 165, 340–349. [Google Scholar] [CrossRef] [Green Version]
- Zou, S.; Zhou, X.; Khan, I.; Weaver, W.W.; Rahman, S. Optimization of the electricity generation of a wave energy converter using deep reinforcement learning. Ocean. Eng. 2022, 244, 110363. [Google Scholar] [CrossRef]
- Gioia, D.G.; Pasta, E.; Brandimarte, P.; Mattiazzo, G. Data-driven control of a Pendulum Wave Energy Converter: A Gaussian Process Regression approach. Ocean. Eng. 2022, 253, 111191. [Google Scholar] [CrossRef]
- Shi, S.; Patton, R.J.; Liu, Y. Robust Data-driven Estimation of Wave Excitation Force for Wave Energy Converters. IFAC-PapersOnLine 2020, 53, 12346–12351. [Google Scholar] [CrossRef]
- Sarkar, D.; Contal, E.; Vayatis, N.; Dias, F. Prediction and optimization of wave energy converter arrays using a machine learning approach. Renew. Energy 2016, 97, 504–517. [Google Scholar] [CrossRef]
- Anderlini, E.; Husain, S.; Parker, G.G.; Abusara, M.; Thomas, G. Towards real-time reinforcement learning control of a wave energy converter. J. Mar. Sci. Eng. 2020, 8, 845. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006; Volume 38, pp. 715–719. [Google Scholar]
- Ko, J.; Fox, D. GP-BayesFilters: Bayesian filtering using Gaussian process prediction and observation models. Auton. Robot. 2009, 27, 75–90. [Google Scholar] [CrossRef] [Green Version]
- Ringwood, J.; Ferri, F.; Ruehl, K.; Yu, Y.H.; Coe, R.; Bacelli, G.; Weber, J.; Kramer, M.M. A competition for WEC control systems. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Jakobsen, M.M.; Kramer, M. RANS-VOF modelling of the wavestar point absorber. Renew. Energy 2017, 109, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Tona, P.; Sabiron, G.; Nguyen, H.N. An energy-maximising MPC solution to the WEC control competition. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; Volume 58899, p. V010T09A034. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Comparing nonlinear hydrodynamic forces in heaving point absorbers and oscillating wave surge converters. J. Ocean. Eng. Mar. Energy 2018, 4, 25–35. [Google Scholar] [CrossRef]
- Wilson, A.; Adams, R. Gaussian process kernels for pattern discovery and extrapolation. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1067–1075. [Google Scholar]
- Coe, R.G.; Bacelli, G.; Cho, H.; Nevarez, V. A Comparative Study on Wave Prediction for WECs; Technical Report; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2018.
- Wilson, D.G.; Robinett, R.D.; Bacelli, G.; Abdelkhalik, O.; Coe, R.G. Extending Complex Conjugate Control to Nonlinear Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 84. [Google Scholar] [CrossRef] [Green Version]
- Price, A.A. New Perspectives on Wave Energy Converter Control. Ph.D Thesis, University of Edinburgh, Edinburgh, UK, 2009. [Google Scholar]
- Guo, B.; Patton, R.J.; Jin, S.; Lan, J. Numerical and experimental studies of excitation force approximation for wave energy conversion. Renew. Energy 2018, 125, 877–889. [Google Scholar] [CrossRef]
- Rubinstein, R. The cross-entropy method for combinatorial and continuous optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Bharadhwaj, H.; Xie, K.; Shkurti, F. Model-predictive control via cross-entropy and gradient-based optimization. In Proceedings of the Learning for Dynamics and Control, PMLR, Zurich, Switzerland, 7–8 June 2020; pp. 277–286. [Google Scholar]
- Pinneri, C.; Sawant, S.; Blaes, S.; Achterhold, J.; Stueckler, J.; Rolinek, M.; Martius, G. Sample-efficient cross-entropy method for real-time planning. arXiv 2020, arXiv:2008.06389. [Google Scholar]
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Shi, S.; Patton, R.J.; Abdelrahman, M.; Liu, Y. Learning a predictionless resonating controller for wave energy converters. In Proceedings of the 38th International Conference on Ocean, Offshore and Arctic Engineering ASME OMAE, Glasgow, UK, 9–14 June 2019. [Google Scholar]


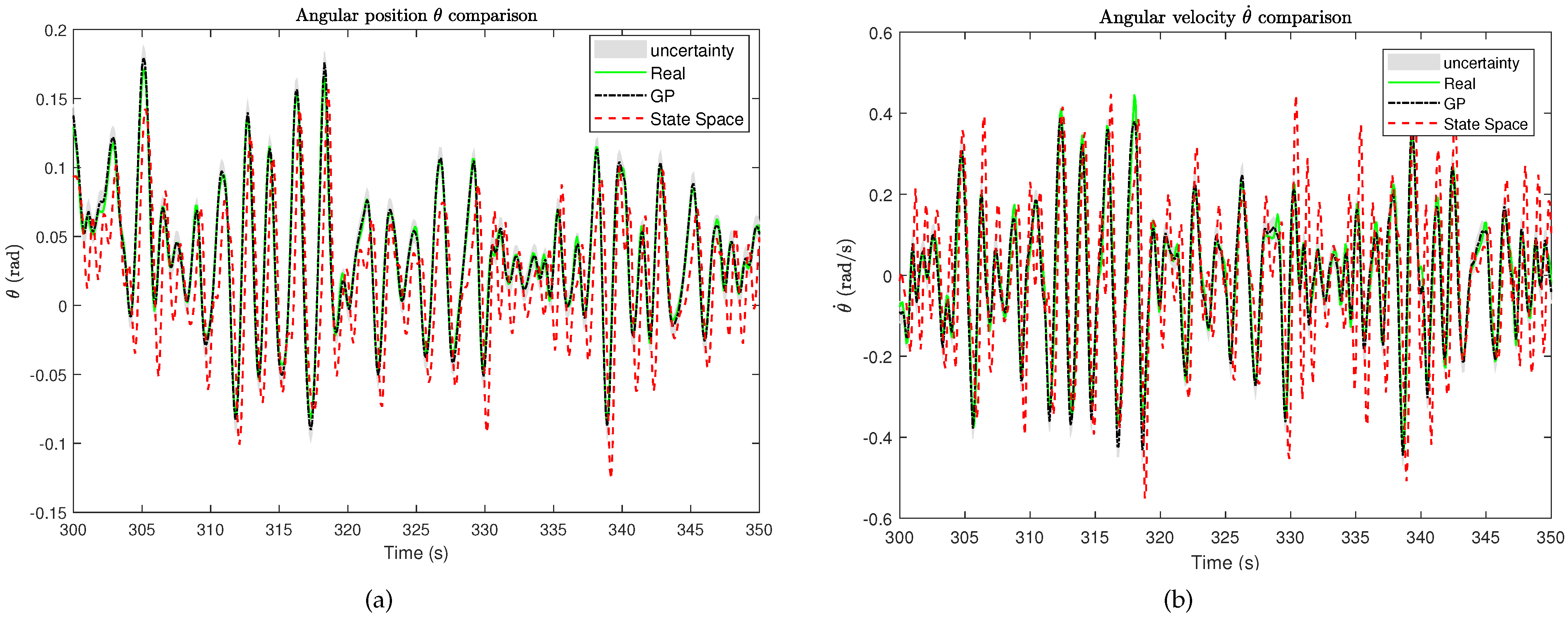



| Comparison Items | GP Regression Model | State-Space Model |
|---|---|---|
| NMSE of angular position () | 0.2971 | 0.9951 |
| NMSE of angular velocity () | 0.3609 | 0.9607 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Shi, S.; Zhang, Z.; Di, Z.; Babayomi, O. Data-Driven Model Predictive Control for Wave Energy Converters Using Gaussian Process. Symmetry 2022, 14, 1284. https://doi.org/10.3390/sym14071284
Liu Y, Shi S, Zhang Z, Di Z, Babayomi O. Data-Driven Model Predictive Control for Wave Energy Converters Using Gaussian Process. Symmetry. 2022; 14(7):1284. https://doi.org/10.3390/sym14071284
Chicago/Turabian StyleLiu, Yanhua, Shuo Shi, Zhenbin Zhang, Zhenfeng Di, and Oluleke Babayomi. 2022. "Data-Driven Model Predictive Control for Wave Energy Converters Using Gaussian Process" Symmetry 14, no. 7: 1284. https://doi.org/10.3390/sym14071284
APA StyleLiu, Y., Shi, S., Zhang, Z., Di, Z., & Babayomi, O. (2022). Data-Driven Model Predictive Control for Wave Energy Converters Using Gaussian Process. Symmetry, 14(7), 1284. https://doi.org/10.3390/sym14071284





