Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling
Abstract
:1. Introduction
- We formally formulate and decompose the problem into three parts, and design an efficient greedy dealing dispatching rules (GDDR) heuristic of which the time complexity is .
- On the basis of GDDR, we firstly design a cooperative co-evolutionary genetic programming (GDDR-CCGP) to characterize different decision points of the problem with three sub-populations, and generate dispatching rules for each decision point while simultaneously exploring the synergistic relationship between dispatching rules by adopting the proposed two-trial evaluation scheme.
- Numerical results demonstrate that the proposed GDDR-CCGP algorithm significantly outperforms the state-of-the-art meta-heuristic algorithms in terms of both solution quality and efficiency.
- We also discuss the importance of three decision points of the two-stage hybrid flow shop scheduling problem, which provides new insights for the design of dispatching rules.
2. Literature Review
3. Problem Description
4. Heuristic Design
4.1. Problem Decomposition
4.2. Greedy Dealing Dispatching Rules Heuristic
| Greedy Dealing Dispatching Rules (GDDR) |
| Step 0. Input three dispatching rules (BFDR, BSDR and JSDR) for each decision point; set job family index . Step 1. For job family k, sort jobs in the non-decreasing order of processing time on the discrete machine , i.e., . Denote this job sequence as and initialize empty batches. Set job index and batch index , where and . Step 2. Greedily try to assign the ith job of to each of , batches that still have space remain, and calculate a priority for each possible batch assignment by applying BFDR; Step 3. Assign the ith job of to the batch with the highest priority, break ties arbitrarily. If , set and go to Step 2; otherwise, go to Step 4. Step 4. If , set and go to Step 1; otherwise, go to Step 5; Step 5. Whenever the batch processor is idle, calculate priorities for all batches queueing in front of the batch processor by applying BSDR; Step 6. Select the batch with the highest priority to process on the batch processor and remove this batch from the queue. Step 7. Whenever the discrete processor is idle, calculate priorities for all queueing jobs in the buffer by applying JSDR. Step 8. Select the job with the highest priority to process on the discrete processor and remove this job from the buffer. Step 9. Repeat Steps 5–8 until all jobs are finished |
5. Genetic Programming-Based Hyper-Heuristic
5.1. Genetic Programming
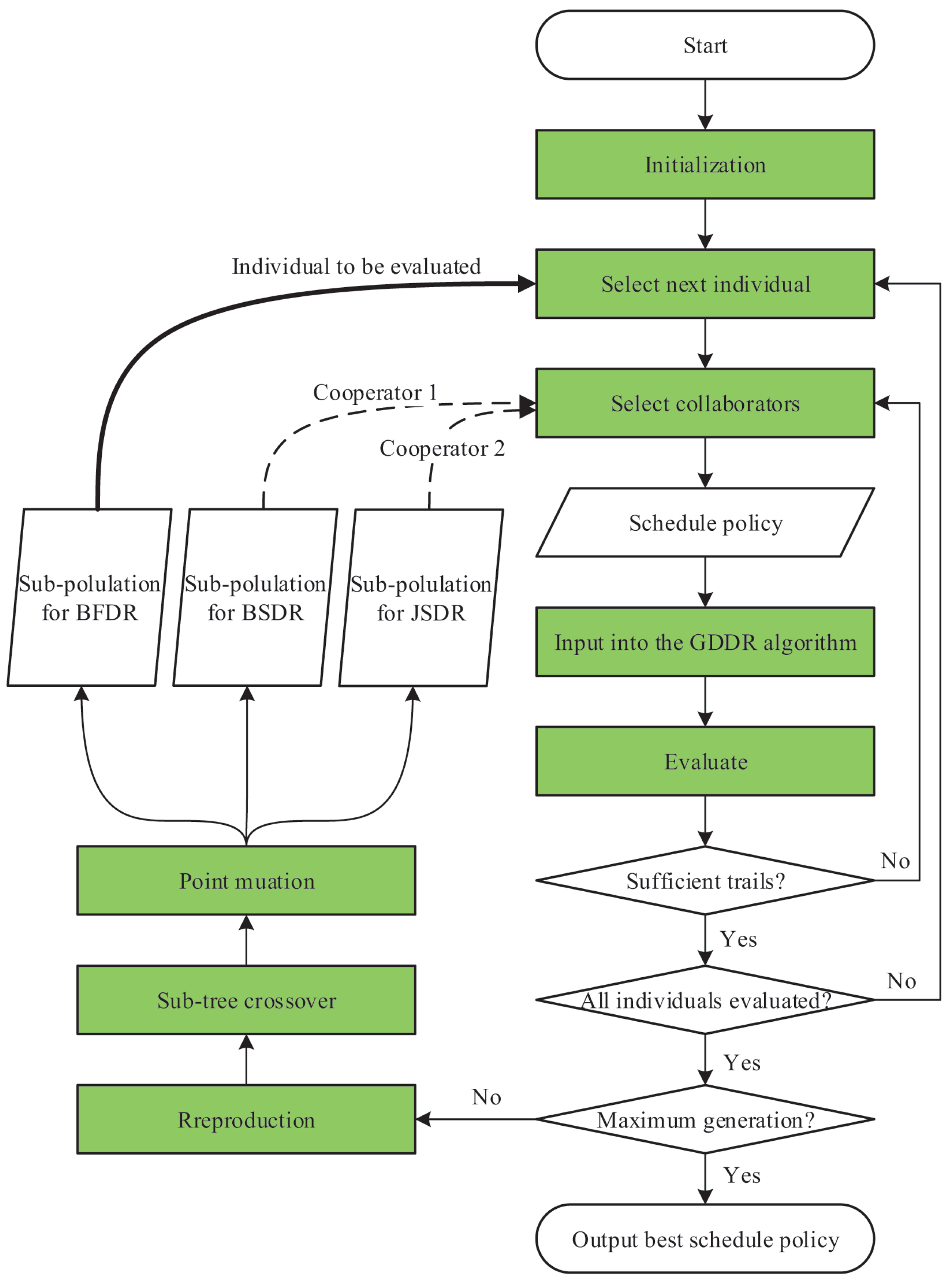
5.2. GDDR-CCGP Algorithm
| Algorithm 1: GDDR-CCGP |
 |
5.3. Fitness Evaluation
| Algorithm 2: eval(s, T) |
 |
6. Computational Experiments
6.1. Terminal Sets and Parameter Settings
6.2. Problem Instances Generation
- job processing time of job i: ;
- batch processing time of job family k: ;
- total number of jobs in job family k: , and .
- : , , , ;
- : , , , ;
- : , , , .
6.3. Comparison Results
- Obj:
- the objective value reached by applying an algorithm on an instance;
- Hh:
- any algorithm h;
- LB:
- the composite lower bound developed by [3];
- Dif:
- the difference in percentage between an algorithm and the lower bound;
- indicates outperforms .
- T1 ( and ), ;
- T2 ( and ), ;
- T3 ( and ), .
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Notations
| n | total number of jobs; |
| m | total number of incompatible job families; |
| b | batch capacity; |
| h | the maximum number of batches the buffer can hold; |
| F | incompatible job families set, where ; |
| total number of jobs in family k, where ; | |
| set of jobs belonging to family k, , ; | |
| number of batches in family k, i.e., , where ; | |
| processing time on the batch processor for family k, where ; | |
| processing time on the discrete processor for job i, where ; | |
| N | job set, where ; |
| B | the batch set, where and ; |
| a sufficient small positive number; | |
| a sufficient large positive number, where . |
Variables
| if job i is assigned to batch l, and 0 otherwise; | |
| if batch l consists of the jobs in job family k, and otherwise, ; | |
| if the position of job i in the process sequence of the discrete processor is less than or | |
| equal to , and otherwise, , for all , let ; | |
| if job i is processed before job j on the discrete processor, and otherwise, ; | |
| the processing time of batch l; | |
| the release time of batch l on the batch processor; | |
| the completion time of job i. |
References
- Mathirajan, M.; Sivakumar, A.I. A literature review, classification and simple meta-analysis on scheduling of batch processors in semiconductor. Int. J. Adv. Manuf. Technol. 2006, 29, 990–1001. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. In Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar]
- Zhang, C.; Shi, Z.; Huang, Z.; Wu, Y.; Shi, L. Flow shop scheduling with a batch processor and limited buffer. Int. J. Prod. Res. 2017, 55, 3217–3233. [Google Scholar] [CrossRef]
- Ahmadi, J.H.; Ahmadi, R.H.; Dasu, S.; Tang, C.S. Batching and scheduling jobs on batch and discrete processors. Oper. Res. 1992, 40, 750–763. [Google Scholar] [CrossRef]
- Branke, J.; Nguyen, S.; Pickardt, C.W.; Zhang, M. Automated design of production scheduling heuristics: A review. IEEE Trans. Evol. Comput. 2015, 20, 110–124. [Google Scholar] [CrossRef] [Green Version]
- Su, L.H.; Yang, D.L.; Chou, H.K. A two-stage flowshop scheduling with limited buffer storage. Asia-Pac. J. Oper. Res. 2009, 26, 503–522. [Google Scholar] [CrossRef]
- Fu, Q.; Sivakumar, A.I.; Li, K. Optimisation of flow-shop scheduling with batch processor and limited buffer. Int. J. Prod. Res. 2012, 50, 2267–2285. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, Z.; Shi, L. Two-stage flow shop with a batch processor and limited buffer. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; pp. 395–400. [Google Scholar]
- Mauluddin, Y. Three-stage flow-shop scheduling model with batch processing machine and discrete processing machine. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 197, p. 14002. [Google Scholar]
- Ross, H.L.F.P.; Corne, D. A promising hybrid GA/heuristic approach for open-shop scheduling problems. In Proceedings of the 11th European Conference on Artificial Intelligence, Amsterdam, The Netherlands, 8–12 August 1994; pp. 590–594. [Google Scholar]
- Rodríguez, J.V.; Petrovic, S.; Salhi, A. A combined meta-heuristic with hyper-heuristic approach to the scheduling of the hybrid flow shop with sequence dependent setup times and uniform machines. In Proceedings of the 3rd Multidisciplinary International Conference on Scheduling: Theory and Applications, MISTA, Paris, France, 28–31 August 2007; pp. 506–513. [Google Scholar]
- Burke, E.K.; McCollum, B.; Meisels, A.; Petrovic, S.; Qu, R. A graph-based hyper-heuristic for educational timetabling problems. Eur. J. Oper. Res. 2007, 176, 177–192. [Google Scholar] [CrossRef] [Green Version]
- Sim, K.; Hart, E.; Paechter, B. A hyper-heuristic classifier for one dimensional bin packing problems: Improving classification accuracy by attribute evolution. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Taormina, Italy, 1–5 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 348–357. [Google Scholar]
- Runka, A. Evolving an edge selection formula for ant colony optimization. In Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation, Montreal, QC, USA, 8–12 July 2009; pp. 1075–1082. [Google Scholar]
- Bader-El-Den, M.; Poli, R.; Fatima, S. Evolving timetabling heuristics using a grammar-based genetic programming hyper-heuristic framework. Memetic Comput. 2009, 1, 205–219. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming II: Automatic Discovery of Reusable Subprograms; MIT Press: Cambridge, MA, USA, 1994; Volume 13, p. 32. [Google Scholar]
- Miyashita, K. Job-shop scheduling with genetic programming. In Proceedings of the 2nd Annual Conference on Genetic and Evolutionary Computation, Las Vegas, NV, USA, 10–12 July 2000; pp. 505–512. [Google Scholar]
- Dimopoulos, C.; Zalzala, A.M. Investigating the use of genetic programming for a classic one-machine scheduling problem. Adv. Eng. Softw. 2001, 32, 489–498. [Google Scholar] [CrossRef]
- Geiger, C.D.; Uzsoy, R.; Aytuğ, H. Rapid modeling and discovery of priority dispatching rules: An autonomous learning approach. J. Sched. 2006, 9, 7–34. [Google Scholar] [CrossRef]
- Geiger, C.D.; Uzsoy, R. Learning effective dispatching rules for batch processor scheduling. Int. J. Prod. Res. 2008, 46, 1431–1454. [Google Scholar] [CrossRef]
- Hildebrandt, T.; Goswami, D.; Freitag, M. Large-scale simulation-based optimization of semiconductor dispatching rules. In Proceedings of the Winter Simulation Conference 2014, Savannah, GA, USA, 7–10 December 2014; pp. 2580–2590. [Google Scholar]
- Shi, Z.; Gao, S.; Du, J.; Ma, H.; Shi, L. Automatic design of dispatching rules for real-time optimization of complex production systems. In Proceedings of the 2019 IEEE/SICE International Symposium on System Integration (SII), Paris, France, 14–16 January 2019; pp. 55–60. [Google Scholar]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. Genetic programming for job shop scheduling. In Evolutionary and Swarm Intelligence Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 143–167. [Google Scholar]
- Park, J.; Nguyen, S.; Zhang, M.; Johnston, M. Genetic programming for order acceptance and scheduling. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancún, Mexico, 20–23 June 2013; pp. 1005–1012. [Google Scholar]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. Automatic design of scheduling policies for dynamic multi-objective job shop scheduling via cooperative coevolution genetic programming. IEEE Trans. Evol. Comput. 2013, 18, 193–208. [Google Scholar] [CrossRef]
- Yska, D.; Mei, Y.; Zhang, M. Genetic programming hyper-heuristic with cooperative coevolution for dynamic flexible job shop scheduling. In Proceedings of the European Conference on Genetic Programming, Parma, Italy, 4–6 April 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 306–321. [Google Scholar]
- Uzsoy, R. Scheduling batch processing machines with incompatible job families. Int. J. Prod. Res. 1995, 33, 2685–2708. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Ozcan, E.; Woodward, J.R. Exploring hyper-heuristic methodologies with genetic programming. In Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 177–201. [Google Scholar]
- Luke, S. Essentials of Metaheuristics. Lulu. 2011. Available online: http://cs.gmu.edu/sean/book/metaheuristics/ (accessed on 1 October 2021).
- Wieg, R.P.; Liles, W.C.; De Jong, K.A. An empirical analysis of collaboration methods in cooperative coevolutionary algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), San Francisco, CA, USA, 7–11 July 2001; Volume 2611, pp. 1235–1245. [Google Scholar]
- Hunt, R.; Johnston, M.; Zhang, M. Evolving “less-myopic” scheduling rules for dynamic job shop scheduling with genetic programming. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 927–934. [Google Scholar]
- Chang, Y.L.; Sueyoshi, T.; Sullivan, R.S. Ranking dispatching rules by data envelopment analysis in a job shop environment. IIE Trans. 1996, 28, 631–642. [Google Scholar] [CrossRef]




| Notation | Description |
|---|---|
| PT | The processing time of a job on the discrete processor |
| BPT | The processing time of a batch on the batch processor |
| BWL | Work load of a batch, calculated by sum of PTs of all jobs in a batch |
| MinBWL | When a job is assigned to a batch, the minimum BWL of the remaining batches |
| MaxBWL | When a job is assigned to a batch, the maximum BWL of the remaining batches |
| BSR | The number of space units remaining for a batch |
| BBT | The time of batch blocking in the batch processor |
| FPTR | Sum of PTs remaining for a job family |
| PTQB | Sum of PTs queueing in the buffer |
| NJQB | Number of jobs queueing in the buffer |
| ERC | A random constant from to 1 |
| Parameter | Value |
|---|---|
| Terminal set of GP for BFDR | PT, BPT, BWL, MinBWL, MaxBWL, FPTR, BSR, 0, 1 |
| Terminal set of GP for BSDR | BPT, BWL, PTQB, NJQB,0, 1 |
| Terminal set of GP for JSDR | PT, PTQB, NJQB, BBT, ERC |
| Function set | +, −, ×, ÷, Max, IfLT, (Neg) |
| Initialization | Ramped-half-and-half tree builder |
| Population size | 500 |
| Generation | 50 |
| Crossover rate | 95% |
| Mutation rate | 5% |
| Elitism | 20 |
| Max. tree depth | 17 |
| Individual selection | Tournament selection (size 7) |
| Cooperators | 1 elite of last generation, 1 random |
| GDSPT | IDE | RDE | GDDR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n-m-b-h | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) |
| 40-2-5-2 | 6.62 | 22.94 | 0.07 | 6.38 | 22.94 | 1.13 | 6.26 | 22.76 | 0.01 | 4.50 a,b,c | 15.90 |
| 40-2-5-3 | 6.72 | 30.60 | 0.07 | 6.53 | 30.17 | 1.06 | 6.39 | 30.17 | 0.00 | 5.16 a,b,c | 25.31 |
| 40-2-10-2 | 2.08 | 6.07 | 0.04 | 2.08 | 6.07 | 0.04 | 2.08 | 6.07 | 0.00 | 1.59 a,b,c | 5.57 |
| 40-2-10-3 | 1.96 | 7.45 | 0.04 | 1.96 | 7.45 | 0.03 | 1.96 | 7.45 | 0.00 | 1.60 a,b,c | 6.65 |
| 40-4-5-2 | 5.45 | 13.50 | 0.06 | 5.03 | 13.50 | 0.95 | 4.76 | 13.50 | 0.00 | 4.93 a | 16.31 |
| 40-4-5-3 | 4.13 | 17.59 | 0.06 | 3.79 | 15.75 | 0.96 | 3.59 | 15.44 | 0.00 | 4.06 b,c | 13.88 |
| 40-4-10-2 | 1.34 | 5.00 | 0.01 | 1.34 | 5.00 | 0.01 | 1.34 | 5.00 | 0.00 | 1.24 | 5.09 |
| 40-4-10-3 | 1.36 | 6.42 | 0.01 | 1.36 | 6.42 | 0.01 | 1.36 | 6.42 | 0.00 | 1.41 | 8.49 |
| 60-2-5-2 | 7.93 | 31.27 | 0.11 | 7.60 | 29.18 | 2.50 | 7.49 | 28.62 | 0.00 | 5.12 a,b,c | 21.22 |
| 60-2-5-3 | 5.17 | 29.18 | 0.12 | 4.97 | 28.29 | 2.45 | 4.88 | 27.66 | 0.00 | 3.94 a,b,c | 22.32 |
| 60-2-10-2 | 2.11 | 8.94 | 0.09 | 2.05 | 8.19 | 1.11 | 2.02 | 7.85 | 0.00 | 1.67 a,b,c | 4.90 |
| 60-2-10-3 | 2.32 | 7.68 | 0.10 | 2.14 | 7.32 | 1.30 | 2.11 | 7.32 | 0.00 | 1.91 a | 5.29 |
| 60-4-5-2 | 5.70 | 18.92 | 0.11 | 5.32 | 18.21 | 2.93 | 5.10 | 16.81 | 0.00 | 4.12 a,b,c | 11.57 |
| 60-4-5-3 | 6.51 | 23.06 | 0.10 | 6.30 | 22.77 | 2.43 | 6.10 | 22.64 | 0.00 | 5.22 a,b,c | 18.83 |
| 60-4-10-2 | 2.40 | 9.21 | 0.07 | 2.11 | 7.32 | 1.09 | 1.99 | 6.64 | 0.00 | 1.96 a | 5.22 |
| 60-4-10-3 | 2.11 | 6.53 | 0.08 | 1.79 | 6.27 | 1.10 | 1.67 | 6.19 | 0.00 | 1.69 a | 4.70 |
| 80-2-5-2 | 7.19 | 28.80 | 0.19 | 6.93 | 28.51 | 5.26 | 6.77 | 27.30 | 0.00 | 4.35 a,b,c | 19.18 |
| 80-2-5-3 | 6.33 | 21.19 | 0.22 | 6.23 | 21.19 | 4.81 | 6.13 | 20.88 | 0.00 | 4.46 a,b,c | 18.04 |
| 80-2-10-2 | 2.52 | 9.49 | 0.11 | 2.42 | 8.83 | 2.19 | 2.39 | 8.58 | 0.00 | 1.69 a,b,c | 4.52 |
| 80-2-10-3 | 2.07 | 9.06 | 0.12 | 1.94 | 8.89 | 2.18 | 1.91 | 8.89 | 0.00 | 1.50 a,b,c | 4.26 |
| 80-4-5-2 | 6.97 | 22.85 | 0.18 | 6.46 | 21.58 | 5.45 | 6.19 | 20.70 | 0.00 | 4.43 a,b,c | 12.62 |
| 80-4-5-3 | 6.60 | 17.39 | 0.18 | 6.40 | 17.34 | 5.15 | 6.11 | 17.20 | 0.00 | 4.31 a,b,c | 11.02 |
| 80-4-10-2 | 2.12 | 6.99 | 0.13 | 1.84 | 6.58 | 2.28 | 1.70 | 6.43 | 0.00 | 1.66 a | 5.84 |
| 80-4-10-3 | 2.48 | 8.53 | 0.13 | 2.09 | 7.45 | 2.21 | 1.92 | 7.45 | 0.00 | 1.72 a,b,c | 5.34 |
| GDSPT | IDE | RDE | GDDR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n-m-b-h | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) |
| 100-2-10-2 | 2.28 | 9.65 | 0.39 | 2.21 | 9.45 | 4.14 | 2.16 | 9.27 | 0.01 | 1.63 a,b,c | 4.58 |
| 100-2-10-3 | 2.42 | 8.37 | 0.16 | 2.32 | 8.25 | 3.91 | 2.28 | 8.19 | 0.01 | 1.64 a,b,c | 5.04 |
| 100-2-20-2 | 1.07 | 4.13 | 0.12 | 0.97 | 3.37 | 1.93 | 0.95 | 3.25 | 0.00 | 0.75 a,b,c | 2.81 |
| 100-2-20-3 | 1.02 | 3.19 | 0.12 | 0.93 | 3.02 | 1.95 | 0.91 | 3.02 | 0.00 | 0.71 a,b,c | 2.31 |
| 100-4-10-2 | 2.28 | 8.37 | 0.16 | 2.03 | 7.88 | 4.37 | 1.89 | 7.70 | 0.00 | 1.68 a,b,c | 5.67 |
| 100-4-10-3 | 2.91 | 8.32 | 0.16 | 2.63 | 7.17 | 4.29 | 2.46 | 6.91 | 0.00 | 1.97 a,b,c | 4.58 |
| 100-4-20-2 | 0.93 | 2.81 | 0.09 | 0.73 | 2.37 | 1.81 | 0.69 | 2.27 | 0.00 | 0.74 a | 2.65 |
| 100-4-20-3 | 0.82 | 3.75 | 0.08 | 0.65 | 2.09 | 1.79 | 0.58 | 1.83 | 0.00 | 0.65 a | 2.87 |
| 100-10-10-2 | 3.29 | 8.24 | 0.11 | 2.53 | 5.59 | 4.32 | 1.99 | 4.70 | 0.00 | 2.32 a,b | 5.50 |
| 100-10-10-3 | 2.89 | 8.64 | 0.11 | 2.18 | 6.11 | 4.37 | 1.72 | 5.30 | 0.00 | 2.04 a,b | 5.34 |
| 200-2-10-2 | 3.27 | 12.24 | 0.71 | 3.22 | 12.18 | 27.22 | 3.16 | 11.77 | 0.01 | 1.67 a,b,c | 6.87 |
| 200-2-10-3 | 3.05 | 8.62 | 0.69 | 3.03 | 8.59 | 26.08 | 2.98 | 8.53 | 0.01 | 1.67 a,b,c | 4.80 |
| 200-2-20-2 | 1.40 | 3.79 | 0.40 | 1.28 | 3.69 | 12.20 | 1.25 | 3.64 | 0.01 | 0.84 a,b,c | 2.14 |
| 200-2-20-3 | 1.54 | 3.93 | 0.41 | 1.40 | 3.93 | 12.94 | 1.37 | 3.93 | 0.01 | 0.94 a,b,c | 2.30 |
| 200-4-10-2 | 2.71 | 12.44 | 0.69 | 2.61 | 12.25 | 27.42 | 2.47 | 11.91 | 0.00 | 1.65 a,b,c | 6.70 |
| 200-4-10-3 | 3.44 | 9.54 | 0.66 | 3.33 | 9.52 | 28.24 | 3.18 | 9.21 | 0.01 | 1.75 a,b,c | 4.36 |
| 200-4-20-2 | 1.41 | 4.06 | 0.41 | 1.20 | 3.38 | 12.19 | 1.07 | 2.98 | 0.01 | 1.00 a,b | 2.63 |
| 200-4-20-3 | 1.46 | 4.06 | 0.41 | 1.19 | 3.08 | 12.26 | 1.08 | 2.94 | 0.00 | 1.02 a,b | 2.44 |
| 200-10-10-2 | 2.90 | 6.51 | 0.67 | 2.65 | 5.84 | 28.64 | 2.13 | 5.74 | 0.00 | 1.82 a,b,c | 4.34 |
| 200-10-10-3 | 2.93 | 6.98 | 0.66 | 2.69 | 6.90 | 28.88 | 2.14 | 6.55 | 0.01 | 1.85 a,b,c | 5.74 |
| 200-10-20-2 | 1.65 | 4.55 | 0.28 | 1.12 | 2.42 | 13.50 | 0.82 | 2.03 | 0.00 | 1.02 a,b | 2.06 |
| 200-10-20-3 | 1.51 | 3.49 | 0.29 | 1.15 | 3.11 | 12.69 | 0.85 | 2.19 | 0.00 | 1.04 a,b | 2.43 |
| 300-2-10-2 | 3.19 | 13.99 | 1.82 | 3.13 | 13.99 | 83.25 | 3.07 | 13.78 | 0.03 | 1.76 a,b,c | 7.65 |
| 300-2-10-3 | 3.37 | 10.31 | 1.81 | 3.36 | 10.31 | 83.09 | 3.31 | 10.21 | 0.02 | 1.92 a,b,c | 7.25 |
| 300-2-20-2 | 1.29 | 4.92 | 0.99 | 1.24 | 4.84 | 37.36 | 1.22 | 4.65 | 0.02 | 0.71 a,b,c | 2.04 |
| 300-2-20-3 | 1.24 | 4.14 | 1.03 | 1.19 | 4.14 | 36.02 | 1.16 | 4.12 | 0.01 | 0.71 a,b,c | 2.06 |
| 300-4-10-2 | 4.42 | 12.21 | 1.83 | 4.25 | 11.96 | 103.03 | 4.02 | 11.30 | 0.01 | 1.97 a,b,c | 5.43 |
| 300-4-10-3 | 3.29 | 7.54 | 1.81 | 3.26 | 7.54 | 99.55 | 3.09 | 7.47 | 0.02 | 1.65 a,b,c | 3.85 |
| 300-4-20-2 | 1.47 | 4.77 | 1.03 | 1.33 | 4.22 | 41.67 | 1.24 | 4.14 | 0.01 | 0.82 a,b,c | 2.03 |
| 300-4-20-3 | 1.49 | 4.37 | 0.99 | 1.30 | 3.80 | 40.71 | 1.19 | 3.62 | 0.01 | 0.81 a,b,c | 1.97 |
| 300-10-10-2 | 3.10 | 8.15 | 1.80 | 2.97 | 6.83 | 105.32 | 2.43 | 6.40 | 0.01 | 1.61 a,b,c | 4.00 |
| 300-10-10-3 | 3.20 | 9.79 | 1.83 | 3.12 | 8.73 | 97.75 | 2.71 | 7.58 | 0.01 | 1.73 a,b,c | 4.77 |
| 300-10-20-2 | 1.62 | 5.35 | 0.88 | 1.21 | 3.31 | 39.39 | 0.93 | 2.96 | 0.01 | 0.99 a,b | 2.60 |
| 300-10-20-3 | 1.64 | 4.70 | 0.89 | 1.27 | 3.64 | 40.20 | 0.97 | 3.26 | 0.01 | 0.95 a,b | 2.59 |
| 400-2-10-2 | 4.13 | 15.82 | 3.83 | 3.92 | 14.82 | 217.06 | 3.77 | 14.45 | 0.03 | 2.26 a,b,c | 9.80 |
| 400-2-10-3 | 4.28 | 11.40 | 4.07 | 4.26 | 11.40 | 161.52 | 4.24 | 11.40 | 0.03 | 2.54 a,b,c | 8.06 |
| 400-2-20-2 | 1.58 | 4.51 | 2.29 | 1.56 | 4.51 | 83.83 | 1.53 | 4.49 | 0.02 | 0.76 a,b,c | 1.77 |
| 400-2-20-3 | 1.49 | 4.76 | 2.03 | 1.45 | 4.76 | 84.41 | 1.41 | 4.68 | 0.02 | 0.70 a,b,c | 1.92 |
| 400-4-10-2 | 3.49 | 11.62 | 3.85 | 3.37 | 11.50 | 198.54 | 3.17 | 10.16 | 0.02 | 1.46 a,b,c | 4.95 |
| 400-4-10-3 | 3.20 | 9.44 | 3.82 | 3.19 | 9.44 | 189.06 | 3.11 | 9.28 | 0.02 | 1.58 a,b,c | 5.25 |
| 400-4-20-2 | 1.46 | 3.61 | 2.02 | 1.38 | 3.54 | 92.61 | 1.28 | 3.52 | 0.01 | 0.81 a,b,c | 1.71 |
| 400-4-20-3 | 1.55 | 4.19 | 1.99 | 1.42 | 3.57 | 99.64 | 1.31 | 3.53 | 0.02 | 0.83 a,b,c | 1.82 |
| 400-10-10-2 | 3.16 | 10.53 | 3.80 | 3.03 | 9.51 | 214.82 | 2.74 | 8.27 | 0.01 | 1.49 a,b,c | 4.02 |
| 400-10-10-3 | 2.97 | 7.74 | 3.78 | 2.92 | 7.60 | 216.61 | 2.57 | 7.60 | 0.01 | 1.42 a,b,c | 4.46 |
| 400-10-20-2 | 1.40 | 4.30 | 2.04 | 1.15 | 2.67 | 98.30 | 0.77 | 2.16 | 0.01 | 0.82 a,b | 2.48 |
| 400-10-20-3 | 1.66 | 4.26 | 2.02 | 1.39 | 3.38 | 106.48 | 0.98 | 2.83 | 0.01 | 1.02 a,b | 2.70 |
| GDSPT | IDE | RDE | GDDR | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n-m-b-h | Avg (%) | Max (%) | Time (s) | Avg (%) | Max (%) | Time (s) | Avg (%) | Max | Time (s) | Avg (%) | Max (%) |
| 600-10-10-2 | 4.55 | 7.92 | 4.14 | 4.22 | 7.04 | 478.53 | 3.72 | 5.87 | 0.02 | 1.42 a,b,c | 2.40 |
| 600-10-20-2 | 1.44 | 2.19 | 1.93 | 1.37 | 2.19 | 321.06 | 0.82 | 1.88 | 0.01 | 0.69 a,b,c | 1.23 |
| 600-20-10-2 | 3.58 | 7.15 | 3.79 | 3.56 | 6.95 | 406.82 | 3.25 | 5.30 | 0.01 | 1.72 a,b,c | 3.34 |
| 600-20-20-2 | 1.34 | 2.90 | 1.88 | 1.22 | 2.57 | 341.80 | 0.61 | 1.72 | 0.01 | 0.61 a,b,c | 1.33 |
| 900-10-10-2 | 3.95 | 10.37 | 11.84 | 3.81 | 9.62 | 613.62 | 3.62 | 9.12 | 0.04 | 1.27 a,b,c | 3.13 |
| 900-10-20-2 | 1.76 | 2.85 | 5.93 | 1.70 | 2.85 | 584.91 | 1.51 | 2.85 | 0.02 | 0.71 a,b,c | 1.17 |
| 900-20-10-2 | 4.58 | 8.97 | 11.67 | 4.29 | 7.41 | 613.89 | 4.03 | 6.83 | 0.03 | 1.48 a,b,c | 2.54 |
| 900-20-20-2 | 1.65 | 3.49 | 5.88 | 1.55 | 2.96 | 584.99 | 1.24 | 2.19 | 0.02 | 0.86 a,b,c | 1.70 |
| 1200-10-10-2 | 6.14 | 14.10 | 26.79 | 5.43 | 13.16 | 638.08 | 5.08 | 12.33 | 0.06 | 1.90 a,b,c | 6.12 |
| 1200-10-20-2 | 1.79 | 3.40 | 13.51 | 1.76 | 3.40 | 621.51 | 1.67 | 3.40 | 0.03 | 0.69 a,b,c | 1.18 |
| 1200-20-10-2 | 5.12 | 10.45 | 26.81 | 4.48 | 8.08 | 643.89 | 4.16 | 7.78 | 0.04 | 1.21 a,b,c | 2.49 |
| 1200-20-20-2 | 1.58 | 2.79 | 12.93 | 1.51 | 2.08 | 616.20 | 1.44 | 1.95 | 0.02 | 0.80 a,b,c | 1.15 |
| BSGP | BatchCCGP | GDDR-CCGP | |
|---|---|---|---|
| BFGP | −686,434.96 (+) | 453,248.68 (+) | 414,854.98 (+) |
| BSGP | 1,139,683.64 (+) | 1,101,289.94 (+) | |
| BatchCCGP | −38,393.70 (o) |
| Improvement Ratio (%) | Dominant Ratio (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GDSPT | IDE | RDE | GDSPT | IDE | RDE | |||||||
| Avg | Best | Avg | Best | Avg | Best | Avg | Best | Avg | Best | Avg | Best | |
| BSGP | 41.45 | −31.17 | 60.99 | −23.19 | 79.14 | −13.04 | 50.13 | 93.48 | 39.48 | 82.61 | 30.26 | 65.22 |
| BFGP | −16.43 | −22.48 | −4.81 | −11.39 | 10.34 | 3.10 | 87.22 | 100.00 | 56.26 | 65.22 | 50.35 | 58.70 |
| BatchCCGP | −29.16 | −37.90 | −19.43 | −29.66 | −8.39 | −19.68 | 92.17 | 100.00 | 80.30 | 93.48 | 63.26 | 76.09 |
| GDDR-CCGP | −27.68 | −40.25 | −17.89 | −32.20 | −6.81 | −22.74 | 90.65 | 100.00 | 80.09 | 93.48 | 61.91 | 78.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Shi, L. Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling. Symmetry 2022, 14, 632. https://doi.org/10.3390/sym14040632
Liu L, Shi L. Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling. Symmetry. 2022; 14(4):632. https://doi.org/10.3390/sym14040632
Chicago/Turabian StyleLiu, Lingxuan, and Leyuan Shi. 2022. "Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling" Symmetry 14, no. 4: 632. https://doi.org/10.3390/sym14040632
APA StyleLiu, L., & Shi, L. (2022). Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling. Symmetry, 14(4), 632. https://doi.org/10.3390/sym14040632





