1. Introduction
The neutrino is a unique particle that breaks the fundamental symmetry between left and right in nature: chiral symmetry or parity
P. It participates in the weak interactions, which break the discrete symmetries, such as
P-symmetry and
C-symmetry, between particles and their antiparticles, and also time reversal symmetry,
T-symmetry. It is proven experimentally that the strong and electromagnetic interactions preserve the aforementioned symmetries. See reviews [
1,
2].
The weak interactions are sensitive only to left-handed neutrinos and right-handed antineutrinos in such a way that -symmetry is preserved for massless neutrinos, according to the Standard Model. However, it was proven by oscillation experiments that neutrinos are massive particles and can be mixed, but with a different pattern than quarks mixing. Such mixing can lead to a violation of -symmetry with an even more rich structure of violation phases than that existing in the quark sector. The neutrino mixing matrix is called the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) mixing matrix.
Neutrino propagation in the sun and in Earth, for which medium is asymmetric, with respect to the presence of particles and antiparticles due to the baryon asymmetry of our universe, can lead to an additional violation of -symmetry. The symmetry of the resonance shape of the probability distribution of neutrino oscillations in matter is also destroyed by the neutrino interaction with matter.
This paper is dedicated to the evaluation of the resonance half-widths of the first maximum for the probability of the total neutrino conversion in the medium. The simplest case of two-neutrino mixing in matter with a constant refraction length is considered. We explore the resonant enhancement of the transition between two neutrino species. We show that the resonant shape of the transition probability is highly asymmetric, contrary to the usual assumption about a symmetric shape of the resonance widths.
2. Framework and Definitions
The probability of transition between the two weak-eigenstates of ultrarelativistic neutrinos,
and
(
) (the symbols
, and
s mean electron, muon, tau, and sterile neutrinos, respectively), in matter [
3]
depends on the mixing function
and the phase
which is proportional to the distance
ℓ traveled by neutrinos. Here,
is the vacuum mixing angle, and
is the mixing angle in matter. The ratio of the neutrino energy,
E, and the neutrino mass squared difference,
, defines the vacuum oscillation length
, and
is the refraction length, where
is the difference of the effective potentials between propagation of the
and
states in matter.
The relations (
2) and (
3) at a fixed vacuum mixing angle
are expressed through two independent dimensionless variables,
and
. For the first time, it was mentioned in [
4,
5] that the mixing function
has a resonance form, with respect to the variable
y. At the resonance
the mixing function (
2) reaches the maximum
with the symmetric half-widths on both sides at half-maxima, with respect to the variable
y:
In the following, we consider the case when the resonance happens for vacuum mixing angles in the first octant , which correspond to positive . In the case , resonance is possible for the opposite signs of or .
It is clear that the half-width (
5) is the supremum of the observable half-widths for the probability (
1), with respect to the variable
y, since there is an additional multiplier
, which is less or equal to 1. This multiplier has an infinite number of maxima, with respect to the variable
x, starting from zero. Let us consider for definiteness the first maximum for probability (
1)
, which corresponds to a total neutrino conversion and is reached at
for fixed
(
4).
The half-widths on both sides at half-maxima of the probability (
1), with respect to the variable
x, are then symmetric and easily calculated
Evaluation of resonance half-widths of the probability (
1), with respect to the variable
y at fixed
(
6), cannot be done analytically and will be considered numerically in the next section.
3. Half-Widths with Respect to the Variable
It is obvious that the probability distribution (
1) around the maximum, with respect to the variable
y at fixed
, is asymmetric with different half-widths
. The equations for new variables
look the same,
but correspond to solutions with different signs
and
, where
describes the ratio of the exact numerical solution of Equation (
8) for the right half-width to the analytical guess of Equation (
5), while
corresponds to the negative ratio of the exact numerical solution of Equation (
8) for the left half-width to the same analytical symmetric solution of Equation (
5).
Equation (
8) can be easily solved numerically by Newton’s method, starting with the points
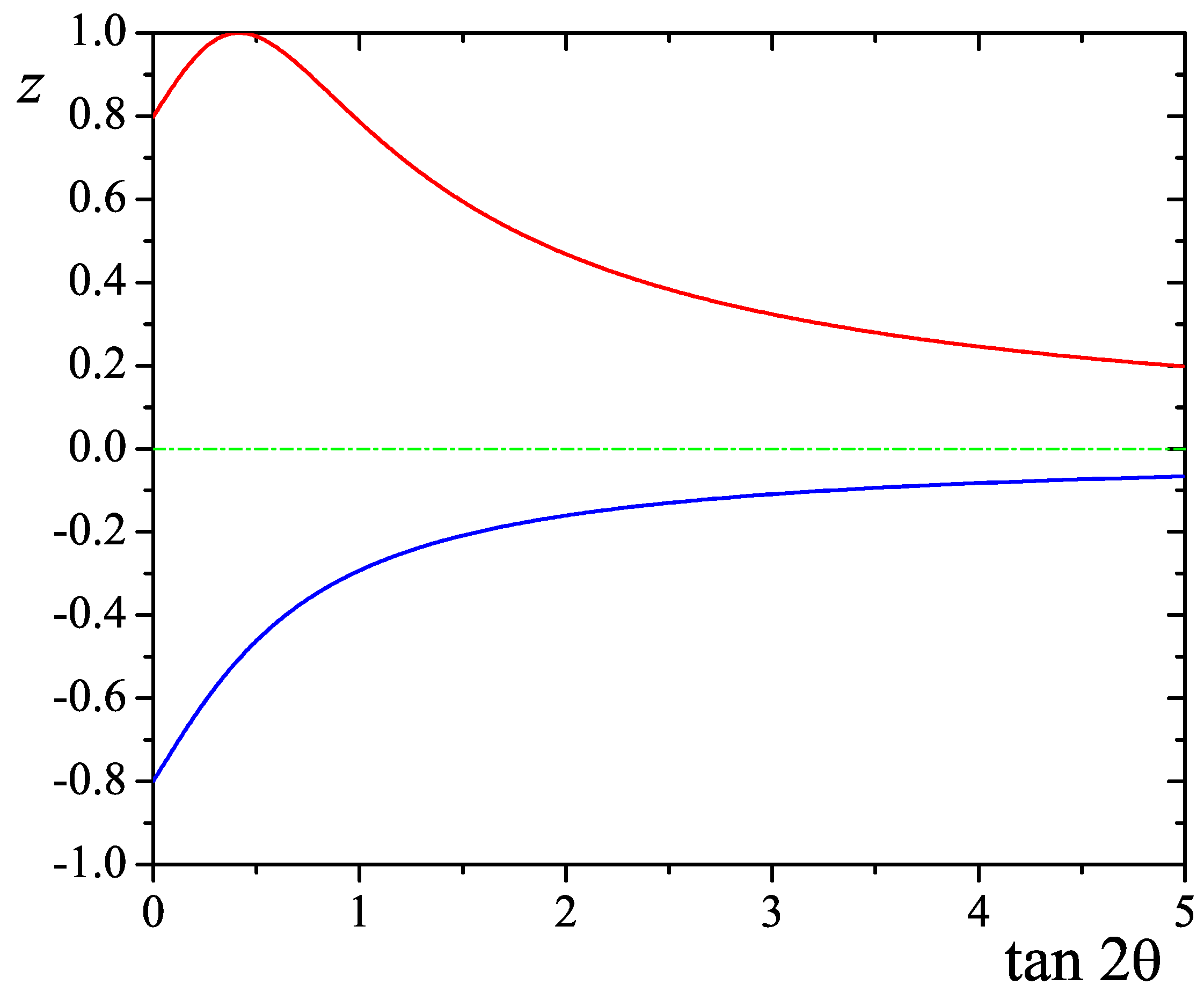
. It is interesting to compare the resonance half-width (
5) with the half-widths of the resonance peak for the probability (
1) (see
Figure 1).
There is only one point
or
at which the right half-width coincides with Equation (
5):
.
The Equation (
8) allows simple investigation of their limiting cases at
and
analytically. In the limiting case of small vacuum mixing angles
, both solutions give the same half-width (see
Figure 1)
where
is a solution of the following transcendental equation:
The asymptotic solutions for the maximal vacuum mixing angle
can be found by substitutions
and
, where
a and
b are positive constants. There is always only one positive root of Equation (
8), which corresponds to the right half-width of the resonance probability peak. In the limiting case,
, we get the solution
, which corresponds to
However, there are infinitely many negative roots at
, which correspond to oscillation peaks on the left side of the first resonance peak at
(
4). The only maximal solution
with
corresponds to the left half-width of the resonance probability peak.
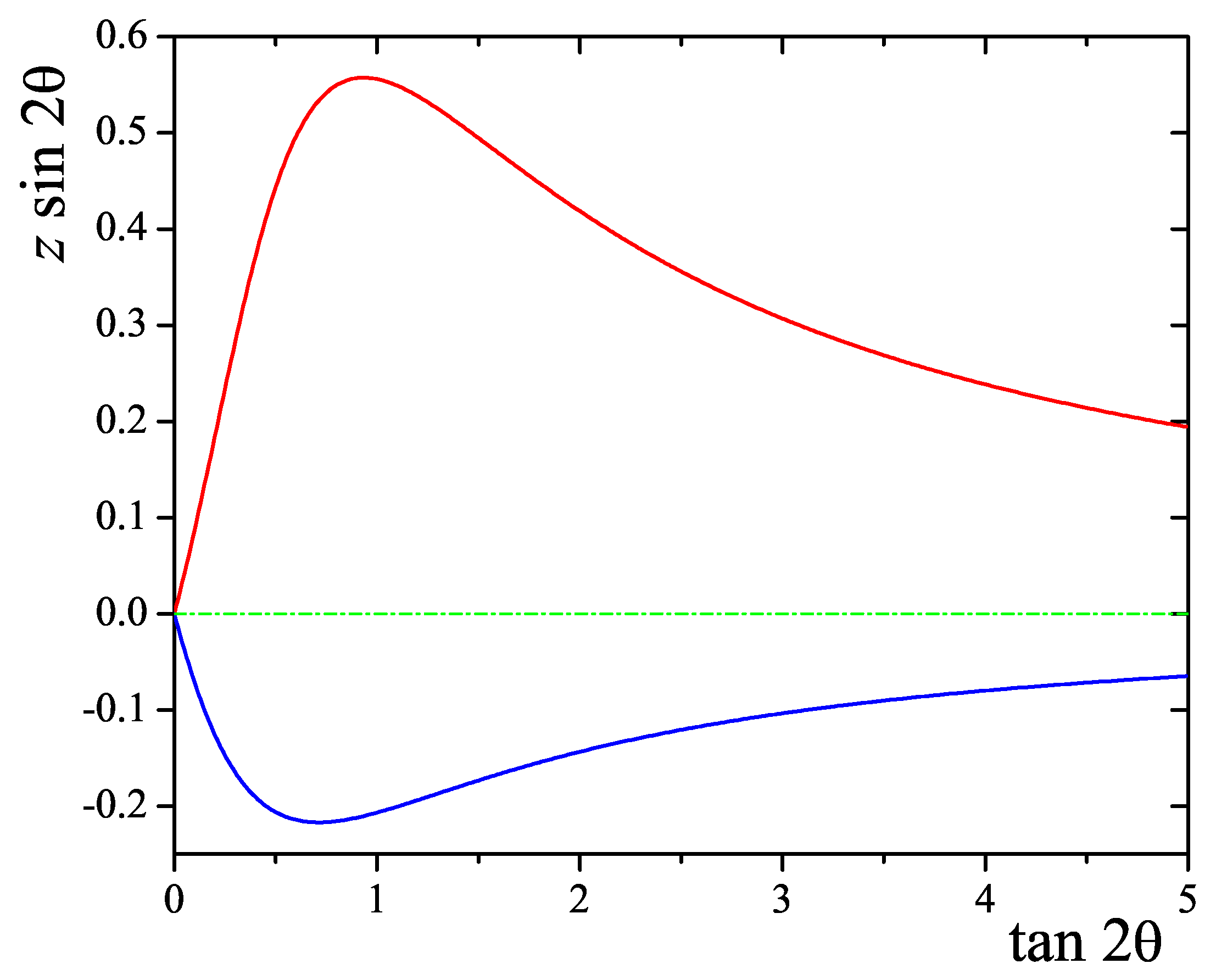
Therefore, in both limiting cases, the absolute values of the widths tend to zero at
(
6), starting from the symmetric peak (
9) at small mixing angles to the maximally asymmetric half-widths ratio
(
11,
12) at the maximal vacuum mixing angle (see
Figure 2).
In the same limiting case
, we can also find the positions of all non-resonance maxima, including the resonance (
)
where
and the corresponding half-widths are
However, due to strong asymmetry in the probability distribution shape, with respect to the location of the absolute maximum, especially in the case of , these formulae cannot give an adequate description of the Mikheyev–Smirnov–Wolfenstein (MSW) resonance width. Therefore, it will be considered in the next section.
4. Full Consideration of the Resonance Width
Let us consider the shapes of the probability distribution (
1) in the two-dimensional
plane. There are two lines that correspond to maximal values of the multipliers in Equation (
1):
and
for the first maximum. The maximum
is reached at the point
, while the condition
defines the ranges, with respect to the variable
y
where
, and with respect to the variable
x
where
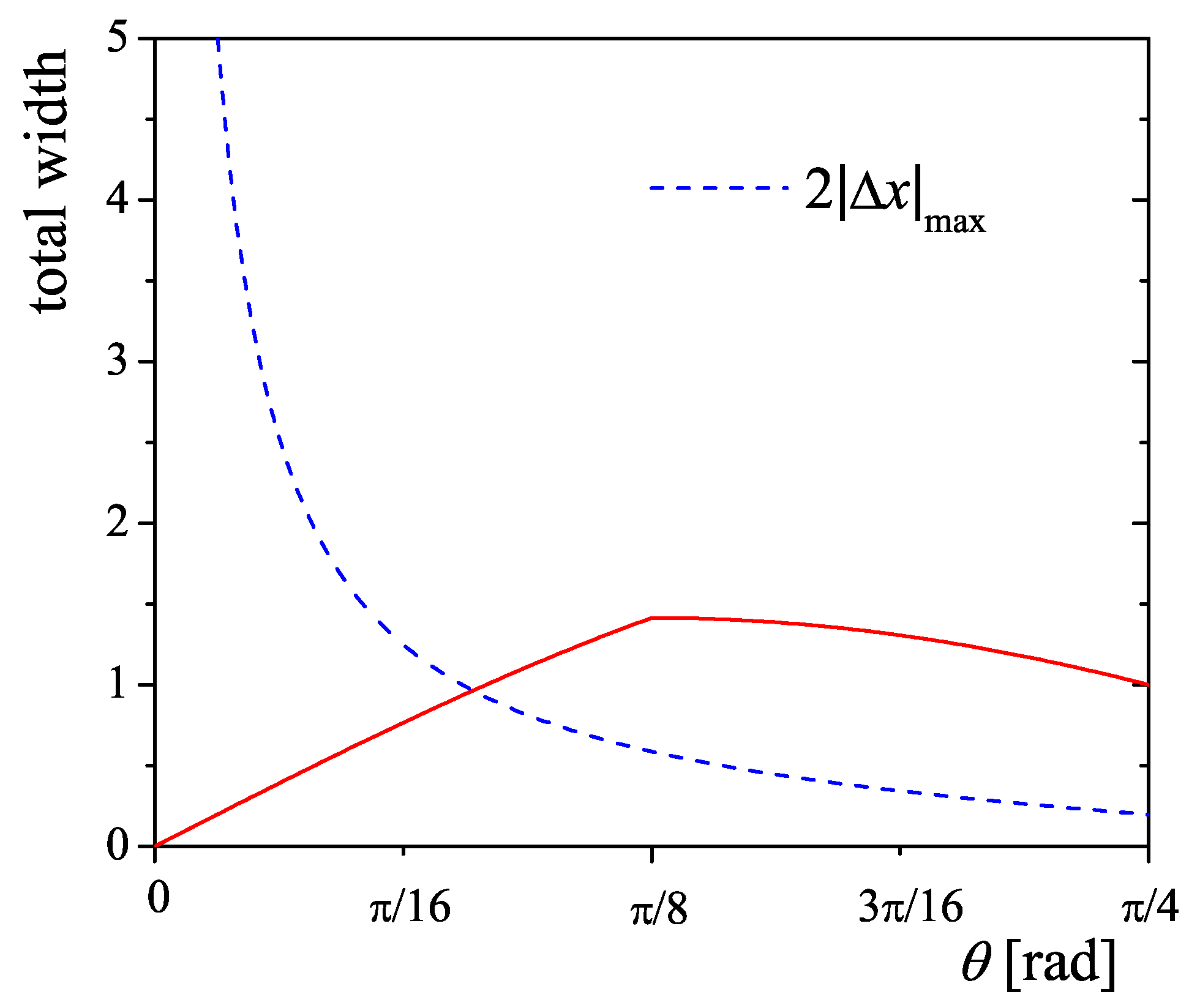
. In
Figure 3, the total width dependence on parameter
are shown.
The solid (red) line presents the total width for the variable
y Equation (
17), while the dashed (blue) line presents the maximal value of width for the variable
x Equation (
18) at fixed
y. From
Figure 3, it is clear that the resonance shapes for the small mixing parameter
and the maximal mixing
are highly asymmetric (
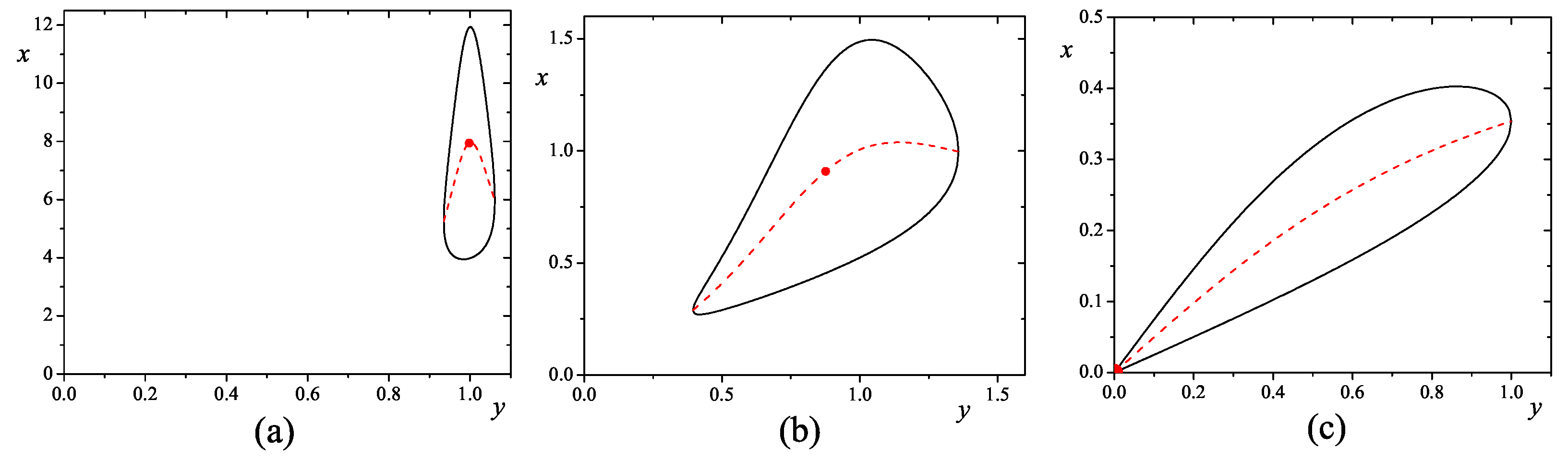
Figure 4a,c).
For small mixing angles (
Figure 4a), the resonance shape has a very narrow width, with respect to the variable
y around 1, and very long ridge, with respect to the variable
x. This resonance disappears at zero mixing in infinity, with respect to the variable
x. The intermediate (between
and
) mixing angle
(
Figure 3) leads to a resonance shape with nearly the same sizes, with respect to the variables
x and
y (
Figure 4b), while the maximal mixing
again shows the asymmetric shape with an absolute maximum at
(
Figure 4c).
5. Applications
In the case of three neutrino mixing, there is a 3 × 3 unitary mixing matrix
:
where the matrix
corresponds to the rotation in the
-plane by an angle
, while
takes into account
violation phase
and
introduces the Majorana phases. It is the well-known PMNS mixing matrix.
Since matter-induced neutrino potential
commutes with
, angle
is not affected by matter. Finally, in the case of neutrino masses
or
, mass matrix commutes approximately with
and commutes with
and
. Therefore, the problem can be reduced with good approximation to two flavours without the effect of the
violation phase
, the Majorana phases
,
, or mixing angle
. Therefore, for the
—
transition we get:
where the two flavours probability
from Equation (
1) depends on the vacuum mixing angle
, mass squared difference
, and the effective potential
. In the last expression,
is the Fermi coupling constant and
is the electron number density in the medium.
In [
6], the authors derived the minimal width of the medium
, below which the probability conversion
is less than 1/2. For a uniform medium in approximation of small vacuum mixing angles at the resonance
, they got the following relation:
where
is the refraction width. Although it is a good approximation for very small vacuum mixing angles (see
Figure 4a),
Figure 4b demonstrates that it is not the case for bigger vacuum mixing angles when corrections to Equation (
21) must be applied. Indeed,
is always reached at
y values less than
. In
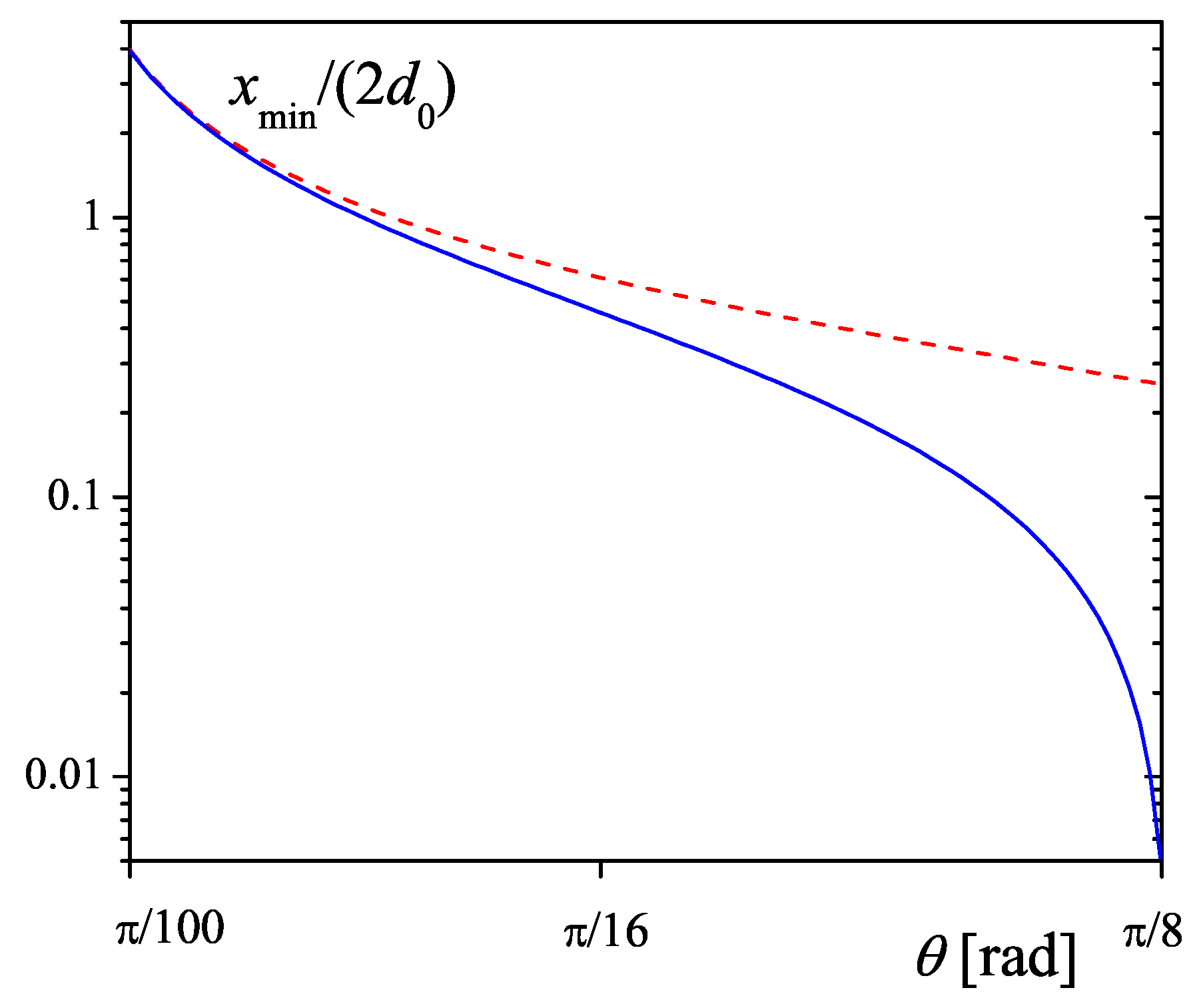
Figure 5, a comparison between the minimal width of the medium from Equation (
21) and a direct calculation using Equations (
16) and (
18) is shown. Direct calculations show that at
, the minimal width of the medium tends to zero:
, where there is maximal deviation from Equation (
21). For the physical value of the mixing angle
, we get from Equation (
21) about 20% bigger value than that obtained from the direct calculations.
At the end of this section, we apply Equations (
16)–(
18) to calculate the shape of the resonance peak in the Earth’s mantle for atmospheric neutrinos. If the mass squared difference is positive
(normal neutrino mass order), the MSW matter enhancement of oscillations will take place between electron and muon neutrinos. For negative mass squared difference (inverted order), the matter oscillation enhancement will take place for the corresponding antineutrinos.
The electron number density in the Earth’s mantle can be estimated assuming a constant matter density
g/cm
3 with an electron fraction number
and Avogadro constant,
, as
. From Equation (
4), the resonance energy is
In order to calculate the distance from the Earth’s atmosphere to the detector, where the total neutrino conversion takes place, we will use Equation (
6),
where
h is the nadir angle and
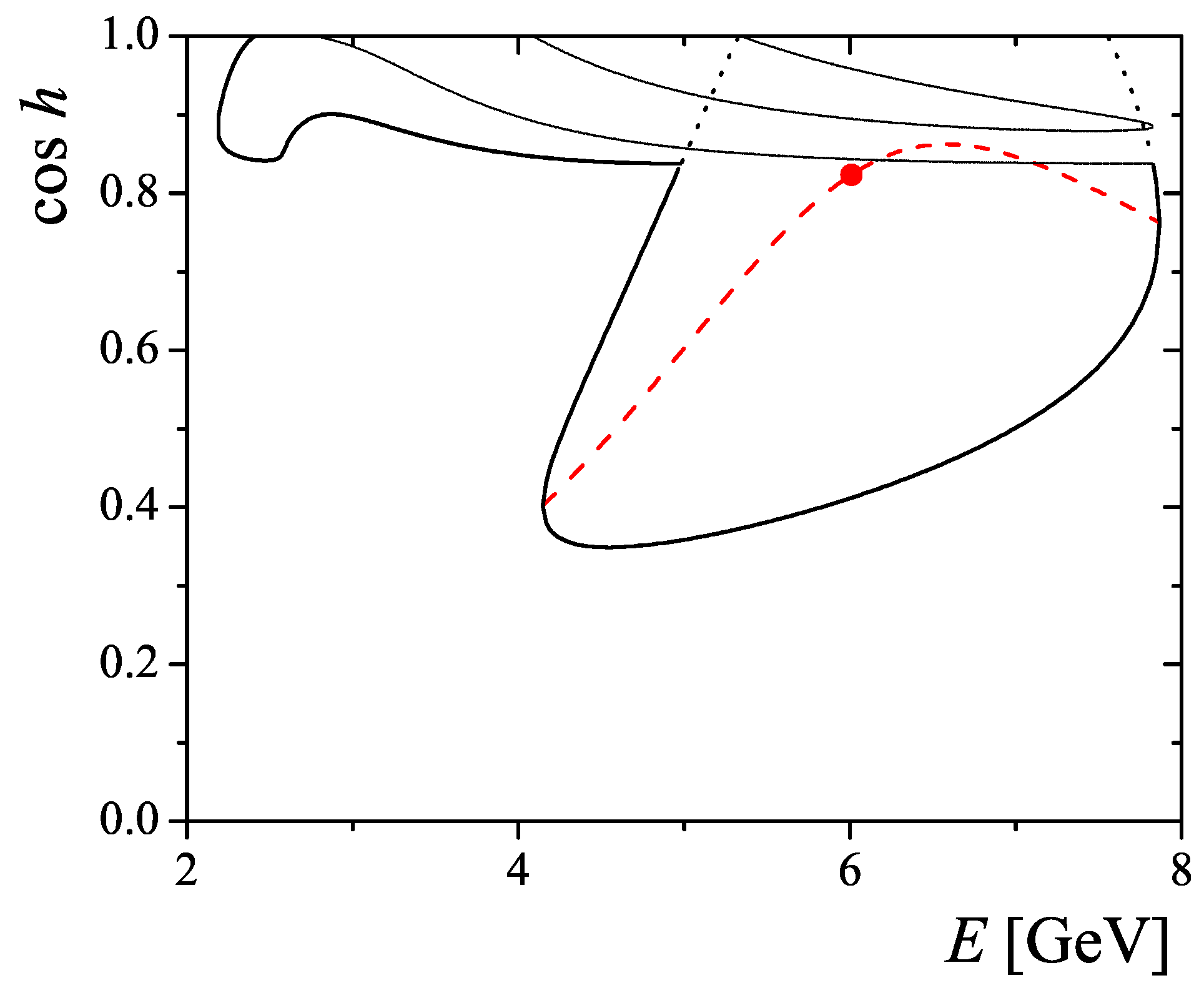
km is the Earth’s radius. The position of the absolute maximum is presented in
Figure 6.
It corresponds to neutrino trajectory in the mantle close to the Earth’s core, which has a radius
km. Therefore, the neutrino trajectories with a nadir angle less than
, crossing both the mantle and the core of the Earth, which have different matter densities and MSW resonance description, is not applicable for this region. The MSW resonance shape (
) is shown in
Figure 6 with a solid line for the applicable region
and with a dotted line for the unphysical case when the Earth’s interior had a constant matter density
.
The resonance shape of the probability distribution of the neutrino trajectories with
cannot be described by the MSW resonance curve (
1). In this region, another matter effect is operative: the interference effect between neutrino wave functions in the mantle and in the core [
7].
6. Discussion
The neutrino propagation in the medium can be described using the MSW approach [
3,
4,
5]. The probability of oscillations between two ultrarelativistic neutrino species for a constant matter density and its constant electron fraction number is described by Equation (
1). There is a phenomenon of resonant enhancement of transition between species, which leads to a maximal mixing angle in the matter
and total neutrino conversion.
It is usually accepted that the resonance half-widths are symmetric and given by Equation (
5). In this paper, we investigate the resonance shape of the probability distribution
Equation (
1) on two independent parameters,
x and
y, which are proportional to the distance
ℓ travelled by the neutrino and neutrino energy
E, correspondingly. Using the analytical Equations (
16)–(
18), for the first maximum it is shown that the resonance shape is highly asymmetric (
Figure 4). Equation (
16) can be easily generalised for the
n-th maximum
while the equations for the half-widths (
17) and (
18) are valid for any resonance maximum.
Our formulae are applicable for any fixed vacuum mixing angles
. However, it should be pointed out that Equation (
4) leads to the solution
at the maximal vacuum mixing angle
. Certainly, such a solution with zero neutrino energy corresponds to an unphysical case, because Equation (
1) is applicable only to a ultrarelativistic neutrino. This limiting case will be considered in details elsewhere.