Abstract
Programming is a vital skill in computer science and engineering-related disciplines. However, developing source code is an error-prone task. Logical errors in code are particularly hard to identify for both students and professionals, and a single error is unexpected to end-users. At present, conventional compilers have difficulty identifying many of the errors (especially logical errors) that can occur in code. To mitigate this problem, we propose a language model for evaluating source codes using a bidirectional long short-term memory (BiLSTM) neural network. We trained the BiLSTM model with a large number of source codes with tuning various hyperparameters. We then used the model to evaluate incorrect code and assessed the model’s performance in three principal areas: source code error detection, suggestions for incorrect code repair, and erroneous code classification. Experimental results showed that the proposed BiLSTM model achieved 50.88% correctness in identifying errors and providing suggestions. Moreover, the model achieved an F-score of approximately 97%, outperforming other state-of-the-art models (recurrent neural networks (RNNs) and long short-term memory (LSTM)).
1. Introduction
Programming is among the most critical skills in the field of computing and software engineering. As a consequence, programming education has received an ever-increasing level of attention. Many educational institutions (universities, colleges, and professional schools) offer extensive programming education options to enhance the programming skills of their students. Indeed, programming has become recognized as a core literacy [1]. Programming skills are developed primarily through repetitive practice, and many universities [2,3,4,5] have created their own programming learning platforms to facilitate such practice by their students. These platforms are often used for programming competitions and serve as automated assessment tools for programming courses [6].
Novice programmers tend to have difficulty developing and debugging source code due to the presence of errors of various types (especially logical errors) and the insufficiency of conventional compilers to detect these errors [7,8].
Example 1.
Consider a simple program that takes an integer input n from the keyboard and generates an output sum s that repetitively adds integers from 1 through n. The solution code is written in C programming language to implement the procedure and is compiled by a conventional compiler. After compiling, the user inputs n = 6 and the program correctly produces sum s = 21 as the output; similarly, input n = 7 produces an output sum s = 28.
| #include <stdio.h> |
| int main(){ |
| int j, l, totalsum = 0; |
| printf(“Give a number: “); |
| scanf(“%d”, &l); |
| for (j = 1; j < = l; j++){ |
| totalsum = totalsum + j; |
| } |
| printf(“Total sum of 1 to %d is: %d\n”, l, totalsum); |
| return (0); |
| } |
Now consider the code below in which a novice programmer has made a mistake (a small logic error) but the compiler executes the program normally and generates output, which, in this case, is incorrect. Specifically, the program has taken input n = 6 and produced output sum s = 15; similarly, input n = 7 produces output sum s = 21.
| #include <stdio.h> |
| int main(){ |
| int j, l, totalsum = 0; |
| printf(“Give a number: “); |
| scanf(“%d”, &l); |
| for (j = 1; j < l; j++){ |
| Totalsum = totalsum + j; |
| } |
| printf(“Total sum of 1 to %d is: %d\n”, l, totalsum); |
| return (0); |
| } |
No compiler has the ability to detect the coding error here. In more complex examples, such logic errors can be difficult to resolve. Environment-dependent logic errors, such as forgetting to include “= 0” for totalsum in the above example, are not uncommon, and even experienced programmers can make errors in source code [9]. It is widely accepted that many known and unknown errors go unrecognized by conventional compilers, which means that programmers often spend valuable time identifying and fixing these errors. To help programmers, especially novice programmers, deal with such source code errors quickly and efficiently, research seeking to shed light on the issue is being actively conducted in programming education [10,11].
A variety of source code and software engineering methods have been proposed, such as source code classification [12,13], code clone detection [14,15], defect prediction [16], program repair [17,18], and code completion [19,20]. Recently, natural language processing (NLP) has been used in a number of domains, including speech recognition, language processing, and machine translation. The most commonly used language models, including bi-gram, GloVe [21], tri-gram, and skip-gram, are examples of NLP-based language models. However, while these models may be useful for relatively short, simple codes, they are considerably less effective for long, complex codes. Today, deep neural network models are being used for language modeling due to their ability to consider long input sequences, and deep neural network-based language models are being developed for source code bug detection, logic error detection, and code completion [20,22,23,24,25]. Recurrent neural networks (RNNs) have been used but are less effective due to gradient vanishing or exploding [26]. Long short-term memory (LSTM) has overcome this problem.
LSTM neural networks consider previous input sequences for prediction or output. However, the functions, classes, methods, and variables of a source code may depend on both previous and subsequent code sections or lines. In such cases, LSTM may not produce optimal results. To fill this gap, we propose a bidirectional LSTM (hereafter BiLSTM) language model to evaluate and repair source codes. A BiLSTM neural network can combine both past and future code sequences to produce output [27]. In constructing and applying our model, we first perform a series of pre-processing tasks on the source code, then encode the code with a sequence of IDs. Next, we train the BiLSTM neural network using the encoded source codes. Finally, the trained BiLSTM model is used for source code evaluation and repair. Our proposed model can be used for different systems (i.e., online judge type, or program/software development where specifications and input/output are well defined) where problems (questions), submission forms (editors), and automatic assessments are involved. We plan to use the proposed model for an intelligent coding environment (ICE) [28] via API (Application Programming Interface). ICE is one of the examples of many services. On the other hand, there are many powerful and intelligent IDEs (i.e., grammatical support) available, but our model (which can be applied for online judge type systems) can provide much smarter feedback by identifying logical errors than conventional IDEs.
The main contributions of our work are summarized below:
- The proposed BiLSTM language model for code evaluation and repair can effectively detect errors (including logical errors) and suggest corrections for incorrect code.
- Application of the proposed model to real-world solution codes collected from the Aizu Online Judge (AOJ) system produced experimental results that indicate superior performance in comparison to other approaches.
- The BiLSTM model can be helpful to students, programmers (especially novice programmers), and professionals, who often struggle to resolve code errors.
- The model accelerates the code evaluation process.
- The proposed model can be used for different real-world programming learning and software engineering related systems and services.
2. Related Works
The wide range of application domains and the functionality of deep neural networks make them powerful and appealing. Recently, machine learning (ML) techniques have been used to solve complex programming-related problems. Accordingly, researchers have begun to focus on the development and application of deep neural network-based models in programming education and software engineering.
In Reference [7], logic errors (LEs) are a type of error that persists after compilation, whereas typical compilers can only detect syntax and semantic errors in codes. This paper proposed a practical approach to identify and discover logic errors in codes for object-oriented-based environments (i.e., C# .Net Framework). Their proposed Object Behavior Environment (OBEnvironment) can help programmers to avoid logical errors based on predefined behaviors by using Alsing, Xceed, and Mind Fusion Components. This approach is not similar to our proposed BiLSTM model, as their model is developed for the C# programming language in the .Net framework. Al-Ashwal et al. [8] introduced a CASE (computer-aided software engineering) tool to identify logical errors in Java programs using both dynamic and static methods. Programmers faced difficulties in identifying logical errors in the codes during testing; sometimes it is necessary to manually check the whole code, which also takes a large amount of time, effort, and cost. They used PMD and Junit tools to identify logical errors on the basis of a list of some common logic errors related to Java. This study is only effective in identifying logical errors in Java programs but will not be effective in other programming languages.
In article [29], an automated logical error detection technique is proposed for functional programming assignments. A large amount of manual and hand-made efforts are required to identify logical errors in test cases. This proposed technique used a reference solution for each assignment (written in OCaml programming language) of students to create a counter-example that contains all the semantic differences between the two programs. This method identified 88 more logical errors that were not identified by the mature test cases. Moreover, this technique can be effective for automatic code repair. The disadvantage of this method is that a reference program is needed to identify logical errors for each incorrect code. In [30], the authors studied a large number of research papers on programming languages and natural languages that were implemented using probabilistic models. They also described how researchers adapted these models to various application domains. Raychev et al. [19] addressed code completion by adopting an n-gram language model and RNN. Their model was quick and effective in code completion tasks. Allamanis et al. [31] proposed a neural stochastic language model to suggest methods and class names in source codes. The model analyzed the meaning of code tokens before making its suggestions and produced notable success in performing method, class, and variable naming tasks.
In article [32], the authors proposed a model for predicting defective regions in source codes on the basis of the code’s semantics. The proposed deep belief network (DBN) was trained to learn the semantic features of the code using token vectors derived from the code’s abstract syntax tree (AST), as every source code contains method, class, and variable names that provide important information. On the basis of this semantic meaning, Pradel et al. [33] introduced a name-based bug detection model for codes.
Song et al. [34] proposed a bidirectional LSTM model to detect malicious JavaScript. In order to obtain semantic information from the code, the authors first constructed a program dependency graph (PDG) for generating semantic slices. The PDG stores semantic information that is later used to create vectors. The approach was shown to have 97.71% accuracy, with an F1-score of 98.29%. In articles [22,24], the authors proposed an LSTM-based model for source code bug detection, code completion, and classification. Both these methods were used to develop the programming skills of novice programmers. Experimental results, obtained by tuning the various hyper parameters and settings of the network, showed that both models achieved better results for bug detection and code completion in comparison with other related models. In [20,23], the authors proposed error detection, logic error detection, and the classification of source codes on the basis of an LSTM model. Both approaches used an attention mechanism that enhanced model scalability. On the basis of various performance scales, both models achieved significant success compared to more sophisticated models. As noted earlier, however, an LSTM-based model considers only previous input sequences for prediction but is unable to consider future sequences. The proposed BiLSTM model has the ability to consider both past and future sequences for output prediction.
In brief, there have been a number of novel and effective neural network and probabilistic models proposed by researchers to solve problems related to source codes. The proposed BiLSTM model is unlike other models in that it considers both the previous and subsequent context of codes to detect errors and offer suggestions that enable programmers and professionals to make the needed repairs efficiently.
3. Proposed Approach
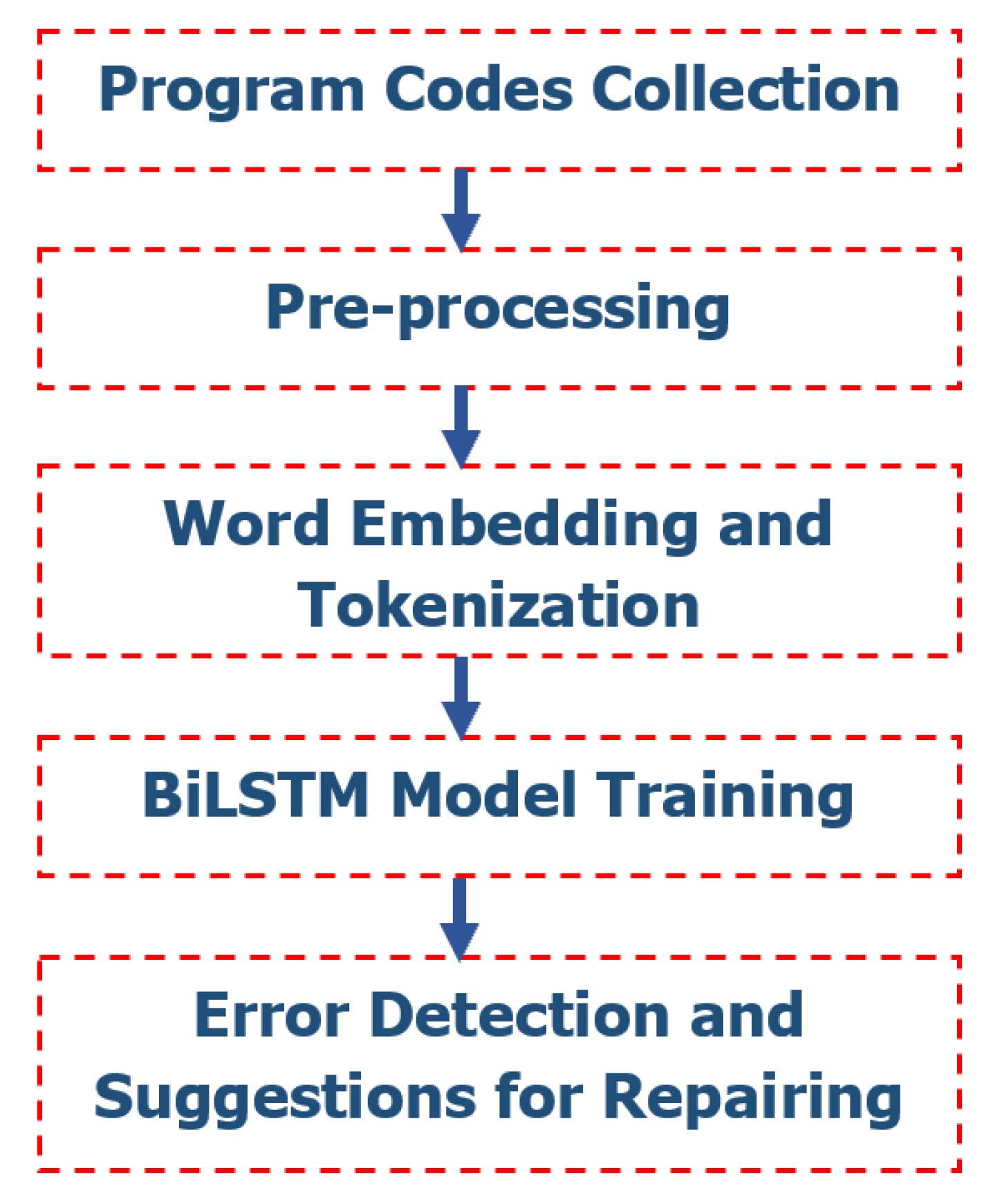
The model that we propose is a language model using a BiLSTM neural network. Figure 1 shows the workflow of the model, proceeding from source code collection to code evaluation by the trained BiLSTM model.

Figure 1.
Workflow of the proposed model.
3.1. BiLSTM Model Architecture
Let I = {i1, i2, i3, ………, it} be the set of encoded IDs of source codes. An RNN then executes for each encoded ID it for t = 1 to n. The output vector of RNN yt can be expressed by the following equations:
where ht is the hidden state output, W is a weight matrix (Wxh is a weight connecting input (x) to hidden layer (h)), b is a bias vector, and tanh is an activation function of the hidden layer. Equation (1) is used to calculate the hidden state output, where the hidden state receives the results of the previous state.
However, due to the problem of gradient vanishing/exploding [26], not all input sequences are used effectively in an RNN. To avoid the problem and produce a better result, the RNN is extended to LSTM. Conceptually, an LSTM network is similar to an RNN, but the hidden layer updating process is replaced by a special unit called a memory cell. LSTM is implemented by applying the following equations:
where σ is a sigmoid function; c, f, i, and o are the cell state, forget gate, input, and output, respectively; and all b are biases. However, there is still a shortcoming in LSTM insofar as it considers only the previous context of the input but cannot consider any future (i.e., subsequent) context.
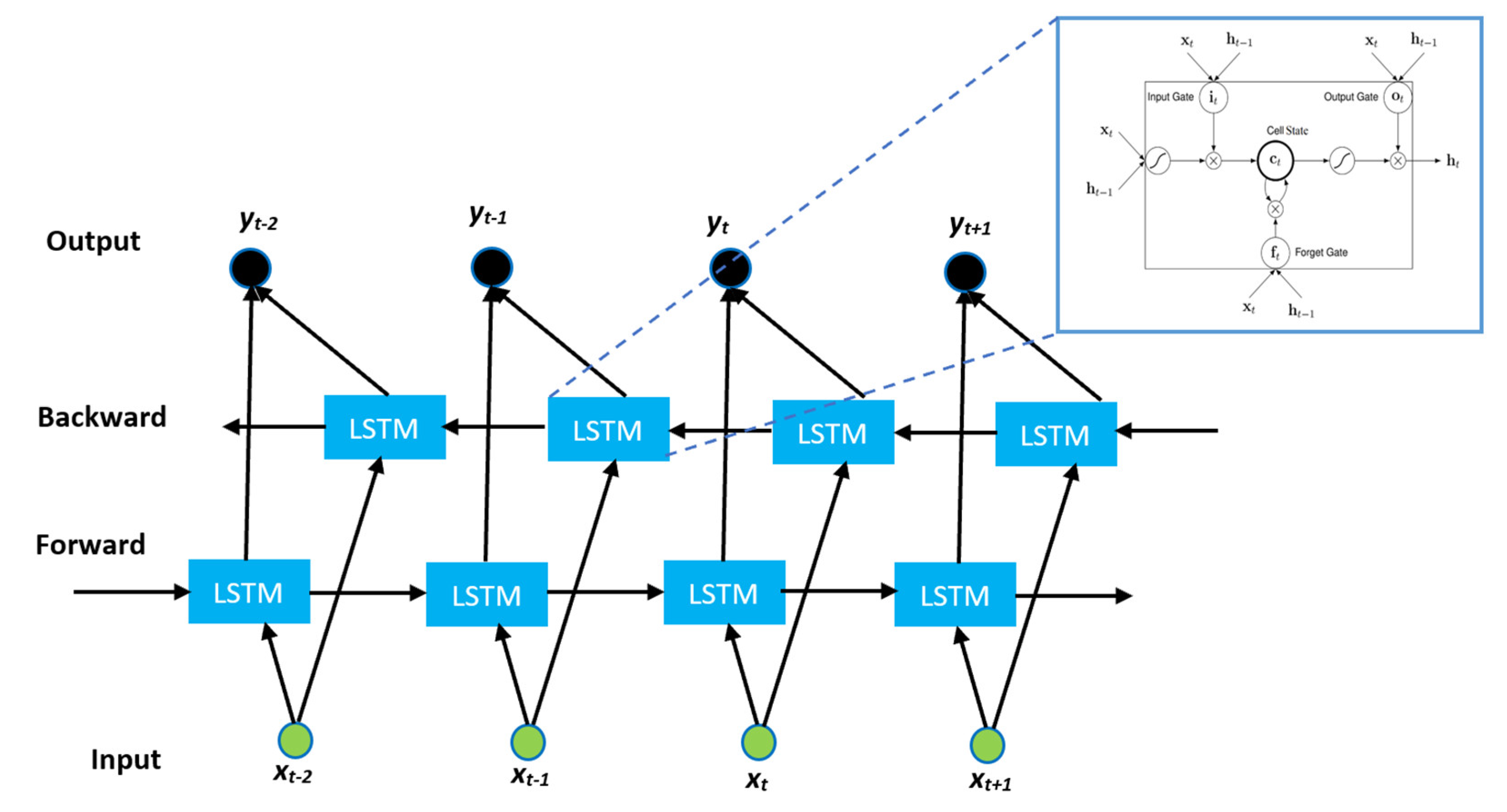
To overcome this limitation, we adopted the BiLSTM model [35], which enables us to consider both the past and future context of source codes, as shown in Figure 2. Here, there are two distinct hidden layers, called the forward hidden layer and backward hidden layer. The forward hidden layer considers the input in ascending order, i.e., t = 1, 2, 3, ..., T. On the other hand, the backward hidden layer considers the input in descending order, i.e., t = T, ...,3,2,1. Finally, and are combined to generate output yt. The BiLSTM model is implemented with the following equations:
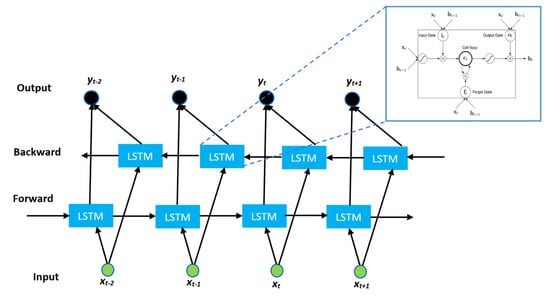
Figure 2.
Overview of the bidirectional long short-term memory (LSTM) model.
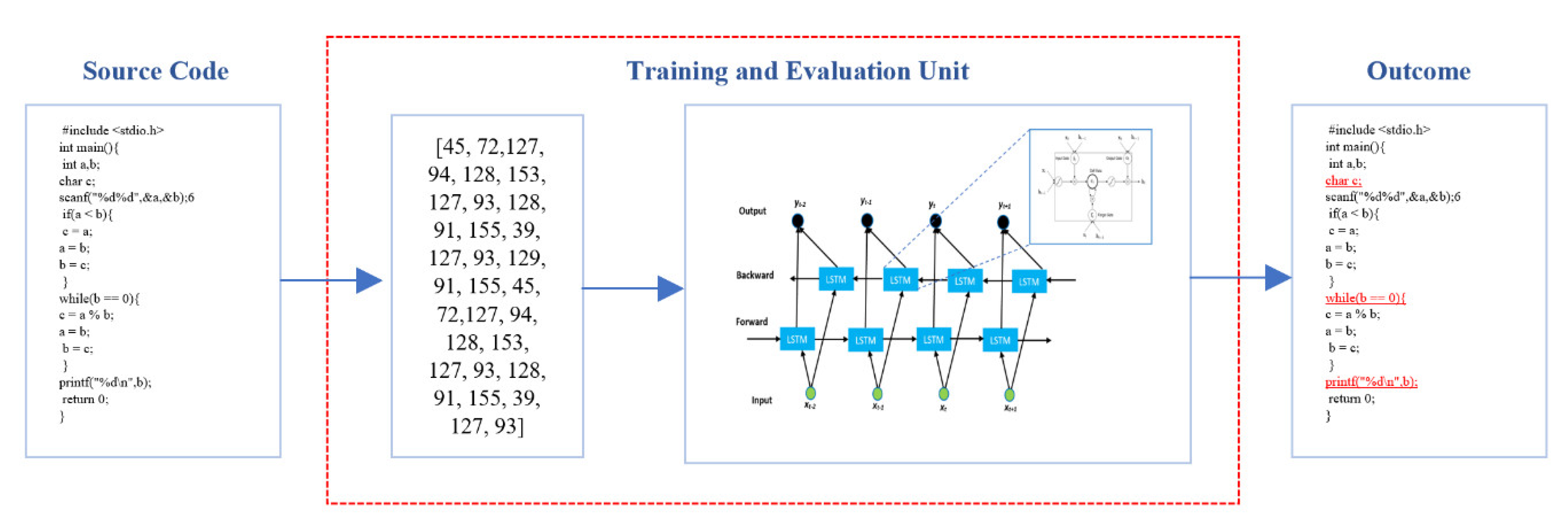
The training and evaluation processes of the proposed model are shown in Figure 3. The bidirectional LSTM network is used as the core processing unit for training and code evaluation. The figure shows the typical input/output style of the model.
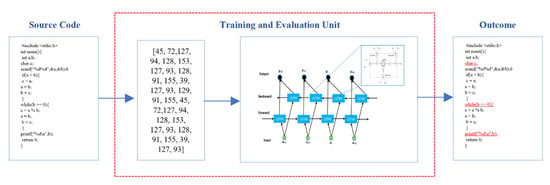
Figure 3.
Typical input/output prototype of the proposed bidirectional LSTM (BiLSTM) model.
3.2. Data Collection and Preprocessing
We collected source codes (written in the C programming language) from the Aizu Online Judge (AOJ) system [5,36]. All unnecessary elements (such as comments, new tabs, blank spaces, new line) were removed from codes.
We considered each keyword, token, variable, number, character, special character, function, and class of the source code as a simple word, then encoded the words with IDs according to Table 1. This process is called word sequencing and encoding, as shown in Figure 4. Finally, we fed the encoded IDs into the BiLSTM neural network for training. Ultimately, the trained BiLSTM model is applied to detect errors and suggest repairs for any incorrect code that is detected.

Table 1.
List of IDs for codes encoding [22].

Figure 4.
Process of source code conversion into encoded IDs.
4. Experimental Results
4.1. Data and Experimental Setup
A series of experiments based on the source codes collected from AOJ was conducted using greatest common divider (GCD) and insertion sort (IS) problem codes. A total of 2482 codes were included in the experiments: 90% for model training, 5% for model validation, and 5% for testing. The average length or number of lines in the GCD and IS solution codes were 18.9 and 30.91, respectively. Moreover, the average sizes of GCD and IS solution codes were 262.45 and 532.28 bytes, respectively. The difficulty or complexity level of solution codes was moderate. To balance the evaluation of the experimental results, we selected an equal number of correct (50%) and incorrect (50%) source codes from each type of problem (GCD and IS). The nature of the error was heterogeneous in the incorrect source codes. We did not select similar or common error typed source codes for training, validation, and testing. Instead, we randomly selected a variety of faulty source codes. To obtain the best results, we tuned the network configurations using hidden neurons of different sizes (e.g., 100, 200, 300, and 400) for the BiLSTM and other models. Training data were saved as .npz format for each type of hidden neuron (200, 300, 400, etc.). Similarly, for the output (error identification and providing suggestions), the model used the same number of hidden neurons. A value of 0.50 was used for the dropout [37] layers to avoid network overfitting. The Adam optimization algorithm [38] was adopted during model training. Particularly in deep learning, Adam optimizer is effectively used for the purpose of model learning. It balances model parameters and loss functions to efficiently update network weights.
Our proposed model is a sequence-to-sequence language model that predicts next words in incorrect codes on the basis of probability. The Softmax activation layer (as defined in Equation (11)) is used to transform the output vector to probability where Softmax takes vector Z = [z1, z2, z3, …, zn] and produces a vector S(z) = [s1, s2, s3, …, sn] for probabilities. The Softmax layer generates the probability for each word (token or ID) if the probability is too low (less than 0.1), which is considered as an error candidate and immediately mark the entire line. At the same time, the model generates a possible correct word instead of the error. To predict the correct word (token or ID), the model (BiLSTM) calculates the code sequences (both forward and backward) to find the best possible word on the basis of the highest probability.
We implemented our experiments on a CPU (Central Processing Unit)-based workstation (RAM: 8 GB; CPU: Intel Core i7-5600U (2.60 GHz); OS: 64-bit Windows 10).
4.2. Evaluation Metrics
We use accuracy and F1-scores as our primary metrics to evaluate the effectiveness of the proposed BiLSTM for detecting code errors and providing code repair suggestions.
Definition 1.
(Error identification accuracy) The model identifies erroneous candidates (words) in the solution codes; the number of correct or actual error candidates (words) out of the total identified error candidates (words) is called error identification accuracy (EIA). The “Number of correctly detected errors” are the errors that actually exist in the code and the “Total number of detected errors” are the errors (may exist or not in the code) detected by the model.
Example 2.
If a model m identifies a total of 11 error candidates (words) in solution code s1, and only 5 of the identified candidates (words) are actually present in the code, the EIA of model m for s1 is approximately 45.45%.
Definition 2.
(Suggestion accuracy) The model generates suggestions for each identified error candidate; the number of correct or actual code repair suggestions out of the total suggestions for error candidates is called suggestion accuracy (SA).
Example 3.
If model m generates a total of 20 suggestions in solution code s2, and only 13 of the total suggestions are correct or true, the SA of model m for s2 is 65%.
Definition 3.
(Correctness of the model) Correctness of the model is calculated as the average of EIA and SA values.
Example 4.
If model m has an EIA value of 45.45% and an SA value of 65%, the correctness of model m will be approximately 55.23%.
Recognizing that correctness of the model (CoM) alone is insufficient to measure the performance of the model, we used three additional evaluation metrics: precision, recall, and F-score. The three measures are defined as follows:
Precision is the ratio of correct error classifications to total error classifications (i.e., true positives to total positives, both true and false). The term TP refers to error code classified as error; similarly, FP refers to the correct code classified as an error. Recall refers to how correctly the model classifies the error codes (the ratio of true positives to true positives plus false negatives). The term FN refers to error code classified as correct. The F-score is the harmonic mean of precision and recall.
4.3. Cross-Entropy
The cross-entropy is an important scale for measuring the performance of probabilistic language models and is defined by the difference between the actual and predicted output of the model. Cross-entropy is calculated by the following equation:
where n is sample length, is an ID within a sample, and probability is calculated for .
4.4. Determining the Number of Epochs and Hidden Units
An epoch is a complete cycle with the full training dataset. Using the optimal number of epochs can improve the performance of the model as well as save time for model training. Our training dataset consisted of two types of problem (GCD and IS) solution codes. We trained our model separately for each of the two types using different hidden units.
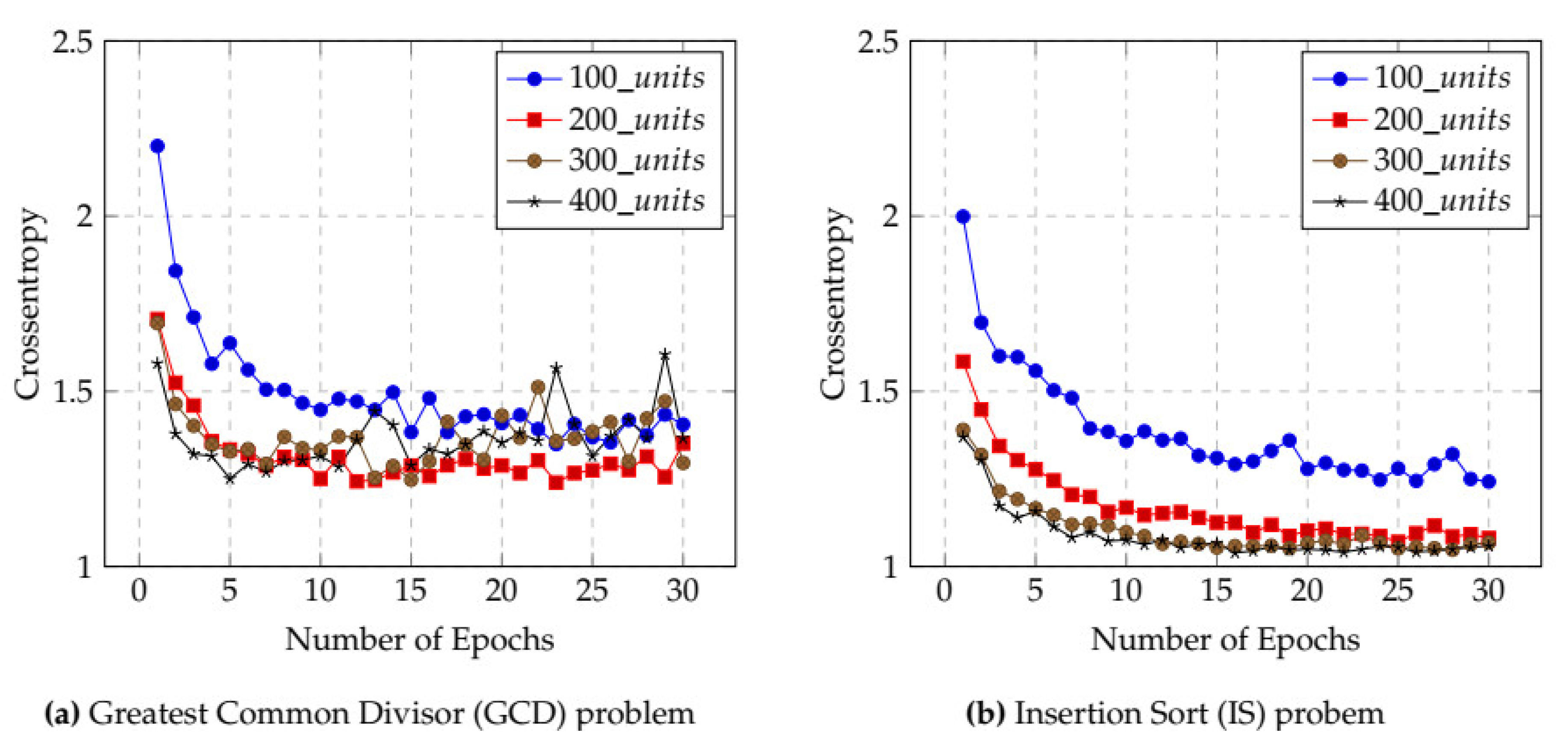
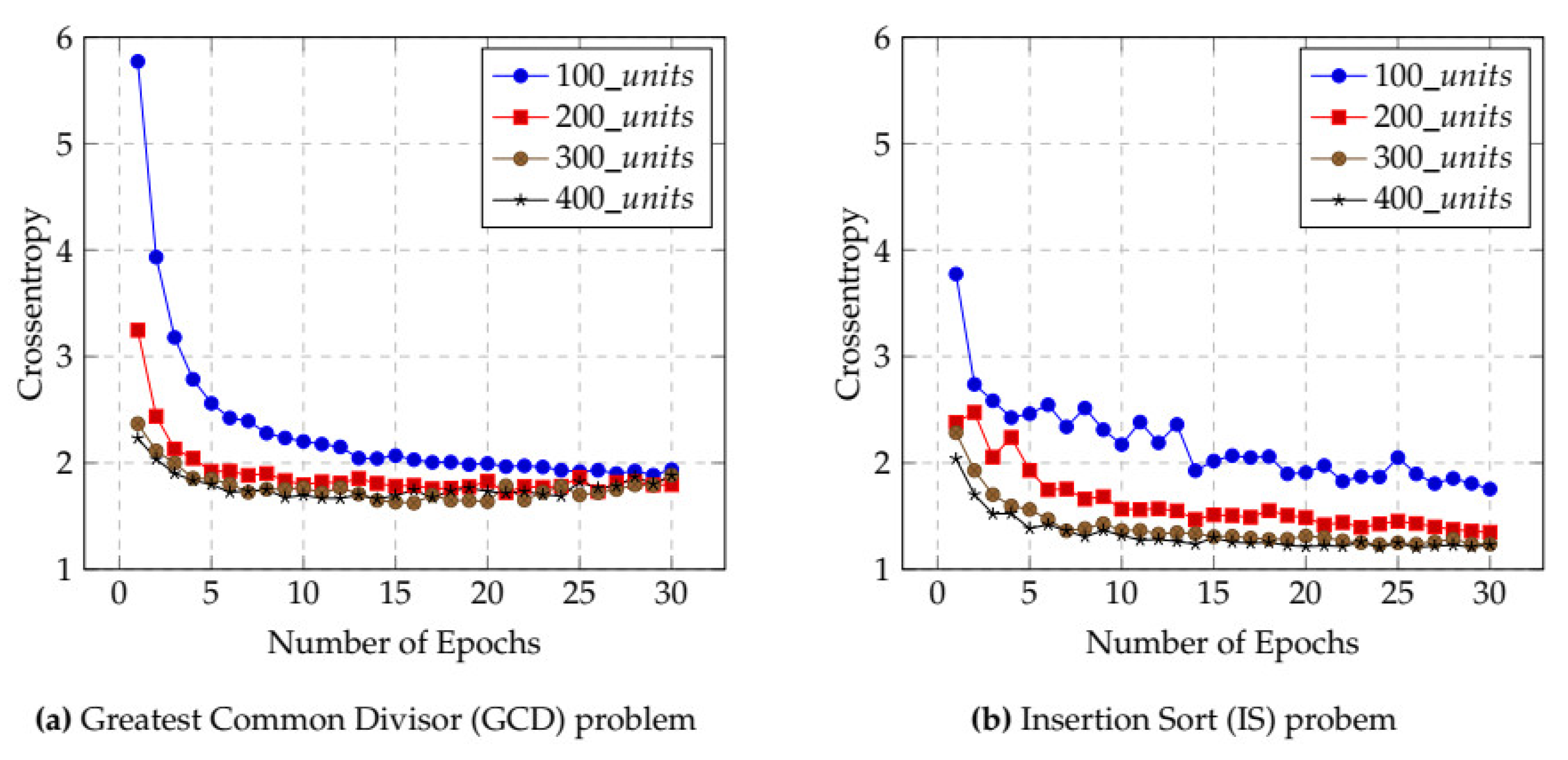
Figure 5 shows the results of the cross-entropy calculations used to select the optimal number of epochs and hidden units (neurons) for the BiLSTM model. Figure 5a gives the results for the GCD case. First, we identified the appropriate number of hidden units for model training. In this case, 200 hidden units produced the lowest cross-entropy. Moreover, cross-entropy was lowest when the number of epochs was between 20 and 25. The indication, then, is that, for the GCD case, the model produced its best performance when the number of hidden units was 200 and the number of epochs was between 20 and 25, and that using these values saves model training time. Similarly, Figure 5b shows that, in the IS case, cross-entropy for the BiLSTM model was lowest when 400 hidden units and between 25 and 30 epochs are used.
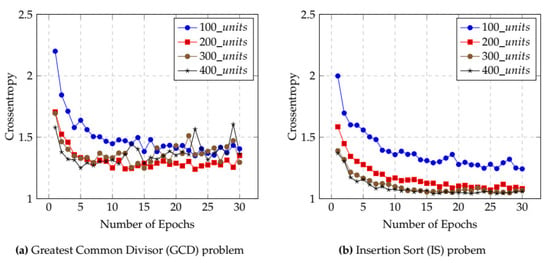
Figure 5.
Influence of cross-entropy on selecting epochs and hidden units for BiLSTM. (a) Greatest Common Divisor (GCD) problem, (b) Insertion Sort (IS) problem.
Figure 6 shows the cross-entropy results for the LSTM model. Figure 6a indicates that, in the GCD case, the cross-entropy of the LSTM model reached its lowest level when 300 hidden units and between 22 and 25 epochs were used. Figure 6b provides the results of when IS codes were used for model training. Here, the LSTM model had minimum cross-entropy when 400 hidden units and between 25 and 30 epochs were used.
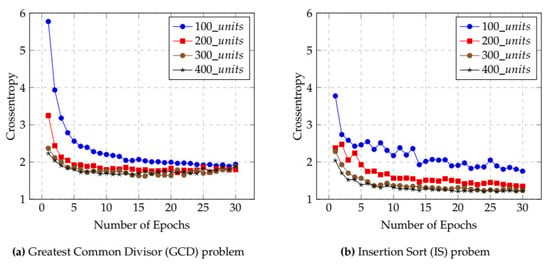
Figure 6.
Influence of cross-entropy on selecting epochs and hidden units for LSTM. (a) Greatest Common Divisor (GCD) problem, (b) Insertion Sort (IS) problem.
Comparative statistics for the lowest cross-entropy of the LSTM and BiLSTM models are given in Table 2. For the LSTM model, 300 and 400 hidden units produced the minimum cross-entropy for the GCD and IS solution codes, respectively. On the other hand, for the BiLSTM model, 200 and 400 hidden units, respectively, produced the lowest cross-entropy. Therefore, we chose these numbers of hidden units (i.e., those producing the minimum cross-entropy) for training and code evaluation.

Table 2.
Comparative lowest crossentropy of LSTM and BiLSTM models for different hidden units.
4.5. Incorrect Source Code Evaluation
We evaluated erroneous source codes using the LSTM and BiLSTM models and compared the performance of the two models. In Figure 7a, an incorrect GCD solution code was evaluated by the LSTM model. Errors were identified in lines 13, 15, 16, and 18 of the code. According to the context of the code, a logical error occurred in line 14, which was supposed to be l = m%n; however, the LSTM model was unable to accurately detect the error. Figure 7b shows an erroneous solution to an IS problem assessed by LSTM. Most of the errors (logical and syntactic) were identified by the model, but an irrelevant error (actually, no error at all) was identified in line 3.

Figure 7.
Source codes evaluation by the LSTM model. (a) Erroneous solution code of GCD problem, (b) Erroneous solution of IS problem.
To compare the error assessment efficiency of the two models (LSTM and BiLSTM), we assessed the same erroneous codes through the BiLSTM model. In Figure 8a, a solution to the GCD problem is evaluated by the BiLSTM model. The model detected errors in lines 13, 14, and 16. On the basis of the context of the code, the model considered the output statement in line 18 to identify the errors. As a result, the BiLSTM model correctly identified logical errors in lines 13 and 14 on the basis of the output details in line 18. In Figure 8b, where an incorrect solution to the IS problem was assessed by the BiLSTM model, the BiLSTM model was able to identify all the errors (logical and syntax) in the code. Errors were identified in lines 6, 16, 17, and 18, considering the full context of the erroneous code. In contrast, it is all but impossible to determine logical errors using a conventional compiler or to even consider the later context of the code. Figure 7 and Figure 8 show that the BiLSTM model properly evaluated the erroneous code on the basis of later context. On the other hand, the LSTM model was incapable of considering later context to detect errors.

Figure 8.
Source codes evaluation by the BiLSTM model. (a) Erroneous solution code of GCD problem, (b) Erroneous solution of IS problem.
4.6. Suggestions for Code Repair
The two models provided suggestions for code repair for each detected error location. Table 3 lists the suggestions based on the GCD problem evaluation described above.

Similarly, Table 4 lists the suggestions based on the IS problem evaluations by the LSTM and BiLSTM models.
Both the LSTM and BiLSTM models provided relevant suggestions for correcting the detected errors. Such suggestions can be useful to programmers, especially novice programmers, to help them quickly repair erroneous codes. However, not all errors are straightforward; some may rely on previous or subsequent lines in the code. In such cases, the BiLSTM model is more efficient than the LSTM model.
4.7. Error Detection Performance
Table 5 shows the comparative performances of the BiLSTM, LSTM, and RNN models for the GCD source code dataset. The CoM of the BiLSTM model was approximately 52.4%, which was much higher than the CoM of the other two models. Note that CoM (as per Equation (13)) was determined on the basis of the correctness of error detection and the suggestions provided for incorrect code. We calculated standard deviation (σ) on the basis of model performance in terms of error identification and suggestion accuracy. The BiLSTM model achieved the lowest deviation (σ: 4.55) compared to other models, which determines that the performance distribution of the model was consistent. Although the BiLSTM model also had the highest precision rate of 98%, there were very few correct codes classified as incorrect. The 95.5% recall rate indicated that there were relatively few false positives. As noted earlier, the F-score is the harmonic mean of the recall and precision ratios and is an important metric to describe model performance. As Table 5 shows, the F-score of the BiLSTM model was highest among the three models, at 96.7%, indicating that our proposed model produced superior true positives with a low rate of false positives.

Table 5.
Performance of the models based on the GCD dataset.
Table 6 shows the comparative results when the models were applied to the IS dataset. Once again, the BiLSTM model outperformed the LSTM and RNN models (CoM: 49.35%; σ: 3.12; precision: 97%; recall: 97%; F-score: 97.0%).

Table 6.
Performance of the models based on the IS dataset.
5. Limitations
Our experiment, including model training, validation, and testing, was conducted using only the C programming language. The performance of the BiLSTM model has not yet been tested using other programming languages. Moreover, we used only two types of solution codes—greatest common divisor (GCD) and insertion sort (IS). It should also be noted that our experimental results show that the BiLSTM model was not flawless—having falsely identified as erroneous code that which was actually correct. Some incorrect suggestions were also produced.
6. Conclusions
It is generally recognized that conventional compilers and other code evaluation systems are unable to reliably detect logic errors and provide proper suggestions for code repair. While neural network-based language models can be effective in identifying errors, standard feedforward neural networks or unidirectional recurrent neural networks (RNNs) have proven insufficient for effective source code evaluation. There are many reasons for this, including code length and the fact that some errors depend on both previous and subsequent code lines. In this paper, we presented an efficient bidirectional LSTM (BiLSTM) neural network model for code evaluation and repair. Importantly, the BiLSTM model has the ability to consider both the previous and subsequent context of the code under evaluation. In developing the model, we first trained the BiLSTM model as a sequence-to-sequence language model using a large number of source codes. We then used the trained BiLSTM model for error detection and to provide suggestions for code repair. Experimental results showed that the BiLSTM model outperformed existing unidirectional LSTM and RNN neural network-based models. The CoM value of the BiLSTM model was approximately 50.88%, with an F-score of approximately 97%. The proposed BiLSTM model thus appears to be effective for detecting errors and providing relevant suggestions for code repair.
In the future, we plan to evaluate our model using larger datasets and different programming languages. We will also seek to optimize various model parameters to improve model performance. We will present real-world performances and experiences obtained from ICE, as well as case studies based on users’ feedback.
Author Contributions
Conceptualization, M.M.R. and Y.W.; Data curation, M.M.R. and Y.W.; Formal analysis, M.M.R.; Funding acquisition, Y.W.; Methodology, M.M.R. and Y.W.; Project administration, Y.W. and K.N.; Resources, Y.W.; Software, M.M.R.; Supervision, Y.W. and K.N.; Validation, M.M.R., Y.W. and K.N.; Visualization, M.M.R.; Writing—original draft, M.M.R.; Writing—review & editing, M.M.R., Y.W. and K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant no. 19K12252).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All source code has been collected from the AOJ system for experimental purposes. URL: http://developers.u-aizu.ac.jp/index and https://onlinejudge.u-aizu.ac.jp/.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vee, A. Understanding Computer Programming as a Literacy. LICS Lit. Compos. Stud. 2013, 1, 42–64. [Google Scholar] [CrossRef]
- Revilla, M.A.; Manzoor, S.; Liu, R. Competitive learning in informatics: The UVa online judge experience. Olymp. Inform. 2008, 2, 131–148. [Google Scholar]
- Petit, J.; Roura, S.; Carmona, J.; Cortadella, J.; Duch, J.; Gimnez, O.; Mani, A.; Mas, J.; Rodrguez-Carbonell, E.; Rubio, E.; et al. Jutge.org: Characteristics and Experiences. IEEE Trans. Learn. Technol. 2018, 11, 321–333. [Google Scholar] [CrossRef]
- Bez, J.L.; Tonin, N.A.; Rodegheri, P.R. URI Online Judge Academic: A tool for algorithms and programming classes. In Proceedings of the 2014 9th International Conference on Computer Science Education, Vancouver, BC, Canada, 22–24 August 2014; pp. 149–152. [Google Scholar] [CrossRef]
- Watanobe, Y. Aizu Online Judge. Available online: https://onlinejudge.u-aizu.ac.jp (accessed on 20 October 2020).
- Mekterović, I.; Brkić, L.; Milašinović, B.; Baranović, M. Building a comprehensive automated programming assessment system. IEEE Access 2020, 8, 81154–81172. [Google Scholar] [CrossRef]
- Ghassan, S. A Practical Approach for Detecting Logical Error in Object Oriented Environment. World Comput. Sci. Inf. Technol. J. 2017, 7, 10–19. [Google Scholar]
- Al-Ashwal, D.; Al-Sewari, E.Z.; Al-Shargabi, A.A. A CASE Tool for JAVA Programs Logical Errors Detection: Static and Dynamic Testing. In Proceedings of the 2018 International Arab Conference on Information Technology (ACIT), Werdanye, Lebanon, 28–30 November 2018; pp. 1–6. [Google Scholar]
- Seo, H.; Sadowski, C.; Elbaum, S.; Aftandilian, E.; Bowdidge, R. Programmers’ build errors: A case study (at google). In Proceedings of the 36th International Conference on Software Engineering (ICSE’14), Hyderabad, India, 31 May–7 June 2014; pp. 724–734. [Google Scholar]
- Minku, L.L.; Mendes, E.; Turhan, B. Data mining for software engineering and humans in the loop. Progress Artif. Intell. 2016, 5, 307–314. [Google Scholar] [CrossRef][Green Version]
- Monperrus, M. Automatic software repair: A bibliography. ACM Comput. Surv. 2018, 51, 1–24. [Google Scholar] [CrossRef]
- Frantzeskou, G.; MacDonell, S.; Stamatatos, E.; Gritzalis, S. Examining the significance of high-level programming features in source code author classification. J. Syst. Softw. 2008, 81, 447–460. [Google Scholar] [CrossRef]
- Mou, L.; Li, G.; Zhang, L.; Wang, T.; Jin, Z. Convolutional neural networks over tree structures for programming language processing. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1287–1293. [Google Scholar]
- White, M.; Tufano, M.; Vendome, C.; Poshyvanyk, D. Deep learning code fragments for code clone detection. In Proceedings of the 31st IEEE/ACM International Conference on Automated Software Engineering, Singapore, 3–7 September 2016; pp. 87–98. [Google Scholar]
- Wei, H.H.; Li, M. Supervised deep features for software functional clone detection by exploiting lexical and syntactical information in source code. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, VIC, Australia, 19–25 August 2017; pp. 3034–3040. [Google Scholar]
- D’Ambros, M.; Lanza, M.; Robbes, R. Evaluating defect prediction approaches: A benchmark and an extensive comparison. Empir. Softw. Eng. 2012, 17, 531–577. [Google Scholar] [CrossRef]
- Pu, Y.; Narasimhan, K.; Solar-Lezama, A.; Barzilay, R. Sk_p: A neural program corrector for mooc. In Proceedings of the 2016 ACM SIGPLAN International Conference on Systems, Programming, Languages and Applications: Software for Humanity, Amsterdam, The Netherlands, 20 October 2016; pp. 39–40. [Google Scholar]
- Gupta, R.; Pal, S.; Kanade, A.; Shevade, S.K. DeepFix: Fixing common c language errors by deep learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), San Francisco, CA, USA, 4–9 February 2017; pp. 1345–1351. [Google Scholar]
- Raychev, V.; Vechev, M.; Yahav, E. Code completion with statistical language models. In Proceedings of the 35th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI’14, Edinburgh, UK, 9–11 June 2014; pp. 419–428. [Google Scholar]
- Rahman, M.M.; Watanobe, Y.; Nakamura, K. A Neural Network Based Intelligent Support Model for Program Code Completion. Sci. Program. 2020, 2020, 7426461. [Google Scholar] [CrossRef]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Teshima, Y.; Watanobe, Y. Bug detection based on LSTM networks and solution codes. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 3541–3546. [Google Scholar]
- Rahman, M.M.; Watanobe, Y.; Nakamura, K. Source Code Assessment and Classification Based on Estimated Error Probability Using Attentive LSTM Language Model and Its Application in Programming Education. Appl. Sci. 2020, 10, 2973. [Google Scholar] [CrossRef]
- Terada, K.; Watanobe, Y. Code Completion for Programming Education based on Recurrent Neural Network. In Proceedings of the 2019 IEEE 11th International Workshop on Computational Intelligence and Applications (IWCIA), Hiroshima, Japan, 9–10 November 2019; pp. 109–114. [Google Scholar]
- Rahman, M.M.; Watanobe, Y.; Nakamura, K. Evaluation of Source Codes Using Bidirectional LSTM Neural Network. In Proceedings of the 2020 3rd IEEE International Conference on Knowledge Innovation and Invention (ICKII), Kaohsiung, Taiwan, 21–23 August 2020; pp. 140–143. [Google Scholar]
- Le, P.; Zuidema, W.H. Quantifying the vanishing gradient and long distance dependency problem in recursive neural networks and recursive LSTMs. In Proceedings of the 1st Workshop on Representation Learning for NLP, Berlin, Germany, 11 August 2016; pp. 87–93. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Intelligent Coding Environment (ICE). Available online: https://onlinejudge.u-aizu.ac.jp/services/ice/ (accessed on 11 December 2020).
- Song, D.; Lee, M.; Oh, H. Automatic and Scalable Detection of Logical Errors in Functional Programming Assignments. In Proceedings of the ACM Programming Languages OOPSLA, Athens, Greece, 20–25 October 2019; Volume 3. 30p. [Google Scholar]
- Allamanis, M.; Barr, E.T.; Devanbu, P.; Sutton, C. A Survey of Machine Learning for Big Code and Naturalness. ACM Comput. Surv. 2018, 51, 37. [Google Scholar] [CrossRef]
- Allamanis, M.; Barr, E.T.; Bird, C.; Sutton, C. Suggesting accurate method and class names. In Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering (ESEC/FSE 2015). Association for Computing Machinery, Bergamo, Italy, 30 August–4 September 2015; pp. 38–49. [Google Scholar] [CrossRef]
- Wang, S.; Liu, T.; Tan, L. Automatically learning semantic features for defect prediction. In Proceedings of the 38th International Conference on Software Engineering (ICSE’16), Austin, TX, USA, 14–22 May 2016; pp. 297–308. [Google Scholar] [CrossRef]
- Pradel, M.; Sen, K. DeepBugs: A learning approach to name-based bug detection. In Proceedings of the ACM Programming Languages, Boston, MA, USA, 4–9 November 2018; Volume 2, pp. 1–147. [Google Scholar] [CrossRef]
- Song, X.; Chen, C.; Cui, B.; Fu, J. Malicious JavaScript Detection Based on Bidirectional LSTM Model. Appl. Sci. 2020, 10, 3440. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Aizu Online Judge. Developers Site (API). 2004. Available online: http://developers.u-aizu.ac.jp/index (accessed on 25 June 2020).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–13. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).