Initial Value Acceleration-Based Alternating Minimization Algorithm for Dynamic Sub-Connected Hybrid Precoding in Millimeter Wave MIMO Systems

Abstract

Symmetry-based sub-connected hybrid precoding is an energy-friendly structure in wireless communications. Most of the prior work set a diagonal constraint on the analog precoder and used a randomly set matrix as the initial analog precoder, which did not match the optimal channel conditions, leading to a decrease in spectral efficiency, and some had huge complexity when calculating the digital precoder. Aiming to solve these problems, this paper proposed a low-complexity hybrid precoding algorithm based on Initial value Acceleration-based Alternating Minimization (IAAM). Leveraging the special structure of analog precoder in sub-connected scheme, we design the analog precoder through low-complexity quadratic programming and use the least square method to obtain the digital precoder. Moreover, we design a heuristic algorithm with the objective function of maximizing the effective channel gain to calculate the initial analog precoder as the starting point for alternating minimization. The simulation results show that the spectral efficiency of this algorithm is at least 17.5% higher than the existing two traditional sub-connected algorithms. Additionally, it increases energy efficiency by at least 12.8% compa with the Orthogonal Matching Pursuit (OMP) algorithm. Its algorithm convergence speed is fast, which increases with the number of RF chains.

1. Introduction

Due to the rapid expansion of wireless network users, the scarcity of spectrum resources has become more and more severe, and people have gradually turned their attention to the millimeter wave, which has abundant spectrum resources [1,2]. Millimeter wave massive MIMO technology uces the physical size of the antenna array by ucing the antenna spacing through the millimeter wave characteristics, which in turn helps to increase the antenna array size to obtain larger array gain to resist attenuation in propagation [3]. Thus, it significantly increases the system capacity while solving the spectrum problem.

The application of massive MIMO technology increases the number of antennas to 64, 128, or even 256, which helps the system generate a directional beam by controlling the phase and amplitude of the signal transmitted by each antenna unit. This can not only effectively enhance the coverage distance of signal transmission, but also uce the interference between adjacent beams, thus greatly improves the system throughput, which has unlimited potential with the increasing number of users and the increasingly more complex signal transmission environment nowadays [4]. This technology is also suitable for applications in millimeter wave communications, which have abundant spectrum resources but are not suitable for long-distance wireless transmission. Therefore, the antenna array scale of the millimeter wave communication system is much larger than that of the traditional communication system. If the precoding scheme still follows the pure digital processing architecture of the traditional communication system, it will greatly increase the amount of data processing and complexity. Additionally, the huge digital and RF links will bring about an increase in cost and power consumption [5,6]. Secondly, if all just use analog components when precoding, it will inevitably bring non-ideal distortion [7]. Therefore, adopting a digital–analog hybrid architecture to convert part of the digital processing work into analog domain beamforming is taken into account. Although the processing performance of the analog domain is slightly worse than that of the digital domain, it can effectively uce the construction cost and power overhead of the system, and the performance difference can also be compensated by architecture design and algorithm optimization. The implementation is that the baseband still uses low-dimensional traditional digital precoding to obtain multiplexing gain, while the RF domain uses phase shifters to implement analog precoding to obtain a higher antenna array gain to realize a wider range of networks coverage and higher transmission rate performance [8]. The current integrated analog beamforming IC is specifically developed for analog phased array applications or hybrid array architectures, in which the hybrid array architecture is a combination of digital beamforming technology and analog beamforming technology.

There are two types of hybrid precoding structures, respectively, called sub-connected and fully-connected according to the connection mode between RF chains and the transmit antennas [9,10]. The sub-connected structure divides the antenna into multiple subsets, which will have a one-on-one connection to different RF chains, respectively. While in fully-connected structure, every RF chain will connect to all antennas through phase shifters [11]. Obviously, the sub-connected structure is more energy friendly in contrast, which is beneficial to improving the energy efficiency of the system. However, there exists a fundamental contradiction between energy efficiency and spectral efficiency: the improvement of energy efficiency will lead to the deterioration of spectral efficiency [12]. Therefore, further optimizing the spectral efficiency of the sub-connected structure has always been a research hotspot.

Omar et al. [8] documented that the millimeter wave channel can be approximated as a sparse channel. According to the sparse channel characteristics, it can be determined that the beamforming gain provided by some of the antenna-RF pairs is not high. The sub-connected structure sacrifices part of the low beamforming gain in exchange for the uction in energy consumption on the RF hardware, which is exactly based on the millimeter wave channel characteristics. Yu et al. [10] proposed a sub-connected structure based on the Succesive Interference Cancellation (SIC) algorithm, which has low complexity. However, it assumes that the digital precoder is a diagonal matrix and requires that the number of RF chains is equal to the number of data streams, which means the digital precoder only allocates power for different data streams. Additionally, the allocation of the RF-antenna pairs is fixed, which means that the channel characteristics are not fully utilized, which has great limitations on spectral efficiency performance. Yu et al. [13] also proposed an alternating minimization algorithm based on Semi-Definite Relaxation (SDR) in sub-connected hybrid precoding, which effectively increases the spectral efficiency, but its computational complexity brought by the convex optimization toolbox during each iteration is too high and it sets an extra diagonal constraint on the analog precoder, which does not match the channel conditions perfectly, resulting in low effective channel gain being obtained. Jing et al. [14] designed a heuristic algorithm to construct the analog and digital precoder of the sub-connected structure. The algorithm complexity is low, but it has a stricter quantitative relationship between the number of data streams, receiving antennas, and RF chains, which cannot be applied to all transmission scenarios. Sungwoo Park et al. [15] deduced the optimal solution of the dynamic sub-connected hybrid precoding scheme, but the calculation amount was too large. So, they designed a low complexity heuristic algorithm based on minimizing the Minkowski-1 norm to allocate the antennas, but the spectral efficiency of this method is not ideal because the algorithm is greedy. Yu [16] also proposed a group-connected structure that compromises between the fully-connected and the sub-connected structure to find a balance between energy efficiency and spectral efficiency, but the performance was generally average.

On the basis of the above analysis, most of the prior work on the sub-connected structure hybrid precoding can not obtain maximum effective channel gain due to setting extra constraints on hybrid precoder, and some have the problem of high computational complexity and too strict control of parameters. In order to avoid performance degradation and limitations of application scenarios due to these problems, this paper proposed an efficient algorithm to realize dynamic sub-connected hybrid precoding, in which an alternating minimization algorithm without any extra constraint was designed to solve the joint design problem of analog and digital precoders. By simplifying the spectral efficiency maximization problem to the effective channel gain maximization problem, we also designed a heuristic algorithm to calculate the initial value of the analog precoder and used it as the starting point of alternating minimization to speed up the convergence and prevent it from falling into a suboptimal solution.

The novel contributions of this paper are as follows:

• Leveraging the special structure of the sub-connected analog precoder, which has unit zero-norm of its row vector, the alternating minimization is completed through the quadratic programming, which maintains the low complexity when designing the analog precoder as well as obtaining higher effective channel gain compa with the traditional algorithms.
• A heuristic algorithm is proposed to calculate the initial value of the analog precoder, which can speed up the convergence and improve the spectral efficiency compa with the randomly set initial value used in traditional alternating minimization.
• The proposed algorithm sets no extra diagonal constraint on the structure of the hybrid precoder and no quantitative relationship between the parameters, which increases the flexibility of its application scenarios.

The remainder of this article is organized as follows. In Section 2, we describe the millimeter wave channel model, and the objective function of antenna subsets allocation with large searching volume is derived. In Section 3, we simplify the original objective function to a decomposable objective function and solve the optimizing problem with the proposed algorithm. In Section 4, we analyze several simulation results of the proposed algorithm, comparing with other existing algorithms. In Section 5, we conclude the paper and propose some future research directions.

2. System Model

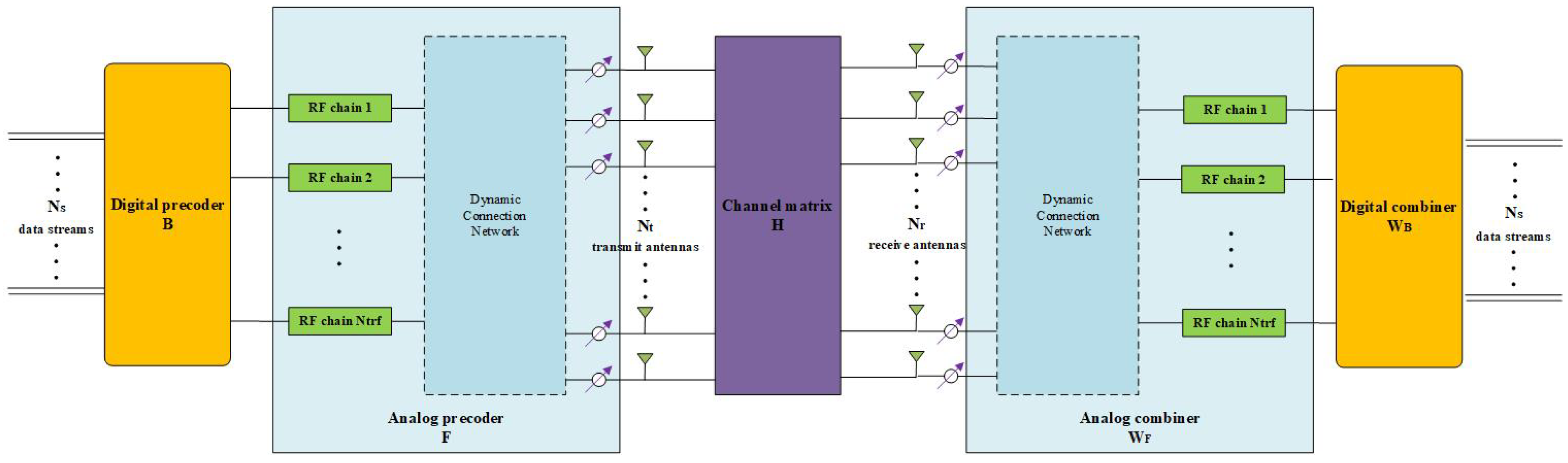
The system framework is shown in Figure 1. This paper considers a point-to-point millimeter-wave MIMO system, adopts the geometric Saleh–Valenzuela channel model, and uses a uniform square planar array (USPA). Because of the symmetrical structure of the precoding system, the hybrid combiner at the receiving end can be designed similarly as the hybrid precoder, so we omit it and focus on the design of precoders.

Assuming the transmitter with ${\mathrm{N}}_{\mathrm{t}}$ antennas sends ${\mathrm{N}}_{\mathrm{s}}$ data streams to the receiver with ${\mathrm{N}}_{\mathrm{r}}$ receiving antennas, the number of RF chains is ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$, and ${\mathrm{N}}_{\mathrm{s}}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}\le {\mathrm{N}}_{\mathrm{t}}$. The baseband signal $\mathrm{y}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{r}}\times 1}$ at the receiver can be written as:

$$\mathrm{y}=\mathrm{HFBx}+\mathrm{n}$$

(1)

where $\mathrm{H}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{r}}\times {\mathrm{N}}_{\mathrm{t}}}$ denotes the millimeter wave channel matrix; $\mathrm{F}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{t}}\times {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}$ is the analog precoding matrix; $\mathrm{B}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}\times {\mathrm{N}}_{\mathrm{s}}}$ is the digital precoding matrix, satisfying ${\parallel \mathrm{FB}\parallel }_{\mathrm{F}}^2={\mathrm{N}}_{\mathrm{s}}$; $\mathrm{x}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{s}}\times 1}$ denotes the transmitted signal; $\mathrm{n}\in {\mathrm{C}}^{{\mathrm{N}}_{\mathrm{r}}\times 1}$ denotes noise vector, obeying complex Gaussian distribution with 0-mean and ${\sigma }^2\mathrm{I}$-covariance. The input signal x satisfies ${\mathrm{E}}_{\mathrm{x}}\left(\mathrm{x}{\mathrm{x}}^{\mathrm{H}}\right)=\mathrm{P}/{\mathrm{N}}_{\mathrm{s}}*{\mathrm{I}}_{{\mathrm{N}}_{\mathrm{s}}}$. ${\mathrm{I}}_{{\mathrm{N}}_{\mathrm{s}}}$ is the ${\mathrm{N}}_{\mathrm{s}}$-dimensional unit matrix, and P is the total output power.

MmWave propagation has limited spatial selectivity or scattering, and the massive MIMO antenna array increases the correlation between the antennas [8]. Therefore, we adopted the geometric Saleh–Valenzuela channel model in this paper, using a uniform square planar array, and the channel matrix H can be expressed as:

$$\mathrm{H}=\sqrt{\frac{N_t{N}_r}{N_{cl}{N}_{\mathrm{ray}}}}\sum _{i=1}^{N_{cl}}\sum _{l=1}^{N_{\mathrm{ray}}}{\alpha }_{il}{a}_r\left({\mathsf{\Phi }}_{il}^r,{\theta }_{il}^r\right)a_t{\left({\mathsf{\Phi }}_{il}^t,{\theta }_{il}^t\right)}^H$$

(2)

where $N_{cl}$ is the number of scattering clusters and $N_{ray}$ is the number of paths in each cluster; ${\alpha }_{il}$ denotes the complex gain of the l-th path of the i-th cluster; ${\varphi }_{il}^r\left({\varphi }_{il}^t\right)$ and ${\theta }_{il}^r\left({\theta }_{il}^t\right)$, respectively, denote the horizontal angle of arrival (departure) and the vertical angle of arrival (departure); $a_r\left({\mathsf{\Phi }}_{il}^r,{\theta }_{il}^r\right)$ and $a_t\left({\mathsf{\Phi }}_{il}^t,{\theta }_{il}^t\right)$ represent the antenna array response vectors at the receiver and the transmitter, respectively, and can be written as:

$$a_t\left({\mathsf{\Phi }}_{il}^t,{\theta }_{il}^t\right)=\frac{1}{\sqrt{N_t}}{\left[\begin{array}{c}1,e^{jkd\left(msin\left({\mathsf{\Phi }}_{il}^t\right)sin\left({\theta }_{il}^t\right)+ncos\left({\theta }_{il}^t\right)\right)},\dots ,\\ e^{jkd\left(\left(\sqrt{N_t}-1\right)sin\left({\mathsf{\Phi }}_{il}^t\right)sin\left({\theta }_{il}^t\right)+\left(\sqrt{N_t}-1\right)cos\left({\theta }_{il}^t\right)\right)}\end{array}\right]}^T$$

(3)

$$a_r\left({\mathsf{\Phi }}_{il}^r,{\theta }_{il}^r\right)=\frac{1}{\sqrt{N_r}}{\left[\begin{array}{c}1,e^{jkd\left(msin\left({\mathsf{\Phi }}_{il}^r\right)sin\left({\theta }_{il}^r\right)+ncos\left({\theta }_{il}^r\right)\right)},\dots ,\\ e^{jkd\left(\left(\sqrt{N_r}-1\right)sin\left({\mathsf{\Phi }}_{il}^r\right)sin\left({\theta }_{il}^r\right)+\left(\sqrt{N_r}-1\right)cos\left({\theta }_{il}^r\right)\right)}\end{array}\right]}^T$$

(4)

where $k=2\pi /\lambda$, $\lambda$ is the wavelength, d is the antenna spacing, and we set $d=\lambda /2$. In addition, in the angle domain, the central angle of the cluster is uniformly distributed, and the angle spread of the multipath component in the cluster obeys the Laplace distribution. Perfect channel state information is assumed to have been obtained through channel estimation [17] and effective feedback techniques [18] in this paper, so we can focus on the precoding design.

Based on Shannon’s theorem, the system spectral efficiency can be expressed as:

$$\mathrm{SE}={log}_2\left(\left|{\mathrm{I}}_{{\mathrm{N}}_{\mathrm{r}}}+\frac{\mathrm{P}}{{\mathrm{N}}_{\mathrm{S}}{\sigma }^2}{\mathrm{HFBB}}^{\mathrm{H}}{\mathrm{F}}^{\mathrm{H}}{\mathrm{H}}^{\mathrm{H}}\right|\right)$$

(5)

where ${\left(·\right)}^{\mathrm{H}}$ represents the conjugate transpose of the matrix, and |·| represents the determinant of the matrix. We set $\mathrm{B}={\left({\mathrm{F}}^{\mathrm{H}}\mathrm{F}\right)}^{-\frac{1}{2}}\widehat{\mathrm{B}}$, and Equation (5) can be equivalent to [15]:

$$\mathrm{SE}={log}_2\left(\left|{\mathrm{I}}_{{\mathrm{N}}_{\mathrm{r}}}+\frac{\mathrm{P}}{{\mathrm{N}}_{\mathrm{S}}{\sigma }^2}{\mathrm{H}}_{\mathrm{eff}}\widehat{\mathrm{B}}{\widehat{\mathrm{B}}}^{\mathrm{H}}{\mathrm{H}}_{\mathrm{eff}}^{\mathrm{H}}\right|\right)$$

(6)

where ${\mathrm{H}}_{\mathrm{eff}}$ represents the effective channel, defined as:

$$\begin{array}{c}{\mathrm{H}}_{\mathrm{eff}}=\mathrm{H}\overline{\mathrm{F}}\hfill \end{array}$$

(7)

$$\begin{array}{c}\overline{\mathrm{F}}=\mathrm{F}{\left({\mathrm{F}}^{\mathrm{H}}\mathrm{F}\right)}^{-\frac{1}{2}}\hfill \end{array}$$

(8)

If the analog precoder F is given, the effective channel ${\mathrm{H}}_{\mathrm{eff}}$ can be determined, and the digital precoder B can be obtained through traditional SVD decomposition. The design of the analog precoder is related to the precoding structure used. The dynamic sub-connected structure used in this article on the transmit side is shown in Figure 1. The dynamic connection network in the Figure 1 is the core of this structure, which is realized by a switch network. The switches dynamically allocate the transmit antennas connected to different phase shifters to the RF link. The switch has smaller power consumption than the phase shifter, although it would generate a certain insertion loss. However, reference [19] shows that the implementation of switch-based hybrid precoding is a promising solution after simulation verification. In the dynamic connection network, each RF chain in the analog precoding process is connected to a non-empty and non-repetitive subset of the transmitting antenna ${\left\{{\mathrm{S}}_{\mathrm{j}}\right\}}_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}$. ${\mathrm{S}}_{\mathrm{j}}$ represents the set of transmit antennas connected to the j-th RF chain. For example, if the i-th transmit antenna is connected to the j-th RF chain, then $\mathrm{i}\in {\mathrm{S}}_{\mathrm{j}}$. Therefore, the constraint for designing the analog precoding matrix can be written as [20]:

$$\left|{\mathrm{F}}_{\mathrm{i},\mathrm{j}}\right|=1_{{\mathrm{S}}_{\mathrm{j}}}\left(\mathrm{i}\right)\forall (\mathrm{i},\mathrm{j})$$

(9)

where $1_{{\mathrm{S}}_{\mathrm{j}}}\left(\mathrm{i}\right)$ can be defined as:

$$1_{\mathrm{Sj}}\left(\mathrm{i}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{i}\in {\mathrm{S}}_{\mathrm{j}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(10)

the set of all non-empty subsets ${\mathrm{S}}_{\mathrm{j}}$ is S, which is defined as follows:

$$\mathrm{S}=\left\{{\left\{{\mathrm{S}}_{\mathrm{j}}\right\}}_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}\mid {\cup }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}{\mathrm{S}}_{\mathrm{j}}=\left\{1,2,\dots ,{\mathrm{N}}_{\mathrm{t}}\right\},{\mathrm{S}}_{\mathrm{j}}\cap {\mathrm{S}}_{\mathrm{k}}=\varnothing ,\forall \mathrm{j}\ne \mathrm{k}.\right\}$$

(11)

and the problem of designing the analog precoding matrix F can be transformed into:

$$\underset{\left\{{\mathrm{S}}_j\right\}\in \mathrm{S}}{max}SE\left(\left\{{\mathrm{S}}_{\mathrm{j}}\right\}\right)$$

(12)

Equation (12) is a joint optimization problem, which requires exhaustive search for the combination of all non-empty and no internal repeating elements subset ${\left\{{\mathrm{S}}_{\mathrm{j}}\right\}}_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}$ to find the optimal solution, and the total search volume is the second type Stirling number [21], as follows:

$$\left|\mathrm{S}\right|=\frac{1}{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}!}\sum _{\mathrm{k}=0}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}!}{(-1)}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}-\mathrm{k}}\left(\begin{array}{c}\mathrm{Nt}\\ \mathrm{k}\end{array}\right){\mathrm{k}}^{\mathrm{N}\mathrm{t}}$$

(13)

The optimal analog precoding matrix can be found by exhaustive search with the search volume of Equation (13), but even if the number of RF chains and transmitting antennas are already small, the search volume is also very large, which is obviously not practical. For example, when ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ = 4 and ${\mathrm{N}}_{\mathrm{t}}$ = 16, the total search volume |S| is also $1.718\times {10}^8$.

3. Proposed Algorithm

In this section, based on the system model in the previous section, we will propose an IAAM based algorithm to implement dynamic sub-connected hybrid precoding.

3.1. Alternating Minimization

As the search volume for exhaustive search through Equation (13) is too large. We need to simplify the objective function. As we all know, the unconstrained full-digital precoding matrix ${\mathrm{F}}_{\mathrm{opt}}$, which is the first ${\mathrm{N}}_{\mathrm{s}}$ volumes of the right singular matrix of the channel matrix H, is the precoding matrix with the best theoretical spectral efficiency. Therefore, the design problem of the analog and digital precoding matrix can be written as:

$$\begin{array}{cc}\underset{\mathrm{F},\mathrm{B}}{min}\hfill & {∥{\mathrm{F}}_{\mathrm{opt}}-\mathrm{FB}∥}_{\mathrm{F}}^2\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & {∥{\mathrm{F}}_{\mathrm{i},:}∥}_0=1,\forall \mathrm{i}\hfill \\ \hfill & \left|{\mathrm{F}}_{\mathrm{i},\mathrm{j}}\right|=1_{\mathrm{Sj}}\left(\mathrm{i}\right),\forall \mathrm{i},\mathrm{j}\hfill \\ \hfill & {\parallel \mathrm{FB}\parallel }_{\mathrm{F}}^2={\mathrm{N}}_{\mathrm{s}}\hfill \end{array}$$

(14)

We use an alternating minimization method to decompose problem (14) into two sub-problems alternately: given analog precoder F, design digital precoder B; given digital precoder B, design analog precoder F. We do this iteratively until the value of the objective function of problem (14) increases compa with the previous iteration, then the analog and digital precoder obtained in the previous iteration will be taken as the optimal solution. The specific iteration process is as follows:

Given the analog precoder F, the digital precoder can be directly calculated through the least squares method and normalized:

$$\mathrm{B}=\frac{\sqrt{{\mathrm{N}}_{\mathrm{s}}}{\mathrm{F}}^{†}{\mathrm{F}}_{\mathrm{opt}}}{{∥{\mathrm{FF}}^{†}{\mathrm{F}}_{\mathrm{opt}}∥}_{\mathrm{F}}}$$

(15)

Given digital precoder B, as the zero norm of each row of the analog precoder F in the given constraints is 1, the objective function of Formula (14) can be expanded as:

$$\underset{1\le j\le N_{\mathrm{rf}}^{\mathrm{t}}}{min}\sum _{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{t}}}\left[{\left({\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},1}}-{\mathrm{F}}_{\mathrm{i},\mathrm{j}}{\mathrm{B}}_{\mathrm{j},1}\right)}^2+{\left({\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},2}}-{\mathrm{F}}_{\mathrm{i},\mathrm{j}}{\mathrm{B}}_{\mathrm{j},2}\right)}^2+\cdots +{\left({\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},{\mathrm{N}}_{\mathrm{s}}}}-{\mathrm{F}}_{\mathrm{i},\mathrm{j}}{\mathrm{B}}_{\mathrm{j},{\mathrm{N}}_{\mathrm{s}}}\right)}^2\right]$$

(16)

where ${\mathrm{F}}_{\mathrm{i},\mathrm{j}}$ denotes the element in the i-th row and the j-th column of F. Formula (16) calculates the non-zero elements of F row by row. It can be found that Formula (16) is a unary quadratic model and has a minimum value. So, the value of ${\mathrm{F}}_{\mathrm{i},\mathrm{j}}$ can be directly calculated and normalized to meet the constraints:

$$\begin{array}{c}{\mathrm{a}}_{\mathrm{i},\mathrm{j}}=\frac{{\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},1}}{\mathrm{B}}_{\mathrm{j},1}+{\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},2}}{\mathrm{B}}_{\mathrm{j},2}+\cdots +{\mathrm{F}}_{{\mathrm{opt}}_{\mathrm{i},{\mathrm{N}}_{\mathrm{s}}}}{\mathrm{B}}_{\mathrm{j},{\mathrm{N}}_{\mathrm{s}}}}{{\mathrm{B}}_{\mathrm{j},1}^2+{\mathrm{B}}_{\mathrm{j},2}^2+\cdots +{\mathrm{B}}_{\mathrm{j},{\mathrm{N}}_{\mathrm{s}}}^2}\hfill \\ {\mathrm{F}}_{\mathrm{i},\mathrm{j}}=\frac{{\mathrm{a}}_{\mathrm{i},\mathrm{j}}}{\left.\mid {\mathrm{a}}_{\mathrm{i},\mathrm{j}}\right]},\mathrm{i}=1,2,\dots ,{\mathrm{N}}_{\mathrm{t}},1\le \mathrm{j}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}\hfill \end{array}$$

(17)

where ${\mathrm{a}}_{\mathrm{i},\mathrm{j}}$ is a virtual variable. Combine Formulas (16) and (17) to design the analog precoder.

The above is the process of the alternating minimization solution, and the algorithm flow is summarized in Algorithm 1.

Algorithm 1 Alternating Optimization Of Hybrid Precoding Matrix.

Input:${\mathrm{F}}_0,{\mathrm{F}}_{\mathrm{opt}}$ Output:$\mathrm{F},\mathrm{B}$  Initialization: In the first iteration, set $\mathrm{F}={\mathrm{F}}_0$, calculate $\mathrm{B}=\frac{\sqrt{{\mathrm{N}}_{\mathrm{s}}}{\mathrm{F}}^{†}{\mathrm{F}}_{\mathrm{opt}}}{{∥{\mathrm{FF}}^{†}{\mathrm{F}}_{\mathrm{opt}}∥}_{\mathrm{F}}}$, $\mathrm{target}={∥{\mathrm{F}}_{\mathrm{opt}}-\mathrm{FB}∥}_{\mathrm{F}}^2,\mathrm{delta}=0$. 1:  while $\mathrm{delta}\ge 0$ do Given B, solve problem (14) by solving problem (16) to obtain F in (17) row by row. Given F, solve problem (14) to obtain B in (15). Set delta = target $-{∥{\mathrm{F}}_{\mathrm{opt}}-\mathrm{FB}∥}_{\mathrm{F}}^2$. Update target =${∥{\mathrm{F}}_{\mathrm{opt}}-\mathrm{FB}∥}_{\mathrm{F}}^2$. 2: return F,B

It is worth noting that, since the minimization objective function ${∥{\mathrm{F}}_{\mathrm{opt}}-\mathrm{FB}∥}_{\mathrm{F}}^2$ is specified, its value will be uced in each iteration, so the convergence of Algorithm 1 can be effectively guaranteed.

3.2. The Design of Initial Value of Analog Precoding Matrix

From the above, we can see that Algorithm 1 needs an initial analog precoding matrix input ${\mathrm{F}}_0$ to begin the iteration. If ${\mathrm{F}}_0$ is set randomly, the algorithm will converge too slowly and fall into a suboptimal solution. Therefore, it is necessary to design the initial value of the analog precoding matrix. Firstly, it can be known from Formulas (9) and (10) that ${\left\{{\mathrm{S}}_{\mathrm{j}}\right\}}_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}$ actually represents the position of non-zero elements in the analog precoding matrix, which means that the function of the analog precoder is to match the optimal channel conditions for the signal to obtain the maximum effective channel gain, so the objective function for designing the analog precoding matrix can be set to maximize ${∥{\mathrm{H}}_{\mathrm{eff}}∥}_{\mathrm{F}}^2$, which can be transformed into:

$$\begin{array}{cc}\hfill {∥{\mathrm{H}}_{\mathrm{eff}}∥}_{\mathrm{F}}^2& =tr\left({\mathrm{H}}_{\mathrm{eff}}^{\mathrm{H}}{\mathrm{H}}_{\mathrm{eff}}\right)\hfill \\ \hfill & =tr\left({\overline{\mathrm{F}}}^{\mathrm{H}}{\mathrm{H}}^{\mathrm{H}}\mathrm{H}\overline{\mathrm{F}}\right)\hfill \end{array}$$

(18)

Therefore, the problem of designing the analog precoder can be expressed as:

$$\begin{array}{c}\underset{\mathrm{F}}{max}tr\left({\overline{\mathrm{F}}}^{\mathrm{H}}{\mathrm{H}}^{\mathrm{H}}\mathrm{H}\overline{\mathrm{F}}\right)\hfill \\ \mathrm{s}.t.\overline{\mathrm{F}}=\mathrm{F}{\left({\mathrm{F}}^{\mathrm{H}}\mathrm{F}\right)}^{-\frac{1}{2}}\hfill \\ {∥{\mathrm{F}}_{\mathrm{i},:}∥}_0=1,\forall \mathrm{i}\hfill \\ \left|{\mathrm{F}}_{\mathrm{i},\mathrm{j}}\right|=1_{{\mathrm{S}}_{\mathrm{j}}}\left(\mathrm{i}\right),\forall \mathrm{i},\mathrm{j}\hfill \\ {∥{\mathrm{F}}_{:\mathrm{j}}∥}_0\ne 0,\forall \mathrm{j}\hfill \\ {\mathrm{S}}_{\mathrm{j}}\in \mathrm{S}\hfill \end{array}$$

(19)

where ${\parallel ·\parallel }_0$ represents the zero norm, ${\mathrm{F}}_{\mathrm{i},:}$ represents the i-th row of matrix F. To ensure the utilization of the RF chains, each column of F has at least one non-zero element.

Since the constraints are discrete and non-convex, it is hard to directly solve the problem (19). Inspi by [15], the reference [15] gives the optimal solution of problem (19) under the unconstrained condition:

$$\widehat{\mathrm{F}}={\mathrm{V}}_{\mathrm{R}}\mathrm{A}$$

(20)

where ${\mathrm{V}}_{\mathrm{R}}$ is the first ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ column of the left eigenvector matrix of ${\mathrm{H}}^{\mathrm{H}}\mathrm{H}$, and A is an arbitrary ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}\times {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ unitary matrix with full rank. This is the optimal solution when the rank of the channel matrix is not greater than the number of RF chains.

Since Formula (20) is the optimal solution of problem (19) under unconstrained conditions, the designing problem of the initial value ${\mathrm{F}}_0$ can be written as:

$$\begin{array}{c}\underset{{\mathrm{F}}_0\in \mathrm{F}}{min}{∥{\mathrm{F}}_0-\widehat{\mathrm{F}}∥}_{\mathrm{F}}^2\\ \mathrm{s}.\mathrm{t}.{∥{\mathrm{F}}_{0_{\mathrm{i},:}}∥}_0=1,\forall \mathrm{i}\\ \left|{\mathrm{F}}_{0_{\mathrm{i},\mathrm{j}}}\right|=1_{{\mathrm{S}}_{\mathrm{j}}}\left(\mathrm{i}\right),\forall \mathrm{i},\mathrm{j}\\ {∥{\mathrm{F}}_{0_{:,\mathrm{j}}}∥}_0\ne 0,\forall \mathrm{j}\end{array}$$

(21)

Based on the above analysis, we propose a heuristic algorithm that uses the matrix $\widehat{\mathrm{F}}$ to calculate the initial value ${\mathrm{F}}_0$. The algorithm flow is shown in Algorithm 2. First, in steps 1 to 16, sort the elements in each row of the matrix $\widehat{\mathrm{F}}$, keep the maximum value, and set the remaining elements to zero. If the 0 norm of each column of $\widehat{\mathrm{F}}$ is not less than 1, then we set it as the initial value ${\mathrm{F}}_0$; otherwise, if all elements in column L of $\widehat{\mathrm{F}}$ are zero, then search for non-zero elements in all the columns in $\widehat{\mathrm{F}}$ whose 0 norm is greater than 1 and assign this value to the element in the L-th column in the same row, set it to zero after assignment, and use the updated $\widehat{\mathrm{F}}$ as the initial value of ${\mathrm{F}}_0$, where $1\le \mathrm{L}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$. In this step, each RF chain is assigned at least one antenna that matches the channel conditions as much as possible, which not only increases the effective channel gain as much as possible but also guarantees the utilization rate of the RF chains; then, in step 17 to step 20, the phase of the non-zero elements in the i-th row of $\widehat{\mathrm{F}}$ is adjusted to the phase of the sum of the elements in the i-th column of the channel matrix H and updated to ${\mathrm{F}}_0$ after normalization, where $1\le \mathrm{i}\le {\mathrm{N}}_{\mathrm{t}}$. The purpose of this step is to make the signal match the channel conditions better and obtain higher effective channel gain by phase modulating the signal. This algorithm is a heuristic algorithm, which is a low-complexity method compa to the exhaustive search.

It is worth noting that the input $\widehat{\mathrm{F}}={\mathrm{V}}_{\mathrm{R}}\mathrm{A}$. In order to obtain a better initial value ${\mathrm{F}}_0$, when running Algorithm 2, we run multiple times and use a different matrix A, and choose the one that gets the largest value of ${∥{\mathrm{HF}}_0∥}_{\mathrm{F}}^2$ as the value of A. Afterwards, we found that the value of A had little influence on the result after Algorithm 1.

Algorithm 2 Iterative initial value of analog precoding matrix.

Input:$\widehat{\mathrm{F}},\mathrm{H}$ Output:${\mathrm{F}}_0$ Initialization:${\mathrm{F}}_0=0$ 1: for$\mathrm{i}=1,2,\dots ,{\mathrm{N}}_{\mathrm{t}}$do 2: ${\mathrm{j}}_0={max}_{1\le \mathrm{j}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}{\widehat{\mathrm{F}}}_{\mathrm{i},\mathrm{j}},$ 3: ${\mathrm{F}}_{0_{\mathrm{i},{\mathrm{j}}_0}}={\widehat{\mathrm{F}}}_{\mathrm{i},{\mathrm{j}}_0}$ 4: while exist ${∥{\mathrm{F}}_{0_{:,\mathrm{j}}}∥}_0=0,1\le \mathrm{j}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ do 5:     ${\mathrm{m}}_0=\varnothing$ 6:     for $\mathrm{j}=1,2,\dots ,{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ do 7:         if ${∥{\mathrm{F}}_{0_{:,\mathrm{j}}}∥}_0=0$ then 8:            ${\mathrm{j}}_0=\mathrm{j}$ 9:         else 10:            if ${∥{\mathrm{F}}_{0_{:,\mathrm{j}}}∥}_0\ge 1$ then 11:                ${\mathrm{m}}_0=\left\{\mathrm{j}\right\}\cup {\mathrm{m}}_0$                           12:     $\left\{{\mathrm{i}}_0,{\mathrm{k}}_0\right\}={min}_{1\le \mathrm{i}\le {\mathrm{N}}_{\mathrm{t}},\mathrm{k}\in {\mathrm{m}}_0}{\mathrm{F}}_{0_{\mathrm{i},\mathrm{k}}}$ 13:     ${\mathrm{F}}_{0_{{\mathrm{i}}_0,{\mathrm{j}}_0}}={\mathrm{F}}_{0_{{\mathrm{i}}_0,{\mathrm{k}}_0}},{\mathrm{F}}_{0_{{\mathrm{i}}_0,{\mathrm{k}}_0}}=0$ 14: for$\mathrm{i}=1,2,\dots ,{\mathrm{N}}_{\mathrm{t}}$do 15:     ${\mathrm{j}}_0=$ find $\left(\left|{\mathrm{F}}_{0_{\mathrm{i},\mathrm{j}}}\right|\ne 0\right),1\le \mathrm{j}\le {\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ 16:     angle $\left({\mathrm{F}}_{0_{\mathrm{i},{\mathrm{j}}_0}}\right)=$ angle $\left({\sum }_{\mathrm{n}=1}^{\mathrm{n}={\mathrm{N}}_{\mathrm{r}}}{\mathrm{H}}_{\mathrm{n},\mathrm{i}}\right)$ 17:     ${\mathrm{F}}_{0_{\mathrm{i},{\mathrm{j}}_0}}=\frac{{\mathrm{F}}_{0_{\mathrm{i},{\mathrm{j}}_0}}}{\left|{\mathrm{F}}_{0_{\mathrm{i},{\mathrm{j}}_0}}\right|}$ 18: return${\mathrm{F}}_0$

Finally, we summarize the whole algorithm flow of the proposed IAAM algorithm in Figure 2.

4. Numerical Simulation Analysis

In this section, we verify the effectiveness of the proposed IAAM algorithm by analyzing the simulation results with different parameters and contrast with optimal pure digital precoding, fixed-sub-connected hybrid precoding, full-connected based OMP algorithm [8], SIC based algorithm [10], and sub-connected based Dynamic Connected (DC) algorithm [14]. The parameters of the channel model are set in

Table 1. Simulation parameters.

Parameter	Value
Number of clusters ${\mathrm{N}}_{\mathrm{cl}}$	4
Number of propagation paths per cluster ${\mathrm{N}}_{\mathrm{ray}}$	20
Antenna array deployed	USPA
Azimuth Angle-of-Arrival (AoA)
and Angle-of-Departure (AoD)	Uniform$[0,2\pi ]$
cluster angles distribution
Angular spread	${10}^{\circ }$
Number of transmitter antennas ${\mathrm{N}}_{\mathrm{t}}$	64
Number of reciever antennas ${\mathrm{N}}_{\mathrm{r}}$	4
Number of RF chains ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$	4
Number of data streams ${\mathrm{N}}_{\mathrm{s}}$	4

. MATLAB R2018a is used for simulation, and the simulation results are based on 1000 random millimeter wave channel samples.

Figure 3 shows the spectral efficiency (SE) of different precoding algorithms with the increasing SNR. It can be seen from Figure 3 that, compa with other sub-connected based methods, the proposed algorithm has the highest spectral efficiency under the same SNR, and is close to the full-connected-based OMP algorithm. The fixed-sub-connected method has poor adaptability to channel conditions and thus has the worst performance. The DC algorithm has better performance than the fixed-sub-connected method because it adaptively allocates antennas, but it only optimizes the analog precoding, which only uses the phase characteristics. The SIC-based algorithm both optimizes the analog and the digital precoding, but its allocation of RF-antenna pairs is fixed, which means the channel characteristics are not fully utilized, so its spectral efficiency performance is only higher than the DC algorithm and the fixed sub-connection. The OMP algorithm is based on a fully-connected structure, which can obtain more beamforming gain from all antennas compa with the sub-connected one, but it also leads to more energy consumption from a large number of phase shifters in exchange.

Then, we conducted a simulation analysis on the system energy efficiency of the proposed algorithm. The energy efficiency calculation formula of the hybrid precoding system is:

$$\mathrm{EE}=\frac{\mathrm{SE}}{{\mathrm{P}}_{\mathrm{common}}+{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}{\mathrm{P}}_{\mathrm{rf}}+{\mathrm{N}}_{\mathrm{t}}{\mathrm{P}}_{\mathrm{pa}}+{\mathrm{N}}_{\mathrm{ps}}{\mathrm{P}}_{\mathrm{ps}}+{\mathrm{N}}_{\mathrm{sw}}{\mathrm{P}}_{\mathrm{sw}}+{\mathrm{P}}_{\mathrm{o}}}$$

(22)

where ${\mathrm{P}}_{\mathrm{common}}$, ${\mathrm{P}}_{\mathrm{rf}}$, ${\mathrm{P}}_{\mathrm{pa}}$, ${\mathrm{P}}_{\mathrm{ps}}$, ${\mathrm{P}}_{\mathrm{sw}}$ and ${\mathrm{P}}_{\mathrm{o}}$ are, respectively, the power of the transmitter, RF chain, power amplifier, phase shifter, switch, and the other circuit components, including baseband processor, filtering, etc. This article sets the simulation parameters as: ${\mathrm{P}}_{\mathrm{common}}$ = ${\parallel \mathrm{FB}\parallel }_{\mathrm{F}}^2$ W, ${\mathrm{P}}_{\mathrm{rf}}$ = 0.3 W, ${\mathrm{P}}_{\mathrm{ps}}$ = 0.05 W, ${\mathrm{P}}_{\mathrm{pa}}$ = 0.3 W, ${\mathrm{P}}_{\mathrm{sw}}$ = 0.01 W, ${\mathrm{P}}_{\mathrm{o}}$ = 0.5 W [22]. ${\mathrm{N}}_{\mathrm{sw}}$ and ${\mathrm{N}}_{\mathrm{ps}}$ are, respectively, the number of switches and the number of phase shifters, defined as follows:

$${\mathrm{N}}_{\mathrm{sw}},{\mathrm{N}}_{\mathrm{ps}}=\left\{\begin{array}{cc}{\mathrm{N}}_{\mathrm{t}}{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}& \mathrm{fully}-\mathrm{connected}\hfill \\ {\mathrm{N}}_{\mathrm{t}}& \mathrm{sub}-\mathrm{connected}\hfill \end{array}\right.$$

(23)

Figure 4 shows a comparison between the proposed IAAM algorithm and the fully-connected based OMP algorithm with the changes in the number of RF chains (${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$). In terms of sub-connected structure, according to Formula (23), both ${\mathrm{N}}_{\mathrm{sw}}$ and ${\mathrm{N}}_{\mathrm{ps}}$ have nothing to do with ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$, while they both increase linearly with ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ in the fully connected structure. Therefore, as ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ increases, the energy consumption of the fully-connected structure increases much faster than that of the sub-connected structure, which means the denominator in Formula (22) increases faster, and because the spectral efficiency(SE) of OMP algorithm is already close to the full-digital precoding, according to Figure 3, the increase in the RF chains only brings about a little increase in spectral efficiency, which is the numerator in Formula (22), thus leading to a continuous drop in its energy efficiency(EE). While the spectral efficiency of the proposed IAAM algorithm increases rapidly with ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ at first, but the increase slows down after the number of RF chains exceeds 8, thus its energy efficiency experiences a slight increase at first. Later, it also decreases with the increase in ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$, but because its overall energy consumption increases slower than the fully-connected structure, its overall energy efficiency declines slower than the fully-connected based OMP algorithm. It can be seen from Figure 4 that the energy efficiency of the proposed sub-connection-based IAAM algorithm is much higher than that of the fully-connected OMP algorithm, and the performance gap gradually expands with the increase in ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$.

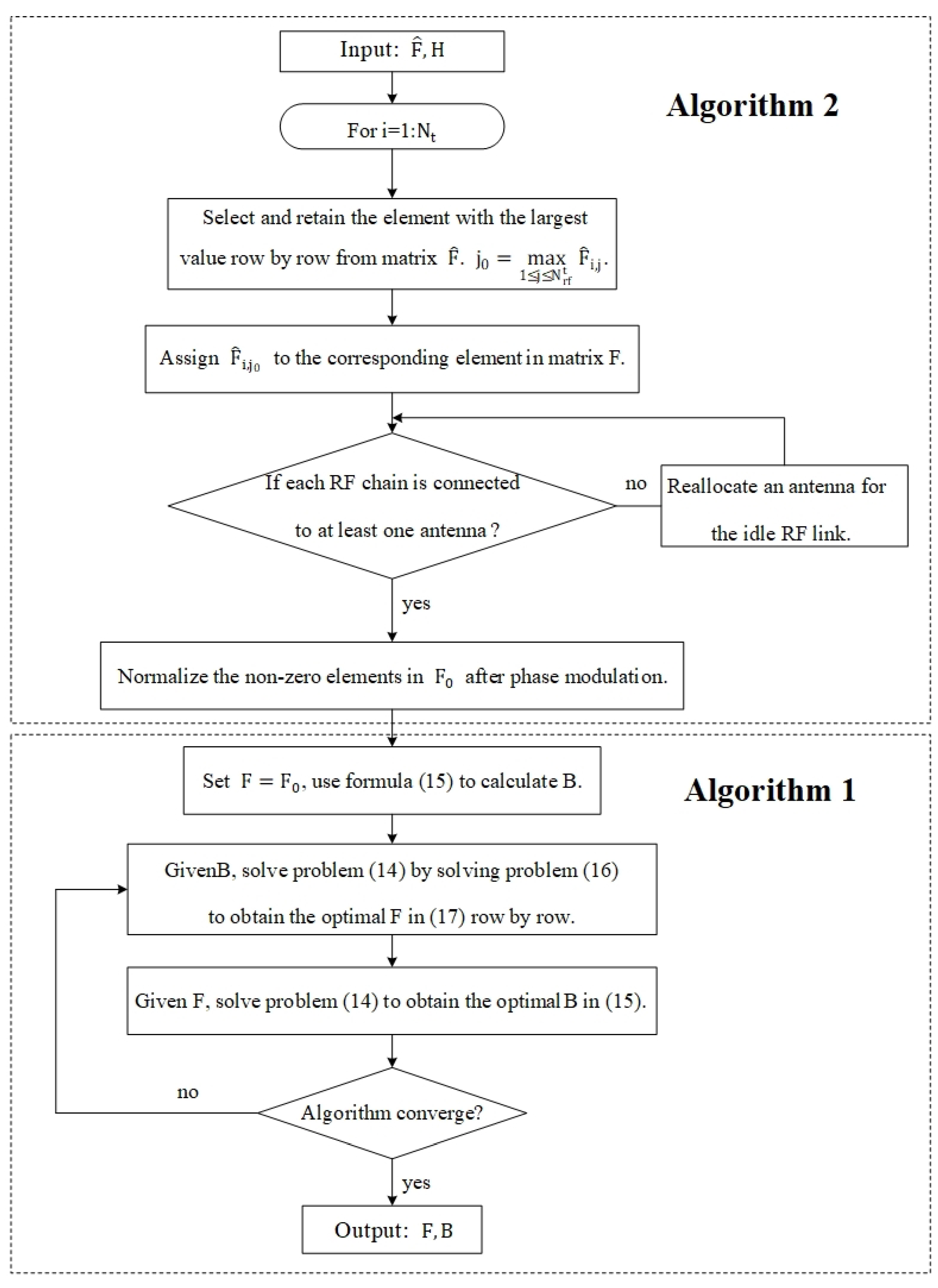
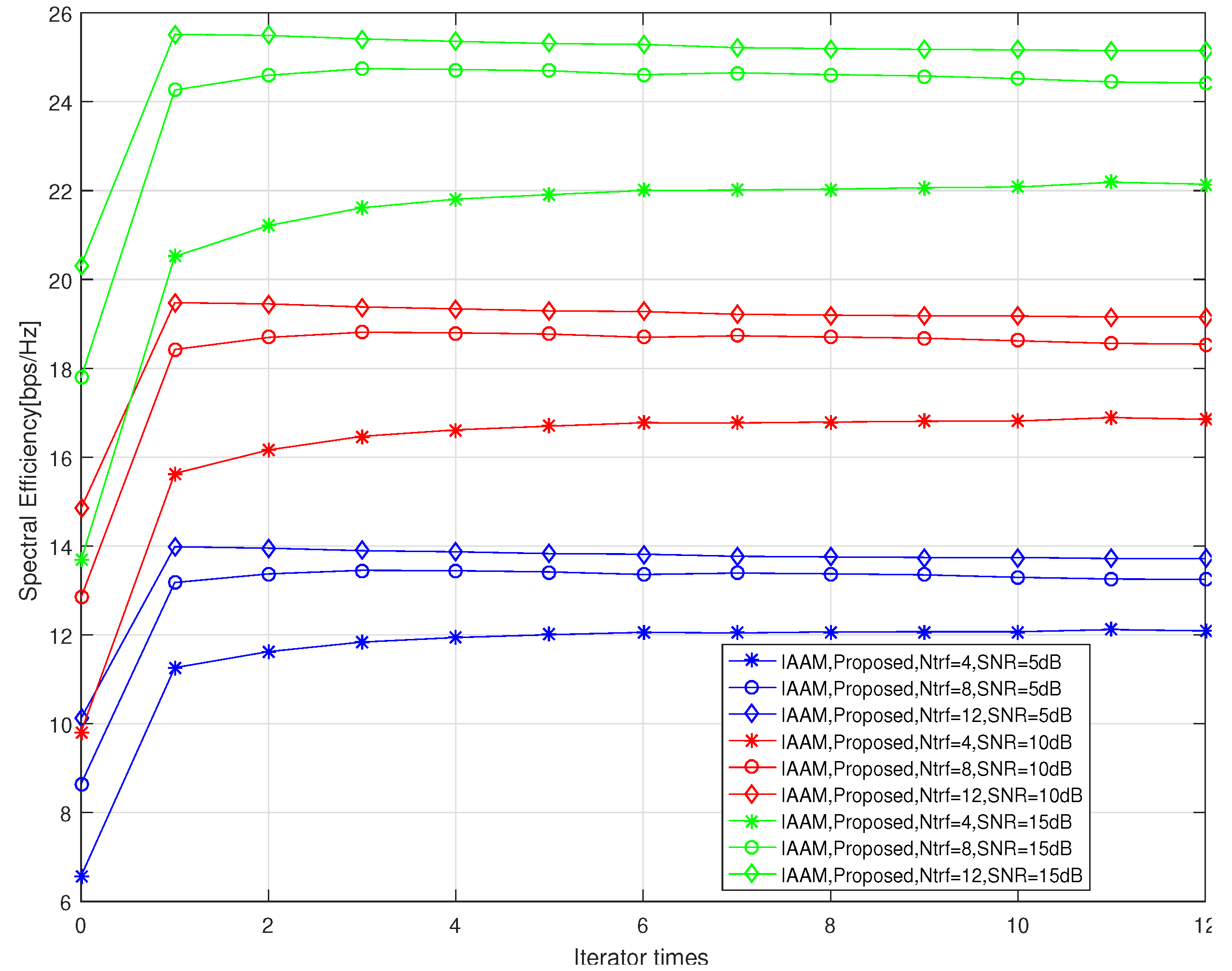
Since the proposed IAAM algorithm needs to be processed in two steps: Algorithms 1 and 2, and Algorithm 1 involves alternating minimization, the convergence speed is also worthy of attention. Figure 5 shows the simulation result of the spectral efficiency of the IAAM algorithm under three different ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ and three different SNR with iteration times. When ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ increases, the result of Formula (20) will be closer to the optimal [15], which makes the performance of the initial value calculated by Algorithm 2 more effective. An excellent initial value can naturally uce the iteration times requi for convergence. It can be seen from Figure 5 that that, regardless of SNR = 5, 10, 15 dB, when ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ = 4, 8, and 12, the numbers of iterations requi for convergence are about 8, 4, and 2, respectively, indicating that the larger ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$, the lower the algorithm’s time complexity, and the better the spectral efficiency performance. Additionally, combined with the conclusion of the energy efficiency simulation result in Figure 4, it can be concluded that this scheme is very practical when the number of RF chains is large, and the energy efficiency is higher than that of the fully-connected hybrid precoding and the algorithm complexity is also low.

After discussing the number of iterations requi for algorithm convergence, the technological complexity of each iteration also needs to be analyzed. For Algorithm 1, the complexity is dominated by getting the pseudo-inverse of the analog precoding matrix when calculating digital precoder, which brings about $\mathrm{O}\left({\mathrm{N}}_{\mathrm{t}}^2{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}\right)$ computations. For Algorithm 2, the computational complexity can be divided into three parts—initially grouping, checking for empty subset and phase modulation—with a total complexity of $\mathrm{O}\left(N_t{N}_{rf}^t+2L{N}_t{N}_{rf}^t+N_t\right)$, in which $\mathrm{L}$ denotes the number of empty subsets after the first round antenna grouping, and we found that the value of $\mathrm{L}$ is always 0 after intensive simulation. Therefore, the overall computational complexity of the proposed IAAM algorithm is given by $\mathrm{O}\left(\mathrm{K}\left({\mathrm{N}}_{\mathrm{t}}^2{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}+N_t{N}_{rf}^t+N_t\right)\right)$ and $\mathrm{K}$ denotes the number of iterations. The SIC-based algorithm has a total computational complexity of $\mathrm{O}\left(M^2\left(N_{rf}^{t}S+N_r\right)\right)$, where $\mathrm{M}$ denotes the number of antennas allocated to each RF chain, and $\mathrm{S}$ denotes the number of iterations, which equals 5 after verification [10]. The OMP-based algorithm owns a computational complexity of $\mathrm{O}\left({\mathrm{N}}_{\mathrm{t}}^2{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}{\mathrm{N}}_{\mathrm{s}}\right)$ [8]. The DC algorithm has a computational complexity of $\mathrm{O}\left(N_t{N}_{rf}^t+L{N}_t{N}_{rf}^t+N_t\right)$ [14].

Table 2. Complexity, and some quantification results of different algorithms with SNR = 10 dB.

Algorithm	Complexity	Spectral Efficiency (bps/Hz)	Energy Efficiency (bps/Hz/J)
Full-digital	∖	24.131	0.089
OMP [8]	$\mathrm{O}\left({\mathrm{N}}_{\mathrm{t}}^2{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}{\mathrm{N}}_{\mathrm{s}}\right)$	20.829	0.517
IAAM, proposed	$\mathrm{O}\left(\mathrm{K}\left({\mathrm{N}}_{\mathrm{t}}^2{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}+N_t{N}_{rf}^t+N_t\right)\right)$	16.761	0.583
SIC [10]	$\mathrm{O}\left({\left(\frac{{\mathrm{N}}_{\mathrm{t}}}{{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}}\right)}^2\left(5{\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}+{\mathrm{N}}_{\mathrm{r}}\right)\right)$	14.261	0.496
DC [14]	$\mathrm{O}\left(N_t{N}_{rf}^t+L{N}_t{N}_{rf}^t+N_t\right)$	10.609	0.369

summarizes the complexities and other quantification results of different algorithms.

The quantification results given in Table 2 are based on ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ = 4. Additionally, from Figure 5, we know that the value of $\mathrm{K}$ in the complexity of IAAM algorithm is 8, and it will decrease with the increase in ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$. As the value of ${\mathrm{N}}_{\mathrm{t}}$ is always very large, the OMP algorithm has the largest computational complexity in the table. The proposed IAAM algorithm has the same magnitude of computational complexity as the SIC algorithm. The complexity of the DC algorithm is the lowest, while its performance is the lowest too. The quantification results also show that the spectral efficiency performance of the proposed algorithm is at least 17.5% higher than the existing two traditional sub-connected algorithms, and it increases at least about 12.8% energy efficiency, compa with the OMP algorithm, even when ${\mathrm{N}}_{\mathrm{rf}}^{\mathrm{t}}$ = 4.

5. Conclusions and Future Directions

In this article, we proposed an IAAM-based algorithm to establish millimeter wave dynamic sub-connected hybrid precoding. We first solved the joint design problem of the analog and digital precoder through alternating minimization and set no extra constraint when solving the problem, thereby avoiding the huge search volume requi for exhaustive search and increasing the flexibility and applicability of the scheme. Then, we designed a heuristic algorithm to calculate the initial value of the analog precoder as the starting point of alternating minimization to prevent the algorithm from converging too slowly and falling into a suboptimal solution. The simulation results show that the IAAM algorithm has better spectral efficiency performance than the two existing sub-connected algorithms. Compa with the fully-connected-based OMP algorithm, it has better energy efficiency performance and lower complexity, and its energy efficiency advantage, as well as the convergence speed, increases rapidly with the number of RF chains. Thus, the proposed algorithm has obvious advantages with a large number of RF chains. In future research, it should be an interesting direction to consider the implementation of the algorithm under the sub-connection structure with energy efficiency as the optimization goal when adding the antenna selection of the transmitter antenna.