Abstract
Total knee replacement is a standard surgical treatment used to treat osteoarthritis in the knee. The implant is complicated, requiring expensive designs and testing as well as a surgical intervention. This research proposes a technique concerning the optimal conformity design of the symmetric polyethylene tibial insert component for fixed-bearing total knee arthroplasty. The Latin Hypercube Sampling (LHS) design of the experiment was used to create 30 cases of the varied tibial insert conformity that influenced the total knee replacement wear volume. The combination of finite element analysis and a surrogate model was performed to predict wear volume according to the standard of ISO-14243:2014 wear test and to determine the optimal conformity. In the first step, the results could predict wear volume between 5.50 to 72.92 mm3/106 cycle. The Kriging method of a surrogate model has then created the increased design based on the efficient global optimization (EGO) method with improving data 10 design points. The result revealed that the optimum design of tibial insert conformity in a coronal and sagittal plane was 0.70 and 0.59, respectively, with a minimizing wear volume of 3.07 mm3/106 cycle. The verification results revealed that the area surface scrape and wear volume are similar to those predicted by the experiment. The wear behavior on the tibial insert surface was asymmetry of both sides. From this study it can be concluded that the optimal conformity design of the tibial insert component can be by using a finite element and surrogate model combined with the design of conformity to the minimized wear volume.
1. Introduction
Knee osteoarthritis is a condition that occurs due to arthritis surface or degenerative joint disease resulting in loss of function and pain in the knee, which often occurs in the elderly. Medically, the treatment of osteoarthritis involves medications and injections to reduce pain, including knee replacement surgery [1]. Joint replacement surgery is the standard and acceptable treatment for people with severe osteoarthritis. In the statistical report, a million knee joint replacement surgeries have been performed worldwide [2]. The objective of knee replacement surgery will help reduce pain from osteoarthritis or accidents and osteoarthritis of the knee and will help restore the knee joint to its original mobility. Correcting pain in a damaged knee with knee replacement surgery and returning a typical knee joint depends on the knee implant and surgical technique. Generally, the total knee arthroplasty (TKA) has consisted of three parts: the femoral component, a tibial insert, and a tibial tray component, in which the available materials were made from metal, ceramic, or polyethylene [3]. The anatomical design of symmetric and asymmetric tibial insert components was introduced in the available commercial usage. Although knee replacements are widely accepted, there have also been reports of failures involving wear between the knee surfaces [4]. According to reports, the most common cause of postoperative failure is wear and tear on the intervertebral disc surfaces 10 to 15 years after surgery [5].
Biomechanically, the surface wear failure of TKA depends on multiple factors such as material, including the manufacturing process, conformity design, and loading from patient activity [6,7]. The TKA wear involved the mechanical contact and the biological reaction between the femoral and tibial insert components [8]. The geometric conformity of the curvature ratio between the femoral and tibia components is a design factor of TKA that affects the contact mechanism and durability of the knee prosthesis [9]. The knee conformity values are typically designed to provide movement similar to normal knee joints and to conform to standard wear tests. The conformity design of commercially available knee implants ranges from approximately 0.5 to 0.9 depending on the design conditions of each type [10,11]. Previous studies have found that TKA design with high conformity in coronal and sagittal planes affected the increased wear in the knee prosthesis [12]. The mechanical wear in TKA is also related to contact stress distribution between the surface of the femoral and tibial insert components. In previous studies, the contact stress distribution in TKA during activity depended on the loading activity and flexion angle, including the geometric conformity design. The low conformity design of TKA revealed the high contact area between the surface of the femoral and tibial insert components during the flexion of the knee joint [13]. In addition, the kinematics of contact point sliding distance during activity also affect the surface wear of the tibial insert component. The medial pivot knee design typically involves a cruciate-retaining (CR) femoral component and a highly congruent polyethylene liner [14]. Moreover, the standard wear test of the knee prosthesis was used as a dedicated test to determine the volume of wear based on the multidirectional loading. The standard ISO 14243 1/3 of wear test involved the load and displacement parameters for wear-testing machines based on load and displacement control corresponding environmental conditions.
The finite element (FE) method is currently widely accepted by biomechanics research, such as stress determine or wear volume in TKA. The reliability, reduced costs, including the proposed approach, and expected outcomes before manufacturing for experiments were the main advantages of FE analysis. Most engineering design situations, in general, require experiments or simulations to evaluate design objectives and constraint functions as a function of design variables. A surrogate model is an engineering technique used when the desired outcome cannot be directly assessed, and a model of the desired outcome is utilized instead [15]. The objective of surrogate modeling is to construct a surrogate as accurately as appropriate using the minimum available simulation evaluations. There are usually three primary steps in the procedure: sample selection (also known as sequential design), construction of the surrogate model and optimizing parameters, and the evaluation of the accuracy of the surrogate [16]. According to previous reports, the FE method investigated total knee arthroplasty designs, leading to improved performance [17]. The study examined interweaving design optimization between the FE method and a surrogate model, utilizing simulation-aided design using a surrogate model [18]. The surrogate model is utilized to reduce contact stress and wear volume employed in the analysis [19]. However, no studies have used surrogate modeling techniques to investigate the design of tibial insert conformity that results in minimum prosthesis wear. Therefore, this research has focused on the conformity of tibial insert design to minimize for wear volume of TKA. The finite element method was used in association with surrogate modeling techniques to assess polyethylene wear. The surrogate model is used in the data analysis to evaluate the first designed group data. Random group data are processed using Latin Hypercube Sampling (LHS) to obtain a design point that is expected to be suitable. These analytical procedures are utilized to form a guideline for determining the relationship between femoral curvature and tibial insert conformity to optimal design.
2. Materials and Methods
2.1. Modeling of TKA
2.1.1. Finite Element (FE) Model
The three-dimensional (3D) FE femoral and tibial insert models based on anatomical symmetry design were used and obtained from a previous study [20]. This study used the explicit dynamics FE analysis solver based on the computationally advanced knee implant analysis and simulations software called ABAQUS Knee Simulator (ABAQUS, Inc., Providence, RI, USA). The solid element type of triangular (R3D3) and hexahedral (C3D8R) were performed, consisting of 31,776 and 34,102 elements for the femoral and tibial insert component shown in Figure 1.
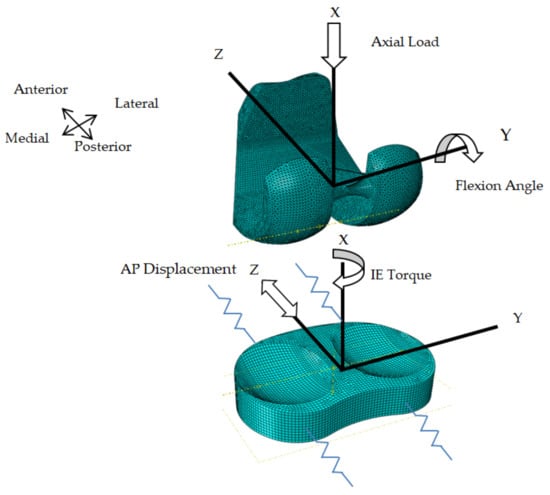
Figure 1.
The 3D FE model consists of the femoral and tibial insert components and boundary condition.
2.1.2. Material Properties and Boundary Conditions
The FE model of the femoral component was developed as a rigid body, while the UHMWPE material was used to create a deformable body for the tibial insert component. According to the mechanical properties, the elastic modulus of UHMWPE was 1048 MPa, and the Poisson ratio was 0.46 [9,21]. The friction coefficient between the femoral and tibial insert components is defined by the value of 0.04 and density of 9.34 × 10−7 g/mm3. [15,22]. As shown in Figure 1, the FE of the femoral and tibial insert components were virtually arranged based on the adjusted position of the lowest surface of the femoral articular being on the tibial insert. For the boundary condition, the applied load were performed based on the ISO-14243-3:2014 standard of knee wear implant test [23], as shown in Figure 1 and Figure 2. The wear simulation included dynamic loads in various directions and data from a human walking investigation that led to the TKA standard test. The axial load, the flexion angle, the displacement of internal-external (IE) torque, and the anterior-posterior (AP) displacement were the loading conditions for the knee simulator based on ISO-14243:2014, as shown in Figure 2a–d, respectively.
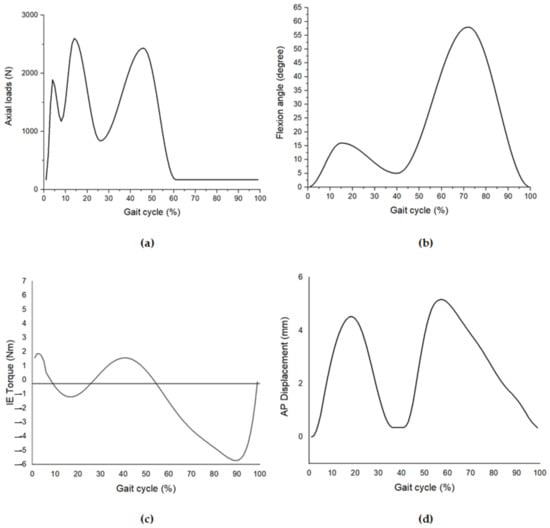
Figure 2.
Loading conditions of ISO−14243:2014 standards. (a) axial loads; (b) flexion angle; (c) internal/external (IE) torque; and (d) anterior/posterior (AP) displacement.
2.1.3. Mesh Convergence Test
In this study, the mesh convergent was also performed to confirm that the results do not change with mesh refinement. Figure 3 shows the result of maximum contact pressure, which is the variation of mesh refinement between the element size of 2.5 mm to 1 mm. The results suggested that the maximum contact pressure generated by elements less than 1 mm had very little change. In addition, Figure 4 shows the maximum contact pressure for the mesh convergence test under dynamic loading for one gait cycle. It can be noticed that the magnitude of maximum contact pressure generated by using the element of 1.2 mm and 1.0 mm displayed a slight fluctuation. Therefore, an element size of 1 mm was used for the simulation in the study.
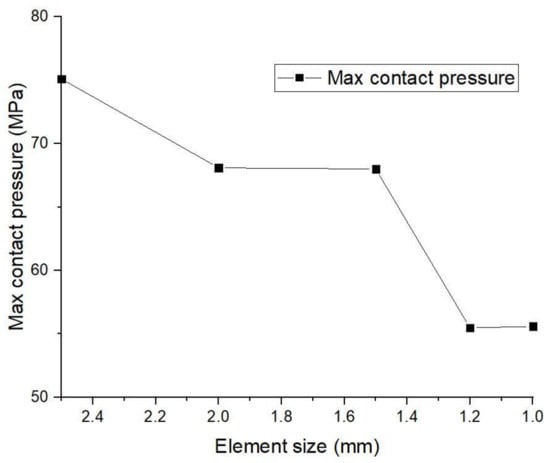
Figure 3.
The result of mesh convergence test for maximum contact pressure.
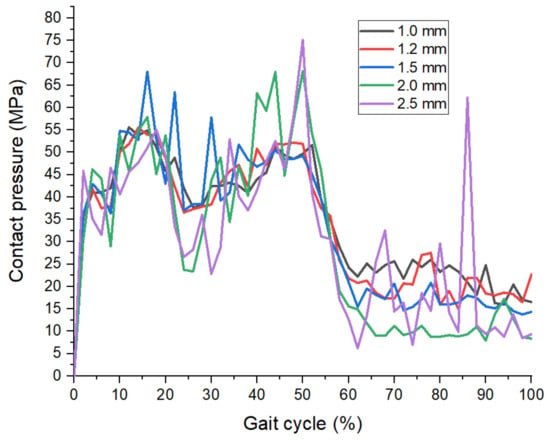
Figure 4.
The result of the mesh convergence test for maximum contact pressure over the entire gait cycle.
2.2. Wear Equation and Computational
According to the wear theory, Archard’s law was applied in the simulation to calculate the surface wear of the tibial insert component, as shown in Equation (1) [24].
H = KwpS
From Equation (1), H represented the wear depth; Kw was the wear factor obtained from laboratory testing; p was the magnitude of contact pressure, and S was the sliding distance during a cycle. In this study, the average wear factor value of 2.643 × 1010 mm3/Nmm was used that obtained from the pin-on-plat wear tests in the multidirectional testing machine [15].
Figure 5 shows the diagram of the wear volume calculation, which is the adaptive refine mesh technique to simulate the calculating of surface wear carried on a Python script file. The initial geometry was started and then generated to the FE model. The nodal result of contact pressure, including sliding distance, was calculated at the first iteration. The wear depth included wear volume and was evaluated by using Archard’s wear law. At the same time, the nodal result was used to calculate the normal force on the contact surface and updated the new positioning of the node by moving it from a calculation of the wear depth. The calculation of the final wear depth and volume was obtained from each number of iteration.
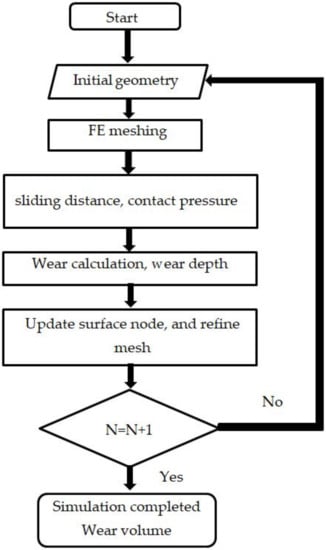
Figure 5.
Diagram of wear simulation in each cycle.
2.3. Design of Experiments (DOE)
In this study, the design of experiments was used to explain variance in conformity of TKA under the hypothesis of minimizing wear volume. Figure 6 showed the conformity defined as the curvature ratio between the femoral and tibial insert components in the coronal and sagittal planes, which are in a range of 0.5 to 0.8 and 0.4 to 0.7, respectively. The articular surface between the femoral and tibial insert components was designed with symmetry in the anteroposterior and sagittal planes. The initial sampling has 30 design scenarios for collecting datasets in the experiment design using LHS, as shown in Figure 7. To perform Latin hypercube sampling, which first decides how many samples points to use, remember which row and column each sample point was taken in. The result of FE analysis was then used to search the optimal design point for TKA conformity using the efficient global optimization (EGO) process.
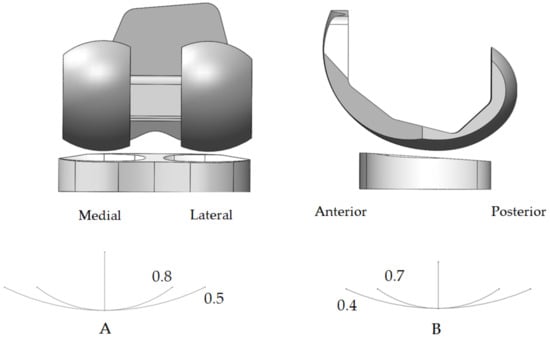
Figure 6.
The upper and lower value of conformity in the study (A) the coronal plane and (B) the sagittal plane.
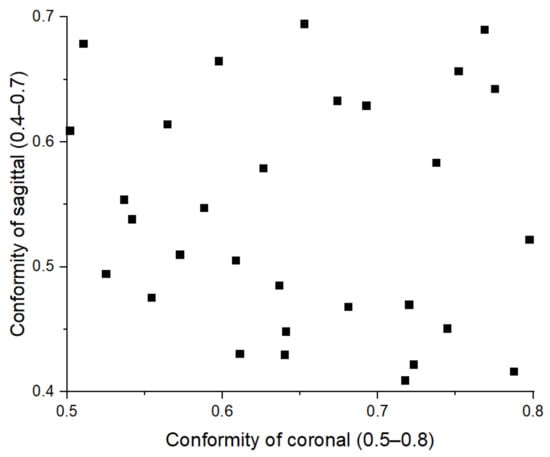
Figure 7.
The initial LHS design of the experiment.
2.4. Surrogate Model Methods
Surrogate models are approximations of the target function or constraint of an optimization problem, simple functions, or functions that take less time to calculate. The value is obtained from the exact random solution of the optimization problem. The surrogate has applied a range of estimation methods. Then the fundamental functions of those solutions are determined when the point of the solutions and the values. The Kriging model used a surrogate model-based engineering design and optimization that predicted interaction between the input and output for optimum point design calculations.
Kriging Method
The Kriging model to predict unknown functions was expressed in the following formula [25,26]:
where and denote the global and local models, respectively. The global model is expressed as
where is a matrix denoting the correlation between the sample points, and is a vector that contains the evaluation value of each sampling point. The Kriging surrogate model denotes a constant global model. The local model has been expressed as
The vector is written in the term of , when is a vector of the sampling points model. The relationship between and is the distance from to . In the Kriging surrogate model, the unknown point in local resources is expressed using stochastic processes. The many design points are created as sampling points. Then, a surrogate model is constructed using a Gaussian random function for the relationship function to estimate the trend using a stochastic process.
2.5. Efficient Global Optimization
The EGO process is one of the optimization techniques combined between the surrogate model and the optimization technique to reduce the optimum cost in the design process [26]. In this work, the Kriging method was selected as the surrogate model for the EGO process. The schematic of the EGO process is shown in Figure 8. The first EGO starts with the creation of initial samples. The LHS was used to design the initial sampling point of the tibial insert [27]. The initial sample data are assessed, and the data are predicted using the kriging method. A definitive optimization is used to find an augmentative point by maximizing the . When the at a point can be shown as
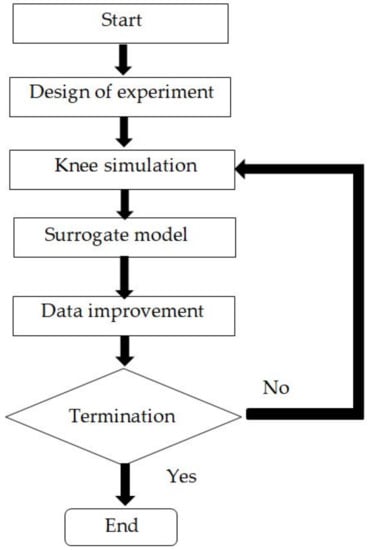
Figure 8.
Flowchart of efficient global optimization.
The point is improved, showing a random variable that is a random variable. The expected improvement is achieved by taking the prospective value. To compute this expectation the notations and are introduced and denote the design and analysis of the computer experiment predictor and its standard error , respectively.
In this note, is Normal (, s2). The right-hand side of Equation (5) is an integral, and applying some integration by parts can improve the closed-form Equation (6).
The average density and distribution functions are represented by and , respectively, which predicts the function from a surrogate model, augmentative random sampling points used on the are loop repeated until data and objective function converge, as illustrated in Figure 9.
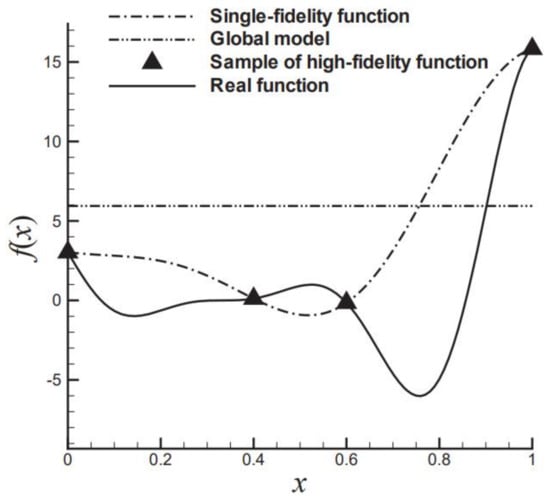
Figure 9.
Schematic of a single-fidelity and multi-fidelity surrogate model: ordinary Kriging model.
2.6. Objective Function and Calculation Condition
The objective function is the minimization of the wear volume on the surface of the tibial component according to the optimal design of conformity. Furthermore, the calculation condition was subject to the range of tibial conformity value in the coronal and sagittal planes, as shown in Equation (7).
2.7. Experiment Test to Wear Test for Validation with Simulation
According to the validation, the joint simulator machine (ProSim pneumatic six-station knee simulator, Simulation Solutions, UK) set up the specific wear test between the femoral and tibial insert components, as shown in Figure 10. The medial size of TKA consisting of femoral, and tibial insert components were used to evaluate the wear volume and included wear scar. The loading condition of the joint simulator consisted of a compressive load of 700 N, which included the symmetry anterior–posterior direction with a sliding distance of 20 mm per 1 cycle. The frequency of the simulator was 1 Hz, which used 50,000 cycles per case. A tibial insert will be ultimately weighed every 10,000 cycles until 50,000 cycles that have each time per case amount to 14 hr/case. The tibial insert has a label blue color before testing on the surface to check that the contact area of wear. The tibial inserts have a loss of weight from wear testing checked by the scales (gram). Conventionally, the tibial insert will be converted from weight (gram) to the final result as wear volume (mm3).

Figure 10.
The machine of joint simulator.
3. Results
3.1. The Result of Simulations
The simulation results estimated the predicted wear of 30 cases with an additional 10 cases, revealing that each tibial insert design affects wear volume due to the variation of the tibial insert conformity. The different conformity leads to different contact areas and scratches on the surface of the tibial insert component. Figure 11 shows the FE result of the wear depth on the surface of the tibial insert component included in six sample cases. It can be noticed that the wear scar is observed with an oval-shape that occurred on the region of both sides of the posterior surface on the tibial insert component. Moreover, the wear behavior on the tibial insert surface was the asymmetry of both sides, caused by the different contact pressure distribution and multi-direction loading. Table 1 shows the magnitude of wear volume in 1 million cycles for a typically sample of 6 cases with various conformity values.
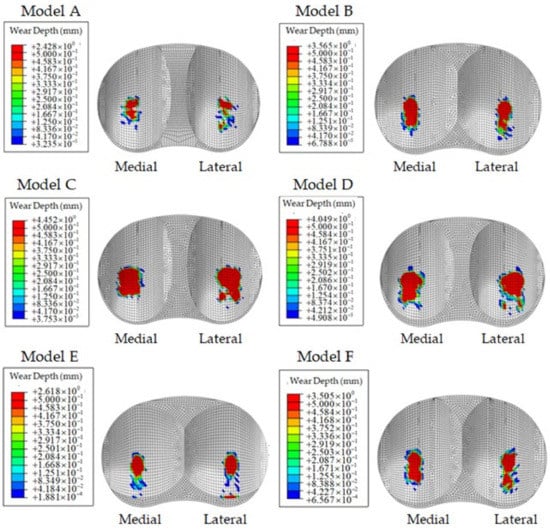
Figure 11.
The FE results of tibial insert wear depth of six samples according to Table 1.

Table 1.
The sample result of wear volume for six from thirty cases.
3.2. Minimization Problem of the Wear Volume Optimization
This study was used in the tibial insert wear as the objective function to solution design and calculation conformity for the minimization wear volume (). Figure 12 shows the additional sampling of the EGO process. In this figure, the wear volume is defined as , and the unit of the is mm3/106 cycle. The details of ten additional sampling by the EGO are shown in Table 2. The minimum wear volume by the EGO with the ordinary Kriging method was found in the ninth iteration with 3.07 mm3/106 cycles. At the optimum point, it was found that the coronal and sagittal conformity were 0.7 and 0.59, respectively. The result of wear depth for the optimal conformity design based on the minimized wear volume using the EGO is shown in Figure 13.
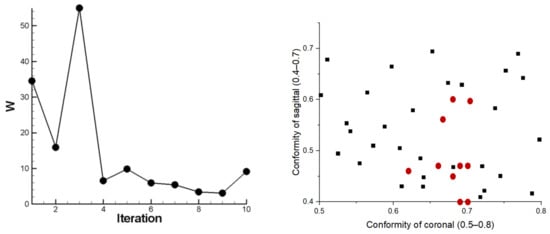
Figure 12.
Collateral sampling in each iteration: the wear volume optimization problem (Left) and additional samples point (Right).

Table 2.
The additional sampling by the EGO using the ordinary Kriging model.
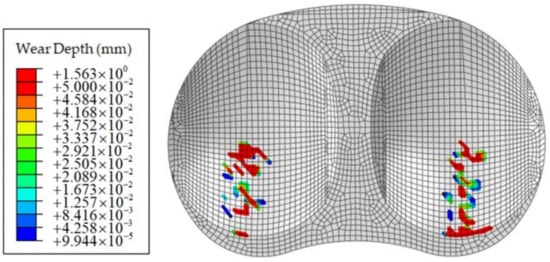
Figure 13.
The result of wear depth for the optimal shape of the tibial insert conformity.
Figure 14 shows the cross-validation results. It was found that the error of value predicted by the EGO with the Kriging surrogate model is acceptable. The slope of the regression line can maintain a slope close to 1.0 and R2 amount 0.9046 for the Kriging method.
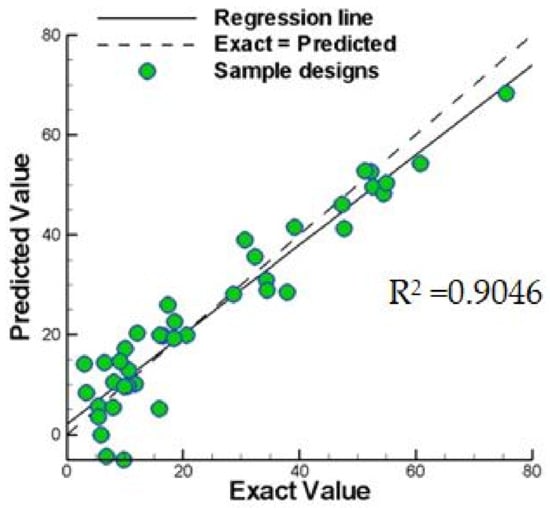
Figure 14.
Cross-validation of six-hump camel-back problem based on ordinary Kriging-based EGO.
3.3. The Relationship Contour of the Design Tibial Insert to Wear Volume
Figure 15 shows the surface response of wear volume for the tibial insert conformity of 40 cases, based on FE analysis according to the surrogate model. The contour plots present the relationship between wear volume and the design parameters consisting of the coronal and sagittal conformities for the proposed ordinary Kriging-based EGOs. According to Figure 15, the optimal designs found by the proposed ordinary Kriging-based EGOs appeared in the blue color that has a wear volume range around 0 to 10 mm3. The optimum design has model conformity of coronal (0.7) and the conformity of sagittal (0.59) that minimizes wear volume of 3.07 mm3/106 cycle.
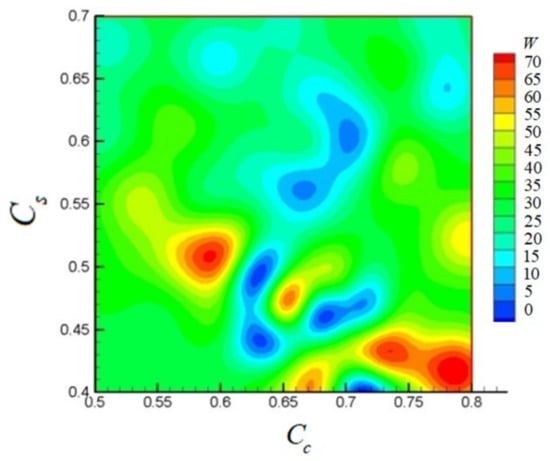
Figure 15.
The surface response plot of wear volume (mm3/Million cycle) according to the parameters design of the conformity of coronal () and conformity of sagittal ().
3.4. Result of Validation between Experimental and Simulation
Figure 16 shows the comparison of wear scar results between FE simulation and experiment under 50,000 cycles. The experimental results showed that the scratch behavior occurred on the tibial insert surface from anterior to posterior and is consistent with the FE simulation. Figure 17 displayed the result of wear volume on the tibial insert component, comparing FE simulation and the experimental method. The magnitude of average wear volume from the experimental method was 2.36 ± 0.57 mm3, whereas the FE result prediction wear volume was 2.38 mm3.
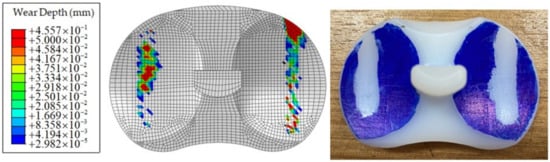
Figure 16.
The comparative result of wear depth between FE simulation (Left) and experimental (Right).
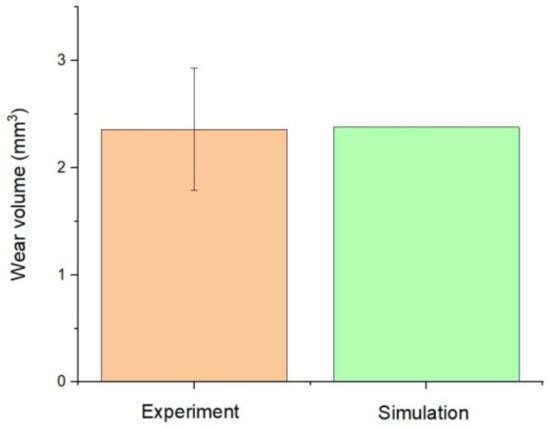
Figure 17.
Comparisons of wear volume between experiments and FE simulation.
4. Discussion
Total knee arthroplasty (TKA) is a standard orthopedic procedure that includes replacing the articular surfaces of the knee joint (femoral condyles and tibial plateau) with smooth metal and polyethylene plastic. TKA attempts to improve the quality of a patient’s life with end-stage osteoarthritis by minimizing pain and improving function [28]. Late infection, bearing wear, and prosthesis loosening are the most typical long-term complications of TKA. Most research reported that the wear of the tibial insert was the critical factor for the limitation of longevity in TKA [4]. Many factors affect the wear of the tibial insert, such as material, sliding distance, load, shape design, etc. [9,12] Some research studied wear in the tibial insert, which was made from different materials such as UHMWPE GUR 1020 and 1050, PEEK, and CFR-PEEK [13,19,22,29,30]. These findings revealed that the material impacted wear volume, with CFR-PEEK outperforming UHMWPE and PEEK. As a result, CFR–PEEK may be a better option for tibial inserts [31]. Furthermore, sliding distance and load also affected wear loss of the tibial insert. There was experimental wear loss of tibial insert using various load conditions and different sliding distances, intermediate and high kinematic conditions, in an anterior and posterior direction [13,32].
The shape and conformity of the bearing surface are crucial for the interaction between the metal component and the polyethylene. The conformity design, particularly the tibial insert and femoral component, affected wear volume. The designed tibial insert with lower contact stress and a wider contact area is the topic of most investigations [33]. Generally, TKA conformity was defined as the ratio of the femoral component radius to the tibial insert radius, which was considered to reduce contact stress [9,11]. Previously, the variation conformity of TKA was designed to determine the contact stress or contact pressure on the tibial insert under various load conditions through experiments [34,35]. Optimal conformity, which resulted in minimal wear volume loss, was potentially difficult and time-consuming to evaluate. As a result, this study used simulations of knee simulators to improve the TKA design [9,11,15]. The importance of design in reducing TKA wear has been highlighted in this paper. The wear was investigated using a finite element re-meshing technique and subroutine script files [11,15,22,30,31]. There are two factors used to design conformity of TKA in coronal and sagittal planes based on the ISO-14243 standard test [36]. The ISO-14243 standard test was used widely for TKA testing to inspect the amount of wear volume on the implant. The standard has developed and changed parameters until the last standard was ISO-14243:2014 [23].
According to previous studies, experiments on the effect of conformity on wear volume in fixed-bearing TKA by simulator found a high wear volume in the high of conformity [36]. The wear volume showed a significant reduction when conformity was reduced. Previous studies with similar test conditions for prosthetic knee pillows found reduced wear volume when conforming to the tibial inserted [37]. Preceding research presented cruciate-retaining (CR) TKA as having a low conformity and revealed that the backside wear of the tibial plateau insert was higher than the posterior-stabilized(PS) TKA, which has high constraints in design [38]. Most of the previous studies have attempted to reduce contact stress to solve the problem of wear in the tibial insert made from polyethylene material. Other studies mentioned that low conformity could help reduce wear volume in TKA; however, the clinical study explained that using a high conforming implant is necessary because the joint limits natural movement [39]. A previous study used the surrogate model to calculate contact points between the TKA and prosthetic knee pillow and found that the initial position of the femoral impacts on the wear volume in an implant. This study showed the process surrogate model for creation and implementation and found that the initial position of the femoral cover that is at the superior/interior position, which is lower than its general position by 10 mm, and at the anterior/posterior by 0 mm, will have the lowest wear volume [17]. Other studies used a surrogate model to analyze TKA, which has created the sample analysis process, and the proposed surrogates can be used with the simulations significantly. The study was performed using simulations with the surrogate contact models with different load conditions, such as anterior–posterior force, superior–inferior force, internal–external torque, and flexion–extension motion. This paper has shown a surrogate model method in which the parameters can be adjusted for analysis to calculate the wear volume [18]. The conclusion of the previous study showed the design process of tibial insert that has low conformity and will have a low wear volume, but cannot be used for general cases because of the limitations of motion in the knee joint. Once the TKA has a high conformity, it will induce many contact stresses commonly used in clinics. Therefore, this research wants to study the conformity of tibial inserts and to optimize the design in order to minimize wear volume, which can be used in clinics.
For the number of simulations, the design of an experiment (DOE) technique was utilized to create a starting sample point. DOE approaches use various simulation designs, such as full factorial, fractional factorial, and LHS. In this study, the LHS method using random functions was created, the design point of which has been distributed between a lower and an upper scope because the approach was commonly utilized widely in the DOE technique of design initial sampling [27]. The simulation is then transferred to a surrogate model, such as Response surface approximation, a Kriging model, or Radial basis neural networks, which are used to create a large number of approved simulations to ensure accuracy [25]. The solution of Kriging is a procedure that requires first Kriging results to estimate the best parameters based on a linear regression that report the relation of the residuals between the regression model and the observations. The EGO is a design optimization process with an algorithm to predict optimum design points, which is the first step in adjusting a design and analysis of computer experiments (DACE) model to incorporate it with initial points design, which means space-filling experimental design. Therefore, the LHS was first used to introduce the initial sampling design and evaluated it using the EGO. The EGO then adapts to appropriate the parameters of a DACE model using maximum probability estimation until the result is satisfactory [26].
According to the optimum conformity design, the results revealed that the conformity value of coronal and sagittal of the tibial insert component are 0.7 and 0.59, respectively, to minimize the wear volume to 3.07 mm3/106 cycle. Previous studies have analyzed different conformities of implants in the coronal and sagittal planes that influence wear volume in each conformity. The result of the wear volumes was approximately 7.8 to 8.5 mm3/106 cycle [40]. Other studies have been designed to identify implant conformity values for three types: a flat, curve, and lipped design. The result showed the lowest to highest wear volume of flat, lipped, and curve designs. This study has a wear volume of 2.3 to 6 mm3/106 cycle, where the lowest wear volume was from the flat design at 2.3 mm3/106 cycle, which has a wear volume similar to this research. However, from previous studies, the flat type implant cannot be used in clinics because the flat implant cannot support the natural movement of the knee [12].
The previous studies performed experiments to compare the knee simulator using simulation with the ISO-14243 standard, which has similar wear volume and scrap area values. The simulation showed wear volume at 1 million cycles for the analysis of wear of TKA [23]. The conclusion of this study indicated that the finite element method could aid the design analysis of TKA, which is reliable and accurate. A previous study tested the new standard, ISO 14243-3:2014, which has a different condition from the initial load’s test. The new standard incurs wear and scrapes at the backside wear of the tibial insert. This study experimented using a knee simulator machine that can test standard knee tests. The condition of the TKA test was an experiment that used two loads: the axial load and the sliding anterior and posterior to check the accuracy of the experiment. It will be compared to the simulation that uses 50,000 cycles as the perimeter. The experiment showed an average wear volume of 2.36 ± 0.57 mm3, and the simulation resulted in a wear volume of 2.38 mm3. The result of both methods showed similar wear volumes. The simulation can predict the wear in the tibial insert with reliability for predictive modeling in this study. To our knowledge, the influent of tibial conformity on wear performance of TKA was reported using finite element analysis and experiments; however, there was no concern in the optimal design of tibial conformity. This study proposes a novel technique for the optimal conformity design of the tibial insert based on the ISO standard wear test, which enlarges the field from the current state of knowledge using the finite element analysis cooperation with a surrogate model. The optimal conformity design of the tibial insert component will then be further developed into the TKA prototypes for actual testing according to the ISO standard test and lead to developing a prototype for a clinical study.
There are some limitations in this study that should be noted as follows:
- 1.
- In consideration of the conformity of the prosthetic knee under the lowest wear volume, this research used the wear co-efficient referenced from the preceding research. It is tested using the ISO-14243 load, where it uses the actual wear coefficient from actual tests. However, this research had studied and found the wear co-efficient from a simplified study to recheck the accuracy of the simulation and the actual test using wear co-efficient trials to achieve the closest value to the actual test.
- 2.
- The prosthetic knee tests for this research used the specific testing machine certified with the ISO-14243. However, the study reduced the perimeters to two conditions: the axial loads and sliding anterior-posterior to recheck the accuracy of the simulation.
- 3.
- The model designed has the conformity value appropriate for production and is used to test, and the accuracy is validated by comparing it to the ISO-14243 standard.
5. Conclusions
This study proposes a novel technique for the optimal conformity design of the tibial insert component to minimize wear volume in TKA. The EGO method consisting of experimental design, FE simulation, surrogate model, and the data improvement with the Kriging method was used to determine the relationship between the conformity and wear volume. Using the combination of a finite element and a surrogate model, the optimal conformity in coronal and sagittal planes were 0.7 and 0.59, respectively, with a minimizing wear volume of 3.07 mm3/106 cycles. A simple experiment was set up to verify the FE simulation, and the result of wear volume and surface area scratch tend to be similar. The application of FE and EGO methods are beneficial in minimizing an unknown function, including a high convergence rate.
Author Contributions
Conceptualization, S.R.; methodology, W.T. and S.R.; software, W.T. and S.R.; validation, W.T. and S.R.; formal analysis, W.T., A.A. and S.R.; investigation, W.T. and S.R.; resources, S.R.; data curation, W.T., A.A. and S.R.; writing—original draft preparation, W.T., A.A., S.S. and S.R.; writing—review and editing, W.T., A.A., S.S. and S.R.; supervision, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable.
Acknowledgments
The authors would like to thank the Center of Excellence in Biomechanics Medicine, Suranaree University of Technology, and Institute of Engineering, Suranaree University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keeney, J.A.; Eunice, S.; Pashos, G.; Wright, R.W.; Clohisy, J.C. What is the evidence for total knee arthroplasty in young patients? A systematic review of the literature. Clin. Orthop. Relat. Res. 2010, 469, 574–583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, M.; Riester, L.; Hunter, G. Nano-hardness measurements of oxidized Zr-2.5Nb and various orthopaedic materials. Trans. Soc. Biomater. 1998, 21, 528. [Google Scholar]
- Naudie, D.D.; Ammeen, D.J.; Engh, G.A.; Rorabeck, C.H. Wear and osteolysis around total knee arthroplasty. J. Am. Acad. Orthop. Surg. 2007, 64, 15–53. [Google Scholar] [CrossRef] [PubMed]
- Vince, K.G. Why knees fail. J. Arthroplast. 2003, 18, 39–44. [Google Scholar] [CrossRef]
- Laskin, R.S. The Genesis total knee prosthesis: A 10-year followup study. Clin. Orthop. Relat. Res. 2001, 388, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Harsha, A.P.; Joyce, T.J. Comparative wear tests of ultra-high molecular weight polyethylene and cross-linked polyethylene. J. Eng. Med. 2013, 227, 600.e8. [Google Scholar] [CrossRef] [PubMed]
- Collier, J.P.; Currier, B.H.; Kennedy, F.E.; Currier, J.H.; Timmins, G.; Jackson, S.K.; Brewer, R.L. Comparison of cross-linked polyethylene materials for orthopedic applications. Clin. Orthop. Relat. Res. 2003, 414, 289–304. [Google Scholar] [CrossRef] [PubMed]
- Villa, T.; Migliavacca, F.; Gastaldi, D.; Colombo, M.; Pietrabissa, R. Contact stresses and fatigue life in a knee prosthesis: Comparison between in vitro measurements and computational simulations. J. Biomech. 2004, 37, 45–53. [Google Scholar] [CrossRef]
- Abdelgaied, A.; Brockett, C.L.; Liu, F.; Jennings, L.M.; Jin, Z.; Fisher, J. The effect of insert conformity and material on total knee replacement wear. Proc. Inst. Mech. Eng. Med. 2014, 228, 98–106. [Google Scholar] [CrossRef] [Green Version]
- D’Lima, D.D.; Chen, P.C.; Colwell, C.W., Jr. Polyethylene contact stresses, articular congruity, and knee alignment. Clin. Orthop. Relat. Res. 2001, 392, 232–238. [Google Scholar] [CrossRef]
- Luger, E.; Sathasivam, S.; Walker, P.S. Inherent differences in the laxity and stability between the intact knee and total knee replacements. Knee 1997, 4, 7–14. [Google Scholar] [CrossRef]
- Brockett, C.L.; Carbone, S.; Fisher, J.; Jennings, L.M. Influence of conformity on the wear of total knee replacement: An experimental study. J. Eng. Med. 2018, 232, 127–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdelgaied, A.; Liu, F.; Brockett, C.; Jennings, L.; Fisher, J.; Jin, Z. Computational wear prediction of artificial knee joints based on a new wear law and formulation. J. Biomech. 2011, 44, 1108–1116. [Google Scholar] [CrossRef]
- Osano, K.; Nagamine, R.; Todo, M.; Kawasaki, M. The Effect of Malrotation of Tibial Component of Total Knee Arthroplasty on Tibial Insert during High Flexion Using a Finite Element Analysis. Sci. World J. 2014, 2014, 695028. [Google Scholar] [CrossRef]
- Knight, L.A.; Pal, S.; Coleman, J.C.; Bronson, F.; Haider, H.; Levine, D.L.; Taylor, M.; Rullkoetter, P.J. Comparison of long-term numerical and experimental total knee replacement wear during simulated gait loading. J. Biomech. 2007, 40, 1550–1558. [Google Scholar] [CrossRef] [PubMed]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling A Practical Guide; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Lin, Y.-C.; Haftka, R.T.; Queipo, N.V.; Fregly, B.J. Two-Dimensional Surrogate Contact Modeling for Computationally Efficient Dynamic Simulation of Total Knee Replacements. J. Biomech. Eng. 2009, 131, 041010-1–041010-8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eskinazi, I.; Fregly, B.J. Surrogate modeling of deformable joint contact using artificial neural networks. Med. Eng. Phys. 2015, 37, 885–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.-C.; Haftka, R.T.; Queipo, N.V.; Fregly, B.J. Surrogate articular contact models for computationally efficient multibody dynamic simulations. Med Eng. Phys. 2010, 32, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Phombut, C.; Rooppakhun, S. The Design of Total Knee Arthroplasty (TKA) Prosthesis Based on Thai Morphology Data Using Reverse Engineering Technique; Technical Report; Suranaree University of Technology: Nakhon Ratchasima, Thailand, 2021. [Google Scholar]
- Petrović Savić, S.; Adamović, D.; Devedžić, G.; Ristić, B.; Matić, A. Contact Stress Generation on the UHMWPE Tibial Insert. Tribol. Ind. 2014, 36, 354–360. [Google Scholar]
- Koh, Y.-G.; Lee, J.-A.; Kang, K.-T. Prediction of Wear on Tibial Inserts Made of UHMWPE, PEEK, and CFR-PEEK in Total Knee Arthroplasty Using Finite-Element Analysis. Lubricants 2019, 7, 30. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-H.; Zhang, W.; Song, D.-Y.; Li, H.; Dong, X.; Zhang, M.; Zhao, F.; Jin, Z.-M.; Cheng, C.-K. The impact of variations in input directions according to ISO 14243 on wearing of knee prostheses. PLoS ONE 2018, 13, e0206496. [Google Scholar] [CrossRef] [Green Version]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981. [Google Scholar] [CrossRef]
- Matheron, G. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Donald, R.J.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive BlackBox Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar]
- Afzal, A.; Kim, K.Y.; Seo, J.W. Effects of Latin hypercube sampling on surrogate modeling and optimization. Int. J. Fluid Mach. Syst. 2017, 10, 240–253. [Google Scholar] [CrossRef]
- Bingham, J.S.; Bukowski, B.R.; Wyles, C.C.; Pareek, A.; Berry, D.J.; Abdel, M.P. Rotating-Hinge Revision Total Knee Arthroplasty for Treatment of Severe Arthrofibrosis. J. Arthroplast. 2019, 34, S271–S276. [Google Scholar] [CrossRef]
- Fisher, J.; Jennings, L.M.; Galvin, A.L.; Jin, Z.M.; Stone, M.H.; Ingham, E. Polyethylene Wear in Total Knees. Clin. Orthop. Relat. Res. 2010, 468, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Netter, J.; Hermida, J.; Flores-Hernandez, C.; Steklov, N.; Kester, M.; D’Limar, D.D. Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty. Lubricants 2015, 3, 381–393. [Google Scholar] [CrossRef]
- Innocenti, B.; Labey, L.; Kamali, A.; Pascale, W.; Pianigiani, S. Development and Validation of a Wear Model to Predict Polyethylene Wear in a Total Knee Arthroplasty: A finite element analysis. Lubricants 2014, 2, 193–205. [Google Scholar] [CrossRef] [Green Version]
- Koh, Y.-G.; Jung, K.-H.; Hong, H.-T.; Kim, K.-M.; Kang, K.-T. Optimal Design of Patient-Specific Total Knee Arthroplasty for Improvement in Wear Performance. J. Clin. Med. 2019, 8, 2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srinivas, G.R.; Deb, A.; Kumar, M.N. A Study on Polyethylene Stresses in MobileBearing and Fixed-Bearing Total Knee Arthroplasty (TKA) using Explicit Finite Element Analysis. J. Long-Term Eff. Med. Implant. 2013, 23, 275–283. [Google Scholar] [CrossRef]
- Abdelgaied, A.; Brockett, C.L.; Liu, F.; Jennings, L.M.; Fisher, J.; Jin, Z. Quantification of the effect of crossshear and applied nominal contact pressure on the wear of moderately cross-linked polyethylene. J. Eng. Med. 2012, 227, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Galvin, A.; Kang, L.; Tipper, J.; Stone, M.; Ingham, E.; Jin, Z.; Fisher, J. Wear of crosslinked polyethylene under different tribological conditions. J. Mater. Sci. Mater. Med. 2006, 17, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Brockett, C.L.; Jennings, L.M.; Hardaker, C.; FisherWear, J. Wear of moderately cross-linked polyethylene in fixed-bearing total knee replacements. J. Eng. Med. 2012, 226, 529–535. [Google Scholar] [CrossRef]
- Galvin, A.L.; Kang, L.; Udofia, I.; Jennings, L.M.; McEwen, H.M.J.; Jin, Z.; Fisher, J. Effect of conformity and contact stress on wear in fixed-bearing. J. Biomech. 2009, 42, 1898–1902. [Google Scholar] [CrossRef] [PubMed]
- Wasielewski, R.C. The causes of insert backside wear in total knee arthroplasty. Clin. Orthop. Relat. Res. 2002, 404, 232–246. [Google Scholar] [CrossRef] [PubMed]
- Ettinger, M.; Zoch, J.M.; Becher, C.; Hurschler, C.; Stukenborg-Colsman, C.; Claassen, L.; Ostermeier, S.; Calliess, T. In vitro kinematics of fixed versus mobile-bearing in unicondylar knee arthroplasty. Arch. Orthop. Trauma Surg. 2015, 135, 871–877. [Google Scholar] [CrossRef]
- Ardestani, M.M.; Moazen, M.; Jin, Z. Contribution of geometric design parameters to knee implant performance: Conflicting impact of conformity on kinematics and contact mechanics. Knee 2015, 22, 217–224. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).