Symmetry Solutions and Conservation Laws for the 3D Generalized Potential Yu-Toda-Sasa-Fukuyama Equation of Mathematical Physics
Abstract
:1. Introduction
2. Solutions of the 3DgYTSF Equation
2.1. Lie Point Symmetries
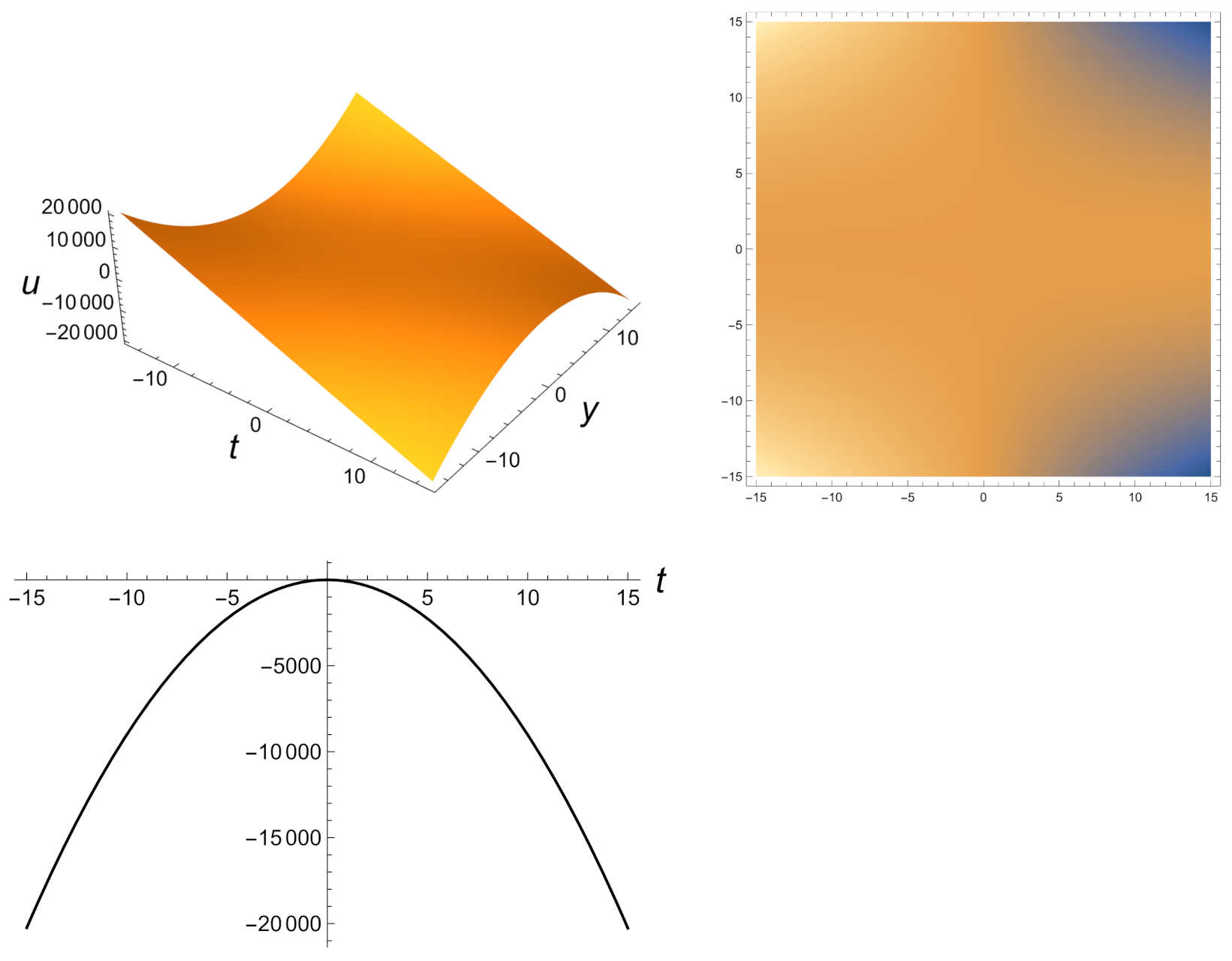
2.2. Group Invariant Solutions under
2.3. Solution via the Incomplete Elliptic Integral
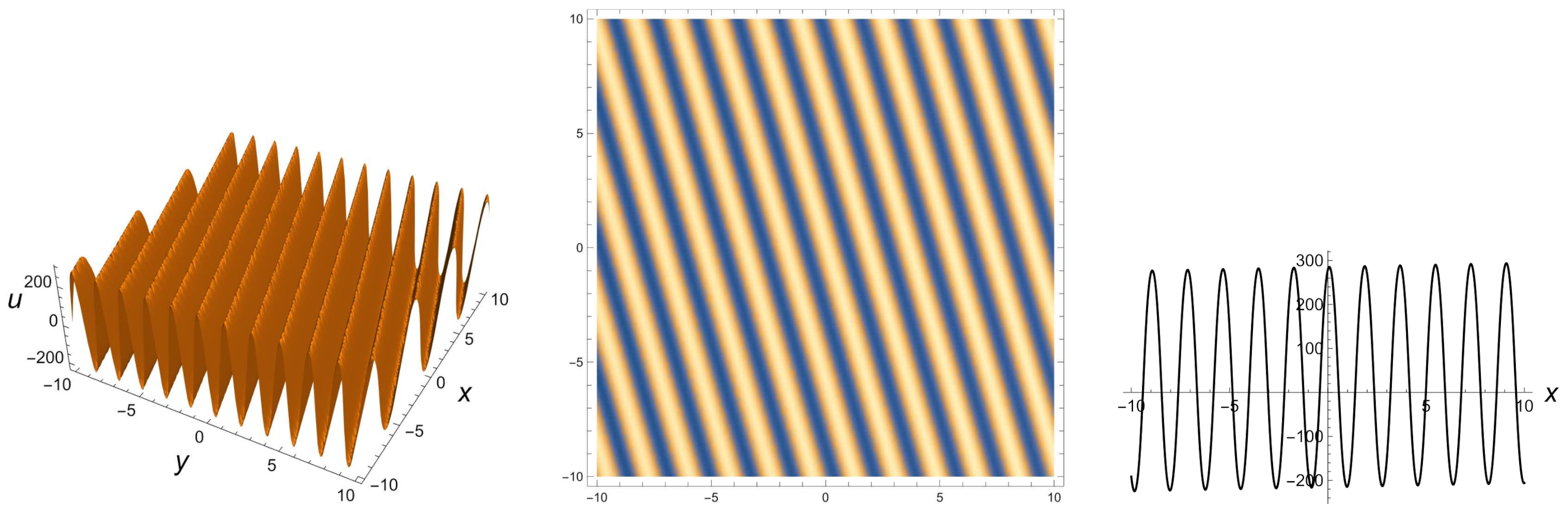
2.4. Group Invariant Solution under
2.5. Group Invariant Solution under
3. Conservation Laws of (2)
3.1. Conservation Laws Using the Multiplier Approach
3.2. Conservation Laws Using Noether’s Approach
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z. Jacobi elliptic function expansion method for the modified Korteweg-de Vries-Zakharov-Kuznetsov and the Hirota equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar]
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zhang, H. A new method for finding exact traveling wave solutions to nonlinear partial differential equations. Phys. Lett. A 2001, 286, 175–179. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Gu, C.H. Soliton Theory and Its Application; Zhejiang Science and Technology Press: Hangzhou, China, 1990. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: New York, NY, USA, 1991. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wang, M.; Li, X.; Zhang, J. The (G′/G)-expansion method and travelling wave solutions for linear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1994; Volumes 1–3. [Google Scholar]
- Ibragimov, N.H. Elementary Lie Group Analysis and Ordinary Differential Equations; John Wiley & Sons: Chichester, NY, USA, 1999. [Google Scholar]
- Simbanefayi, I.; Khalique, C.M. Travelling wave solutions and conservation laws for the Korteweg-de Vries-Bejamin-Bona-Mahony equation. Results Phys. 2018, 8, 57–63. [Google Scholar] [CrossRef]
- Noether, E. Invariante variationsprobleme. Nachr. v. d. Ges. d. Wiss. zu Göttingen. Math.-Phys. Klasse 1918, 2, 235–257. [Google Scholar]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Leveque, R.J. Numerical Methods for Conservation Laws, 2nd ed.; Birkhäuser-Verlag: Basel, Switzerland, 1992. [Google Scholar]
- Mikhailov, A.V.; Shabat, A.B.; Yamilov, R.I. On an extension of the module of invertible transformations. Dokl. Akad. Nauk SSSR 1987, 295, 288–291. [Google Scholar]
- Mikhailov, A.V.; Shabat, A.B.; Yamilov, R.I. Extension of the module of invertible transformations and classification of integrable systems. Commun. Math. Phys. 1988, 115, 1–19. [Google Scholar] [CrossRef]
- Sjöberg, A. Double reduction of PDEs from the association of symmetries with conservation laws with applications. Appl. Math. Comput. 2007, 84, 608–616. [Google Scholar] [CrossRef]
- Sjöberg, A. On double reductions from symmetries and conservation laws. Nonlinear Anal. Real World Appl. 2009, 10, 3472–3477. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Yasar, E.; Özer, T. On symmetries, conservations laws and similarity solutions of foam drainage equation. Int. J. Non-Linear Mech. 2011, 46, 357–362. [Google Scholar] [CrossRef]
- Polat, G.G.; Orhan, Ö.; Özer, T. On new conservation laws of fin equation. Adv. Math. Phys. 2014, 695408. [Google Scholar] [CrossRef]
- Leach, P.G.L. Lie symmetries and Noether symmetries. Appl. Anal. Discrete Math. 2012, 6, 238–246. [Google Scholar] [CrossRef]
- Mei, F.X.; Zheng, G.H. On the Noether symmetry and Lie symmetry of mechanical systems. Acta Mech. Sin. 2002, 18, 414–419. [Google Scholar]
- Yu, S.J.; Toda, K.; Sasa, N.; Fukuyama, T. N soliton solutions to the Bogoyavlenskii-Schiff equation and a quest for the soliton solution in (3 + 1) dimensions. J. Phys. A Math. Gen. 1998, 31, 3337–3347. [Google Scholar] [CrossRef]
- Yan, Z. New families of nontravelling wave solutions to a new (3 + 1)-dimensional potential-YTSF equation. Phys. Lett. A 2003, 318, 78–83. [Google Scholar] [CrossRef]
- Zeng, X.; Dai, Z.; Li, D. New periodic soliton solutions for the (3 + 1)-dimensional potential-YTSF equation. Chaos Solitons Fractals 2009, 42, 657–661. [Google Scholar] [CrossRef]
- Wang, Y.P. Solving the (3 + 1)-dimensional potential-YTSF equation with Exp-function method. J. Phys. Conf. Ser. 2008, 96, 012186. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M. A modification of extended homoclinic test approach to solve the (3 + 1)-dimensional potential-YTSF equation. Chin. Phys. Lett. 2011, 28, 040202. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Multiple invariant solutions of the 3D potential Yu-Toda-Sasa-Fukuyama equation via symmetry technique. Int. J. Mod. Phys. B 2020, 34, 2050188. [Google Scholar] [CrossRef]
- Huang, L.; Manafian, J.; Singh, G.; Nisar, K.S.; Nasution, M.K.M. New lump and interaction soliton, N-soliton solutions and the LSP for the (3+1)-D potential-YTSF-like equation. Results Phys. 2021, 29, 104713. [Google Scholar] [CrossRef]
- Plaatjie, K.; Khalique, C.M. On the solutions and conservation laws of the Yu–Toda–Sasa–Fukuyama equation of plasma physics. Results Phys. 2021, 29, 104706. [Google Scholar] [CrossRef]
- Ma, H.; Cheng, Q. A Deng N-soliton solutions and localized wave interaction solutions of a (3 + 1)-dimensional potential-Yu–Toda–Sasa–Fukuyama equation. Mod. Phys. Lett. B 2021, 35, 2150277. [Google Scholar] [CrossRef]
- Dong, M.J.; Tian, S.F.; Wang, X.B.; Zhang, T.T. Lump-type solutions and interaction solutions in the (3 + 1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation. Anal. Math. Phys. 2019, 9, 1511–1523. [Google Scholar] [CrossRef]
- Li, Z.Q.; Tian, S.F.; Wang, H.; Yang, J.J.; Zhang, T.T. Characteristics of the lump, lumpoff and rouge wave solutions in a (3 + 1)-dimensional generalized potential Yu-Toda-Sasa-Fukuyama equation. Mod. Phys. Lett. 2019, 33, 1950291. [Google Scholar] [CrossRef]
- Jadaun, V.; Singh, N.R. Soliton solutions of generalized (3 + 1)-dimensional Yu-Toda-Sasa-Fukuyama equation using Lie symmetry analysis. Anal. Math. Phys. 2020, 10, 42. [Google Scholar] [CrossRef]
- Billing, J.; King, A.C. Wave Motion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kudryashov, N.A. Analytical Theory of Nonlinear Differential Equations; Institute of Computer Investigations: Moskow/Igevsk, Russia, 2004. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Institute of Computer Science: Moscow/Izhevsk, Russia, 2004. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integration, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Sarlet, W. Comment on ‘Conservation laws of higher order nonlinear PDEs and the variational conservation laws in the class with mixed derivatives’. J. Phys. A Math. Theor. 2010, 43, 458001. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalique, C.M.; Plaatjie, K.; Diteho, O.L. Symmetry Solutions and Conservation Laws for the 3D Generalized Potential Yu-Toda-Sasa-Fukuyama Equation of Mathematical Physics. Symmetry 2021, 13, 2058. https://doi.org/10.3390/sym13112058
Khalique CM, Plaatjie K, Diteho OL. Symmetry Solutions and Conservation Laws for the 3D Generalized Potential Yu-Toda-Sasa-Fukuyama Equation of Mathematical Physics. Symmetry. 2021; 13(11):2058. https://doi.org/10.3390/sym13112058
Chicago/Turabian StyleKhalique, Chaudry Masood, Karabo Plaatjie, and Oageng Lawrence Diteho. 2021. "Symmetry Solutions and Conservation Laws for the 3D Generalized Potential Yu-Toda-Sasa-Fukuyama Equation of Mathematical Physics" Symmetry 13, no. 11: 2058. https://doi.org/10.3390/sym13112058
APA StyleKhalique, C. M., Plaatjie, K., & Diteho, O. L. (2021). Symmetry Solutions and Conservation Laws for the 3D Generalized Potential Yu-Toda-Sasa-Fukuyama Equation of Mathematical Physics. Symmetry, 13(11), 2058. https://doi.org/10.3390/sym13112058






