Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers
Abstract
:1. Introduction
2. Physical Model and Governing Equations
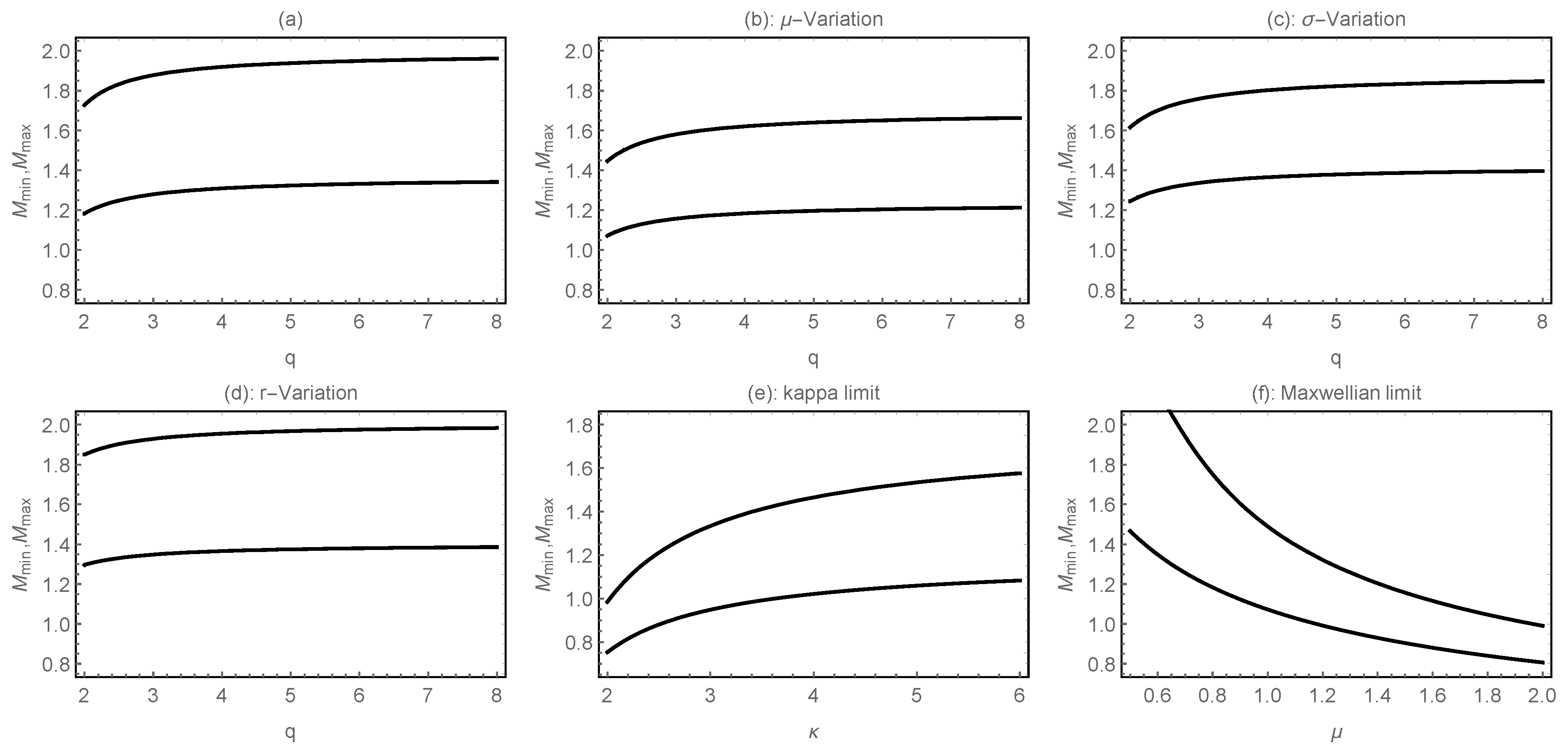
3. Sagdeev Potential Approach
- (i)
- ,
- (ii)
- gives the minimum/critical Mach number,
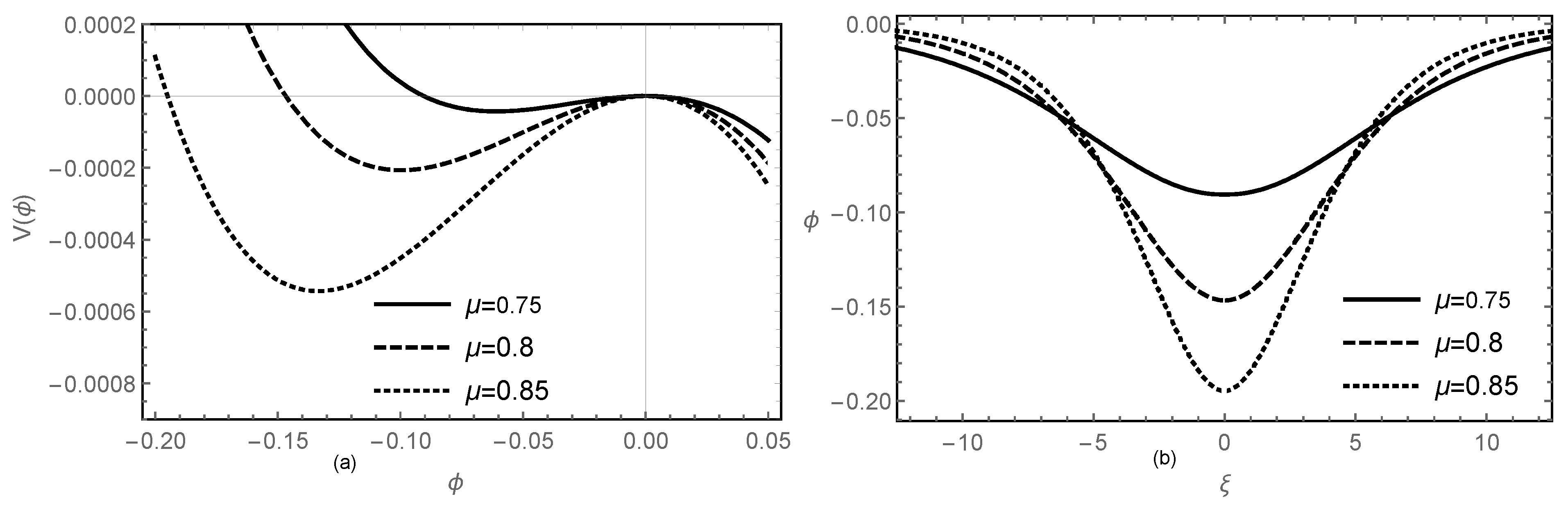
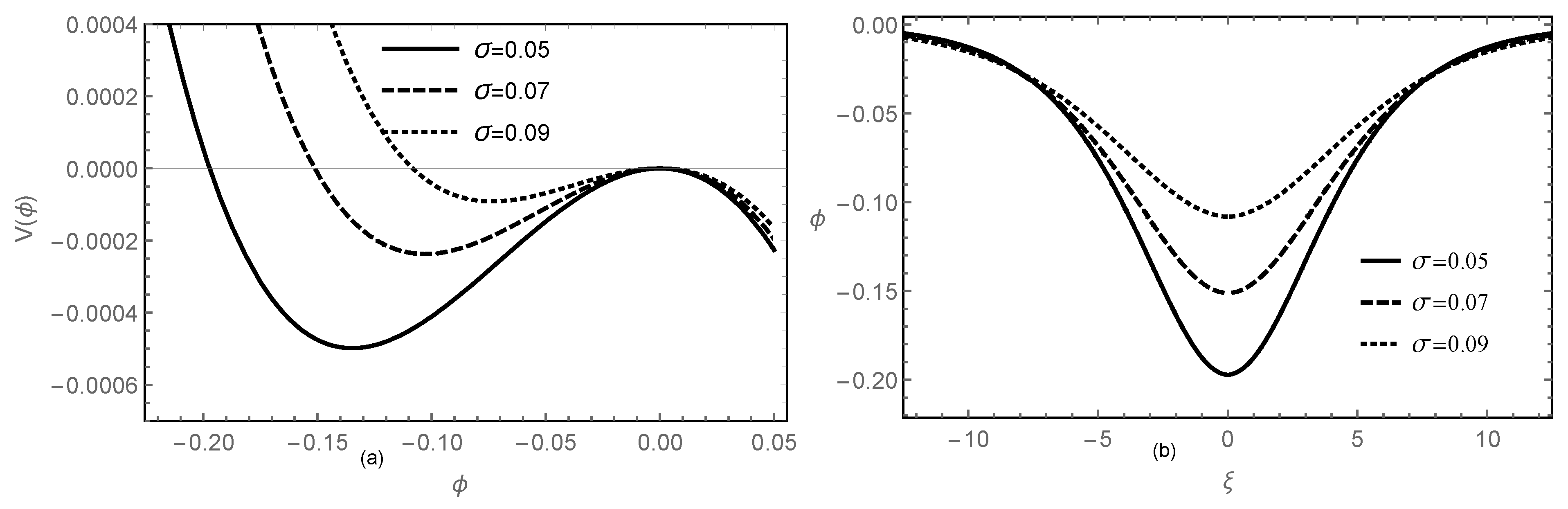
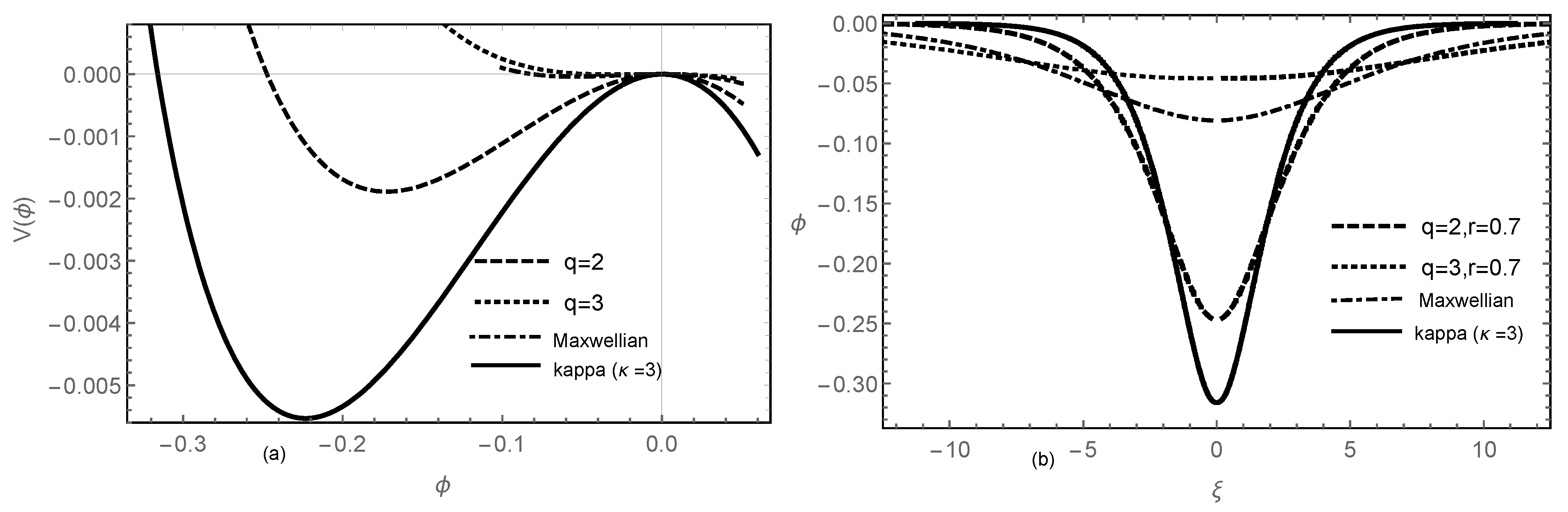
4. Unmodulated Electron-Acoustic Solitary Waves
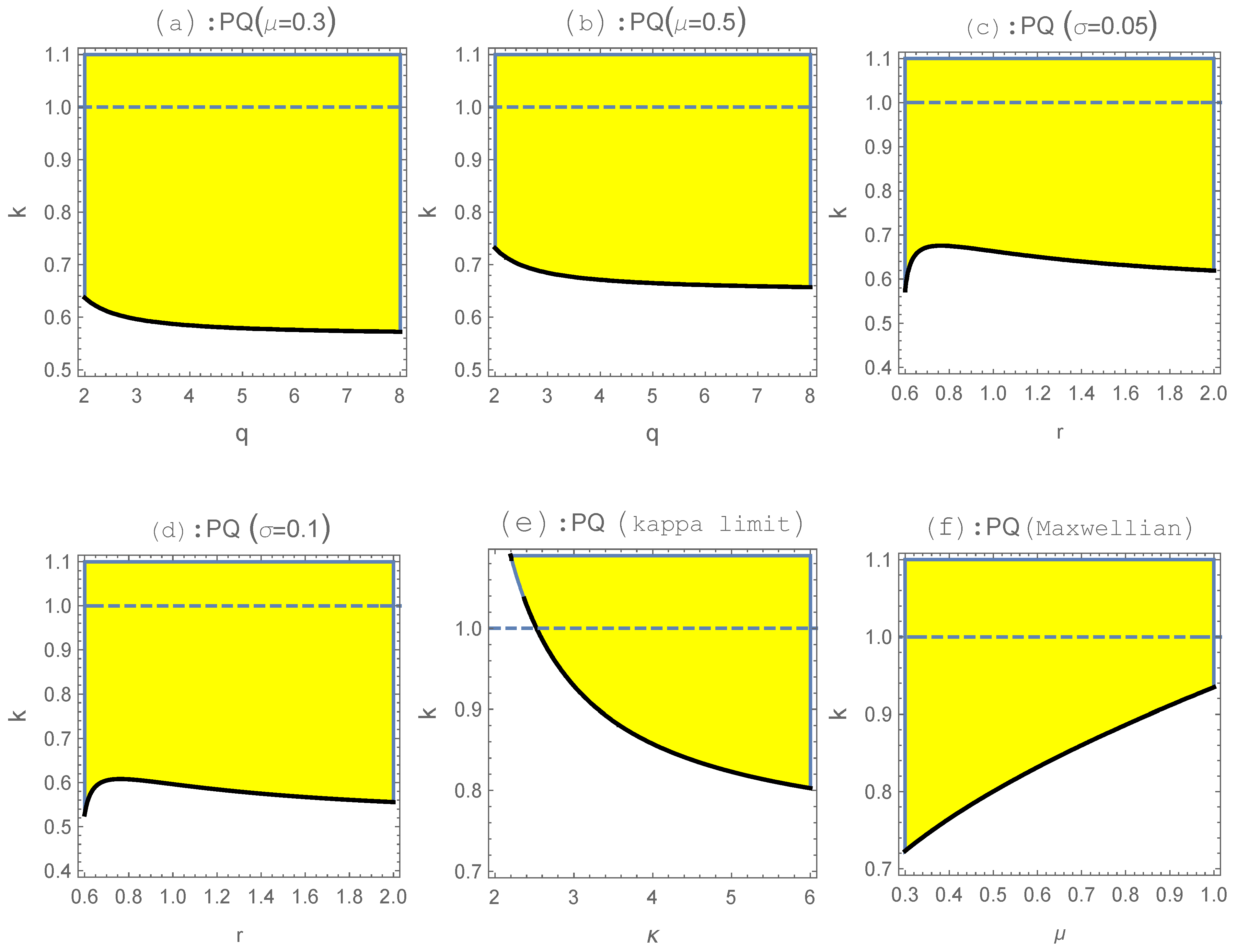
5. Nonlinear Schrödinger Equation and Modulational Instability
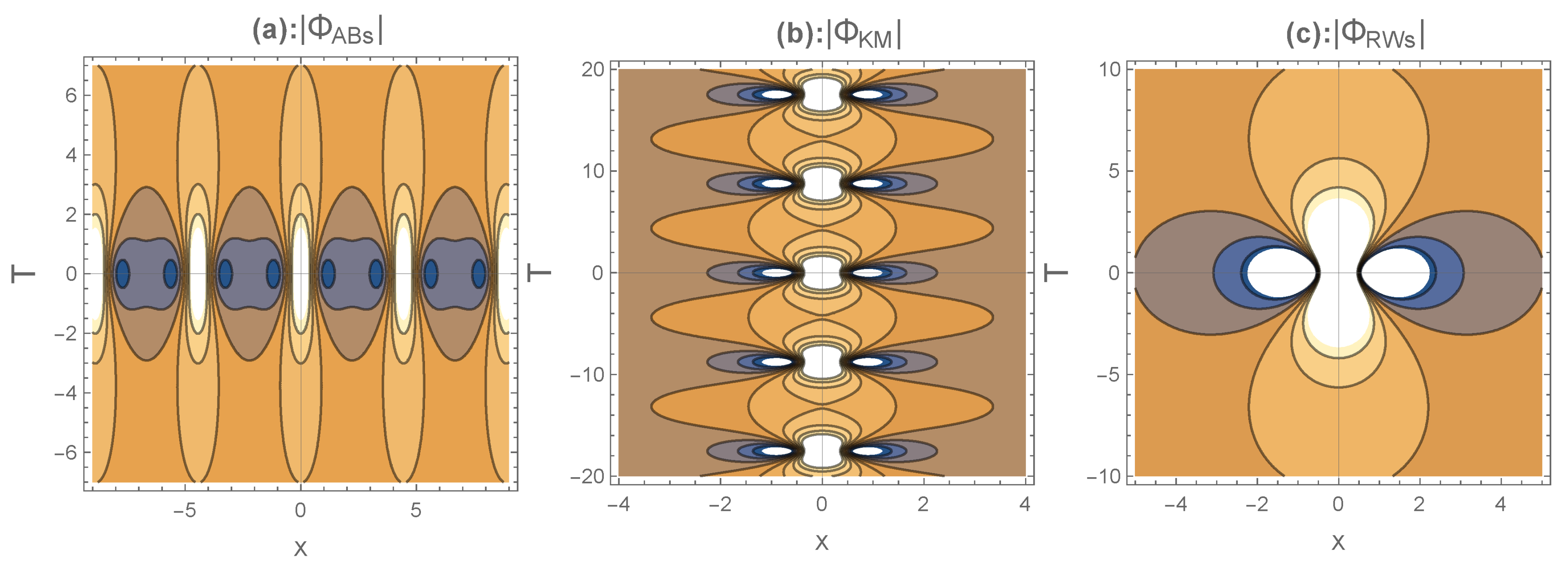
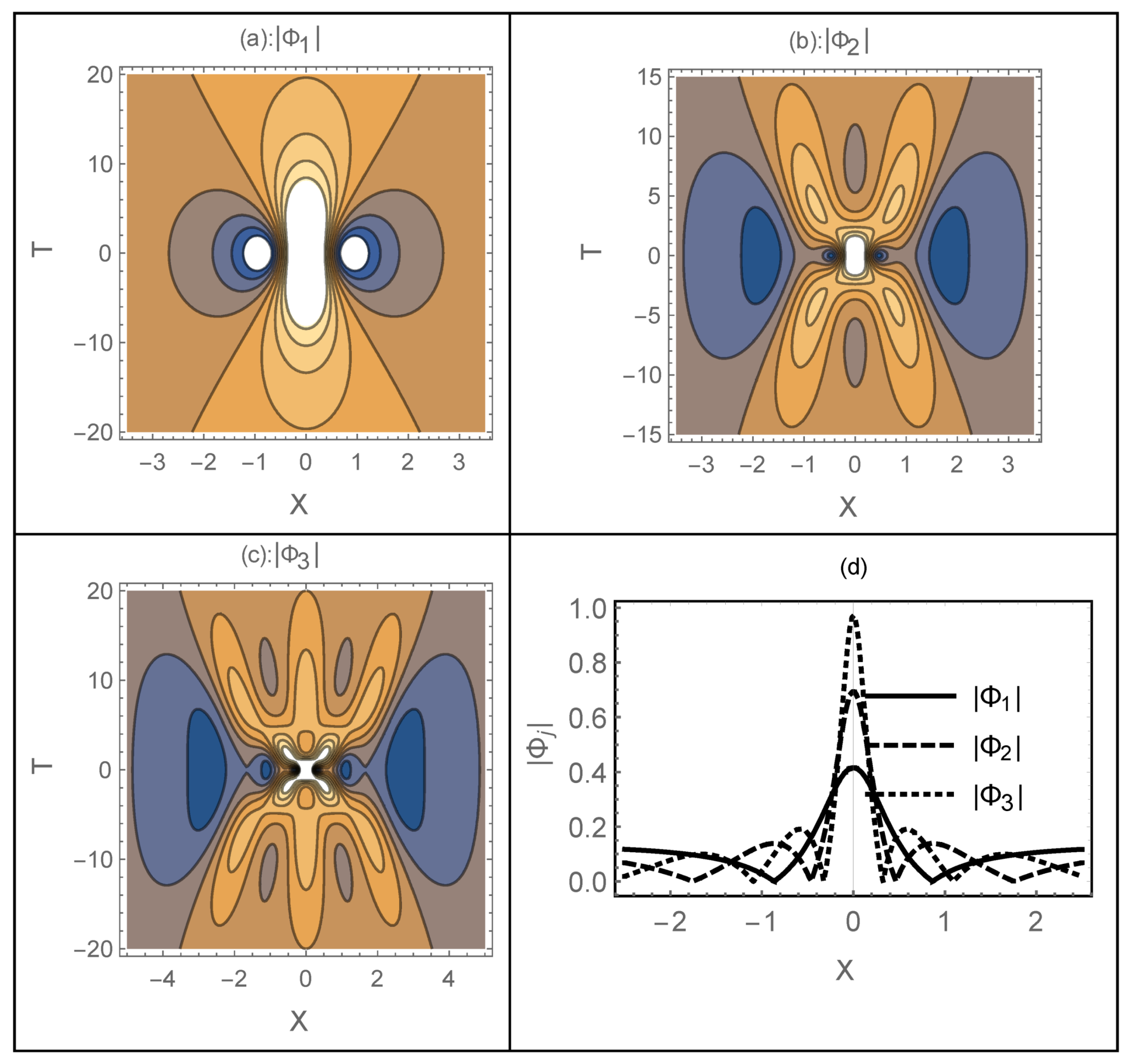
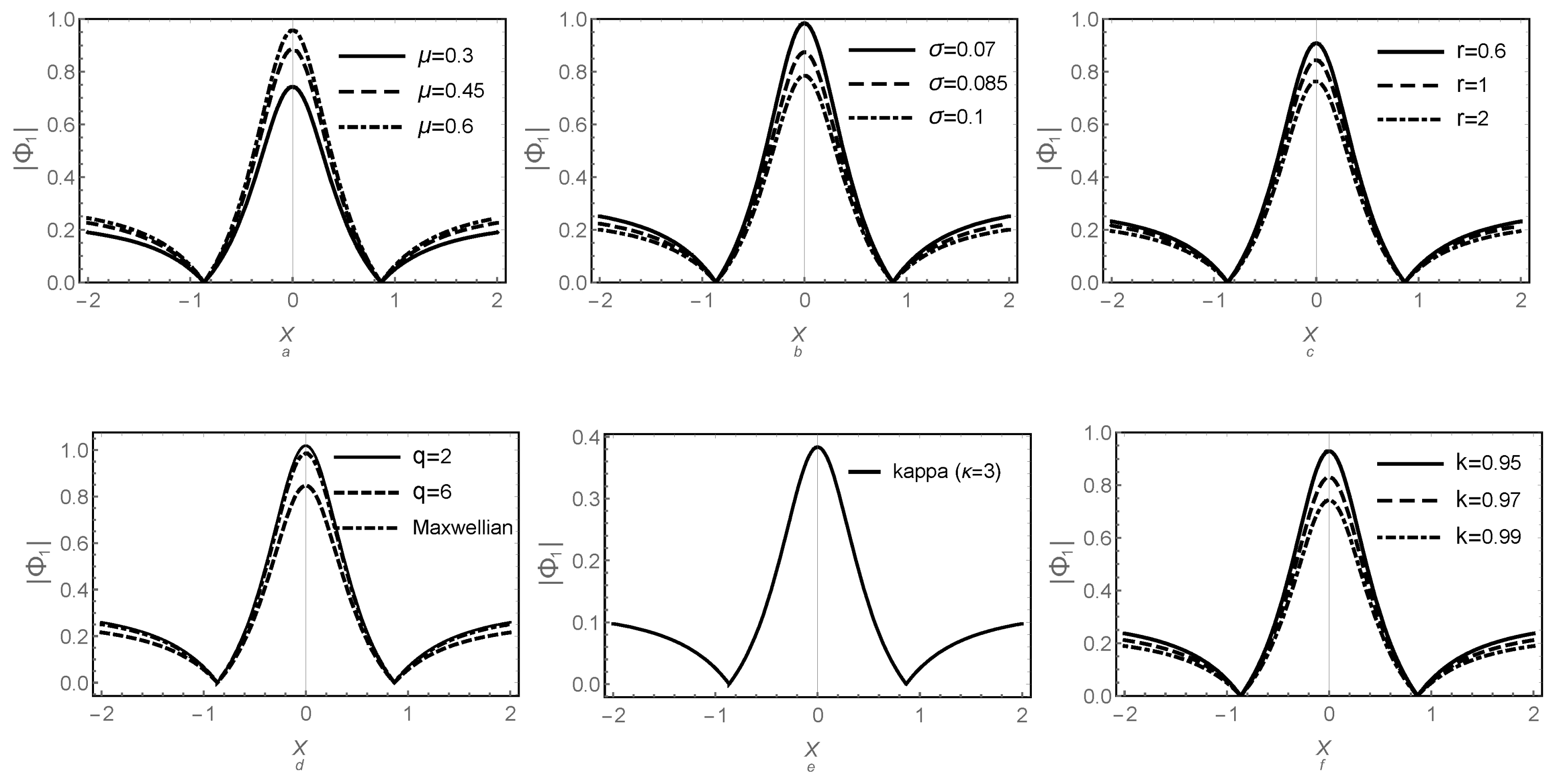
6. Electron Acoustic RWs and Breathers
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fried, B.D.; Gould, R.W. Longitudinal ion oscillations in a hot plasma. Phys. Fluids 1961, 4, 139–147. [Google Scholar] [CrossRef]
- Henry, D.; Treumann, R.A. Propagation of electronic longitudinal modes in a non-Maxwellian plasma. J. Plasma Phys. 1972, 8, 311–319. [Google Scholar] [CrossRef]
- Matsumoto, H.; Kojima, H.; Miyatake, T.; Omura, Y.; Okada, M.; Nagano, I.; Tsutsui, M. Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys. Res. Lett. 1994, 21, 2915–2918. [Google Scholar] [CrossRef]
- Bale, S.D.; Kellogg, P.J.; Larsen, D.E.; Lin, R.P.; Goetz, K.; Lepping, R.P. Bipolar electrostatic structures in the shock transition region: Evidence of electron phase space holes. Geophys. Res. Lett. 1998, 25, 2929–2932. [Google Scholar] [CrossRef]
- Pickett, J.S.; Chen, L.J.; Kahler, S.W.; Santolik, O.; Goldstein, M.L.; Lavraud, B.; Décréau, P.M.E.; Kessel, R.; Lucek, E.; Lakhina, G.S.; et al. On the generation of solitary waves observed by Cluster in the near-Earth magnetosheath. Nonlinear Process. Geophys. 2005, 12, 181–193. [Google Scholar] [CrossRef] [Green Version]
- Tokar, R.L.; Gary, S.P. Electrostatic hiss and the beam driven electron acoustic instability in the dayside polar cusp. Geophys. Res. Lett. 1984, 11, 1180–1183. [Google Scholar] [CrossRef]
- Pottelette, R.; Ergun, R.E.; Treumann, R.A.; Berthomier, M.; Carlson, C.W.; McFadden, J.P.; Roth, I. Modulated electron-acoustic waves in auroral density cavities: FAST observations. Geophys. Res. Lett. 1999, 26, 2629–2632. [Google Scholar] [CrossRef]
- Pickett, J.S.; Kahler, S.W.; Chen, L.J.; Huff, R.L.; Santolik, O.; Khotyaintsev, Y.; Décréau, P.M.E.; Winningham, D.; Frahm, R.; Goldstein, M.L.; et al. Solitary waves observed in the auroral zone: The Cluster multi-spacecraft perspective. Nonlinear Process. Geophys. 2004, 11, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Dubouloz, N.; Pottelette, R.; Malingre, M.; Treumann, R.A. Generation of broadband electrostatic noise by electron acoustic solitons. Geophys. Res. Lett. 1991, 18, 155–158. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Singh, S.V.; Kakad, A.P.; Pickett, J.S. Generation of electrostatic solitary waves in the plasma sheet boundary layer. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Dillard, C.S.; Vasko, I.Y.; Mozer, F.S.; Agapitov, O.V.; Bonnell, J.W. Electron-acoustic solitary waves in the Earth’s inner magnetosphere. Phys. Plasmas 2018, 25, 022905. [Google Scholar] [CrossRef]
- Watanabe, K.; Taniuti, T. Electron-Acoustic Mode in a Plasma of Two-Temperature Electrons. J. Phys. Soc. Jpn. 1977, 43, 1819–1820. [Google Scholar] [CrossRef]
- Stix, T.H. Waves in Plasmas; AIP: New York, NY, USA, 1992. [Google Scholar]
- Gary, S.P.; Tokar, R.L. The electron-acoustic mode. Phys. Fluids 1985, 28, 2439–2441. [Google Scholar] [CrossRef]
- Berthomier, M.; Pottelette, R.; Malingre, M.; Khotyaintsev, Y. Electron-acoustic solitons in an electron-beam plasma system. Phys. Plasmas 2000, 7, 2987–2994. [Google Scholar] [CrossRef]
- Mace, R.L.; Hellberg, M.A. The Korteweg–de Vries–Zakharov–Kuznetsov equation for electron-acoustic waves. Phys. Plasmas 2001, 8, 2649–2656. [Google Scholar] [CrossRef]
- Mamun, A.A.; Shukla, P.K.; Stenflo, L. Obliquely propagating electron-acoustic solitary waves. Phys. Plasmas 2002, 9, 1474–1477. [Google Scholar] [CrossRef]
- Shukla, P.K.; Mamun, A.A.; Eliasson, B. 3D electron-acoustic solitary waves introduced by phase space electron vortices in magnetized space plasmas. Geophys. Res. Lett. 2004, 31, L07803. [Google Scholar] [CrossRef] [Green Version]
- Singh, K.; Saini, N.S. Effect of anisotropic pressure on electron acoustic oscillatory and monotonic shocks in superthermal magnetoplasma. Radio Sci. 2019, 54, 1192–1203. [Google Scholar] [CrossRef]
- Mace, R.L.; Hellberg, M.A. A dispersion function for plasmas containing superthermal particles. Phys. Plasmas 1995, 2, 2098–2109. [Google Scholar] [CrossRef]
- Summers, D.; Thorne, R.M.; Matsumoto, H. Evaluation of the modified plasma dispersion function for half-integral indices. Phys. Plasmas 1996, 3, 2496–2501. [Google Scholar] [CrossRef]
- Abid, A.A.; Khan, M.Z.; Lu, Q.; Yap, S.L. A generalized AZ-non-Maxwellian velocity distribution function for space plasmas. Phys. Plasmas 2017, 24, 033702. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Feldman, W.C.; Anderson, R.C.; Bame, S.J.; Gary, S.P.; Gosling, J.T.; McComas, D.J.; Thomsen, M.F.; Paschmann, G.; Hoppe, M.M. Electron velocity distributions near the Earth’s bow shock. J. Geophys. Res. Space Phys. 1983, 88, 96–110. [Google Scholar]
- Masood, W.; Schwartz, S.J.; Maksimovic, M.; Fazakerley, A.N. Electron velocity distribution and lion roars in the magnetosheath. Ann. Geophys. 2006, 24, 1725–1735. [Google Scholar] [CrossRef] [Green Version]
- Masood, W.; Schwartz, S.J. Observations of the development of electron temperature anisotropies in Earth’s magnetosheath. J. Geophys. Res. 2008, 106, A01216. [Google Scholar] [CrossRef]
- Asano, Y.; Nakamura, R.; Shinohara, I.; Fujimoto, M.; Takada, T.; Baumjohann, W.; Owen, C.J.; Fazakerley, A.N.; Runov, A.; Nagai, T.; et al. Electron flat-top distributions around the magnetic reconnection region. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, M.N.; Shah, H.A.; Murtaza, G.; Schwartz, S.J.; Mahmood, F. Parallel propagating electromagnetic modes with the generalized distribution function. Phys. Plasmas 2004, 11, 3819–3829. [Google Scholar] [CrossRef]
- Qureshi, M.N.; Nasir, W.; Masood, W.; Yoon, P.H.; Shah, H.A.; Schwartz, S.J. Terrestrial lion roars and non-Maxwellian distribution. J. Geophys. Res. Space Phys. 2014, 119, 10059–10067. [Google Scholar] [CrossRef] [Green Version]
- Shah, K.H.; Qureshi, M.N.; Masood, W.; Shah, H.A. Electron acoustic nonlinear structures in planetary magnetospheres. Phys. Plasmas 2018, 25, 042303. [Google Scholar] [CrossRef]
- Sagdeev, R.Z. Reviews of Plasma Physics; Leontovich, M.A., Ed.; Consultants Bureau: New York, NY, USA, 1966. [Google Scholar]
- Albalawi, W.; El-Tantawy, S.A.; Salas, A.H. On the rogue wave solution in the framework of a Korteweg–de Vries equation. Results Phys. 2021, 30, 104847. [Google Scholar] [CrossRef]
- Tiofack, C.G.L.; Douanla, D.V.; Mohamadou, A.; Ismaeel, S.M.E.; El-Tantawy, S.A. Dust-acoustic modulated structures in self-gravitating magnetized electron depleted dusty plasmas: Multi-rogue waves and dark soliton collisions. Eur. Phys. J. Plus 2021, 136, 699. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; El-Tantawy, S.A. Simulation study on nonlinear structures in nonlinear dispersive media. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 053117. [Google Scholar] [CrossRef]
- Irfan, M.; Ali, S.; El-Tantawy, S.A.; Ismaeel, S.M.E. Three dimensional ion-acoustic rogons in quantized anisotropic magnetoplasmas with trapped/untrapped electrons. ChaosInterdiscip. J. Nonlinear Sci. 2019, 29, 103133. [Google Scholar] [CrossRef] [PubMed]
- El-Tantawy, S.A.; Salas, A.H.; Alharthi, M.R. On the Analytical and Numerical Solutions of the Linear Damped NLSE for Modeling Dissipative Freak Waves and Breathers in Nonlinear and Dispersive Mediums: An Application to a Pair-Ion Plasma. Front. Phys. 2021, 9, 580224. [Google Scholar] [CrossRef]
- Salas, A.H.; El-Tantawy, S.A.; Castillo, H.J.E. The hybrid finite difference and moving boundary methods for solving a linear damped nonlinear Schrödinger equation to model rogue waves and breathers in plasma physics. Math. Probl. Eng. 2020, 2020, 6874870. [Google Scholar] [CrossRef]
- Bansal, S.; Gill, T.S.; Aggarwal, M. Oblique modulation of electron acoustic waves in superthermal plasma. Phys. Scr. 2019, 94, 105603. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef] [Green Version]
- Akhmediev, N.; Ankiewicz, A.; Taki, M. Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 2009, 373, 675–678. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ankiewicz, A.; Devine, N.; Akhmediev, N. Are rogue waves robust against perturbations? Phys. Lett. A 2009, 373, 3997–4000. [Google Scholar] [CrossRef]
- Kuznetsov, E.A. Solitons in a parametrically unstable plasma. Akad. Nauk. SSSR Dokl. 1977, 236, 575–577. [Google Scholar]
- Ma, Y.C. The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 1979, 60, 43–58. [Google Scholar] [CrossRef]
- Ruderman, M.S. Freak waves in laboratory and space plasmas. Eur. Phys. J. Spec. Top. 2010, 185, 57–66. [Google Scholar] [CrossRef] [Green Version]
- El-Bedwehy, N.A. Freak waves in GaAs semiconductor. Physica B 2014, 442, 114–117. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alshehri, M.H.; Duraihem, F.Z.; El-Sherif, L.S. Dark soliton collisions and method of lines approach for modeling freak waves in a positron beam plasma having superthermal electrons. Results Phys. 2020, 19, 103452. [Google Scholar] [CrossRef]
- Singh, K.; Saini, N.S. The evolution of rogue wave triplets and super rogue waves in superthermal polarized space dusty plasma. Phys. Plasmas 2019, 26, 113702. [Google Scholar] [CrossRef]
- Almutlak, S.A.; El-Tantawy, S.A.; Shan, S.A.; Ismaeel, S.M. Multidimensional freak waves in electron depleted dusty magnetoplasmas having superthermal ion with two temperatures. Eur. Phys. J. Plus 2019, 134, 513. [Google Scholar] [CrossRef]
- Akhtar, N.; El-Tantawy, S.A.; Mahmood, S.; Wazwaz, A.-M. On the dynamics of dust-acoustic and dust-cyclotron freak waves in a magnetized dusty plasma. Rom. Rep. Phys. 2019, 71, 403. [Google Scholar]
- El-Tantawy, S.A.; Wazwaz, A.M. Anatomy of modified Korteweg–de Vries equation for studying the modulated envelope structures in non-Maxwellian dusty plasmas: Freak waves and dark soliton collisions. Phys. Plasmas 2018, 25, 092105. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Shan, S.A.; Akhtar, N.; Elgendy, A.T. Impact of electron trapping in degenerate quantum plasma on the ion-acoustic breathers and super freak waves. Chaos Solitons Fract. 2018, 113, 356–364. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Ali, S.; Maroof, R.; Wazwaz, A.-M.; El-Labany, S.K. On the super freak waves in multicomponent plasmas having two-negative ions: Xe+ − F− − SF6− and Ar+ − F− − SF6− plasmas. Indian J. Phys. 2017, 91, 939–946. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Aboelenen, T. Simulation study of planar and nonplanar super rogue waves in an electronegative plasma: Local discontinuous Galerkin method. Phys. Plasmas 2017, 24, 052118. [Google Scholar] [CrossRef]
- El-Tantawy, S.A. Ion-acoustic waves in ultracold neutral plasmas: Modulational instability and dissipative rogue waves. Phys. Lett. A 2017, 381, 787–791. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Wazwaz, A.M.; Ali Shan, S. On the nonlinear dynamics of breathers waves in electronegative plasmas with Maxwellian negative ions. Phys. Plasmas 2017, 24, 022105. [Google Scholar] [CrossRef]
- Turing, A. Philosophical the royal biological transqfctions society sciences. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef] [PubMed]
- Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A 2009, 80, 033610. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Rogue waves in space dusty plasmas. Phys. Plasmas 2017, 24, 113701. [Google Scholar] [CrossRef]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Stenflo, L.; Marklund, M. Rogue waves in the atmosphere. J. Plasma Phys. 2010, 76, 293–295. [Google Scholar] [CrossRef] [Green Version]
- Bailung, H.; Sharma, S.K.; Nakamura, Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 2011, 107, 255005. [Google Scholar] [CrossRef]
- Merriche, A.; Tribeche, M. Electron-acoustic rogue waves in a plasma with Tribeche–Tsallis–Cairns distributed electrons. Ann. Phys. 2017, 376, 436–447. [Google Scholar] [CrossRef]
- Ullah, S.; Masood, W.; Siddiq, M.; Rizvi, H. Oblique modulation and envelope excitations of nonlinear ion sound waves with cubic nonlinearity and generalized (r, q) distribution. Phys. Scr. 2019, 94, 125604. [Google Scholar] [CrossRef]
- Ullah, S.; Masood, W.; Siddiq, M. Electron acoustic envelope solitons in non-Maxwellian plasmas. Eur. Phys. J. D 2020, 74, 1–9. [Google Scholar] [CrossRef]
- Liu, J.G.; Xiong, W.P. Multi-wave, breather wave and lump solutions of the Boiti–Leon–Manna–Pempinelli equation with variable coefficients. Results Phys. 2020, 19, 103532. [Google Scholar] [CrossRef]
- Singh, K.; Saini, N.S. Breather Structures and Peregrine Solitons in a Polarized Space Dusty Plasma. Front. Phys. 2020, 8, 602229. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Genty, G.; Wetzel, B.; Akhmediev, N.; Dias, F.; Dudley, J.M. Observation of Kuznetsov–Ma soliton dynamics in optical fiber. Sci. Rep. 2012, 2, 1–5. [Google Scholar] [CrossRef]
- Danehkar, A.; Saini, N.S.; Hellberg, M.A.; Kourakis, I. Electron-acoustic solitary waves in the presence of a suprathermal electron component. Phys. Plasmas 2011, 18, 072902. [Google Scholar] [CrossRef] [Green Version]
- Lakhina, G.S.; Singh, S.V.; Rubia, R.; Sreeraj, T. A review of nonlinear fluid models for ion-and electron-acoustic solitons and double layers: Application to weak double layers and electrostatic solitary waves in the solar wind and the lunar wake. Phys. Plasmas 2018, 25, 080501. [Google Scholar] [CrossRef]
- Verheest, F.; Hellberg, M.A. Effects of hot electron inertia on electron-acoustic solitons and double layers. Phys. Plasmas 2015, 22, 072303. [Google Scholar] [CrossRef] [Green Version]
- Kourakis, I.; Shukla, P.K. Modulational instability and localized excitations of dust-ion acoustic waves. Phys. Plasmas 2003, 10, 3459. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.K. Modulation of dust acoustic waves with non-adiabatic dust charge fluctuations. Phys. Lett. A 2003, 320, 226–233. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, W.; Jahangir, R.; Masood, W.; Alkhateeb, S.A.; El-Tantawy, S.A. Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers. Symmetry 2021, 13, 2029. https://doi.org/10.3390/sym13112029
Albalawi W, Jahangir R, Masood W, Alkhateeb SA, El-Tantawy SA. Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers. Symmetry. 2021; 13(11):2029. https://doi.org/10.3390/sym13112029
Chicago/Turabian StyleAlbalawi, Wedad, Rabia Jahangir, Waqas Masood, Sadah A. Alkhateeb, and Samir A. El-Tantawy. 2021. "Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers" Symmetry 13, no. 11: 2029. https://doi.org/10.3390/sym13112029
APA StyleAlbalawi, W., Jahangir, R., Masood, W., Alkhateeb, S. A., & El-Tantawy, S. A. (2021). Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers. Symmetry, 13(11), 2029. https://doi.org/10.3390/sym13112029






