Construction of Analytic Solution to Axisymmetric Flow and Heat Transfer on a Moving Cylinder
Abstract
1. Introduction
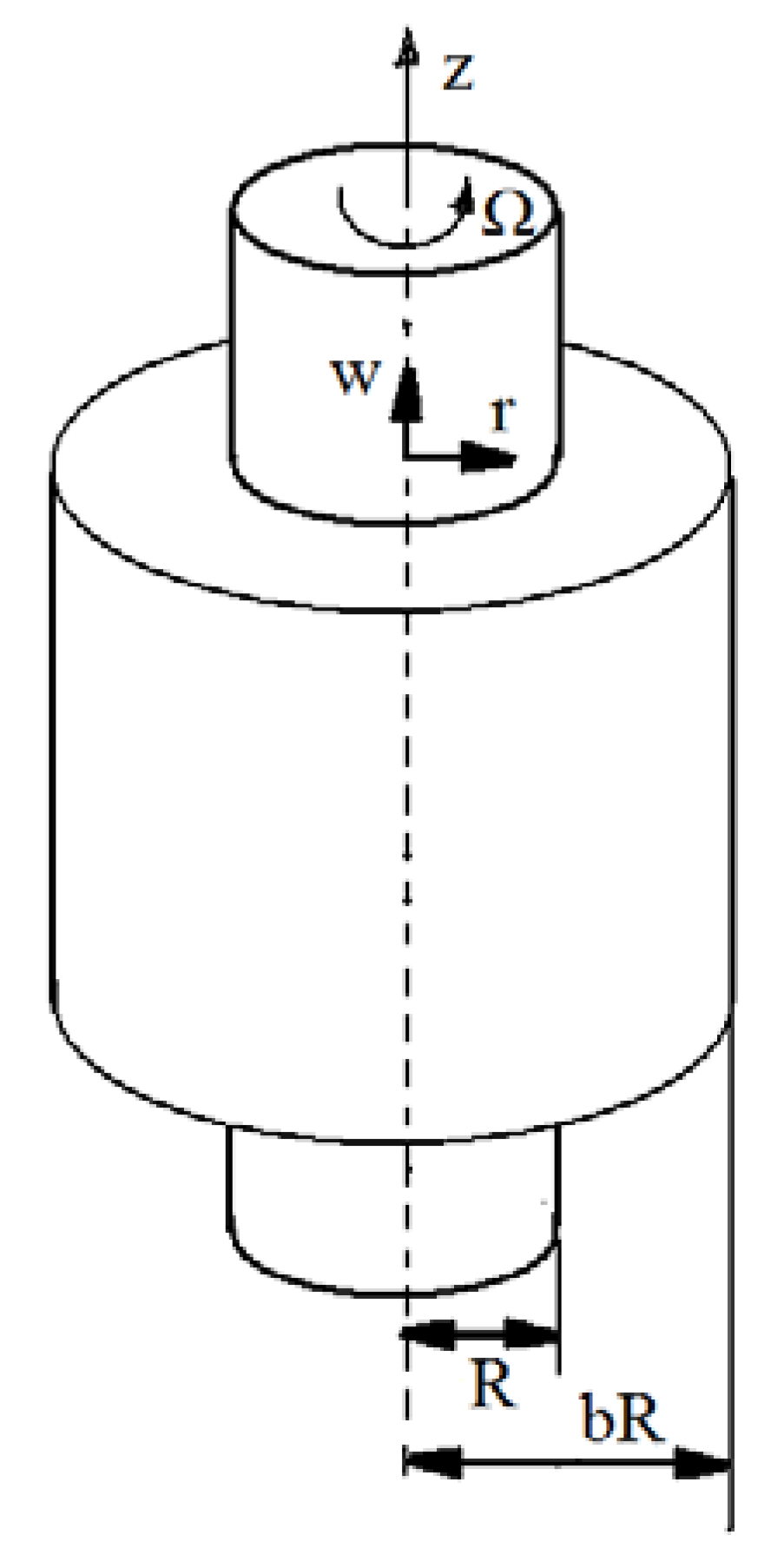
2. Equations of Motion
3. Basics of the Optimal Auxiliary Functions Method (OAFM)
4. Application of the Optimal Auxiliary Functions Method
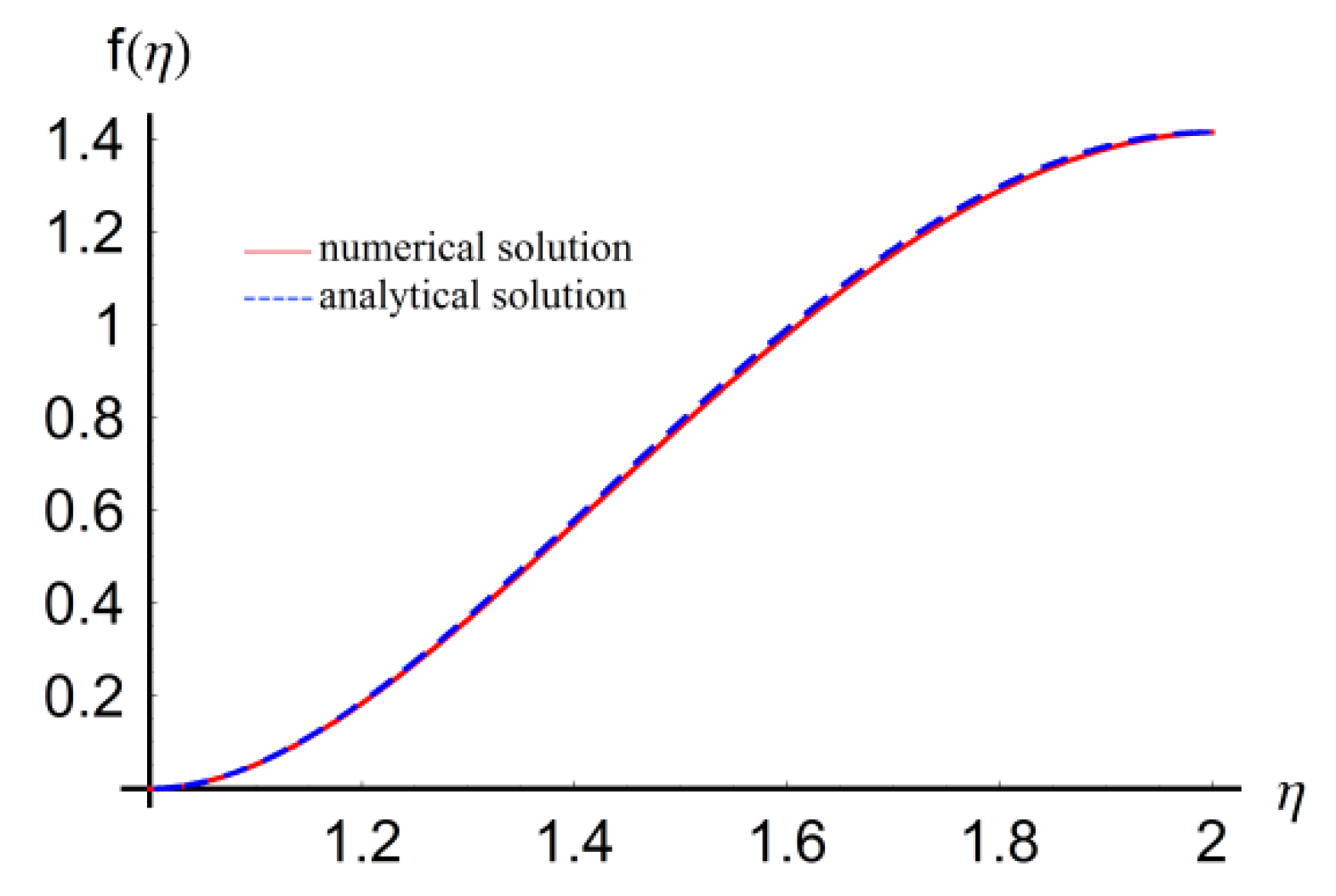
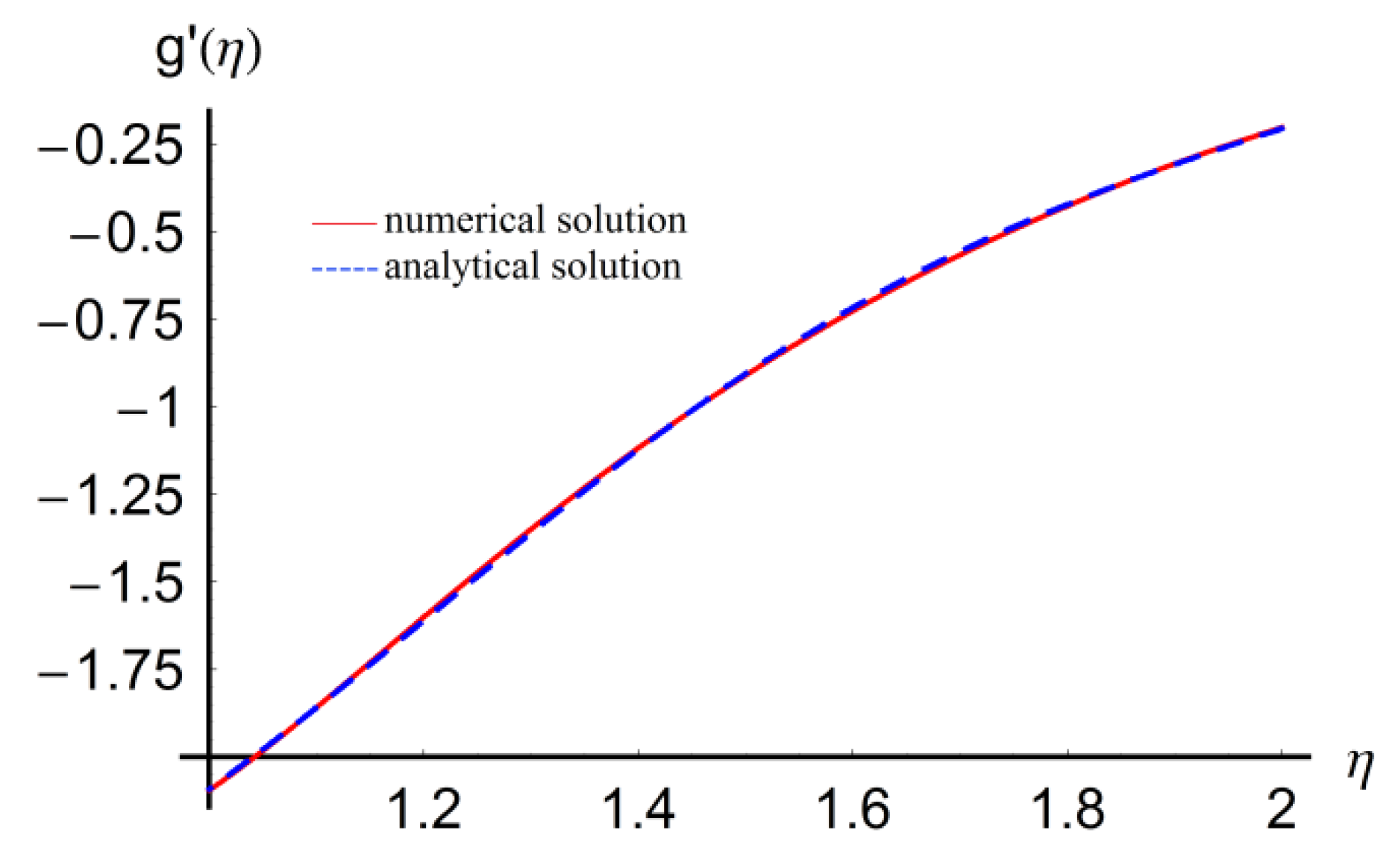
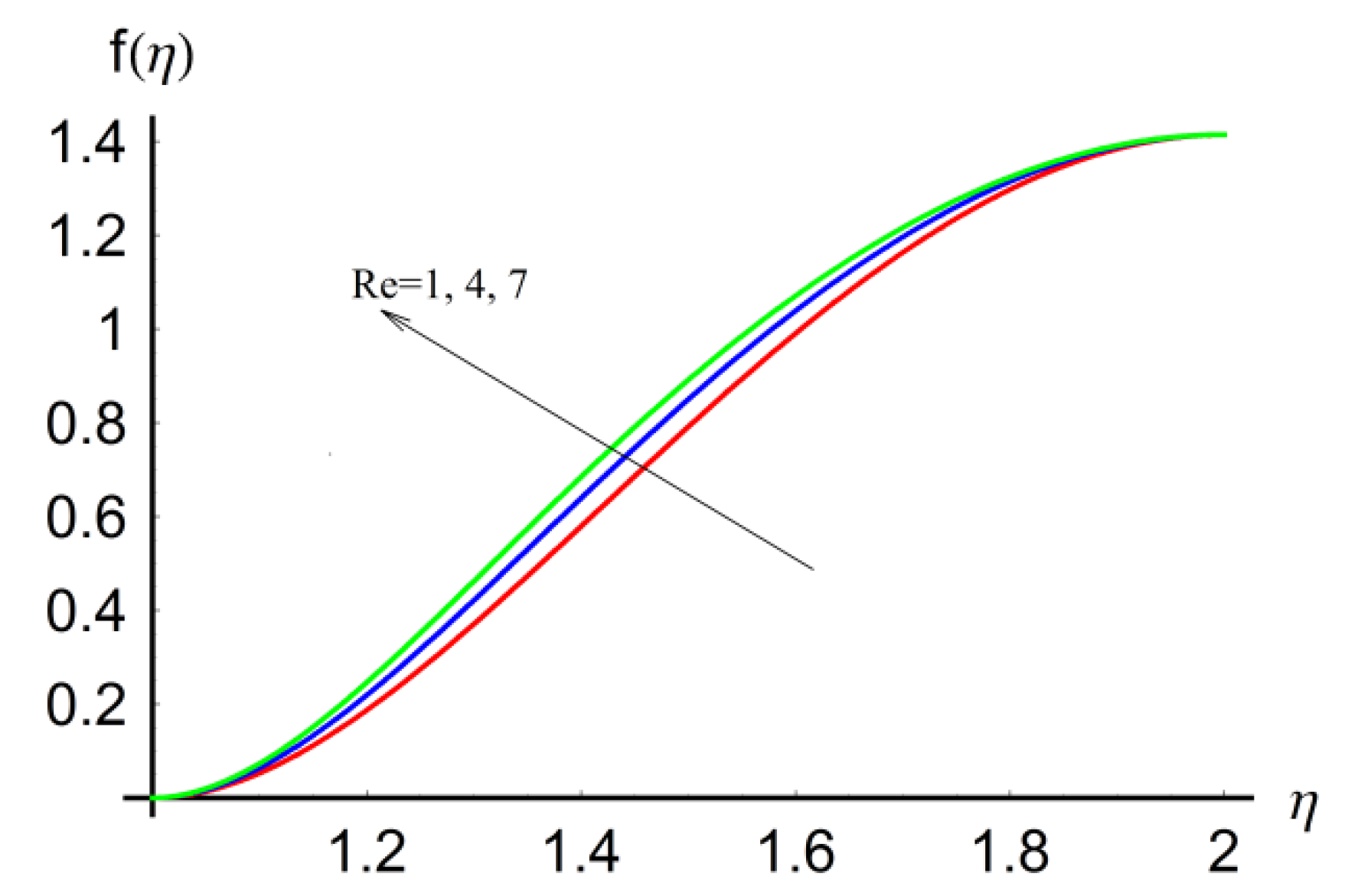
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gorla, R.S.R. The final approach to steady state in an axisymmetric stagnation flow following a change in free stream velocity. Appl. Sci. Res. 1983, 40, 247–251. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkhe, A.J.; Neth, G. Unsteady axisymmetric stagnation-point floor of a viscousfluid on a cylinder. Int. J. Eng. Sci. 1999, 37, 1143–1157. [Google Scholar] [CrossRef]
- Weidman, P.D.; Putkaradze, V. Axisymmetric stagnation flow obliquely impinging on a circular cylinder. Eur. J. Mech. B Fluids 2003, 22, 123–131. [Google Scholar] [CrossRef]
- Resnic, C.; Grosan, T.; Pop, I. Heat transfer in axisymmetric stagnation flow on a thin cylinder. Studia Univ. Babes Bolyai Math. 2008, LIII, 119–125. [Google Scholar]
- Ahmed, I.; Sajid, M.; Hayat, T.; Ayub, M. Unsteady axisymmetric flow of a second-grade fluid over a radially stretching sheet. Comp. Math. Appl. 2008, 56, 1351–1357. [Google Scholar] [CrossRef]
- Hong, L.; Wang, C.Y. Annular axisymmetric stagnation flow on a moving cylinder. Int. J. Eng. Sci. 2009, 47, 141–152. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, M. Effect of heat transfer on magnetohydrodynamic axisymmetric flow between two stretching sheets. Z. Naturforsch. 2010, 65, 961–968. [Google Scholar] [CrossRef]
- Doo, C.; Huang, S.J.; Zhang, M.J. On 3D axisymmetric invested stagnation point flow related to Navier-Stokes equations. Nonlinear Anal. Forum 2011, 16, 67–75. [Google Scholar]
- Nadeem, S.; Rehman, A.; Vajravelu, K.; Lee, J.; Lee, C. Axisymmetric stagnation flow of a micropolarnanofluid in a moving cylinder. Math. Probl. Eng. 2012. [Google Scholar] [CrossRef]
- Shahzad, A.; Ali, R.; Khan, M. On the exact solution for axisymmetric flow and heat transfer over a nonlinear radially stretching sheet. Chim. Phys. Lett. 2012, 29, 084705. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A.; Awais, M. MHD axisymmetric flow of third grade fluid between stretching sheets with heat transfer. Comput. Fluids 2013, 36, 103–108. [Google Scholar] [CrossRef]
- Mastroberardino, A. Series solutions of annular axisymmetric stagnation flow and heat transfer on moving cylinder. Appl. Math. Mech. 2013, 34, 1043–1054. [Google Scholar] [CrossRef]
- Rosca, A.V.; Rosca, N.C.; Pop, I. Axisymmetric stagnation point flow and heat transfer towards a permeable moving flat plate with surface slip condition. Appl. Math. Comput. 2014, 233, 139–151. [Google Scholar]
- Hazarika, G.C.; Sarmah, A. Effect of magnetic field on flow near an axisymmetric stagnation point on a moving cylinder. Int. J. Modern Eng. Res. Tech. 2014, 1, 46–54. [Google Scholar]
- Weidman, P. Axisymmetric rotational stagnation point flow impinging on a flat liquid surface. Eur. J. Mech. B Fluids 2016, 56, 188–191. [Google Scholar] [CrossRef]
- Khan, M.; Rahman, M.; Manzur, M. Axisymmetric flow and heat transfer to a modified second grade fluid over a radially stretching sheet. Results Phys. 2017, 7, 878–889. [Google Scholar] [CrossRef]
- Azam, M.; Khan, M.; Alshomrani, A.S. Effects of magnetic field and partial slip on unsteady axisymmetric flow of Caureaunanofluid over a radially stretching surface. Results Phys. 2017, 7, 2671–2682. [Google Scholar] [CrossRef]
- Nadeem, A.; Mahmood, A.; Siddique, J.I.; Zhao, L. Axisymmetric magnetohydrodynamic flow of nanofluidunder heat generation/absorption effects. Appl. Math. Sci. 2017, 11, 2059–2087. [Google Scholar]
- Mahapatra, T.R.; Sidqui, S. Heat transfer in non-axisymmetric Homanstagnation point flows towards a stretching sheet. Eur. J. Mech. B Fluids 2017, 65, 522–529. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V.; Madescu, G.; Dragan, F. Dynamic response of a permanent magnet synchronous generator to a wind gust. Energies 2019, 12, 915. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. An efficient analytical approach to investigate the dynamics of a misaligned multirotor system. Mathematics 2020, 8, 1083. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Vibration of nonlinear nonlocal elastic column with initial imperfections. Springer Proc. Phys. 2018, 198, 49–56. [Google Scholar]
- Marinca, V.; Herisanu, N. Explicit and exact solutions to cubic Duffing and double-well Duffing equations. Math. Comput. Model. 2011, 53, 604–609. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marinca, V.; Herisanu, N. Construction of Analytic Solution to Axisymmetric Flow and Heat Transfer on a Moving Cylinder. Symmetry 2020, 12, 1335. https://doi.org/10.3390/sym12081335
Marinca V, Herisanu N. Construction of Analytic Solution to Axisymmetric Flow and Heat Transfer on a Moving Cylinder. Symmetry. 2020; 12(8):1335. https://doi.org/10.3390/sym12081335
Chicago/Turabian StyleMarinca, Vasile, and Nicolae Herisanu. 2020. "Construction of Analytic Solution to Axisymmetric Flow and Heat Transfer on a Moving Cylinder" Symmetry 12, no. 8: 1335. https://doi.org/10.3390/sym12081335
APA StyleMarinca, V., & Herisanu, N. (2020). Construction of Analytic Solution to Axisymmetric Flow and Heat Transfer on a Moving Cylinder. Symmetry, 12(8), 1335. https://doi.org/10.3390/sym12081335



