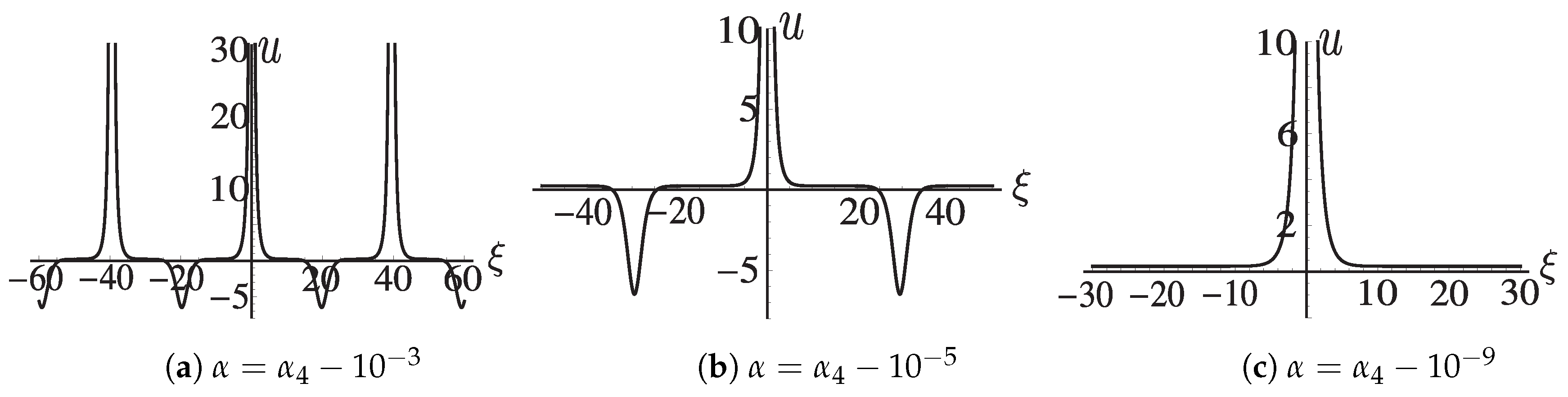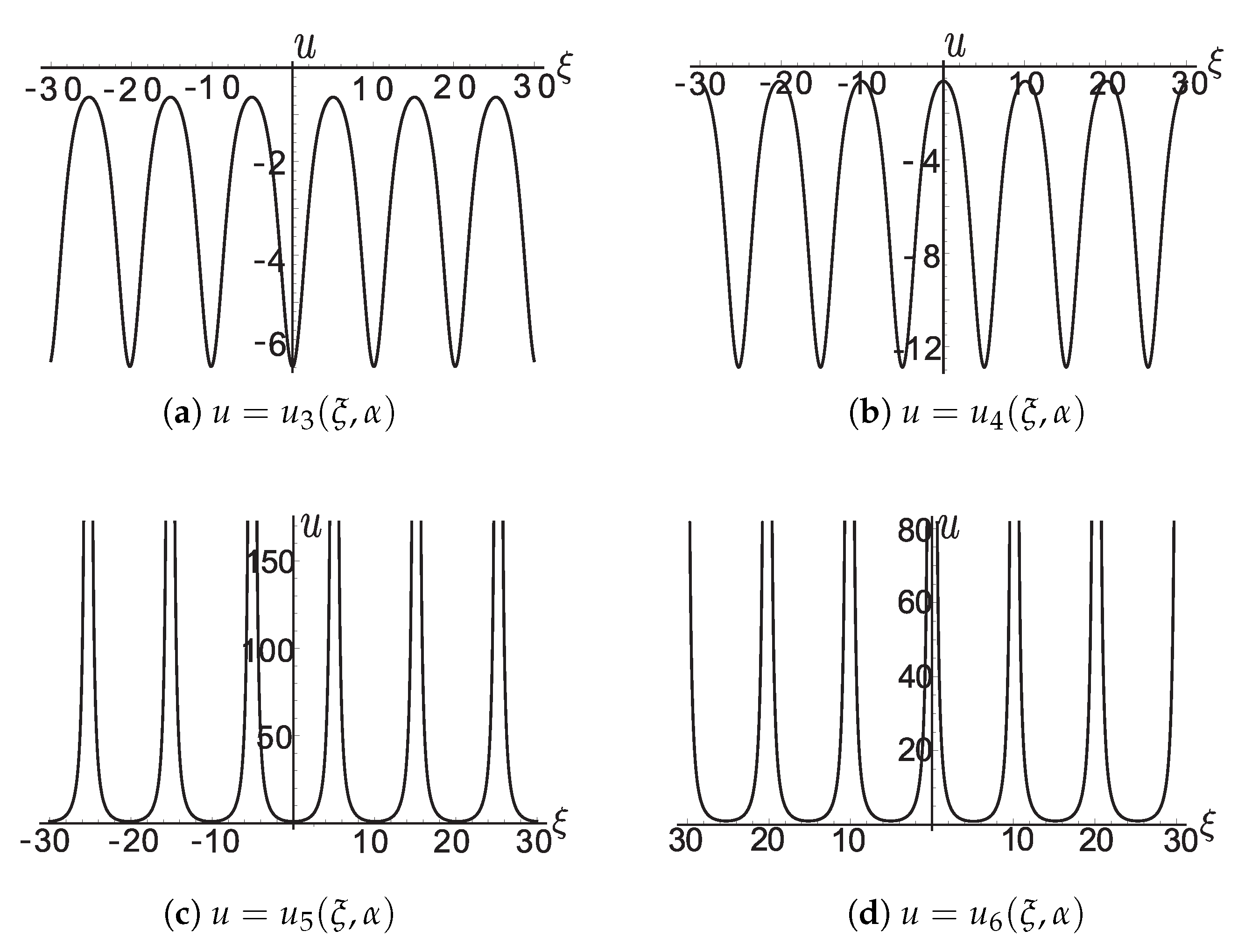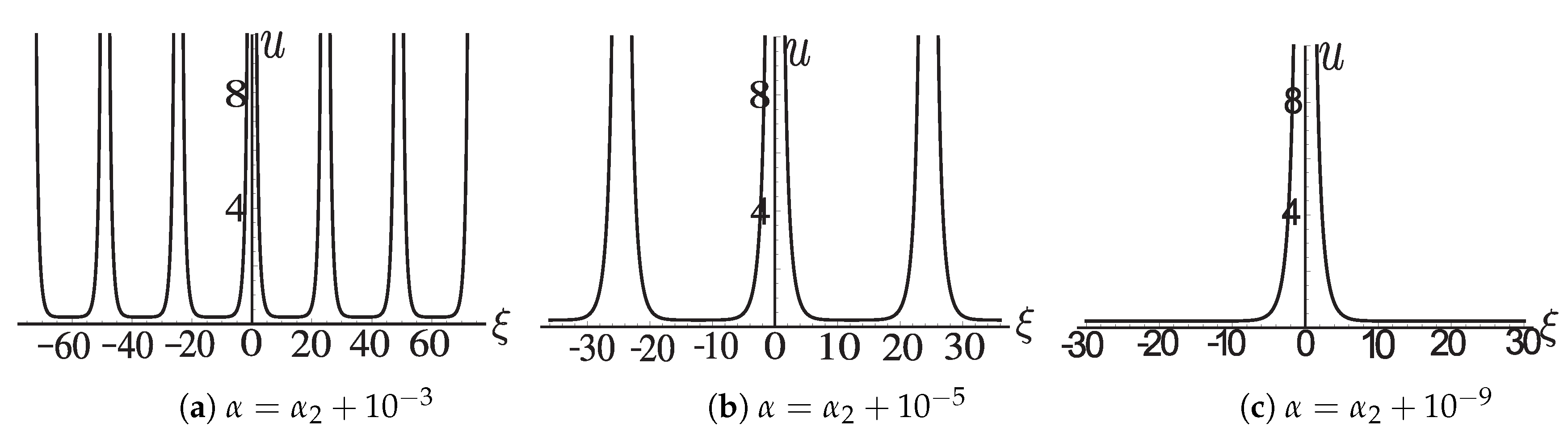Periodic Wave Solutions and Their Asymptotic Property for a Modified Fornberg–Whitham Equation

Abstract

Recently, periodic traveling waves, which include periodically symmetric traveling waves of nonlinear equations, have received great attention. This article uses some bifurcations of the traveling wave system to investigate the explicit periodic wave solutions with parameter $\alpha$ and their asymptotic property for the modified Fornberg–Whitham equation. Furthermore, when $\alpha$ tends to given parametric values, the elliptic periodic wave solutions become the other three types of nonlinear wave solutions, which include the trigonometric periodic blow-up solution, the hyperbolic smooth solitary wave solution, and the hyperbolic blow-up solution.

1. Introduction

The Fornberg–Whitham equation

$$u_t-u_{xxt}+u_x+u{u}_x=3u_x{u}_{xx}+u{u}_{xxx}$$

(1)

appeared in the study of qualitative behaviors of wave-breaking [1,2]. In [3], Fornberg and Whitham obtained a peak solution of the form $u(x,t)=Aexp(-\frac{1}{2}|x-\frac{4}{3}t|)$ for Equation (1). We can see the similarity between Equation (1) and the well-known Camassa–Holm equation

$$u_t+2k{u}_x-u_{xxt}+3u{u}_x=2u_x{u}_{xx}+u{u}_{xxx}.$$

(2)

If $k=0$, then Equation (2) has the peakon solution $u(x,t)=cexp(-|x-ct\left|\right)$ [4]. If $k\ne 0$, then Equation (2) has the peakon solution $u(x,t)=(c+k)exp(-|x-ct\left|\right)-k$ [5]. In addition to the distinction in the coefficients, there exists a great difference, i.e., for $k=0$, Equation (2) possesses the property of complete integrability and bi-Hamiltonian structure while Equation (1) does not have such advantage [6].

Since the appearance of the Camassa–Holm equation Equation (2), a huge amount of work has been carried out to study the dynamic properties of Equation (2). Equation (2) has been proved to possess the global existence, the precise blow-up scenario, the blow-up set and the blow-up rate for the strong solutions [7,8,9,10]. It has also been confirmed that the peakon of Equation (2) are orbitally stable [11,12].

In [13], Liu and Qian suggested a generalized Camassa–Holm equation

$$u_t+2k{u}_x-u_{xxt}+3u^2{u}_x=2u_x{u}_{xx}+u{u}_{xxx}.$$

(3)

Similarly, by softening the nonlinear term, He et al. [14] studied the peakons and solitary waves for the modified Fornberg–Whitham equation

$$u_t-u_{xxt}+u_x+u^2{u}_x=3u_x{u}_{xx}+u{u}_{xxx}.$$

(4)

However, little attention has been given to the periodic traveling wave solutions in their study.

Recently, periodic traveling waves of nonlinear equations have received great attention. For instance, Angulo et al. [15] mentioned that the cnoidal waves of KdV equation converge to the limit soliton when the period tends to infinity. The detailed study was presented by Neves [16]. In [17], the periodic asymptotics of a class of stationary nonlinear Schrödinger equations has been studied together with the existence of dark soliton. The authors [18] showed that the limit forms of the periodic loop solutions of the Kudryashov–Sinelshchikov equation contained loop soliton solutions, smooth periodic wave solutions, and periodic cusp wave solutions.

In this paper, we study the explicit periodic wave solutions and their asymptotic property for Equation (4) using bifurcation analysis [19,20,21,22,23,24,25,26]. Also, some periodic wave solutions are symmetric [27]. First, we obtain two types of explicit periodic wave solutions, elliptic smooth periodic wave solutions and periodic blow-up solutions with a parameter $\alpha$. Secondly, we reveal that there exist four parametric values. When $\alpha$ tends to these parametric values, these elliptic periodic wave solutions can become other three types of nonlinear wave solutions, the hyperbolic smooth solitary wave solutions, the hyperbolic blow-up solutions and the trigonometric periodic blow-up solutions.

This paper is organized as follows. In Section 2, we give some preliminaries. Our main results are listed in Section 3. In Section 4, we provide derivation to our main results. A short conclusion is given in Section 5.

2. Preliminaries

To derive our results, we give some preliminaries in this section. For given constant c, substituting $u=\phi \left(\xi \right)$ with $\xi =x-ct$ into Equation (4), it follows that

$$-c{\phi }^{\prime }+c{\phi }^{‴}+{\phi }^{\prime }+{\phi }^2{\phi }^{\prime }=3{\phi }^{\prime }{\phi }^{″}+\phi {\phi }^{‴}.$$

(5)

Integrating (5) once, we have

$$(\phi -c){\phi }^{″}=\frac{1}{3}{\phi }^3+(1-c)\phi -{\left({\phi }^{\prime }\right)}^2+g,$$

(6)

where g is an integral constant. Letting $y={\phi }^{\prime }$, we get a planar system

$$\left\{\begin{array}{cc}\hfill & \frac{\mathrm{d}\phi }{\mathrm{d}\xi }=y,\hfill \\ & \frac{\mathrm{d}y}{\mathrm{d}\xi }=\frac{\frac{1}{3}{\phi }^3+(1-c)\phi -y^2+g}{\phi -c},\hfill \end{array}\right.$$

(7)

with the first integral

$${(\phi -c)}^2{y}^2=\frac{2}{15}{\phi }^5-\frac{1}{6}c{\phi }^4+\frac{2}{3}(1-c){\phi }^3+(g-c(1-c)){\phi }^2-2gc\phi +h,$$

(8)

where h is another integral constant.

Assuming that $\alpha$ and c (double root) are two real roots of the equation

$$\frac{2}{15}{\phi }^5-\frac{1}{6}c{\phi }^4+\frac{2}{3}(1-c){\phi }^3+(g-c(1-c)){\phi }^2-2gc\phi +h=0,$$

(9)

we get its other two roots $\beta$ and $\gamma$ of forms

$$\beta =\frac{1}{8}\left(-3c-4\alpha +\sqrt{-320+320c-23c^2-24c\alpha -48{\alpha }^2}\right),$$

(10)

and

$$\gamma =\frac{1}{8}\left(-3c-4\alpha -\sqrt{-320+320c-23c^2-24c\alpha -48{\alpha }^2}\right).$$

(11)

Solving equations $\beta =\gamma$, $\alpha =\beta$, and $\alpha =\gamma$ respectively, we get the four numbers ${\alpha }_i$$(i=1-4)$ of forms

$$\begin{array}{cc}\hfill {\alpha }_1& =\frac{-3c+2\sigma }{12},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\alpha }_2& =\frac{-3c+\sigma }{12},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\alpha }_3& =\frac{-3c-\sigma }{12},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\alpha }_4& =\frac{-3c-2\sigma }{12},\hfill \end{array}$$

(15)

where

$$\sigma =\sqrt{15(16c-16-c^2)}.$$

(16)

From above expressions we get the following lemma.

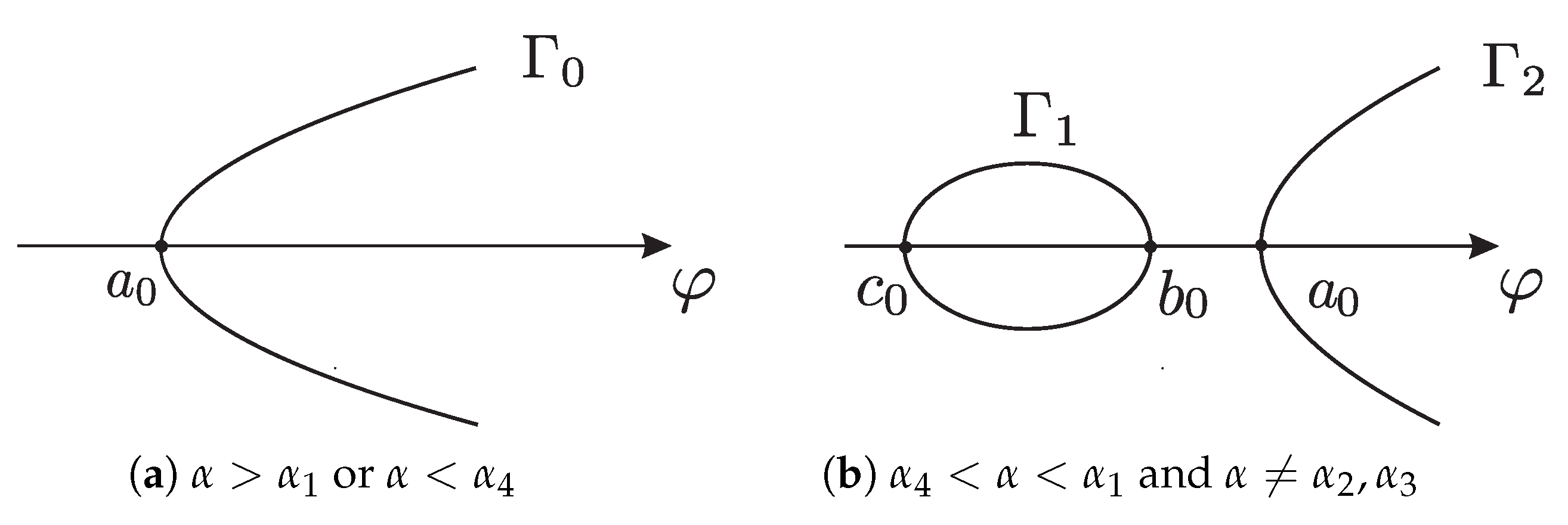
Lemma 1.

To make σ real, denote $c_1=4\left(2-\sqrt{3}\right)$, $c_2=4\left(2+\sqrt{3}\right)$, when constant wave velocity $c\in (c_1,c_2)$, there are the following facts.

(1) ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and ${\alpha }_4$ are real and satisfy inequality

$${\alpha }_4<{\alpha }_3<{\alpha }_2<{\alpha }_1.$$

(17)

(2) If $\alpha <{\alpha }_4$ or $\alpha >{\alpha }_1$, then β and γ are complex. If ${\alpha }_4\le \alpha \le {\alpha }_1$, then β and γ are real and there exists the following properties.

(i) When $\alpha ={\alpha }_1$, it follows that

$$\beta =\gamma ={\alpha }_2<\alpha ={\alpha }_1.$$

(18)

(ii) When $\alpha \in ({\alpha }_2,{\alpha }_1)$, it follows that

$$\gamma <\beta <\alpha .$$

(19)

(iii) When $\alpha ={\alpha }_2$, it follows that

$$\gamma ={\alpha }_4<\beta =\alpha ={\alpha }_2.$$

(20)

(iv) When $\alpha \in ({\alpha }_3,{\alpha }_2)$, it follows that

$$\gamma <\alpha <\beta .$$

(21)

(v) When $\alpha ={\alpha }_3$, it follows that

$$\alpha =\gamma ={\alpha }_3<\beta ={\alpha }_1.$$

(22)

(vi) When $\alpha \in ({\alpha }_4,{\alpha }_3)$, it follows that

$$\alpha <\gamma <\beta .$$

(23)

(vii) When $\alpha ={\alpha }_4$, it follows that

$$\alpha ={\alpha }_4<\beta =\gamma ={\alpha }_2.$$

(24)

According to the above inequalities, we give some notations as follows:

$$a_0=\left\{\begin{array}{cc}\alpha ,\hfill & when\alpha \in ({\alpha }_2,{\alpha }_1)or\alpha >{\alpha }_{1}or\alpha <{\alpha }_4,\hfill \\ \beta ,\hfill & when\alpha \in ({\alpha }_3,{\alpha }_2)or\alpha \in ({\alpha }_4,{\alpha }_3).\hfill \end{array}\right.$$

(25)

$$b_0=\left\{\begin{array}{cc}\beta ,\hfill & when\alpha \in ({\alpha }_2,{\alpha }_1)or\alpha >{\alpha }_{1}or\alpha <{\alpha }_4,\hfill \\ \alpha ,\hfill & when\alpha \in ({\alpha }_3,{\alpha }_2),\hfill \\ \gamma ,\hfill & when\alpha \in ({\alpha }_4,{\alpha }_3).\hfill \end{array}\right.$$

(26)

$$c_0=\left\{\begin{array}{cc}\gamma ,\hfill & when\alpha \in ({\alpha }_2,{\alpha }_1)or\alpha \in ({\alpha }_3,{\alpha }_2)or\alpha >{\alpha }_{1}or\alpha <{\alpha }_4,\hfill \\ \alpha ,\hfill & when\alpha \in ({\alpha }_4,{\alpha }_3).\hfill \end{array}\right.$$

(27)

Using above these notations, on the φ-y plane we obtain some special points $(a_0,0)$, $(b_0,0)$, $(c_0,0)$. Via (2.4) we display the orbits passing these special points as Figure 1.

3. Our Main Results

In this section, we state our main results. The pictures of Proposition 1 are included in the Appendix A.

Proposition 1.

For given $c\in \left(4\left(2-\sqrt{3}\right),4\left(2+\sqrt{3}\right)\right)$ and arbitrary real number α, if let

$$\xi =x-ct,$$

(28)

and β, γ be in (10)–(11), and ${\alpha }_i$$(i=1-4)$ be in (12)–(15), then Equation (4) has the following explicit periodic wave solutions.

(1) If $\alpha <{\alpha }_4$ or $\alpha >{\alpha }_1$, then the explicit periodic wave solutions are

$$u_1(\xi ,\alpha )=\frac{A_1+\alpha -(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1+\mathrm{cn}\left({\eta }_1\xi ,k_1\right)},$$

(29)

and

$$u_2(\xi ,\alpha )=\frac{A_1+\alpha +(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1-\mathrm{cn}\left({\eta }_1\xi ,k_1\right)},$$

(30)

where

$$A_1=\sqrt{{(b_1-\alpha )}^2+a_1^2},$$

(31)

$$k_1=\sqrt{\frac{A_1+b_1-\alpha }{2A_1}},$$

(32)

$${\eta }_1=\sqrt{\frac{2A_1}{15}},$$

(33)

$$a_1^2=-\frac{{(b_0-c_0)}^2}{4},$$

(34)

and

$$b_1=\frac{b_0+c_0}{2}.$$

(35)

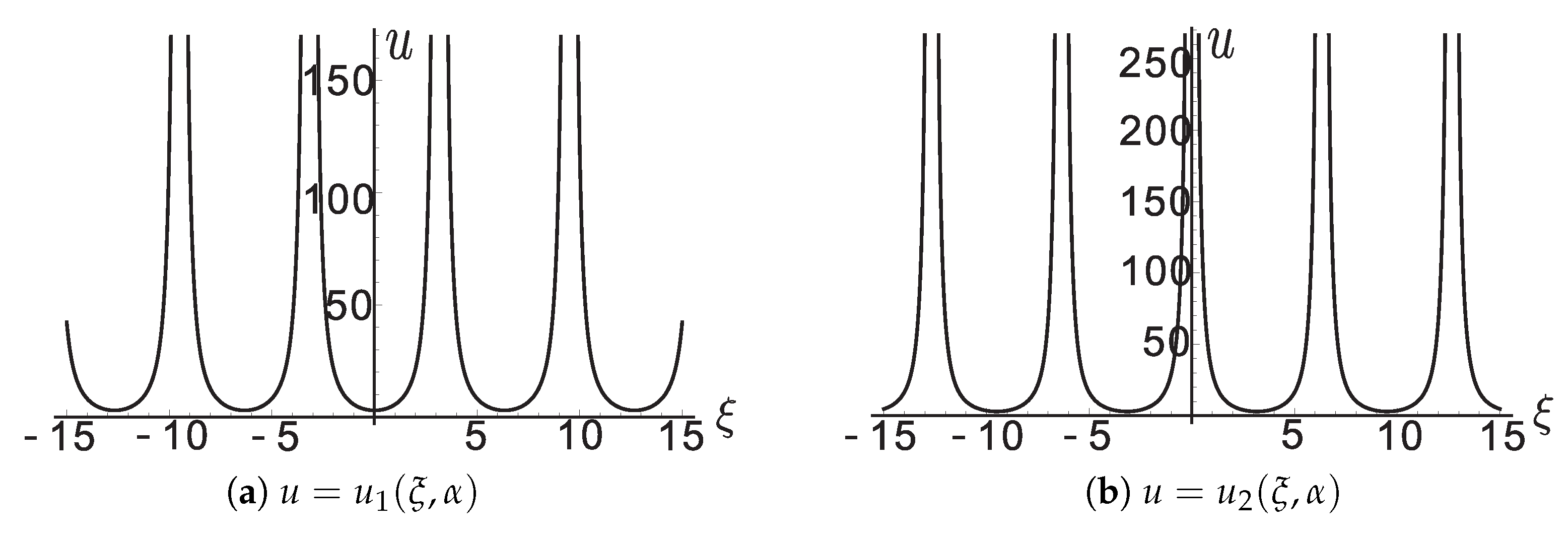
For the graphics of $u_1(\xi ,\alpha )$ and $u_2(\xi ,\alpha )$ with $c=8$ and $\alpha =3>{\alpha }_1$, see Figure A1a,b.

These two solutions possess the following limits.

${\left(1\right)}_a$ When $\alpha \to {\alpha }_1+0$, $u_1(\xi ,\alpha )$ becomes the trigonometric periodic blow-up solution

$$u_1^{\circ }\left(\xi \right)={\alpha }_3+\frac{\sigma }{4{\cos }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)},$$

(36)

and $u_2(\xi ,\alpha )$ becomes the trigonometric periodic blow-up solution

$$u_1^{*}\left(\xi \right)={\alpha }_3+\frac{\sigma }{4{\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}.$$

(37)

${\left(2\right)}_b$ When $\alpha \to {\alpha }_4-0$, $u_1(\xi ,\alpha )$ becomes the smooth solitary wave solution

$$u_2^{\circ }\left(\xi \right)={\alpha }_2-\frac{\sigma }{4}{\mathrm{sech}}^2\left(\sqrt{\frac{\sigma }{120}}\xi \right),$$

(38)

and $u_2(\xi ,\alpha )$ becomes the hyperbolic single blow-up solution

$$u_2^{*}\left(\xi \right)={\alpha }_4+\frac{\sigma }{4}{\coth }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right).$$

(39)

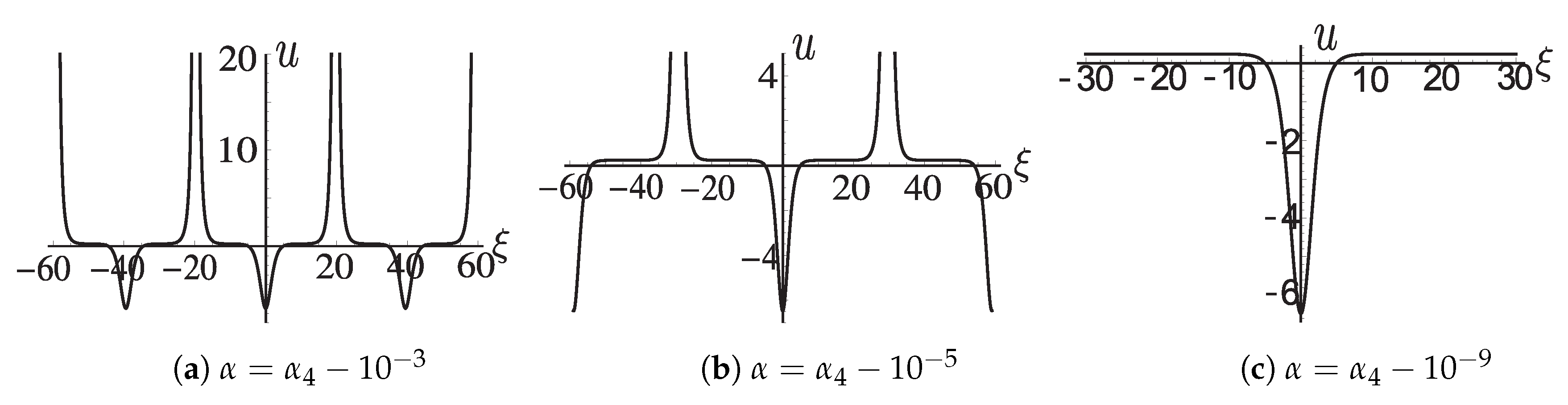
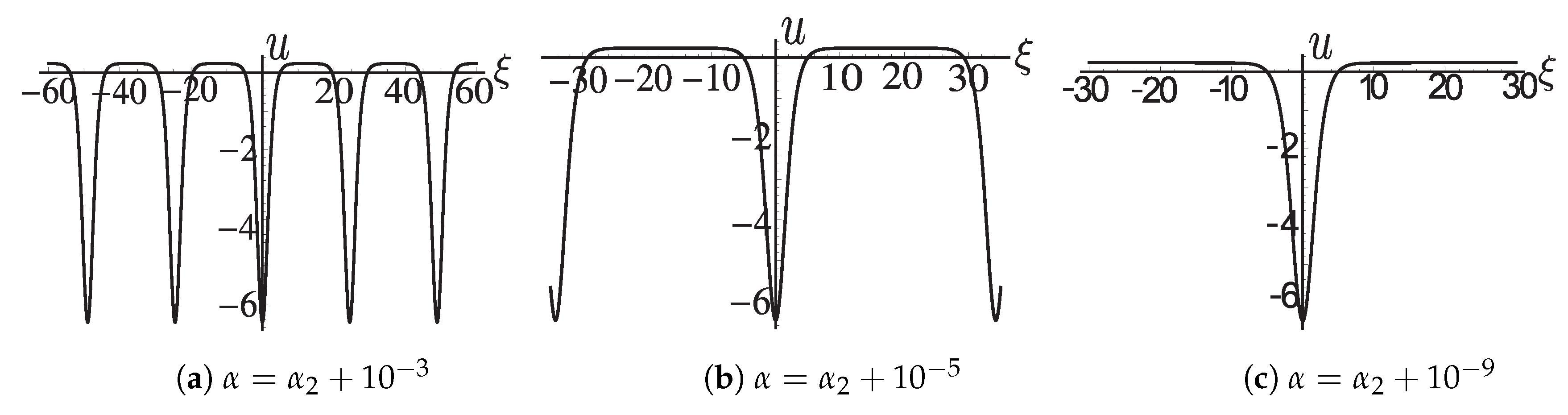
For the varying figures of $u=u_1(\xi ,\alpha )$ when $c=8$, and $\alpha \to {\alpha }_4-0$ where ${\alpha }_4=-2(1+\sqrt{5})$, see Figure A2a–c. For the varying figures of $u=u_2(\xi ,\alpha )$ when $c=8$, ${\alpha }_4=-2(1+\sqrt{5})$ and $\alpha \to {\alpha }_4-0$, see Figure A3a–c.

(2) If $\alpha$ satisfies ${\alpha }_4<\alpha <{\alpha }_1$ and $\alpha \ne {\alpha }_2,{\alpha }_3$, then the explicit periodic wave solutions are

$$u_3(\xi ,\alpha )=c_0+(b_0-c_0){\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right),$$

(40)

$$u_4(\xi ,\alpha )=\frac{b_0-k_2{a}_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-k_2{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)},$$

(41)

$$u_5(\xi ,\alpha )=\frac{a_0-b_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)},$$

(42)

and

$$u_6(\xi ,\alpha )=c_0+\frac{a_0-c_0}{{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)},$$

(43)

where

$$k_2=\sqrt{\frac{b_0-c_0}{a_0-c_0}},$$

(44)

$${\eta }_2=\frac{\sqrt{a_0-c_0}}{\sqrt{30}},$$

(45)

and $a_0$, $b_0$, $c_0$ are in (25)–(27).

For the figures of $u=u_i(\xi ,\alpha )$$(i=3,4,5,6)$ with $c=8$ and $\alpha =1$, see Figure A4a–d.

These four solutions possess the following limits.

${\left(1\right)}_a$ When $\alpha \to {\alpha }_1-0$ or $\alpha \to {\alpha }_3$, the smooth periodic wave solutions $u_3(\xi ,\alpha )$ and $u_4(\xi ,\alpha )$ become the trivial solution $u_3^{\circ }\left(\xi \right)={\alpha }_3$, and the elliptic periodic blow-up solutions $u_5(\xi ,\alpha )$, $u_6(\xi ,\alpha )$ respectively become the trigonometric periodic blow-up solution $u_1^{\circ }\left(\xi \right)$ and $u_1^{*}\left(\xi \right)$ given (36) and (37).

${\left(2\right)}_b$ When $\alpha \to {\alpha }_4+0$ or $\alpha \to {\alpha }_2$, the smooth periodic wave solution $u_3(\xi ,\alpha )$ becomes the smooth solitary wave solution $u_2^{\circ }\left(\xi \right)$ given in (38), the smooth periodic wave solution $u_4(\xi ,\alpha )$ and the periodic blow-up solution $u_5(\xi ,\alpha )$ become the trivial solution $u_3^{☆}\left(\xi \right)={\alpha }_2$, and the elliptic periodic blow-up solution $u_6(\xi ,\alpha )$ becomes the hyperbolic single blow-up solution $u_2^{*}\left(\xi \right)$ given in (39). For the varying figures of $u=u_3(\xi ,\alpha )$ when $c=8$, ${\alpha }_2=-2+\sqrt{5}$ and $\alpha \to {\alpha }_2+0$, see Figure A5a–c. For the varying figures of $u=u_6(\xi ,\alpha )$ when $c=8$, ${\alpha }_2=-2+\sqrt{5}$ and $\alpha \to {\alpha }_2+0$, see Figure A6a–c.

4. The Derivation of Main Results

In this section, we give the derivation for our main results listed in Proposition 1. First, we derive $u_i(\xi ,\alpha )$$(i=1,2)$ and their limit forms.

(1) If $\alpha >{\alpha }_1$ or $\alpha <{\alpha }_4$, then via Lemma 1 we know that Equation (9) has four roots c, $\alpha$, $\beta$ and $\gamma$. The root c is a double real root. $\alpha$ is a simple real root. $\beta$ and $\gamma$ are two complex roots. From Figure 1a we see that on $\phi -y$ plane there is an open orbit ${\mathsf{\Gamma }}_0$ passing the point $(a_0,0)$. The open orbit ${\mathsf{\Gamma }}_0$ possesses expression

$$y^2=\frac{2}{15}(\phi -a_0)[{(\phi -b_1)}^2+a_1^2],\mathrm{for}\phi \ge \alpha ,$$

(46)

where $a_1^2$ and $b_1$ are given in (34) and (35).

Substituting (46) into $\frac{d\phi }{d\xi }=y$ and integrating it along ${\mathsf{\Gamma }}_0$, we have

$${\int }_{a_0}^{\phi }\frac{ds}{\sqrt{(s-a_0)\left[{\left(s-b_1\right)}^2+a_1^2\right]}}=\sqrt{\frac{2}{15}}\left|\xi \right|,$$

(47)

and

$${\int }_{\phi }^{+\infty }\frac{ds}{\sqrt{(s-a_0)\left[{\left(s-b_1\right)}^2+a_1^2\right]}}=\sqrt{\frac{2}{15}}\left|\xi \right|.$$

(48)

Completing the integral in (47) and (48), we get

$$\frac{A_1+a_0-\phi }{A_1-a_0+\phi }=\mathrm{cn}\left(\sqrt{\frac{2A_1}{15}}\xi ,k_1\right),$$

(49)

and

$$\frac{\phi -a_0-A_1}{\phi -a_0+A_1}=\mathrm{cn}\left(\sqrt{\frac{2A_1}{15}}\xi ,k_1\right),$$

(50)

where $A_1$ and $k_1$ are listed in (31) and (32). Respectively solving Equation (49) and Equation (50) for $\phi$ and noting that $u=\phi \left(\xi \right)$, we obtain $u_1(\xi ,\alpha )$ and $u_2(\xi ,\alpha )$ of forms (29) and (30).

Since the period of the function $cn(\tau ,k)$ is 4K, where

$$K={\int }_0^{\frac{\pi }{2}}\frac{\mathrm{d}\theta }{\sqrt{1-k^2{\sin }^2\theta }},$$

(51)

This completes the derivations of $u_i(\xi ,\alpha )$$(i=1,2)$.

Now we show the limits of $u_i(\xi ,\alpha )$$(i=1,2)$ as $\alpha \to {\alpha }_1+0$ or $\alpha \to {\alpha }_4-0$.

($1^0$) When $\alpha \to {\alpha }_1+0$, it follows that

$$\left\{\begin{array}{cc}\hfill & \beta \to -\frac{3c+\sigma }{12}={\alpha }_3,\hfill \\ \hfill & \gamma \to -\frac{3c+\sigma }{12}={\alpha }_3,\hfill \end{array}\right.$$

(52)

which implies that $a_0\to {\alpha }_1$, $b_0\to {\alpha }_3$ and $c_0\to {\alpha }_3$.

Thus, we have

$$\left\{\begin{array}{cc}\hfill & A_1\to \frac{\sigma }{4},\hfill \\ \hfill & k_1\to 0,\hfill \\ \hfill & \mathrm{cn}\left(\sqrt{\frac{2A_1}{15}}\xi ,k_1\right)\to \mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,0\right)=\cos \left(\sqrt{\frac{\sigma }{30}}\xi \right).\hfill \end{array}\right.$$

(53)

Further we have

$$\begin{array}{cc}\hfill u_1(\xi ,\alpha )& =\frac{A_1+\alpha -(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1+\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}\hfill \\ \hfill & \to \frac{(5\sigma -3c)-(\sigma +3c)\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,0\right)}{12\left[1+\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,0\right)\right]}\hfill \\ \hfill & =\frac{(5\sigma -3c)-(\sigma +3c)\cos \left(\sqrt{\frac{\sigma }{30}}\xi \right)}{12\left[1+\cos \left(\sqrt{\frac{\sigma }{30}}\xi \right)\right]}\hfill \\ \hfill & =-\frac{1}{12}(\sigma +3c)+\frac{\sigma }{4{\cos }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & ={\alpha }_3+\frac{\sigma }{4{\cos }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & =u_1^{\circ }\left(\xi \right),\hfill \end{array}$$

(54)

and

$$\begin{array}{cc}\hfill u_2(\xi ,\alpha )& =\frac{A_1+\alpha +(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1-\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}\hfill \\ \hfill & \to \frac{(5\sigma -3c)+(\sigma +3c)\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,0\right)}{12\left[1-\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,0\right)\right]}\hfill \\ \hfill & =\frac{5\sigma -3c+(\sigma +3c)\cos \left(\sqrt{\frac{\sigma }{30}}\xi \right)}{12\left[1-\cos \left(\sqrt{\frac{\sigma }{30}}\xi \right)\right]}\hfill \\ \hfill & =-\frac{1}{12}(\sigma +3c)+\frac{\sigma }{4{\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & ={\alpha }_3+\frac{\sigma }{4{\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & =u_1^{*}\left(\xi \right).\hfill \end{array}$$

(55)

This implies that the property ${\left(1\right)}_a$ is true.

($2^0$) When $\alpha \to {\alpha }_4-0$, it follows that

$$\left\{\begin{array}{cc}\hfill & \beta \to {\alpha }_2,\hfill \\ \hfill & \gamma \to {\alpha }_2,\hfill \end{array}\right.$$

(56)

which implies that $a_0\to {\alpha }_4$, $b_0\to {\alpha }_3$ and $c_0\to {\alpha }_2$.

Thus, we have

$$\left\{\begin{array}{cc}\hfill & k_1\to 1,\hfill \\ \hfill & A_1\to \frac{\sigma }{4},\hfill \\ \hfill & {\eta }_1\to \sqrt{\frac{\sigma }{30}},\hfill \\ \hfill & \mathrm{cn}\left(\sqrt{\frac{2A_1}{15}}\xi ,k_0\right)\to \mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,1\right)=\mathrm{sech}\left(\sqrt{\frac{\sigma }{30}}\xi \right).\hfill \end{array}\right.$$

(57)

Further it follows that

$$\begin{array}{cc}\hfill u_1(\xi ,\alpha )& =\frac{A_1+\alpha +(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1+\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}\hfill \\ \hfill & \to \frac{\sigma -3c-(5\sigma +3c)\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,1\right)}{12\left[1+\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,1\right)\right]}\hfill \\ \hfill & =\frac{\sigma -3c-(5\sigma +3c)\mathrm{sech}\left(\sqrt{\frac{\sigma }{30}}\xi \right)}{12\left[1+\mathrm{sech}\left(\sqrt{\frac{\sigma }{30}}\xi \right)\right]}\hfill \\ \hfill & =\frac{\sigma -3c}{12}-\frac{\sigma }{4}{\mathrm{sech}}^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & ={\alpha }_2-\frac{\sigma }{4}{\mathrm{sech}}^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & =u_2^{\circ }\left(\xi \right),\hfill \end{array}$$

(58)

and

$$\begin{array}{cc}\hfill u_2(\xi ,\alpha )& =\frac{A_1+\alpha -(A_1-\alpha )\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}{1-\mathrm{cn}\left({\eta }_1\xi ,k_1\right)}\hfill \\ \hfill & \to \frac{\sigma -3c+(5\sigma +3c)\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,1\right)}{12\left[1-\mathrm{cn}\left(\sqrt{\frac{\sigma }{30}}\xi ,1\right)\right]}\hfill \\ \hfill & =\frac{\sigma -3c+(5\sigma +3c)\mathrm{sech}\left(\sqrt{\frac{\sigma }{30}}\xi \right)}{12\left[1-\mathrm{sech}\left(\sqrt{\frac{\sigma }{30}}\xi \right)\right]}\hfill \\ \hfill & =-\frac{1}{12}(2\sigma +3c)+\frac{\sigma }{4}{\coth }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & ={\alpha }_4+\frac{\sigma }{4}{\coth }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & =u_2^{*}\left(\xi \right).\hfill \end{array}$$

(59)

This implies that the property ${\left(1\right)}_b$ holds.

Secondly, we derive $u_j(\xi ,\alpha )$$(j=3,4,5,6)$ and their limit forms.

(2) If $\alpha \in ({\alpha }_4,{\alpha }_1)$ and $\alpha \ne {\alpha }_2$, ${\alpha }_3$, then from Lemma 1 we see that Equation (9) has four real roots c, $\alpha$, $\beta$ and $\gamma$. The root c is a double real root. The other three roots are simple real roots. From the expressions (25)–(27) of $a_0$, $b_0$, $c_0$ and Figure 1b, we can see that there exists a closed orbit ${\mathsf{\Gamma }}_1$ passing the points $(b_0,0)$, $(c_0,0)$, and there is an open orbit ${\mathsf{\Gamma }}_2$ passing $(a_0,0)$ on $\phi -y$ plane. The closed orbit ${\mathsf{\Gamma }}_1$ possesses expression

$$y^2=\frac{2}{15}(a_0-\phi )(b_0-\phi )(\phi -c_0),\mathrm{where}{c}_0\le \phi \le b_0,$$

(60)

and the open orbit ${\mathsf{\Gamma }}_2$ has expression

$$y^2=\frac{2}{15}(\phi -a_0)(\phi -b_0)(\phi -c_0),\mathrm{where}\phi \ge a_0.$$

(61)

Substituting the above two expressions into $\frac{d\phi }{d\xi }=y$ and integrating it along the two orbits, we have

$${\int }_{c_0}^{\phi }\frac{ds}{\sqrt{(a_0-s)(b_0-s)(s-c_0)}}=\frac{\sqrt{2}}{\sqrt{15}}\left|\xi \right|(\mathrm{along}{\mathsf{\Gamma }}_1\mathrm{and}{c}_0<\phi \le b_0<a_0),$$

(62)

$${\int }_{\phi }^{b_0}\frac{ds}{\sqrt{(a_0-s)(b_0-s)(s-c_0)}}=\frac{\sqrt{2}}{\sqrt{15}}\left|\xi \right|(\mathrm{along}{\mathsf{\Gamma }}_1\mathrm{and}{c}_0\le \phi <b_0<a_0),$$

(63)

$${\int }_{a_0}^{\phi }\frac{ds}{\sqrt{(s-a_0)(s-b_0)(s-c_0)}}=\frac{\sqrt{2}}{\sqrt{15}}\left|\xi \right|(\mathrm{along}{\mathsf{\Gamma }}_2\mathrm{and}{c}_0<b_0<a_0<\phi ),$$

(64)

and

$${\int }_{\phi }^{\infty }\frac{ds}{\sqrt{(s-a_0)(s-b_0)(s-c_0)}}=\frac{\sqrt{2}}{\sqrt{15}}\left|\xi \right|(\mathrm{along}{\mathsf{\Gamma }}_2\mathrm{and}{b}_0<a_0\le \phi <\infty ).$$

(65)

Completing the above four integrals, the four equations respectively become

$${\mathrm{sn}}^{-1}\left(\sqrt{\frac{\phi -c_0}{b_0-c_0}}\xi ,k_2\right)=\sqrt{\frac{a_0-c_0}{30}}\left|\xi \right|,$$

(66)

$${\mathrm{sn}}^{-1}\left(\sqrt{\frac{(a_0-c_0)(b_0-\phi )}{(b_0-c_0)(a_0-\phi )}}\xi ,k_2\right)=\sqrt{\frac{a_0-c_0}{30}}\left|\xi \right|,$$

(67)

$${\mathrm{sn}}^{-1}\left(\sqrt{\frac{\phi -a_0}{\phi -b_0}}\xi ,k_2\right)=\sqrt{\frac{a_0-c_0}{30}}\left|\xi \right|,$$

(68)

and

$${\mathrm{sn}}^{-1}\left(\sqrt{\frac{a_0-c_0}{\phi -c_0}}\xi ,k_2\right)=\sqrt{\frac{a_0-c_0}{30}}\left|\xi \right|,$$

(69)

where $k_2$ is given in (44). Solving the above four equations for $\phi$ respectively and noting that $u=\phi \left(\xi \right)$, we get the solutions $u_j(\xi ,\alpha )$$(j=3,4,5,6)$ of the forms (40)–(43).

Since the period of the function $sn(\tau ,k)$ is $4K$, it follows that the period of the function $sn({\eta }_2\xi ,k_2)$ is $4K/{\eta }_2$.

Now we derive the limit forms. First, we derive the limit forms $2_a$. From the expressions (25)–(27), we have the following limits.

(i) When $\alpha \to {\alpha }_1-0$, it follows that

$$\left\{\begin{array}{cc}\hfill & a_0=\alpha \to \frac{-3c+2\sigma }{12}={\alpha }_1,\hfill \\ \hfill & b_0=\beta \to \frac{-3c-\sigma }{12}={\alpha }_3,\hfill \\ \hfill & c_0=\gamma \to \frac{-3c-\sigma }{12}={\alpha }_3.\hfill \end{array}\right.$$

(70)

(ii) When $\alpha \to {\alpha }_3+0$, it follows that

$$\left\{\begin{array}{cc}\hfill & a_0=\beta \to \frac{-3c+2\sigma }{12}={\alpha }_1,\hfill \\ \hfill & b_0=\alpha \to \frac{-3c-\sigma }{12}={\alpha }_3,\hfill \\ \hfill & c_0=\gamma \to \frac{-3c-\sigma }{12}={\alpha }_3.\hfill \end{array}\right.$$

(71)

(iii) When $\alpha \to {\alpha }_3-0$, it follows that

$$\left\{\begin{array}{cc}\hfill & a_0=\beta \to \frac{-3c+2\sigma }{12}={\alpha }_1,\hfill \\ \hfill & b_0=\gamma \to \frac{-3c-\sigma }{12}={\alpha }_3,\hfill \\ \hfill & c_0=\alpha \to \frac{-3c-\sigma }{12}={\alpha }_3.\hfill \end{array}\right.$$

(72)

Thus, when $\alpha \to {\alpha }_1-0$ or $\alpha \to {\alpha }_3$, we have

$$\left\{\begin{array}{cc}\hfill & b_0-c_0\to 0,\hfill \\ \hfill & k_2=\sqrt{\frac{b_0-c_0}{a_0-c_0}}\to 0,\hfill \\ \hfill & a_0-c_0\to \frac{\sigma }{4},\hfill \\ \hfill & {\eta }_2=\sqrt{\frac{a_0-c_0}{30}}\to \sqrt{\frac{\sigma }{120}},\hfill \end{array}\right.$$

(73)

and further have

$$u_3(\xi ,\alpha )=c_0+(b_0-c_0){\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)\to {\alpha }_3,$$

(74)

$$u_4(\xi ,\alpha )=\frac{b_0-k_2{a}_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-k_2{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\to {\alpha }_3,$$

(75)

$$\begin{array}{cc}\hfill u_5(\xi ,\alpha )& =\frac{a_0-b_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\hfill \\ \hfill & \to \frac{(2\sigma -3c)+(\sigma +3c){\mathrm{sn}}^2\left(\sqrt{\frac{\sigma }{120}}\xi ,0\right)}{12[1-{\mathrm{sn}}^2\left(\sqrt{\frac{\sigma }{120}}\xi ,0\right)]}\hfill \\ \hfill & =\frac{(2\sigma -3c)+(\sigma +3c){\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}{12\left[1-{\sin }^2\left(\sqrt{\frac{\sigma }{8}}\xi \right)\right]}\hfill \\ \hfill & =-\frac{1}{12}(\sigma +3c)+\frac{\sigma }{4{\cos }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & ={\alpha }_3+\frac{\sigma }{4{\cos }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & =u_1^{\circ }\left(\xi \right),\hfill \end{array}$$

(76)

and

$$\begin{array}{cc}\hfill u_6(\xi ,\alpha )& =c_0+\frac{a_0-c_0}{{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\hfill \\ \hfill & \to -\frac{1}{12}(\sigma +3c)+\frac{\sigma }{4{\mathrm{sn}}^2\left(\sqrt{\frac{\sigma }{120}}\xi ,0\right)}\hfill \\ \hfill & =-\frac{1}{12}(\sigma +3c)+\frac{\sigma }{4{\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & ={\alpha }_3+\frac{\sigma }{4{\sin }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & =u_1^{*}\left(\xi \right).\hfill \end{array}$$

(77)

These complete the derivations for limit forms ${\left(2\right)}_a$.

Secondly, we derive the limit forms ${\left(2\right)}_b$. Similarly, from (25)–(27) we get the following limits.

(iv) When $\alpha \to {\alpha }_2+0$, we have

$$\left\{\begin{array}{cc}\hfill & a_0=\alpha \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & b_0=\beta \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & c_0=\gamma \to \frac{-3c-2\sigma }{12}={\alpha }_4.\hfill \end{array}\right.$$

(78)

(v) When $\alpha \to {\alpha }_2-0$, we have

$$\left\{\begin{array}{cc}\hfill & a_0=\beta \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & b_0=\alpha \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & c_0=\gamma \to \frac{-3c-2\sigma }{12}={\alpha }_4.\hfill \end{array}\right.$$

(79)

(vi) When $\alpha \to {\alpha }_4+0$, it follows that

$$\left\{\begin{array}{cc}\hfill & a_0=\beta \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & b_0=\gamma \to \frac{-3c+\sigma }{12}={\alpha }_2,\hfill \\ \hfill & c_0=\alpha \to \frac{-3c-2\sigma }{12}={\alpha }_4.\hfill \end{array}\right.$$

(80)

Thus, when $\alpha \to {\alpha }_2$ or $\alpha \to {\alpha }_4+0$, we have

$$\left\{\begin{array}{cc}\hfill & b_0-c_0\to \frac{\sigma }{4},\hfill \\ \hfill & k_2=\sqrt{\frac{b_0-c_0}{a_0-c_0}}\to 1,\hfill \\ \hfill & a_0-c_0\to \frac{\sigma }{4},\hfill \\ \hfill & {\eta }_2=\sqrt{\frac{a_0-c_0}{30}}\to \sqrt{\frac{\sigma }{120}},\hfill \end{array}\right.$$

(81)

and further have

$$\begin{array}{cc}\hfill u_3(\xi ,\alpha )& =c_0+(b_0-c_0){\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)\hfill \\ \hfill & \to -\frac{1}{12}(2\sigma +3c)+\frac{3\sigma }{12}{\mathrm{sn}}^2\left(\sqrt{\frac{\sigma }{120}}\xi ,1\right)\hfill \\ \hfill & =-\frac{1}{12}(2\sigma +3c)+\frac{\sigma }{4}{\tanh }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & =\frac{\sigma -3c}{12}-\frac{\sigma }{4}{\mathrm{sech}}^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & ={\alpha }_2-\frac{\sigma }{4}{\mathrm{sech}}^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & =u_2^{\circ }\left(\xi \right),\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill u_6(\xi ,\alpha )& =c_0+\frac{a_0-c_0}{{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\hfill \\ \hfill & \to -\frac{1}{12}(2\sigma +3c)+\frac{\frac{\sigma }{4}}{{\mathrm{sn}}^2\left(\sqrt{\frac{\sigma }{120}}\xi ,1\right)}\hfill \\ \hfill & =-\frac{1}{12}(2\sigma +3c)+\frac{\frac{\sigma }{4}}{{\tanh }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)}\hfill \\ \hfill & =-\frac{1}{12}(2\sigma +3c)+\frac{\sigma }{4}{\coth }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & ={\alpha }_4+\frac{\sigma }{4}{\coth }^2\left(\sqrt{\frac{\sigma }{120}}\xi \right)\hfill \\ \hfill & =u_2^{*}\left(\xi \right),\hfill \end{array}$$

(83)

$$u_4(\xi ,\alpha )=\frac{b_0-k_2{a}_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-k_2{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\to {\alpha }_2,$$

(84)

and

$$u_5(\xi ,\alpha )=\frac{a_0-b_0{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}{1-{\mathrm{sn}}^2\left({\eta }_2\xi ,k_2\right)}\to {\alpha }_2.$$

(85)

Hereto we have finished the derivations for our main results.

5. Conclusions

In this paper, we have studied the explicit smooth periodic wave solutions and periodic blow-up solutions and their asymptotic property for Equation (4). In Proposition 1, the explicit expressions of these solutions and their limits have been shown. Based on these results, Equation (4) possesses explicit periodic wave solutions, and solitary wave solution has been exposed. Furthermore, we have found that the periodic blow-up solution $u_1(\xi ,\alpha )$ can converge to the smooth solitary wave solution $u_2^{\circ }\left(\xi \right)$. On the other hand, this example shows that not only the cnoidal wave solution but also the periodic blow-up solution can converge to the smooth solitary wave solution.

Furthermore, a new phenomenon about the periodic solution has been discovered. In [16], the author proved that when the period tends to ∞, the cnoidal waves of KdV equation, on compact sets, converge to the limit soliton. In our paper, it has been found that when the period $T_1$ tends to $\frac{2\pi \sqrt{30}}{\sqrt{\sigma }}$, the elliptic periodic blow-up solutions $u_1(\xi ,\alpha )$ and $u_2(\xi ,\alpha )$ become the trigonometric periodic blow-up solution $u_1^{\circ }\left(\xi \right)$ and $u_1^{*}\left(\xi \right)$ respectively. Also, when the period $T_2$ tends to $\frac{2\pi \sqrt{30}}{\sqrt{\sigma }}$, $u_5(\xi ,\alpha )$ and $u_6(\xi ,\alpha )$ become $u_1^{\circ }\left(\xi \right)$ and $u_1^{*}\left(\xi \right)$ respectively.

Finally, the correctness of all the solutions are also validated by the mathematical software.