Buckling of Corrugated Ring under Uniform External Pressure
Abstract
1. Introduction
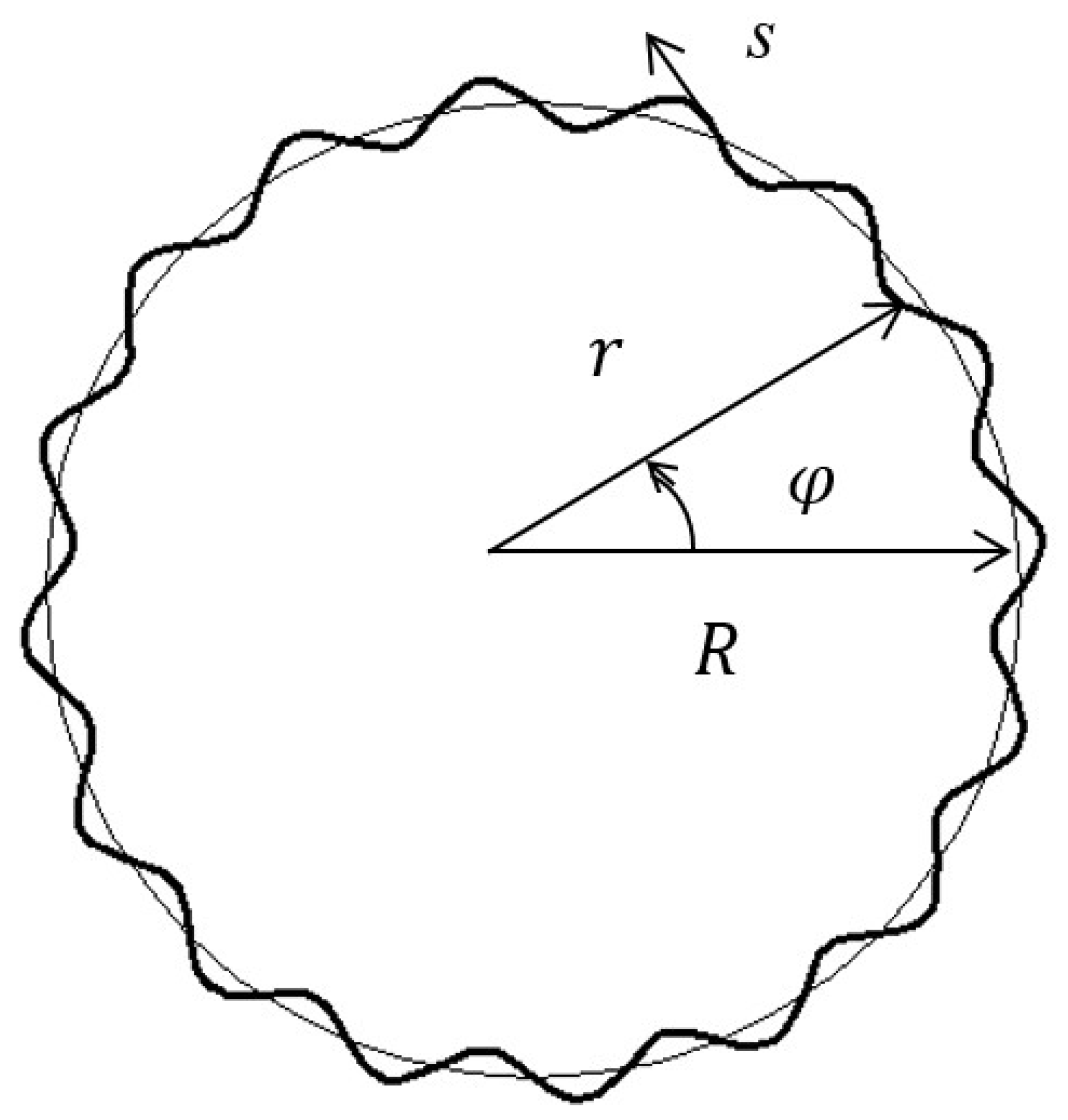
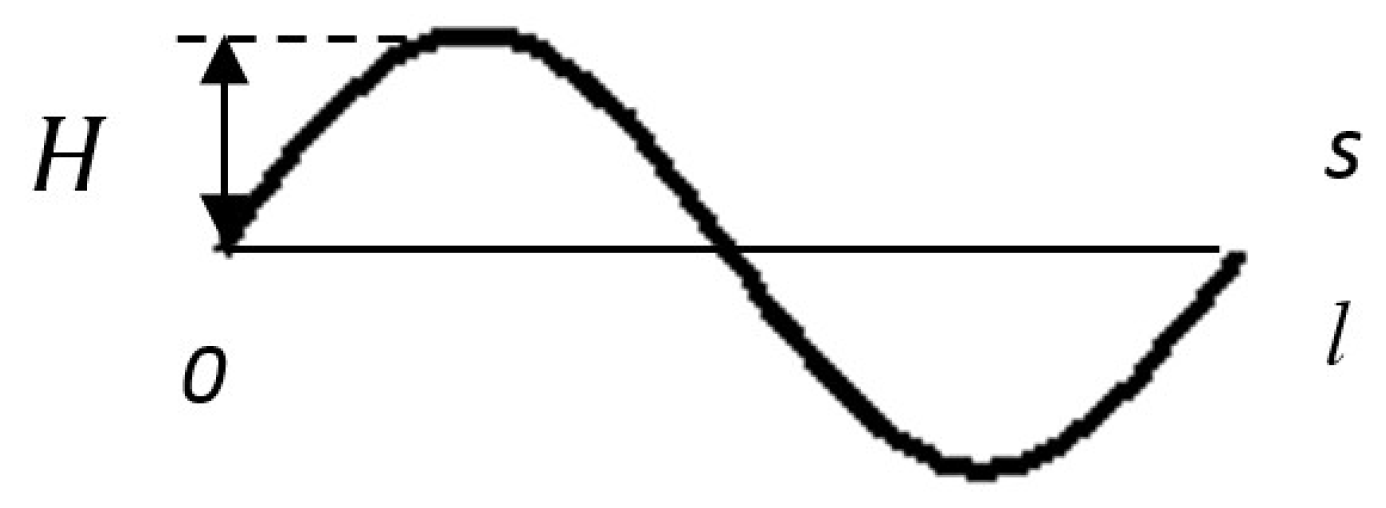
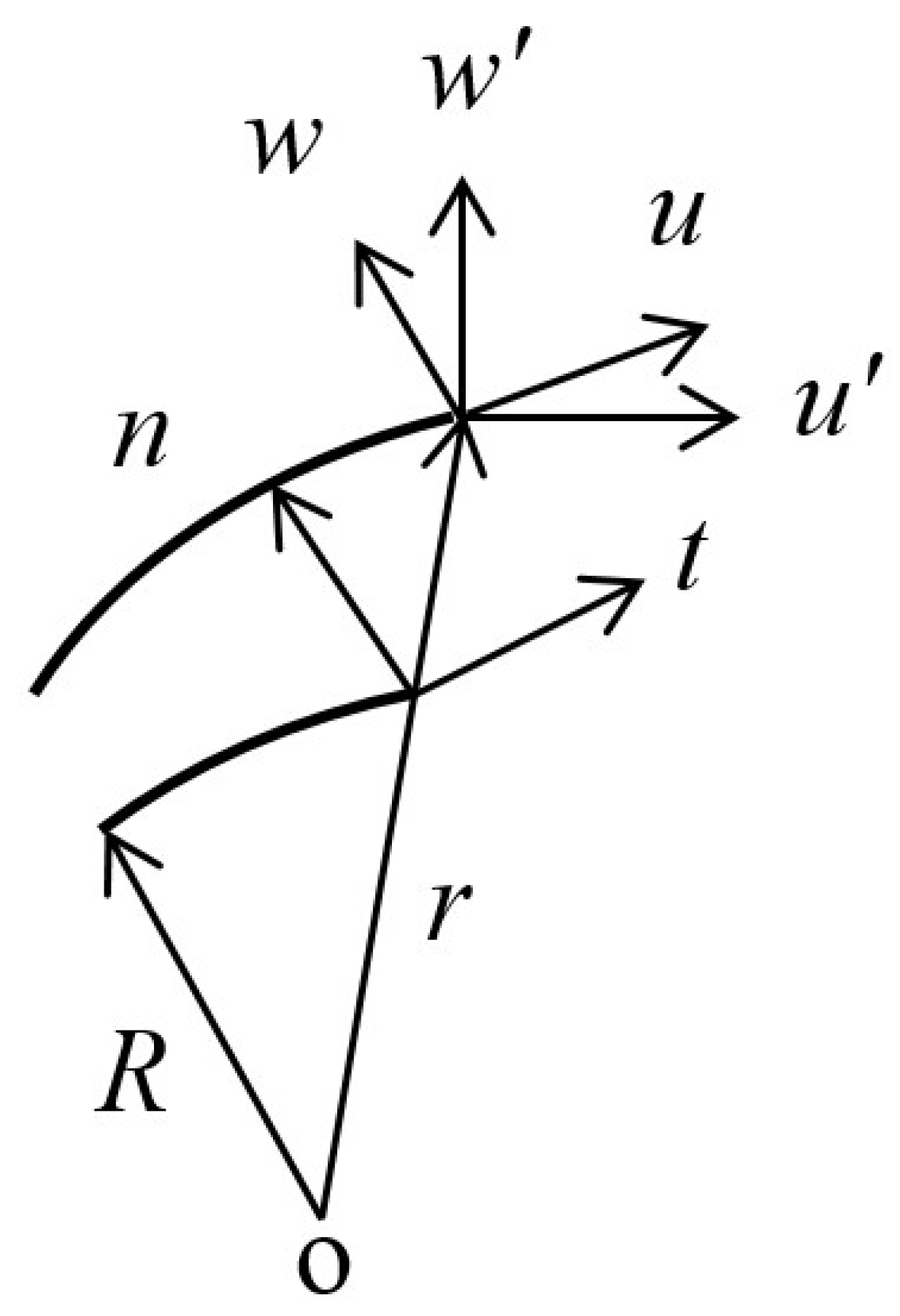
2. A Statement of the Problem
3. Equivalent Bending Stiffness Approach
- (a)
- the applicability of the equivalent bending stiffness approach to the stability problems;
- (b)
- estimation of the error caused by neglecting the curvature of the basic circular ring in determining equivalent bending stiffness;
- (c)
- estimation of the accuracy of the buckling pressure obtained with the equivalent bending stiffness approach and the possibility of its refinement.
4. Asymptotic Homogenization Method
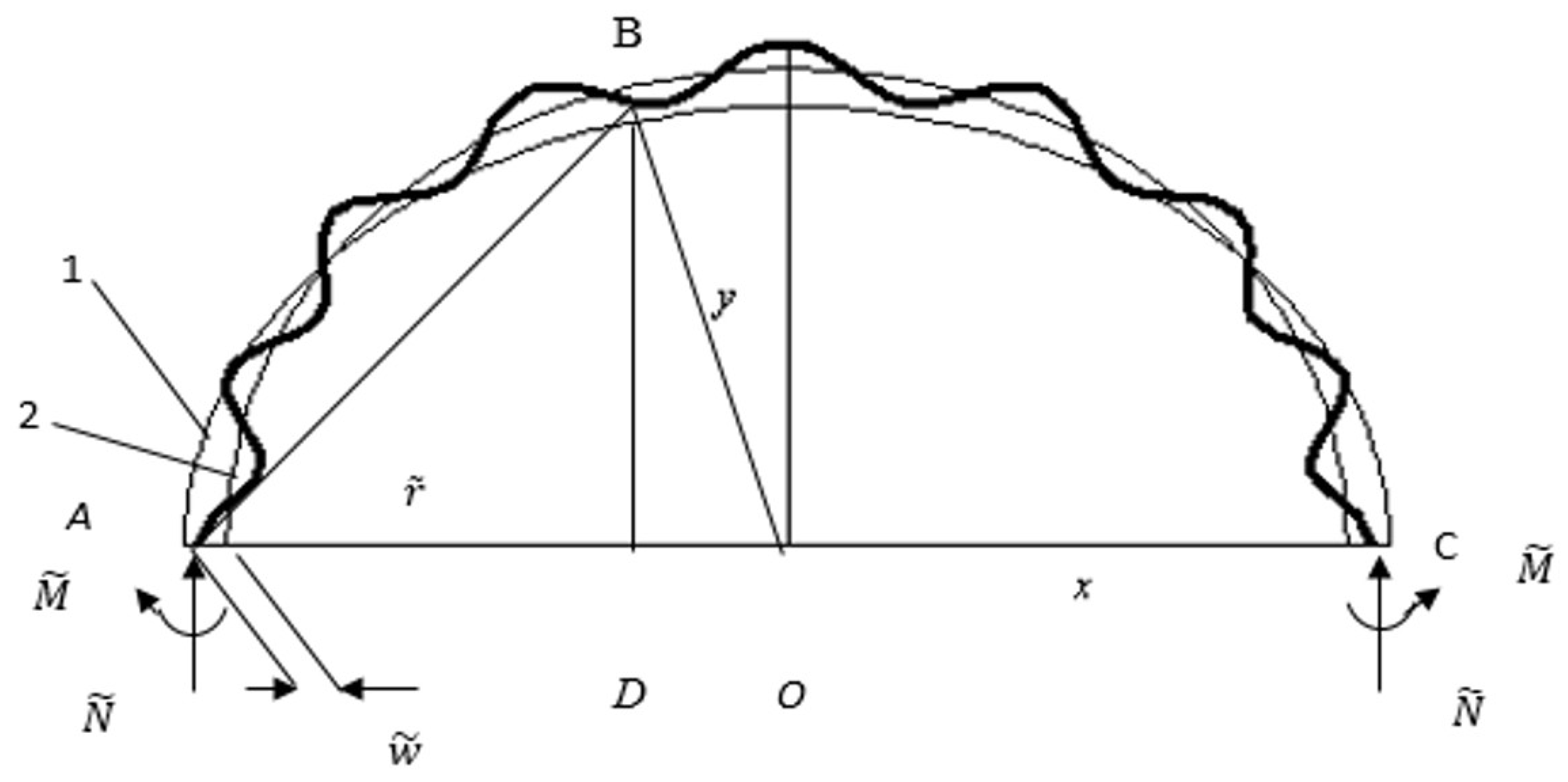
5. Using the Imperfection Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Abbreviations
| ODE | Ordinary Differential Equation |
| FEA | finite element analysis |
References
- Dayyani, I.; Shaw, A.D.; Flores, E.I.S.; Friswell, M.I. The mechanics of composite corrugated structures: A review with applications in morphing aircraft. Comp. Struct. 2015, 133, 358–380. [Google Scholar] [CrossRef]
- Adriaenssens, S.; Dejong, M. Form finding of corrugated shell structures for seismic design and validation using non-linear pushover analysis. Eng. Struct. 2019, 181, 362–373. [Google Scholar]
- Malek, S.; Williams, C.J.K. The equilibrium of corrugated plates and shells. Nexus Netw. J. 2017, 19, 619–627. [Google Scholar] [CrossRef]
- Manko, Z.; Beben, D. Research on steel shell of a road bridge made of corrugated plates during backfilling. J. Bridge Eng. 2005, 10, 592–603. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, M.; Hassanein, M.F.; Zhong, J.; Ding, H.; An, L. Study on elastic global shear buckling of curved girders with corrugated steel webs: Theoretical analysis and FE modelling. Appl. Sci. 2018, 8, 2457. [Google Scholar] [CrossRef]
- Semenyuk, N.P. Stability of corrugated arches under external pressure. Int. Appl. Mech. 2013, 49, 211–219. [Google Scholar] [CrossRef]
- Ross, C.; Humphries, M. The buckling of corrugated circular cylinders under uniform external pressure. Thin Walled Struct. 1993, 17, 259–271. [Google Scholar] [CrossRef]
- Semenyuk, N.P.; Zhukova, N.B.; Ostapchuk, V.V. Stability of corrugated composite noncircular cylindrical shells under external pressure. Int. Appl. Mech. 2007, 43, 1380–1389. [Google Scholar] [CrossRef]
- Semenyuk, N.P.; Babich, I.Y. Stability of longitudinally corrugated cylindrical shells under uniform surface pressure. Int. Appl. Mech. 2007, 43, 1236–1247. [Google Scholar] [CrossRef]
- Semenyuk, N.P.; Zhukova, N.B.; Neskhodovskaya, N.A. Stability of orthotropic corrugated cylindrical shells under axial compression. Mech. Comp. Mater. 2002, 38, 243–250. [Google Scholar] [CrossRef]
- Norman, A.D.; Seffen, K.A.; Guest, S.D. Multistable corrugated shells. Proc. R. Soc. A 2008, 464, 1653–1672. [Google Scholar] [CrossRef]
- Wang, X.J.; Wang, Z.M.; Wang, N. Finite element analysis for the stiffness and the buckling of corrugated tubes in heat exchanger. Adv. Mater. Res. 2012, 468–471, 1675–1680. [Google Scholar] [CrossRef]
- Wennberg, D.; Wennhage, P.; Stichel, S. Orthotropic models of corrugated sheets in finite element analysis. Int. Sci. Res. Netw. Mech. Eng. 2011, 2011, 979532. [Google Scholar] [CrossRef]
- Sowiński, K. Buckling of shells with special shapes with corrugated middle surfaces–FEM study. Eng. Struct. 2019, 179, 310–320. [Google Scholar] [CrossRef]
- Dolgikh, D.V.; Kiselev, V.V. Corrugation of a flexible ring under external hydrostatic compression. J. Appl. Math. Mech. 2010, 74, 204–213. [Google Scholar] [CrossRef]
- Andreeva, L.E. Elastic Elements of Instruments; Israel Program for Scientific Translations: Jerusalem, Israel, 1966. [Google Scholar]
- Seydel, E.B. Schubknickversuche Mit Wellblechtafeln; Jahrbuch d. Deutsch; Versuchsanstallt für Luftfahrt. E.V.: Munich/Berlin, Germany, 1931; Volume 4, pp. 233–235. [Google Scholar]
- Briassoulis, D. Equivalent orthotropic properties of corrugated sheets. Comput. Struct. 1986, 23, 129–138. [Google Scholar] [CrossRef]
- Donnell, L.H. The flexibility of corrugated pipes under longitudinal forces and bending. Trans. ASME 1932, 54, 69–75. [Google Scholar]
- Ye, Z.; Berdichevsky, V.L.; Yu, W. An equivalent classical plate model of corrugated structures. Int. J. Solids Struct. 2014, 51, 2073–2083. [Google Scholar] [CrossRef]
- Xia, Y.; Friswell, M.I.; Flores, E.I.S. Equivalent models of corrugated panels. Int. J. Solids Struct. 2012, 49, 1453–1462. [Google Scholar] [CrossRef]
- Nguyen-Minh, N.; Tran-Van, N.; Bui-Xuan, T.; Nguyen-Thoi, T. Static analysis of corrugated panels using homogenization models and a cell-based smoothed Mindlin plate element. Front. Struct. Civ. Eng. 2019, 13, 251–272. [Google Scholar] [CrossRef]
- Kolpakov, A.G.; Rakin, S.I. Calculation of the effective stiffness of the corrugated plate by solving the problem on the plate cross-section. J. Appl. Mech. Tech. Phys. 2016, 57, 757–767. [Google Scholar] [CrossRef]
- Kolpakov, A.A.; Kolpakov, A.G. Discussion of the effective stiffnesses in: Ye, Berdichevsky, and Yu [Int. J. Solids Struct. 51 (2014) 2073–2083]. Int. J. Solids Struct. 2019, 174–175, 145–146. [Google Scholar] [CrossRef]
- Gimena, L.; Gimena, F.; Gonzaga, P. Structural analysis of a curved beam element defined in global coordinates. Eng. Struct. 2008, 30, 3355–3364. [Google Scholar] [CrossRef]
- Mercuri, V.; Balduzzi, G.; Asprone, D.; Auricchio, F. Structural analysis of non-prismatic beams: Critical issues, accurate stress recovery, and analytical definition of the Finite Element (FE) stiffness matrix. Eng. Struct. 2020, 213, 110252. [Google Scholar] [CrossRef]
- Andrianov, I.V.; Diskovsky, A.A.; Kholod, E.G. Homogenization method in the theory of corrugated plates. Tech. Mech. 1998, 18, 123–133. [Google Scholar]
- Syerko, E.; Diskovsky, A.A.; Andrianov, I.V.; Comas-Cardona, S.; Binetruy, C. Corrugated beams mechanical behavior modeling by the homo–genization method. Int. J. Solids Struct. 2013, 50, 928–936. [Google Scholar] [CrossRef][Green Version]
- Andrianov, I.V.; Awrejcewicz, J.; Diskovsky, A.A. Design optimization of FGM beam in stability problem. Eng. Comput. 2019, 36, 248–270. [Google Scholar] [CrossRef]
- Andrianov, I.I.; Awrejcewicz, J.; Diskovsky, A.A. The optimal design of a functionally graded corrugated cylindrical shell under axisymmetric loading. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 387–398. [Google Scholar] [CrossRef]
- Andrianov, I.V.; Diskovsky, A.A.; Syerko, E. Optimal design of a circular diaphragm using the homogenization approach. Math. Mech. Solids 2017, 22, 283–303. [Google Scholar] [CrossRef]
- Feodosiev, V.I. Advanced Stress and Stability Analysis, Worked Examples; Springer: Berlin, Germany, 2005. [Google Scholar]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Andrianov, I.V.; Awrejcewicz, J.; Manevitch, L.I. Asymptotical Mechanics of Thin-Walled Structures: A Handbook; Springer: Berlin, Germany, 2004. [Google Scholar]
- Manevich, L.I.; Andrianov, I.V.; Oshmyan, V.G. Mechanics of Periodically Heterogeneous Structures; Springer: Berlin, Germany, 2002. [Google Scholar]
- Ziegler, H. Principles of Structural Stability, 2nd ed.; Springer: Basel, Switzerland, 1977. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Panovko, Y.a.G.; Gubanova, I.I. Stability and Oscillations of Elastic Systems Paradoxes, Fallacies, and New Concepts; Consultants Bureau: New York, NY, USA, 1965. [Google Scholar]
- Grigolyuk, E.I.; Kabanov, V.V. Stability of Shells; Nauka: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Vol’mir, A.S. Stability of Deformable Systems; Foreign Technology Division, Air Force Systems Command; Wright-Patterson Air Force Base: Dayton, OH, USA, 1967. [Google Scholar]
- Thielemann, W.; Esslinger, M. Beul- und Nachbeulverhalten isotropic Zylinder unter Äussendruck. Stahlbau 1967, 36, 161–174. [Google Scholar]
- Myachenkov, V.I. The stability of cylindrical shells under axisymmetric transverse pressure. Sov. Appl. Mech. 1970, 6, 19–23. [Google Scholar] [CrossRef]
- Zevin, A.A. Estimates of eigenvalue of self-adjont boundary-value problems with periodic coefficients. Ukr. Math. J. 1998, 50, 719–722. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Romano, A. On the derivation of thermomechanical balance equations for continuous systems with a nonmaterial interface. Int. J. Eng. Sci. 1987, 25, 1459–1468. [Google Scholar] [CrossRef]
- Dell’Isola, F. Linear growth of a liquid droplet divided from its vapour by a “Soap Buble”–like fluid Interface. Int. J. Eng. Sci. 1989, 27, 1053–1067. [Google Scholar] [CrossRef][Green Version]

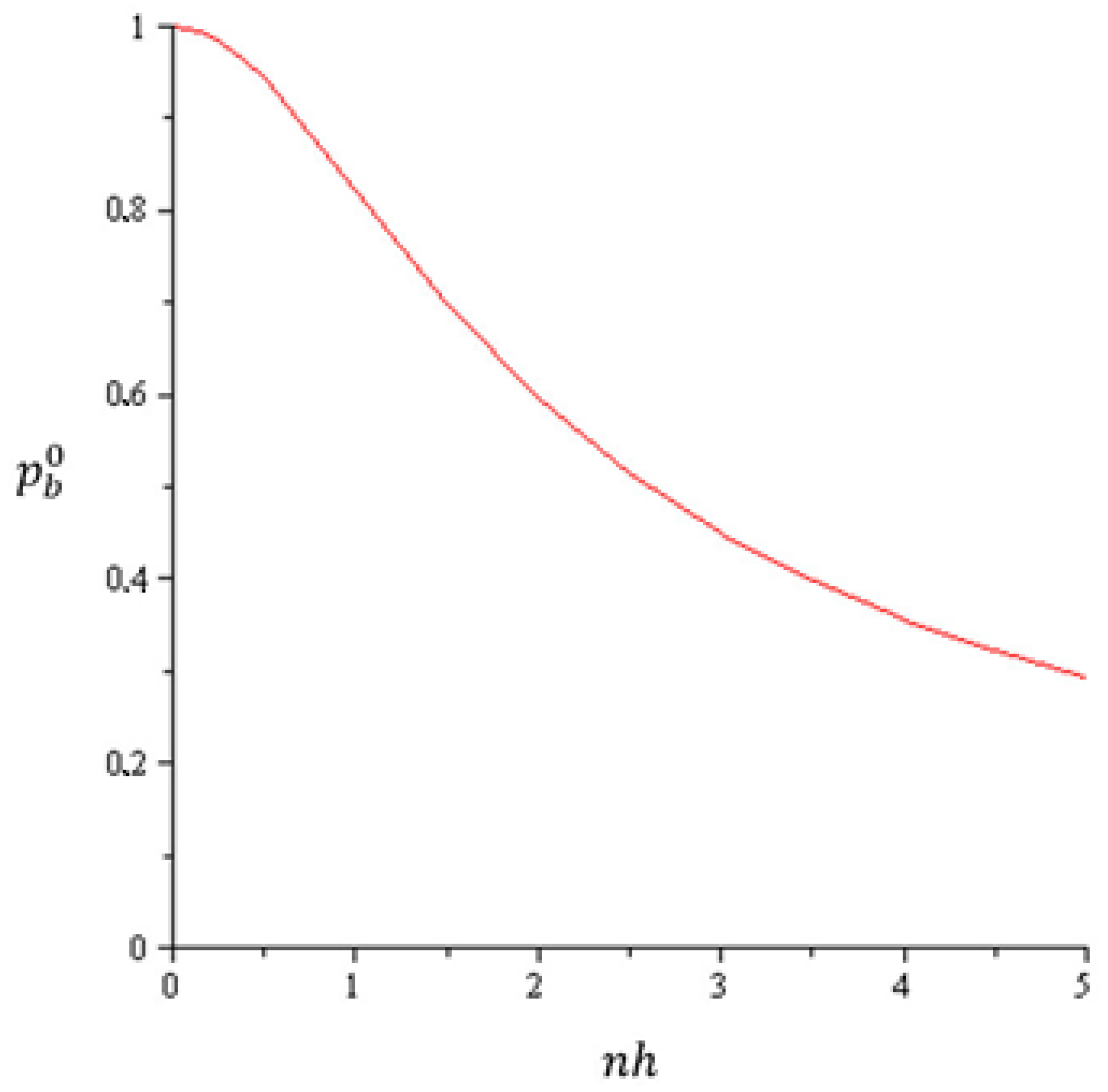
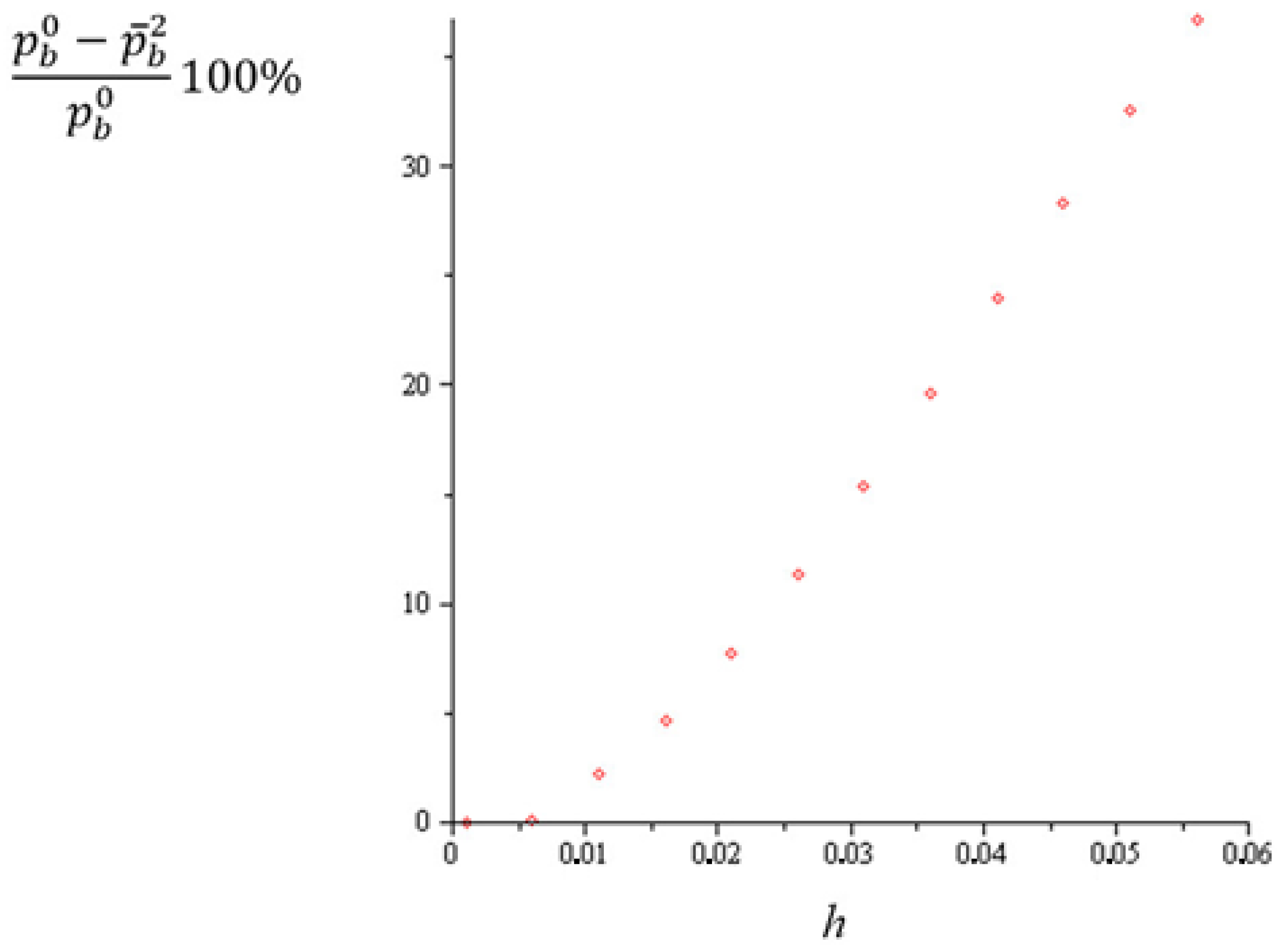

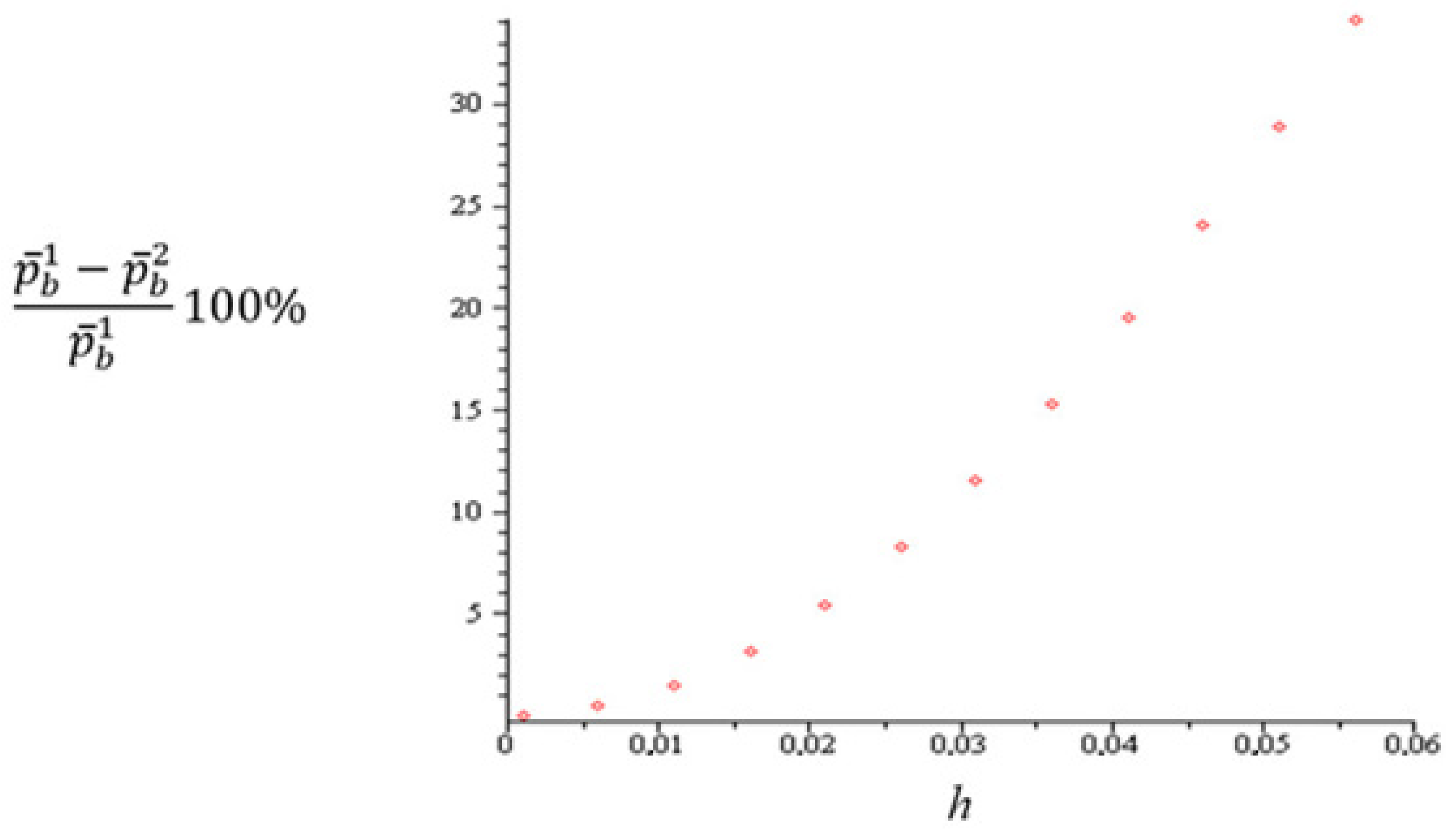
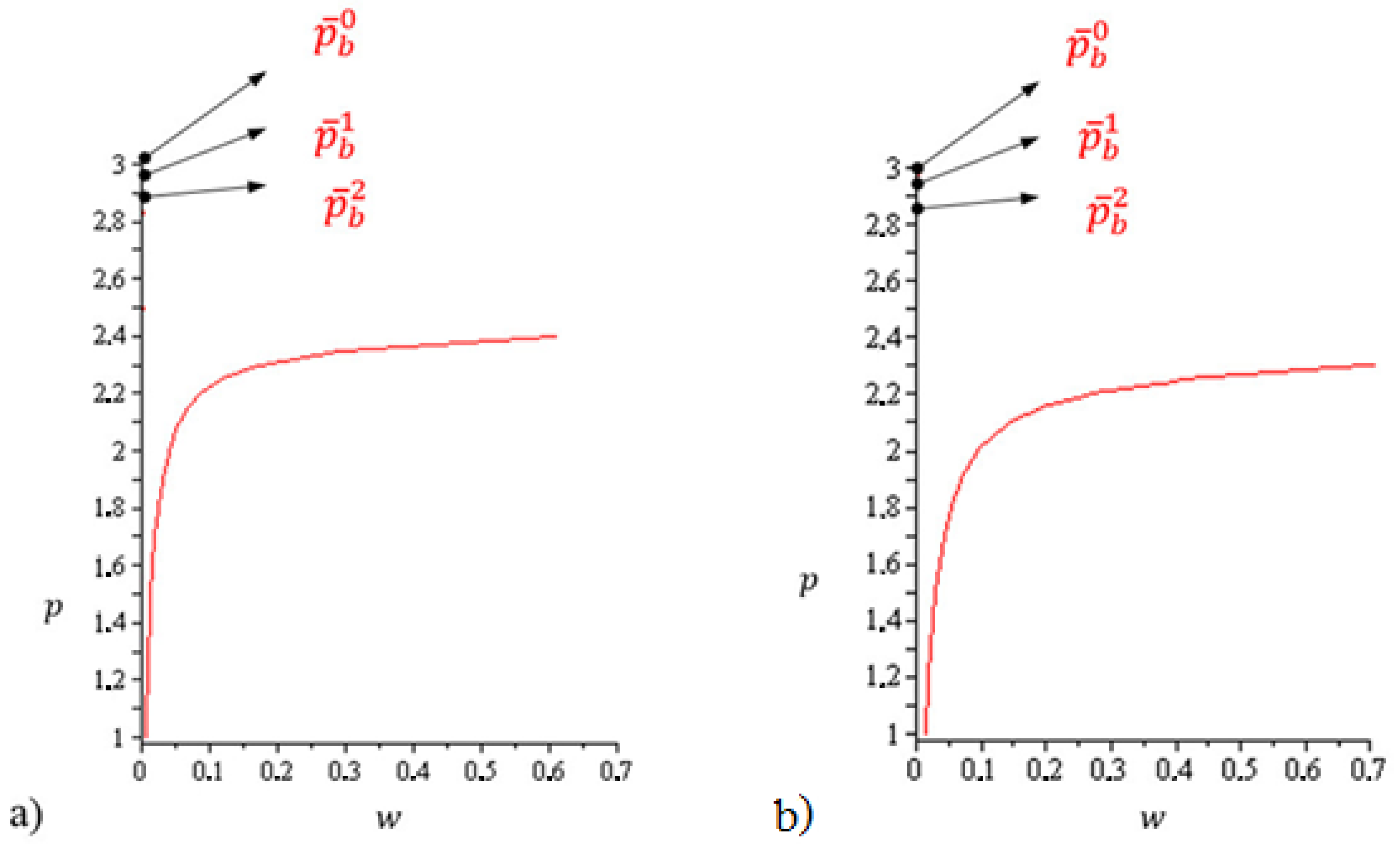
| nh = 1.6 | n = 160; h = 0.01 | n = 80; h = 0.02 | n = 40; h = 0.04 | n = 20; h = 0.08 | n = 16; h = 0.1 |
|---|---|---|---|---|---|
| pb | 0.6767 | 0.6767 | 0.6767 | 0.6766 | 0.6764 |
| Number of Iteration/Pressure | p = −1 | p = −1.5 | p = −2 |
|---|---|---|---|
| 3 | Δ3 = 0.8% | Δ3 = 1.09% | Δ3 = 12% |
| 4 | Δ4 = 0.01% | Δ4 = 1.06% | Δ4 = 3.18% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrianov, I.I.; Andrianov, I.V.; Diskovsky, A.A.; Ryzhkov, E.V. Buckling of Corrugated Ring under Uniform External Pressure. Symmetry 2020, 12, 1250. https://doi.org/10.3390/sym12081250
Andrianov II, Andrianov IV, Diskovsky AA, Ryzhkov EV. Buckling of Corrugated Ring under Uniform External Pressure. Symmetry. 2020; 12(8):1250. https://doi.org/10.3390/sym12081250
Chicago/Turabian StyleAndrianov, Igor I., Igor V. Andrianov, Alexander A. Diskovsky, and Eduard V. Ryzhkov. 2020. "Buckling of Corrugated Ring under Uniform External Pressure" Symmetry 12, no. 8: 1250. https://doi.org/10.3390/sym12081250
APA StyleAndrianov, I. I., Andrianov, I. V., Diskovsky, A. A., & Ryzhkov, E. V. (2020). Buckling of Corrugated Ring under Uniform External Pressure. Symmetry, 12(8), 1250. https://doi.org/10.3390/sym12081250




