Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding
Abstract
1. Introduction
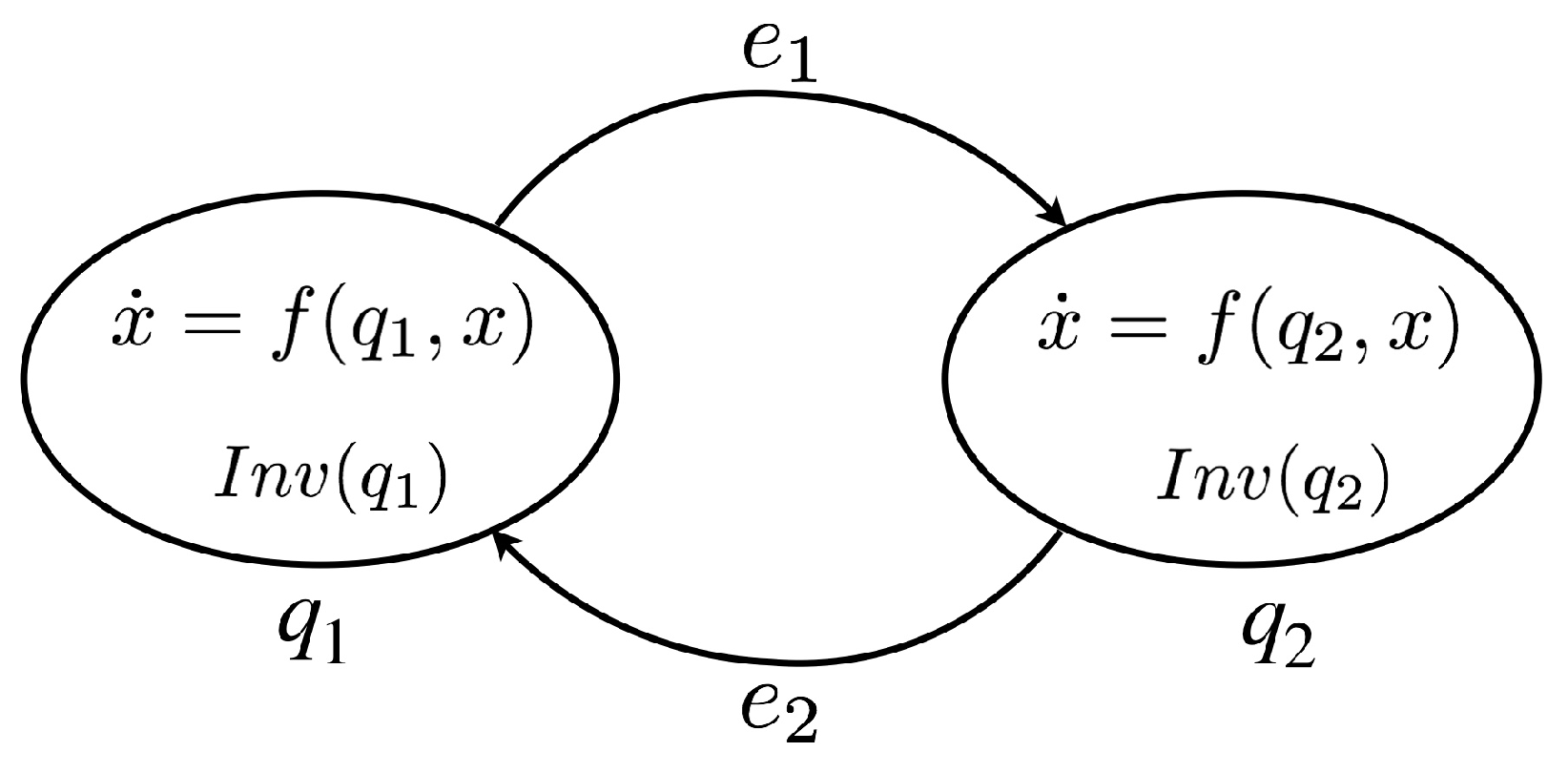
2. Hybrid Automata
- Q is a set of discrete states ;
- X is a set of continuous state vectors ;
- is a set of initial hybrid states ;
- F is a set of vector fields : ;
- I is a set of continuous invariants : , where restricts the continuous evolution within ;
- E is a set of discrete transitions to switch between discrete states ;
- G is a set of guard conditions : ;
- R is a set of reset maps : .
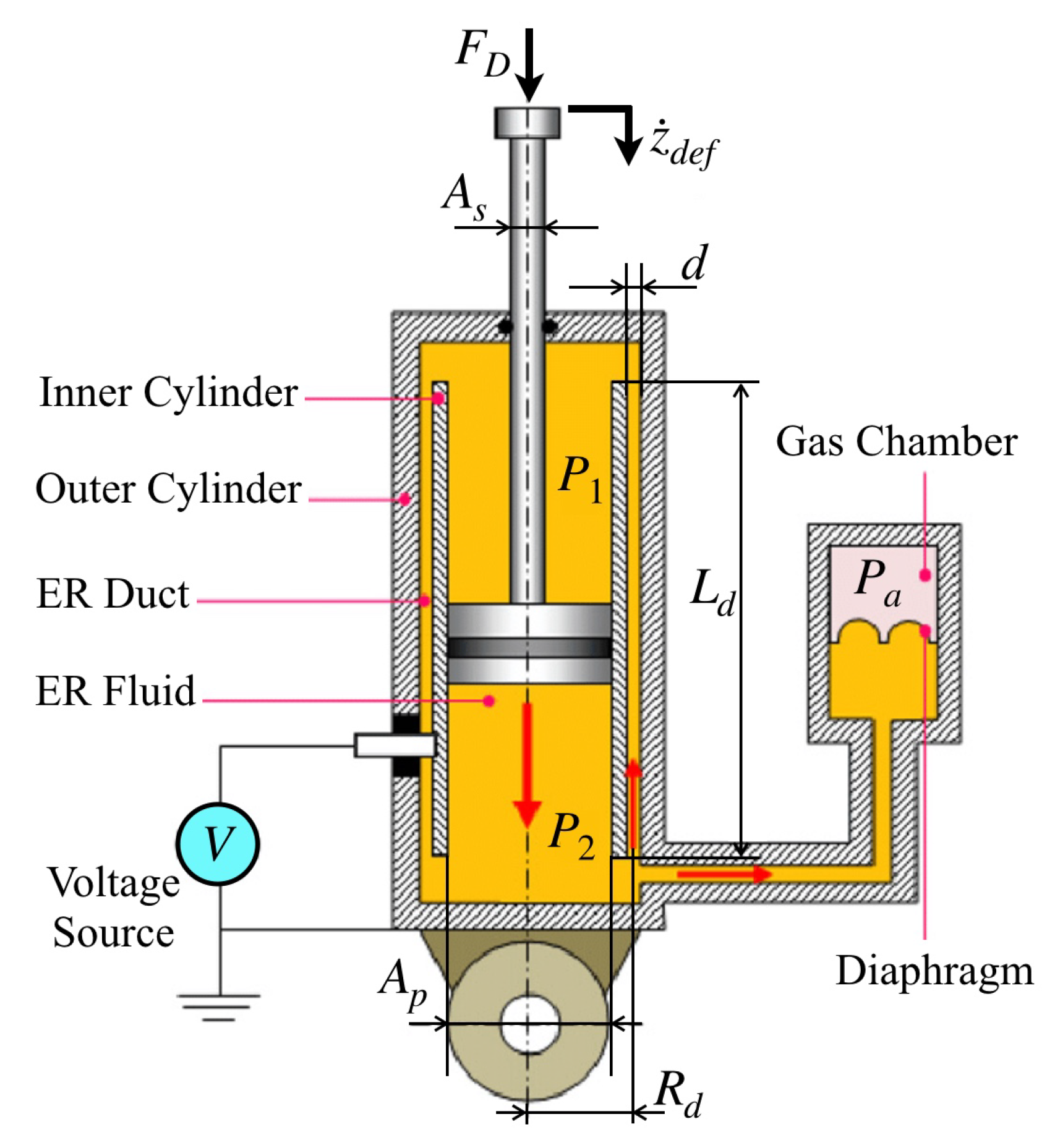
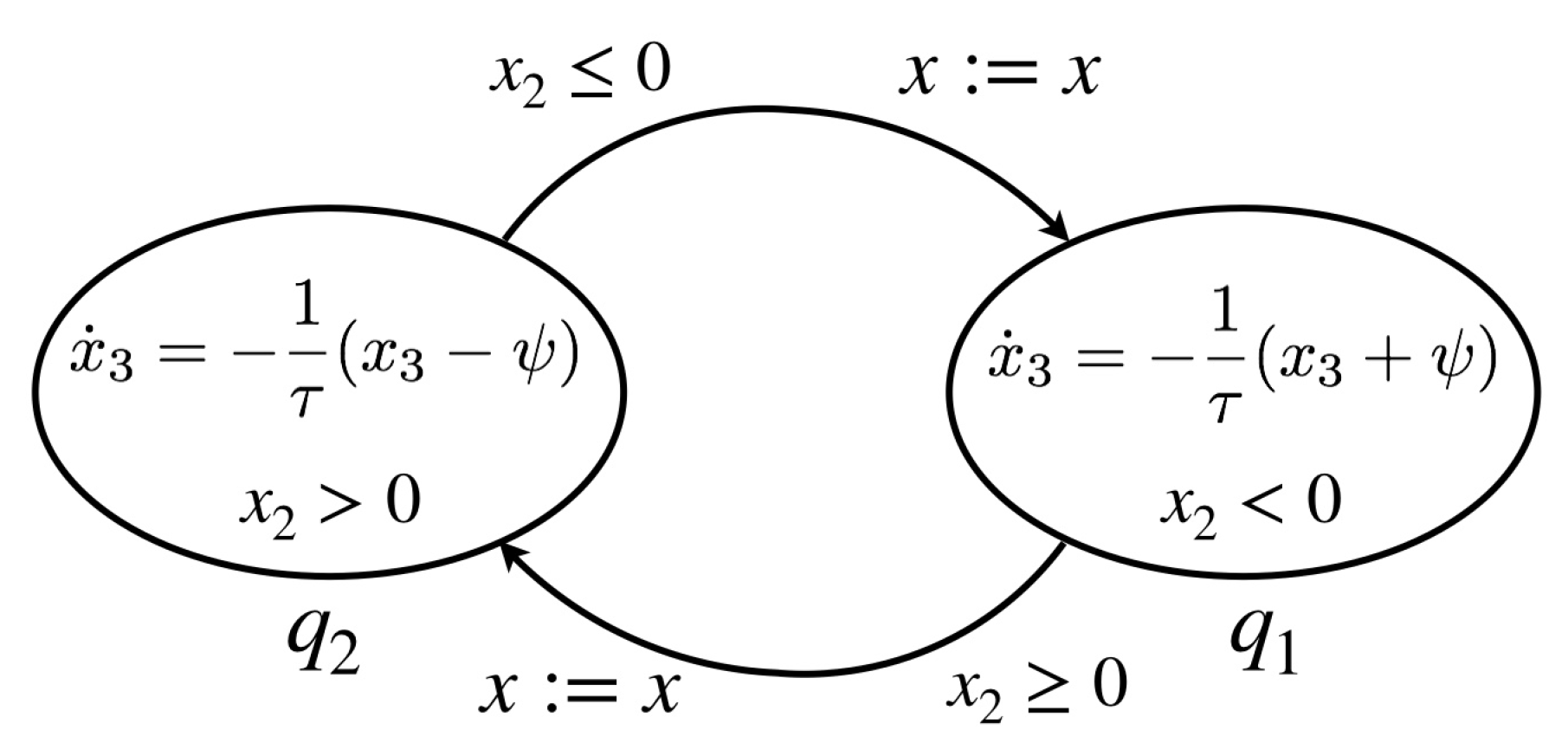
3. Modelling of Electro-Rheological Damper
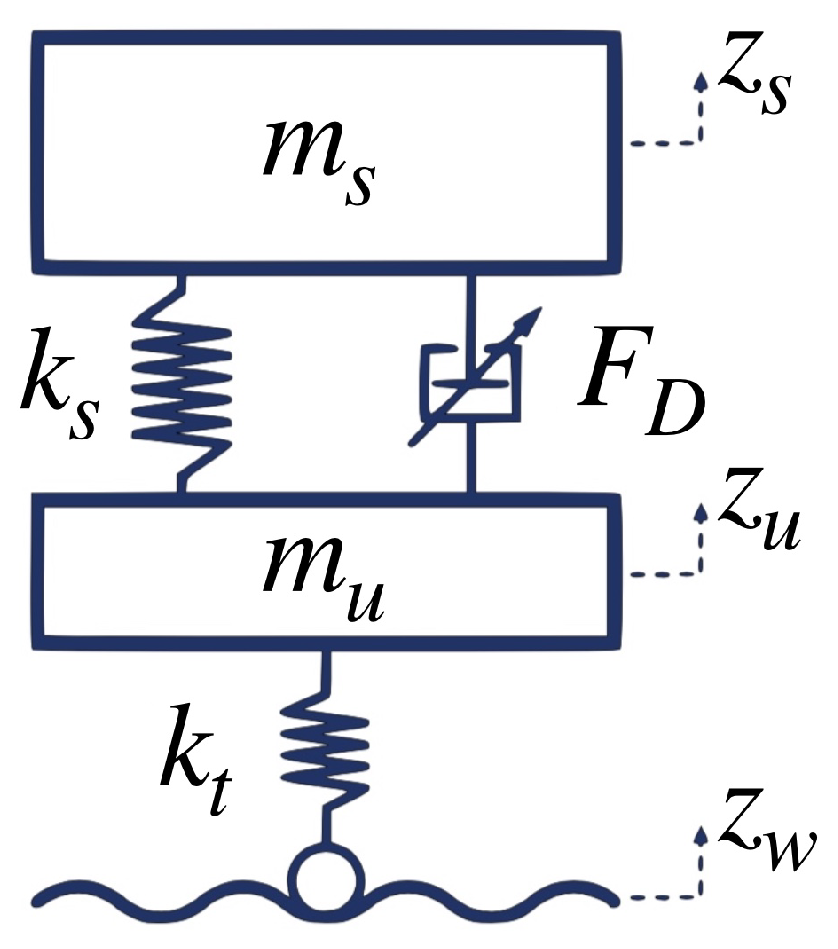
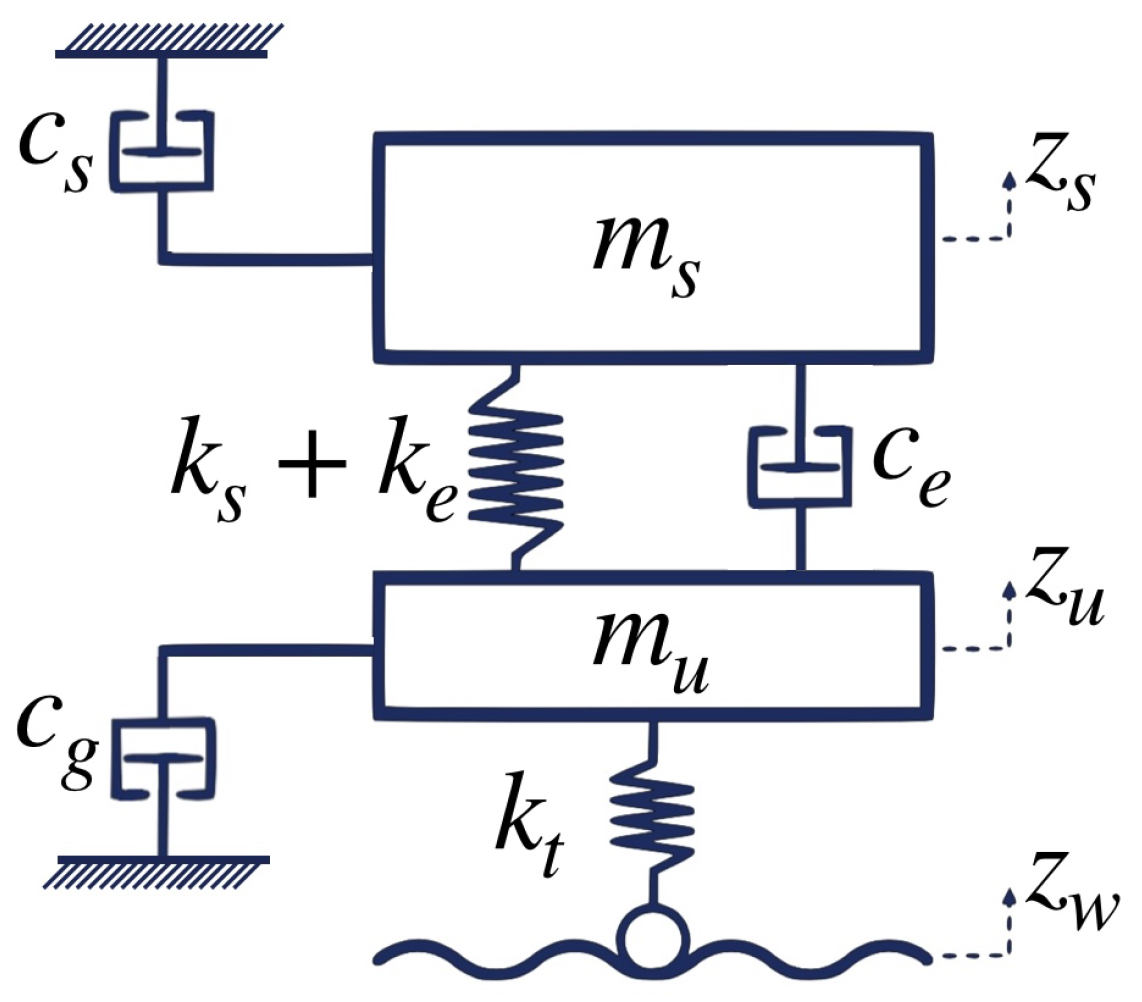
4. The Quarter Car Suspension Model
5. The Sliding Mode Controller Design
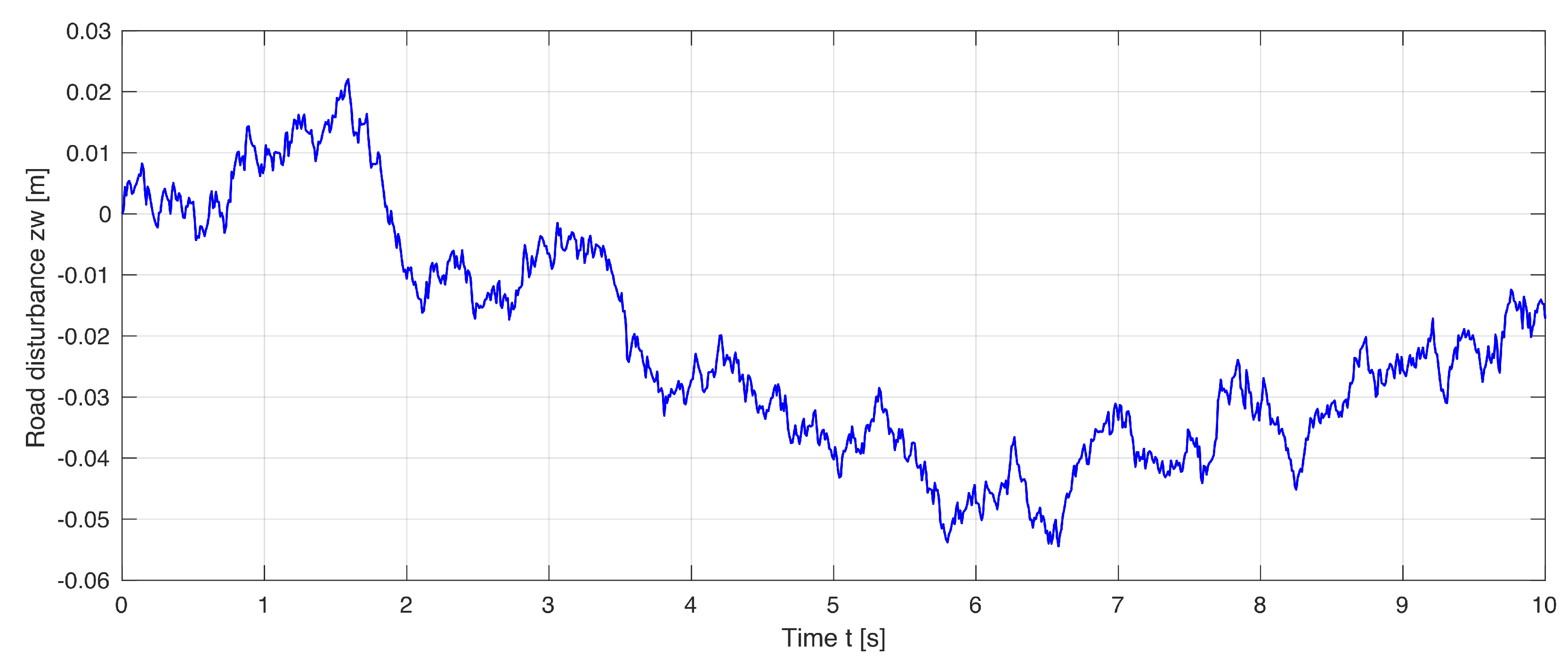
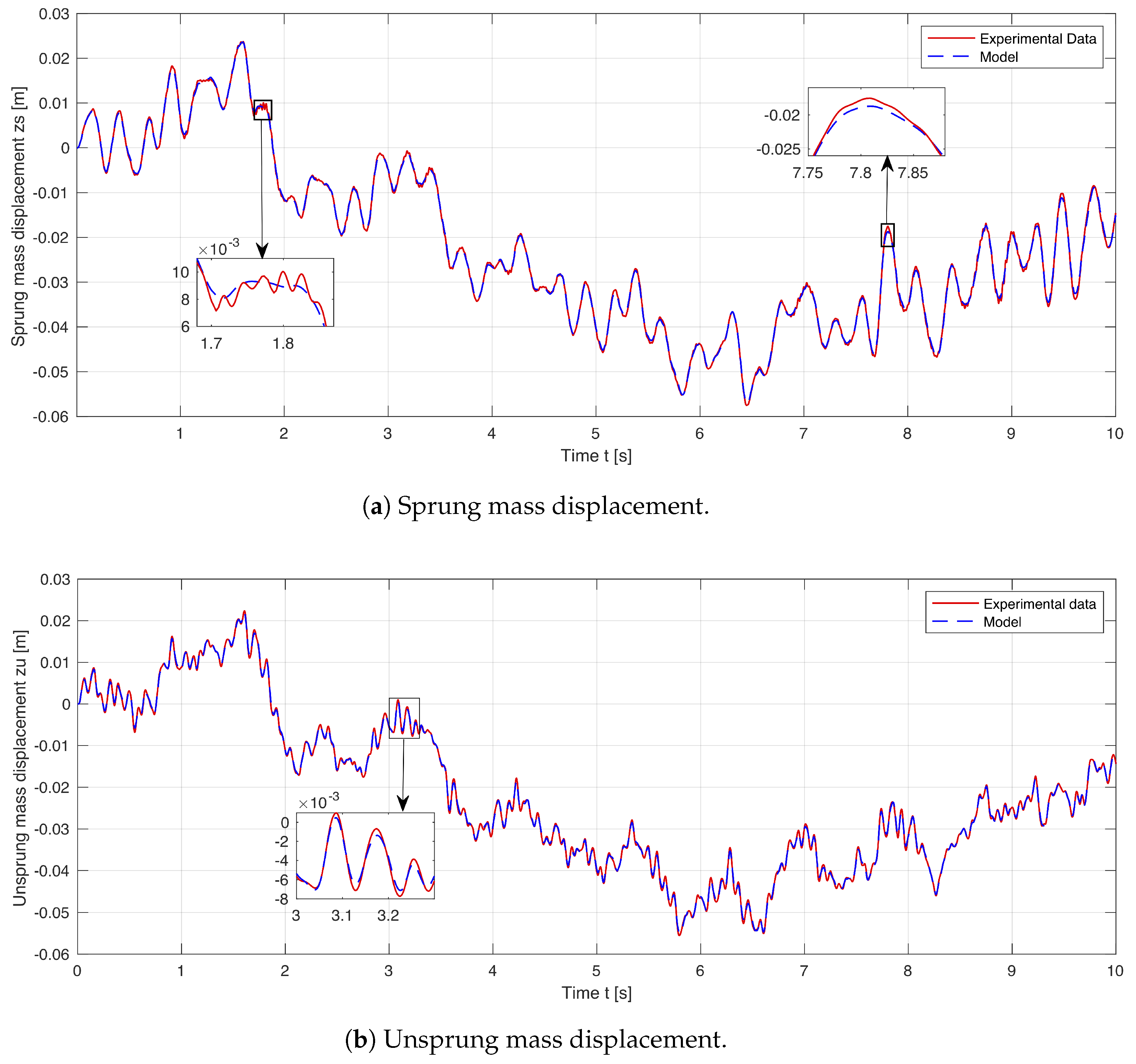
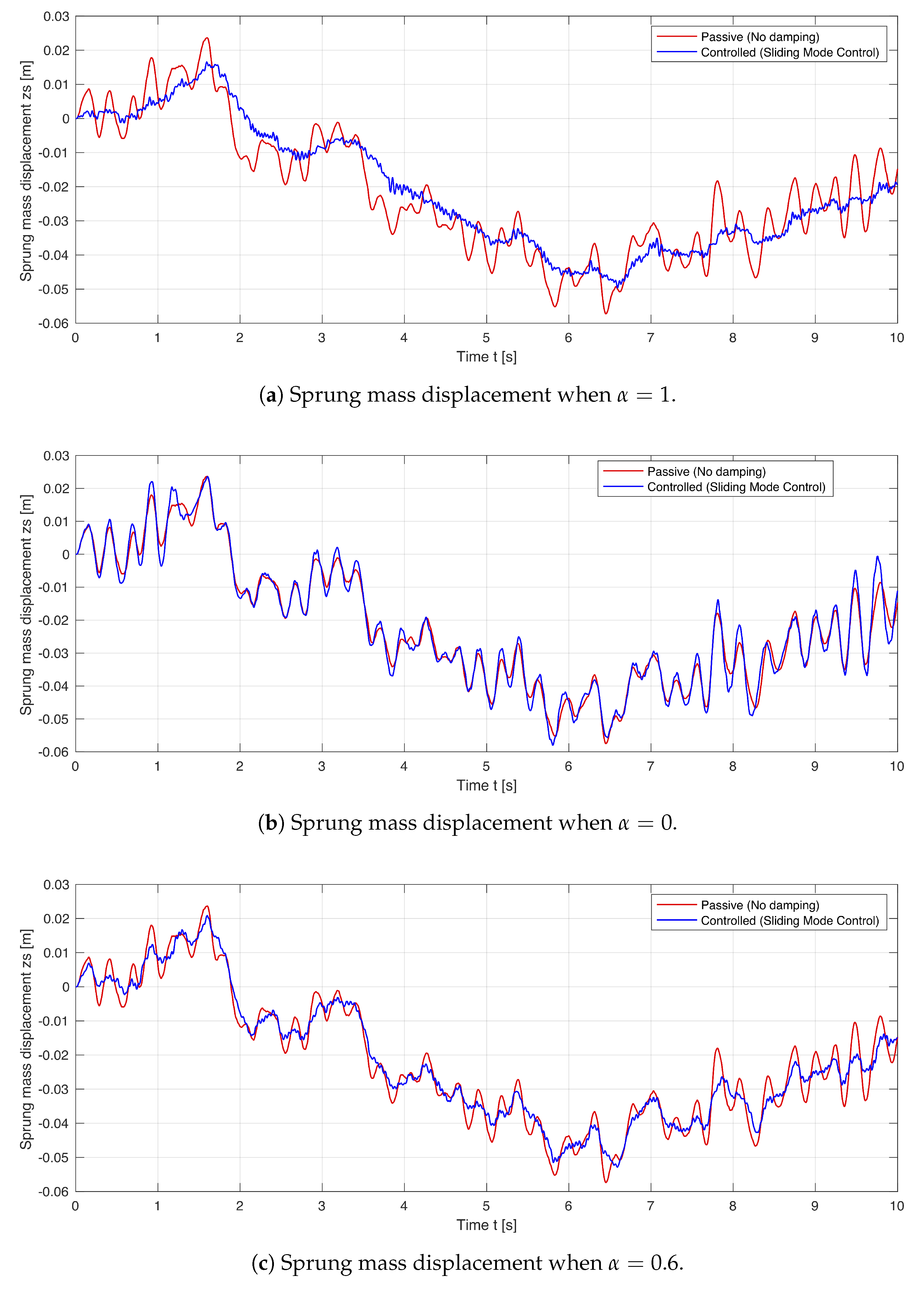
6. Prototype Implementation and Simulation Results
7. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Yagiz, N.; Hacioglu, Y. Backstepping control of a vehicle with active suspensions. Control. Eng. Pract. 2008, 16, 1457–1467. [Google Scholar] [CrossRef]
- Ribbens, W.B. Chapter 7—Vehicle Motion Controls. In Understanding Automotive Electronics, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 343–408. ISBN 9780128104347. [Google Scholar]
- Nekoui, M.A.; Hadavi, P. Optimal control of an active suspension system. In Proceedings of the 14th International Power Electronics and Motion Control Conference, Ohrid, Macedonia, 6–8 September 2010; Volume 16, ISBN 978-1-4244-7856-9. [Google Scholar] [CrossRef]
- Alvarez-Sanchez, E. A Quarter-Car Suspension System: Car Body Mass Estimator and Sliding Mode Control. Procedia Technol. 2013, 7, 208–214. [Google Scholar] [CrossRef]
- Yerrawar, R.N.; Arakerimath, R.R. Performance assessment and control policies for semiactive suspension using SIMSCAPE. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 9–10 September 2016; pp. 1163–1168. [Google Scholar]
- Gandhi, P.; Adarsh, S.; Ramachandran, K.I. Performance Analysis of Half Car Suspension Model with 4 DOF using PID, LQR, FUZZY and ANFIS Controllers. Procedia Comput. Sci. 2017, 115, 2–13. [Google Scholar] [CrossRef]
- Chen, Y. Skyhook Surface Sliding Mode Control on Semi-Active Vehicle Suspension System for Ride Comfort Enhancement. Engineering 2009, 1, 23–32. [Google Scholar] [CrossRef]
- Savaresi, S.; Silani, E.; Bittanti, S. Acceleration driven damper (ADD): An optimal control algorithm for comfort oriented semi-active suspensions. ASME Trans. J. Dyn. Syst. Meas. Control. 2005, 127, 218–229. [Google Scholar] [CrossRef]
- Savaresi, S.; Spelta, C. Mixed skyhook and ADD: Approaching the filtering limits of a semi-active suspension. ASME Trans. J. Dyn. Syst. Meas. Control. 2007, 129, 382–392. [Google Scholar] [CrossRef]
- Choi, S.B.; Lee, S.K.; Park, Y.P. A hysteresis model for the field-dependent damping force of a magnetorheological damper. J. Sound Vib. 2001, 245, 375–383. [Google Scholar] [CrossRef]
- Gaul, L.; Nitsche, R. Friction control for vibration suppression. Mech. Syst. Signal Process. 2000, 14, 139–150. [Google Scholar] [CrossRef]
- Kim, Y.; Langari, R.; Hurlebaus, S. Semiactive nonlinear control of a building with a magnetorheological damper system. Mech. Syst. Signal Process. 2009, 23, 300–315. [Google Scholar] [CrossRef]
- Kamath, G.M.; Wereley, N.M. A nonlinear viscoelastic-plastic model for electrorheological fluids. Smart Mater. Struct. 1997, 6, 351. [Google Scholar] [CrossRef]
- Dyke, S.; Spencer Jr, B.; Sain, M.; Carlson, J. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater. Struct. 1996, 5, 565. [Google Scholar] [CrossRef]
- Guo, S.; Yang, S.; Pan, C. Dynamic modeling of magnetorheological damper behaviors. J. Intell. Mater. Syst. Struct. 2006, 17, 3–14. [Google Scholar] [CrossRef]
- Makris, N.; Burton, S.A.; Taylor, D.P. Electrorheological damper with annular ducts for seismic protection applications. Smart Mater. Struct. 1996, 5, 551. [Google Scholar] [CrossRef]
- Unger, A.; Schimmack, F.; Lohmann, B.; Schwarz, R. Application of LQ-based semi-active suspension control in a vehicle. Control. Eng. Pract. 2013, 21, 1841–1850. [Google Scholar] [CrossRef]
- Fallah, M.S.; Bhat, R.; Xie, W.F. H∞ robust control of semi-active Macpherson suspension system: New applied design. Veh. Syst. Dyn. 2010, 48, 339–360. [Google Scholar] [CrossRef]
- Passenberg, B.; Caines, P.E.; Leibold, M.; Stursberg, O.; Buss, M. Optimal control for hybrid systems with partitioned state space. IEEE Trans. Autom. Control. 2013, 58, 2131–2136. [Google Scholar] [CrossRef]
- Prabakar, R.S.; Sujatha, C.; Narayanan, S. Optimal semi-active preview control response of a half car vehicle model with magnetorheological damper. J. Sound Vib. 2009, 326, 400–420. [Google Scholar] [CrossRef]
- Zareh, S.H.; Khayyat, A.A.A. Fuzzy inverse model of magnetorheological dampers for semi-active vibration control of an eleven-degrees of freedom suspension system. J. Syst. Des. Dyn. 2011, 5, 1485–1497. [Google Scholar] [CrossRef]
- Takahashi, M.; Kumamaru, T.; Yoshida, K. Integrated controller design for automotive semi-active suspension considering vehicle behavior with steering input. J. Syst. Des. Dyn. 2010, 4, 712–724. [Google Scholar] [CrossRef]
- Rao, K.D. Modeling, Simulation and Control of Semi Active Suspension System for Automobiles under MATLAB Simulink using PID Controller. IFAC Proc. Vol. 2014, 47, 827–831. [Google Scholar] [CrossRef]
- Zapateiro, M.; Luo, N.; Karimi, H.R.; Vehi, J. Vibration control of a class of semiactive suspension system using neural network and backstepping techniques. Mech. Syst. Signal Process. 2009, 23, 1946–1953. [Google Scholar] [CrossRef]
- Guo, D.L.; Hu, H.Y.; Yi, J.Q. Neural network control for a semi-active vehicle suspension with a magnetorheological damper. J. Vib. Control. 2004, 10, 461–471. [Google Scholar] [CrossRef]
- Sun, L.; Cai, X.; Yang, J. Genetic algorithm-based optimum vehicle suspension design using minimum dynamic pavement load as a design criterion. J. Sound Vib. 2007, 301, 18–27. [Google Scholar] [CrossRef]
- Available online: https://fmi-standard.org/ (accessed on 11 January 2020).
- Aljarbouh, A.; Caillaud, B. Chattering-free simulation of hybrid dynamical systems with the functional mock-up interface 2.0. In Proceedings of the First Japanese Modelica Conferences, Tokyo, Japan, 23–24 May 2016; Volume 124, pp. 95–105. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Caillaud, B. On the Regularization of Chattering Executions in Real Time Simulation of Hybrid Systems. In Proceedings of the Baltic Young Scientists Conference, the 11th Baltic Young Scientists Conference, Tallinn, Estonia, 10–14 August 2015; p. 49. Available online: https://hal.archives-ouvertes.fr/hal-01246853 (accessed on 14 January 2020).
- Aljarbouh, A.; Caillaud, B. Simulation for hybrid systems: Chattering path avoidance. In Proceedings of the 56th Conference on Simulation and Modelling (SIMS 56), Linkoping, Sweden, 7–9 October 2015; Volume 119, pp. 175–185. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Zeng, Y.; Duracz, A.; Caillaud, B.; Taha, W. Chattering-free simulation for hybrid dynamical systems semantics and prototype implementation. In Proceedings of the 19th IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC) and 15th International Symposium on Distributed Computing and Applications for Business Engineering (DCABES), Paris, France, 24–26 August 2016; pp. 412–422. [Google Scholar] [CrossRef]
- Aljarbouh, A. Non-standard zeno-free simulation semantics for hybrid dynamical systems. In Verification and Evaluation of Computer and Communication Systems; Springer International Publishing: Cham, Switzerland, 2019; pp. 16–31. [Google Scholar]
- Choi, S.B. Vibration control of electrorheological seat suspension with human-body model using sliding mode control. J. Sound Vib. 2007, 303, 391–404. [Google Scholar] [CrossRef]

| Discrete State | Dynamics | Invariant |
|---|---|---|
| Transition | Reset | Guard |
|---|---|---|
| Parameter | Value | Unit |
|---|---|---|
| 2.28 | kg | |
| 0.26 | kg | |
| 1399 | N/m | |
| 186 | N/m | |
| 23 | N·s/m | |
| 12,270 | N/m | |
| 40 | ms | |
| 5000 | N·s/m | |
| 3000 | N·s/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljarbouh, A.; Fayaz, M. Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding. Symmetry 2020, 12, 1286. https://doi.org/10.3390/sym12081286
Aljarbouh A, Fayaz M. Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding. Symmetry. 2020; 12(8):1286. https://doi.org/10.3390/sym12081286
Chicago/Turabian StyleAljarbouh, Ayman, and Muhammad Fayaz. 2020. "Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding" Symmetry 12, no. 8: 1286. https://doi.org/10.3390/sym12081286
APA StyleAljarbouh, A., & Fayaz, M. (2020). Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding. Symmetry, 12(8), 1286. https://doi.org/10.3390/sym12081286





