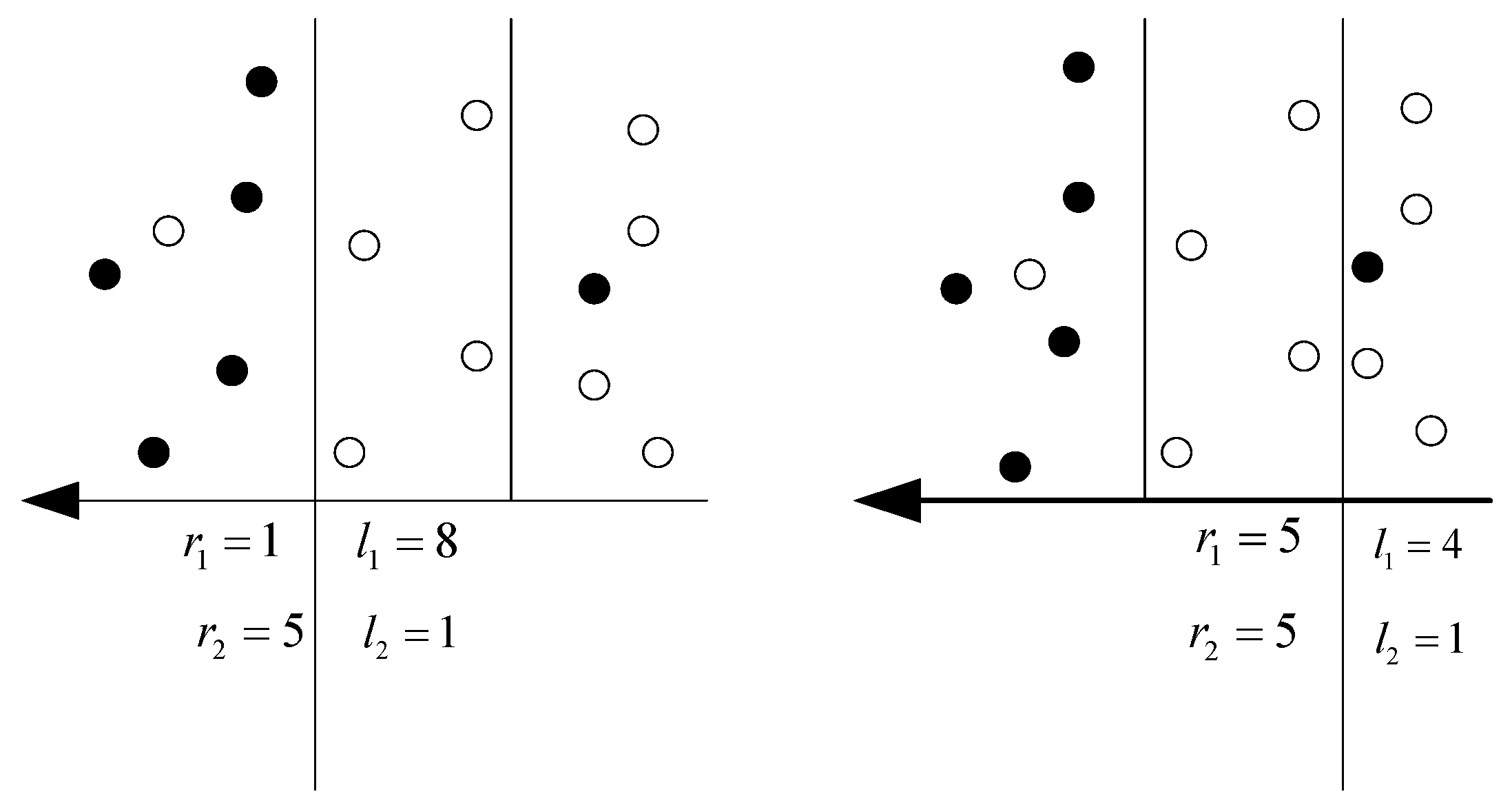1. Introduction
Incomplete economic information refers to people’s incomplete grasp of market information due to their limited cognitive ability. That is, the market cannot produce and allocate enough information effectively under the economic system. In real life—due to the cost of information collection and dissemination—rice information cannot be transmitted in a timely way to every market participant who needs information. Then result is the restriction of information flow and application. Moreover, the market price cannot reflect the supply and demand situation of the market sensitively, and the market supply and demand situation cannot change sensitively with the guidance of the price. The most serious one may cause the failure of the market mechanism, so improving the integrity of incomplete economic information has become an important research topic.
In fact, the discretization of data is not a new topic. Before the emergence of rough set theory, the problem of human discretization (or quantization) was studied extensively and many research results were obtained due to the need of numeric calculation. Rough set theory is an effective method to improve the completeness of incomplete economic information by analyzing the decision table and obtaining the knowledge of indiscernible relation.
Most of original research on rough set theory is published in Polish. At the time of publishing, it did not attract the attention of the international computer science and mathematics circles, and its research area was only limited to some countries in Eastern Europe. It was not until the late 1980s that it attracted the attention of scholars from all over the world [
1]. In 1991, Z. Pawlak’s monograph “Rough Set: Theoretical Aspects of Reasoning about Data” systematically elaborated on rough set theory, which laid a rigorous mathematical foundation for the rough set theory. The publication of the book marked the rough set research boom. The rough set and Boolean logic method proposed by Skowron et al. Are complete. In theory, all possible combinations of discrete breakpoint sets can be found out. However, the complexity of the algorithm is exponential and cannot be applied in practical problems. Nguyen proposed several improved greedy algorithms based on the separability of breakpoints to instances. In general, it is not easy to select the optimal metric, but it is especially effective to solve a problem by using the improved greedy algorithm after selecting the optimal metric. It belongs to local optimization search algorithm; it is not practical for the whole problem. While Chen Caiyun uses genetic algorithm to search the best discrete breakpoint set, which belongs to the whole search algorithm. The second kind of algorithm is the rough set discretization algorithm proposed from different angles. The main problem is that the selection of candidate segmentation points is subjective, and the efficiency of some discrete algorithms is also worth considering. To date, rough set theory has been successfully applied in many scientific and engineering fields such as pattern recognition, machine learning, decision support, process control, predictive modeling, etc. [
2]. The rough set theory is based on the classification mechanism, which understands the classification as an equivalence relation in a particular space, and the equivalence relation constitutes the division of the space [
3]. Rough set theory understands knowledge as the division of data, and each divided set is called the concept. The main idea is to use knowledge bases of known knowledge to approximate inaccurate or uncertain knowledge-with-knowledge from known knowledge bases [
4].
Rough set theory has two main categories in the application of information science: one is non-decision analysis, and the content mainly includes data compression, reduction, clustering and machine discovery [
5]; the other type is the analysis of decision-making, which mainly includes decision analysis and rule extraction. Of course, it can also be used for preprocessing of raw data, such as data compression and reduction. As a mathematical tool for dealing with uncertainty and inaccuracy, rough set theory has received increasing attention in the international academic community in recent years [
6].
Discretization is one of the important issues with rough sets. The rough set method proposed by Z. Pawlak with the indistinguishable relationship as the core deals with discrete attribute values, while the actual life data are mostly continuous attribute values. Therefore, data needs to be discretized, which has become the bottleneck in the practicality of rough set theory [
7]. The essence of discretization can be attributed to the problem of using the selected breakpoints to divide the space formed by conditional attributes. It is a space partitioning and optimization coding problem [
8]. This problem has been extensively studied in the fields of pattern recognition taxonomy, coding, and image coding [
9,
10]. However, how to combine the predecessors’ research and existing theories to develop a discretization method that is useful for rough set knowledge is a worthwhile question.
This study presents a rough set based on big-data discretization algorithm of incomplete economic information, novelty and innovation points of this method is that of incomplete economic information added in the first place, and then on the basis of supplementary data using rough set in keeping the original decision system of indiscernibility relation at the same time, the less possible breakpoint set segmentation space, which is formed by the continuous attribute values and classification identification of the relevant information accurately improve the computational efficiency and incomplete economic information more complete. The algorithm designed in this study effectively fills in incomplete economic information, improves the efficiency of economic information circulation, makes the market mechanism more flexible and makes outstanding contributions to the development and progress of the economic field.
2. Discrete Algorithm Design of Rough Set Incomplete Economic Information
2.1. The Algorithm for Filling of Incomplete Economic Information Based on Deep Learning
In recent years, domestic and foreign professionals have proposed a large number of the methods for filling of incomplete economic information, but those methods can only deal with small-scale data. Hence, the algorithm for filling of incomplete economic information based on deep learning is proposed in the study. First, the three-layer network model is constructed, and the output of each layer network is set as the output of the upper layer network, and the uppermost layer is set as the acquired feature output. During training, the network initialization parameters are extracted from top to bottom training, and finally the back propagation algorithm is used to fine tune all parameters [
11].
In order to extract the monitoring objectives of each layer of the network training, the instance data are first set as input, and an overlay automatic encoder is established to extract the two-layer features of the instance data. The schematic diagram of the superimposed automatic encoder is shown in
Figure 1:
In
Figure 1,
y represents the reconstructed data set and
is the coding factor. In this study, the original economic information
that has not been processed is set as the network input and the first layer feature
can be extracted in the lowermost layer, where
is the feature factor. The feature
is set as the input of the upper layer network, and the second layer feature
is obtained. The training is mainly based on local training, and the weight needs to be updated with the second layer feature training and cannot interfere with the lower layer network. According to this method, the laminated network parameters can be initialized, and finally the backpropagation algorithm is used to fine tune the body parameters [
12]. In this way, two layers features
and
of the original data instance can be extracted.
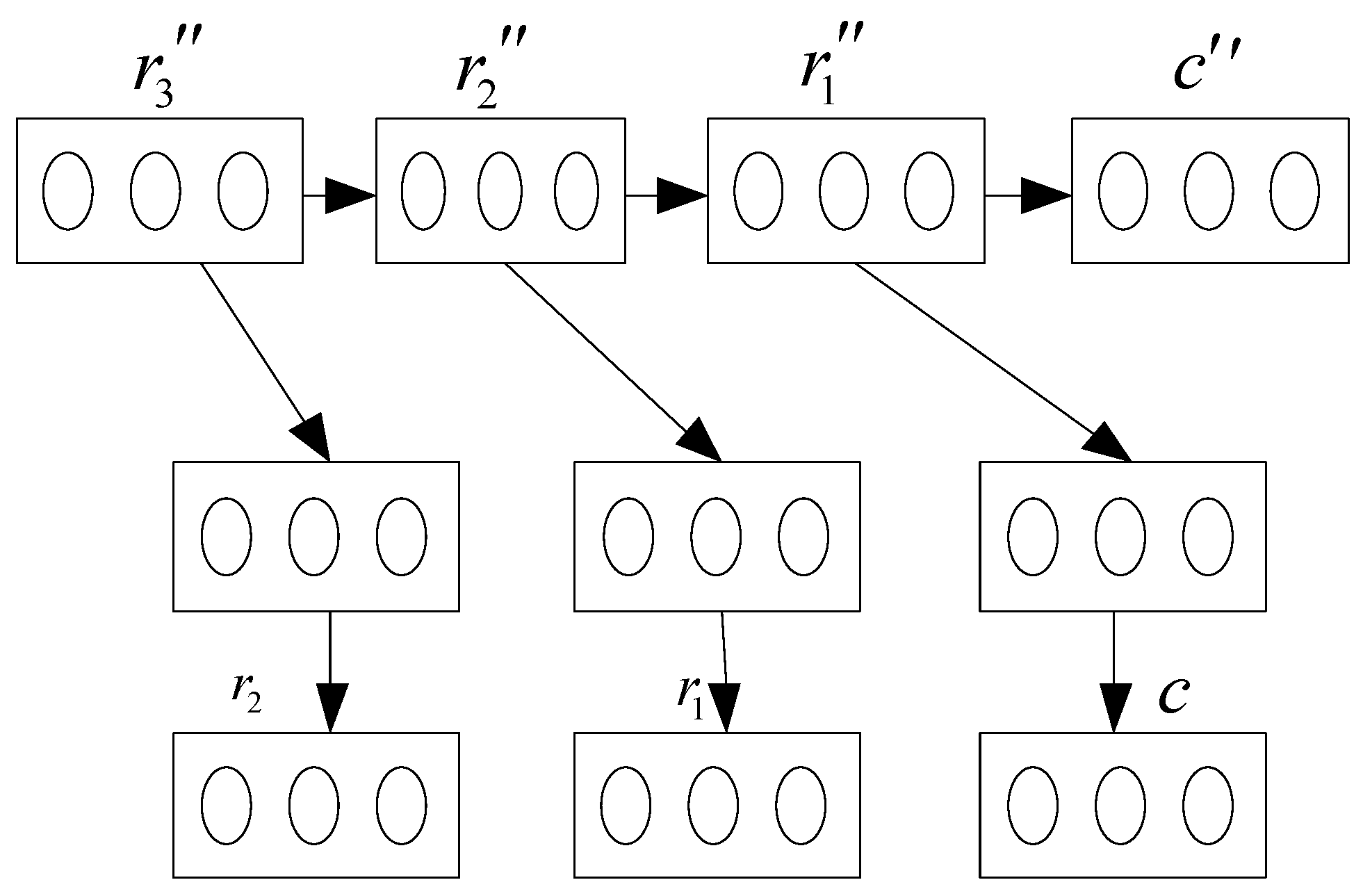
Based on the superimposed automatic encoder, a three-layer deep filling network model is constructed. The schematic diagram of the three-layer deep-fill network model is shown in
Figure 2:
In
Figure 2, The supervisory data are set to
,
and
3 in sequence, and the network parameters of each layer are initialized using a layer-by-layer training form. The first step is to add noise to the data instance
, the second step extracts some attributes and sets the attribute value to 0 and finally obtains the simulation example
of incomplete economic information; when the input is
, the first layer features
and
of the incomplete economic information are extracted, and then the first layer feature
of the instance
is deeply learned by the superposition encoder in
. Set
as supervisory data,
as input, the second layer features
and
of
can be obtained. The first layer feature
of the instance
is obtained in
using a superimposed automatic encoder. Finally, set
as supervisory data,
as input, the third layer features
and
of
can be obtained. The deep learning network approximates the instance features in turn, and the interference of incomplete economic information at each layer is reduced. When reaching the top layer of the network, the big-data features can be obtained [
13].
The instances are sequentially extracted in the data set R, and the deep learning network is trained. After the training, the network parameters are updated. When the global network is stable, the network parameters , and are extracted.
After extracting the network parameters, the depth features of each data in the dataset of incomplete economic information are extracted [
14]. For incomplete economic information
, you need to set the attribute value of its incomplete attribute to 0 and establish
.
is divided and set to input, and its depth feature
is obtained using Equation (1).
Then, Formula (2) is used to restore incomplete economic information and obtain the filling value
of incomplete economic information:
2.2. The Discretization Algorithm Based on Breakpoint Discrimination in Rough Set
Rough set is an important mathematical tool for dealing with inaccurate data. Unlike evidence theory and fuzzy set theory, the rough set theory does not require any prior knowledge or additional information about the data [
15]. In the rough set theory, the data table is called the information system. In the context of data, there is a large amount of undecidable data in the complete economic information after filling. Therefore, using discretization algorithm based on breakpoint discrimination in rough set, under the premise of maintaining the original indistinguishable relationship of the decision system, the space formed by the continuous attribute value of the complete economic information is divided by using as few breakpoint sets as possible [
16].
Assume that in the context of big data, the decision-making system for the complete economic information after filling is
,
U is the finite set of objects (the domain);
R is the set of attributes;
V is the set of attribute values;
f is the information function. Each continuous condition attribute
, and C is a subset. In the domain, its finite attribute values
V are sorted as follows.
The candidate breakpoint for the complete economic information after the filling is
where
;
represents the
m-th breakpoint of attribute a and
;
is the total number of breakpoints for attribute a and set
(
) is a set of instances.
In the case where decision attribute value of the completed economic information is
j, the instances belong to both
X, and the value of attribute a is smaller than the value of breakpoint
, and its number is
In the case where decision attribute value of the completed economic information is
j, the instances belong to both
X, and the value of attribute a is bigger than the value of breakpoint
, and its number is
Then
where
and
are the attribute factors,
is the type of decision and
d represents the decision factor. The breakpoint
of the set
X is inserted, and the instance of the decision attribute value
j in the set
X is divided into an
x subset of less than
and an
x subset of greater than or equal to
[
17]. Since the different breakpoints are different in the insertion position of the set
X, the instance distribution position of the decision attribute
j is different, and thus the ability of different breakpoints to distinguish the decision attribute value
j is different. In the example set shown in
Figure 3, “•” indicates the instance with the decision attribute value of 1 and “∘” indicates the instance with the decision attribute value of 0. Obviously, breakpoint
is better at distinguishing decision-making classes in the instance set than breakpoint
. For any breakpoint
in set
X, we use
to indicate the discriminative power of the breakpoint to the decision attribute value of
j. For any breakpoint in set
X, we use the discriminative power to represent the breakpoint’s decision attribute value.
is the weighted mean of breakpoint
for the discriminative power of
decision attribute values. Therefore,
is the indicator for selecting breakpoints [
18].
2.2.1. Calculation Method for
In the following, the ability to distinguish the filled complete economic information breakpoint from the decision attribute value j is calculated. First, the following concepts are introduced.
is the probability that the instance decision attribute value is equal to j and belongs to the x in the filled complete economic information set ;
is the probability that the instance decision attribute value is not equal to j and belongs to x in the filled complete economic information set ;
is the total number of instances of the decision attribute value j in the filled complete economic information set ;
is a total example of the filled economic information set .
It can be seen from the observation that if the value of the breakpoint of the completed complete economic information is high, it means that the instance of the decision attribute value j is concentrated on the side; then its will be very high, which means that the instance of the decision attribute value is not equal to j is distributed on the other side of . This indicates that has the strong ability to distinguish the decision attribute value j. Therefore, the value of is used to represent the ability of the filled complete economic information breakpoint to distinguish the decision attribute value j.
Step 1 is calculated;
Step 2 is calculated;
Step 3 is calculated.
2.2.2. Calculation Method for
Through analysis, we get that if the fully populated complete economic information breakpoint is of high importance, then the value of
is correspondingly high. The larger the value of
is, the higher the breakpoints
ability to distinguish decision-making classes is. This shows that the filled complete economic information breakpoint
is also important and has the priority of choice [
19]. The value of breakpoint
can be expressed as
2.2.3. Discrete Algorithm Design Based on Big Data
With the continuous integration of Internet of things, social network, cloud computing and other technologies into our lives, as well as the rapid development of existing computing power, storage space and network bandwidth, the accumulated data of human beings in the Internet, communications, finance, business, medical care and many other fields continue to grow and accumulate. In particular, the huge amount of big data generated in the economic field leads to the decline of the integrity of economic information and the increase of the amount of incomplete economic information. Therefore, it is imperative to use rough sets to process incomplete economic information under the background of big data. The design process of discretization algorithm for incomplete economic information based on rough set of big data are as follows:
Suppose
P is the selected set of economic information breakpoints,
L is the set of equivalence classes into which the instance is divided by the breakpoint set
P and C is the set of candidate breakpoints.
is the equivalent class of the completed economic information decision system that has been divided by P, so if
, the
is
Based on the above analysis, the discretization algorithm based on breakpoint discrimination ability is given below.
Algorithm based on breakpoint discrimination ability (algorithm 1):
- Step 1
; .
- Step 2
For , should be calculated;
- Step 3
Select maximum breakpoint of and add it to P;
- Step 4
For all , if divides the equivalence class X into and , then remove X from L and add equivalence classes and to L;
- Step 5
If the instances have the same decision in each of the equivalence classes of L, then stop; otherwise go to Step 2.
Assume that the domain of the completed economic information decision system after filling is
U and
P is used to represent the equivalence relation determined by the decision attribute equal to the attribute value.
Q is the equivalence relation cluster determined by the equality of arbitrary condition attributes of the complete economic information decision system after filling, which forms an initial division on
U.
The process of selecting the filled complete economic information breakpoints by the algorithm of this study is essentially the process of merging attribute values.
(1) Assume that the algorithm in this study forms a new equivalence partition on
U according to the equivalence relation
, then there is only one merge:
and respectively indicate the compatibility before and after discretization of the completed economic information decision system and . Therefore, the compatibility of the completed economic information decision system after filling is unchanged.
(2) Similarly, when the combination of equivalence classes is two or more, the compatibility of the completed economic information decision system after filling does not change [
20].
The calculation process is shown in
Figure 4 below.
3. Experimental Process and Analysis
Experiments were carried out to verify the effectiveness of the discretization algorithm of rough set incomplete economic information designed in this study based on big data. First, the filling performance test of incomplete economic information is carried out, and then the discretization performance test is carried out.
(1) Filling performance test of incomplete economic information
In order to verify the effectiveness of the proposed algorithm, the proposed algorithm is compared with two filling algorithms FIMUS and DMI. A portion of the data are removed from the data set of 10 G incomplete economic information to simulate the incomplete economic information set. After the filling is completed, the padding value is compared with the real value to obtain the filling precision of the algorithm.
This study artificially creates two economic information missing values, single mode missing and multi-mode missing. In single mode, each data object is allowed to contain only one missing value, while multipattern allows each data object to contain multiple missing values [
21,
22], and the missing values vary. The missing data are simulated by selecting 1%, 3%, 5% and 10% of the data from the data set and deleting some of the attribute values of the data.
This article uses two criteria to measure the fill accuracy of the algorithm. The first standard is called the
standard, which measures the degree to which the fill value matches the true value. The second criterion is RMSE, which measures the average error between the fill value and the true value. According to the definition of two standards, for an algorithm, the larger the value of
is, the higher the filling accuracy of the algorithm is. Conversely, the smaller the value of RMSE is, the lower the fill accuracy of the algorithm is. The results of the filling are shown in
Table 1:
It can be seen from
Table 1 that for any kind of missing combination, with the increase of data missing rate, the
obtained by the algorithm FIMUS and DMI are decreasing, that is, the filling precision of the two algorithms for incomplete economic information decreases with the increase of data missing rate. As the data loss rate increases, the RMSE obtained by the algorithms FIMUS and DMI increases continuously, that is the filling accuracy of the two algorithms decreases as the data missing rate increases [
23,
24]. The algorithm proposed in this study has an RMSE fill value of less than 0.2. Therefore, in terms of RMSE, the filling accuracy of the proposed algorithm is significantly higher than that of FIMUS and DMI.
This is because the method in this study adopts the filling algorithm of incomplete economic information based on deep learning. Through the feature extraction of the existing information and deep learning, the supplementary filling value can be obtained. Therefore, the accuracy of the calculation result is high.
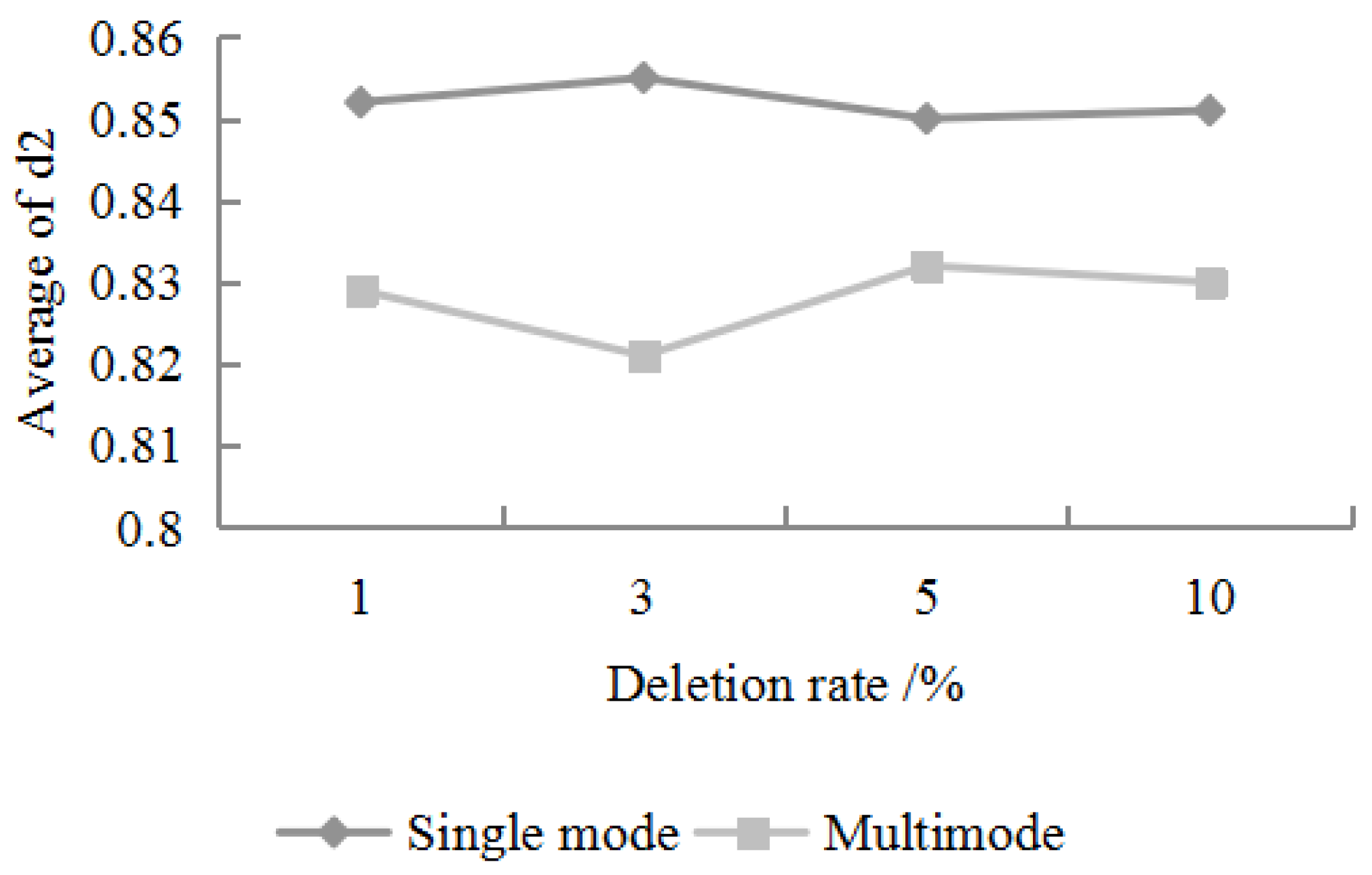
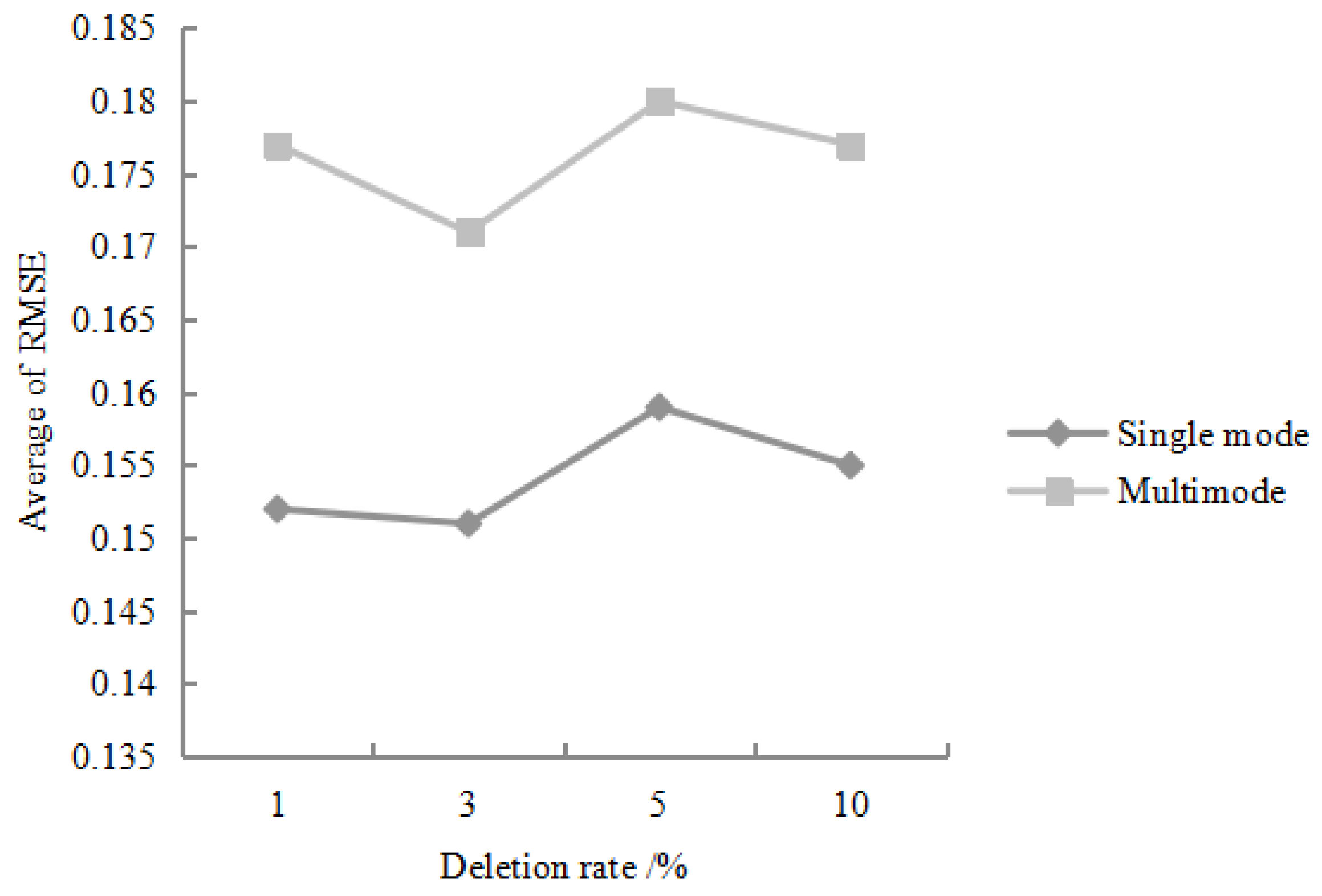
For any missing combination, different economic information is randomly selected as the training data. After running the algorithm 20 times, the average value of the
value and the average value of the RMSE obtained by the statistical algorithm are shown in
Figure 5 and
Figure 6:
It can be seen from
Figure 5 and
Figure 6 that the filling accuracy of the algorithm is relatively stable. Specifically, when the data deletion rate is between 1% and 10%,
can be stably maintained above 0.8, and the RMSE value is stable between 0.15 and 0.2. In addition, for any one of the missing rates, the filling accuracy of the single missing mode is significantly higher than the filling accuracy of the multiple missing mode [
25]. This is because the multi-fill mode has a large amount of missing data, and its interference with feature extraction and restoration is higher than that of the single-missing mode.
(2) Discretization performance test results
In order to verify the discretization test performance of the algorithm, a total of 9 groups of samples with different sizes were set up, and the incomplete economic information is filled. The discrete experiments were carried out with the method in this study, based on information entropy algorithm and based on breakpoint importance algorithm. and the number of different samples is set. The detailed settings are shown in
Table 2.
In order to verify the validity of the proposed algorithm, an identification test of incomplete economic information was carried out. The experimental process was divided into the following steps:
Discrete the incomplete economic information data set with the selected three methods;
Select the information entropy algorithm for attribute reduction, use the inductive value reduction algorithm to perform value reduction and get the rules. Finally, test the knowledge gained.
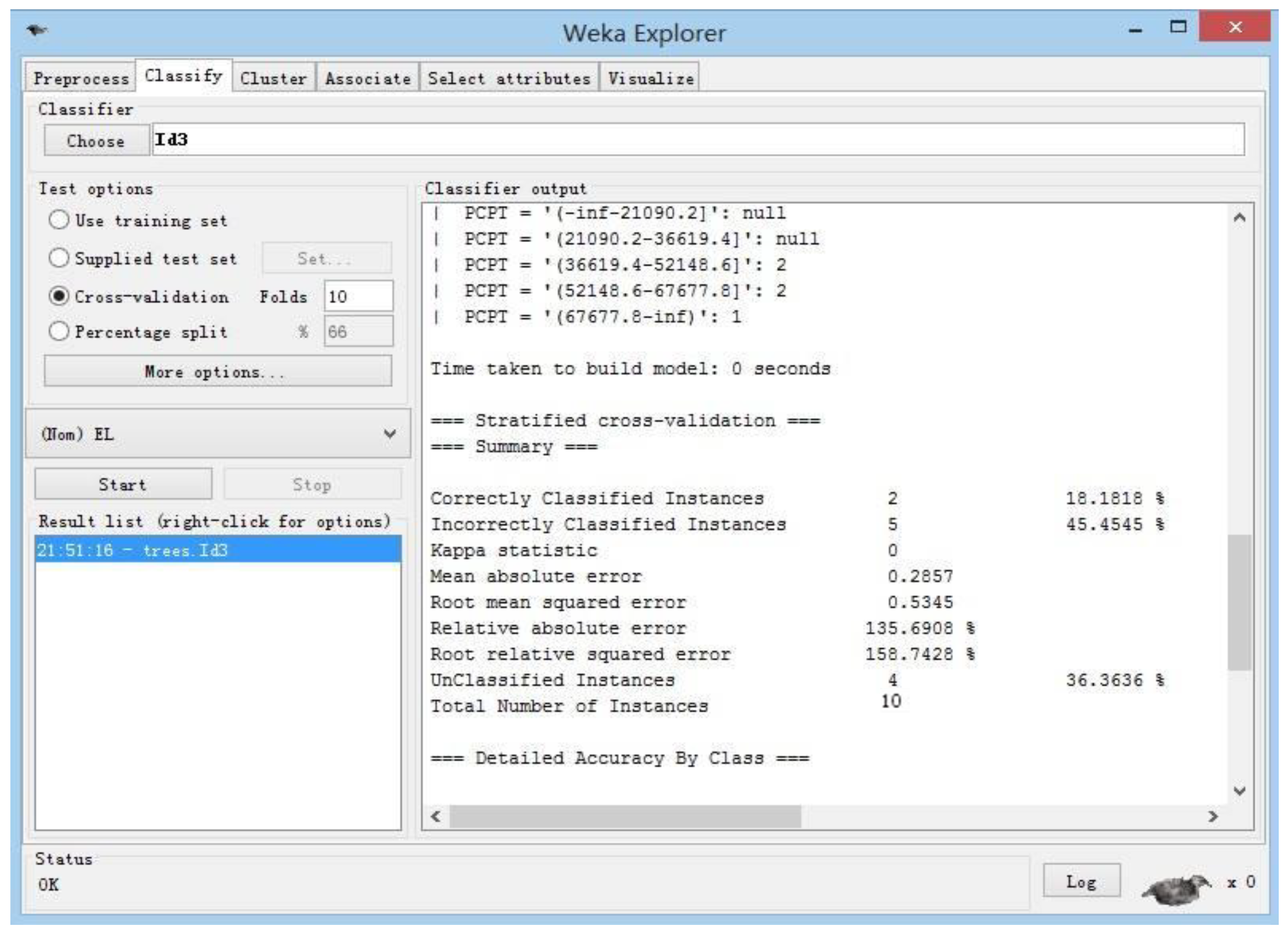
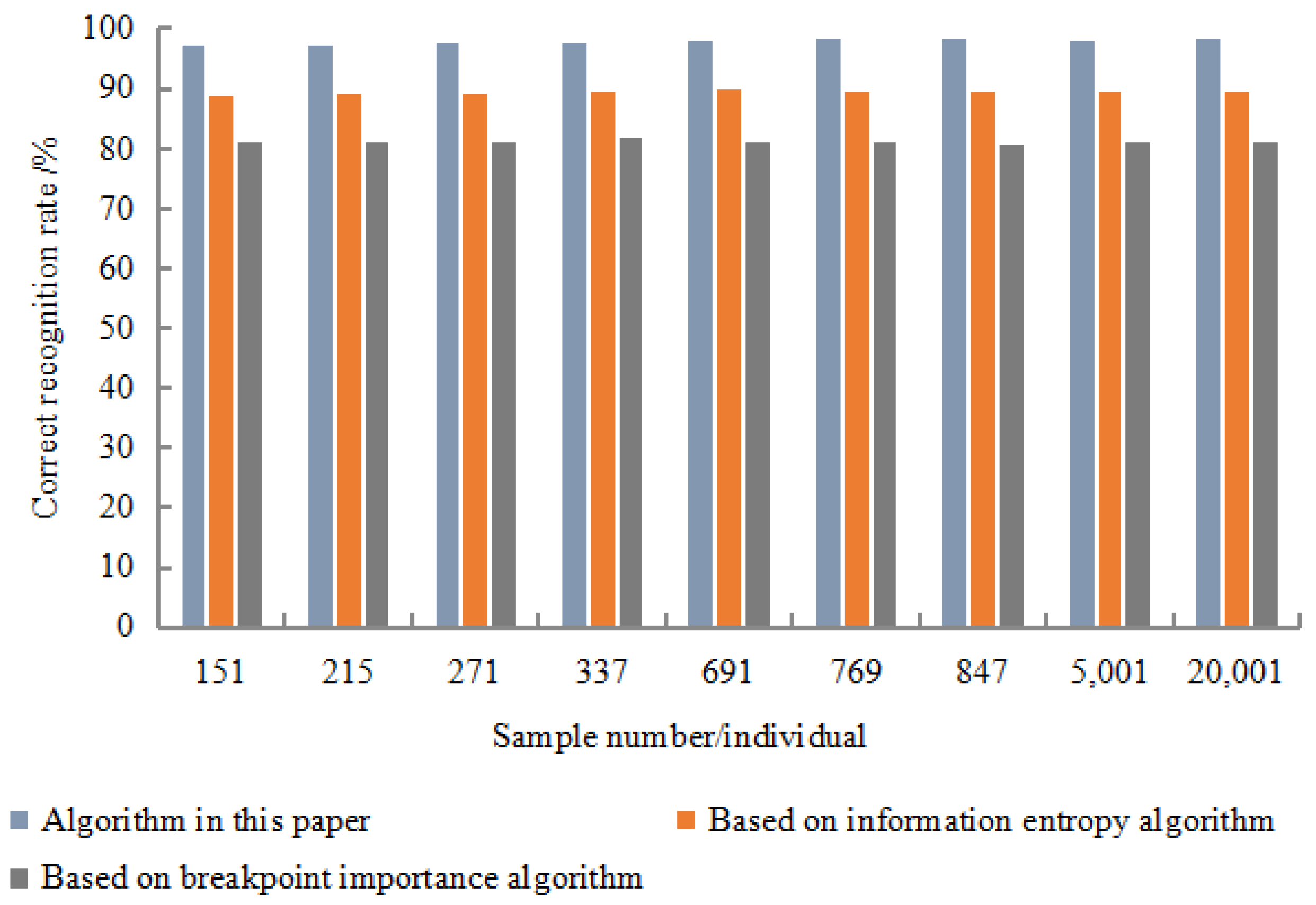
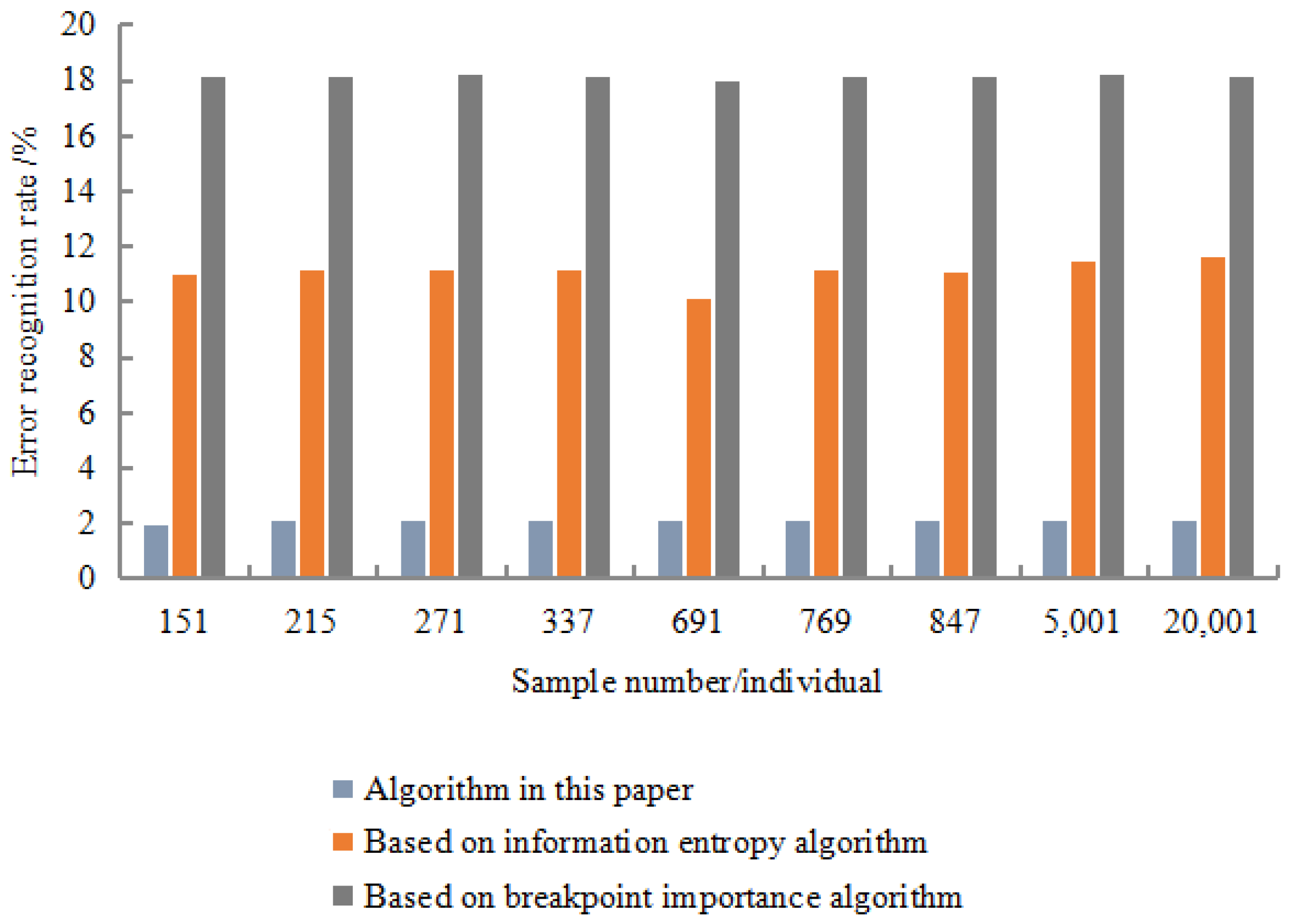
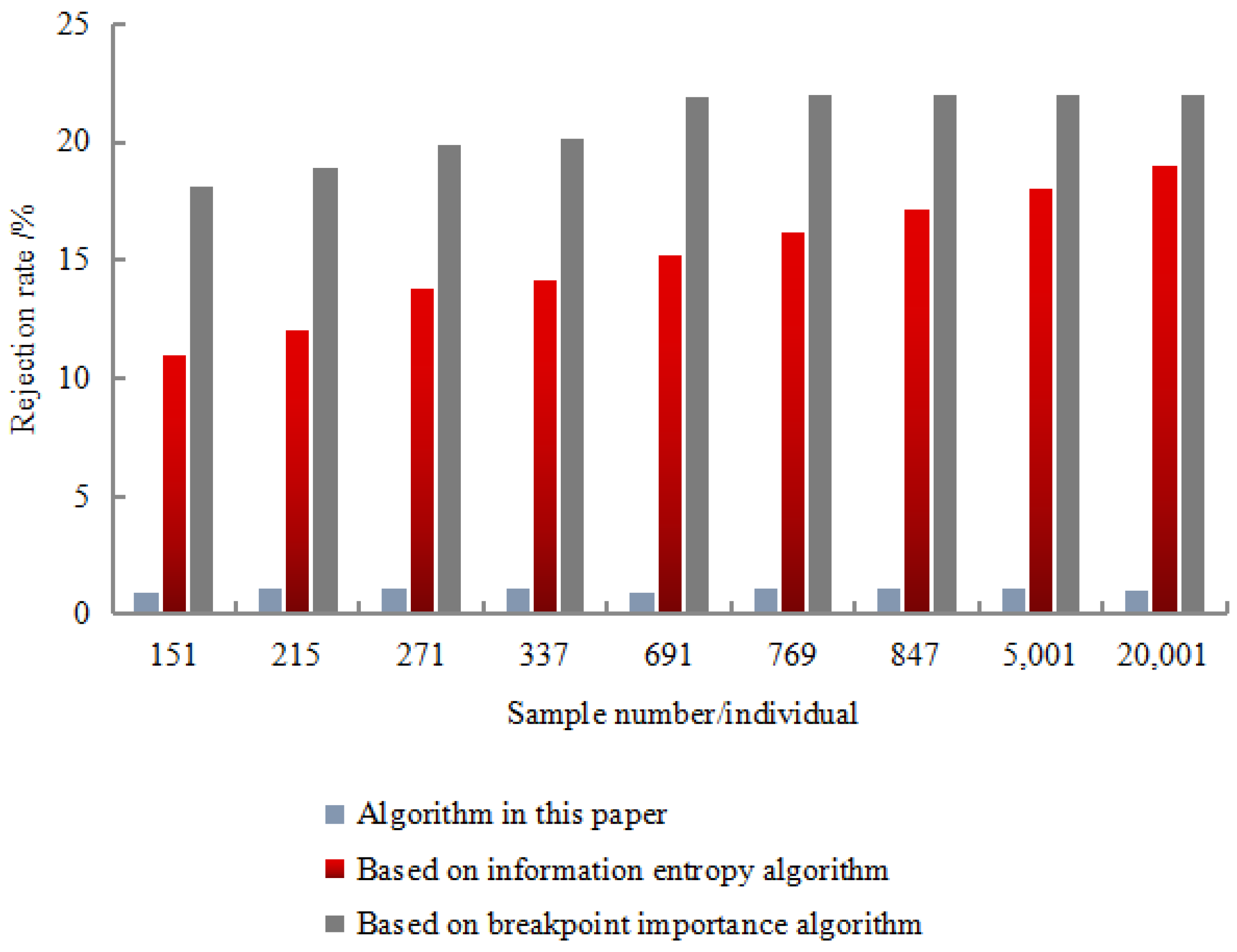
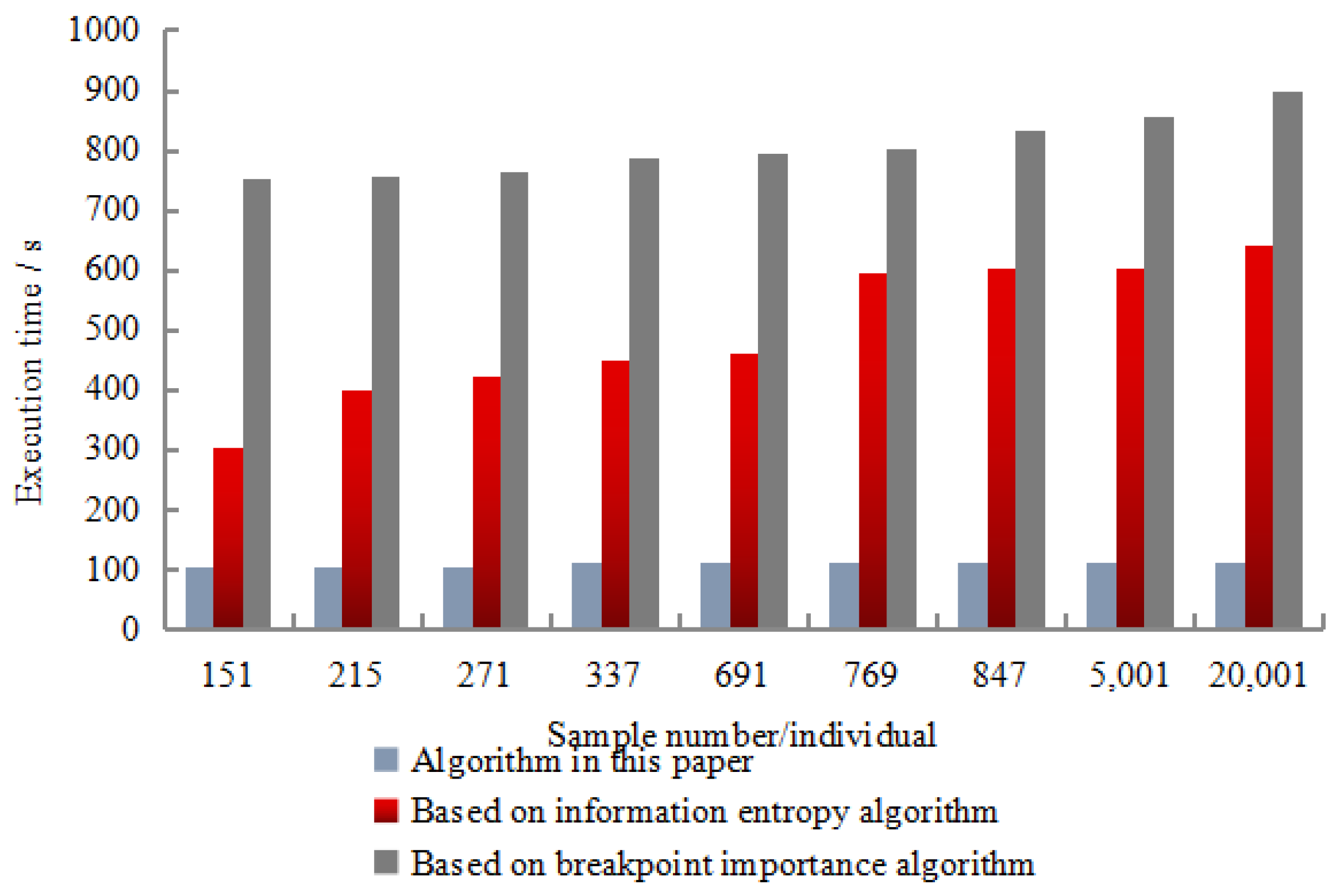
Each data set was randomly selected 50% for the learning of the training set, and the remaining 50% were identified and tested using the obtained inference rules. The recognition results are shown in
Figure 7,
Figure 8,
Figure 9 and
Figure 10.
The experimental results show that the correct recognition rate was as high as 98.67%, the error recognition rate was as low as 2.01%, and the rejection recognition rate was as low as 1.01%. In terms of calculation time, the algorithm had the shortest calculation time, and the minimum value was only 101 s. The experimental resulted show that the recognition effect of this algorithm was better than the entropy algorithm based on information and the importance algorithm of breakpoints. Moreover, it showed strong robustness in the detection resulted. This was mainly due to the discretization algorithm based on rough set breakpoint discrimination. Under the premise of maintaining the original indistinguishable relationship of decision-making system, this algorithm used as few breakpoints as possible to divide the space formed by the continuous attribute values of existing economic information.
4. Discussion
The discretization algorithm utilizes the concept of consistency level of decision system in rough set. The consistency level of the decision-making system is obtained through calculation, clustering and partitioning, and the clustering parameter factors are adjusted repeatedly to ensure the consistency level of the decision-making system. Using discriminant functions to filter candidate breakpoints is a common discretization algorithm, such as one based on the importance of breakpoints. You can distinguish the number of instances of breakpoints to measure the importance of breakpoints. The higher the value of the instance pair, the more important the breakpoint is and the more likely it is to choose a breakpoint. According to the differences of different candidate breakpoint decision-making ability, this study puts forward a rough set based on the large data incomplete economic information discretization algorithm, experimental results show that when the data deletion rate is between 1%–10%, the stable can remain above 0.8, the RMSE value stable between 0.15–0.2, shows that this algorithm for incomplete economic information filling effect is good, the main reason is that the algorithm using deep learning does not completely fill in economic information. First, a three-layer network model is constructed. The output of each layer is set as the output of the upper layer, and the upper layer is set as the acquired feature output. In the training process, network initialization parameters were extracted from the top to the bottom and all parameters were fine-tuned with the back propagation algorithm, which improved the filling effect of incomplete economic information. The correct recognition rate of the algorithm designed in this study is up to 98.67% and the error recognition rate and reject recognition rate are lower than the other two algorithms. The calculation time of the algorithm is the shortest, with the minimum value only 101 s, which indicates that the algorithm USES rough sets to realize the discretization of supplementary economic information, with high computational efficiency and recognition accuracy.
In conclusion, the effectiveness of the algorithm is verified by the experimental results the incomplete economic information has a good filling effect. When the sample size and condition attributes are large, it still has a higher computational efficiency and a higher identification accuracy, which plays an important role in improving the flow rate of economic information.
5. Conclusions
Although rough set theory has only been developed for little more than twenty years, the research results obtained are remarkable. Its successful application in the computer field (data decision and analysis, machine learning, pattern recognition, etc.) has gradually been valued. In order to make the incomplete economic information complete, improve the calculation speed and realize the accurate classification and recognition of relevant economic information, a rough set incomplete economic information discretization algorithm based on big data is proposed. First, incomplete economic information is filled in. Then the decision-making ability of candidate breakpoints is analyzed. After discretization of continuous attributes, the decision system keeps the original consistency. While keeping the original indiscernibility of decision system, the rough set is used to segment the space formed by continuous attribute values with as few breakpoints as possible, so as to accurately classify and recognize the relevant information. The experimental results show that the algorithm is effective and has high efficiency when the number of samples is great and condition attributes are large.
Due to the complexity of the actual problem, this method is not suitable for discretization of all data sets. It is necessary to continuously explore new discretization algorithms to meet the needs of different data sets. In the future—with the development of the economy and social progress—economic data are bound to grow at an alarming rate and the requirements for economic information will become more stringent, so we are bound to find a more effective way to deal with these incomplete economic information. Research must keep pace with the times, introduce more advanced technologies to fill and discretize incomplete economic information, make economic information circulation more inspiration, complete data and promote economic progress.