Abstract
A mathematical model for forecasting the transmission of the COVID-19 outbreak is proposed to investigate the effects of quarantined and hospitalized individuals. We analyze the proposed model by considering the existence and the positivity of the solution. Then, the basic reproduction number —the expected number of secondary cases produced by a single infection in a completely susceptible population—is computed by using the next-generation matrix to carry out the stability of disease-free equilibrium and endemic equilibrium. The results show that the disease-free equilibrium is locally asymptotically stable if , and the endemic equilibrium is locally asymptotically stable if . Numerical simulations of the proposed model are illustrated. The sensitivity of the model parameters is considered in order to control the spread by intervention strategies. Numerical results confirm that the model is suitable for the outbreak that occurred in Thailand.
1. Introduction
It is well-known that the world is battling with a new infectious disease, namely, a novel coronavirus disease. This disease was renamed by the WHO to COVID-19 on February 2020 [1]. The disease was first found in Wuhan, Hubei, China in December 2019. The first case was found in the Huanan seafood market, which is a seafood and wet animals market [2]. Recently, there has been no evidence to confirm the source of this disease; it may have been a bat or a pangolin [3,4,5,6], which are the most likely. Two enormous infectious disease problems have already happened earlier by a coronavirus, which are SARS-CoV in 2003 and MERS-CoV in 2012 [7,8]. The direct contact with the virus in secretion on the surfaces or breath droplets from infected humans is the main transmitted channel of COVID-19 from human to human. Moreover, vaccine and directional treatment have not been found to control the spreading of the disease.
Infected individuals have many symptoms such as cough, difficulty in breathing, and fever [9], because the respiratory system can be destroyed by a coronavirus. These outbreaks have affected people and economics around the world, since many governments used lockdown policies to reduce the spreading of the disease. Many shops, supermarkets, department stores, and public places were shut down to prevent people from contact with each other. Social distancing is used to maintain the distance between people, and to stop crowded social events.
Nowadays, the number of infected individuals is increasing every day. By data from the World Health Organization (WHO), there are a cumulative confirmed cases and deaths as of 1 June 2020 [10]. At present, the numbers have increased to a cumulative confirmed cases and deaths, reported on 12 July 2020 [11].
To understand the behavior of infectious diseases, mathematical models are investigated to predict the transmission dynamics for controlling and planning strategies [12,13,14,15]. Several pieces of research proposed mathematical models to forecast the spreading of infections such as HIV [16,17,18,19], tuberculosis [20], Ebola [21,22,23,24], Dengue [14,15,25], Zika [12,26,27], MERS [28,29,30], and SARS [29,31,32].
Since this outbreak is a global problem, there are many mathematical models to predict the behavior of transmission for COVID-19 [33]. In this paper, we develop a new system of differential equations to describe the behavior of COVID-19 transmission from human to human. We consider the dynamics of populations by using six phages of infection, these are susceptible class, latent class, infected class, quarantine class, hospitalized class, and recovery class. An analysis of the proposed model is investigated. We consider the invariant region, the existence of the solution, the positivity of the solution, equilibria, the basic reproduction number, and stability of the endemic equilibria. These help us to explain the solution to the proposed model. Moreover, we show the simulation of the solutions and analyze the sensitivity of the parameters in the model. The main contribution is related to considering many ways as much as possible. We also use the model to predict the behavior of COVID-19 for real situations in Thailand.
The remainder of this paper is structured as follows: The model formulation is introduced in Section 2, and the existence of the solution, positivity of the solution, equilibria, and stability analysis of the model is presented in Section 3. In Section 4, numerical simulations are illustrated, followed by the sensitivity analysis in Section 5. The case study of the model to fit with the actual data from Thailand is presented in Section 6. Finally, conclusions are presented in Section 7.
2. Mathematical Model
In this section, we express the model formulation of COVID-19. Based on the classical SIR model [34], SIRD model [2], SEIR model [35], and others model [36,37]—and taking into account the behavior of the COVID-19 [38]—we proposed a new epidemiology-generalized model of COVID-19 outbreak, namely, the SLIQHR (Susceptible-Latent-Infectious-Quarantine-Hospitalized-Recovery) model. We investigate the latent class and quarantine class which is not in the hospital in the model, as humans in the latent class can transmit the virus to nearby people. Moreover, we consider the parameter related to death from the infection.
The constant total population at time t, denoted by , is separated into six subpopulation classes. These are susceptible class , latent class , infectious class , quarantine class , hospitalized class , and recovery class . We have . The model under assumptions can be written by the system of ordinary differential equations as follows:
where is a recruited rate; and are the transmission coefficient per unit of time per person in the susceptible class contact with latent class and infectious class, respectively; is the transition rate (per unit time) from latent compartment L to infectious compartment I; is the transition rate (per unit time) from latent compartment L to quarantine compartment Q; k is the rate at which a human leaves the infectious class by becoming quarantine and hospitalized; is the proportion of populations infectious by becoming isolation from others; is the proportion progression from infectious class to hospitalized class; is the rate from infectious class to quarantine class; is the transition rate (per unit time) from quarantine compartment Q to recovery compartment R; is the transition rate (per unit time) from quarantine compartment Q to hospitalized compartment H; is the rate of hospitalized class H become recovery class R; is the disease induced death rate; and is the natural death rate. A flowchart of the model (1) is shown in Figure 1.
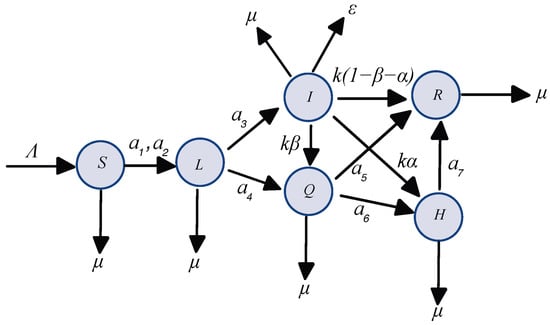
Figure 1.
Flowchart of the (Susceptible-Latent-Infectious-Quarantine-Hospitalized-Recovery) model.
3. Analysis of the Model
In this section, we study the invariant region of the solution of the proposed model (1), the positivity of the solution, and the equilibria of the model. Then, the basic reproduction number of the model is obtained. We also investigate local stability of both disease-free equilibrium and endemic equilibrium.
3.1. Invariant Region
The invariant region is obtained from the bounded situation of the model. Here, . It follows that
This inequality can be expressed in a general solution as
where is the initial values, i.e., at
Further, we can observe that as Thus, it can be concluded that is bounded as Therefore, the feasible region of the model in the non-negative region is defined as
3.2. Existence of the Solution
The existence of the solution is an important tool to confirm that the solution of the proposed model (1) exists. If the solution exists, we can find the approximate solutions or deal with its solution to forecast the dynamics of the disease transmission.
Lemma 1
(Derrick and Groosman theorem [39]). Let Ω denote the region
and suppose that satisfies the Lipchitz condition
whenever the pairs and belong to Ω where k is a positive constant. Then, there is a constant such that there exists a unique continuous vector solution of of the system in the interval .
It is important to note that the condition is satisfied by the requirement that are continuous and bounded in Ω.
Theorem 1.
The solution of the model (1) with the initial conditions exists and is unique in for all
3.3. Positivity of the Solution
Theorem 2.
The solution of the model (1) with the initial conditions is positive in for all
Proof.
Positivity of : The first equation of system (1) given by can be expressed without loss of generality as an inequality as . After applying integration by a separable method, the solution can be obtained as . We can conclude that .
Similarly, can be shown to be positive by the same procedure. Therefore, the solution of the model system (1) is a positive quantity in for all □
3.4. Equilibria
Setting all equations in the system (1) to be zero and solving all variables, we get two equilibrium points:
- (i)
- The disease-free equilibrium (DFE)
- (ii)
- The endemic equilibriumwherewith and .
3.5. The Basic Reproduction Number ()
The number of secondary infectious produced by one infectious individual in a completely susceptible population is the basic reproduction number . We determine by using the next-generation matrix [40].
The Jacobian matrices of f and v are given by F and V, respectively
and
The eigenvalues of are
Therefore, the spectral radius is .
3.6. Stability of Disease-Free Equilibrium (DFE)
Theorem 3.
The disease-free equilibrium point () is locally asymptotically stable if .
3.7. Stability of the Endemic Equilibrium
Theorem 4.
The endemic equilibrium point () exists and is locally asymptotically stable if
Proof.
The endemic equilibrium point
where
Thus, the endemic equilibrium point exists and is positive if
The Jacobian matrix of the model system (1) at is given as
The characteristic equation from equation is
where
The eigenvalues of are
and the roots of
Let us consider
then, there is no positive real root by the Descartes’ rule of signs [41] provided
This means that
Since all eigenvalues of have negative real part for , the endemic equilibrium point of the model system (1) is locally asymptotically stable if . □
4. Numerical Simulations
In this section, the numerical results of the system (1) are carried out using Matlab with the initial values:
Figure 2 shows a computer simulation of the system (1) with the parametric values , and in which . The solution trajectory tends to the disease-free equilibrium , as proved in Theorem 3.
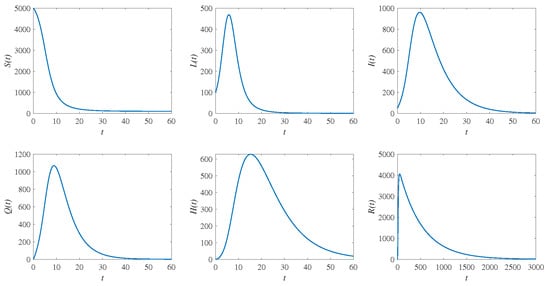
Figure 2.
Simulation results of system (1). The time series of susceptible population , latent population , infectious population , quarantine population , hospitalized population , and recovery population , respectively. The solution trajectory tends toward the disease-free equilibrium (DFE) when .
Figure 3 shows a computer simulations of the system (1) with the parametric values and in which . The solution trajectories tend to the endemic equilibrium , as proved in Theorem 4.
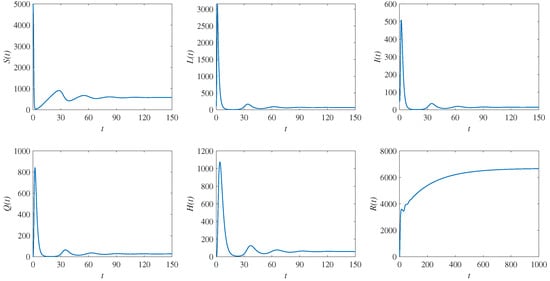
Figure 3.
Simulation results of system (1). The time series of susceptible population , latent population , infectious population , quarantine population , hospitalized population , and recovery population , respectively. The solution trajectories tend toward the endemic equilibrium when .
5. Sensitivity Analysis
We carried out sensitivity analysis [42] in order to determine the relative significance of model parameters on disease transmission. The analysis shows the impact of parameters on the basic reproduction number in order to control the spread of COVID-19 disease. The explicit expression of is given by
Since depends on eight parameters, all sensitivity indices can be carried out and expressed below:
The sensitivity indices of the basic reproduction number with respect to the parameters are shown in Table 1. The parameters that have positive indices, i.e., , have a positive effect on the basic reproduction number. It means that the increase in the number of latent population and infectious population with the rate and may lead to an outbreak. Furthermore, the parameter in which their sensitivity indices are negative, i.e., , have a negative effect to minimize the endemicity of the disease. From Table 1, we give the examples of parameters and effected on all classes as shown in Figure 4 and Figure 5, respectively.

Table 1.
Sensitivity indices table.
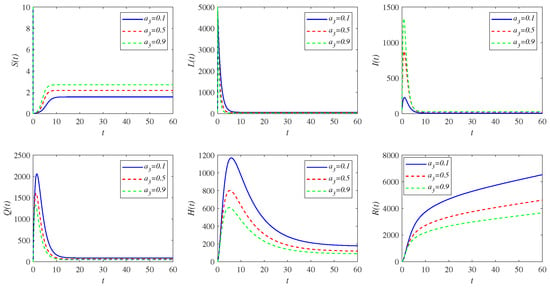
Figure 4.
Simulation results of system (1) focused on changes in the transition rate (per unit time) from latent compartment L to infectious compartment I, i.e., .
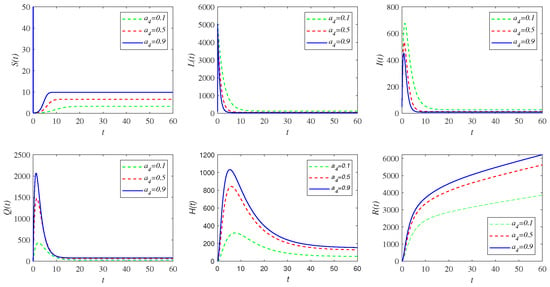
Figure 5.
Simulation results of system (1) focused on changes in the transition rate (per unit time) from latent compartment L to quarantine compartment Q, i.e., .
6. The Case Study of Thailand
In this section, the numerical simulations of the model system (1) will be compared with the real data, focused on the number of infectious individuals and the number of hospitalized individuals. The real data are taken from the Department of Disease Control, Ministry of Public Health, Thailand [43]. The confirmation of infected people is collected by COVID-19 swab test. The starting point is 3 February 2020, when the COVID-19 disease outbreak began, and the collected data end on the 158th day.
In Figure 6, the confirmed cases of infectious class simulated from the model (red solid line) fitted well to the reported COVID-19 cases data (blue circle) with . The confirmed cases of hospitalized class simulated from the model (red solid line) is nearly close to the real data (blue circle) with , as shown in Figure 7.
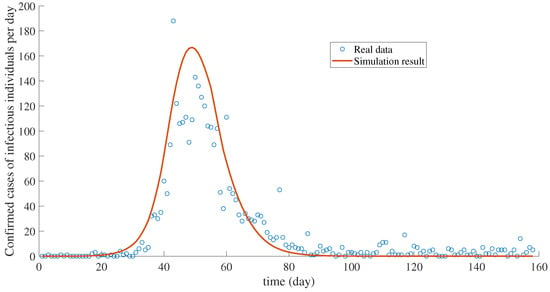
Figure 6.
The number of confirmed cases of infectious individuals per day.
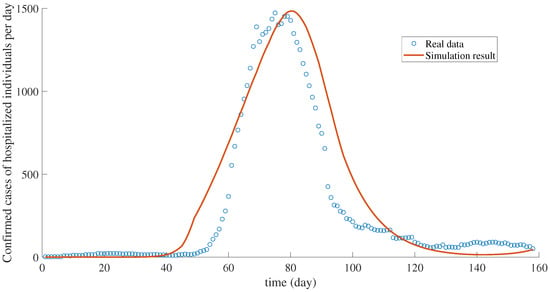
Figure 7.
The number of confirmed cases of hospitalized individuals per day.
7. Conclusions and Discussion
We have proposed the epidemiology-generalized model of COVID-19 outbreak which is composed of the susceptible , latent , infectious , quarantine , hospitalized , and recovery populations. The model is developed from the past models, for example, the SIR model and SEIR model. This outbreak has some properties different from previous SARS and MERS outbreaks. The major difference from others is the latent class. After humans get 2019-nCoV (novel coronavirus 2019), the symptoms do not appear for at least 14 days, which is a long time to transmit the virus to nearby humans. This is the major problem of COVID-19 that causes the disease to spread around the world. Our proposed model gives a fitted approximation of the data from Thailand with forecast of the confirmed infectious and hospitalized cases. The basic reproduction number which is obtained from the model analysis provides the condition for considering the stability of the equilibrium. The sensitivity analysis of the parameters in the model provides that the quarantine and hospitalized classes are the best way to control the transmission of the disease because the change of model parameters and let us know the quarantine policy is a suitable way to reduce the spreading of COVID-19 outbreak. From the results, we can say that the proposed model may be a suitable tool for predicting the outbreak.
Author Contributions
Conceptualization, D.P. and K.T.; data curation, K.T.; formal analysis, K.T.; investigation, D.P., K.T. and I.C.; methodology, I.C.; software, K.T.; resources, D.P.; validation, D.P., K.T. and I.C.; visualization, K.T. and I.C.; writing—original draft, D.P. and K.T.; writing—review & editing, I.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This research project was financially supported by Mahasarakham University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. Coronavirus Disease 2019 (Covid-19): Situation Report. Available online: https://www.who.int/dg/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020 (accessed on 1 July 2020).
- Fanelli, D.; Piazza, F. Analysis and forecast of covid-19 spreading in china, italy and france. Chaos Solitons Fractals 2020, 134, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Randhawa, G.; Soltysiak, M.; Roz, H.; de Souza, C.; Hill, K.; Kari, L. Machine learning using intrinsic genomic signatures for rapid classification of novel pathogens: Covid-19 case study. PLoS ONE 2020, 15, e0232391. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Yang, X.L.; Wang, X.G.; Hu, B.; Zhang, L.; Zhang, W.; Chen, H.D. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020, 579, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Xiao, K.; Zhai, J.; Feng, Y.; Zhou, N.; Zhang, X.; Zou, J.J.; Zhang, Z. Isolation of sars-cov-2-related coronavirus from malayan pangolins. Nature 2020, 583, 286–289. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Q.; Zhang, Z. Probable pangolin origin of sars-cov-2 associated with the Covid-19 outbreak. Curr. Biol. 2020, 134, 1–5. [Google Scholar] [CrossRef]
- World Health Organization. Consensus Document on the Epidemiology of Severe Acute Respiratory Syndrome (Sars). Available online: https://www.who.int/csr/sars/WHOconsensus.pdf (accessed on 12 July 2020).
- World Health Organization. Middle East Respiratory Syndrome Coronavirus (Mers-Cov). Available online: https://www.who.int/news-room/fact-sheets/detail/middle-east-respiratory-syndrome-coronavirus-(mers-cov) (accessed on 12 July 2020).
- Atangana, A. Modelling the spread of Covid-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef]
- World Health Organization. Coronavirus Disease 2019 (Covid-19): Situation Report. 133. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200712-covid-19-sitrep-133.pdf (accessed on 12 July 2020).
- World Health Organization. Coronavirus Disease 2019 (Covid-19): Situation Report. 174. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200712-covid-19-sitrep-174.pdf (accessed on 12 July 2020).
- Suparit, P.; Wiratsudakul, A.; Modchang, C. A mathematical model for zika virus transmission dynamics with a time-dependent mosquito biting rate. Theor. Med. Model. 2018, 15, 1–11. [Google Scholar] [CrossRef]
- Bocharov, G.; Volpert, V.; Ludewig, B.; Meyerhans, A. Mathematical Immunology of Virus Infections; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- Sardar, T.; Chattopadhyay, J. A mathematical model of dengue transmission with memory. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 511–525. [Google Scholar] [CrossRef]
- Wu, C.; Wong, P.Y. Dengue transmission: Mathematical model with discrete time delays and estimation of the reproduction number. J. Biol. Dyn. 2019, 13, 1–25. [Google Scholar] [CrossRef]
- Sazonov, I.; Grebennikov, D.; Kelbert, M.; Meyerhans, A.; Bocharov, G. Viral Infection Dynamics Model Based on a Markov Process with Time Delay between Cell Infection and Progeny Production. Mathematics 2020, 8, 1207. [Google Scholar] [CrossRef]
- Zheltkova, V.; Argilaguet, J.; Peligero, C.; Bocharov, G.; Meyerhans, A. Prediction of PD-L1 inhibition effects for HIV-infected individuals. PLoS Comput. Biol. 2019, 15, E1007401. [Google Scholar] [CrossRef]
- Shcherbatova, O.; Grebennikov, D.; Sazonov, I.; Meyerhans, A.; Bocharov, G. Modeling of the HIV-1 Life Cycle in Productively Infected Cells to Predict Novel Therapeutic Targets. Pathogens 2020, 9, 255. [Google Scholar] [CrossRef] [PubMed]
- Romanyukha, A.A.; Nosova, E.A. Modeling Spread of HIV as a Result of Social Maladjustment. Autom. Remote Control 2012, 73, 2071–2082. [Google Scholar] [CrossRef]
- Avilov, K.K.; Romanyukha, A.A.; Borisov, S.E.; Belilovsky, E.M.; Nechaeva, O.B.; Karkach, A.S. An approach to estimating tuberculosis incidence and case detection rate from routine notification data. Int. Tuberc. Lung Dis. 2015, 19, 288–294. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, K.; Li, C.; Hong, G.; Zhang, X.; Shan, M.; Li, H.; Wang, J. Mathematical models for devising the optimal ebola virus disease eradication. J. Transl. Med. 2017, 1–10. [Google Scholar] [CrossRef]
- Rhoubari, Z.; Besbassi, H.; Hattaf, K.; Yousfi, N. Mathematical modeling of ebola virus disease in bat population. J. Transl. Med. 2018, 1–7. [Google Scholar] [CrossRef]
- Berge, T.; Lubuma, J.-S.; Moremedi, G.; Morris, N.; Kondera-Shava, R. A simple mathematical model for ebola in africa. J. Biol. Dyn. 2017, 11, 42–74. [Google Scholar] [CrossRef]
- Deepa, O.S.; Nallamalli, S.; SinghNaik, L.; Teja, G. Mathematical model for transmission of ebola. Procedia Comput. Sci. 2015, 48, 741–745. [Google Scholar] [CrossRef][Green Version]
- Carvalho, S.; da Silva, S.; da Cunha Charret, I. Mathematical modeling of dengue epidemic: Control methods and vaccination strategies. Theory Biosci. 2019, 138, 223–239. [Google Scholar] [CrossRef]
- Bonyah, E.; Okosun, K. Mathematical modeling of zika virus. Asian Pac. J. Trop. Dis. 2016, 6, 673–679. [Google Scholar] [CrossRef]
- Biswas, S.; Ghosh, U.; Sarkarb, S. Mathematical model of zika virus dynamics with vector control and sensitivity analysis. Infect. Dis. Model. 2020, 5, 23–41. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Ma, W.; Bai, P. A novel dynamic model describing the spread of the mers-cov and the expression of dipeptidyl peptidase 4. Comput. Math. Methods Med. 2017, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Liang, K. Mathematical model of infection kinetics and its analysis for Covid-19, sars and mers. Infect. Genet. Evol. 2020, 82, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Lamwong, J.; Tang, I.; Pongsumpun, P. Mers model of thai and south korean population. Curr. Appl. Sci. Technol. 2018, 18, 1–13. [Google Scholar]
- Herrera, G.; Fernandez-Merodo, J.; Mulas, J.; Pastor, M. A landslide forecasting model using ground based sar data: The portalet case study. Eng. Geol. 2013, 105, 220–230. [Google Scholar] [CrossRef]
- Goulard, M.; Laurent, T.; Thomas-Agnan, C. About predictions in spatial sar models: Optimal and almost optimal strategies. Spat. Econ. Anal. 2017, 12, 304–325. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Torresa, D.M. Mathematical modeling of covid-19 transmission dynamics with a case study of wuhan. Chaos Solitons Fractals 2020, 135, 1–6. [Google Scholar] [CrossRef]
- Postnikov, E. Estimation of Covid-19 dynamics “on a back-of-envelope”: Does the simplest sir model provide quantitative parameters and predictions? Chaos Solitons Fractals 2020, 135, 109841. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J. Modeling and forecasting the covid-19 pandemic in india. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Shereen, M.; Khan, S.; Kazmi, A.; Bashir, N.; Siddique, R. Covid-19 infection: Origin, transmission, and characteristics of human coronaviruses. J. Adv. Res. 2020, 24, 91–98. [Google Scholar] [CrossRef]
- Arino, J.; Portet, S. A simple model for Covid-19. Infect. Dis. Model. 2020, 5, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Van Bavel, J.J.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Drury, J. Using social and behavioural science to support Covid-19 pandemic response. Nat. Hum. Behav. 2020, 4, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Derrick, N.; Grossman, S. Differential Equation with Application; Addision Wesley Publishing Company, Inc.: Reading, MA, USA, 1976. [Google Scholar]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Bhaskar, A.; Song, Y. Descartes’ rule of signs and the identifiability of population demographic models from genomic variation data. Ann. Stat. 2014, 42, 2469–2493. [Google Scholar] [CrossRef] [PubMed]
- Chitnisa, N.; Hymanb, J.; Cushing, J. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Ministry of Public Health, Department of Disease Control. COVID-19 Situation Reports. Available online: https://covid19.ddc.moph.go.th/en (accessed on 1 July 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).