An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots
Abstract
1. Introduction
2. Development of the Scheme
3. Generalization of the Method
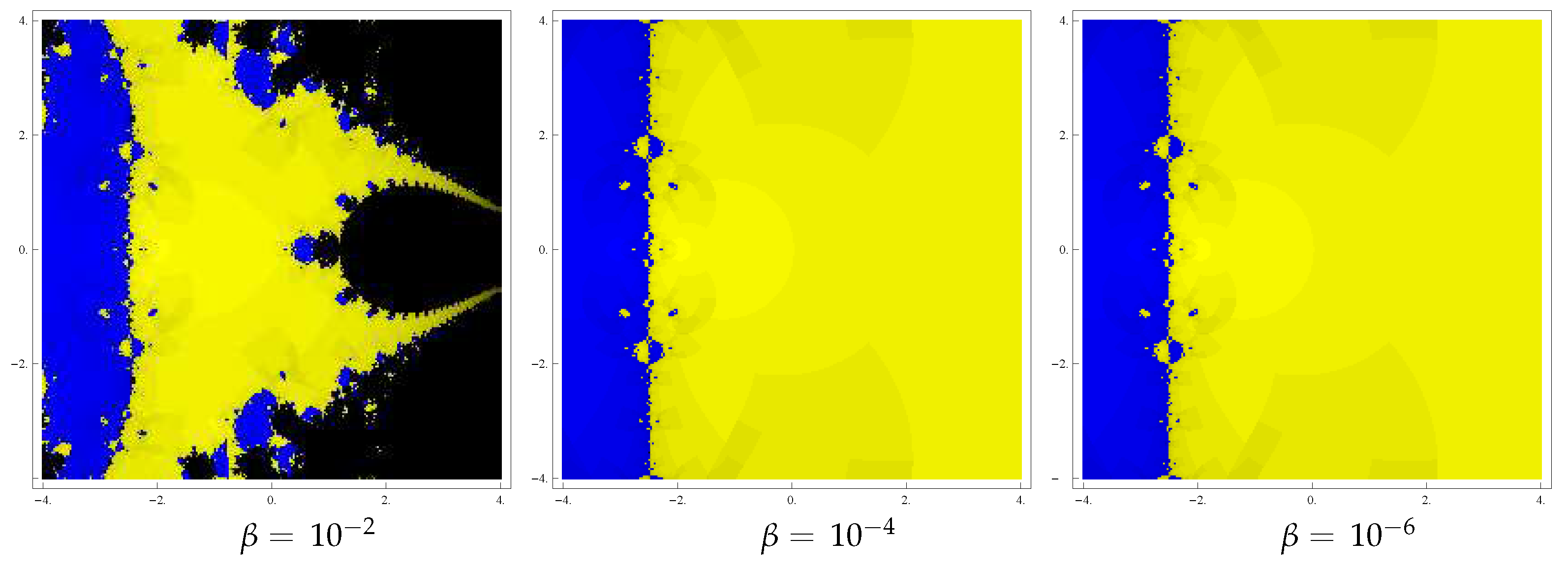
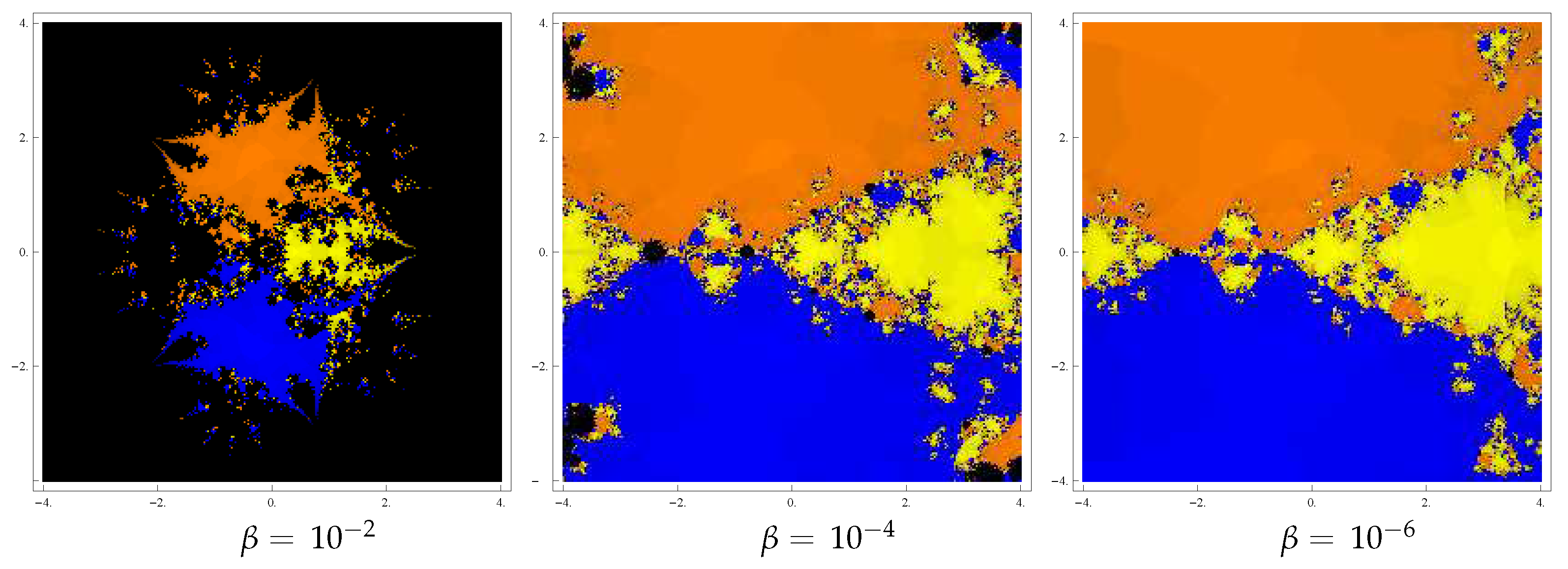
4. Basins of Attraction
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tetsuro, Y. Historical Developments in Convergence Analysis for Newton’s and Newton-Like Methods. In Numerical Analysis: Historical Developments in the 20th Century; Brezinski, C., Wuytack, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 241–263. [Google Scholar]
- Kantorovich, L.V. On Newton’s Method. In Collected Works on Approximation Analysis of the Leningrad Branch of the Institute; Trudy Mat. Inst. Steklov.; Academy of Sciences of the Soviet Union: Moscow, Russia, 1949; pp. 104–144. [Google Scholar]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008. [Google Scholar]
- Schröder, E. Über unendlich viele Algorithmen zur Auflösung der Gleichungen. Math. Ann. 1870, 2, 317–365. [Google Scholar] [CrossRef]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1977, 27, 257–269. [Google Scholar] [CrossRef]
- Dong, C. A family of multipoint iterative functions for finding multiple roots of equations. Int. J. Comput. Math. 1987, 21, 363–367. [Google Scholar] [CrossRef]
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar]
- Li, S.G.; Cheng, L.Z.; Neta, B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput. Math. Appl. 2010, 59, 126–135. [Google Scholar] [CrossRef]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 4199–4206. [Google Scholar] [CrossRef]
- Sharifi, M.; Babajee, D.K.R.; Soleymani, F. Finding the solution of nonlinear equations by a class of optimal methods. Comput. Math. Appl. 2012, 63, 764–774. [Google Scholar] [CrossRef]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 270, 387–400. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. Constructing a family of optimal eighth-order modified Newton-type multiple-zero finders along with the dynamics behind their purely imaginary extraneous fixed points. J. Comp. Appl. Math. 2018, 333, 131–156. [Google Scholar] [CrossRef]
- Kansal, M.; Kanwar, V.; Bhatia, S. On some optimal multiple root-finding methods and their dynamics. Appl. Appl. Math. 2015, 10, 349–367. [Google Scholar]
- Behl, R.; Alsolami, A.J.; Pansera, B.A.; Al-Hamdan, W.M.; Salimi, M.; Ferrara, M. A new optimal family of Schrder’s method for multiple zeros. Mathematics 2019, 7, 1076. [Google Scholar] [CrossRef]
- Behl, R.; Salimi, M.; Ferrara, M.; Sharifi, S.; Alharbi, S.K. Some real-life applications of a newly constructed derivative free iterative scheme. Symmetry 2019, 11, 239. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1982. [Google Scholar]
- Kumar, D.; Sharma, J.R.; Argyros, I.K. Optimal one-point iterative function free from derivatives for multiple roots. Mathematics 2020, 8, 709. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Jäntschi, L. On a class of optimal fourth order multiple root solvers without using derivatives. Symmetry 2019, 11, 1452. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Argyros, I.K. Development of optimal eighth order derivative-free methods for multiple roots of nonlinear equations. Symmetry 2019, 11, 766. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Vrscay, E.R.; Gilbert, W.J. Extraneous fixed points, basin boundaries and chaotic dynamics for Schröder and König rational iteration functions. Numer. Math. 1988, 52, 1–16. [Google Scholar] [CrossRef]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–46. [Google Scholar] [CrossRef]
- Jézéquel, F. Dynamical Control of Approximation Methods; Habilitationa diriger des recherches, Universit Pierre et Marie Curie: Paris, France, 2005. [Google Scholar]
- Chand, P.B.; Chicharro, F.I.; Jain, P. Optimal fourth-order Weerakoon-Fernando-type methods for multiple roots and their dynamics. Mediterr. J. Math. 2019, 16, 67. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Magreñán, Á.A. A study of dynamics via Möbius conjugacy map on a family of sixth-order modified Newton-like multiple-zero finders with bivariate polynomial weight functions. J. Comput. Appl. Math. 2018, 344, 608–623. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.; Torregrosa, J.R. On developing fourth-order optimal families of methods for multiple roots and their dynamics. Appl. Math. Comput. 2018, 265, 520–532. [Google Scholar] [CrossRef]
- Sidorov, N.; Sidorov, D.; Li, Y. Basins of attraction and stability of nonlinear systems’ equilibrium points. Differ. Equ. Dyn. Syst. 2019. [Google Scholar] [CrossRef]
- Neta, B.; Scott, M.; Chun, C. Basin attractors for various methods for multiple roots. App. Math. Comp. 2012, 218, 5043–5066. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newtons method using fifth order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; McGraw-Hill Book Company: New York, NY, USA, 1992. [Google Scholar]
| Methods | k | ACOC | CPU | |||
|---|---|---|---|---|---|---|
| LM−1 | 6 | 4.000 | 0.0776 | |||
| LM−2 | 6 | 4.000 | 0.0942 | |||
| SSM | 6 | 4.000 | 0.0782 | |||
| ZM | 6 | 4.000 | 0.0634 | |||
| SM | 6 | 4.000 | 0.0935 | |||
| KM | 6 | 4.000 | 0.0624 | |||
| SM−1 | 6 | 4.000 | 0.0724 | |||
| SM−2 | 6 | 4.000 | 0.0745 | |||
| NM | 5 | 4.000 | 0.0615 |
| Methods | k | ACOC | CPU | |||
|---|---|---|---|---|---|---|
| LM−1 | 4 | 4.000 | 0.8274 | |||
| LM−2 | 4 | 4.000 | 1.1072 | |||
| SSM | 4 | 4.000 | 1.1076 | |||
| ZM | 4 | 4.000 | 1.1066 | |||
| SM | 4 | 4.000 | 1.2947 | |||
| KM | 4 | 4.000 | 1.0952 | |||
| SM−1 | 3 | 0 | 4.000 | 0.3284 | ||
| SM−2 | 3 | 0 | 4.000 | 0.3375 | ||
| NM | 3 | 0 | 4.000 | 0.3124 |
| Methods | k | ACOC | CPU | |||
|---|---|---|---|---|---|---|
| LM−1 | 4 | 4.000 | 1.6382 | |||
| LM−2 | 4 | 4.000 | 1.7935 | |||
| SSM | 4 | 4.000 | 1.9031 | |||
| ZM | 4 | 4.000 | 1.8720 | |||
| SM | 4 | 4.000 | 1.9655 | |||
| KM | 4 | 4.000 | 1.9026 | |||
| SM−1 | 4 | 4.000 | 1.4802 | |||
| SM−2 | 4 | 4.000 | 1.4922 | |||
| NM | 4 | 4.000 | 1.4656 |
| Methods | k | ACOC | CPU | |||
|---|---|---|---|---|---|---|
| LM−1 | 4 | 4.000 | 1.4512 | |||
| LM−2 | 4 | 4.000 | 2.2314 | |||
| SSM | 4 | 4.000 | 2.2615 | |||
| ZM | 4 | 4.000 | 2.3088 | |||
| SM | 4 | 4.000 | 2.7610 | |||
| KM | 4 | 4.000 | 2.2926 | |||
| SM−1 | 4 | 4.000 | 0.7223 | |||
| SM−2 | 4 | 4.000 | 0.7407 | |||
| NM | 4 | 4.000 | 0.5931 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Kumar, D.; Sharma, J.R.; Cesarano, C.; Agarwal, P.; Chu, Y.-M. An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots. Symmetry 2020, 12, 1038. https://doi.org/10.3390/sym12061038
Kumar S, Kumar D, Sharma JR, Cesarano C, Agarwal P, Chu Y-M. An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots. Symmetry. 2020; 12(6):1038. https://doi.org/10.3390/sym12061038
Chicago/Turabian StyleKumar, Sunil, Deepak Kumar, Janak Raj Sharma, Clemente Cesarano, Praveen Agarwal, and Yu-Ming Chu. 2020. "An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots" Symmetry 12, no. 6: 1038. https://doi.org/10.3390/sym12061038
APA StyleKumar, S., Kumar, D., Sharma, J. R., Cesarano, C., Agarwal, P., & Chu, Y.-M. (2020). An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots. Symmetry, 12(6), 1038. https://doi.org/10.3390/sym12061038






