New Uniform Motion and Fermi–Walker Derivative of Normal Magnetic Biharmonic Particles in Heisenberg Space

Abstract

In the present paper, we firstly discuss the normal biharmonic magnetic particles in the Heisenberg space. We express new uniform motions and its properties in the Heisenberg space. Moreover, we obtain a new uniform motion of Fermi–Walker derivative of normal magnetic biharmonic particles in the Heisenberg space. Finally, we investigate uniformly accelerated motion (UAM), the unchanged direction motion (UDM), and the uniformly circular motion (UCM) of the moving normal magnetic biharmonic particles in Heisenberg space.

1. Introduction

In relativistic physics, mathematical description of the motion of the particle is given by its kinematics. Kinematic features of a particle moving through a continuous, differentiable curve or geometric features of the curve itself in space are mostly described by the moving orthogonal frame such as Frenet–Serret frame, parallel frame, rotation minimizing frame, etc. Generally, the factors affecting this motion are not discussed with the exception of projectiles and falling bodies. These studies have been recently improved by considering the quantities that influence the motion, i.e., mass and force. Thus, dynamics of the motion of the particle can be discussed by using the mathematical description and geometric characterization in a given space [1,2].

The description of UAM in relativity has been reviewed and the concept of a UAM of a viewer in standard space time is investigated in-depth in [3]. Approach to the viewer may be noticed as a Lorentzian, offering a different construction of a stationary regular space. The trajectories of UAM are shown as the prolongation on the space time of some integral curves of the new vector field defined on a convinced fiber bundle in the space time.

Therefore, they found a new geometric approach to provide that an inextensible UAM viewer does not abandon in a limited appropriate time. The investigation of these motions has an observed technological and physical fascinate because they correlate to the orbits of some artificial satellites, planets or stars.

The notion of the UAM was analyzed in detail by giving its novel geometric characterization by Fuente and Romero [4]. The description of the unchanged direction motion (UDM) was presented by extending the UAM by Fuente, Romero, and Torres [5]. The intrinsic definition of the uniformly circular motion (UCM) was given by Fuente, Romero, and Torres as a particular case of a planar motion [5].

Practically, essential details of the Landau–Hall structure are obtained as among the additional solution individuals of the Lorentz force formulation. Hence, this as well indicates that magnetic particles are utilized to resolve a variational issue [6,7,8,9].

As it can be seen in the literature, the major patterns to be taken into account were the situations of magnetic curves in Riemannian spaces and in Riemannian surfaces of constant sectional curvature consecutively regarding situations of less simple curvature, different signatures, and higher dimensions [10,11,12,13].

Research on magnetic particles have been concentrated on a shifting charged particle, which usually is free of any kind of exterior force within its motion, in a connected magnetic field [14,15,16,17]. On the other hand, this is genuine to presume that there could possibly be a few exterior forces impacting the tendencies of the particle including gravitational force, frictional force, normal force, etc. Simply by encouraged this point, we research new uniform motion of velocity magnetic biharmonic particles and some vector fields with Fermi–Walker derivative in Heisenberg space. In [18], we already characterized the frictional magnetic curves on a 3-dimensional Riemannian manifold by providing a straightforward exposition of physical modeling of special magnetic trajectories. Considering the Riemannian geometry and standard methods of differential geometry, we aim to investigate another significant magnetic trajectories on the 3D Riemannian manifold.

2. The Heisenberg Group and Magnetic Particles

Heisenberg group with 3-dimension can easily be mentioned as ${\mathbb{R}}^3$ offered by way of the subsequent multiplication:

$$(\overline{x},\overline{y},\overline{z})(x,y,z)=(\overline{x}+x,\overline{y}+y,\overline{z}+z-\frac{1}{2}\overline{x}y+\frac{1}{2}x\overline{y}).$$

A basis of left invariant vector fields is presented by simply

$$\begin{array}{ccc}\hfill {\mathbf{e}}_1& =& \frac{\partial }{\partial x},\hfill \\ \hfill {\mathbf{e}}_2& =& \frac{\partial }{\partial y}+x\frac{\partial }{\partial z},\hfill \\ \hfill {\mathbf{e}}_3& =& \frac{\partial }{\partial z}.\hfill \end{array}$$

The only non-trivial bracket relations are

$$[{\mathbf{e}}_1,{\mathbf{e}}_2]={\mathbf{e}}_3.$$

We will construct Riemannian metric

$$g_h={(dx)}^2+{(dy)}^2+{(dz-xdy)}^2.$$

The Levi–Civita connection in the Heisenberg group is defined by D. Koszul formula and the Lie bracket relations we obtain

$$\begin{array}{ccc}\hfill {\nabla }_{{\mathbf{e}}_1}{\mathbf{e}}_1& =& {\nabla }_{{\mathbf{e}}_2}{\mathbf{e}}_2={\nabla }_{{\mathbf{e}}_3}{\mathbf{e}}_3=0,\hfill \\ \hfill {\nabla }_{{\mathbf{e}}_1}{\mathbf{e}}_2& =& -{\nabla }_{{\mathbf{e}}_2}{\mathbf{e}}_1=\frac{1}{2}{\mathbf{e}}_3,\hfill \\ \hfill {\nabla }_{{\mathbf{e}}_1}{\mathbf{e}}_3& =& {\nabla }_{{\mathbf{e}}_3}{\mathbf{e}}_1=-\frac{1}{2}{\mathbf{e}}_2,\hfill \\ \hfill {\nabla }_{{\mathbf{e}}_2}{\mathbf{e}}_3& =& {\nabla }_{{\mathbf{e}}_3}{\mathbf{e}}_2=\frac{1}{2}{\mathbf{e}}_1.\hfill \end{array}$$

A magnetic field $\mathcal{B}$ defined on manifold $\left(M^n,g\right)$ is a 2 form such that its new Lorentz force is a new field $\varphi$ presented by

$$\begin{array}{cc}\mathcal{B}(\mathcal{Y},\mathcal{X})=g(\varphi (\mathcal{Y}),\mathcal{X}),& \forall \mathcal{Y},\mathcal{X}\in X(M^n).\end{array}$$

From Levi–Civita connection, magnetic particles $\zeta$ satisfies

$${\nabla }_{{\zeta }^{\prime }}{\zeta }^{\prime }=\varphi ({\zeta }^{\prime }).$$

Also [2], Lorentz force $\varphi$ can be presented by

$$\varphi (\mathcal{Y})=\mathcal{B}\times \mathcal{Y}.$$

Let $\alpha$ be a regular biharmonic particle and $\mathcal{B}$ be a magnetic field in Heisenberg space. We call the particle $\alpha$ a normal biharmonic magnetic particle, if the normal field of the particle satisfies the following Lorenz equation

$${\nabla }_{s}N=\varphi (N)=\mathcal{B}\times N.$$

3. Uniform Motion for Normal Biharmonic Magnetic Particles

In this part, we characterize the uniformly motion of moving charged particles with unit speed velocity magnetic biharmonic particles. We obtain necessary and sufficient provisions that have to be satisfied with the biharmonic particle with Frenet curvatures of world line of magnetic particles. We present the following definitions of UDM, UAM, and UCM [19,20].

Definition 1.

Let${\nabla }_s^{fw}$ be Fermi–Walker derivative associated with Levi Civita connection ∇ of h. Fermi–Walker derivative is defined by

$${\nabla }_s^{fw}\mathcal{R}={\nabla }_s\mathcal{R}-h\left(\mathbf{T},\mathcal{R}\right){\nabla }_s\mathbf{T}+h({\nabla }_s\mathbf{T},\mathcal{R})\mathbf{T},$$

where $\mathcal{R}$ is any vector field along with the particle, h is metric, T is the tangent field, ∇ is the derivative operator [20].

Definition 2.

The field $\mathbf{X}$ observes a UAM iff

$${\nabla }_s^{fw}({\nabla }_s\mathbf{X})=0.$$

Definition 3.

The field $\mathbf{X}$ observes a UDM iff

$${\left|{\nabla }_s\mathbf{X}\right|}^2=constant,$$

and

$${\left|{\nabla }_s^{fw}({\nabla }_s\mathbf{X})\right|}^2=constant.$$

Definition 4.

The field $\mathbf{X}$ observes a UCM iff

$${\nabla }_s^{fw}({\left|{\nabla }_s\mathbf{X}\right|}^{-1}{\nabla }_s\mathbf{X})=0.$$

Lemma 1.

$\varphi \left(\mathbf{T}\right)$ is Fermi–Walker parallel iff

$$\begin{array}{c}(\frac{\delta \omega +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2(\upsilon +{\mathsf{\Phi }}^0)]-\frac{\chi \delta }{2\omega }sin2\mathsf{\Phi }{ϝ}^2)=0,\\ (-\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]+\frac{\chi \delta }{\omega }ϝsin\mathsf{\Phi }({\mathsf{\Phi }}^0+\upsilon ))=0,\\ (-\frac{\omega \delta +{\chi }^{\prime }}{\omega }[\upsilon ϝsin\mathsf{\Phi }({\mathsf{\Phi }}^0+\upsilon )+\frac{1}{2}cos\mathsf{\Phi }sin2\mathsf{\Phi }{ϝ}^3]-\frac{\chi \delta }{\omega }{\mathsf{\Phi }}^0ϝcos\mathsf{\Phi })=0,\end{array}$$

where $ϝ=sin\varrho ,\nu =cos\varrho .$

Proof. 

Fermi–Walker definition of $\varphi \left(\mathbf{T}\right)$ is obtained by

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}\varphi \left(\mathbf{T}\right)& =& (\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]\hfill \\ & & -\frac{\chi \delta }{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }){\mathbf{e}}_1+(-\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\hfill \\ & & -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]+\frac{\chi \delta }{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )){\mathbf{e}}_2\hfill \\ & & +(-\frac{\omega \delta +{\chi }^{\prime }}{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }\hfill \\ & & \times {ϝ}^{3}sin\mathsf{\Phi }(s)]-\frac{\chi \delta }{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ){\mathbf{e}}_3.\hfill \end{array}$$

It provides us the theorem. □

Lemma 2.

$\varphi \left(\mathbf{N}\right)$ is Fermi–Walker parallel iff

$$\begin{array}{c}(\frac{\delta }{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-\omega \upsilon -\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi })=0\\ (-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]-\omega ϝcos\mathsf{\Phi }+\frac{{\delta }^2}{\omega }ϝsin\mathsf{\Phi }({\mathsf{\Phi }}^0+\upsilon ))=0\\ (-\frac{\delta }{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }]-\omega sin\mathsf{\Phi }ϝ-{\mathsf{\Phi }}^0ϝcos\mathsf{\Phi })=0.\end{array}$$

Proof. 

Fermi–Walker derivative of $\varphi \left(\mathbf{N}\right)$ is given by

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}\varphi \left(\mathbf{N}\right)& =& (\frac{\delta }{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-\omega \upsilon \hfill \\ & & -\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }){\mathbf{e}}_1+(-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\hfill \\ & & -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]-\omega cos\mathsf{\Phi }ϝ+\frac{{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0\hfill \\ & & +\upsilon )){\mathbf{e}}_2+(-\frac{\delta }{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^3\hfill \\ & & \times sin\mathsf{\Phi }]-\omega sin\mathsf{\Phi }ϝ-\frac{{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ){\mathbf{e}}_3.\hfill \end{array}$$

By using parallelism we obtain lemma. □

Lemma 3.

$\varphi \left(\mathbf{B}\right)$ is Fermi–Walker parallel iff

$$\begin{array}{c}(\frac{-{\delta }^2}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-{\chi }^{\prime }\upsilon )=0\\ (\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]-{\chi }^{\prime }cos\mathsf{\Phi }ϝ)=0\\ (\frac{{\delta }^2}{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]-{\chi }^{\prime }sin\mathsf{\Phi }ϝ)=0\end{array}$$

Proof. 

From Fermi–Walker derivative we have following.

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}\varphi \left(\mathbf{B}\right)& =& (\frac{-{\delta }^2}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-{\chi }^{\prime }\upsilon ){\mathbf{e}}_1\hfill \\ & & +(\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]-{\chi }^{\prime }cos\mathsf{\Phi }ϝ){\mathbf{e}}_2\hfill \\ & & +(\frac{{\delta }^2}{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]-{\chi }^{\prime }sin\mathsf{\Phi }ϝ){\mathbf{e}}_3.\hfill \end{array}$$

This completes the proof. □

3.1. Uniformly Accelerated Motion (UAM)

In this detail, we recognize UAM in Heisenberg space.

$\varphi \left(\mathbf{T}\right)$ observes UAM iff

$$\begin{array}{c}(\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]\\ -\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime }))cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi })=0,\\ (-\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]\\ +\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime }))sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon ))=0,\\ (-\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }\\ \times {ϝ}^{3}sin\mathsf{\Phi }]-\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime })){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ)=0.\end{array}$$

By using the Fermi–Walker derivative and the following equation we have the above system.

$$\begin{array}{ccc}\hfill {\nabla }_s\varphi \left(\mathbf{T}\right)& =& (-{\omega }^2\upsilon -\frac{\chi \delta }{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }+\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\hfill \\ & & +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]){\mathbf{e}}_1+(-{\omega }^{2}cos\mathsf{\Phi }(s)ϝ+\frac{\chi \delta }{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0\hfill \\ & & +\upsilon )-\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]){\mathbf{e}}_2\hfill \\ & & -({\omega }^{2}sin\mathsf{\Phi }ϝ+\frac{\chi \delta }{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{\omega \delta +{\chi }^{\prime }}{\omega }[\upsilon sin\mathsf{\Phi }\hfill \\ & & \times ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]){\mathbf{e}}_3.\hfill \end{array}$$

This gives us the subsequent equation

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}{\nabla }_s\varphi \left(\mathbf{T}\right)& =& (\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-\frac{1}{\omega }(\delta {\chi }^{\prime }\hfill \\ & & +\delta (\omega \delta +{\chi }^{\prime }))cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }){\mathbf{e}}_1+(-\frac{1}{\omega }({\chi }^{\prime \prime }-\chi {\delta }^2)[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\hfill \\ & & -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]+\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime }))sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )){\mathbf{e}}_2\hfill \\ & & +(-\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }\hfill \\ & & \times {ϝ}^{3}sin\mathsf{\Phi }]-\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime })){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ){\mathbf{e}}_3.\hfill \end{array}$$

The $\varphi \left(\mathbf{N}\right)$ observes a UAM iff

$$\begin{array}{c}(-\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta \times [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )])=0,\\ (\frac{{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }])=0,\\ (-\frac{{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }])=0.\end{array}$$

By using Fermi–Walker derivative and following equation we have above system.

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}{\nabla }_s\varphi \left(\mathbf{N}\right)& =& (-\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0\hfill \\ & & +\upsilon )]){\mathbf{e}}_1+(\frac{{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\hfill \\ & & -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]){\mathbf{e}}_2+(-\frac{{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [\upsilon sin\mathsf{\Phi }\hfill \\ & & \times ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]){\mathbf{e}}_3.\hfill \end{array}$$

The $\varphi \left(\mathbf{B}\right)$ observes a UAM iff

$$\begin{array}{c}({\chi }^{″}\upsilon +\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\chi \delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\\ +{sin}^2\mathsf{\Phi }{sin}^2\varrho ({\mathsf{\Phi }}^0+\upsilon )])=0,\\ ({\chi }^{″}cos\mathsf{\Phi }ϝ-\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )\\ +\chi \delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }])=0,\\ ({\chi }^{″}sin\mathsf{\Phi }ϝ+\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\chi \delta [\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0\\ +\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }])=0.\end{array}$$

From the Fermi–Walker derivative and the following equation, we have the above system.

$$\begin{array}{ccc}\hfill {\nabla }_s^{fw}{\nabla }_s\varphi \left(\mathbf{B}\right)& =& ({\chi }^{″}\upsilon +\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\chi \delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\hfill \\ & & +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]){\mathbf{e}}_1+({\chi }^{″}cos\mathsf{\Phi }ϝ-\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)\hfill \\ & & \times sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\chi \delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3\hfill \\ & & \times {sin}^2\mathsf{\Phi }]){\mathbf{e}}_2+({\chi }^{″}sin\mathsf{\Phi }ϝ+\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\chi \delta [\upsilon \hfill \\ & & \times sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]){\mathbf{e}}_3.\hfill \end{array}$$

Figure 1 demonstrates the magnetic trajectories of N-magnetic particle with UAM.

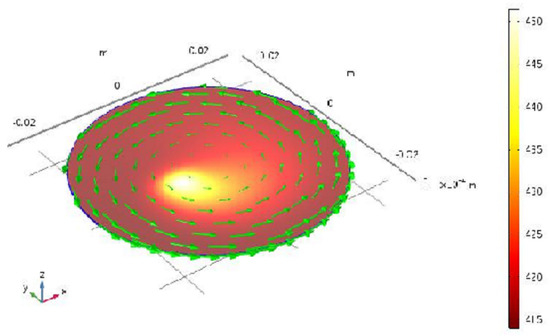
Figure 1. Magnetic trajectories of the N-magnetic particle with UAM.

3.2. Unchanged Direction Motion (UDM)

In this detail, we recognize UDM in Heisenberg space.

$\varphi \left(\mathbf{T}\right)$ observes UDM iff

$$\begin{array}{c}(-{\omega }^2\upsilon -\frac{\chi \delta }{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }+\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0\\ +{\upsilon )])}^2+(-{\omega }^{2}cos\mathsf{\Phi }ϝ+\frac{\chi \delta }{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )\\ -\frac{\omega \delta +{\chi }^{\prime }}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]{)}^2+({\omega }^{2}sin\mathsf{\Phi }ϝ\\ +\frac{\chi \delta }{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{\omega \delta +{\chi }^{\prime }}{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]{)}^2=r_1,\end{array}$$

and

$$\begin{array}{c}(\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]-\frac{1}{\omega }(\delta {\chi }^{\prime }\\ +\delta (\omega \delta +{\chi }^{\prime }))cos\mathsf{\Phi }{ϝ}^2{sin\mathsf{\Phi })}^2+(-\frac{1}{\omega }({\chi }^{\prime \prime }-\chi {\delta }^2)[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\\ -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }{]+\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime }))sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon ))}^2\\ +(-\frac{1}{\omega }({\chi }^{″}-\chi {\delta }^2)[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]\\ -\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime })){\mathsf{\Phi }}^0{cos\mathsf{\Phi }ϝ)}^2=r_2,\end{array}$$

where $r_1,r_2$ are constants.

The $\varphi \left(\mathbf{N}\right)$ observes a UDM iff

$$\begin{array}{c}(\omega \upsilon +\frac{{\omega }^2+{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }(s)-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0\\ +{\upsilon )])}^2+(\frac{{\omega }^2+{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )-\omega cos\mathsf{\Phi }ϝ-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon \\ \times cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2{\mathsf{\Phi }])}^2+(\omega sin\mathsf{\Phi }ϝ+\frac{{\omega }^2+{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ\\ +\frac{\delta }{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]{)}^2=r_3,\end{array}$$

and

$$\begin{array}{c}(-\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0\\ +{\upsilon )])}^2+(\frac{{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0ϝ\upsilon \\ \times cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2{\mathsf{\Phi }])}^2+(-\frac{{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{1}{\omega }({\omega }^2\\ +{\delta }^2{)\delta [\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }])}^2=r_4,\end{array}$$

where $r_3,r_4$ are constants.

The $\varphi \left(\mathbf{B}\right)$ observes a UDM iff

$$\begin{array}{c}((-{\chi }^{\prime }+\omega \delta )\upsilon -\chi cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\\ +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon ){])}^2+((-{\chi }^{\prime }+\omega \delta )cos\mathsf{\Phi }ϝ\\ +\chi sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\\ -cos\mathsf{\Phi }{ϝ}^3{sin}^2{\mathsf{\Phi }])}^2+((-{\chi }^{\prime }+\omega \delta )sin\mathsf{\Phi }ϝ-\chi {\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ\\ +\frac{{\delta }^2}{\omega }{[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi })}^2=r_5,\end{array}$$

and

$$\begin{array}{c}({\chi }^{″}\upsilon +\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\chi \delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\\ +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon ){])}^2+({\chi }^{″}cos\mathsf{\Phi }ϝ-\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0\\ +\upsilon )+\chi \delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]{)}^2\\ +({\chi }^{″}sin\mathsf{\Phi }ϝ+\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\chi \delta [\upsilon sin\mathsf{\Phi }\\ ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }{])}^2=r_6,\end{array}$$

where $r_5,r_6$ are constants.

Figure 2 demonstrates the magnetic trajectories of N-magnetic particle with UDM.

$$\begin{array}{c}ϝ({\mathsf{\Phi }}^0+\upsilon )\\ +{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]-\frac{1}{\omega }(\delta {\chi }^{\prime }+\delta (\omega \delta +{\chi }^{\prime })){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ))=0,\end{array}$$

where $\vartheta ={\left|{\nabla }_s\varphi \left(\mathbf{T}\right)\right|}^{-1}.$

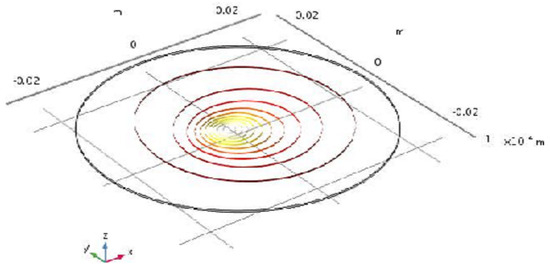
Figure 2. Magnetic trajectories of the N-magnetic particle with UAM.

The $\varphi \left(\mathbf{N}\right)$ observes a UCM iff

$$\begin{array}{c}(-{\psi }^{\prime }(\omega \upsilon +\frac{{\omega }^2+{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\\ +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )])+\psi (-\frac{{\delta }^2}{\omega }cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }\\ -\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2+{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]))=0,\\ +({\psi }^{\prime }(\frac{{\omega }^2+{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )-\omega cos\mathsf{\Phi }ϝ-\frac{\delta }{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\\ -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }])+\psi (\frac{{\delta }^2}{\omega }sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )\\ +\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]))=0,\\ +(-{\psi }^{\prime }(\omega sin\mathsf{\Phi }ϝ+\frac{{\omega }^2+{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{\delta }{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )\\ +{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }])+\psi (-\frac{{\delta }^2}{\omega }{\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ\\ +\frac{1}{\omega }({\omega }^2+{\delta }^2)\delta [\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]))=0,\end{array}$$

where $\psi ={\left|{\nabla }_s\varphi \left(\mathbf{N}\right)\right|}^{-1}.$ Figure 3 demonstrates the magnetic trajectories of N-magnetic particle with UCM.

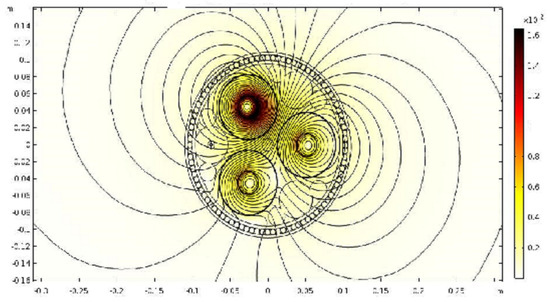
Figure 3. Magnetic trajectories of the N- magnetic particle with UDM.

The $\varphi \left(\mathbf{B}\right)$ observes a UCM iff

$$\begin{array}{c}({\chi }^{\prime }((-{\chi }^{\prime }+\omega \delta )\upsilon -\chi cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }-\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{ϝ}^2\\ +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )])+\chi ({\chi }^{″}\upsilon +\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)cos\mathsf{\Phi }{ϝ}^{2}sin\mathsf{\Phi }\\ -\chi \delta [{\mathsf{\Phi }}^0{cos}^2\mathsf{\Phi }{sin}^2\varrho +{sin}^2\mathsf{\Phi }{ϝ}^2({\mathsf{\Phi }}^0+\upsilon )]))=0,\\ +({\chi }^{\prime }((-{\chi }^{\prime }+\omega \delta )cos\mathsf{\Phi }ϝ+\chi sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+\frac{{\delta }^2}{\omega }[{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }\\ -cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }])+\chi ({\chi }^{″}cos\mathsf{\Phi }ϝ-\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3)sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0\\ +\upsilon )+\chi \delta [{\mathsf{\Phi }}^0ϝ\upsilon cos\mathsf{\Phi }-cos\mathsf{\Phi }{ϝ}^3{sin}^2\mathsf{\Phi }]))=0,\\ +({\chi }^{\prime }((-{\chi }^{\prime }+\omega \delta )sin\mathsf{\Phi }ϝ-\chi {\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ+\frac{{\delta }^2}{\omega }[\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )\\ +{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi })+\chi ({\chi }^{″}sin\mathsf{\Phi }ϝ+\frac{1}{\omega }(-{\chi }^{\prime }\omega +{\delta }^3){\mathsf{\Phi }}^{0}cos\mathsf{\Phi }ϝ\\ +\chi \delta [\upsilon sin\mathsf{\Phi }ϝ({\mathsf{\Phi }}^0+\upsilon )+{cos}^2\mathsf{\Phi }{ϝ}^{3}sin\mathsf{\Phi }]))=0,\end{array}$$

where $\chi ={\left|{\nabla }_s\varphi \left(\mathbf{N}\right)\right|}^{-1}.$

Figure 4 and Figure 5 demonstrate the magnetic trajectories of N-magnetic particle with UCM.

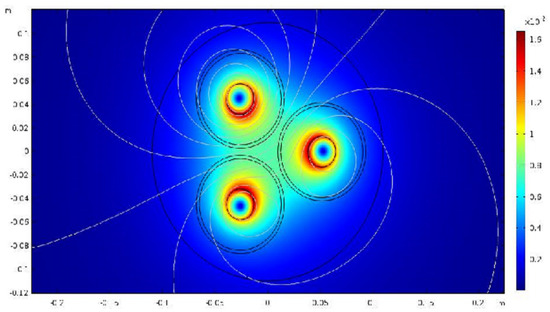
Figure 4. Magnetic trajectories of the N-magnetic particle with UCM.

Figure 5. Magnetic trajectories of the N-magnetic particle with UCM.

4. Conclusions

In this work, we investigate the special type of magnetic trajectories such that it corresponds to a moving charged particle in an associated magnetic field in Heisenberg space. This study differs from the former studies in the literature since it is considered in the Heisenberg space. We consider uniformly accelerated motion (UAM), the unchanged direction motion (UDM), and the uniformly circular motion (UCM) of the moving normal magnetic biharmonic particles in Heisenberg space.

In future studies, we will investigate the physical implications of the external force on a charged particle by obtaining different trajectories in different space time structures such as considering Heisenberg space time, de Sitter space time, Anti de Sitter space time, etc. Finally, this study leads up to the research of classifying the magnetic trajectories associated with characterizing moving binormal biharmonic magnetic particles in de Sitter space.