Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate
Abstract
1. Introduction
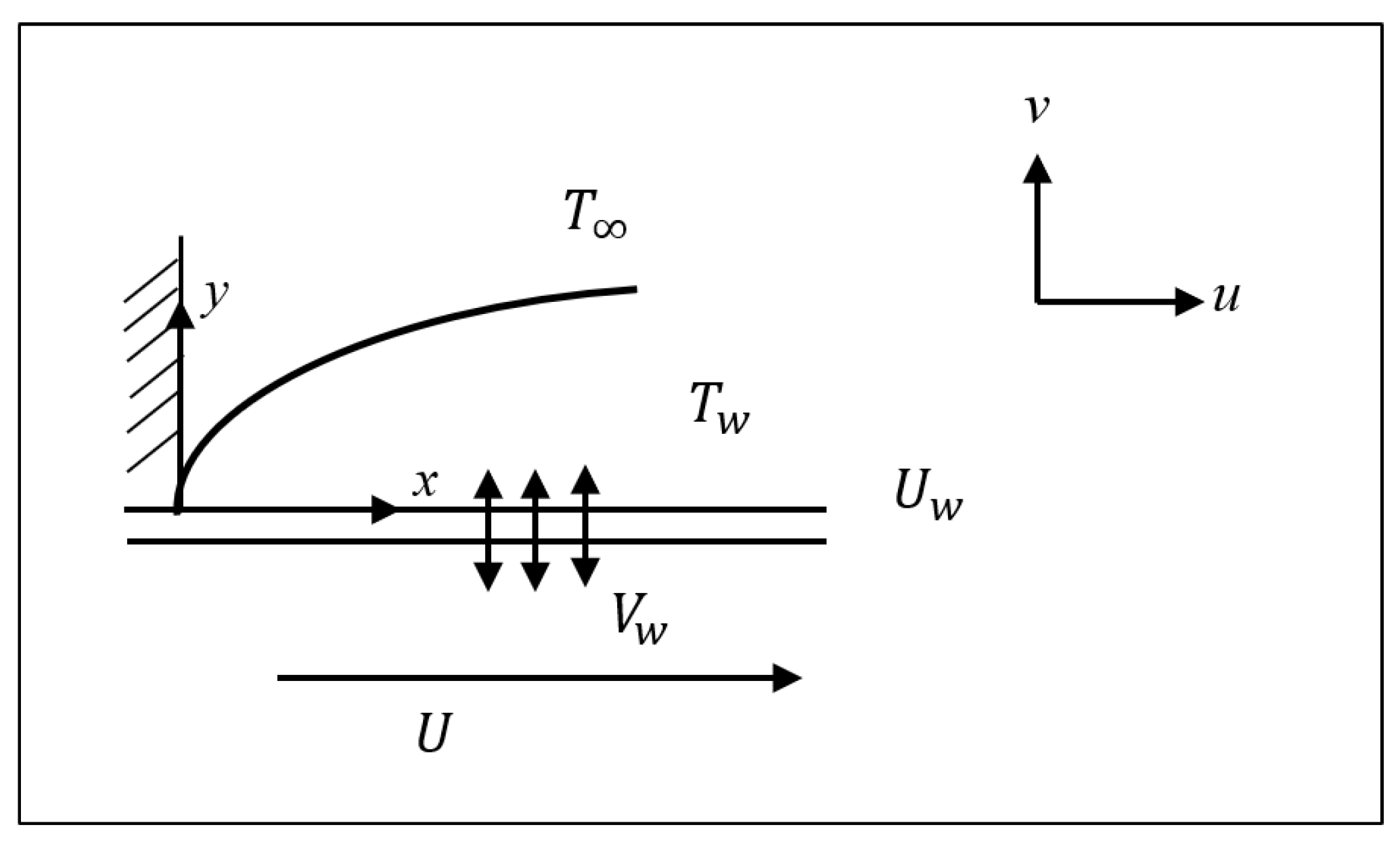
2. Description of Flow Problem
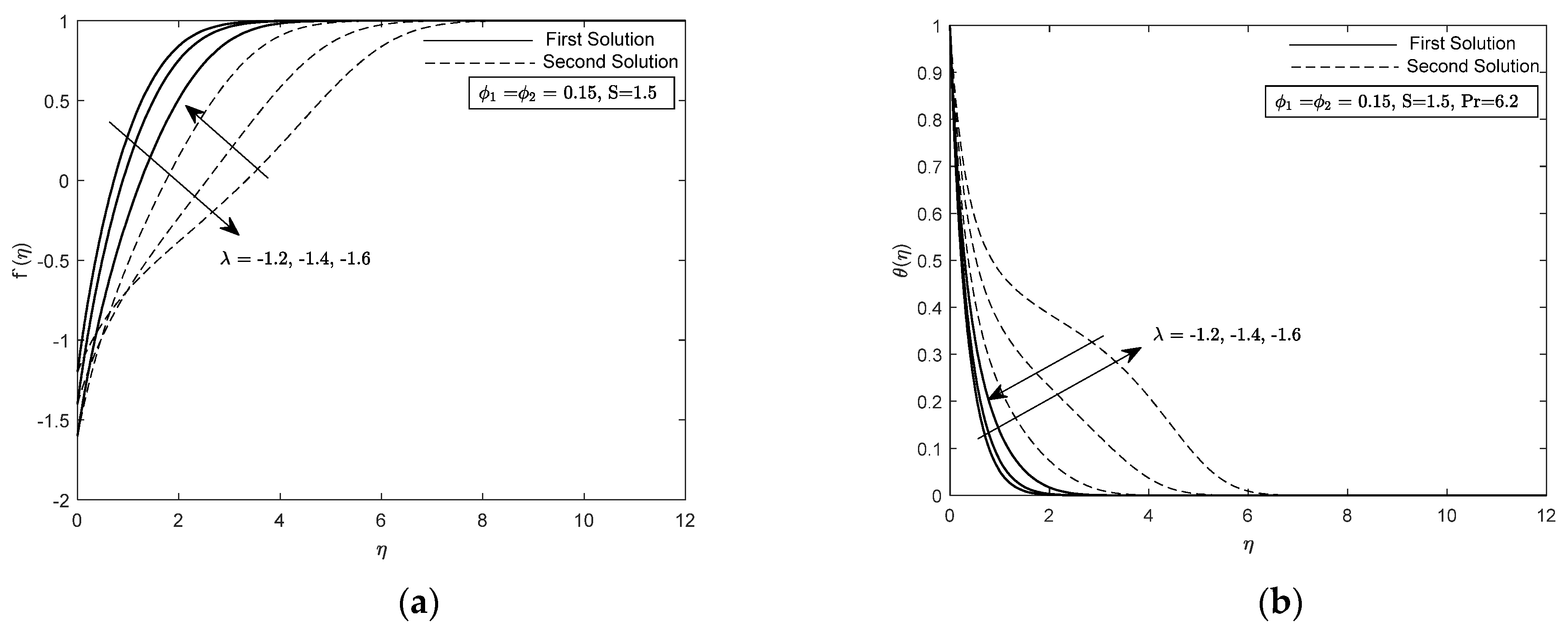
3. Stability Solution
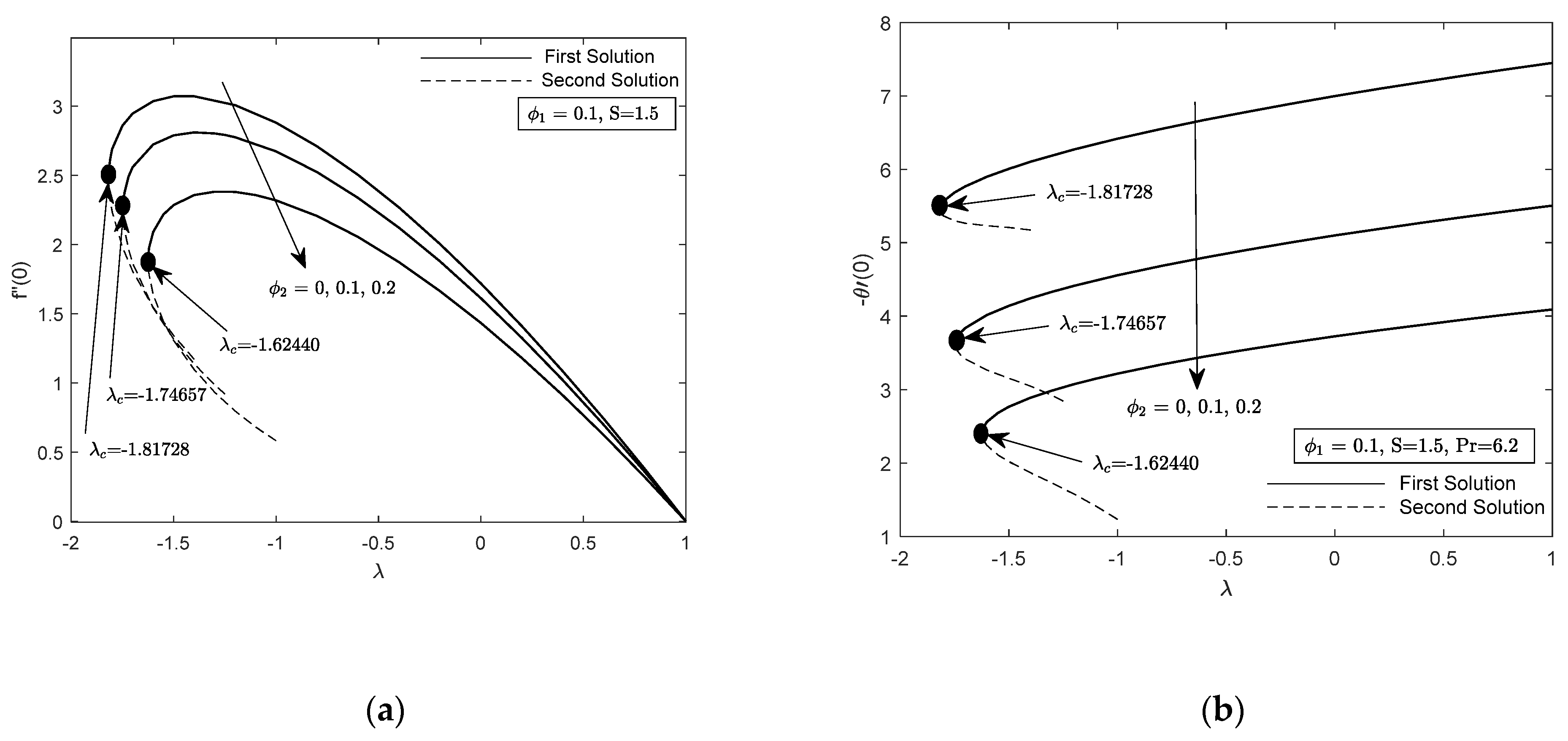
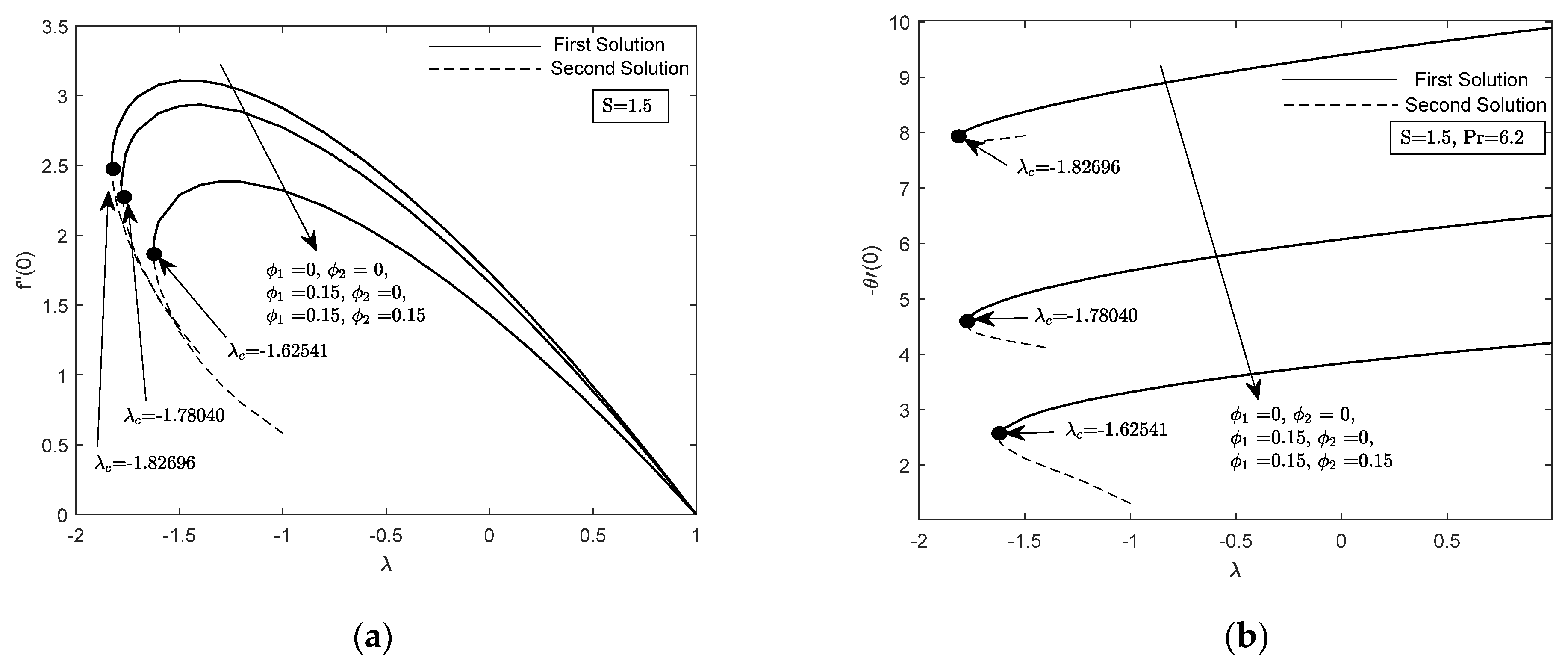
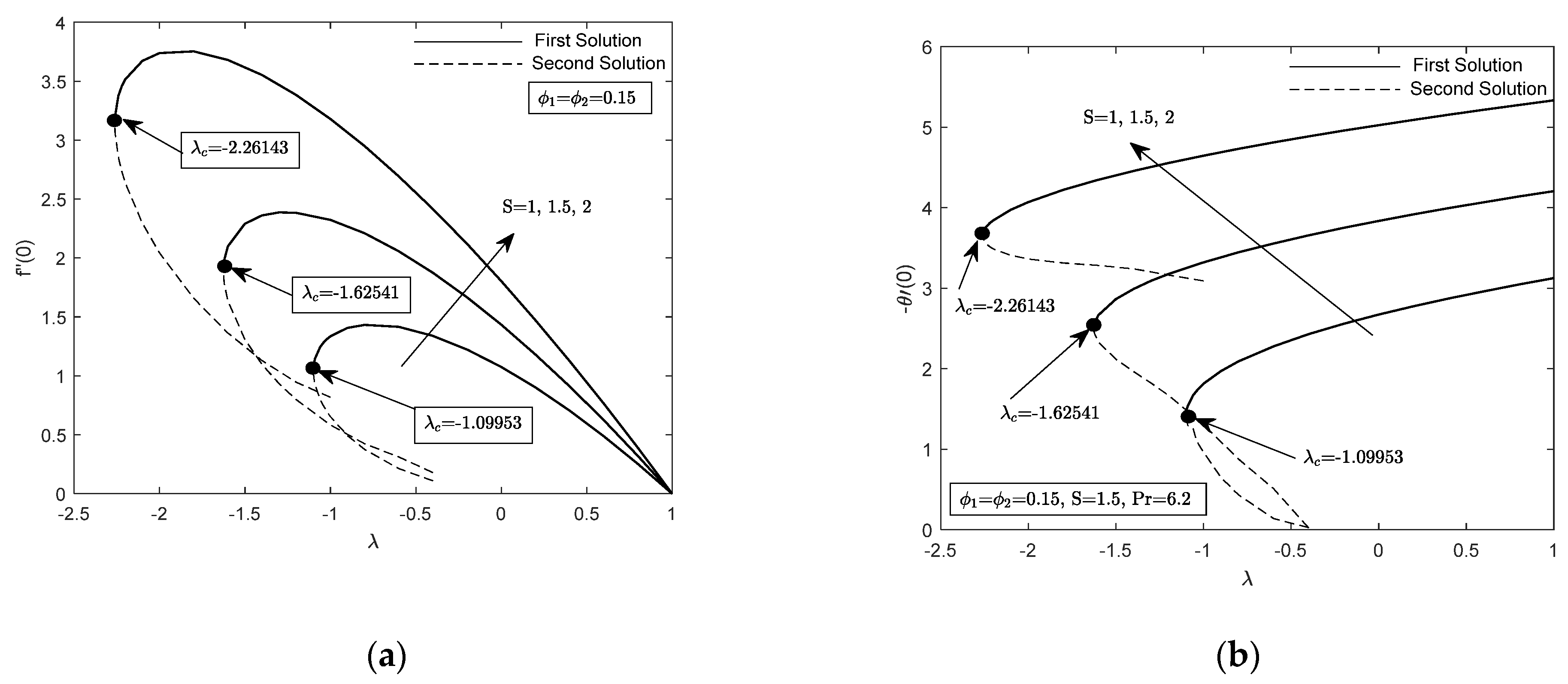
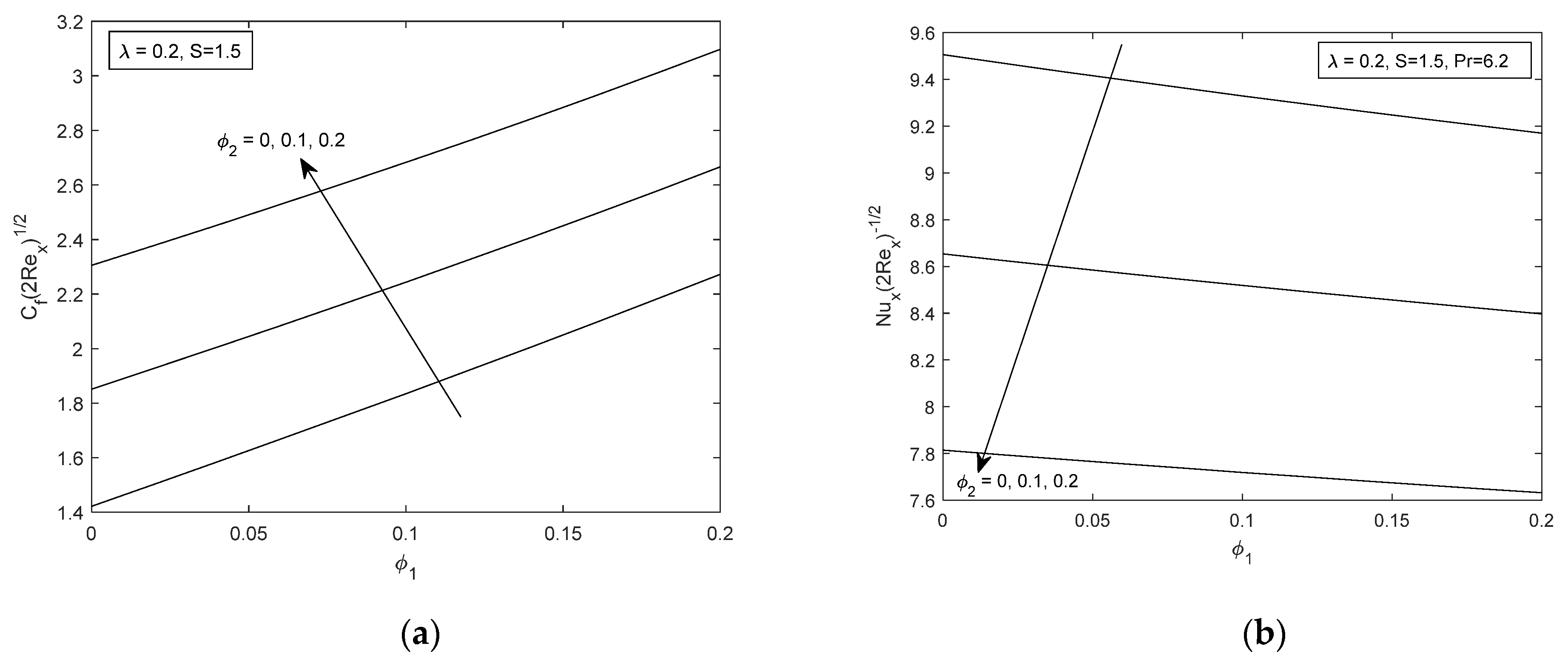
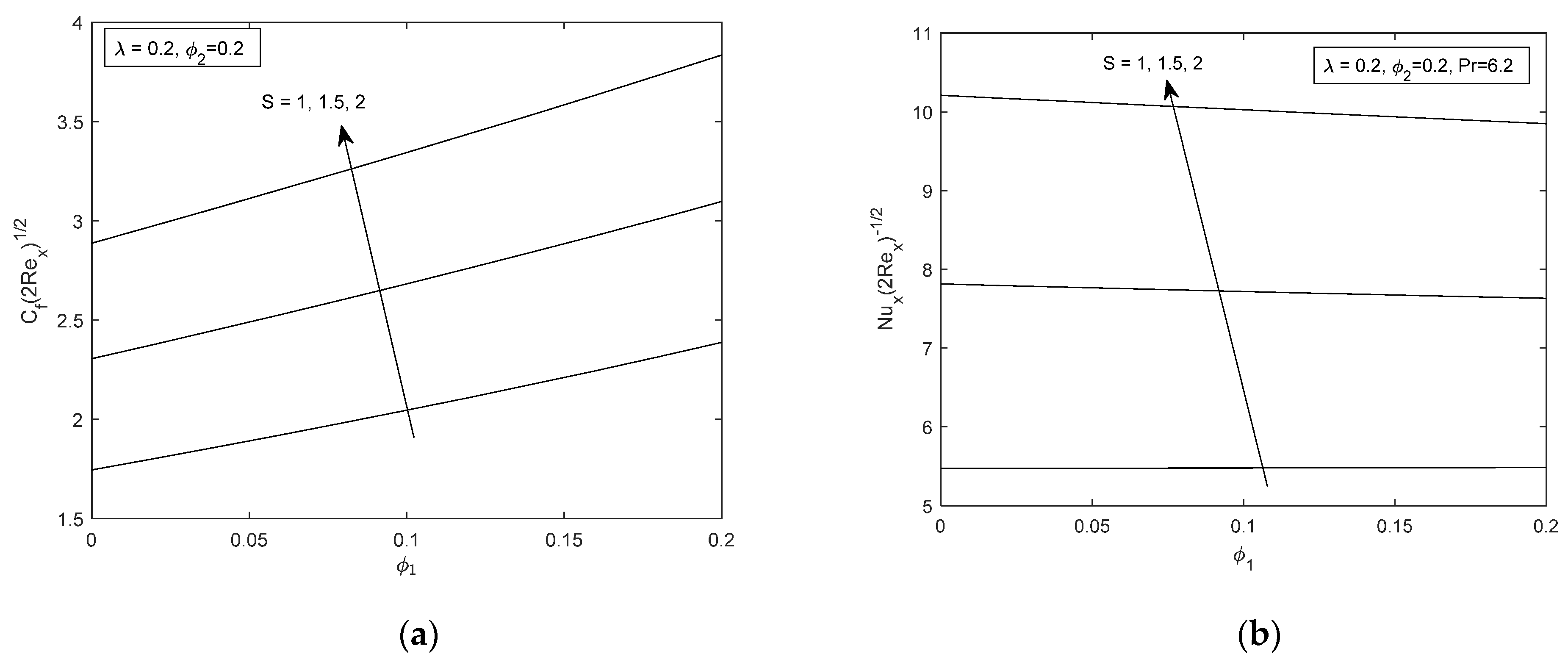
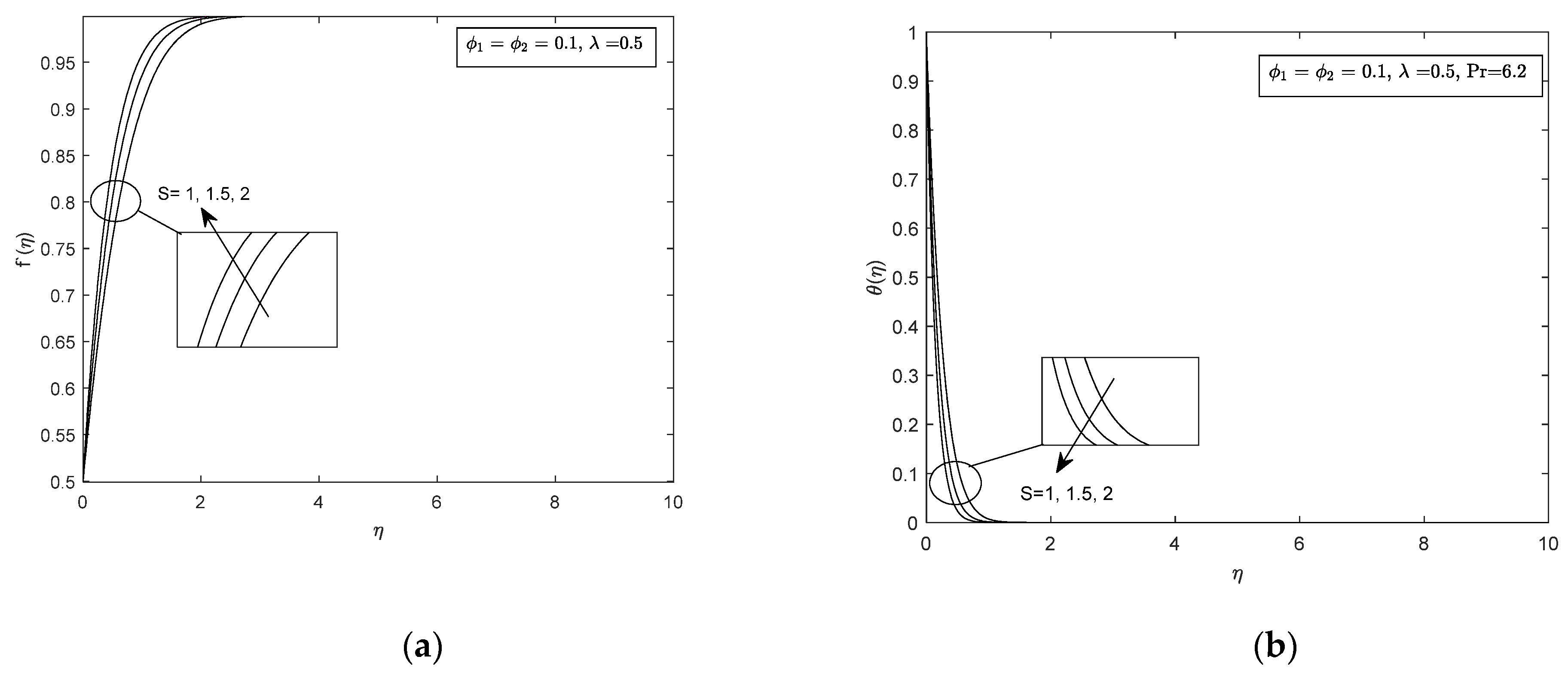
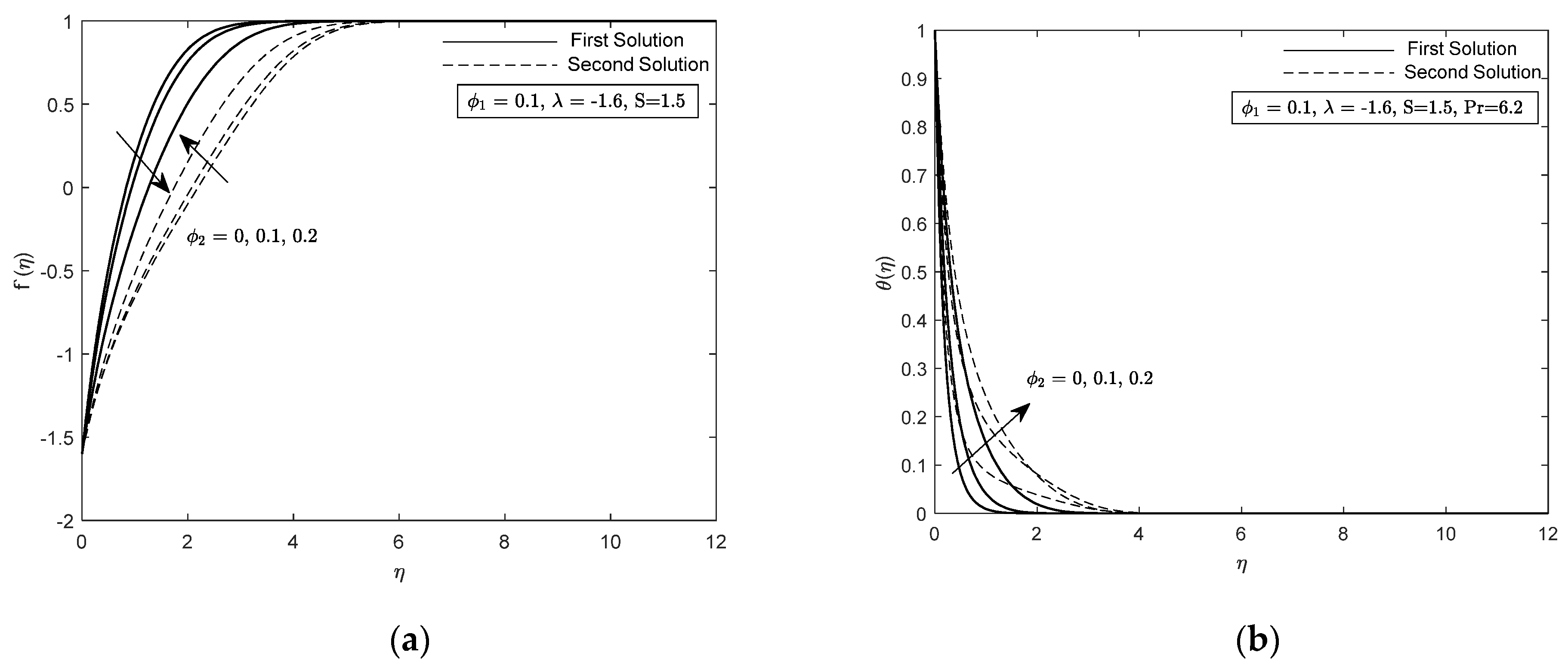
4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ODE | Ordinary Differential Equation |
| Pr | Prandtl number |
| T | Temperature |
| U | Uniform free stream |
| S | Suction/injection parameter |
| Plate heat flux | |
| Nux | Local Nusselt number |
| Rex | Reynolds number |
| Skin friction coefficient | |
| Condition on plate | |
| ∞ | Ambient condition |
| hnf | Hybrid nanofluid |
| nf | Nanofluid |
| f | Fluid |
| α | Thermal diffusivity |
| μ | Dynamic viscosity |
| ρ | Density |
| ψ | Stream function |
| η | Similarity variables |
| θ | Dimensionless temperature |
| (ρCp)f | Specific heat for base fluid |
| Cp | Specific heat at constant pressure |
| τ | Dimensionless time |
| k | Thermal conductivity |
| Concentration of nanoparticles | |
| ϒ | Eigenvalues |
| υ | Kinematic viscosity |
References
- Busemann, A. Ludwig Prandtl. 1875–1953. Biogr. Mem. Fellows R. Soc. 1960, 5, 193–205. [Google Scholar]
- Duwairi, H.M.; Tashtoush, B.; Damseh, R.A. On heat transfer effects of a viscous fluid squeezed and extended between two parallel plates. Heat Mass Transf. 2004, 41, 112–117. [Google Scholar]
- Arifuzzaman, S.M.; Islam, M.M.; Haque, M.M. Combined heat and mass transfer steady flow of a viscous over a vertical plate with large suction. Int. J. Sci. Technol. Soc. 2015, 3, 236–242. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, L.; Chen, G.; Ma, L. Coupling effects of viscous sheet and ambient fluid on boundary layer flow and heat transfer in Power law fluids. J. Heat Transf. 2019, 141, 061701. [Google Scholar] [CrossRef]
- Anyanwu, O.E.; Raymond, D.; Adamu, A.K.; Ogwumu, O.D. Viscous and Joule dissipation effects on heat transfer in MHD Poiseuille flow in the presence of radial magnetic field. FUW Trends Sci. Technol. J. 2017, 2, 171–186. [Google Scholar]
- Venkateswarlu, M.; Kumar, M.P. Soret and heat source effects on MHD flow of a viscous fluid in a parallel porous plat channel in presence of slip condition. U.P.B Sci. Bull. Ser. D 2017, 79, 171–186. [Google Scholar]
- Raju, K.C.; Reddy, D.B.S. Effect of chemical reaction, thermo-diffusion, hall effects on MHD convective heat and mass transfer flow of a viscous fluid in a vertical channel bounded by stretching and stationary walls. Int. J. Sci. Innov. Math. Res. 2019, 7, 12–24. [Google Scholar]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.E. Anomalously thermal conductivity enhancement in nanotube suspension. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Long, N.M.A.N.; Suali, M.; Ishak, A.; Bachok, N.; Arifin, N.M. Unsteady stagnation point flow and heat transfer over stretching/shrinking sheet. Appl. Sci. 2011, 11, 3520–3524. [Google Scholar]
- Mohyud-Din, S.T.; Zaidi, Z.A.; Khan, U.; Ahmed, N. On heat and mass transfer analysis of a nanofluid between rotating plates. Aerosp. Sci. Technol. 2015, 46, 514–522. [Google Scholar] [CrossRef]
- Zhu, J.; Chu, P.; Sui, J. Exact analytical nanofluid flow and heat transfer involving asymmetric wall heat fluxes with nonlinear velocity slip. Math. Probl. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Bakar, N.A.A.; Bachok, N.; Arifin, N.M. Boundary layer stagnation-point flow over a stretching/shrinking cylinder in a nanofluid: A stability analysis. Indian J. Pure Appl. Phys. 2019, 57, 106–117. [Google Scholar]
- Mishra, S.R.; Baag, S.; Bhatti, M.M. Study of heat and mass transfer on MHD Walters B nanofluid flow induced by stretching plate surface. Alex. Eng. J. 2018, 57, 2435–2443. [Google Scholar] [CrossRef]
- Prasad, P.D.; Kumar, R.V.M.S.S.K.; Varma, S.V.K. Heat and mass transfer analysis for the MHD flow of a nanofluid with radiation absorption. Ain Shams Eng. J. 2018, 9, 801–813. [Google Scholar] [CrossRef]
- Farooq, M.; Ahmad, S.; Javed, M.; Anjum, A. Melting heat transfer in squeezed nanofluid flow through Darcy Forchheimer medium. J. Heat Transf. 2019, 141, 012402. [Google Scholar] [CrossRef]
- He, W.; Tongraie, D.; Lotfipour, A.; Purfattah, F.; Karimipour, A.; Afrand, M. Effect of twisted tape inserts and nanofluid on flow field and heat transfer characteristics in a tube. Commun. Heat Mass Transf. 2020, 110, 104440. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary layer behavior on continuous solid surfaces II. The boundary layer on a continuous flat surface. AIChE J. 1961, 7, 221–225. [Google Scholar]
- Blasius, H. Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Angew. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Tsou, F.K.; Sparrow, E.M.; Goldstein, R.J. Flow and heat transfer in the boundary layer on a continuous moving surface. Int. J. Heat Mass Transf. 1967, 10, 219–235. [Google Scholar] [CrossRef]
- Tsai, S.-Y.; Hsu, T.H. Thermal transport of a continuous moving plate in a non-Newtonian fluid. Comput. Math. Appl. 1995, 29, 99–108. [Google Scholar] [CrossRef]
- Bataller, R.C. Radiation Effects in the Blasius Flow. Appl. Math. Comput. 2008, 198, 333–338. [Google Scholar]
- Haile, E.; Shankar, B. Boundary layer flow of nanofluids over a moving surface in the presence of thermal radiation, viscous dissipation and chemical reaction. Appl. Appl. Math. 2015, 10, 952–969. [Google Scholar]
- Maliki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Hartnett, J.P. Mass transfer cooling. In Handbook of Heat Transfer Applications, 2nd ed.; McGraw-Hill: New York, NY, USA, 1985; pp. 1–111. [Google Scholar]
- Masad, J.A.; Nayfeh, A.H. Effects of suction and wall shaping on the fundamental parametric resonance in boundary layers. Phys. Fluids A Fluid Dyn. 1992, 4, 963–974. [Google Scholar] [CrossRef]
- Rosali, H.; Ishak, A.; Pop, I. Micropolar fluid flow towards stretching/shrinking sheet in a porous medium with suction. Int. Commun. Heat Mass Transf. 2012, 39, 826–829. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Effects of viscous dissipation and suction/injection on MHD nanofluid flow over a wedge with porous medium and slip. Alex. Eng. J. 2016, 55, 3115–3123. [Google Scholar] [CrossRef]
- Subamowo, G.M.; Akinshilo, A.; Yinusa, A.A. Two-dimensional flow analysis of nanofluid through porous channel with suction/injection at slowly expanding/contracting walls using variation of parameter method. Transp. Phenom. Nano Micro Scales 2019, 7, 120–129. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef]
- Kausar, M.S.; Hussanan, A.; Mamat, A.; Ahmad, B. Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation. Symmetry 2019, 11, 659. [Google Scholar] [CrossRef]
- Olatundun, A.T.; Makinde, O.D. Analysis of Blasius flow of hybrid nanofluids over a convectively heated surface. Defect Diffus. Forum 2017, 377, 29–41. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary layer flow over a moving surface in nanofluid with suction/injection. Acta Mech. Sin. 2012, 28, 34–40. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mimi, E.A. Effect of hybrid and single nanofluids on the performance characteristics of chilled water air conditioning system. Appl. Therm. Eng. 2019, 163, 114398. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosure filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1985, 20, 171–179. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thomson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
| Thermophysical Properties | |||
|---|---|---|---|
| Alumina Oxide (Al2O3) | 36 | 773 | 3880 |
| Titanium Oxide (TiO2) | 8.7 | 690 | 4010 |
| Water | 0.613 | 4179 | 997.1 |
| Thermophysical | Hybrid Nanofluids |
|---|---|
| Density | |
| Heat capacity | |
| Viscosity | |
| Thermal conductivity |
| 0 | 0 | 1.4217 | 9.5054 | 1.4217 | 9.5054 |
| 0.1 | 1.4099 | 7.0938 | 1.8348 | 9.3293 | |
| 0.2 | 1.3008 | 5.3806 | 2.2724 | 9.1699 | |
| 0.1 | 0 | 1.4225 | 6.8347 | 1.8511 | 8.6534 |
| 0.1 | 1.3248 | 5.1875 | 2.2435 | 8.5188 | |
| 0.2 | 1.1727 | 4.0088 | 2.6661 | 8.3972 | |
| 0.2 | 0 | 1.3195 | 4.9333 | 2.3051 | 7.8144 |
| 0.1 | 1.1799 | 3.8055 | 2.6826 | 7.7189 | |
| 0.2 | 1.0149 | 2.9931 | 3.0971 | 7.6317 |
| λ | First Solution | Second Solution | |
|---|---|---|---|
| 0 | −1.81725 | 0.0068 | −0.0068 |
| −1.815 | 0.0614 | −0.0580 | |
| −1.8 | 0.1772 | −0.1510 | |
| 0.1 | −1.74653 | 0.0076 | −0.0076 |
| −1.746 | 0.0299 | −0.2303 | |
| −1.7 | 0.3015 | −0.2431 | |
| 0.2 | −1.62439 | 0.0054 | −0.0054 |
| −1.624 | 0.0250 | −0.0243 | |
| −1.6 | 0.2085 | −0.1708 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aladdin, N.A.L.; Bachok, N. Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate. Symmetry 2020, 12, 1064. https://doi.org/10.3390/sym12071064
Aladdin NAL, Bachok N. Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate. Symmetry. 2020; 12(7):1064. https://doi.org/10.3390/sym12071064
Chicago/Turabian StyleAladdin, Nur Adilah Liyana, and Norfifah Bachok. 2020. "Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate" Symmetry 12, no. 7: 1064. https://doi.org/10.3390/sym12071064
APA StyleAladdin, N. A. L., & Bachok, N. (2020). Boundary Layer Flow and Heat Transfer of Al2O3-TiO2/Water Hybrid Nanofluid over a Permeable Moving Plate. Symmetry, 12(7), 1064. https://doi.org/10.3390/sym12071064





