Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry
Abstract
1. Introduction
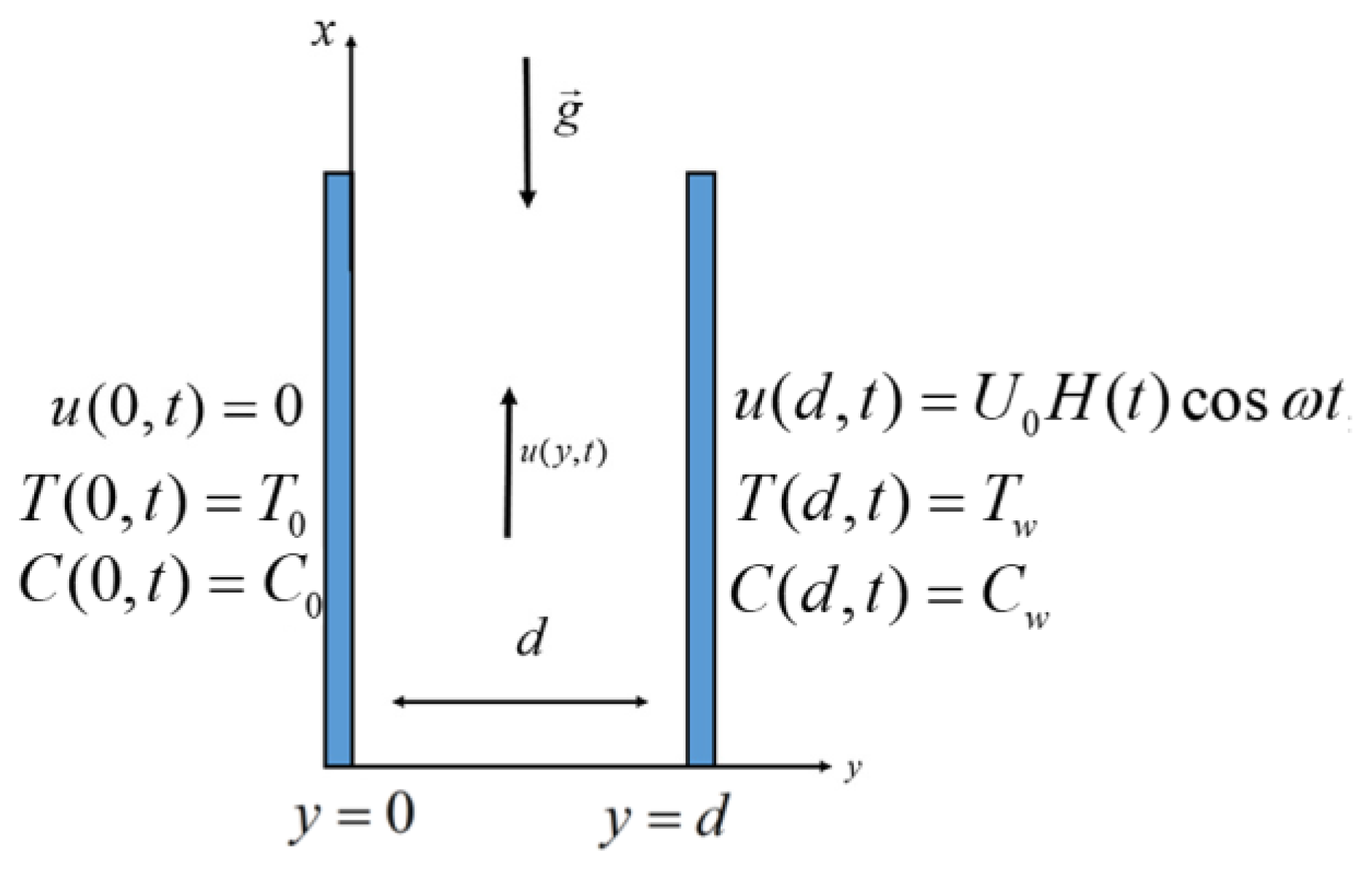
2. Mathematical Modelling
3. Generalization of the Classical Model
4. The Solution of the Heat and Mass Equations
5. Velocity Profile Calculations
6. Skin Friction, Rate of Heat Transfer, and Rate of Mass Transfer
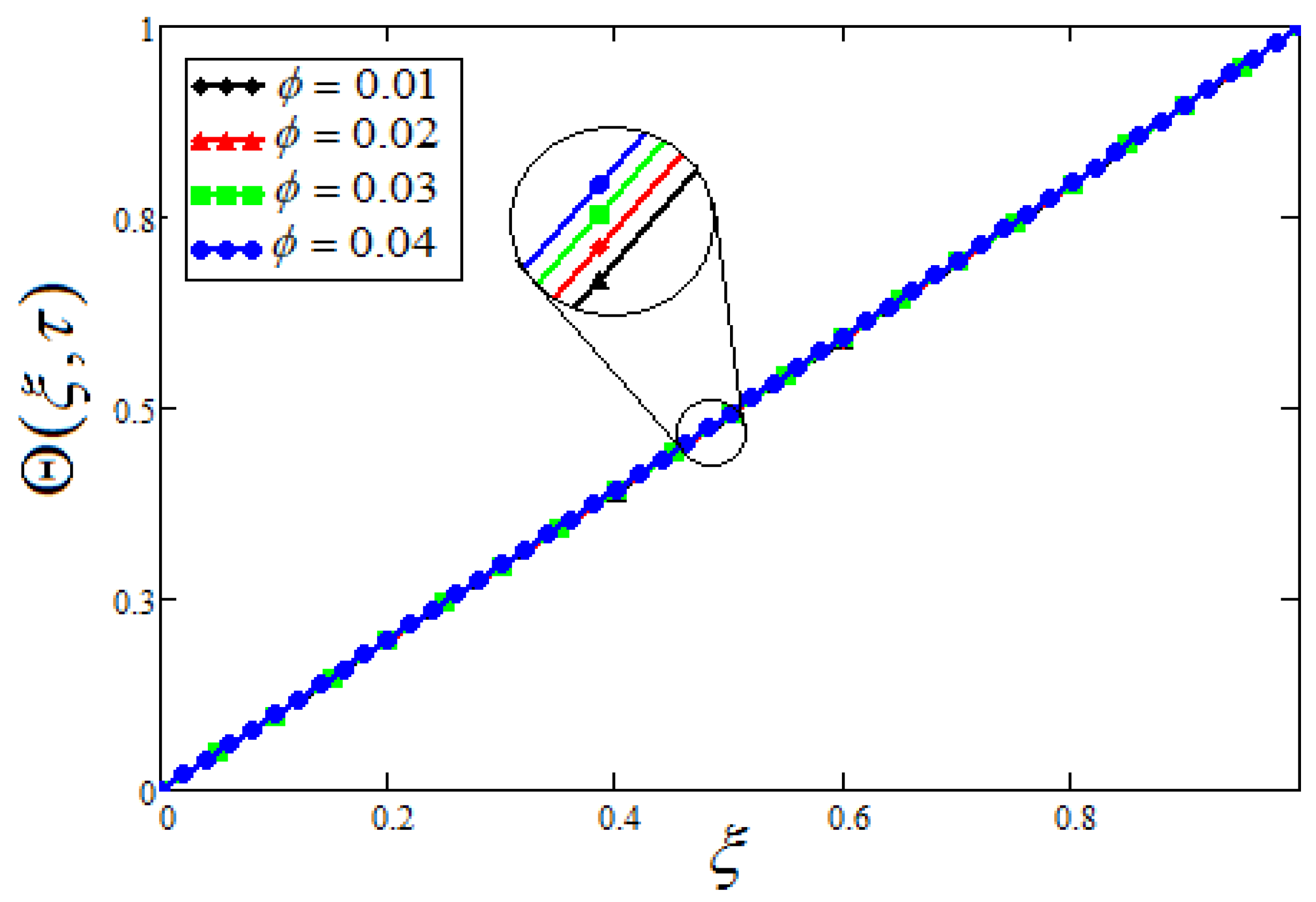
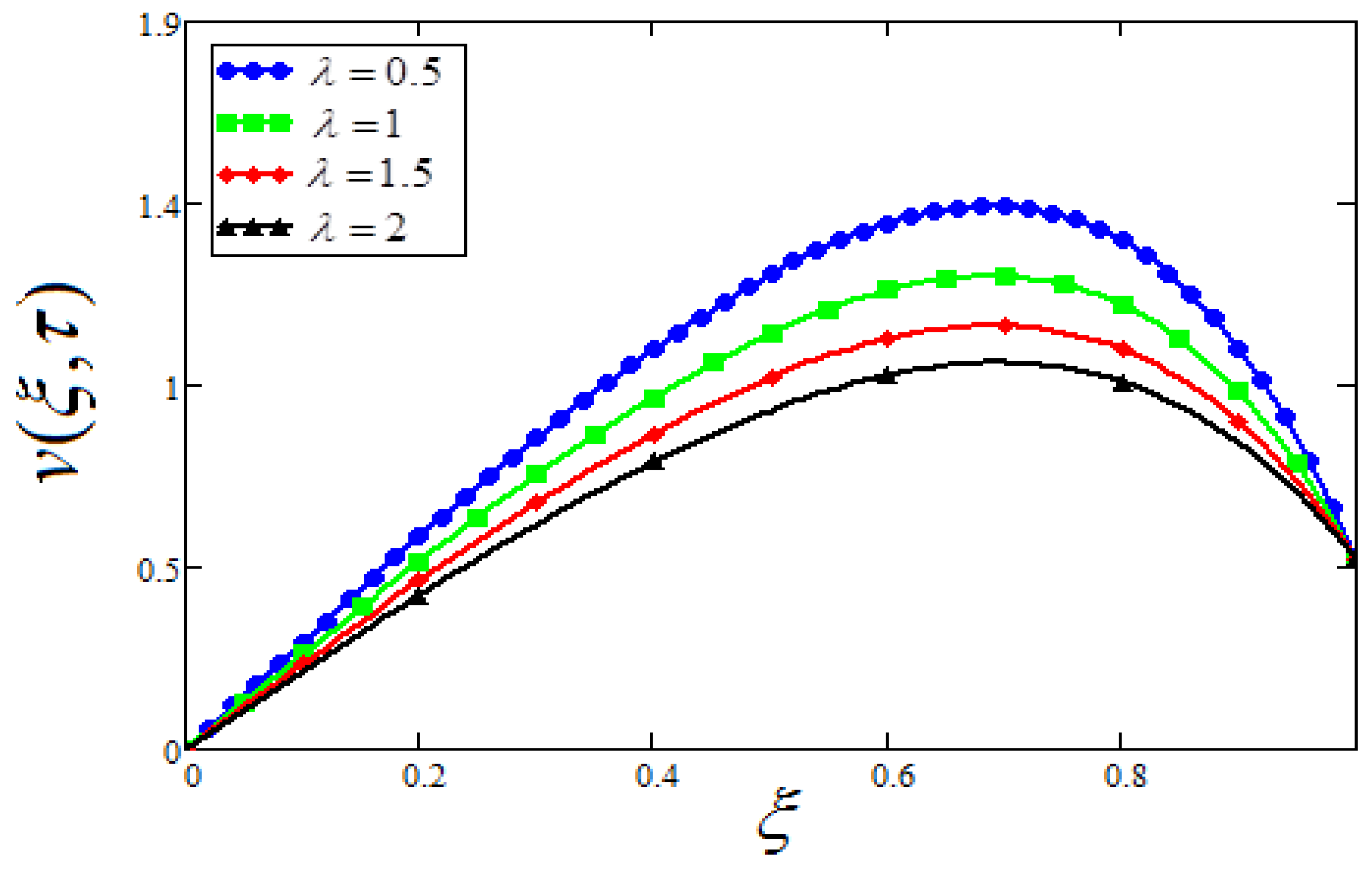
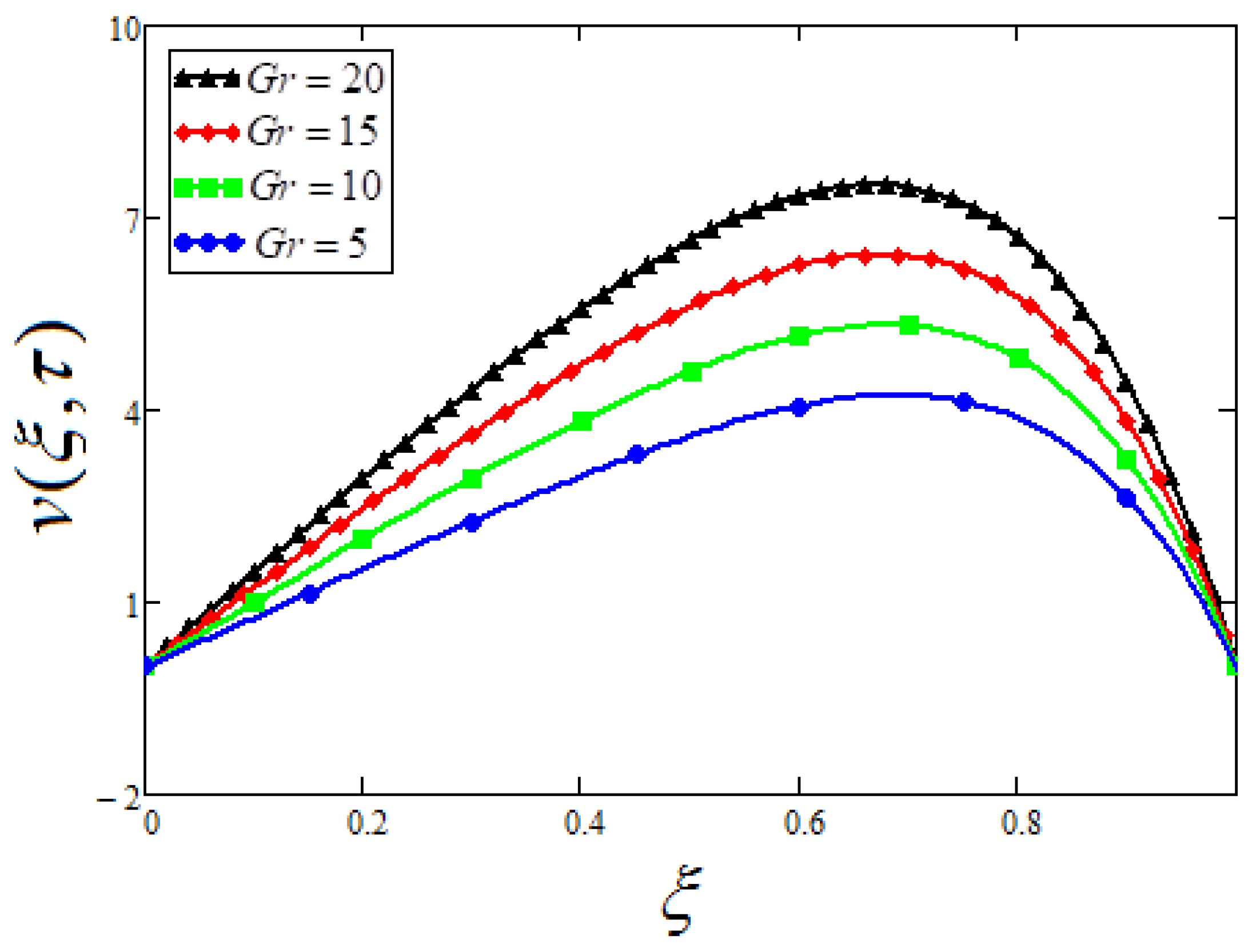
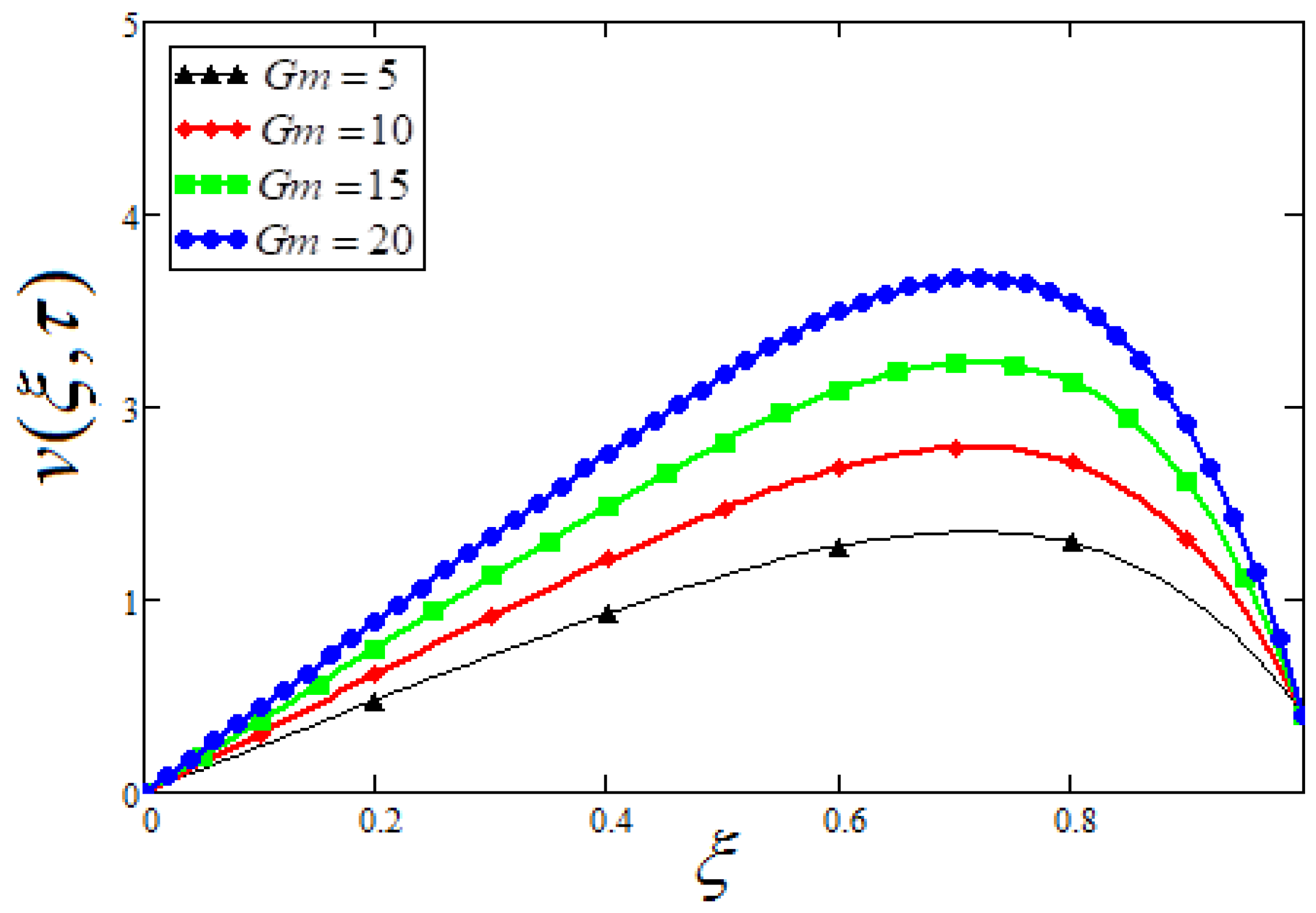
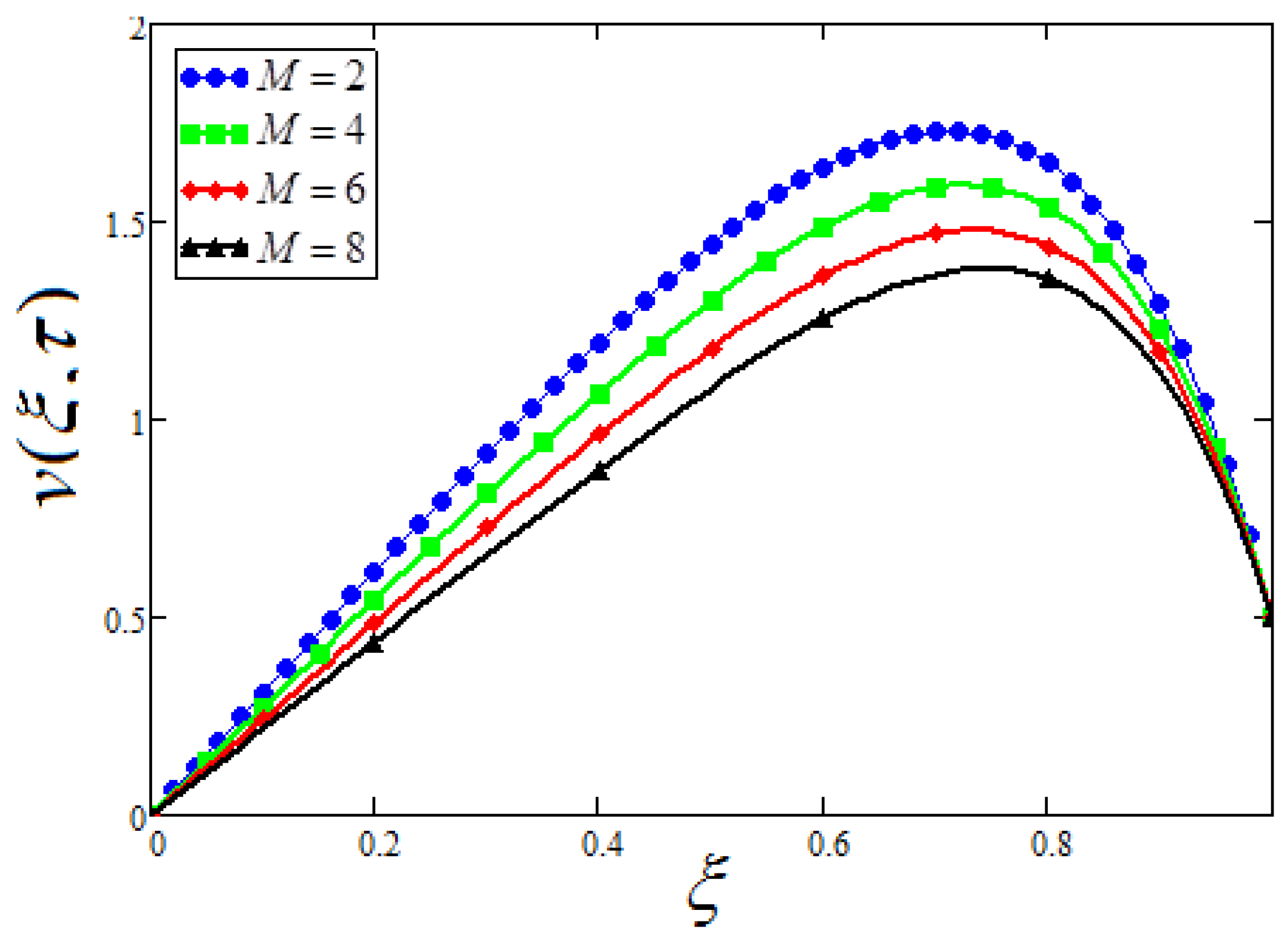
7. Parametric Study
8. Conclusions
- ❖
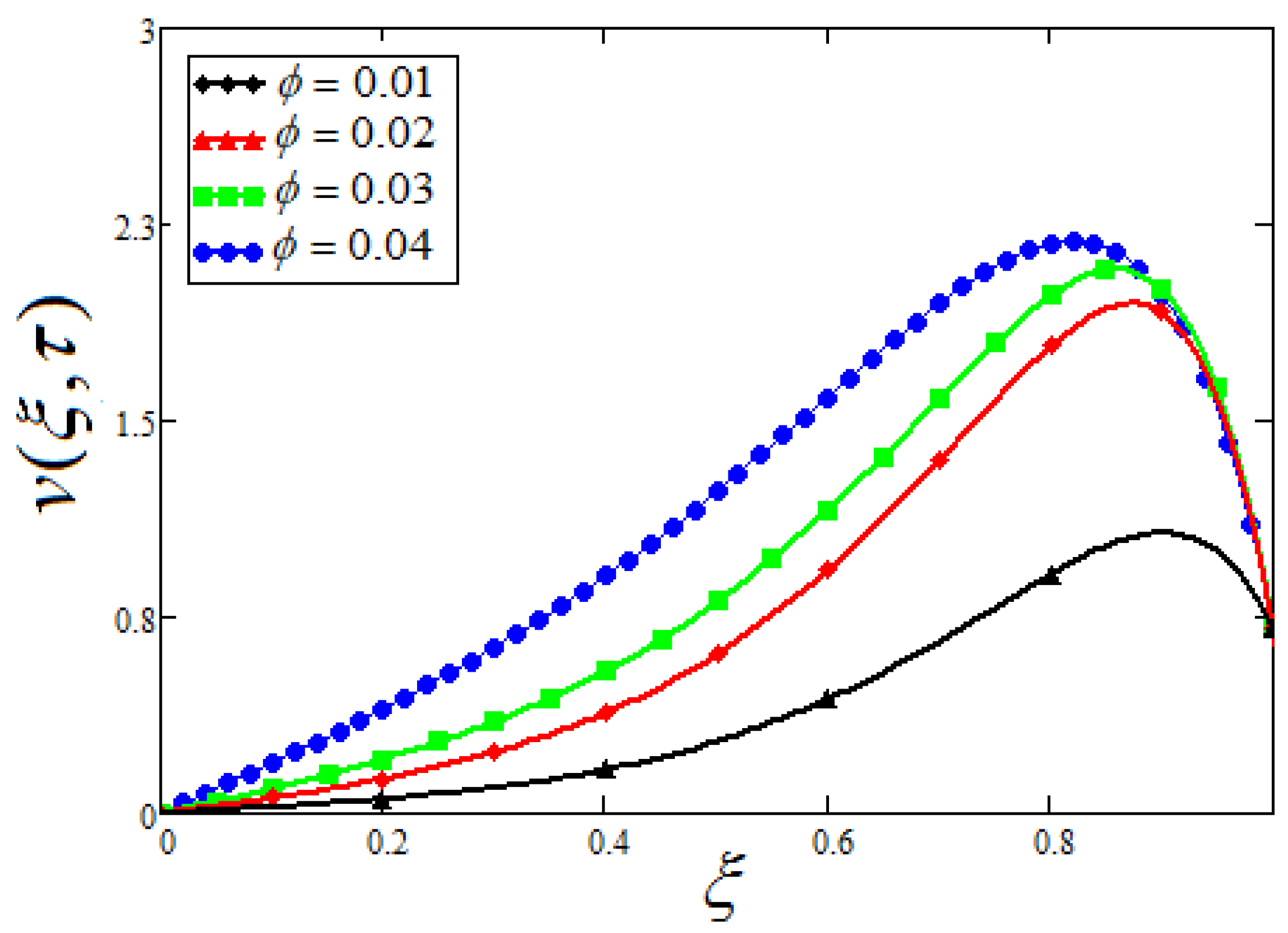
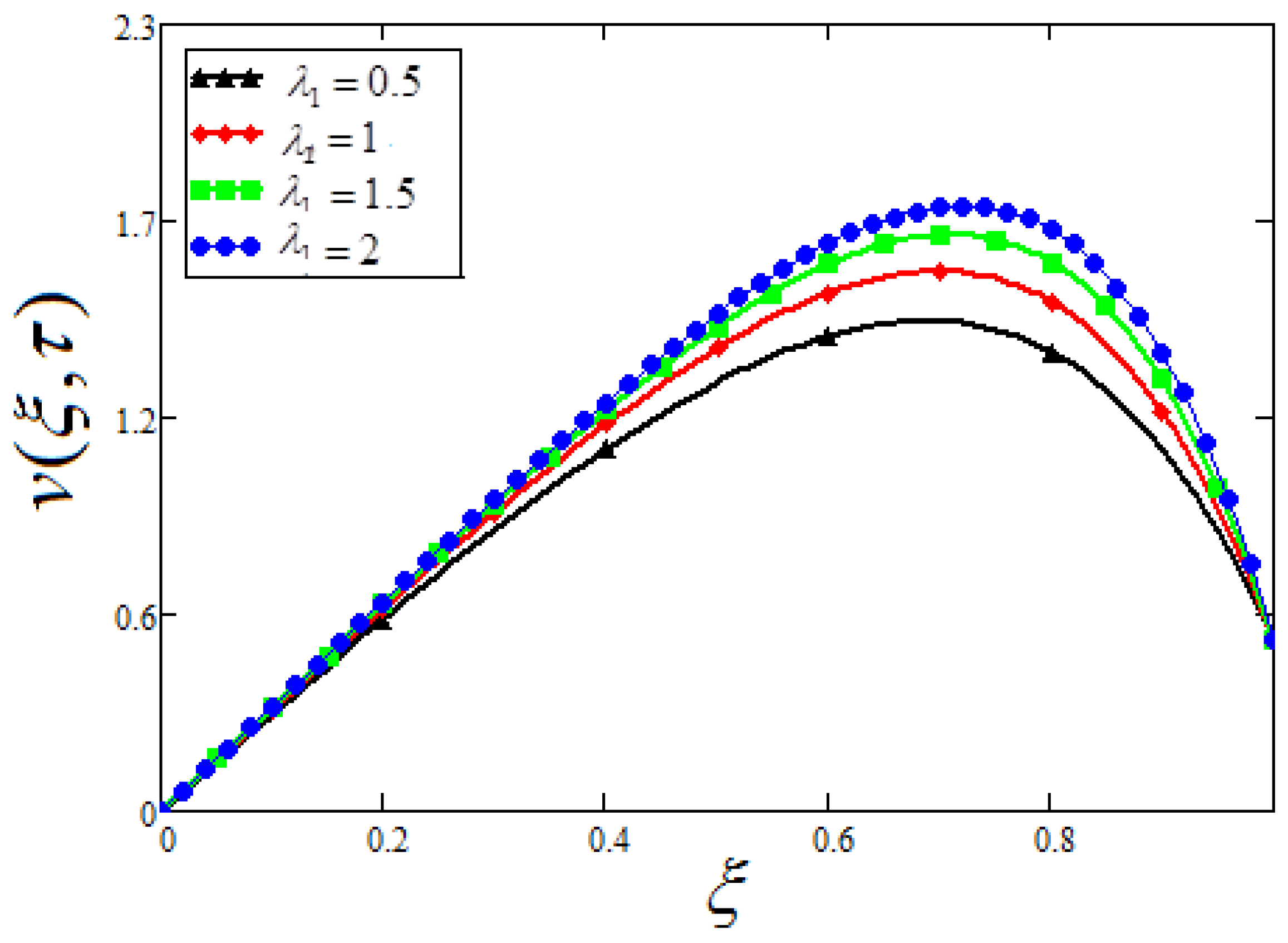
- The velocity profile shows that by increasing the volume fraction of the nanoparticles, the fluid becomes more viscous and as a result, the concrete will be denser and hence will be stronger.
- ❖
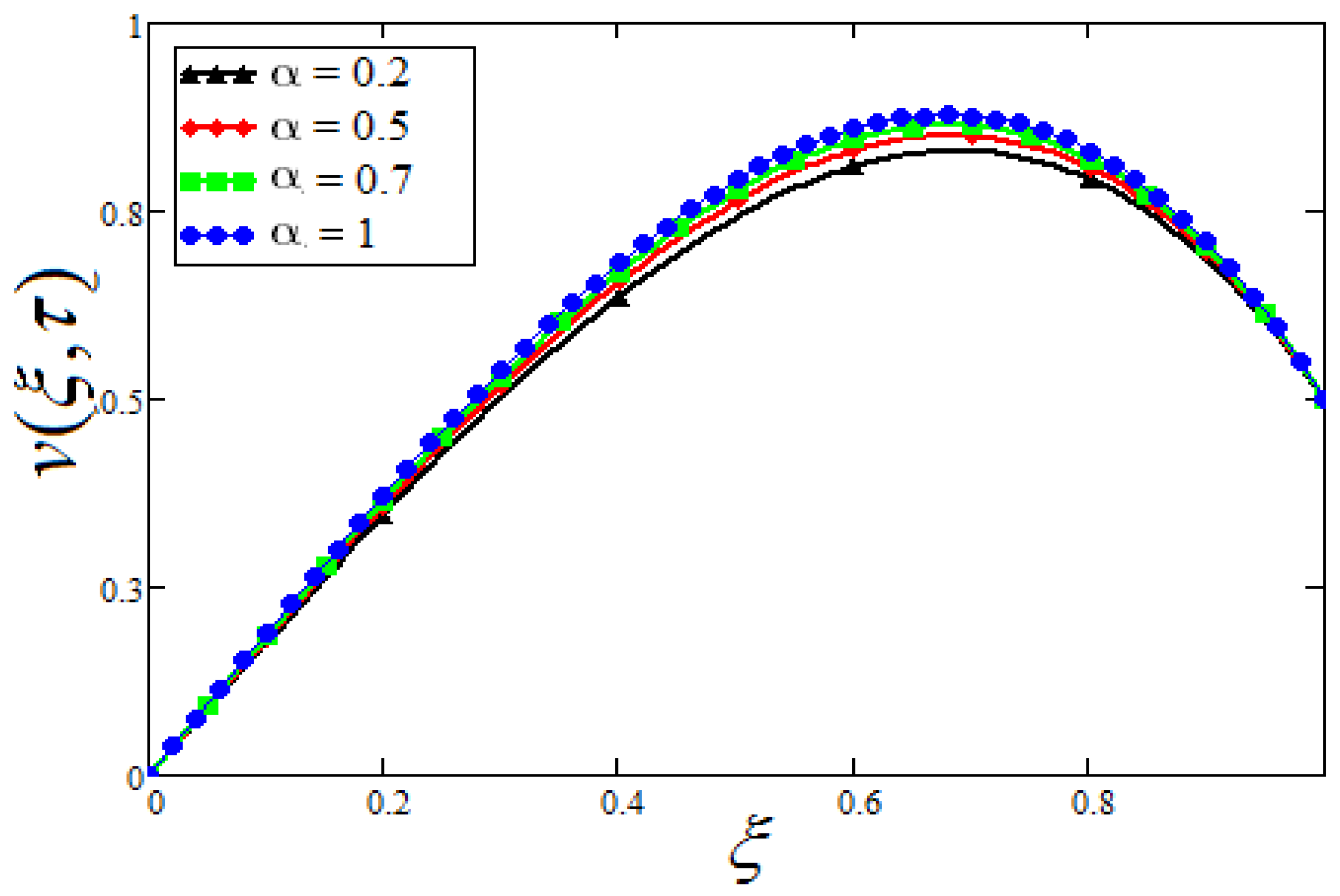
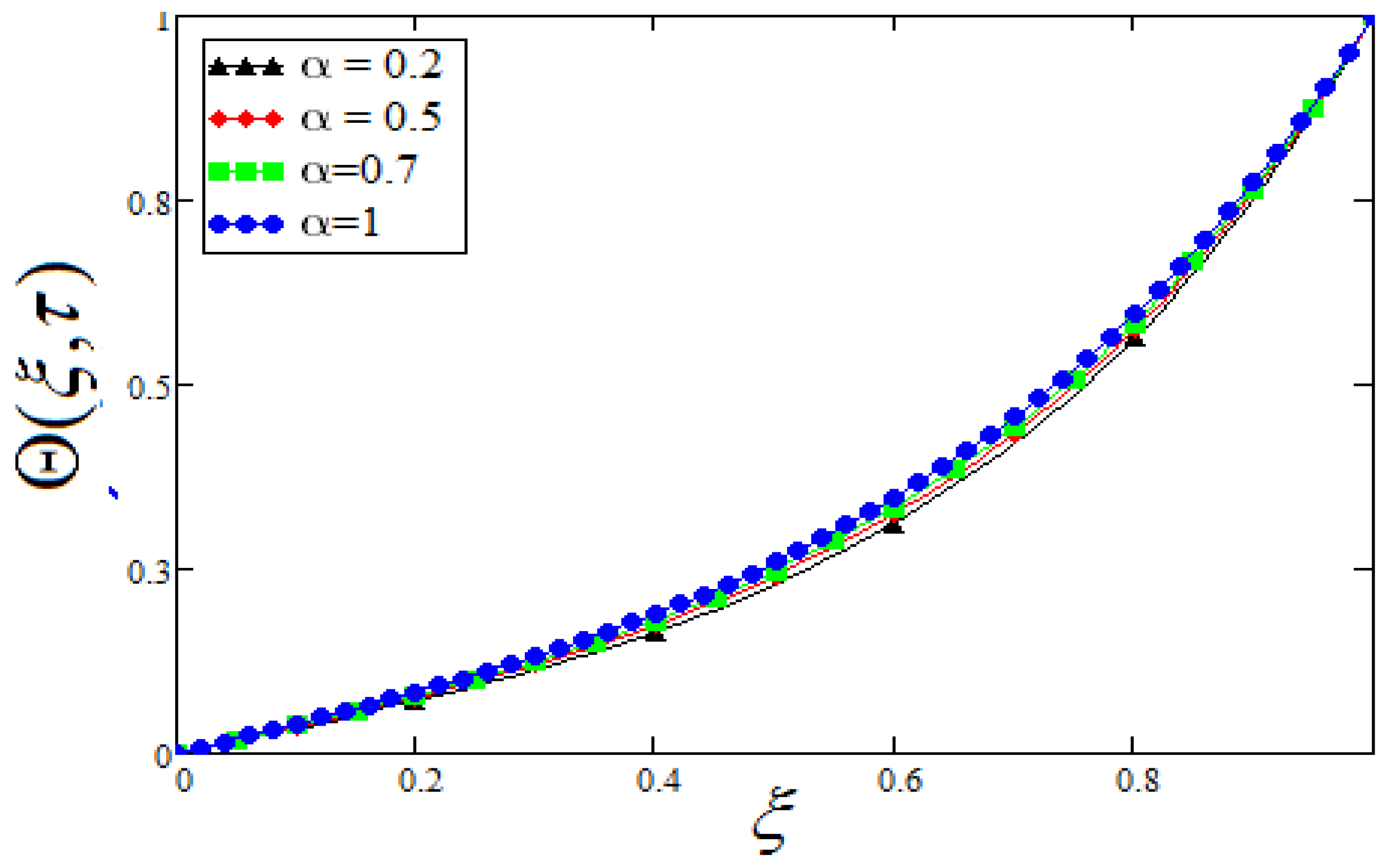
- The concrete will be stronger for lesser values of , as the lesser values of reduces the velocity profile, because of the higher viscous forces and weaker thermal forces.
- ❖
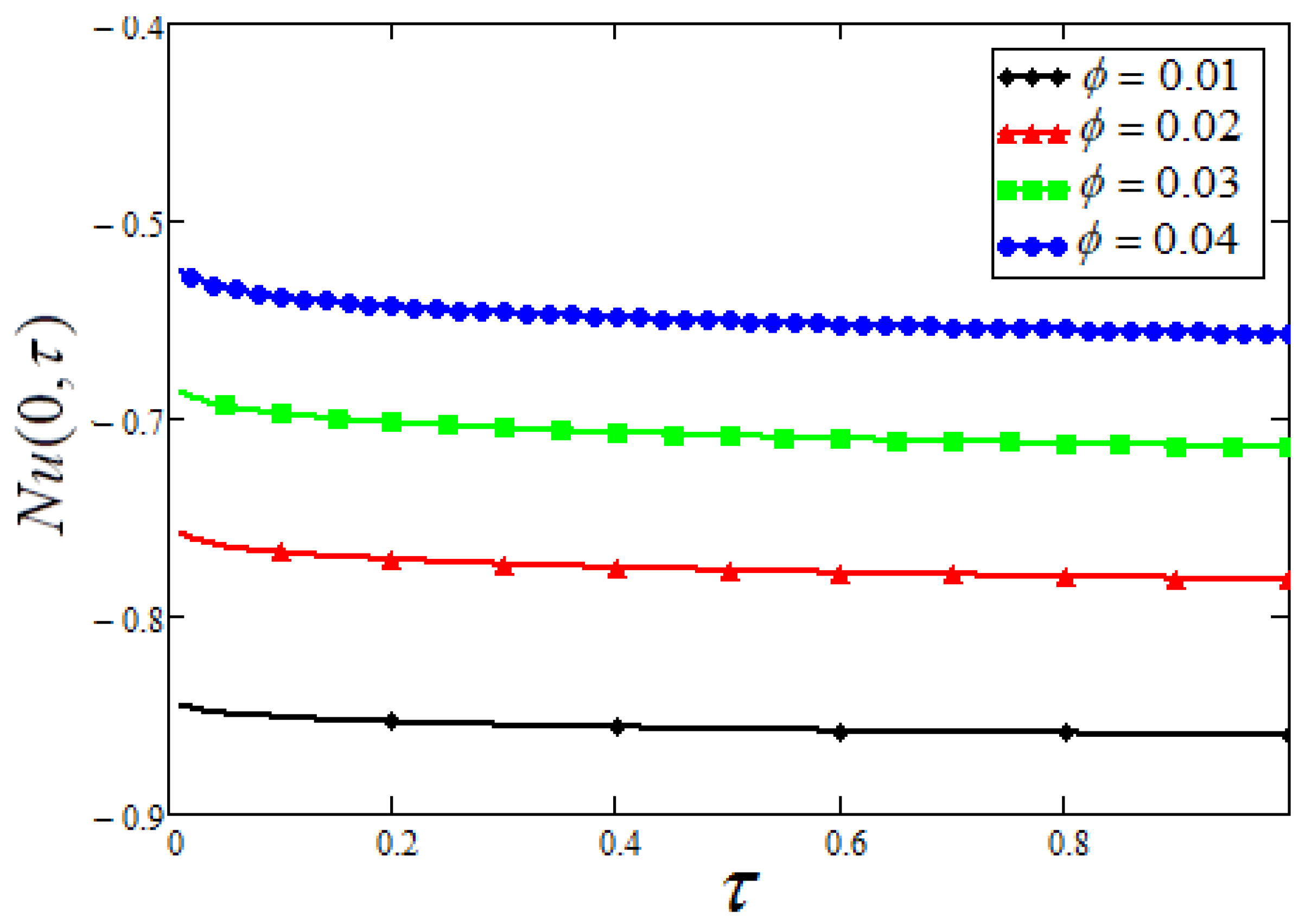
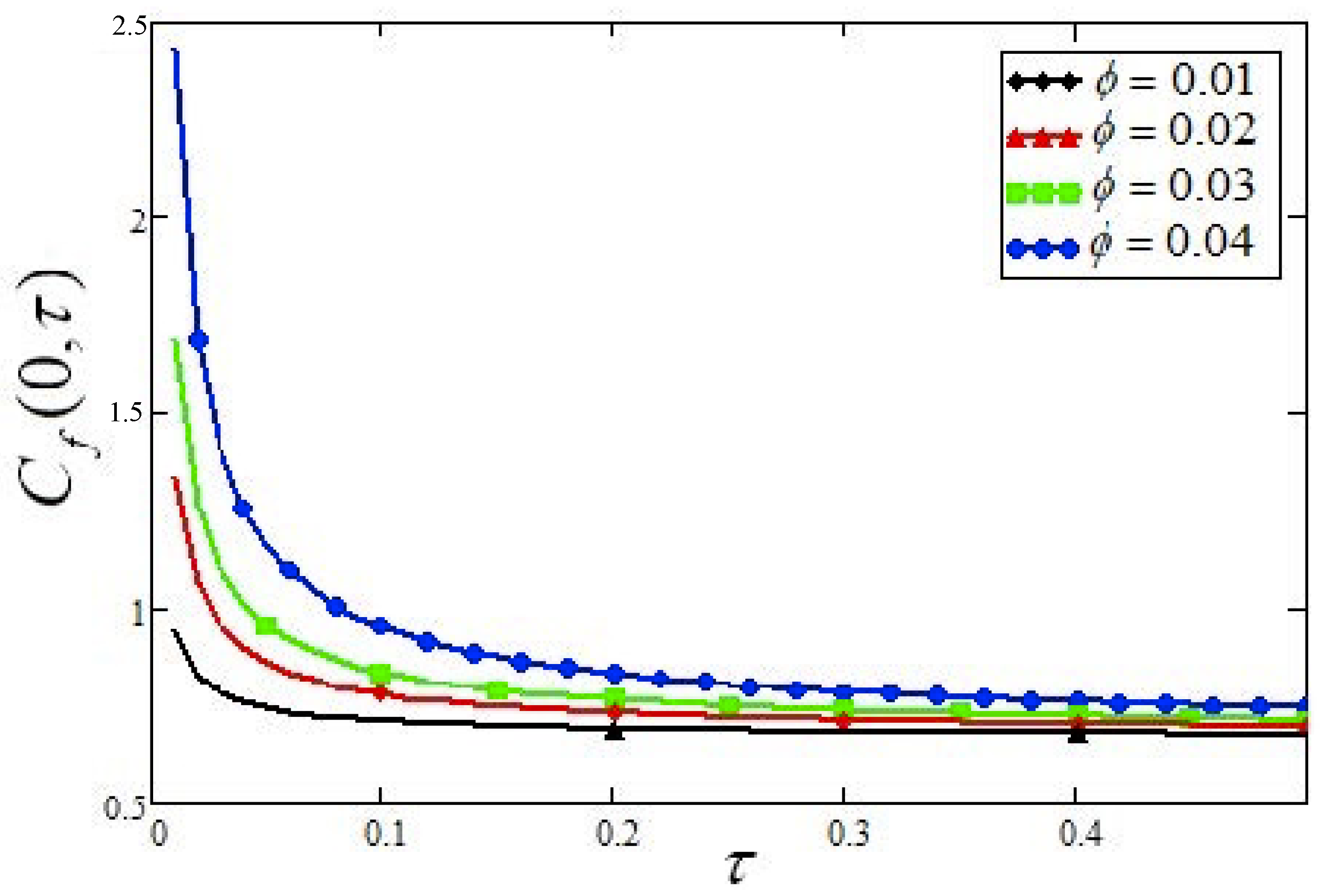
- Also, suspended nanoparticles in cement-concrete skin friction increase 15.26% which shows that increasing the binding strength of cement slurry and aging resistance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Reynolds number | Jeffrey fluid parameter | ||
| Peclet number | dynamic viscosity | ||
| Jeffrey fluid parameter | electrical conductivity | ||
| Schmidt number | applied magnetic field | ||
| Hartmann number | gravitational acceleration | ||
| thermal Grashof number | thermal expansion | ||
| mass Grashof number | mass expansion | ||
| density |
References
- Whitaker, R.H.; Brann, R. Mineral Composition. Patent US7651559B2, 26 January 2010. [Google Scholar]
- Roco, M.C.; Williams, R.S.; Alivisatos, P. Nanotechnology Research Directions: IWGN Workshop Report. Vision for Nanotechnology R&D in the Next Decade; National Science and Technology Council: Arlington, VA, USA, 1999. [Google Scholar]
- Sobolev, K.; Flores, I.; Torres-Martinez, L.; Valdez, P.; Zarazua, E.; Cuellar, E. Engineering of SiO 2 nanoparticles for optimal performance in nano cement-based materials. In Nanotechnology in Construction 3; Springer: Berlin/Heidelberg, Germany, 2009; pp. 139–148. [Google Scholar]
- Gann, D. A review of nanotechnology and its potential applications for construction. SPRU Univ. Sussex 2002, 2002, 28. [Google Scholar]
- Bartos, P.J. Nanotechnology in construction: A roadmap for development. In Nanotechnology in Construction 3; Springer: Berlin/Heidelberg, Germany, 2009; pp. 15–26. [Google Scholar]
- Sobolev, K.; Flores, I.; Hermosillo, R.; Torres-Martínez, L. Nanomaterials and nanotechnology for high-performance cement composites. Presented at the Presented at the ACI Session on Nanotechnology of Concrete: Recent Developments Future Perspectives, Denver, CO, USA, 7 November 2006. [Google Scholar]
- Sobolev, K.; Gutiérrez, M.F. How nanotechnology can change the concrete world. Am. Ceram. Soc. Bull. 2005, 84, 14. [Google Scholar]
- Zaki, S.; Ragab, K.S. How nanotechnology can change concrete industry. In Proceedings of the “1st International Conference” Sustainable Built Environment Infrastructures in Developing Countries, Bandung, Indonesia, 2–3 November 2009; p. 2170-0095. [Google Scholar]
- Hadi, A.A.A. Nanoparticles concentration and environmental effects on cogeneration system in cement industry. Int. J. Eng. Res. Gen. Sci. 2015, 3, 786–798. [Google Scholar]
- Nazari, A.; Riahi, S.; Riahi, S.; Shamekhi, S.F.; Khademno, A. Influence of Al2O3 nanoparticles on the compressive strength and workability of blended concrete. J. Am. Sci. 2010, 6, 6–9. [Google Scholar]
- Morsy, M.; Alsayed, S.; Aqel, M. Hybrid effect of carbon nanotube and nano-clay on physico-mechanical properties of cement mortar. Constr. Build. Mater. 2011, 25, 145–149. [Google Scholar] [CrossRef]
- Malhotra, V.M.; Mehta, P.K. High-Performance, High-Volume Fly Ash Concrete: Materials, Mixture Proportioning, Properties, Construction Practice, and Case Histories; Supplementary Cementing Materials for Sustainable Development: Ottawa, ON, Canada, 2002. [Google Scholar]
- Raki, L.; Beaudoin, J.; Alizadeh, R.; Makar, J.; Sato, T. Cement and concrete nanoscience and nanotechnology. Materials 2010, 3, 918–942. [Google Scholar] [CrossRef]
- Bahmani, S.H.; Huat, B.B.; Asadi, A.; Farzadnia, N. Stabilization of residual soil using SiO2 nanoparticles and cement. Constr. Build. Mater. 2014, 64, 350–359. [Google Scholar] [CrossRef]
- Shekari, A.; Razzaghi, M. Influence of nano particles on durability and mechanical properties of high performance concrete. Procedia Eng. 2011, 14, 3036–3041. [Google Scholar] [CrossRef]
- Givi, A.N.; Rashid, S.A.; Aziz, F.N.A.; Salleh, M.A.M. Experimental investigation of the size effects of SiO2 nano-particles on the mechanical properties of binary blended concrete. Compos. Part B Eng. 2010, 41, 673–677. [Google Scholar] [CrossRef]
- Kang, S.; Hong, S.I.; Choe, C.R.; Park, M.; Rim, S.; Kim, J. Preparation and characterization of epoxy composites filled with functionalized nanosilica particles obtained via sol–gel process. Polymer 2001, 42, 879–887. [Google Scholar] [CrossRef]
- Edelstein, A.S.; Cammaratra, R. Nanomaterials: Synthesis, Properties and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Sobolev, K. Mechano-chemical modification of cement with high volumes of blast furnace slag. Cem. Concr. Compos. 2005, 27, 848–853. [Google Scholar] [CrossRef]
- Sobolev, K. Effect of complex admixtures on cement properties and the development of a test procedure for the evaluation of high-strength cements. Adv. Cem. Res. 2003, 15, 67–76. [Google Scholar] [CrossRef]
- Li, G. Properties of high-volume fly ash concrete incorporating nano-SiO2. Cem. Concr. Res. 2004, 34, 1043–1049. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Int. J. Therm. Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Arasteh, H.; Mashayekhi, R.; Goodarzi, M.; Motaharpour, S.H.; Dahari, M.; Toghraie, D. Heat and fluid flow analysis of metal foam embedded in a double-layered sinusoidal heat sink under local thermal non-equilibrium condition using nanofluid. J. Therm. Anal. Calorim. 2019, 138, 1461–1476. [Google Scholar] [CrossRef]
- Yousefzadeh, S.; Rajabi, H.; Ghajari, N.; Sarafraz, M.M.; Akbari, O.A.; Goodarzi, M. Numerical investigation of mixed convection heat transfer behavior of nanofluid in a cavity with different heat transfer areas. J. Therm. Anal. Calorim. 2019, 1–25. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohseni-Gharyehsafa, B.; Ghazvini, M.; Goodarzi, M.; Jilte, R.D.; Kumar, R. Comparing various machine learning approaches in modeling the dynamic viscosity of CuO/water nanofluid. J. Therm. Anal. Calorim. 2019, 1–15. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of heat transfer enhancement in a forward-facing contracting channel using FMWCNT nanofluids. Numer. Heat Transf. Part A Appl. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Gholamalizadeh, E.; Pahlevanzadeh, F.; Ghani, K.; Karimipour, A.; Nguyen, T.K.; Safaei, M.R. Simulation of water/FMWCNT nanofluid forced convection in a microchannel filled with porous material under slip velocity and temperature jump boundary conditions. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Jalali, E.; Ali Akbari, O.; Sarafraz, M.M.; Abbas, T.; Safaei, M.R. Heat transfer of oil/MWCNT nanofluid jet injection inside a rectangular microchannel. Symmetry 2019, 11, 757. [Google Scholar] [CrossRef]
- Bahiraei, M.; Jamshidmofid, M.; Goodarzi, M. Efficacy of a hybrid nanofluid in a new microchannel heat sink equipped with both secondary channels and ribs. J. Mol. Liq. 2019, 273, 88–98. [Google Scholar] [CrossRef]
- Giwa, S.O.; Sharifpur, M.; Goodarzi, M.; Alsulami, H.; Meyer, J.P. Influence of base fluid, temperature, and concentration on the thermophysical properties of hybrid nanofluids of alumina–ferrofluid: Experimental data, modeling through enhanced ANN, ANFIS, and curve fitting. J. Therm. Anal. Calorim. 2020, 1–19. [Google Scholar] [CrossRef]
- Peng, Y.; Zahedidastjerdi, A.; Abdollahi, A.; Amindoust, A.; Bahrami, M.; Karimipour, A.; Goodarzi, M. Investigation of energy performance in a U-shaped evacuated solar tube collector using oxide added nanoparticles through the emitter, absorber and transmittal environments via discrete ordinates radiation method. J. Therm. Anal. Calorim. 2020, 139, 2623–2631. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Dareh Baghi, A.; Safaei, M.R.; Leon, A.S.; Ghomashchi, R.; Goodarzi, M.; Lin, C.-X. Assessment of Iron Oxide (III)–Therminol 66 Nanofluid as a Novel Working Fluid in a Convective Radiator Heating System for Buildings. Energies 2019, 12, 4327. [Google Scholar] [CrossRef]
- Karimipour, A.; Bagherzadeh, S.A.; Taghipour, A.; Abdollahi, A.; Safaei, M.R. A novel nonlinear regression model of SVR as a substitute for ANN to predict conductivity of MWCNT-CuO/water hybrid nanofluid based on empirical data. Phys. A Stat. Mech. Its Appl. 2019, 521, 89–97. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.; Doğan, S.; Avrutin, V.; Cho, S.-J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 11. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Gedanken, A. A template-free, sonochemical route to porous ZnO nano-disks. Microporous Mesoporous Mater. 2008, 110, 553–559. [Google Scholar] [CrossRef]
- Ludi, B.; Niederberger, M. Zinc oxide nanoparticles: Chemical mechanisms and classical and non-classical crystallization. Dalton Trans. 2013, 42, 12554–12568. [Google Scholar] [CrossRef]
- Nochaiya, T.; Sekine, Y.; Choopun, S.; Chaipanich, A. Microstructure, characterizations, functionality and compressive strength of cement-based materials using zinc oxide nanoparticles as an additive. J. Alloys Compd. 2015, 630, 1–10. [Google Scholar] [CrossRef]
- Arefi, M.R.; Rezaei-Zarchi, S. Synthesis of zinc oxide nanoparticles and their effect on the compressive strength and setting time of self-compacted concrete paste as cementitious composites. Int. J. Mol. Sci. 2012, 13, 4340–4350. [Google Scholar] [CrossRef] [PubMed]
- Flores-Velez, L.M.; Dominguez, O. Characterization and properties of Portland cement composites incorporating zinc-iron oxide nanoparticles. J. Mater. Sci. 2002, 37, 983–988. [Google Scholar] [CrossRef]
- Taylor-Lange, S.C.; Riding, K.A.; Juenger, M.C. Increasing the reactivity of metakaolin-cement blends using zinc oxide. Cem. Concr. Compos. 2012, 34, 835–847. [Google Scholar] [CrossRef]
- Nguyen, T.M.T.; Wang, P.-W.; Hsu, H.-M.; Cheng, F.-Y.; Shieh, D.-B.; Wong, T.-Y.; Chang, H.-J. Dental cement’ biological and mechanical properties improved by ZnO nanospheres. Mater. Sci. Eng. C 2019, 97, 116–123. [Google Scholar] [CrossRef]
- Gowda, R.; Narendra, H.; Mourougane, R.; Nagabhushana, B. Performance of Nano-SiO 2 and Nano-ZnO 2 on Compressive Strength and Microstructure Characteristics of Cement Mortar. In Sustainable Construction and Building Materials; Springer: Berlin/Heidelberg, Germany, 2019; pp. 13–22. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Taj, M.; Ullah, I.; Aldawsari, A.M.; Thounthong, P.; Sooppy Nisar, K. MHD Flow and Heat Transfer in Sodium Alginate Fluid with Thermal Radiation and Porosity Effects: Fractional Model of Atangana–Baleanu Derivative of Non-Local and Non-Singular Kernel. Symmetry 2019, 11, 1295. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A. A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid. Eur. Phys. J. Plus 2017, 132, 54. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Khan, I.; Gohar, M.; Saqib, M. On the applications of nanofluids to enhance the performance of solar collectors: A comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional models. Eur. Phys. J. Plus 2017, 132, 540. [Google Scholar] [CrossRef]
- Asif, M.; Ul Haq, S.; Islam, S.; Abdullah Alkanhal, T.; Khan, Z.A.; Khan, I.; Nisar, K.S. Unsteady Flow of Fractional Fluid between Two Parallel Walls with Arbitrary Wall Shear Stress Using Caputo–Fabrizio Derivative. Symmetry 2019, 11, 449. [Google Scholar] [CrossRef]
- Gohar, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Shah, A. The unsteady flow of generalized hybrid nanofluids: Applications in cementitious materials. J. Aust. Ceram. Soc. 2018, 55, 657–666. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. New direction in fractional differentiation. Math. Nat. Sci. 2017, 1, 18–25. [Google Scholar] [CrossRef][Green Version]
- Sheikh, N.A.; Ali, F.; Khan, I.; Gohar, M. A theoretical study on the performance of a solar collector using CeO2 and Al2O3 water based nanofluids with inclined plate: Atangana–Baleanu fractional model. ChaosSolitons Fractals 2018, 115, 135–142. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Fetecau, C. Flow of a viscoelastic fluid with the fractional Maxwell model between two side walls perpendicular to a plate. Appl. Math. Comput. 2008, 200, 459–464. [Google Scholar] [CrossRef]
- Siddique, I.; Vieru, D. Exact solution for the rotational flow of a generalized second grade fluid in a circular cylinder. Acta Mech. Sin. 2009, 25, 777–785. [Google Scholar] [CrossRef]
- Hristov, J. The non-linear Dodson diffusion equation: Approximate solutions and beyond with formalistic fractionalization. Math. Nat. Sci. 2017, 1, 1–17. [Google Scholar] [CrossRef][Green Version]
- Atangana, A.; Bildik, N. The use of fractional order derivative to predict the groundwater flow. Math. Probl. Eng. 2013, 2013, 543026. [Google Scholar] [CrossRef]
- Besbes, S.D.; Guillopé, C. Non-isothermal flows of viscoelastic incompressible fluids. Nonlinear Anal. 2001, 44, 919–942. [Google Scholar] [CrossRef]
- Djabi, A.; Merouani, A.; Aissaoui, A. A frictional contact problem with wear involving elastic-viscoplastic materials with damage and thermal effects. Electron. J. Qual. Theory Differ. Equ. 2015, 2015, 1–18. [Google Scholar] [CrossRef]
- Kothandapani, M.; Srinivas, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. Int. J. Non-Linear Mech. 2008, 43, 915–924. [Google Scholar] [CrossRef]
- Artemov, M.A.; Baranovskii, E.S. Solvability of the Boussinesq Approximation for Water Polymer Solutions. Mathematics 2019, 7, 611. [Google Scholar] [CrossRef]
- Ali, F.; Gohar, M.; Khan, I. MHD flow of water-based Brinkman type nanofluid over a vertical plate embedded in a porous medium with variable surface velocity, temperature and concentration. J. Mol. Liq. 2016, 223, 412–419. [Google Scholar] [CrossRef]
- Zakian, V. Numerical inversion of Laplace transform. Electron. Lett. 1969, 5, 120–121. [Google Scholar] [CrossRef]
- Reches, Y. Nanoparticles as concrete additives: Review and perspectives. Constr. Build. Mater. 2018, 175, 483–495. [Google Scholar] [CrossRef]
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| Properties | Concrete | |
|---|---|---|
| 2300 | 5.61 × 103 | |
| 1.160 | 1.046 | |
| 41.086 | 0.880 | |
| 1.57 | 1.25 |
| Enhancement (%) | ||||||
|---|---|---|---|---|---|---|
| 0.00 | 0.2 | 0.5 | 0.5 | 2 | 0.596 | |
| 0.01 | 0.2 | 0.5 | 0.5 | 2 | 0.645 | 8.221% |
| 0.02 | 0.2 | 0.5 | 0.5 | 2 | 0.669 | 12.24% |
| 0.03 | 0.2 | 0.5 | 0.5 | 2 | 0.681 | 14.26% |
| 0.04 | 0.2 | 0.5 | 0.5 | 2 | 0.687 | 15.26% |
| Enhancement (%) | ||||
|---|---|---|---|---|
| 0.00 | 2 | 0.2 | 0.603 | |
| 0.01 | 2 | 0.2 | 0.675 | 11.94% |
| 0.02 | 2 | 0.2 | 0.758 | 25.70% |
| 0.03 | 2 | 0.2 | 0.854 | 41.62% |
| 0.04 | 2 | 0.2 | 0.969 | 60.69% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikh, N.A.; Chuan Ching, D.L.; Khan, I.; Ahmad, A.; Ammad, S. Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry. Symmetry 2020, 12, 1037. https://doi.org/10.3390/sym12061037
Sheikh NA, Chuan Ching DL, Khan I, Ahmad A, Ammad S. Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry. Symmetry. 2020; 12(6):1037. https://doi.org/10.3390/sym12061037
Chicago/Turabian StyleSheikh, Nadeem Ahmad, Dennis Ling Chuan Ching, Ilyas Khan, Afnan Ahmad, and Syed Ammad. 2020. "Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry" Symmetry 12, no. 6: 1037. https://doi.org/10.3390/sym12061037
APA StyleSheikh, N. A., Chuan Ching, D. L., Khan, I., Ahmad, A., & Ammad, S. (2020). Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry. Symmetry, 12(6), 1037. https://doi.org/10.3390/sym12061037







