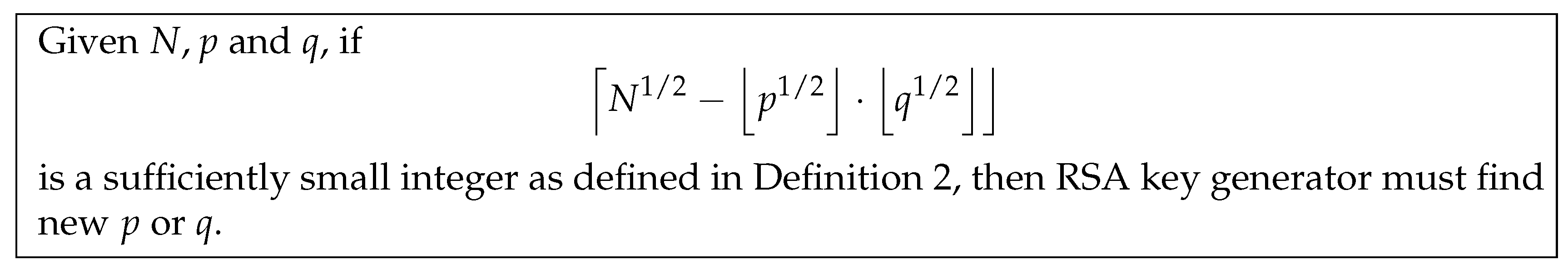A New LSB Attack on Special-Structured RSA Primes

Abstract

Asymmetric key cryptosystem is a vital element in securing our communication in cyberspace. It encrypts our transmitting data and authenticates the originality and integrity of the data. The Rivest–Shamir–Adleman (RSA) cryptosystem is highly regarded as one of the most deployed public-key cryptosystem today. Previous attacks on the cryptosystem focus on the effort to weaken the hardness of integer factorization problem, embedded in the RSA modulus, $N=pq$. The adversary used several assumptions to enable the attacks. For examples, p and q which satisfy Pollard’s weak primes structures and partial knowledge of least significant bits (LSBs) of p and q can cause N to be factored in polynomial time, thus breaking the security of RSA. In this paper, we heavily utilized both assumptions. First, we assume that p and q satisfy specific structures where $p=a^m+r_p$ and $q=b^m+r_q$ for $a,b$ are positive integers and m is a positive even number. Second, we assume that the bits of $r_p$ and $r_q$ are the known LSBs of p and q respectively. In our analysis, we have successfully factored N in polynomial time using both assumptions. We also counted the number of primes that are affected by our attack. Based on the result, it may poses a great danger to the users of RSA if no countermeasure being developed to resist our attack.

1. Introduction

One of the earliest asymmetric key cryptosystems is the Rivest–Shamir–Adleman (RSA) cryptosystem, introduced by Rivest, Shamir and Adleman in 1978 [1]. Its simple and easy-to-understand mathematical design makes it compelling to be used in the early ages of digital cyberspace technology. Since then, it is considered as the most widely known asymmetric key cryptosystem. In its key generation algorithm, an RSA modulus, $N=pq$ is computed where p and q, called RSA primes are two distinct primes such that $p<q<2p$. From the values of p and q, another parameter called RSA public exponent, e is obtained which satisfies $e<\varphi \left(N\right)$ and $gcd(e,\varphi (N\left)\right)=1$ where $\varphi \left(N\right)=(p-1)(q-1)$. An RSA private exponent, d that satisfies $ed\equiv 1(modN)$ then is computed. One of the security strength of RSA is integer factorization problem and it is embedded in the RSA modulus since p and q are very large $n-$bit primes (typically, $n=1024$). The problem is deemed infeasible to be solved by current computing machines and the best algorithm to solve the problem, called general number field sieve (GNFS) [2] is still running in sub-exponential time.

Past attacks on RSA by Pollard in 1974 [3] have shown that primes with particular structures are vulnerable to be factored in polynomial time, which is easily computed by any modern computers. In his attacks, Pollard showed that if $p-1$ or $q-1$ are constituted of small primes, then there is a factoring algorithm to factor $N=pq$ in polynomial time. Another method in attacking RSA assumes that several bits of p and q are known by the adversary and this weakens the hardness of factoring N. Particularly, ref. [4] showed that $1/2$ least significant bits (LSBs) of the RSA primes are sufficient to factor N in polynomial time. Random reconstruction algorithm by Heninger and Shacham also showed that it can efficiently recover all of the RSA keys given 0.57 fraction of the random bits of each p and q [5]. Later, Maitra et al. [6] provided a combinatorial model of Heninger’s work and was able to reconstruct the LSBs of RSA primes using modified brute-force by shortening the total search space.

The LSBs discussed in the prior attacks of RSA are commonly gathered by side-channel attack. It is one of the prominent methods to collect the physical outputs or side-effects of cryptographic devices during the computing processes [7]. The outputs or side-effects include but are not limited to the computational time and power of decryption [8,9], emission heat and electromagnetic radiation of the devices [10], cache behavior [11] and sound of processor during computations [12].

About This Paper

The results in this paper are the extensions from our papers in [13] and [14]. In this paper, we assume that certain LSBs of the RSA primes are known. We show that only a small amount of LSBs are required in our attack to factor N in polynomial time given that the RSA primes satisfy specified structures. We also show the abundance of primes that can satisfy the structures and no proper checking mechanism has been done in any standard RSA libraries to hinder the usage of such primes. This shows the risks inherent in the existing method to generate RSA keys may produces RSA modulus that falls under our attack.

2. Preliminaries

In this section, we provide some helpful lemmas which results are applied to make our attack successful.

Lemma 1.

Let $a,r\in {\mathbb{Z}}^{+}$ and $m\ge 2$ be an even number. If $\sqrt{a^m+r}=a^{m/2}+ϵ$ then $ϵ<\frac{r}{2a^{m/2}}$.

Proof. 

Let $a^m+r$ be an integer where $a\in {\mathbb{Z}}^{+}$. Then

$$\begin{array}{c}\sqrt{a^m+r}<\sqrt{a^m+\frac{r^2}{4}{a}^{-m}+r}=\sqrt{{(a^{m/2}+\frac{r}{2}{a}^{-m/2})}^2}=a^{m/2}+\frac{r}{2}{a}^{-m/2}\hfill \end{array}$$

Since $\sqrt{a^m+r}=a^{m/2}+ϵ$ then $ϵ<\frac{r}{2a^{m/2}}$. This terminates the proof. □

Suppose $N=pq$ is a valid RSA modulus where $p=a^m+r_p$ and $q=b^m+r_q$. Let $a,b\in {\mathbb{Z}}^{+}$, we can see that $ab$ is unknown if p and q are secret values. Using the result from Lemma 1, we find the lower and upper bounds of $N^{1/2}-{\left(ab\right)}^{m/2}$ in the following lemma.

Lemma 2.

Let $a,b\in {\mathbb{Z}}^{+}$ and $m\ge 2$ be an even number such that $a<b<{(2a^m+1)}^{\frac{1}{m}}$. Suppose $N=(a^m+r_p)(b^m+r_q)$ where $r_p\le r_q<N^{\gamma }$. If $r_p<2a^{m/2}$ and $r_q<2b^{m/2}$ then ${\left(r_p{r}_q\right)}^{1/2}<N^{1/2}-{\left(ab\right)}^{m/2}<\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1$.

Proof. 

To prove the lower bound, first we need to show that $a^m{r}_q+b^m{r}_p>2{\left(ab\right)}^{m/2}{\left(r_p{r}_q\right)}^{1/2}$. Observe that

$$\begin{array}{c}{\left(a^{m/2}{r}_q^{1/2}-b^{m/2}{r}_p^{1/2}\right)}^2=a^m{r}_q+b^m{r}_p-2{\left(ab\right)}^{m/2}{\left(r_p{r}_q\right)}^{1/2}.\hfill \end{array}$$

Since ${\left(a^{m/2}{r}_q^{1/2}-b^{m/2}{r}_p^{1/2}\right)}^2$ will always be positive value, it implies that $a^m{r}_q+b^m{r}_p>2{\left(ab\right)}^{m/2}{\left(r_p{r}_q\right)}^{1/2}$. Then

$$\begin{array}{ccc}\sqrt{(a^m+r_p)(b^m+r_q)}\hfill & =& \sqrt{{\left(ab\right)}^m+a^m{r}_q+b^m{r}_p+r_p{r}_q}\hfill \\ & >& \sqrt{{\left(ab\right)}^m+2{\left(ab\right)}^{m/2}{\left(r_p{r}_q\right)}^{1/2}+r_p{r}_q}\hfill \\ & =& \sqrt{{\left(a{b}^{m/2}+{\left(r_p{r}_q\right)}^{1/2}\right)}^2}\hfill \\ & =& {\left(ab\right)}^{m/2}+{\left(r_p{r}_q\right)}^{1/2}\hfill \end{array}$$

Thus, $\sqrt{(a^m+r_p)(b^m+r_q)}-{\left(ab\right)}^{m/2}=N^{1/2}-{\left(ab\right)}^{m/2}>{\left(r_p{r}_q\right)}^{1/2}$. To prove the upper bound, since $\sqrt{a^m+r_p}=a^{m/2}+{ϵ}_1$ and $\sqrt{b^m+r_q}=b^{m/2}+{ϵ}_2$. Then, based on Lemma 1,

$$\begin{array}{ccc}{N}^{1/2}\hfill & =& \sqrt{(a^m+r_p)(b^m+r_q)}=\sqrt{(a^m+r_p)}\sqrt{(b^m+r_q)}\hfill \\ & =& (a^{m/2}+{ϵ}_1)(b^{m/2}+{ϵ}_2)={\left(ab\right)}^{m/2}+a^{m/2}{ϵ}_2+b^{m/2}{ϵ}_1+{ϵ}_1{ϵ}_2\hfill \\ & <& {\left(ab\right)}^{m/2}+a^{m/2}\frac{r_q}{2b^{m/2}}+b^{m/2}\frac{r_p}{2a^{m/2}}+\frac{r_p}{2a^{m/2}}\frac{r_q}{2b^{m/2}}\hfill \end{array}$$

(1)

If $r_p<2a^{m/2}$ and $r_q<2b^{m/2}$ then

$$\begin{array}{ccc}\frac{r_p}{2a^{m/2}}\frac{r_q}{2b^{m/2}}\hfill & =& \frac{r_p{r}_q}{4{\left(ab\right)}^{m/2}}<\frac{4{\left(ab\right)}^{m/2}}{4{\left(ab\right)}^{m/2}}\hfill \\ & =& 1.\hfill \end{array}$$

(2)

If $a<b<{(2a^m+1)}^{\frac{1}{m}}$, then Equation (1) becomes

$$\begin{array}{ccc}{N}^{1/2}-{\left(ab\right)}^{m/2}\hfill & <& a^{m/2}\frac{r_q}{2b^{m/2}}+b^{m/2}\frac{r_p}{2a^{m/2}}+1\hfill \\ & =& {\left(\frac{a}{b}\right)}^{m/2}\frac{r_q}{2}+{\left(\frac{b}{a}\right)}^{m/2}\frac{r_p}{2}+1\hfill \\ & <& {\left(1\right)}^{m/2}\frac{r_q}{2}+{\left(2\right)}^{m/2}\frac{r_p}{2}+1\hfill \\ & =& \frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1.\hfill \end{array}$$

This terminates the proof. □

By obtaining the lower and upper bounds of $N^{1/2}-{\left(ab\right)}^{m/2}$ in Lemma 2, we have gathered a result that can be useful in our attack later. Throughout this paper, we focus on the RSA primes in the forms of $p=a^m+r_p$ and $q=b^m+r_q$. Therefore, we define LSBs in the next definition based on these forms.

Definition 1

(Least Significant Bits (LSBs) of Primes). Let $l_1,l_2,m\in {\mathbb{Z}}^{+}$. Suppose $p=a^m+r_p$ and $q=b^m+r_q$ are primes. Suppose there exist unknown $a_0$ and $b_0$ such that

$$p={(2^{l_1}·a_0)}^m+r_p$$

(3)

and

$$q={(2^{l_2}·b_0)}^m+r_q.$$

(4)

Then we define $r_p$ and $r_q$ to be k-many LSBs of p and q respectively where $k\le l_{1}m,l_{2}m$ satisfies

$$r_p\equiv p(mod{2}^{l_{1}m})$$

(5)

and

$$r_q\equiv q(mod{2}^{l_{2}m}).$$

(6)

To identify primes that satisfy Equations (3) and (4), we observe the binary representations of $a^m$ and $b^m$. Their LSBs must have k many consecutive 0’s to satisfy $p=a^m+r_p$ and $q=b^m+r_q$. Particularly, let $r_{p_i}$ be the binary representation of a and $r_{q_i}$ be the binary representation of b where $i=1,2,\dots ,n$. Observe

$$\begin{array}{c}{a}^m=\underset{n-k\mathrm{many}\mathrm{bits}\mathrm{of}1\mathrm{and}0’\mathrm{s}}{\underbrace{r_{p_1}{r}_{p_2}\dots r_{p_{(n-k)}}}}\stackrel{k\mathrm{many}\mathrm{bits}\mathrm{of}0’\mathrm{s}}{\overbrace{r_{p_{(n-k+1)}}\dots r_{p_n}}}\hfill \end{array}$$

(7)

$$\begin{array}{c}{b}^m=\underset{n-k\mathrm{many}\mathrm{bits}\mathrm{of}1\mathrm{and}0’\mathrm{s}}{\underbrace{r_{q_1}{r}_{q_2}\dots r_{q_{(n-k)}}}}\stackrel{k\mathrm{many}\mathrm{bits}\mathrm{of}0’\mathrm{s}}{\overbrace{r_{q_{(n-k+1)}}\dots r_{q_n}}}\hfill \end{array}$$

(8)

The random reconstruction algorithm [5], which was improved by [6], is one of the efficient algorithms used to find the LSBs of RSA primes. Thus, it can be utilized to find the values of $r_p$ and $r_q$ that satisfy Equations (5) and (6).

3. Our Attack

Before we proceed to show how N can be factored in polynomial time using previous results, we define the term ‘sufficiently small’ that is used to justify our attack.

Definition 2.

We define sufficiently small value in this paper to be a value smaller than the largest feasible value of the lowest security level to be brute forced by current computing machine.

Remark 1.

The latest recommendation for key management by NIST [15] stated that the lowest security level is 112-bit. This implies that the largest feasible value of this security level to be brute forced by current computing machine is $2^{112}$. Based on Definition 2, a value lower than $2^{112}$ is considered sufficiently small. This value can be changed in the future, depends on the future advancements of computing technology.

Now we are ready to show how RSA modulus can be factored in polynomial time by using this next theorem.

Theorem 1.

Let $a,b\in {\mathbb{Z}}^{+}$ and $m\ge 2$ be an even number such that $a<b<{(2a^m+1)}^{\frac{1}{m}}$. Suppose $N=pq=(a^m+r_p)(b^m+r_q)$ is a valid RSA modulus. Let $r_p\equiv p(mod{2}^m)$ and $r_q\equiv q(mod{2}^m)$ where $r_p<2a^{m/2}$ and $r_q<2b^{m/2}$ such that $max\{r_p,r_q\}<2^k$. If $2^{k-1}\left(2^{\frac{m}{2}}+1\right)$ is a sufficiently small value as defined in Definition 2 and k many LSBs of p and q are known then N can be factored in polynomial time.

Proof. 

From Lemma 2 we can see that ${\left(r_p{r}_q\right)}^{1/2}<N^{1/2}-{\left(ab\right)}^{m/2}<\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1$. Thus,

$$\begin{array}{cc}{N}^{1/2}-\left(\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1\right)\hfill & <{\left(ab\right)}^{m/2}<N^{1/2}-{\left(r_p{r}_q\right)}^{1/2}.\hfill \end{array}$$

(9)

Suppose $r_p$ and $r_q$ are known LSBs of p and q respectively. The LSB values may be obtained from side-channel attacks described previously in Section 1. Since $max\{r_p,r_q\}<2^k$, then the difference between the upper and lower bounds of Equation (9) is

$$\begin{array}{ccc}{N}^{1/2}-{\left(r_p{r}_q\right)}^{1/2}-N^{1/2}+\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1\hfill & <& 2^k\left(2^{\frac{m}{2}-1}+\frac{1}{2}\right)-{\left({\left(min\{r_p,r_q\}\right)}^2\right)}^{1/2}+1\hfill \\ & =& 2^k\left(\frac{2^{\frac{m}{2}}+1}{2}\right)-min\{r_p,r_q\}+1\hfill \\ & =& 2^{k-1}\left(2^{\frac{m}{2}}+1\right)-min\{r_p,r_q\}+1\hfill \end{array}$$

(10)

which is the size for set of integers to find ${\left(ab\right)}^{m/2}$. If $2^{k-1}\left(2^{\frac{m}{2}}+1\right)$ is sufficiently small as defined in Definition 2, then we can find ${\left(ab\right)}^{m/2}$ in polynomial time. By computing ${\left({\left(ab\right)}^{m/2}\right)}^2$, we find ${\left(ab\right)}^m$. Then

$$\begin{array}{ccc}N-r_p{r}_q\hfill & \equiv & (a^m+r_p)(b^m+r_q)-r_p{r}_q\hfill \\ & \equiv & {\left(ab\right)}^m+a^m{r}_q+b^m{r}_p\hfill \\ & \equiv & a^m{r}_q+b^m{r}_p(mod{\left(ab\right)}^m).\hfill \end{array}$$

Observe that from $r_p<2a^{m/2}$ and $r_q<2b^{m/2}$, then we can have $a^m{r}_q+b^m{r}_p<{\left(ab\right)}^m$. Thus, we obtain the full integer $a^m{r}_q+b^m{r}_p$ without modular reduction. Since the values of $r_p,r_q,{\left(ab\right)}^m$ and $a^m{r}_q+b^m{r}_p$ are known, we can find the roots of the following quadratic equation

$$X^2-(a^m{r}_q+b^m{r}_p)X+\left({\left(ab\right)}^m{r}_p{r}_q\right).$$

We find that $x_1=a^m{r}_q$ and $x_2=b^m{r}_p$. Since $r_p$ and $r_q$ are known, we can can obtain

$$a^m=\frac{x_1}{r_q}\mathrm{and}{b}^m=\frac{x_2}{r_p}.$$

Thus we can factor N by calculating

$$\frac{N}{b^m+r_q}=a^m+r_p.$$

 □

The next remark justifies our selection criteria on parameter m.

Remark 2.

Let $\mathbb{A}$ be the set of possible value of ${\left(ab\right)}^{m/2}$. From Equation (9), we know that $\mathbb{A}$ will yield a set of numbers between $N^{1/2}-\left(\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1\right)$ and $N^{1/2}-{\left(r_p{r}_q\right)}^{1/2}$. If $m\ge 2$ is an even integer, then ${\left(ab\right)}^{m/2}$ will be an integer and causes $\mathbb{A}$ to be a finite set. However, if m is a positive odd integer, then ${\left(ab\right)}^{m/2}$ will be a real value and causes $\mathbb{A}$ to be an infinite set. The latter consequence will make our method to be infeasible since there are infinite possible values of ${\left(ab\right)}^{m/2}$ to be tried on. Therefore, m must be an even integer equals or greater than 2.

The following is an example to illustrate the result from Theorem 1.

Example 1.

We use RSA-2048 modulus in this example. Specifically, we are given

$$\begin{array}{ccc}N\hfill & =& 25443213484803330676546636060506767271319211956273880351374351825\hfill \\ & & 46256158013255117739836500456730264902937246910852858138318236603\hfill \\ & & 28796126064275138262348021411229982061934595317738337964801727892\hfill \\ & & 54233470084592231117946043667803816674367149523326731127008733355\hfill \\ & & 36182425074366173327195127004160399499185526019310064433935140944\hfill \\ & & 60366015740466980367515605709366458027738329608044170750026717443\hfill \\ & & 54815841155246667831512956948961180313537576080810878904128457697\hfill \\ & & 49463326499780838181084411701695971249384738323330037734781899087\hfill \\ & & 42844727615199026762546947725863259415895257407078268520959081886\hfill \\ & & 49384624121217162949627607660163\hfill \end{array}$$

Suppose from side-channel attack described previously, we know the 12 LSBs of p and q. Particularly,

$$p=\underset{unknown1024bits}{\underbrace{1\dots 0000000000}}+\underset{known12-bits}{\underbrace{101111001001}}$$

and

$$q=\underset{unknown1024bits}{\underbrace{1\dots 0000000000}}+\underset{known12-bits}{\underbrace{100111101011}}$$

where

$$r_p={\left(101111001001\right)}_2=3017$$

(11)

and

$$r_q={\left(100111101011\right)}_2=2539$$

(12)

Then we set

$$\begin{array}{ccc}i\hfill & =& ⌈{\left(r_p{r}_q\right)}^{1/2}⌉\hfill \\ & =& 2768.\hfill \end{array}$$

Then we calculate

$$\sigma ={\left(\left[\sqrt{N}\right]-i\right)}^{2}andz\equiv N-\left(r_p{r}_q\right)(mod\sigma )$$

(13)

and solve the equation

$$x_{1,2}=X^2-zX+\sigma r_p{r}_q=0$$

(14)

We find that neither $\frac{x_1}{r_q}+r_p$ nor $\frac{x_2}{r_p}+r_q$ are integers. This means $x_1$ and $x_2$ are not our final solutions. It also means $\sigma \ne {\left(ab\right)}^m$ at this point. To find the correct σ, we have to iterate the computation of Equations (13) and (14) using iterations of increasing values of i. This search can be done in polynomial time as i should be less than $\frac{r_q}{2}+2^{\frac{m}{2}-1}{r}_p+1=7304$ as stated in Lemma 2. In this case, we find the correct σ when $i=2811$. That is, we compute

$$\begin{array}{ccc}\sigma \hfill & =& {\left(\left[\sqrt{N}\right]-i\right)}^2\hfill \\ & =& 25443213484803330676546636060506767271319211956273880351374351825\hfill \\ & & 46256158013255117739836500456730264902937246910852858138318236603\hfill \\ & & 28796126064275138262348021411229982061934595317738337964801727892\hfill \\ & & 54233470084592231117946043667803816674367149523326731127008733355\hfill \\ & & 36182425074366173327195127004160399499185525929621955792730967217\hfill \\ & & 57093357794065292733692579733017882760046777578179801403516768246\hfill \\ & & 29246851968098638468612026451713499821263832772646855070783021404\hfill \\ & & 05118967588741443353965388245391488440871378163462453288885183603\hfill \\ & & 73902790724858882651191332644704993553711430100366047804022517832\hfill \\ & & 60459933438910410000000000000000\hfill \end{array}$$

and

$$\begin{array}{ccc}z\hfill & =& N-\left(r_p{r}_q\right)(mod\sigma )\hfill \\ & =& 89688108641204173727032726579464016876338230259763485752676915520\hfill \\ & & 29864369346509949197255689891871480293629009304972476804922737433\hfill \\ & & 08164023833345436293443443589110393948271190234563044828085133601\hfill \\ & & 59867584445896715483689419368903401441113556150811582658621838273\hfill \\ & & 0671222071693656405388924690682306752949627600000000.\hfill \end{array}$$

Using values of σ and z, we solve the equation

$$x_{1,2}=X^2-zX+\sigma r_p{r}_q=0.$$

(15)

The solutions of Equation (15) are used to compute

$$\begin{array}{ccc}\frac{N}{\frac{x_1}{r_q}+r_p}\hfill & =& p\hfill \\ & =& 2076325666953480903251061985643543068723624934635381548413863\hfill \\ & & 1458070722097244580144040973758980302401303555418169933522406\hfill \\ & & 1662229162879643933792870833231736875142501533422110427899095\hfill \\ & & 3517812060123279372587614099731233402621448865880933141145360\hfill \\ & & 5245689592204158590965166633547679145670950934175191147210000\hfill \\ & & 3017\hfill \end{array}$$

and

$$\begin{array}{ccc}\frac{N}{\frac{x_2}{r_p}+r_q}\hfill & =& q\hfill \\ & =& 1225396087413168498292617260986889571145024632726919066571061\hfill \\ & & 6588749446565648362779666067127897821347705191543359716126834\hfill \\ & & 5944097932917669169852614268434890176706523882967335716979529\hfill \\ & & 9071636233133238459212674004750005745005313778479423967599274\hfill \\ & & 3740090403457711105290569800062341129610183840357926739210000\hfill \\ & & 2539.\hfill \end{array}$$

Hence, N has been successfully factored in polynomial time.

Remark 3.

From Example 1, we show that as small as 12-bits of LSBs are required to successfully execute our attack. Hence, this put our method in advantage since it does not necessarily depend on side-channel attack [7] to gather the LSBs. Instead, by using our method, an adversary can use brute-force approach to find the correct LSBs since the required LSBs can be very small.

4. Numbers of Primes with Vulnerable Specialized Structures Against Random Reconstruction Algorithm

From Equations (7) and (8) we can see that $r_{p_1}$ until $r_{p_{(n-k)}}$ must be another binary representation of a squared number. The same case also applies on $r_{q_1}$ until $r_{q_{(n-k)}}$ In the next Theorem, we count the number of squared numbers with $n-k$ bit.

Theorem 2.

If n is any large positive integer and k is a small positive integer then there are at least $⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋$ squared numbers between $2^{n-k-1}$ and $2^{n-k}-1$.

Proof. 

Let $X=\left\{x_i^2\right\}$ for $i=\{1,2,3,\dots \}$ be the set of all squared numbers between $2^{n-k-1}$ and $2^{n-k}-1$. Particularly,

$$2^{n-k-1}<x_i^2<2^{n-k}-1.$$

Then

$$\begin{array}{c}{2}^{\frac{1}{2}(n-k-1)}<x_i<{\left(2^{n-k}-1\right)}^{\frac{1}{2}}\Rightarrow 2^{\frac{1}{2}(n-k-1)}<x_i<{\left(\left(2^{\frac{n-k}{2}}-1\right)\left(2^{\frac{n-k}{2}}+1\right)\right)}^{\frac{1}{2}}.\hfill \end{array}$$

(16)

To find the least number of i, the amount of squared numbers between $2^{n-k-1}$ and $2^{n-k}-1$, we compute the difference between the upper bound and the lower bound of Equation (16) in integer form. That is,

$$\begin{array}{ccc}⌊{\left(\left(2^{\frac{n-k}{2}}-1\right)\left(2^{\frac{n-k}{2}}+1\right)\right)}^{\frac{1}{2}}-2^{\frac{1}{2}(n-k-1)}⌋\hfill & >& ⌊{\left(\left(2^{\frac{n-k}{2}}-1\right)\left(2^{\frac{n-k}{2}}-1\right)\right)}^{\frac{1}{2}}-2^{\frac{1}{2}(n-k-1)}⌋\hfill \\ & =& ⌊{\left({\left(2^{\frac{n-k}{2}}-1\right)}^2\right)}^{\frac{1}{2}}-2^{\frac{1}{2}(n-k-1)}⌋\hfill \\ & =& ⌊2^{\frac{n-k}{2}}-1-2^{\frac{1}{2}(n-k-1)}⌋.\hfill \\ & =& ⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)-1⌋.\hfill \end{array}$$

If n is any large positive integer and k is a small positive integer then

$$⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)-1⌋\approx ⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋.$$

This terminates the proof. □

Theorem 3.

Let $a,b\in {\mathbb{Z}}^{+}$ and $m\ge 2$ be an even number such that $a<b<{(2a^m+1)}^{\frac{1}{m}}$. Suppose $N=pq=(a^m+r_p)(b^m+r_q)$ be a valid RSA modulus. Let $r_p\equiv p(mod{2}^m)$ and $r_q\equiv q(mod{2}^m)$ where $r_p<2a^{m/2}$ and $r_q<2b^{m/2}$ such that $max\{r_p,r_q\}<2^k$. Let $x>0$ be an integer where $x^2$ is the smallest squared number with n-bit size. If $2^{k-1}\left(2^{\frac{m}{2}}+1\right)$ is a sufficiently small value as defined in Definition 2 and k many LSBs of p and q are known, then there are at most

$$\frac{⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋}{2}\left(\frac{2^k}{log{\left(x\right)}^2}+\frac{2^k}{log{\left(x+⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋\right)}^2}\right)$$

candidates of p and q with size of n-bit such that $p=a^m+r_p$ and $q=b^m+r_q$ satisfy Theorem 1.

Proof. 

Let $x>0$ be an integer where $x^2$ is the smallest squared number with $n-k$-bit. Let $f\left(x\right)$ be the prime-counting function between $x^2$ and $x^2+max\{r_p,r_q\}$. Then

$$\begin{array}{ccc}{\pi }_1^{\ast }\left(x\right)=\frac{x^2+max\{r_p,r_q\}}{log(x^2+max\{r_p,r_q\})}-\frac{x^2}{log{x}^2}\hfill & \approx & \frac{x^2+max\{r_p,r_q\}}{log{x}^2}-\frac{x^2}{log{x}^2}\hfill \\ & =& \frac{x^2+max\{r_p,r_q\}-x^2}{log{x}^2}=\frac{max\{r_p,r_q\}}{log{x}^2}\hfill \\ & <& \frac{2^k}{log{x}^2}.\hfill \end{array}$$

From Theorem 2, we know there are approximately $⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋$ squared numbers with $n-k$-bit size where $n-k$ is a large integer suitably used in RSA. Thus, ${\pi }_1^{\ast }\left(x\right)$ for the consecutive squared numbers are as follows:

$$\begin{array}{cc}\hfill {\pi }_1^{\ast }\left(x\right)& <\frac{2^k}{log{\left(x\right)}^2}\hfill \\ \hfill {\pi }_1^{\ast }(x+1)& <\frac{2^k}{log{(x+1)}^2}\hfill \\ \hfill {\pi }_1^{\ast }(x+2)& <\frac{2^k}{log{(x+2)}^2}\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⋮\hfill \\ \hfill {\pi }_1^{\ast }\left(x+⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋\right)& <\frac{2^k}{log{\left(x+⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋\right)}^2}.\hfill \end{array}$$

(17)

The summation of Equation (17) can be represented in the sum of arithmetic progression formula where the number of i terms is multiplied by the sum of the first and last number in the progression and dividing by 2. That is,

$$\begin{array}{ccc}{\pi }_2^{\ast }=\sum _{i=0}^{⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)-1⌋}\frac{2^k}{log{\left(x+i\right)}^2}\hfill & <& \frac{⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋}{2}\left({\pi }_1^{\ast }\left(x\right)+{\pi }_1^{\ast }\left(x+⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋\right)\right)\hfill \\ & <& \frac{⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋}{2}\left(\frac{2^k}{log{\left(x\right)}^2}+\frac{2^k}{log{\left(x+⌊2^{\frac{n-k}{2}}\left(1-2^{-\frac{1}{2}}\right)⌋\right)}^2}\right)\hfill \end{array}$$

(18)

This terminates the proof. □

Result from Theorem 3 shows there is a significant amount of primes that satisfy Theorem 1.

5. Comparative Analysis

Here we compare our results with the existing attacks with known bits of primes. The authors of [16] introduced partial key exposure attacks with assumption that certain bits of primes can be known by the adversary. They showed that $2/3$ bits of p or q are sufficient to factor N using integer programming technique. Later, ref. [17] reduced this value to $1/2$ using LLL algorithm. The attack from Herrmann and May later on required the known bits to be arranged in random blocks [18].

Heninger and Shacham’s attack is motivated by the so-called cold boot attack which targets the memory in electronic chips to reconstruct the bits of the private keys given that the bits are from random positions [5]. They successfully conducted the attack if $0.57$ random bits of the primes are known. It should be noted here their fraction value is much lower if they consider the random bits of RSA private exponent, d ($d_p$ and $d_q$ in the case of CRT-RSA). Using a similar method, ref. [6] proved that if the total LSBs from both p and q known is at least 50% of the total length of N, then N can be factored using lattice-based method. Our method, unlike existing methods, utilize k-many LSBs of the primes where k is less than the value of $2^{k-1}\left(2^{\frac{m}{2}}+1\right)$ which is sufficiently small as defined in Definition 2, as shown in Theorem 1.

The summaries of all the attacks are compiled in

Table 1. Comparison of our method against existing attacks with known bits of primes.

Attacks	Position of Known Bits	Bits of Primes Need to Be Known	Comments/ Remarks	Advantages/ Disadvantages
Rivest and Shamir (1985)	LSBs or MSBs	$2/3$ of the bits of p or q	Solving integer programming problem	Advantages: Fast speed Disadvantages: Requires a lot of known bits
Coppersmith (1996)	LSBs or MSBs	$1/2$ of the bits of p or q	Using lattice- based method
Herrmann and May (2008)	Any position (in blocks)	${log}_e\left(2\right)\approx 0.7$ of the bits of p or q	Number of blocks $\approx loglogN$
Heninger and Shacham (2009)	Any position	$r_p=N^{{\delta }_1}$ $r_q=N^{{\delta }_2}$ ${\delta }_1+{\delta }_2\ge 0.57$ of the bits of p or q	Using random reconstruction algorithm (RRA)
Maitra et al. (2010)	LSBs	$r_p=N^{{\delta }_1}$ $r_q=N^{{\delta }_2}$ ${\delta }_1+{\delta }_2\ge 0.5$ of the bits of p or q	Using RRA together with lattice-based method
Our method: Theorem 1	LSBs	$r_p,r_q<2^k$ where $2^k$ is sufficiently small as in Definition 2. That is $r_p,r_q<N^{\frac{k}{{log}_{2}N}}$.	Side-channel attack of complexity $O\left(2^k\right)$ where $2^k$ is sufficiently small as in Definition 2.	Advantages: Fast speed, requires less known bits Disadvantages: Requires specific hardware to conduct side-channel attack

.

From Table 1, we can see that our method required less LSBs for the attack to be successful when compared to [5,6]. That is, the attack required less computational time and space to be executed. It is easy to see that if $N\approx 2^{2048}$ and $k=80$, then $r_p,r_q<N^{0.039}$. This is a substantial improvement from previous works.

We would like to point out the trade-off of our attack, namely the characteristics as mentioned in Theorem 1. Nevertheless, our analysis shows that if $r_p$ and $r_q$ are bounded to $2^k$ where k is stated as in Definition 2, the side-channel attack can be conducted in reasonable time in order to identify whether the primes in physical devices fall under the category as mentioned. This results in our research to be of importance for real-world implementation of the RSA cryptosystem. Moreover, we have shown in Section 4 that the number of primes satisfying our conditions are exponentially many. This shows the importance of our attack.

6. Countermeasure of the Attack

Although the attack seems to target a niche set of primes, there is no immediate noticeable detection that can be implemented to overcome the attack. This means the prevention from utilizing the weak primes must be applied in the RSA key generator with the full knowledge of the secret parameters, p and q. The countermeasure is depicted in Figure 1.

Since the computation is minimal, the prevention of the attack can be applied in the real-world RSA implementation.

Example 2.

For a toy example of this countermeasure method, we revisit the values in Example 1. Given $N,p,q$ from Example 1, we compute

$$⌈N^{1/2}-⌊p^{1/2}⌋·⌊q^{1/2}⌋⌋=2811.$$

Since 2811 is definitely sufficiently small based on Definition 2, an RSA key generator must find new p and q. Let

$$\begin{array}{ccc}p\hfill & =& 10373821590420718162568315912935402272816716250952617784159371685\hfill \\ & & 44340371332193665789760371540571568043597631052985984619935841269\hfill \\ & & 00533099600902588040933556878478965238617603915696057625198338769\hfill \\ & & 03361223061009707594893117366305299494205202223327617461773922102\hfill \\ & & 7548212123977286017508681549015403870522203136301\hfill \\ q\hfill & =& 11233601978358194938103618628808793989586489373749842937474042065\hfill \\ & & 13933235347992919444792393988509367460666790358619415756939475813\hfill \\ & & 80412937835561807122090537966641130001194088391044588117638361372\hfill \\ & & 99643968716613613967481916652898906661611644105170965584735585835\hfill \\ & & 3331398195279380078798660391902694277601327538353\hfill \end{array}$$

be the the new p and q. Then,

$$\begin{array}{ccc}N\hfill & =& 11653538274128513578568669090454309990749271193335847349122392459\hfill \\ & & 01318960034317752307651515404527551518430900334308748335133453988\hfill \\ & & 21286310578795557118148985154417613224899775560303891043729606906\hfill \\ & & 29637177530605885689603305847327219925303871989047949044982302417\hfill \\ & & 19652217537589201420247464831069631221516545858847199510976358555\hfill \\ & & 34569641991568190286013308968767353183943188900880965338613790529\hfill \\ & & 14898692740675146768914029502466472816780769463189924714976665682\hfill \\ & & 15047424802978071513075475252664886423135404769620269065551233781\hfill \\ & & 80576090100374515694019647558981694450446331689603531906067965349\hfill \\ & & 37648446600588401959096464052253\hfill \end{array}$$

be the new RSA modulus, N. We compute

$$\begin{array}{ccc}⌈N^{1/2}-⌊p^{1/2}⌋·⌊q^{1/2}⌋⌋\hfill & =& 91788620433890001811698154984784049754386699417980052\hfill \\ & & 34196964320832189804911338215937374325313217127978801\hfill \\ & & 050344028808215933053746159321527280081664264988.\hfill \end{array}$$

which is larger than $2^{112}$. Hence N is safe from our attack.

7. Conclusions

We have shown an attack on RSA modulus, $N=pq$ where $p=a^m+r_p$ and $b^m+r_q$ for $r_p$ and $r_q$ are k LSBs of p and q respectively. Our attack can be mounted successfully in polynomial time if the LSBs of the primes are known and satisfy the conditions. We also show that there is a significant number of primes with respect to their sizes that are vulnerable to our attack. This imposes a great threat to the RSA users who might not realize that their RSA primes may fall under these vulnerable primes. However, our suggestion on how to detect the vulnerable primes during the key generation process may help to overcome this problem so that the RSA cryptosystem can still be applied.