A Two-Tier Partition Algorithm for the Optimization of the Large-Scale Simulation of Information Diffusion in Social Networks
Abstract
1. Introduction
- Difficulties in the storage, management, and analysis of big data. For large-scale social networks, such as WeChat and Weibo, the scale of data is very large—usually hundreds of millions or even billions. It is difficult to manage such unstructured data based on traditional file storage or relational databases. When the network scale is too large, the time consumption of connectivity is not acceptable in the traditional relational database, let alone in the analysis and calculation of network indexes such as node degree, cascades, and so on.
- Difficulties with the implementation of the simulation of large-scale social networks. Existing high-performance simulation engines, including MPI-based(Message Passing Interface) simulation tools, GPU-based(Graphic Processing Unit) simulation engines [10], and so on, cannot obtain high performance in the simulation of large-scale social networks because of the strong correlations in the network. Too many interactions among nodes decrease the performance greatly, especially when the nodes are distributed in different machines.
2. Related Works
3. The Spark-Based Large-Scale Simulation of Information Siffusion in Social Networks
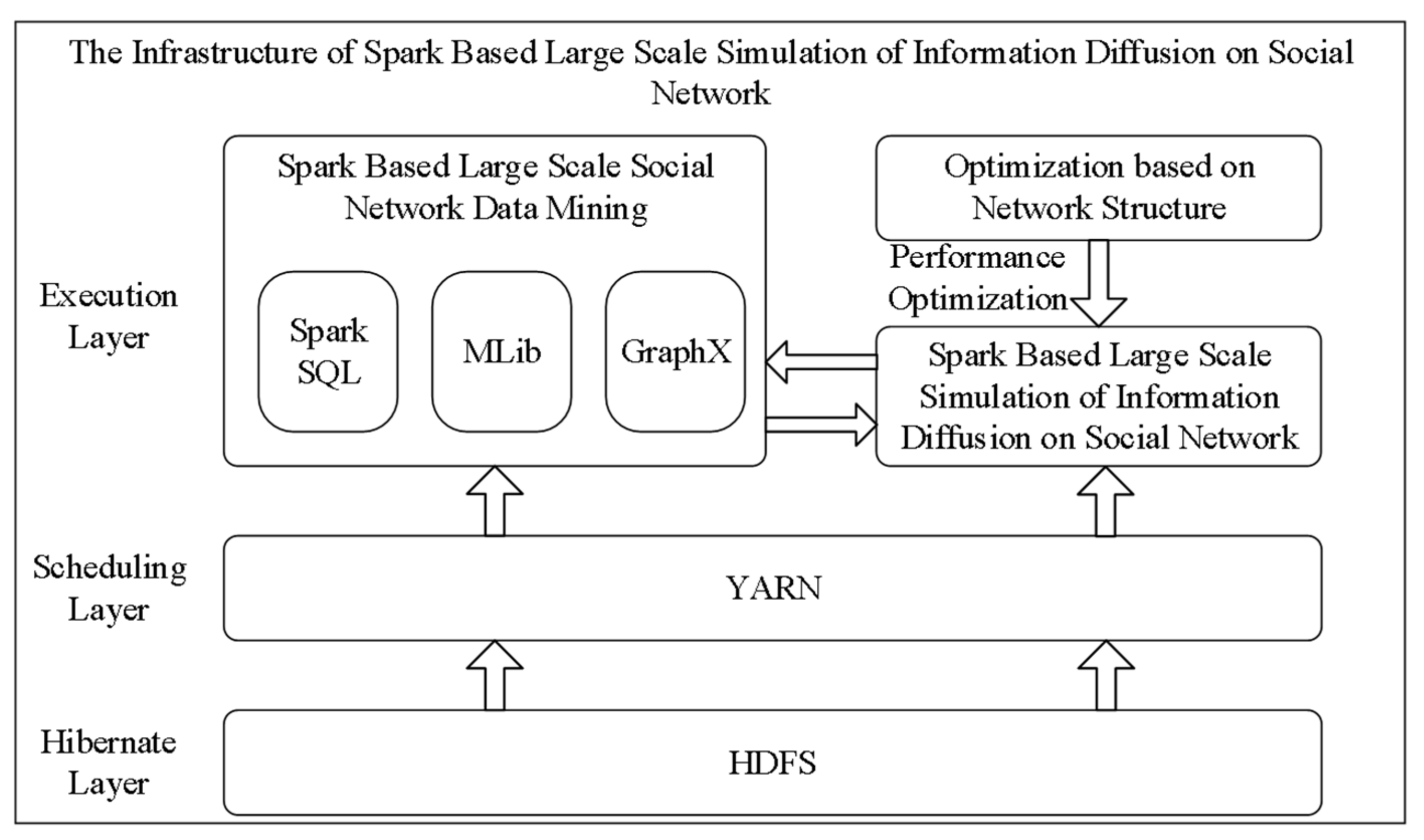
3.1. The Infrastructure of Simulation
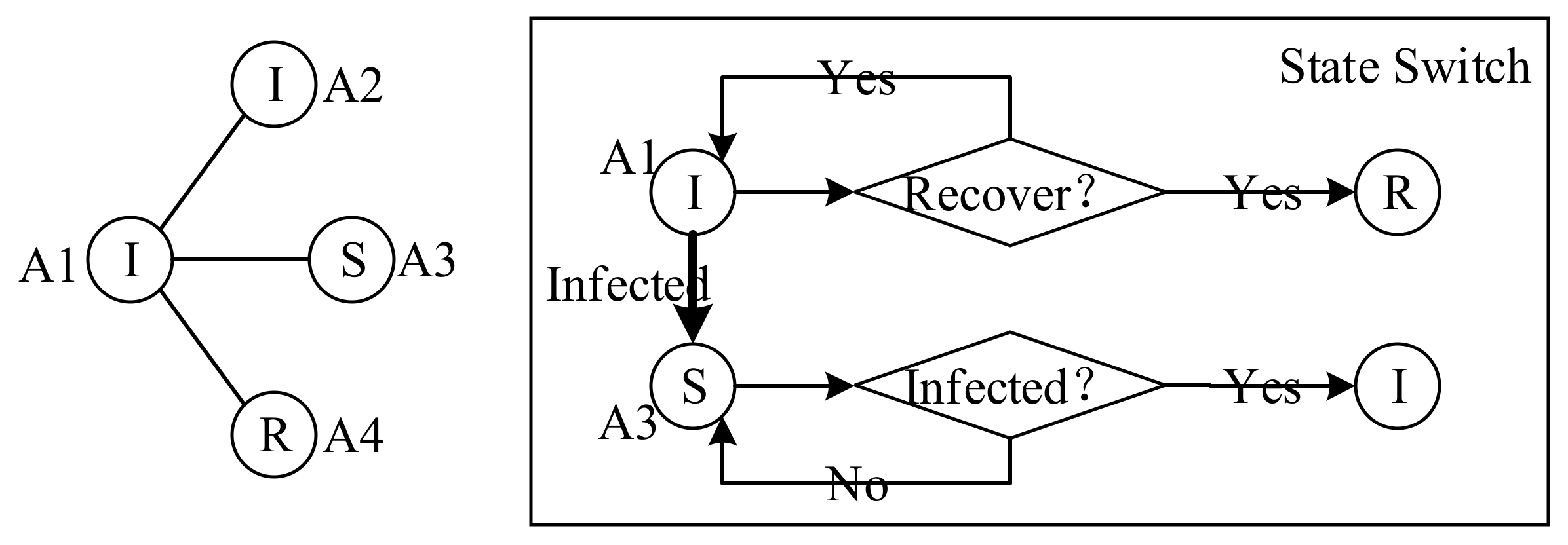
3.2. The Agent Model
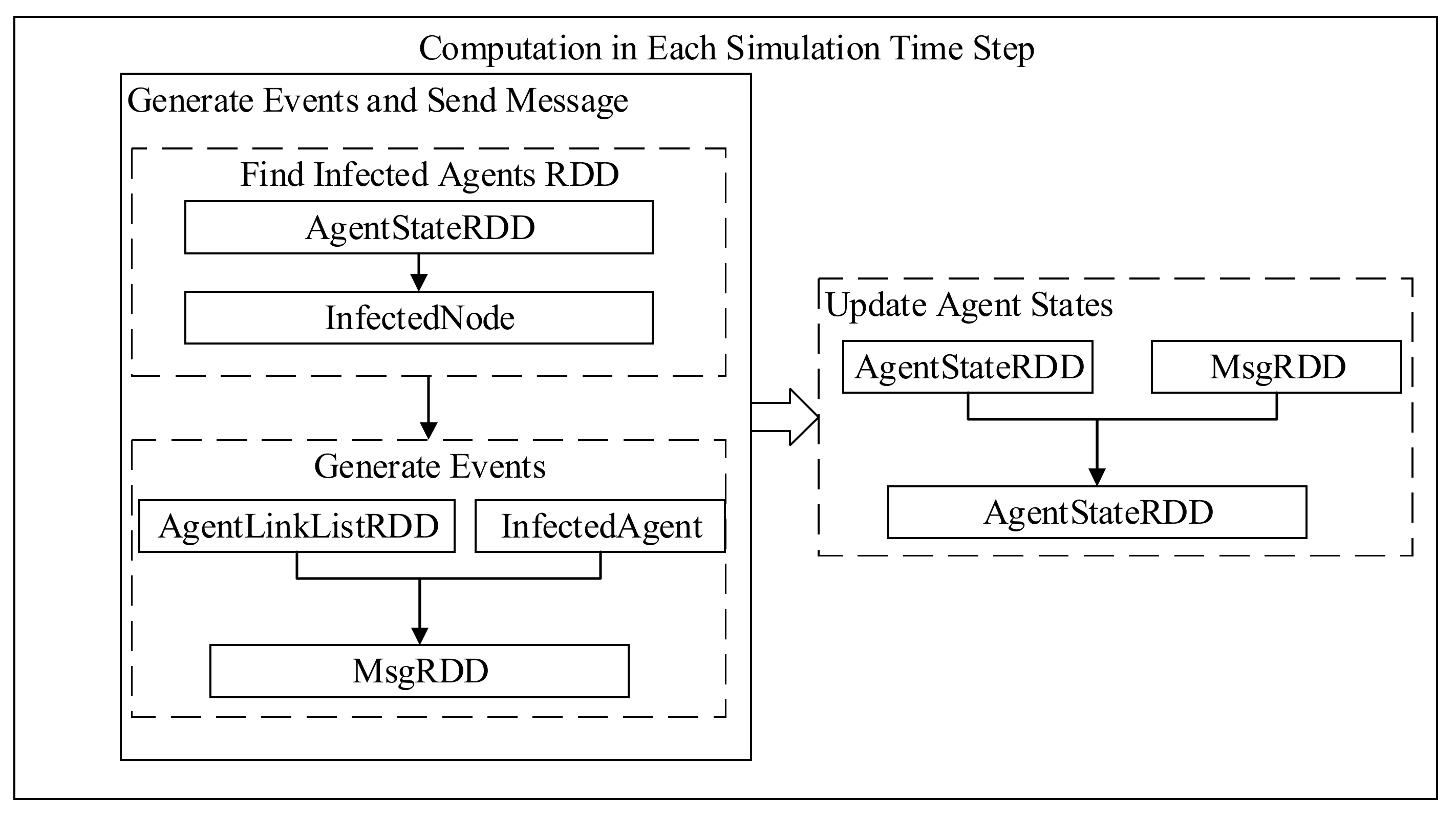
3.3. The Implementation of a Simulation Kernel in Spark
3.3.1. The Design of Data Structure
3.3.2. Scheduling Mechanism
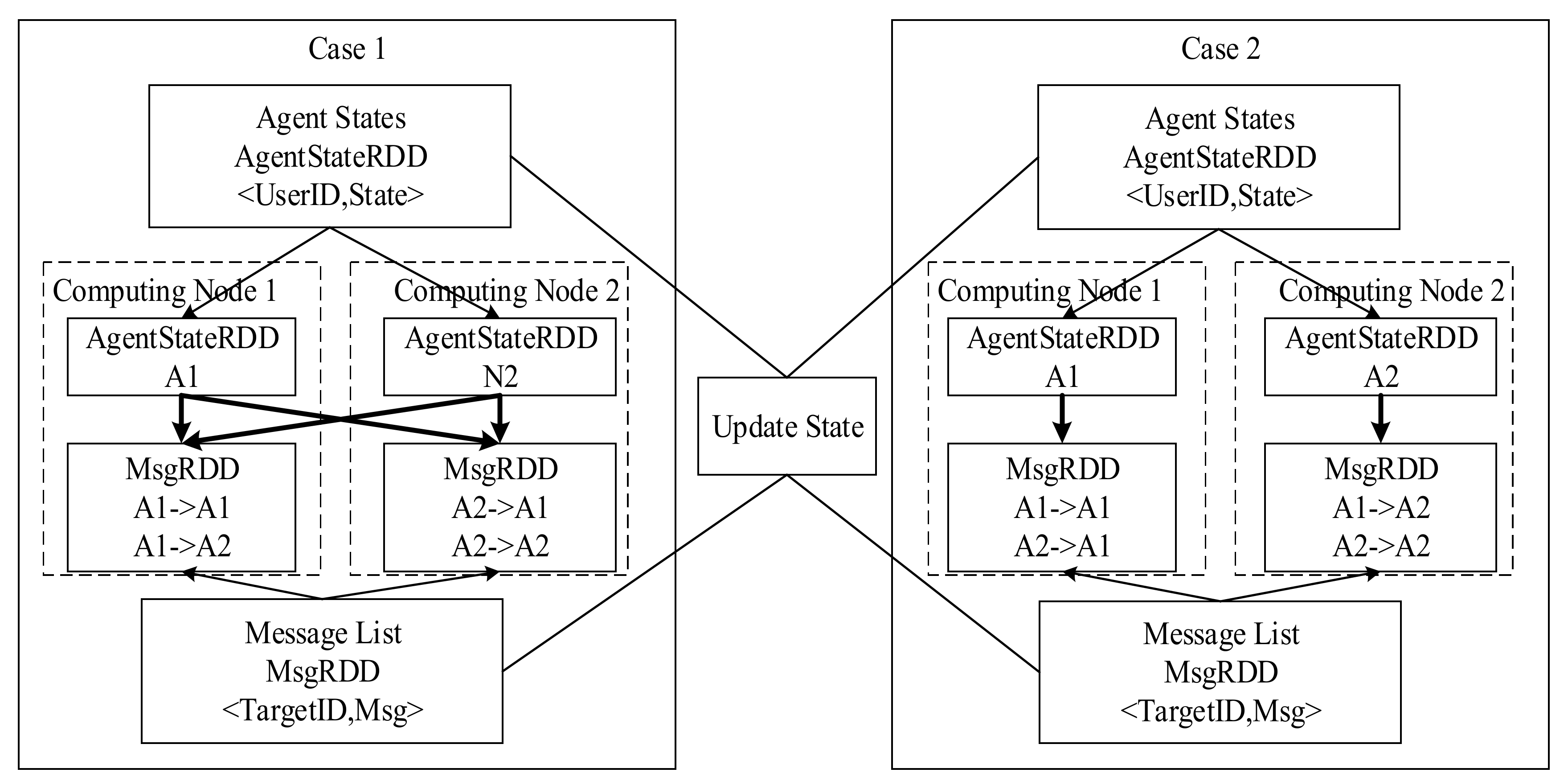
The Design of the Message Passing Mechanism
The Design of the State Update Mechanism
4. Optimization
4.1. Figures, Tables, and Schemes
4.2. The Partition Based on Network Structure
4.2.1. The Principle of the Two-Tier Partition
4.2.2. Community Detection
4.2.3. Graph Cut
4.2.4. The Flow of Two-Tier Partition
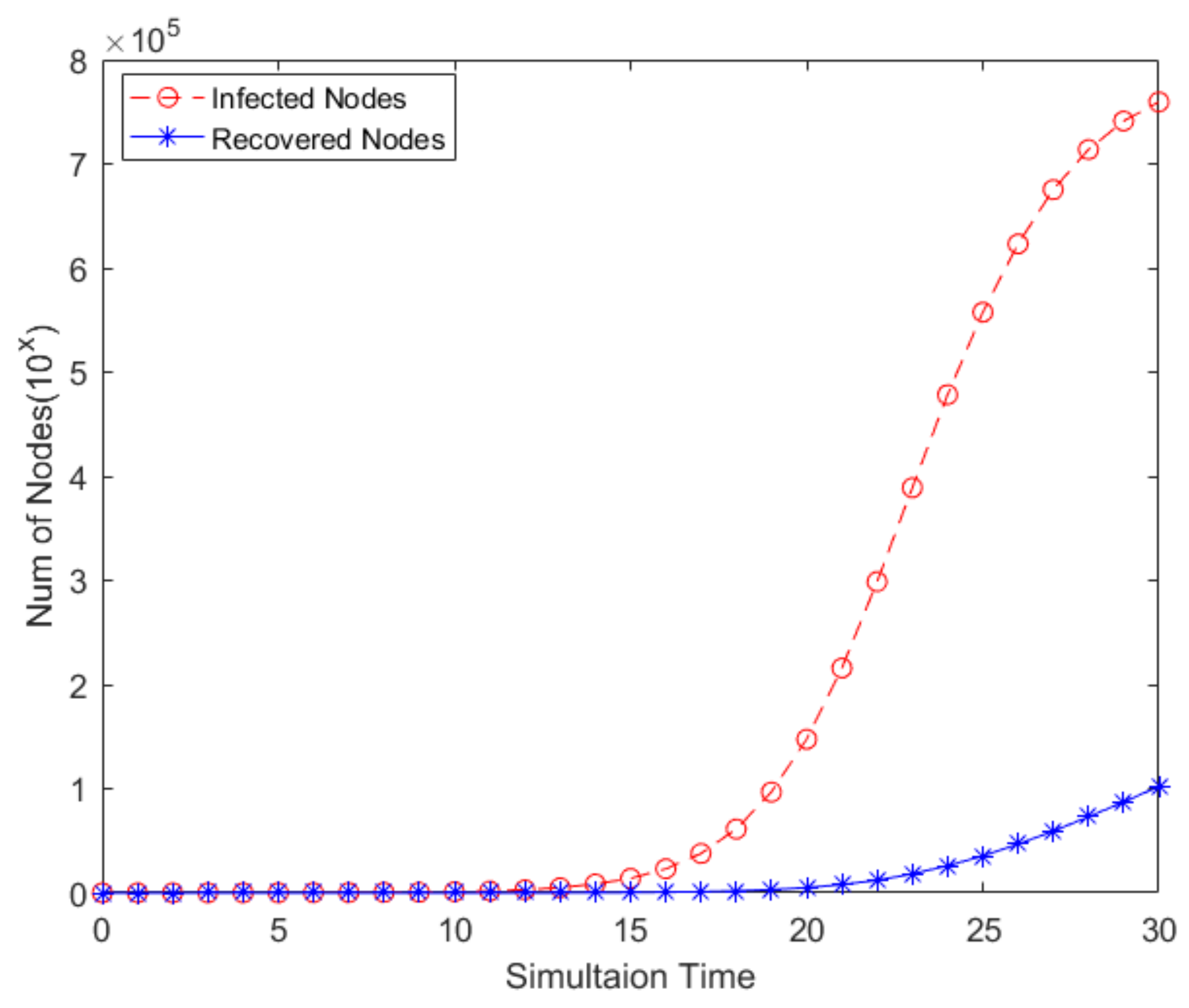
5. Experiments
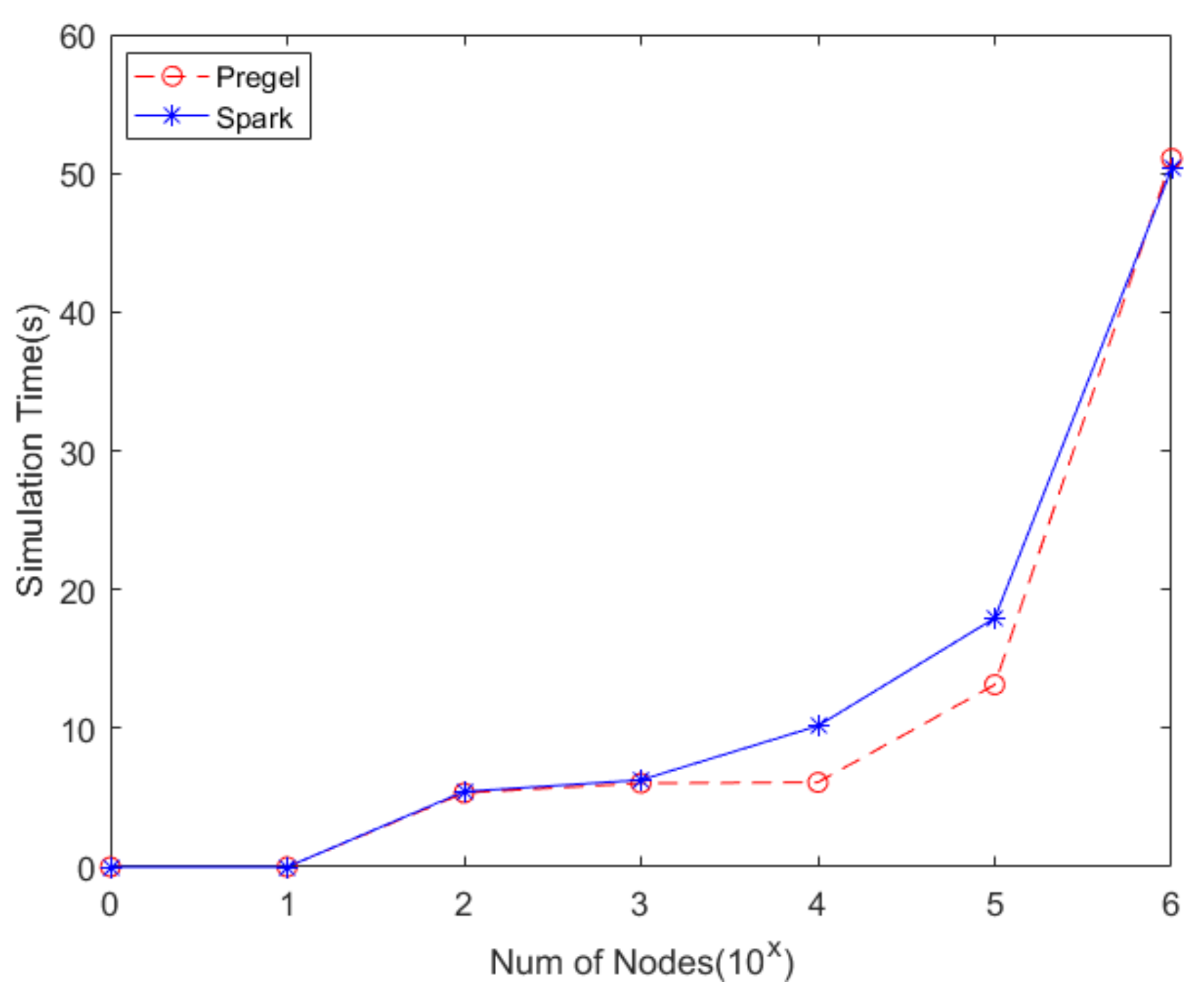
5.1. Experiments of Performance in Different Scales
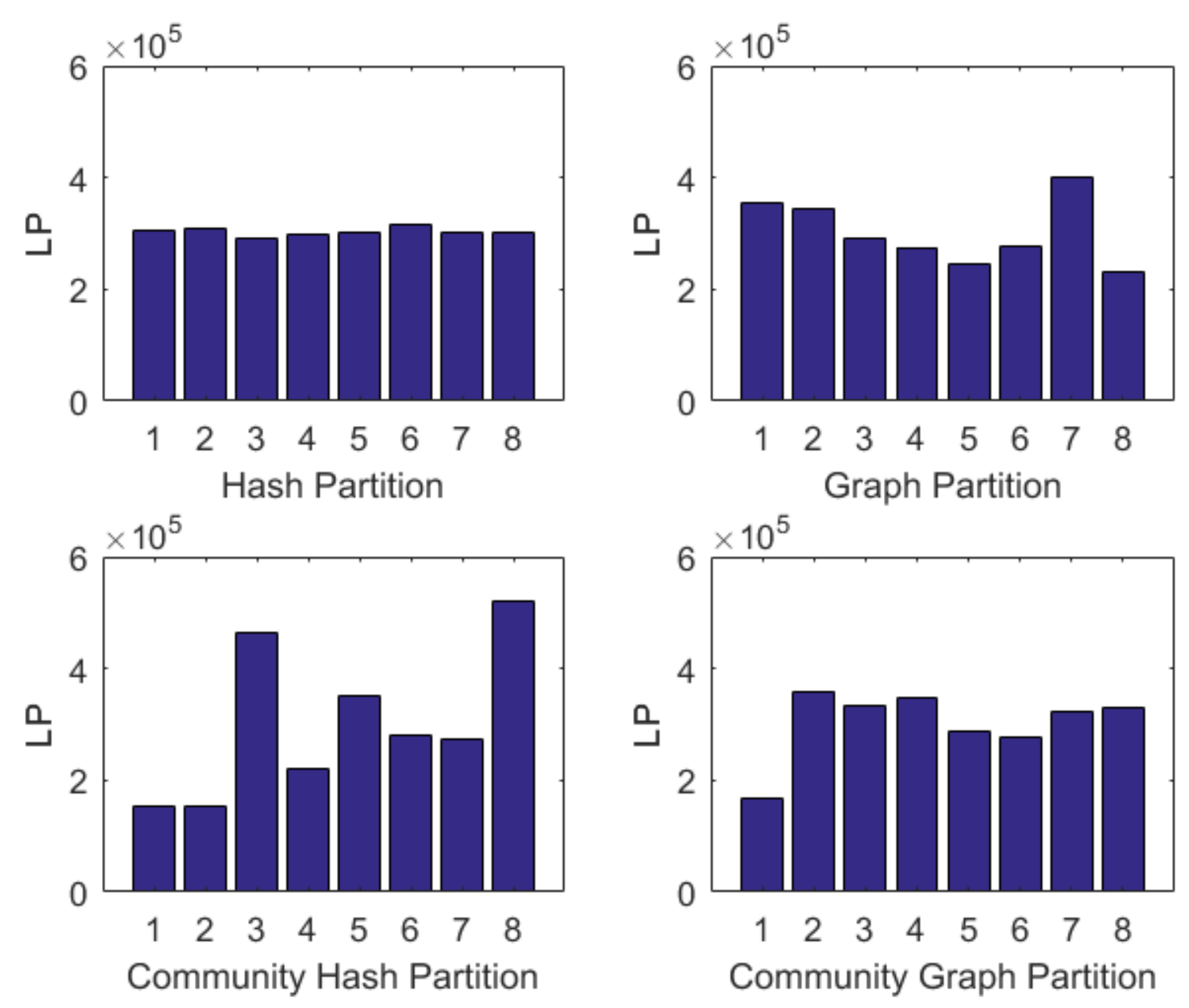
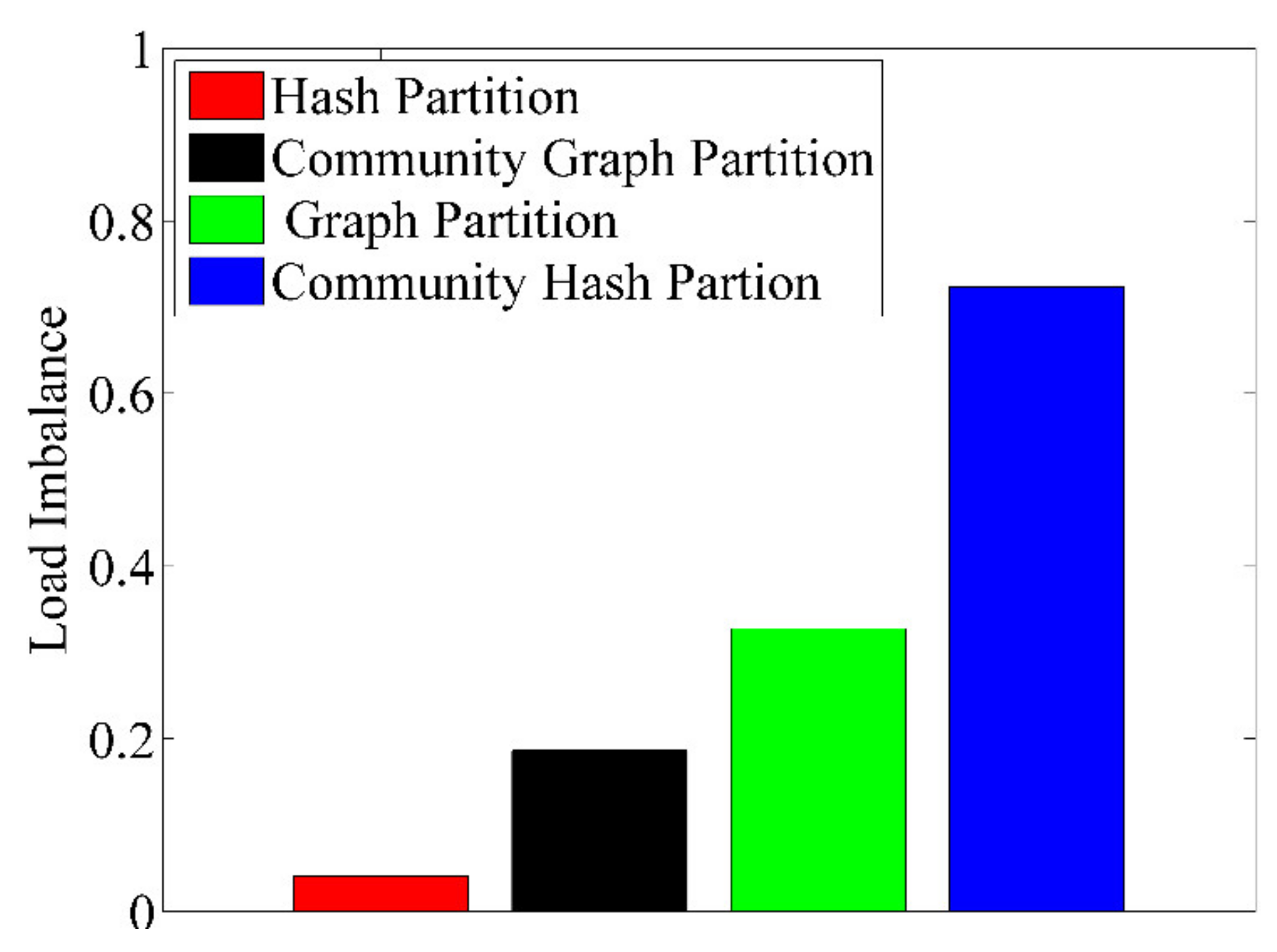
5.2. Experiments of Two-Tier Partition
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wechat 2018. In Wechat Data Report 2018; Wechat: Singapore, 2019; Available online: https://support.weixin.qq.com/cgi-bin/mmsupport-bin/getopendays (accessed on 19 May 2020).
- Fang, B.; Jia, Y.; Han, Y. Core scientific issues of social network analysis. research status and future prospects. CAS Bull. 2015, 2, 187–199. [Google Scholar]
- Liu, W.; Sidhu, A.; Beacom, A.M.; Valente, T. Social Network Theory. In The International Encyclopedia of Media Effects; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Fang, B. Online Social Network Analysis; Electronic Industry Press: Beijing, China, 2014. [Google Scholar]
- Zhang, J.; Li, X. Artificial society -sociological simulation based on Agent. Syst. Eng. 2005, 23, 13–20. [Google Scholar]
- Sklar, E. Software Review: NetLogo, a Multi-Agent Simulation Environment. Artif. Life 2007, 13, 303–311. [Google Scholar] [CrossRef]
- Minar, N.; Burkhart, R.; Langton, C.; Askenazy, M. The Swarm Simulation System–A Toolkit for Building Multi-agent Simulations; Santa Fe Institute: Santa Fe, NM, USA, 1996. [Google Scholar]
- North, M.J.; Collier, N.; Vos, J.R. Experiences creating three implementations of the repast agent modeling toolkit. ACM Trans. Model. Comput. Simul. 2006, 16, 1–25. [Google Scholar] [CrossRef]
- Railsback, S.F.; Lytinen, S.; Jackson, S.K. Agent-based Simulation Platforms: Review and Development Recommendations. Simulation 2006, 82, 609–623. [Google Scholar] [CrossRef]
- Zhen, L.; Gang, G.; Bin, C.; Xiaogang, Q. Accelerating Large Scale Artificial Society Simulation with CPU/GPU Based Heterogeneous Parallel Method. In Proceedings of the IEEE/ACM International Symposium on Distributed Simulation & Real Time Applications, London, UK, 21–23 September 2016. [Google Scholar]
- Walker, S.J. Big Data: A Revolution That Will Transform How We Live, Work, and Think. Int. J. Advert. 2014, 33, 181–183. [Google Scholar] [CrossRef]
- Google. Sorting 1 PB with MapReduce. Available online: http://googleblog.blogspot.com/2008/11/sorting-1pb-with-mapreduce.html,20081111 (accessed on 21 November 2019).
- Matei, Z.; Mosharaf, C.; Franklin, J.; Shenker, M.; Ion, S. Spark: Cluster Computing with Working Sets. In Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing, Berkeley, CA, USA, 22–25 June 2010. [Google Scholar]
- Charlse, M.; Michael, J. agent-based modeling and simulation. In Proceedings of the 2009 Winter Simulation Conference, Austin, TX, USA, 13 December 2009; pp. 86–98. [Google Scholar]
- Allan, R. Survey of Agent Based Modelling and Simulation Tools; Science and Technology Facilities Council: Washington, DC, USA, 2010. [Google Scholar]
- Mittal, A.; Krejci, C.C.; Dorneich, M.C. An agent-based approach to designing residential renewable energy systems. Renew. Sustain. Energy Rev. 2019, 112, 1008–1020. [Google Scholar] [CrossRef]
- Griffin, F.A.; Stanish, C. An Agent-Based Model of Prehistoric Settlement Patterns and Political Consolidation in the Lake Titicaca Basin of Peru and Bolivia. Struct. Dyn. 2007, 2, 2. [Google Scholar]
- Testa, J.W.; Mock, K.J.; Taylor, C.; Koyuk, H.; Coyle, J.R.; Waggoner, R. Agent-based modeling of the dynamics of mammal-eating killer whales and their prey. Mar. Ecol. Prog. Ser. 2012, 466, 275–291. [Google Scholar] [CrossRef]
- Lee, K.; Park, J. A Hadoop-Based Output Analyzer for Large-Scale Simulation Data. In Proceedings of the The Fourth IEEE International Conference on Big Data & Cloud Computing, Sydney, Australia, 3 December 2014. [Google Scholar]
- Sethia, P.; Karlapalem, K. A multi-agent simulation framework on small Hadoop cluster. Eng. Appl. Artif. Intell. 2011, 24, 1120–1127. [Google Scholar] [CrossRef]
- Kärger, J.; Ruthven, D.M.; Theodorou, D.N. Molecular Dynamics Simulations. In Diffusion in Nanoporous Materials; Wiley: Hoboken, NJ, USA, 2012; pp. 227–273. [Google Scholar]
- Youbo, L.; Yang, L.; Junyong, L.; Yong, L.; Jianting, L.; Su, D. Hadoop Based Distributed Computing Framework for Large-scale Cascading Failure Simulation and Analysis of Power System. Autom. Electr. Power Syst. 2016, 40, 90–97. [Google Scholar]
- He, L.; Fen, D.; Wang, R.; Su, P.-R.; Ying, L.-Y. Worm simulation of large-scale online social network based on MapReduce. J. Softw. 2013, 7, 1666–1682. [Google Scholar] [CrossRef]
- Chuan, A.; Bin, C.; Liang, L.; Jian, J.; He, L.; Lai, K.; Qiu, X. Design and implementation of large-scale network propagation simulation method inspired by Pregel mechanism. Sci. Sin. Inf. 2018, 48, 932–946. [Google Scholar]
- Kang, L.; Zhang, X.; Li, F.; Tian, Y. Graph partitioning method for social networks based on communication load balancing. Comput. Eng. Appl. 2018, 54, 66–71. [Google Scholar]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2009, 486, 75–174. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef]
- Clauset, A. Finding local community structure in network. Phys. Rev. E 2005, 72, 1–7. [Google Scholar] [CrossRef]
- Fieldler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed]
- Kernighan, B.W.; Lin, S. An Efficient Heuristic Procedure for Partitioning Graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]

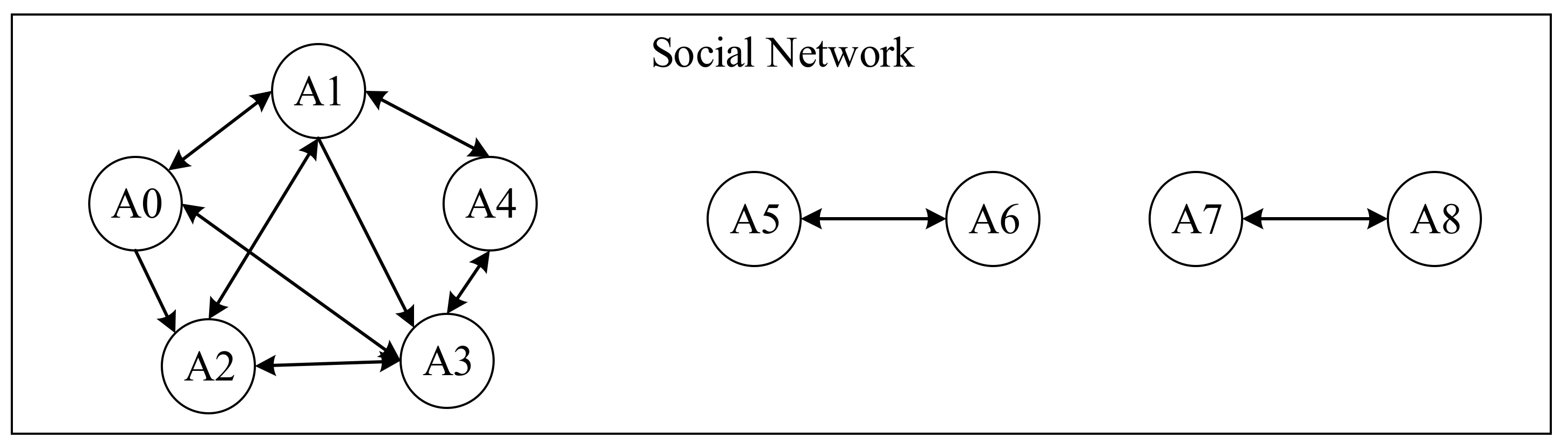
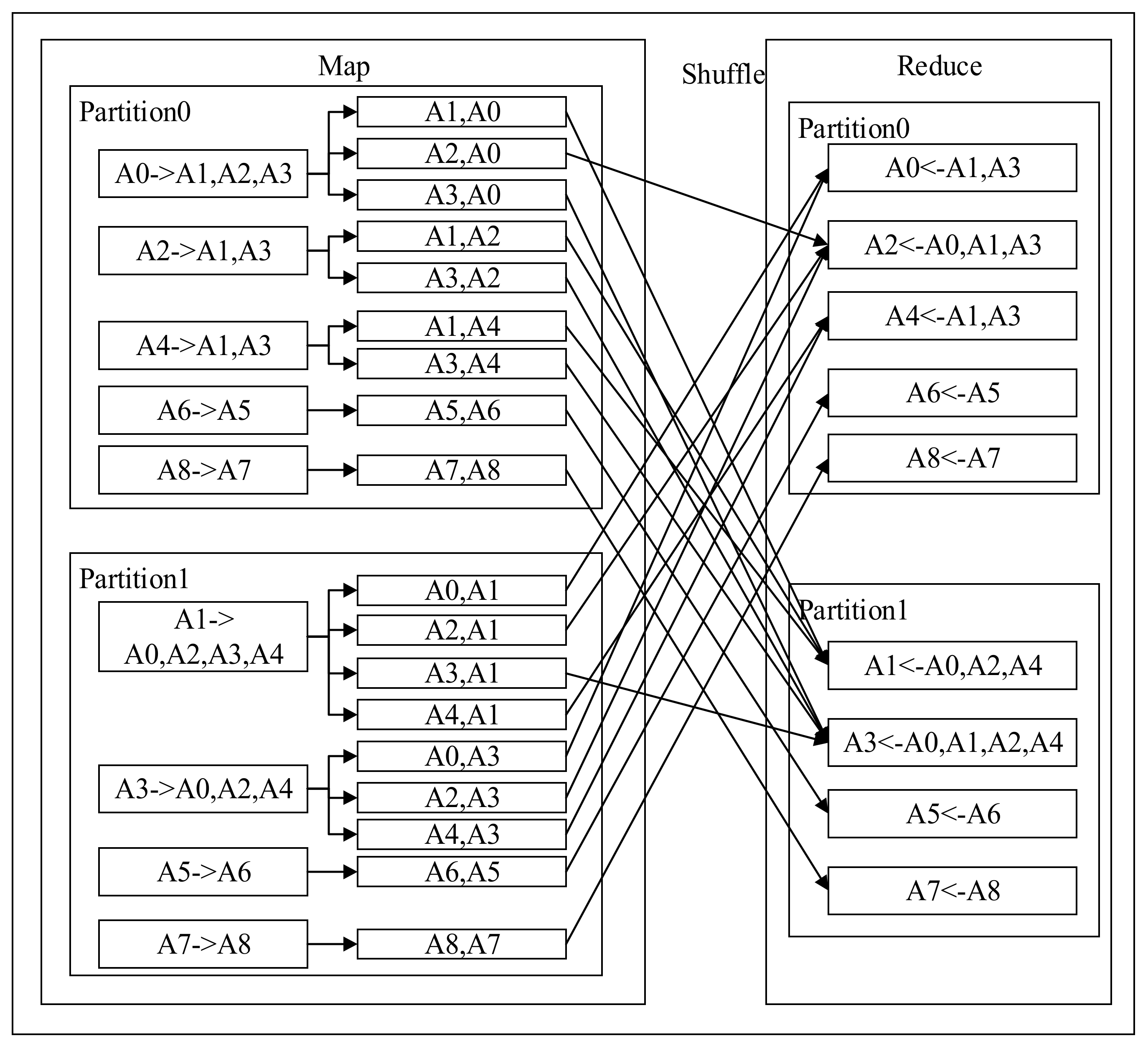


| Name | Stored Information | Data Type | Description |
|---|---|---|---|
| AgentStateRDD | Agent state | <Key,Value>RDD | Record the state change of agent |
| AgentLinkListRDD | Neighboring Agents of Agent | <Key,Value>RDD | Record the neighboring agents list of agent |
| MsgRDD | Message | <Key,Value>RDD | Record the messages list received by agent |
| InfectedAgentBroadcast | Infected Agent | Broadcast | Record infected agents |
| InfectedAgentRDD | Infected Agent | <Key,Value>RDD | Record infected agents |
| Algorithm the Two-tier Partition |
| Input: Adjacent set ; represents the neighbor list of vertex i. |
| , represents the number of partitions. |
| Output:, represents the index of located partition for vertex i. |
| 1. ← find community of all vertexes with LPA() |
| 2. for each community do |
| 3. statistic compute load of all vertexes in this community as |
| 4. end |
| 5. |
| 6. for each edge in do |
| 7. construct community relation of source community and target community from |
| 8. end |
| 9. ← statistic community relations |
| 10. ← construct simplify network with and |
| 11. ←GraphPartition(,) |
| Order of Magnitude of Network Size | Hundred | Thousand | Ten Thousand | Hundred Thousand | Million |
|---|---|---|---|---|---|
| The number of nodes | 100 | 1000 | 10,000 | 100,000 | 1,000,000 |
| The number of edges | 1143 | 10,739 | 111,392 | 112,0837 | 11,183,970 |
| Partition Algorithm | Hash Partition | Graph Partition | Community Hash | Community Graph |
|---|---|---|---|---|
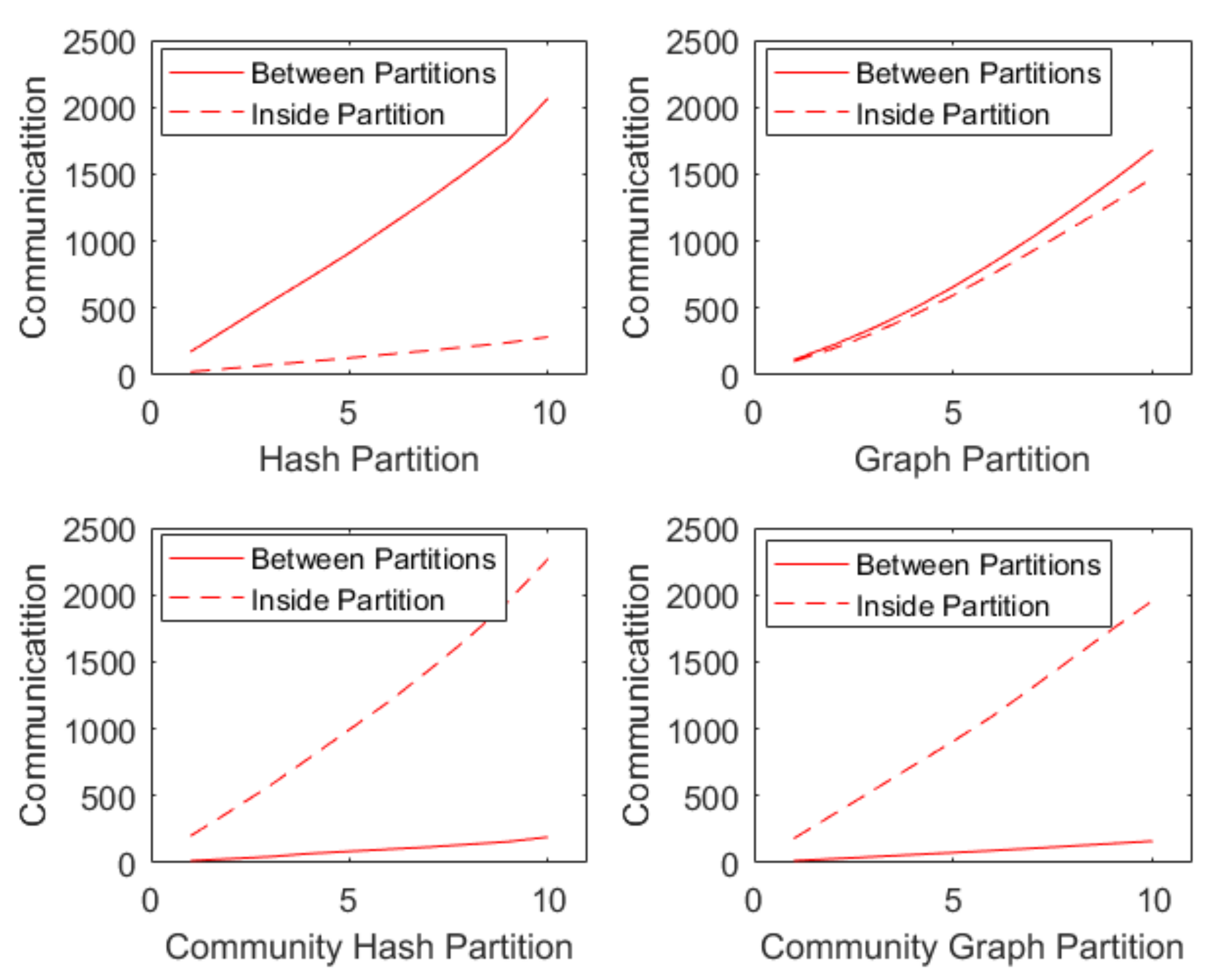
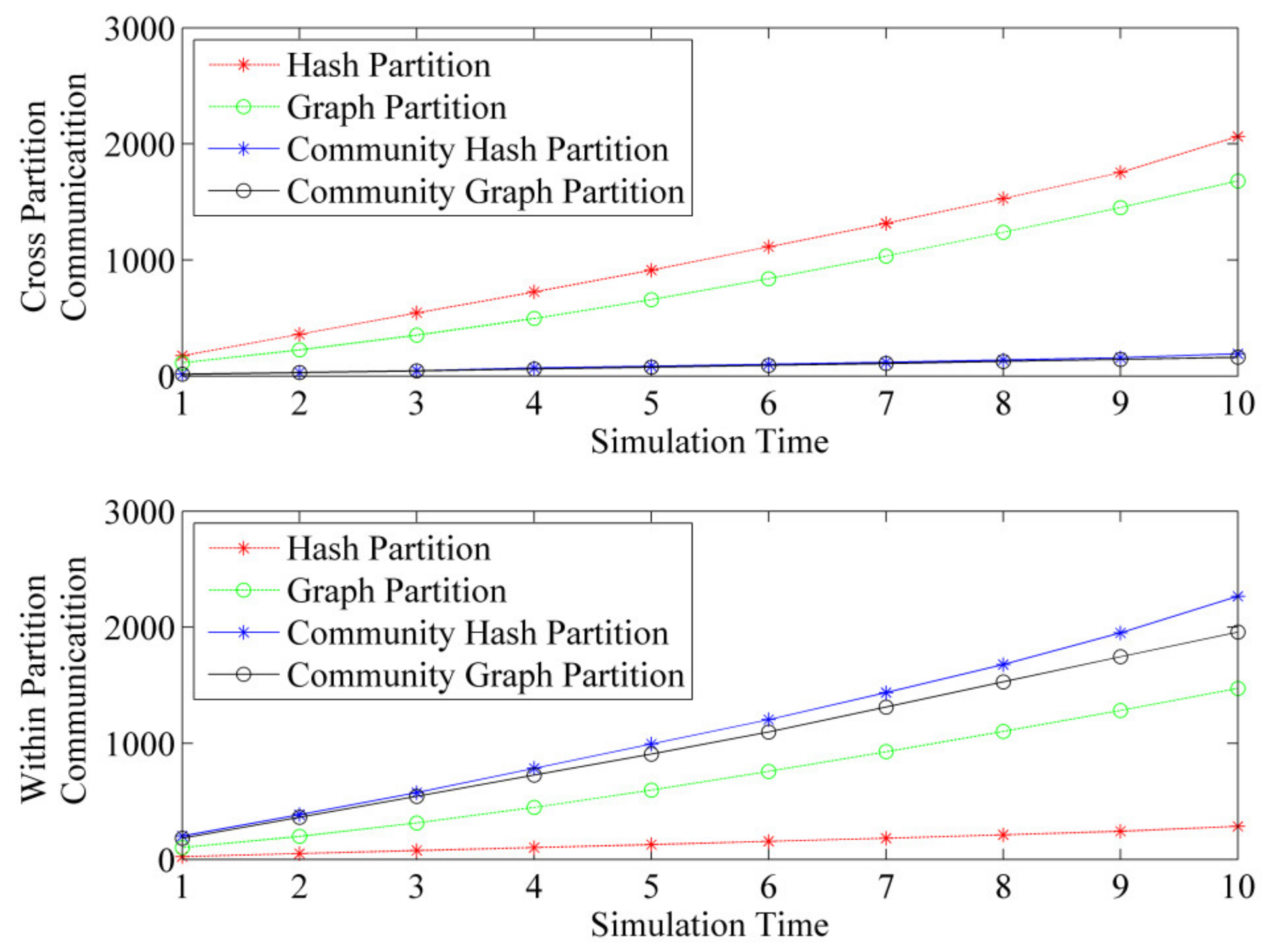
| The proportion of cross-partition communication | 87.9% | 53.3% | 7.8% | 7.6% |
| The proportion of inter-partition communication | 12.1% | 46.7% | 92.2% | 92.4% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, H.; Ning, D.; Zhu, M.; Ai, C.; Qiu, X.; Dai, W. A Two-Tier Partition Algorithm for the Optimization of the Large-Scale Simulation of Information Diffusion in Social Networks. Symmetry 2020, 12, 843. https://doi.org/10.3390/sym12050843
Chen B, Chen H, Ning D, Zhu M, Ai C, Qiu X, Dai W. A Two-Tier Partition Algorithm for the Optimization of the Large-Scale Simulation of Information Diffusion in Social Networks. Symmetry. 2020; 12(5):843. https://doi.org/10.3390/sym12050843
Chicago/Turabian StyleChen, Bin, Hailiang Chen, Dandan Ning, Mengna Zhu, Chuan Ai, Xiaogang Qiu, and Weihui Dai. 2020. "A Two-Tier Partition Algorithm for the Optimization of the Large-Scale Simulation of Information Diffusion in Social Networks" Symmetry 12, no. 5: 843. https://doi.org/10.3390/sym12050843
APA StyleChen, B., Chen, H., Ning, D., Zhu, M., Ai, C., Qiu, X., & Dai, W. (2020). A Two-Tier Partition Algorithm for the Optimization of the Large-Scale Simulation of Information Diffusion in Social Networks. Symmetry, 12(5), 843. https://doi.org/10.3390/sym12050843





