CryptoDL: Predicting Dyslexia Biomarkers from Encrypted Neuroimaging Dataset Using Energy-Efficient Residue Number System and Deep Convolutional Neural Network
Abstract
1. Introduction
2. An Overview of Deep CNN for Image Dataset Classification
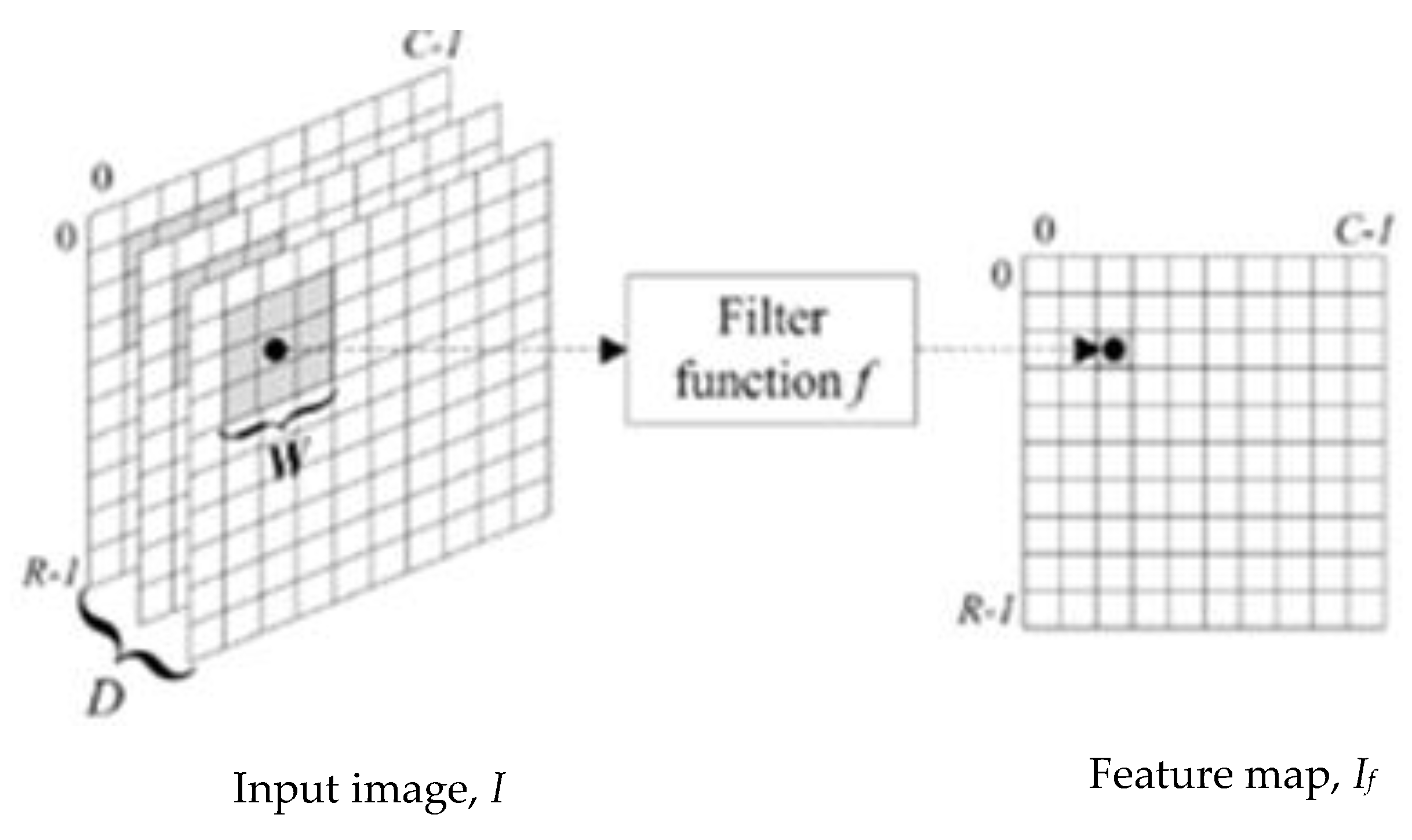
- Convolutional Layer: A convolutional layer is a series of small parameterized filters that operate on the input data domain. In this study, inputs are raw brain images and encrypted brain images data. The aim of the convolutional layers is to learn abstract features from the data [45]. Every filter is an n × n matrix called a stride. In this case, we have n = 3. We convolve the pixels in the input image and evaluate the dot product, called feature maps, of the filter values and related values in the pixel neighbour. For example, the stride is a pair of numbers (3,3), in which, in each step, we slide a three-unit filter to the left or down. In summary, given a brain MRI image I (Figure 1), consisting of R rows, C columns, and D layers, a 2D function I (x, y, z) where 0 ≤ x < R, 0 ≤ y < C, and 0 ≤ z < D are spatial coordinates, amplitude I is called the intensity at any point on the 2D set with coordinates (x, y, z) [46]. The process of extracting feature maps is defined in Equation (1):where If is the convolved image, and Wi,j,k are coefficients of kernels or strides for convolving 2D arrays.
- Activation Layer: The feature maps from convolutional layers are inputted through a nonlinear activation function to produce another stride called feature maps [4]. After each convolutional layer, we used a nonlinear activation function. Each activation function performs some fixed mathematical operations on a single number, which it accepts as input. In practice, there are several activation functions from which one could choose. These include ReLU (ReLU (z) = max (0, z)), Sigmoid, Tanh functions, and several other ReLU variants such as leaky ReLU and parameter ReLU [4,45]. ReLU is an acronym for rectified linear unit.
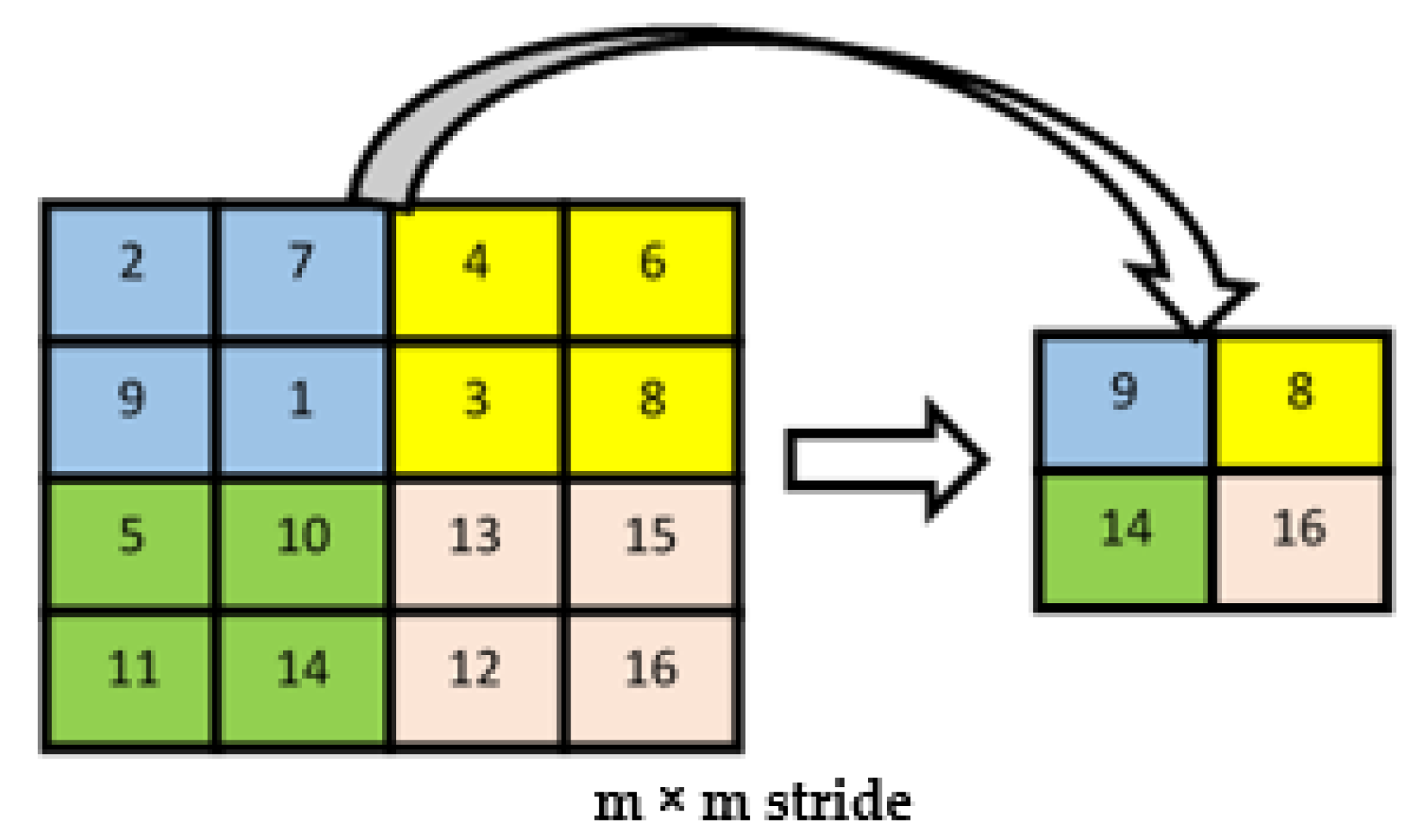
- Pooling Layer: A pooling layer, also known as sub-sampling layer, is next after an activation layer. The pooling layer takes small grid regions as input and performs operations on them to produce a single number for each region. Different kinds of pooling layers have been implemented in previous studies, with max-pooling and average pooling being the two most common. The pooling layers give CNN some translational invariance because a slight shift of the input image may result in a slight change in activation maps. In max-pooling (Figure 2), the value of the largest pixel among all the pixels is considered in the receptive field of the filter, while the average of all the pixel values is considered in average pooling.
- Fully Connected Layer: The fully connected layer has the same structure as classical feed-forward network hidden layers. This layer is named because each neuron in this layer is linked in the previous layer to all neurons, where each connection represents a value called weight. Every neuron’s output is the dot product of two vectors, that is, neuron output in the preceding layers and the corresponding weight for each neuron.
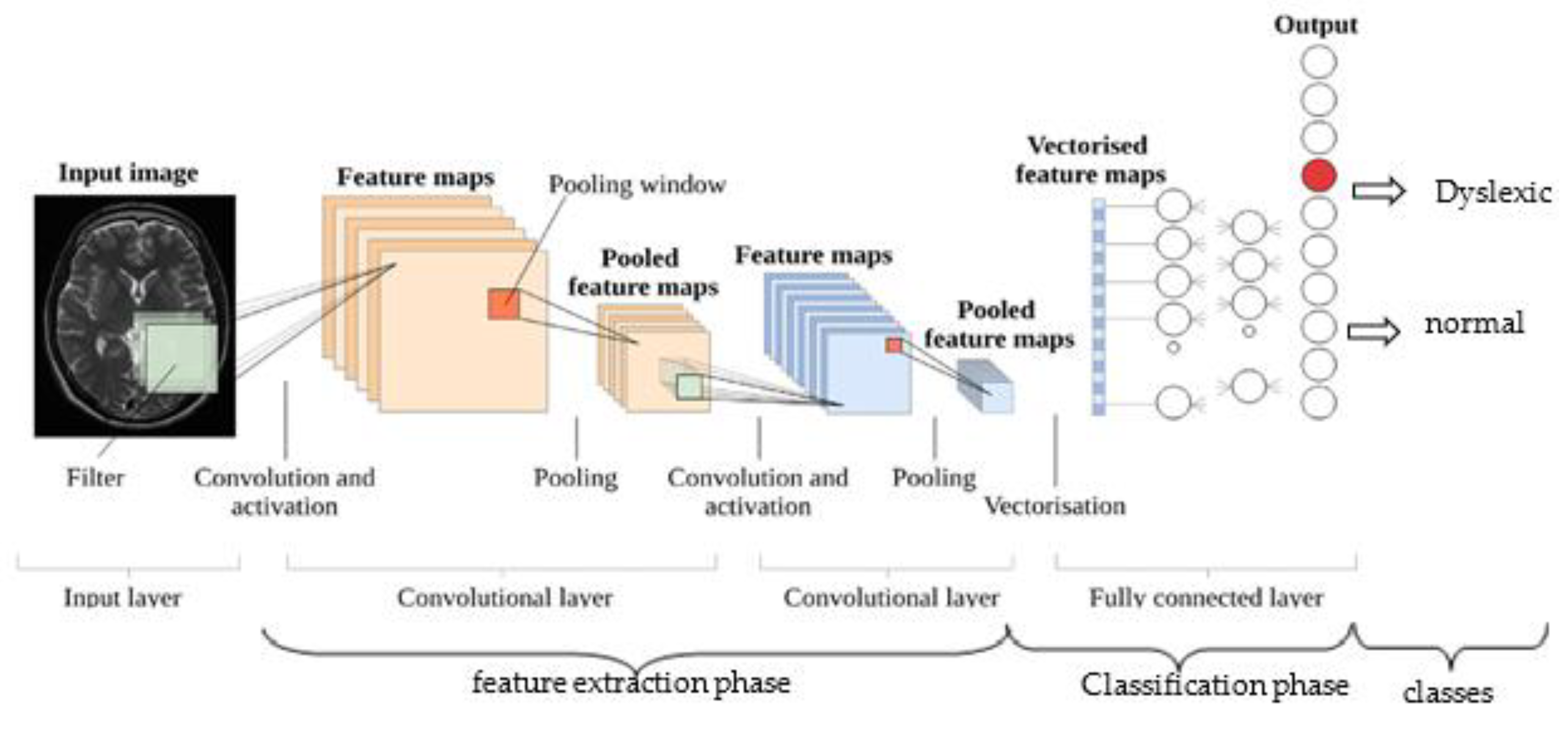
- Dropout Layer: This layer is also called dropout regularization. A model sometimes gets skewed to the training dataset on many occasions, and when the testing dataset is added, it generates high errors. In this situation, a problem of overfitting has occurred. To avoid overfitting during the training process, we used a dropout layer. In this layer, by setting them to zero in each iteration, we dropout a set of connections at random in the fully connected layers. This value drop prevents overfitting from occurring, so that the final model will not be fully fit to the training dataset. Batch normalization is also used to resolve internal covariance shift issues within the feature maps by smoothing the gradient flow, thus helping to improve network generalization. Figure 3 shows the building blocks of the simplified deep CNN classifier for brain images.
3. Background of Residue Number System and Image Encryption
4. Materials and Methods
4.1. Participants
4.2. Brain Images Acquisition and Pre-Processing
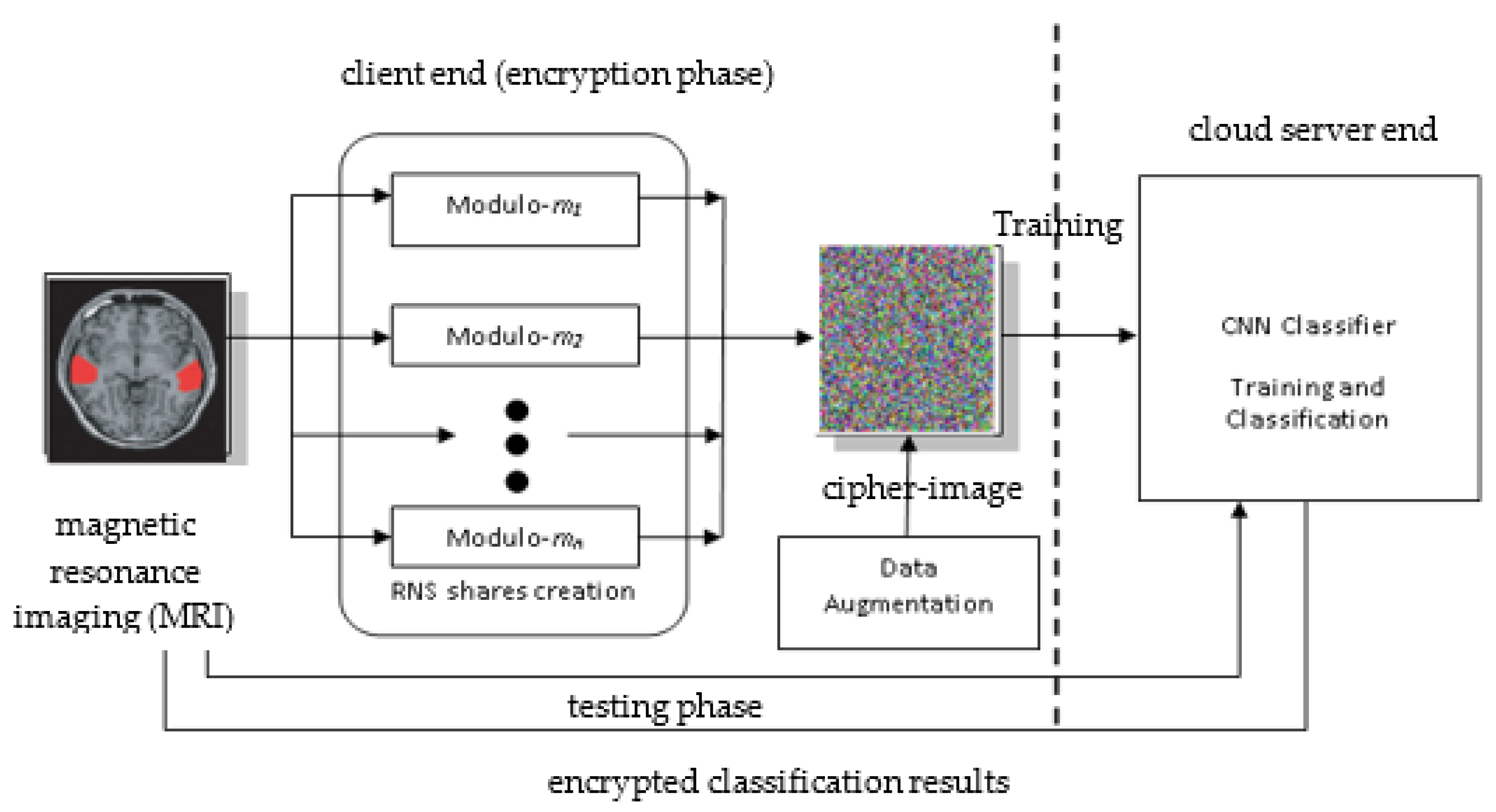
4.3. Proposed Conceptual Framework for Secure Brain Image Classification
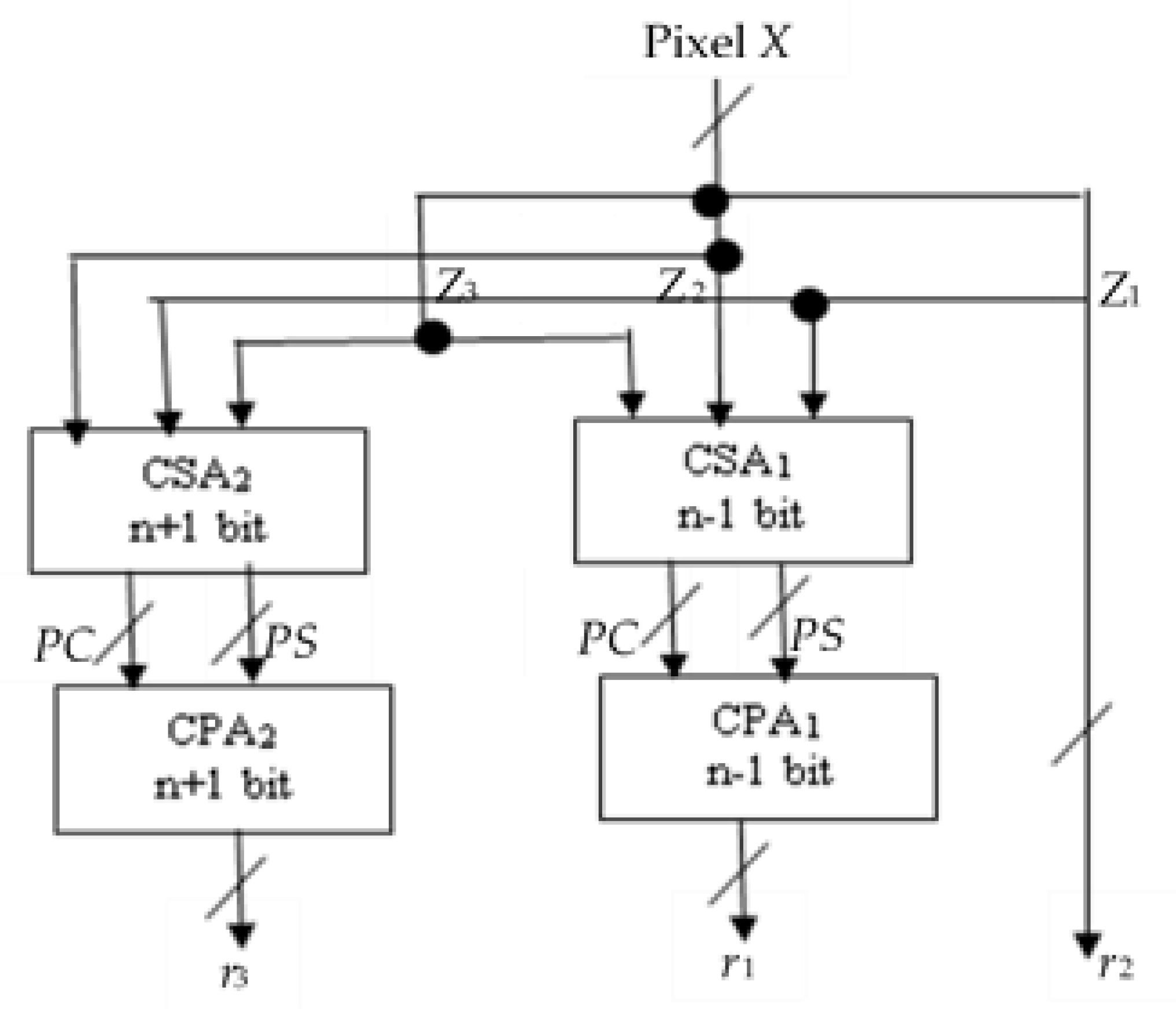
4.4. Design of RNS Pixel-Bitstream Encoder for Image Encryption
- r2 is the n least significant bit (LBS) of integer X and is computed directly from modulo −2n processor.
- For r1 and r3, X is partitioned into two n-bit blocks, Z1 and Z2, and one (n + 1)-bit block Z3, where
4.4.1. Case 1: Modulo −2n − 1
4.4.2. Case 2: Modulo −2n+1 − 1
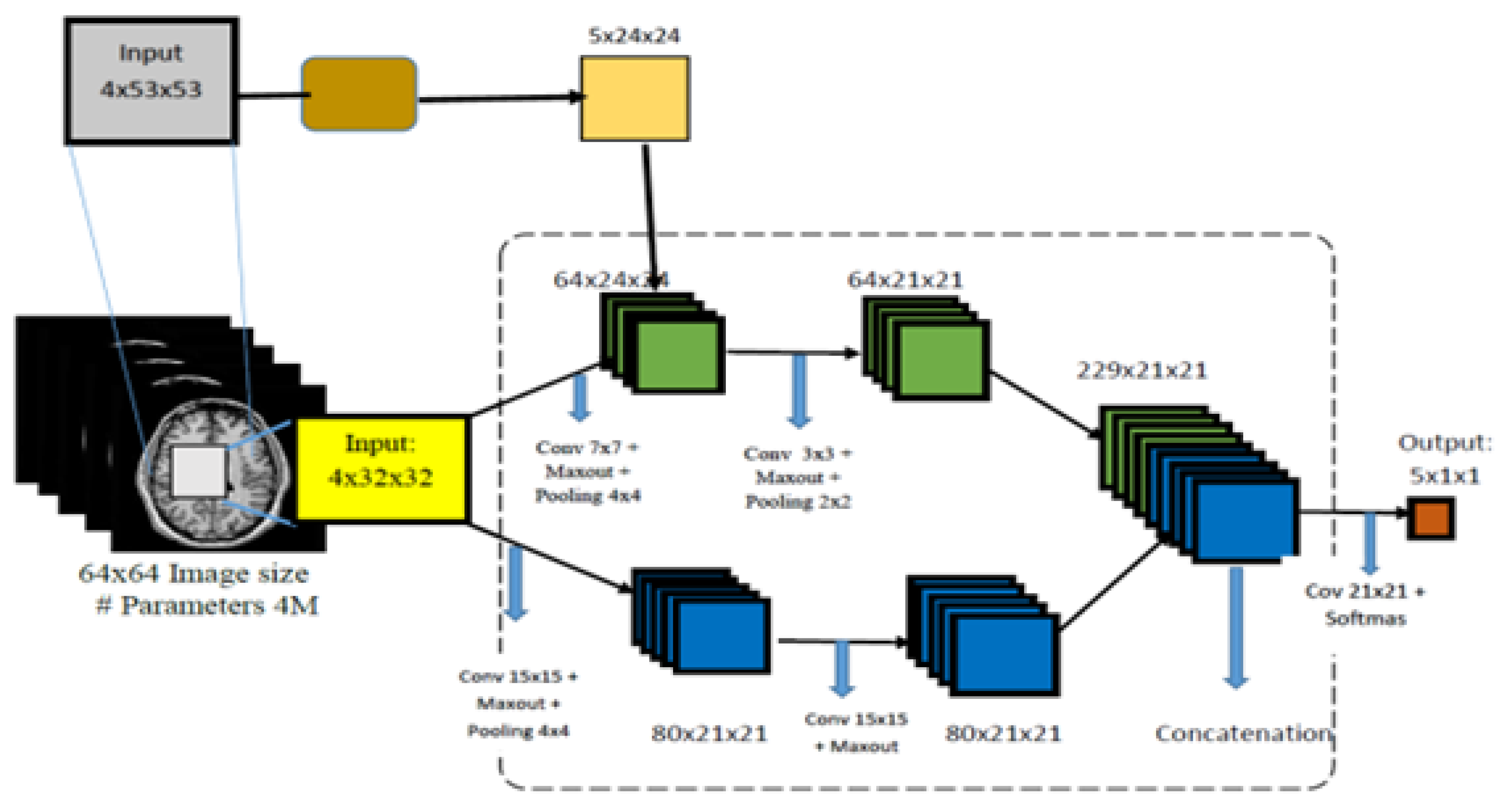
4.5. Deep CNN Architecture, Training, and Classification
5. Experimental Results and Discussion
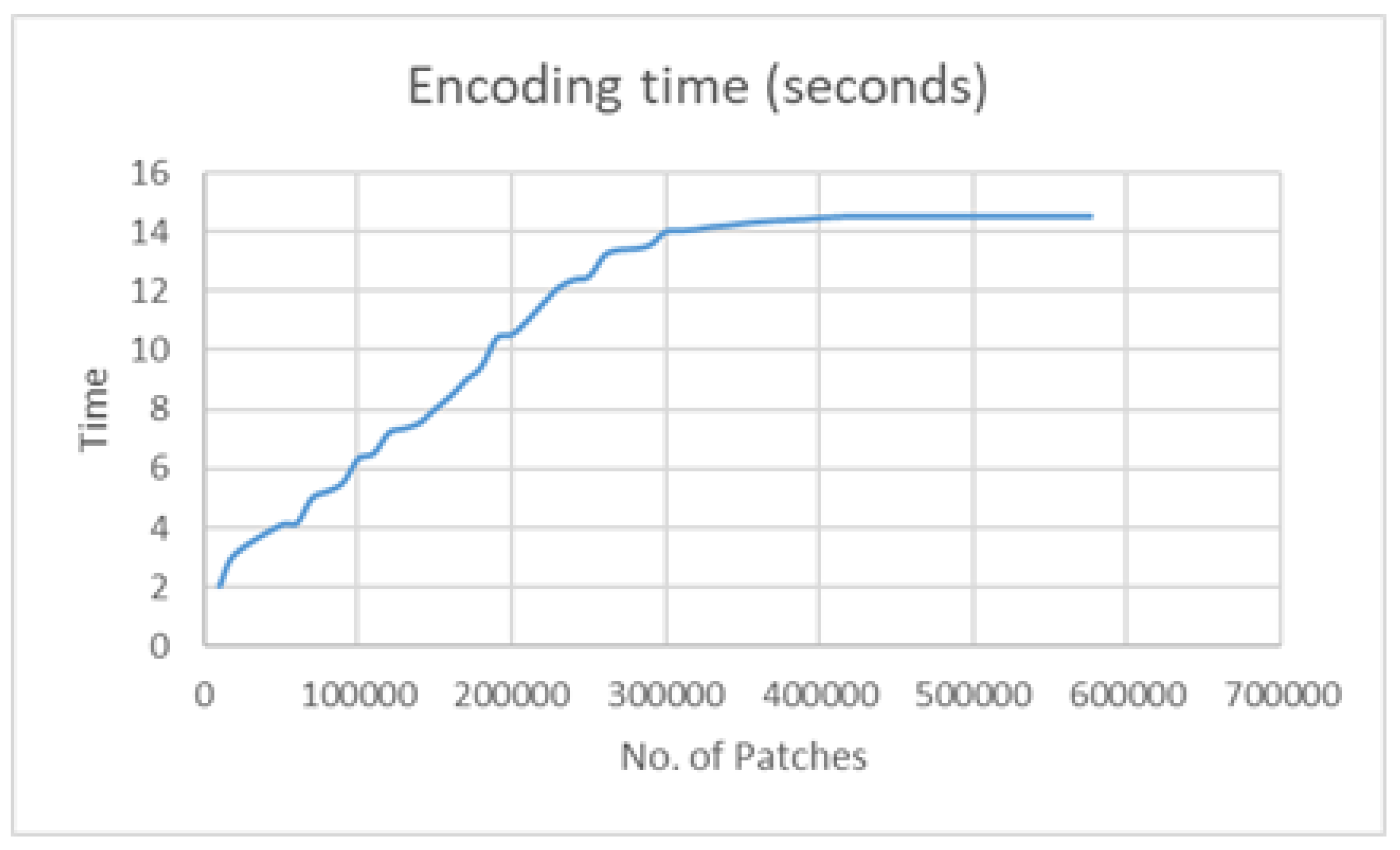
5.1. Implementation of the Proposed Pixel-Bitstream Encoder and Encryption Time Analysis
5.2. Analysis of Pixel-Bitstream Encoder Performance
5.2.1. Design Analysis
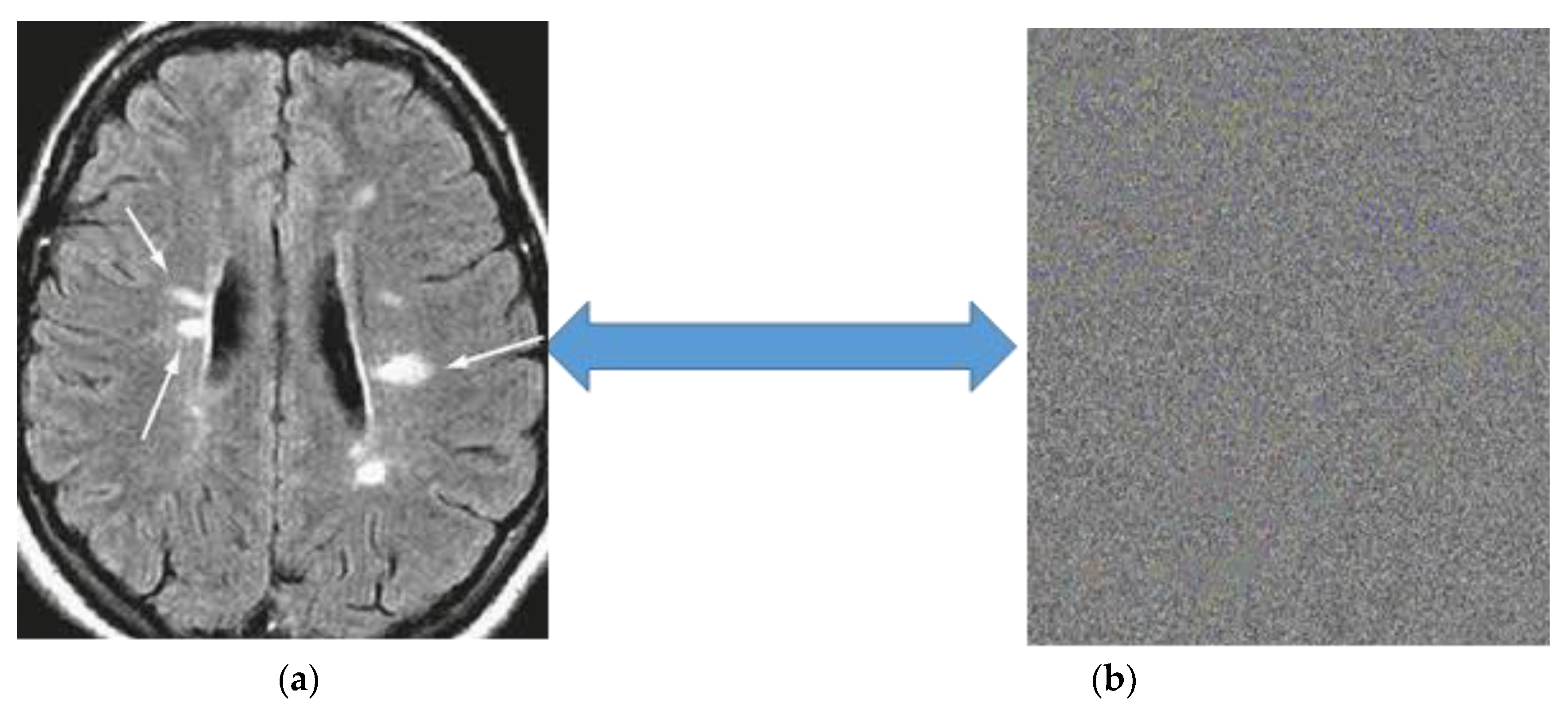
5.2.2. Cipher Image Analysis
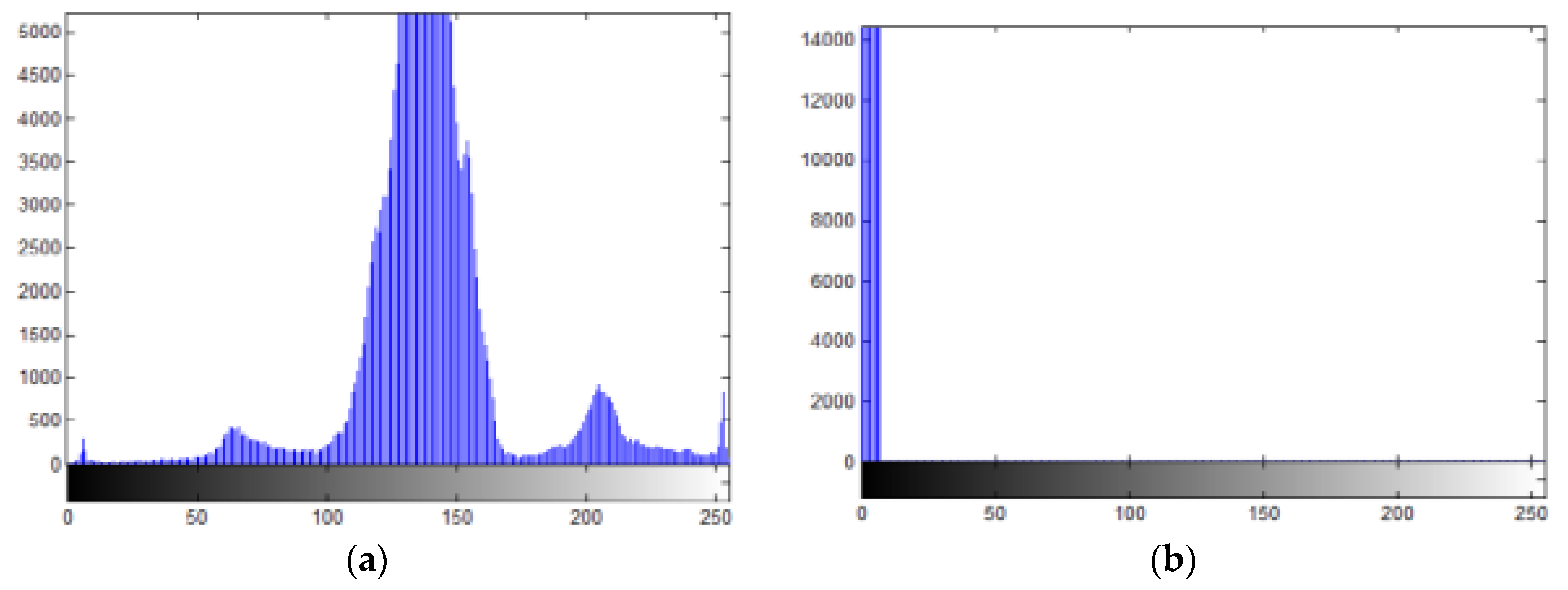
5.2.3. Histogram Analysis
5.2.4. Correlation Coefficient Analysis
5.3. Analysis of the Proposed Cascaded Deep CNN Classifier Performance
- Accuracy: Accuracy tests the percentage of dyslexic subjects correctly classified as positive. For computation of the classifier accuracy, Equation (14) is used.
- Sensitivity: Sensitivity is a measure of the percentage of dyslexic subjects that is correctly classified or predicted to be positive by the classifier. It is also known as the true positive rate (TPR) or recall. For the computation of sensitivity, Equation (15) is used.
- Specificity: Specificity, or the true negative rate (TNR), tests the percentage of correctly classified non-dyslexic subjects. This indicates accuracy in identifying non-dyslexic subjects [82], as shown in Equation (16).
- ROC and Area under ROC (AUC): The receiver operating characteristics (ROC) curve plots the sensitivity curve against specificity, and thus provides a representation of the trade-off between correctly classified positive instances and incorrectly classified negative instances [83]. Area under ROC (AUC) is computed directly from this curve.
5.4. Summary of Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, D.; Wu, G.; Suk, H. Deep Learning in Medical Image Analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef] [PubMed]
- Biomarker Working Group. Biomarkers and surrogate endpoints: Preferred definitions and conceptual framework. Clin. Pharmacol. Ther. 2001, 69, 89–95. [Google Scholar]
- Sharin, U.; Abdullah, S.N.H.S.; Omar, K.; Adam, A.; Sharis, S. Prostate Cancer Classification Technique on Pelvis CT Images. Int. J. Eng. Technol. 2019, 8, 206–213. [Google Scholar]
- Lundervold, A.S.; Lundervold, A. An overview of deep learning in medical imaging focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef] [PubMed]
- Elnakib, A.; Soliman, A.; Nitzken, M.; Casanova, M.F.; Gimel’farb, G.; El-Baz, A. Magnetic resonance imaging findings for dyslexia: A review. J. Biomed. Nanotechnol. 2014, 10, 2778–2805. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.F.; Lee, J.S.; Kirby, R. Brain imaging findings in dyslexia. Pediatr. Neonatol. 2010, 51, 89–96. [Google Scholar] [CrossRef]
- Casanova, M.F.; El-Baz, A.; Elnakib, A.; Giedd, J.; Rumsey, J.M.; Williams, E.L.; Andrew, E.S. Corpus callosum shape analysis with application to dyslexia. Transl. Neurosci. 2010, 1, 124–130. [Google Scholar] [CrossRef]
- Farr, L.; Mancho-For, N.; Montal, M. Estimation of Brain Functional Connectivity in Patients with Mild Cognitive Impairment. Brain Sci. 2019, 9, 350. [Google Scholar] [CrossRef]
- Wajuihian, S.O.; Naidoo, K.S. Dyslexia: An overview. Afr. Vis. Eye Health 2011, 70, 89–98. [Google Scholar] [CrossRef][Green Version]
- Yuzaidey, N.A.M.; Din, N.C.; Ahmad, M.; Ibrahim, N.; Razak, R.A.; Harun, D. Interventions for children with dyslexia: A review on current intervention methods. Med. J. Malays. 2018, 73, 311–320. [Google Scholar]
- Tamboer, P.; Vorst, H.C.M.; Ghebreab, S.; Scholte, H.S. Machine learning and dyslexia: Classification of individual structural neuro-imaging scans of students with and without dyslexia. NeuroImage Clin. 2016, 11, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Płoński, P.; Gradkowski, W.; Altarelli, I.; Monzalvo, K.; van Ermingen-Marbach, M.; Grande, M.; Hein, S.; Marchewka, A.; Bogorodzki, P.; Ramus, F.; et al. Multi-parameter machine learning approach to the neuroanatomical basis of developmental dyslexia. Hum. Brain Mapp. 2017, 38, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Ravi, D.; Wong, C.; Deligianni, F.; Berthelot, M.; Andreu-Perez, J.; Lo, B.; Yang, G.-Z. Deep Learning for Health Informatics. IEEE J. Biomed. Health Inform. 2017, 21, 4–21. [Google Scholar] [CrossRef] [PubMed]
- Dash, S.; Acharya, B.R.; Mittal, M.; Ajith, A.; Kelemen, A. Deep Learning Techniques for Biomedical and Health Informatics; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yu, L.; Chen, H.; Dou, Q.; Qin, J.; Heng, P.A. Integrating Online and Offline 3D Deep Learning for Automated Polyp Detection in Colonoscopy Videos. IEEE J. Biomed. Health Inform. 2016, 2194, 1–11. [Google Scholar]
- Oyedotun, O.K.; Olaniyi, E.O. Deep Learning in Character Recognition Considering Pattern Invariance Constraints. Int. J. Syst. Appl. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Ren, J. Investigation of Convolutional Neural Network Architectures for Image-based Feature Learning and Classification; University of Washington: Bothell, WA, USA, 2016. [Google Scholar]
- Zhu, Q.; Lv, X. 2P-DNN: Privacy-Preserving Deep Neural Networks Based on Homomorphic Cryptosystem. arXiv 2018, arXiv:1807.08459. [Google Scholar]
- Pengtao, X.; Bilenko, M.; Finley, T.; Gilad-Bachrach, R.; Lauter, K.; Naehrig, M. Crypto-Nets: Neural Networks over Encrypted Data. arXiv 2014, arXiv:1412.6181. [Google Scholar]
- Mahmood, A.; Hamed, T.; Obimbo, C.; Dony, R. Improving the Security of the Medical Images. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 137–146. [Google Scholar] [CrossRef][Green Version]
- Al-Haj, A.; Abandah, G.; Hussein, N. Crypto-based algorithms for secured medical image transmission. IET Inf. Secur. 2015, 9, 365–373. [Google Scholar] [CrossRef]
- Gatta, M.T.; Al-Latief, S.T.A. Medical image security using modified chaos-based cryptography approach. J. Phys. Conf. Ser. 2018, 1003, 1–6. [Google Scholar] [CrossRef]
- Dowlin, N.; Gilad-Bachrach, R.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. CryptoNets: Applying neural networks to Encrypted data with high throughput and accuracy—Microsoft research. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 24 February 2016; pp. 1–12. [Google Scholar]
- Chao, J.; Badawi, A.A.; Unnikrishnan, B.; Lin, J.; Mun, C.F.; Brown, J.M.; Campbell, J.P.; Chiang, M.; Kalpathy-Cramer, J.; Chandrasekhar, V.R.; et al. CaRENets: Compact and Resource-Efficient CNN for Homomorphic Inference on Encrypted Medical Images. arXiv 2019, arXiv:1901.10074. [Google Scholar]
- Koppu, S.; Viswanatham, V.M. A Fast Enhanced Secure Image Chaotic Cryptosystem Based on Hybrid Chaotic Magic Transform. Model. Simul. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box. Symmetry 2018, 10, 399. [Google Scholar] [CrossRef]
- Safari, A.; Kong, Y. Four tap Daubechies filter banks based on RNS. In Proceedings of the IEEE 2012 International Symposium on Communications and Information Technologies (ISCIT), Gold Coast, QLD, Australia, 2–5 October 2012; pp. 952–955. [Google Scholar]
- Bankas, E.K.; Gbolagade, K.A. A New Efficient RNS Reverse Converter for the 4-Moduli Set. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2014, 8, 328–332. [Google Scholar]
- Navin, A.H.; Oskuei, A.R.; Khashandarag, A.S.; Mirnia, M. A Novel Approach Cryptography by using Residue Number System. In Proceedings of the ICCIT, 6th International Conference on Computer Science and Convergence Information Technology IEEE, Seogwipo, Korea, 29 November–1 December 2011. [Google Scholar]
- Abdul-mumin, S.; Gbolagade, K.A. Mixed Radix Conversion based RSA Encryption System. Int. J. Comput. Appl. 2016, 150, 43–47. [Google Scholar] [CrossRef]
- Alhassan, S.; Gbolagade, K.A. Enhancement of the Security of a Digital Image using the Moduli Set. J. Adv. Res. Comput. Eng. Technol. 2013, 2, 2223–2229. [Google Scholar]
- Youssef, M.I.; Eman, A.E.; Elghany, M.A. Multi-Layer Data Encryption using Residue Number System in DNA Sequence. Int. J. Comput. Appl. 2012, 45, 19–24. [Google Scholar]
- Youssef, M.I.; Emam, A.E.; Saafan, S.M.; Elghany, M.A.B.D. Secured Image Encryption Scheme Using both Residue Number System and DNA Sequence. Online J. Electron. Electr. 2013, 6, 656–664. [Google Scholar]
- Sirichotedumrong, W.; Maekawa, T.; Kinoshita, Y.; Kiya, H. Privacy-Preserving Deep Neural Networks with Pixel-based Image Encryption Considering Data Augmentation in the Encrypted Domain. In Proceedings of the IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Liu, X.; Zou, Y.; Kuang, H.; Ma, X. Face Image Age Estimation Based on Data Augmentation and Lightweight Convolutional. Symmetry 2020, 12, 146. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognition: A self. Biol. Cybern. 1980, 202, 193–202. [Google Scholar] [CrossRef]
- Yadav, S.S.; Jadhav, S.M. Deep convolutional neural network based medical image classification for disease diagnosis. J. Big Data 2019, 6, 1–18. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. arXiv 2019, arXiv:1901.06032. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Ali, A. A New Channel Boosted Convolutional Neural Network using Transfer Learning. arXiv 2018, arXiv:1804.08528. [Google Scholar]
- Rahman, A.; Muniyandi, R.C. An Enhancement in Cancer Classification Accuracy Using a Two-Step Feature Selection Method Based on Artificial Neural Networks with 15 Neurons. Symmetry 2020, 12, 271. [Google Scholar] [CrossRef]
- Niethammer, M.; Styner, M.; Aylward, S.; Zhu, H.; Oguz, I.; Yap, P.-T.; Shen, D. Information Processing in Medical Imaging. In Proceedings of 25th International Conference, IPMI 2017; Hutchison, D., Ed.; Springer: Boone, NC, USA, 2017. [Google Scholar]
- Cole, J.H.; Poudel, R.P.K.; Tsagkrasoulis, D.; Caan, M.W.A.; Steves, C.; Spector, T.D.; Montana, G. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. Neuroimage 2017, 1–25. [Google Scholar] [CrossRef]
- Hesamifard, E.; Takabi, H.; Ghasemi, M. CryptoDL: Deep Neural Networks over Encrypted Data. arXiv 2017, arXiv:1711.05189. [Google Scholar]
- Chervyakov, N.I.; Lyakhov, P.A.; Valueva, M.V.; Valuev, G.V.; Kaplun, D.I.; Efimenko, G.A.; Gnezdilov, D.V. Area-Efficient FPGA Implementation of Minimalistic Convolutional Neural Network Using Residue Number System. In Proceedings of the IEEE 23rd Conference of Frust Association, Bologna, Italy, 13–16 November 2018; pp. 112–118. [Google Scholar]
- Dimauro, G.; Impedovo, S.; Pirlo, G. A New Technique for Fast Number Comparison in the Residue Number System. IEEE Trans. Comput. 1993, 42, 608–612. [Google Scholar] [CrossRef]
- Gbolagade, K.A.; Cotofana, S.D. An O(n) Residue Number System to Mixed Radix Conversion Technique. In Proceedings of the IEEE Conference on Very Large Scale Integration, Taipei, Taiwan, 24–27 May 2009; pp. 521–524. [Google Scholar]
- Abdul-mumin, S.; Gbolagade, K.A. An Improved Residue Number System Based RSA Cryptosystem. Int. J. Emerg. Technol. Comput. Appl. Sci. 2017, 20, 70–74. [Google Scholar]
- Lotfinejad, M.M.; Mosleh, M.; Noori, H. A novel generic three-moduli set and its optimum arithmetic residue to binary converters. In Proceedings of the 2010 the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–29 February 2010; pp. 112–116. [Google Scholar]
- Cao, B.; Srikanthan, T.; Chang, C.H. Design of residue-to-binary converter for a new 5-moduli superset residue number system. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems, Vancouver, BC, Canada, 23–26 May 2004. [Google Scholar]
- Płoński, P.; Gradkowski, W.; Marchewka, A.; Jednoróg, K.; Bogorodzki, P. Dealing with the heterogeneous multi-site neuroimaging data sets: A discrimination study of children dyslexia. In Brain Informatics and Health. BIH 2014, Lecture Notes in Computer Science, 8609; Ślȩzak, D., Tan, A.H., Peters, J.F., Schwabe, L., Eds.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Dale, A.M.; Fischl, B.; Sereno, M.I. Cortical Surface-Based Analysis: I. Segmentation and Surface Reconstruction. Neuroimage 1999, 9, 179–194. [Google Scholar] [CrossRef]
- Sun, X.; Shi, L.; Luo, Y.; Yang, W.; Li, H.; Liang, P.; Li, K.; Mok, V.C.T.; Chu, W.C.W.; Wang, D. Histogram—Based normalization technique on human brain magnetic resonance images from different acquisitions. Biomed. Eng. Online 2015, 14, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kleesiek, J.; Urban, G.; Hubert, A.; Schwarz, D.; Maier-Hein, K.; Bendszus, M.; Briller, A. Neuroimage Deep MRI brain extraction: A 3D convolutional neural network for skull stripping. Neuroimage 2016, 129, 460–469. [Google Scholar] [CrossRef] [PubMed]
- Im, K.; Raschle, N.M.; Smith, S.A.; Ellen, G.P.; Gaab, N. Atypical Sulcal Pattern in Children with Developmental Dyslexia and At-Risk Kindergarteners. Cereb. Cortex 2016, 26, 1138–1148. [Google Scholar] [CrossRef] [PubMed]
- Tamboer, P.; Scholte, H.S.; Vorst, H.C.M. Dyslexia and voxel-based morphometry: Correlations between five behavioural measures of dyslexia and gray and white matter volumes. Ann. Dyslexia 2015, 65, 121–141. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Penwarden, N.; Ji, Q. An Image Segmentation Framework Based on Patch Segmentation Fusion. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; pp. 1–5. [Google Scholar]
- Alkinani, M.H.; El-Sakka, M.R. Patch-based models and algorithms for image denoising: A comparative review between patch-based images denoising methods for additive noise reduction. EURASIP J. Image Video Process. 2017, 58, 1–27. [Google Scholar] [CrossRef]
- Parhami, B. Digital/analog arithmetic with continuous-valued residues. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009. [Google Scholar]
- Omondi, A.; Premkumar, B. Residue Number Systems: Theory and Implementation. In Covent Garden, London; Imperial College Press: London, UK, 2007. [Google Scholar]
- Jaberipur, G.; Belghadr, A.; Nejati, S. Impact of diminished-1 encoding on residue number systems arithmetic units and converters. Comput. Electr. Eng. 2019, 75, 61–76. [Google Scholar] [CrossRef]
- Shin, H.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep Convolutional Neural Networks for Computer-Aided Detection: CNN Architectures, Dataset Characteristics and Transfer Learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Kafi, M.; Maleki, M.; Davoodian, N. Research in Veterinary Science Functional histology of the ovarian follicles as determined by follicular fluid concentrations of steroids and IGF-1 in Camelus dromedarius. Res. Vet. Sci. 2015, 99, 37–40. [Google Scholar] [CrossRef]
- Bengio, Y. Deep Learning of Representations: Looking Forward. In Statistical Language and Speech Processing. SLSP 2013, Lecture Notes in Computer Science, 7978; Dediu, A.H., Martín-Vide, C., Mitkov, R., Truthe, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nguyen, Q.; Mukkamala, M.C.; Hein, M. Neural Networks Should be Wide Enough to Learn Disconnected Decision Regions. arXiv 2018, arXiv:1803.00094. [Google Scholar]
- Havaei, M.; Davy, A.; Warde-Farley, D.; Biard, A.; Courville, A.; Bengio, Y.; Pal, C.; Jodoin, P.; Larochelle, H. Brain Tumor Segmentation with Deep Neural Networks. Med. Image Anal. 2017, 35, 18–31. [Google Scholar] [CrossRef]
- Kamnitsas, K.; Ledig, C.; Newcombe, V.F.J.; Simpson, J.P.; Kane, A.D.; Menon, D.K.; Rueckert, D.; Glocker, B. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Med. Image Anal. 2017, 36, 61–78. [Google Scholar] [CrossRef]
- Dou, Q.; Chen, H.; Yu, L.; Zhao, L.; Qin, J.; Wang, D.; Mok, V.C.T.; Shi, L.; Heng, P. Automatic Detection of Cerebral Microbleeds from MR Images via 3D Convolutional Neural Networks. IEEE Trans. Med. Imaging 2016, 35, 1182–1195. [Google Scholar] [CrossRef]
- Dou, Q.; Yu, L.; Chen, H.; Jin, Y.; Yang, X.; Qin, J.; Heng, P. 3D deeply supervised network for automated segmentation of volumetric medical images. Med. Image Anal. 2017, 41, 40–54. [Google Scholar] [CrossRef] [PubMed]
- Payan, A.; Montana, G. Predicting Alzheimer’s disease: A neuroimaging study with 3D convolutional neural networks. arXiv 2015, arXiv:1502.02506. [Google Scholar]
- Amerineni, R.; Gupta, R.S.; Gupta, L. CINET: A Brain-Inspired Deep Learning Context—Integrating Neural Network Model for Resolving Ambiguous Stimuli. Brain Sci. 2020, 10, 64. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Krizhevsky, A.; Sustskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 84–90. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Computer Vision – ECCV 2014. Lecture Notes in Computer Science, 8689; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Germany.
- Maroosi, A.; Muniyandi, R.C. Accelerated Execution of P Systems with Active Membranes to solve the N-Queens Problem. Theor. Comput. Sci. 2014, 551, 39–54. [Google Scholar]
- Maroosi, A.; Muniyandi, R.C.; Sundararajan, E.; Zin, A.M. Parallel and Distributed Computing Models on a Graphics Processing Unit to Accelerate Simulation of Membrane Systems. Stimul. Model. Pract. Theory 2014, 47, 60–78. [Google Scholar]
- Othman, A.; Muniyandi, R.C. Elliptic Curve Diffie-Hellman Random Keys Using Artificial Neural Network and Genetic Algorithm for Secure Data over Private Cloud. Inf. Technol. J. 2016, 15, 77–83. [Google Scholar] [CrossRef]
- Zhou, Y.; Panetta, K.; Agaian, S. An image scrambling algorithm using parameter based M-sequences. In Proceedings of the 2008 International Conference on Machine Learning and Cybernetics, Kunming, China, 12–15 July 2008. [Google Scholar]
- Somaraj, S.; Hussain, M.A. A Novel Image Encryption Technique Using RGB Pixel Displacement for Color Images. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016. [Google Scholar]
- Wang, Y.; Wong, K.W.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Solitons Fractals 2009, 41, 1773–1783. [Google Scholar] [CrossRef]
- Macaš, M.; Novak, D.; Kordik, P.; Lhotska, L.; Vyhnalek, M.; Brzezny, R. Dyslexia Detection from Eye Movements Using Artificial Neural Networks. In Proceedings of the European Medical and Biological Engineering Conference, Prague, Czech Republic, 20–25 November 2005; pp. 1–10. [Google Scholar]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Xia, Z.; Su, M.; Shu, H.; Gong, G. Disrupted white matter connectivity underlying developmental dyslexia: A machine learning approach. Hum. Brain Mapp. 2016, 37, 1443–1458. [Google Scholar] [CrossRef] [PubMed]
- Sarah, B.; Nicole, C.; Ardag, H.; Madelyn, M.; Holland, S.K.; Tzipi, H. An fMRI Study of a Dyslexia Biomarker. J. Young Investig. 2014, 26, 1–4. [Google Scholar]
- Spoon, K.; Crandall, D.; Siek, K. Towards Detecting Dyslexia in Children’s Handwriting Using Neural Networks. In Proceedings of the International Conference on Machine Learning AI for Social Good Workshop, Long Beach, CA, USA, 15 June 2019; pp. 1–5. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 1–54. [Google Scholar] [CrossRef]
- Bost, R.; Popa, R.A.; Tu, S.; Goldwasser, S. Machine Learning Classification over Encrypted Data. In Proceedings of the NDSS Conference, San Diego, CA, USA, 8–11 February 2015; pp. 1–14. [Google Scholar]
- Tanaka, M. Learnable Image Encryption. In Proceedings of the IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Taichung, Taiwan, 19–21 May 2018; pp. 1–2. [Google Scholar]


| Virtex-4 FPGA Delay in Seconds | Spartan-3 FPGA Delay in Seconds | ||||||
|---|---|---|---|---|---|---|---|
| n | Critical Path (2n+1 − 1) | Proposed Encoder | State-of-the-Art (2) | % Improvement | Proposed Encoder | State-of-the-Art (2) | % Improvement |
| 4 | 25 − 1 | 23.7 | 25.6 | 7.4 | 25.5 | 30.1 | 15.3 |
| 5 | 26 − 1 | 29.9 | 33.7 | 11.3 | 35.2 | 39.7 | 11.3 |
| 8 | 29 − 1 | 37.1 | 48.5 | 23.5 | - | - | - |
| 11 | 212 − 1 | 56.8 | 68.3 | 16.8 | - | - | - |
| Adjacent Portions | Correlation Coefficient (r) |
|---|---|
| Portion1 | −0.0293 |
| Portion2 | 0.0082 |
| Portion3 | −0.0275 |
| Portion4 | −0.0111 |
| Portion5 | −0.0659 |
| Whole Images | −0.0073 |
| Before Encoding | After Encoding | |||||
|---|---|---|---|---|---|---|
| Training Iterations | Accuracy (%) | Sensitivity (%) | Specificity (%) | Accuracy (%) | Sensitivity (%) | Specificity (%) |
| 150 | 57.47 ± 2.58 | 40.19 ± 2.13 | 53.62 ± 2.33 | 39.66 ± 2.09 | 33.28 ± 2.51 | 37.18 ± 2.85 |
| 225 | 59.13 ± 3.76 | 61.23 ± 3.72 | 54.91 ± 3.19 | 58.39 ± 3.44 | 58.72 ± 3.06 | 53.31 ± 3.41 |
| 350 | 70.68 ± 4.02 | 65.29 ± 2.97 | 66.84 ± 2.88 | 63.42 ± 3.19 | 61.97 ± 2.89 | 62.00 ± 2.99 |
| 450 | 80.22 ± 4.46 | 71.33 ± 3.85 | 72.53 ± 4.12 | 68.99 ± 3.87 | 67.81 ± 4.73 | 68.03 ± 3.96 |
| 500 | 84.56 ± 4.91 | 76.25 ± 4.64 | 78.21 ± 4.33 | 73.19 ± 4.18 | 70.33 ± 4.46 | 71.43 ± 4.11 |
| Author(s) and Year | Image Encrypted Algorithm | Deep Learning Classifier Used | Source of Dataset Used | Accuracy (%) | Reference No. |
|---|---|---|---|---|---|
| Tanaka (2018) | Block-based | Pyramidal Residue Network | CIFER Dataset | 56.80 | [89] |
| Sirichotedumrong et al. (2019) | Pixel-based | ResNet-18 | CIFER Dataset | 86.99 | [35] |
| Chao et al. (2019) | - | CaRENets | MNIST Dataset | 73.10 | [25] |
| Proposed | Pixel-based | Two-Pathway Cascaded Deep CNN | Kaggle Brain MRI Dataset | 73.19 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usman, O.L.; Muniyandi, R.C. CryptoDL: Predicting Dyslexia Biomarkers from Encrypted Neuroimaging Dataset Using Energy-Efficient Residue Number System and Deep Convolutional Neural Network. Symmetry 2020, 12, 836. https://doi.org/10.3390/sym12050836
Usman OL, Muniyandi RC. CryptoDL: Predicting Dyslexia Biomarkers from Encrypted Neuroimaging Dataset Using Energy-Efficient Residue Number System and Deep Convolutional Neural Network. Symmetry. 2020; 12(5):836. https://doi.org/10.3390/sym12050836
Chicago/Turabian StyleUsman, Opeyemi Lateef, and Ravie Chandren Muniyandi. 2020. "CryptoDL: Predicting Dyslexia Biomarkers from Encrypted Neuroimaging Dataset Using Energy-Efficient Residue Number System and Deep Convolutional Neural Network" Symmetry 12, no. 5: 836. https://doi.org/10.3390/sym12050836
APA StyleUsman, O. L., & Muniyandi, R. C. (2020). CryptoDL: Predicting Dyslexia Biomarkers from Encrypted Neuroimaging Dataset Using Energy-Efficient Residue Number System and Deep Convolutional Neural Network. Symmetry, 12(5), 836. https://doi.org/10.3390/sym12050836






