Abstract
Modeling fluid flows is a general procedure to handle engineering problems. Here we present a systematic study of the flow and heat transfer around a circular cylinder by introducing a new representative appropriate drag coefficient concept. We demonstrate that the new modified drag coefficient may be a preferable dimensionless parameter to describe more appropriately the fluid flow physical behavior. A break in symmetry in the global structure of the entire flow field increases the difficulty of predicting heat and mass transfer behavior. A general simple drag model with high accuracy is further developed over the entire range of Reynolds numbers met in practice. In addition, we observe that there may exist an inherent relation between the drag and heat and mass transfer. A simple analogy model is established to predict heat transfer behavior from the cylinder drag data. This finding provides great insight into the underlying physical mechanism.
1. Introduction
Flow over an object is omnipresent both in nature [1,2,3] and in many engineering applications [4,5,6]. For instance, the motion of swimming and flying animals [1], growth of stalagmites [2], fall motion of hailstones [3], motion of pollutants in the atmosphere [7], complex motion of the drill string in the field of petroleum engineering [8], and flow over bridge piers, chimney stacks, offshore structures, and tower structures in civil engineering [9], aircrafts in the field of aerospace [10], nuclear fuel rods in the atomic field [5], power battery cooling structures in the field of new energy vehicles [11], heat exchanger tubes in thermal engineering [12], etc. The fluid dynamic drag [13,14,15], active and passive methods for drag reduction [16,17,18], boundary layer flow [19], flow-induced vibration [5], behavior of turbulent fluid motion [20], and instability in the wake shear layer [21,22,23] are of interest in numerous fields. Owing to its practical importance in engineering applications and theoretical significance in understanding fundamental fluid mechanics, the flow over a circular cylinder has attracted extensive study interest from both scientists and engineers. Therefore, the flow and heat transfer characteristics of circular cylinders in cross flow have been the subject of many theoretical, experimental, and numerical studies; thus, a large number of results exist and are available in the literature.
2. Literature Review
The flow over bluff bodies like spheres [24,25,26] and circular cylinders [27,28,29,30] is a classical problem in fluid mechanics. Yao et al. [9] focused on the influence of turbulence on the wind pressure and aerodynamic behavior of smooth circular cylinders. Liang and Duan [12] studied numerically the flow past a yawed circular cylinder using large eddy simulation. They pointed out that the boundary condition of the two end-plates has a significant effect on the flow behaviors in the wake. Sarıoğlu et al. [18] investigated experimentally the effect of a rod on the flow around a square cylinder at incidence. Lin et al. [21] carried out an experimental study on nonstationary three-dimensional aspects of flow past a circular cylinder and found that the flow behaviors are critically affected by the presence of a separation bubble. Ahmed and Wagner [28] focused on the vortex shedding and transition frequencies associated with flow around a circular cylinder. During an oil drilling process, complex motion of the drill string [31,32] and the settling velocity of drill cuttings in drilling fluids [33,34] have been the focus of investigations in the field of petroleum engineering. Leth-Espensen et al. [35] presented a biomass devolatilization model describing both spherical and cylindrical particles for suspension firing. Duan et al. [7] investigated the flow and heat transfer past a sphere, and they first proposed the appropriate drag coefficient to replace the inertia type definition proposed by Sir Isaac Newton.
It seems to be a common perception that the drag and customary drag coefficient would preferably have a uniform variation trend. In fact, this is a wrong perception caused by the inertia type definition. An extension research of the previous work (Reference [7]) was conducted in the present paper. The flow past a circular cylinder was investigated by introducing a new representative appropriate drag coefficient concept originally presented in Reference [7] for spheres. The Kutta-Joukowski theorem states that the force experienced by a body in a uniform stream is equal to the product of the fluid density, stream velocity, and circulation and has a direction perpendicular to the stream velocity [36]. Appling the Kutta-Joukowski theorem, the motion of flying animals, high-speed aircrafts, and cylinders of various shapes may be easily converted into a specific type of problem (Figure 1).
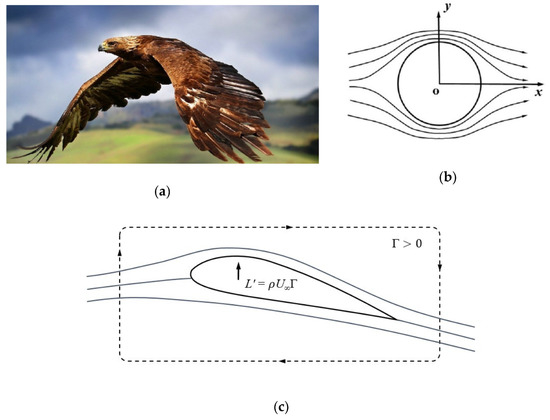
Figure 1.
Flow past an object. (a) Flight of an eagle; (b) flow past a circular cylinder; (c) flow past an airfoil.
The flow over a circular cylinder is a classic example of flow over a bluff body and frequently serves as a benchmark to help understand flow separation and vortex shedding [37]. Extensive studies have been carried out on this classic problem in the past century. A literature survey indicates that resistance formulas for a wide range of Reynolds (Re) numbers are rarely reported, especially concerning the absence of a classical drag relationship in the entire range of Re numbers. Therefore, based on a systematic summary of previous studies, we have developed such a general empirical model for accurate prediction of the appropriate drag coefficient.
Historical experimental data for drag and heat transfer of the flow around a circular cylinder were critically examined. Analogous investigations have been reported by many researchers working in the flow and heat and mass transfer area, including internal flows [38] and external flows [7]. For external flows, Duan et al. [7] found that there exists a relation between the drag and heat transfer in spheres. For internal flows, Duan and He [38] presented an extended Reynolds analogy for slip flow heat transfer in microchannels. To the authors’ best knowledge, the internal relationship between the drag and heat transfer for cylinders has not been revealed in the existing literature. Here we present drag and heat transfer results which demonstrate that there may exist an inherent relation between the drag and heat transfer in cylinders. The appropriate drag coefficient may be associated with the Nusselt number. Thus, a simple model is proposed to predict heat transfer behavior from drag data.
Drag estimation of bodies moving through fluids is a crucial concern in engineering practice [1]. For a uniform stream past a circular cylinder, the usual definition of the drag coefficient CD is [39]
where F represents the drag force on the circular cylinder per unit length, ρ is the fluid density, is the relative velocity of the fluid and the object, A is the projected area of the body in the direction of the flow, and D is the cylinder diameter.
It is well known that in a viscous cross flow, the drag acting on a circular cylinder is due to friction and inertia. Earlier efforts and significant contributions were made by Stokes [40], Oseen [41], and Lamb [42] to obtain theoretical solutions for creeping flows. Van Dyke [43] introduced the development of theoretical solutions for spheres and circular cylinders. A first approximation for the drag coefficient on a cylinder is known as the Oseen solution, and it is expressed as follows [41]
where = 0.577216… is Euler’s constant and Re is the Reynolds number defined by . Tomotika and Aoi [44] derived and presented expansion formulas of the drag force at small Reynolds numbers. As a result of their efforts, a second approximation of the drag coefficient was presented [44]:
where is a constant defined by . Further, a third approximation of the drag coefficient is expressed as [44]
Subsequently, further research was conducted by Proudman and Pearson [45], Kaplun [46], and Tamada et al. [47] in order to determine expansion formulas of drag force. Due to the complexity and difficulty of mathematically solving Navier-Stokes equations, it is quite difficult to extend the availability of the analytical solutions to higher Reynolds numbers. The correlation between the drag coefficient and Reynolds number can only be determined by means of experiment.
For historical reasons, it is a common practice to use dynamic pressure to nondimensionalize the drag experienced by bodies. The drag coefficient can also be expressed by the following general expression [44]:
where μ represents the viscosity. The constants Bm may be acquired via solving the following simultaneous linear algebraic equations:
where are functions of the Re number, and they may be expressed by
where and are the modified Bessel functions of the first and second kind, respectively. Furthermore, substituting Equation (5) into Equation (1), the general formula of CD can be written as
A literature survey shows that drag correlations for a wide range of Re numbers are rarely reported. In particular, there is no such correlation for drag in the entire range of Re numbers. The old drag coefficient diagrams were used in almost all the relevant literature and texts. When researchers verify the accuracy and reliability of the results they have obtained, they all have to use traditional drag coefficient diagrams. Therefore, a new drag coefficient diagram with rich and reliable data and a general drag model is necessary. Based on this situation, we extensively collected historical experimental data and mapped them on the latest drag coefficient-Re diagram (Figure 2). The historical experimental data collected by Schlichting [48] and other experimental results from Dryden and Hill [49], Delany and Sorensen [50], Tritton [51], Roshko [52], and Achenbach [53] for the drag coefficient of circular cylinders all fall on a single curve. The new drag coefficient diagram refers to a wide range of Re numbers and can greatly facilitate engineering applications, and it can be updated in the texts of fluid mechanics and heat transfer, since it is of great significance to teaching and scientific research.
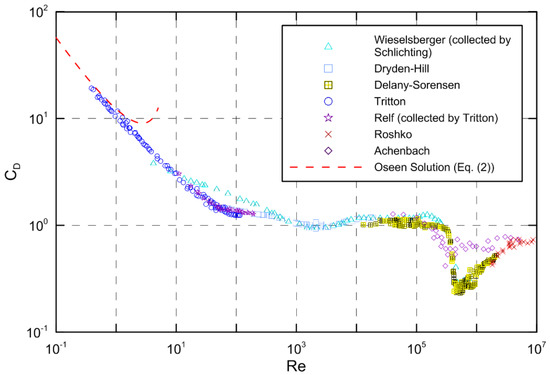
Figure 2.
Latest traditional drag coefficient diagram.
3. Results and Discussion
3.1. Drag Force-Velocity Diagram
It is intuitive to people that the resistance of a moving body increases rapidly with velocity. For bluff-body flows, trend graphs of resistance and velocity over a broad range of Re are rarely seen in the literature, especially for flow around circular cylinders. Based on the results of previous experimental studies [48,49,50,51,52,53], a resistance-velocity diagram over a broad range of Re numbers was obtained, and it is illustrated in Figure 3. The relative velocity range is from 1.5 × 10−3 to 1.5 × l03 m/s, which roughly covers all the flow conditions that exist in nature and in engineering applications, and the corresponding Reynolds number range is from 1 to 106.
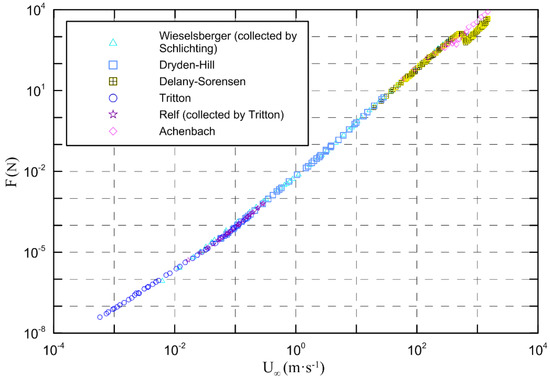
Figure 3.
Drag force-velocity diagram.
The classic shape of the drag coefficient curve versus Reynolds number for circular cylinders is presented in Figure 2 and also appears in every fluid mechanics text. Figure 3 shows the typical trend that the drag on a circular cylinder increases with increasing flow velocity of the fluid; however, there is a significant reduction in the customary drag coefficient CD with increasing Re number (Figure 2). Obviously, the drag and the customary drag coefficient have a roughly opposite changing trend, which may be undesirable and unreasonable. As can be seen from Figure 2, with increasing Re number, the drag coefficient first decreases, then it is nearly invariant in a wide range of Re number with a rise of Re up to 2.0 × 105; however, as a matter of fact, the drag coefficient is closely related to the Reynolds number in this regime. The most remarkable variation in CD occurs in the critical Reynolds number range (3–4) × 105, where CD decreases from its subcritical value of 1.2 to the supercritical value of 0.2. The sudden drop in the drag coefficient marks the end of the subcritical regime and the beginning of the critical regime. In detail, this decrease in CD is a result of the transition from laminar to turbulent flow in the boundary layer [54]. After that, CD rises again in the supercritical regime, and it gradually approaches a constant value in the transcritical regime [55]. This variation trend is strange and ruleless, which further demonstrates that the customary drag coefficient may be not a proper dimensionless parameter to describe and represent the drag.
3.2. The Concept of Appropriate Drag Coefficient and Its Physical Meaning
Although extensive investigations on flow past circular cylinders have been conducted in pressurized wind tunnels, due to the limitations of the conditions, most of the experimental works were carried out below the critical Reynolds number Re < 4 × 105. In the supercritical and transcritical flow regimes, generally the behavior of the flow around circular cylinders is abnormally sensitive to the Reynolds number or a very small perturbation, so there are some differences in the results of different researchers (see Figure 2).
In fluid dynamics, the drag coefficient is an important dimensionless group which is utilized to quantify the drag of a body in a moving fluid. Therefore, the drag coefficient is a crucially important dimensionless parameter when calculating resistance, and we hope it can hint as to the variation trend of resistance. However, it is clear that the traditional drag coefficient does not possess this important characteristic, and its change trend with the Reynolds number may be also easily misleading. A very representative example is shown on Wikipedia [56], where the relevant statement is expressed as follows: “the drag coefficient is utilized in the resistance relation in which a lower drag coefficient indicates the body will have less aerodynamic or hydrodynamic drag”. Through the above analysis, we can see that this expression is not rigorous, since a smaller value of drag coefficient does not necessary imply that the drag acting on the body is lower. This demonstrates that the customarily used drag coefficient may not be a desirable and appropriate dimensionless parameter to describe the fluid flow physical behavior. It seems to be a common perception that the drag and customary drag coefficient would preferably have a uniform variation trend. In fact, this is a wrong perception caused by Newton’s definition, and herein lies the significance of our research work.
Thus, in this work, we propose the use of a new, more representative drag coefficient quantity, namely, the modified drag coefficient that is defined in the following manner [7].
By comparison with Equation (1), it is clearly observed that the above definition of the appropriate drag coefficient is simpler and easier to use. Furthermore, by the use of Equation (8), the appropriate drag coefficient can also be expressed as follows:
From the above formula, it is noted that the new drag coefficient is directly related to the constants Bm. Using the definition of the modified drag coefficient for spheres and cylinders, the general drag expressions may be restated respectively as
A striking similarity in the equation structure emerges between the drag expressions in terms of the modified drag coefficient and the linear Stokes drag expression for spheres [57]. The linear Stokes drag of spheres at low Reynolds numbers may be expressed as
The Stokes drag for spheres is also referred to as the Stokes-Einstein-Sutherland equation, and it was developed based on the analytical solution of Navier-Stokes equations by Sir George Gabriel Stokes [40].
Based on the discussion above, we observe that the proposed dimensionless group DC is desirable and reasonable in representing the drag and also shows more physical meaning. As a consequence, it is more appropriate and convenient to work out drag problems using Equation (9).
3.3. General Drag Model over the Entire Range of Reynolds Numbers
Historical experimental drag data for circular cylinders were processed and presented according to the definition of the modified drag coefficient. Figure 4 demonstrates the appropriate drag coefficient of circular cylinders as a function of the Re number. It can be seen that the modified drag coefficient rises with increasing Re number as the drag force itself does. From Figure 3 and Figure 4, it is observed that the drag and the modified drag coefficient have roughly the same variation trend with increasing Re number. Figure 4 is more reasonable and intuitive in reflecting the original physical behavior and natural tendency. Therefore, Figure 4 does serve as a significant visual aid in drag analysis and optimum structural design. Furthermore, the curve is relatively smooth and there does not exist a minimum for DC. This means that the definition of the appropriate drag coefficient is more scientific and reasonable. Figure 2 demonstrates that the customary drag coefficient is a fairly complicated function of the Re number, while the appropriate drag coefficient curve is relatively very smooth (Figure 4), so it is easier to obtain a relatively simple expression to accurately describe the flow characteristics over the entire range of Re numbers.
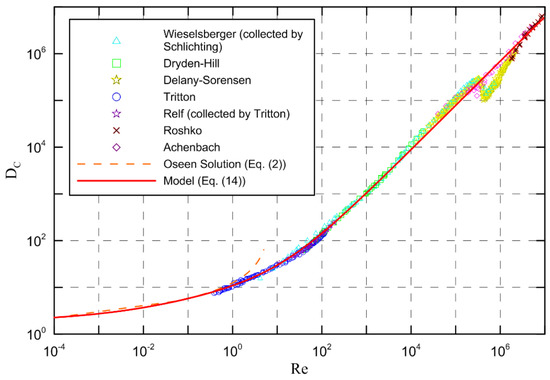
Figure 4.
Appropriate drag coefficient diagram.
Due to the absence of a classical drag relationship over the entire range of Re numbers, based on the systematic summary of previous research, according to the definition of the appropriate drag coefficient, an extensive empirical model of the appropriate drag coefficient with great accuracy was developed by means of a weighted least square fit in the entire Re number range. The simple model obtained is expressed as follows:
As can be seen from Figure 2 and Figure 4, the modified drag coefficient curve is smoother than the traditional drag coefficient curve. The model developed is in good agreement with the analytical solution and almost all experimental data. Using the appropriate drag coefficient definition to solve the problems of flow past an object, the change in resistance of the object with the velocity of the fluid can be intuitively reflected by the relation between the appropriate drag coefficient and Re number in the graph. The above discussion demonstrates that the new modified drag coefficient may be a preferable dimensionless parameter to describe fluid flow physical behavior so that fluid flow problems can be solved in a simple and intuitive manner.
3.4. Relationship between the Drag and Heat Transfer
For convection heat transfer from cylinders, Tomotika et al. obtained the Oseen solution, and they proposed a mean Nusselt number correlation which is valid at low Reynolds numbers and of very limited utility [58]. Lately, Khan et al. [59] performed an analytical study on heat transfer from cylinders and proposed the corresponding relationship. The analytical solution of the average Nusselt number obtained for both thermal boundary conditions is expressed as follows:
A large number of experimental studies on convection heat transfer from cylinders were performed by researchers. Based on experimental data, Kramers [60] suggested a mean Nusselt number correlation for 0.1 ≤ Re ≤ 104.
The correlation by Kramers is recommended due to its simplicity. In addition, Fand [61] analyzed the results of other investigators for liquids and air and correlated previous researchers’ and his experimental data by an equation as follows:
Owing to the similarity of governing differential equations for heat and mass transfer, analogy has been developed as a useful tool [62]. Based on the classical analogical approach, some analogy studies were carried out on the flow of fluids through a fluidized bed [63], turbulent flow in circular pipes [64,65], fully developed turbulent flow of power law fluids [66], slip flow heat transfer in microchannels [38], drag-reduced turbulent channel flow [67], and material evaporation behavior [68]. It is an efficient and applicable approach to predict heat and mass transfer coefficients from hydrodynamic results, especially for complex engineering problems. The change of the thermal field for different Reynolds numbers can be predicted from that of flow [69], particularly for the heat transfer behavior of the wake behind a heated body. This means the role played by the heat flux has a similar nature to that of the drag. It was found that there may exist a strong similarity between the drag and heat and mass transfer. It is expected that one transport process may be associated with another transport process, allowing one to be determined if the other is known. For example, an analogy exists between the diffusion of heat and electrical charge. This part focuses on an analogy between the appropriate drag coefficient and the mean Nusselt number.
In general, engineers may be interested in the availability of simple models which can be applied to extended studies. Through in-depth comparisons and analyses of heat transfer correlations and the new drag model, based on comprehensive consideration of simplicity, ease of use, and high accuracy, an analogy between drag and heat transfer for cylinders was developed. The analogy is applicable for a wide range of Reynolds numbers, 0.1 ≤ Re ≤ 105, and it may approximately hold for flow with higher Reynolds number. The rough analogy may be expressed as follows:
It is well known that the thermal field and concentration field can be related to the velocity field through Re. It is established that a relationship exists between momentum transfer and heat and mass diffusivities via Equation (18). The key engineering parameters, the Nusselt number and the Sherwood number, can be predicted using the presented analogy in the calculation and analysis of heat and mass transfer for convenience due to the simplicity of this expression, but there may be some loss in accuracy. Here, Equation (18) is valid for gases in which Pr is near unity in the heat transfer process. Therefore, in order to extend the availability of the simple analogy, the Prandtl number effect was considered and added in a more exact analogy. The exact analogy was developed for a wide range of Reynolds numbers, 0.1 ≤ Re ≤ 105.
The above model for circular cylinders is presented as (7.5 + 2.5Re0.45)Nu/Pr0.4, and it is compared with the drag experimental results in Figure 5. The flow and heat transfer data in Figure 5 come from experimental studies, in which the heat transfer data were collected by Whitaker [70], and other experimental data were from Sanitjai and Goldstein [71] and Perkins and Leppert [72]. The presented model does provide a means to approximately predict the Nusselt number for the whole range of Reynolds numbers, even if no experimental results exist! In particular, this may be quite important due to the lack of information on heat transfer for high-Reynolds-number flows in the literature. In addition, the obtained results also provide a theoretical basis for the design and optimization of the shape and thermal barrier coating system of high-speed aircrafts.
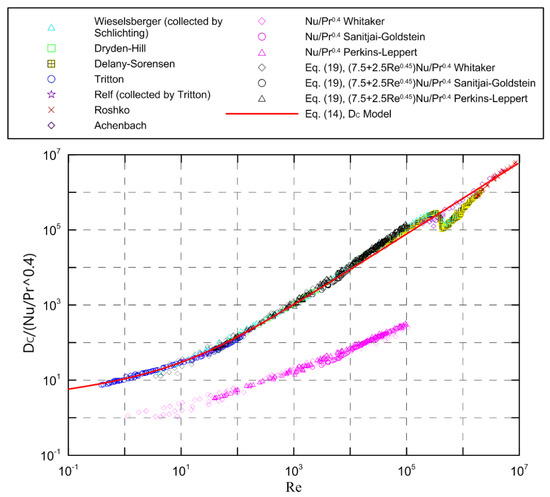
Figure 5.
Comparison of drag experimental results and heat transfer experimental data with the developed model (Equation (19)).
An inherent relation between the drag and heat and mass transfer was obtained by analogy with hydrodynamic drag data. The strong analogy further proves that the new modified drag coefficient may be a proper dimensionless parameter to describe and represent the drag, and it provides great insight into the mechanism of different transport phenomena.
4. Conclusions
The flow over regular-shaped bodies like spheres and circular cylinders represents a classical and conventional problem in hydromechanics. It was found that the customary drag coefficient may not be a proper dimensionless parameter to describe and represent the drag for flow past bluff bodies.
In the present work, it was demonstrated that a new modified drag coefficient may be a preferable dimensionless parameter to describe fluid flow physical behavior and reflect the real variation trend of drag force. A general simple drag model with fundamental accuracy was developed and is universally valid for all Reynolds number regimes. It is convenient to predict the hydrodynamic drag on cylinders utilizing the general simple model.
It was observed that there may exist a strong similarity between the drag and heat and mass transfer. It was established in this paper that a relation exists between the drag and heat transfer around a circular cylinder. This may be quite crucial due to the lack of information on the Nusselt number and the Sherwood number for most bluff bodies in the existing literature. In this context, the presented model does offer a method for predicting the Nusselt number and the Sherwood number for flow over other body shapes. The proposed simple means may provide great insight into the design and optimization of the shape and thermal barrier coating system of high-speed aircrafts.
In future research work, we will further extend analogies to other body shapes employing the appropriate drag coefficient concept.
Author Contributions
Conceptualization, H.M. and Z.D.; Methodology, H.M. and Z.D.; Formal analysis, H.M. and Z.D.; Investigation, H.M.; Validation, Z.D.; Writing—original draft, H.M.; Writing—review and editing, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China under No. 2017YFB0102101 and the National Natural Science Foundation of China under No. 51576013.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | cross-sectional area, m2 |
| Bm | constants |
| CD | drag coefficient |
| D | cylinder, sphere diameter, m |
| DC | appropriate drag coefficient |
| F | drag force, N |
| Im, Km | modified Bessel function |
| Nu | surface-average Nusselt number |
| Pr | Prandtl number |
| Re | Reynolds number, |
| S | constant |
| Sh | Sherwood number |
| free stream velocity, m/s | |
| Euler’s constant | |
| coefficient is a function of the Reynolds number | |
| μ | dynamic viscosity, N·s/m2 |
| ν | kinematic viscosity, m2/s |
| ρ | density, kg/m3 |
| D | drag |
| ∞ | for fluid at free stream conditions |
References
- Floryan, D.; Van Buren, T.; Smits, A.J. Efficient cruising for swimming and flying animals is dictated by fluid drag. Proc. Natl. Acad. Sci. USA 2018, 115, 8116–8118. [Google Scholar] [CrossRef] [PubMed]
- Parmentier, J.; Lejeune, S.; Maréchal, M.; Bourges, F.; Genty, D.; Terrapon, V.; Maréchal, J.-C.; Gilet, T. A drop does not fall in a straight line: A rationale for the width of stalagmites. Proc. R. Soc. A 2019, 475, 20190556. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.K.; Chueh, C.C. A numerical study on the ventilation coefficients of falling lobed hailstones. Atmos. Res. 2020, 234, 104737. [Google Scholar] [CrossRef]
- Churbanov, A.G.; Iliev, O.; Strizhov, V.F.; Vabishchevich, P.N. Numerical simulation of oxidation processes in a cross-flow around tube bundles. Appl. Math. Model. 2018, 59, 251–271. [Google Scholar] [CrossRef]
- Lai, J.; Sun, L.; Yang, J.; Li, P.; Xi, Z.; Gao, L.; He, C. Experimental and numerical analyses on flow-induced vibration of a nuclear engineering test reactor internal. Nucl. Eng. Des. 2018, 340, 335–346. [Google Scholar] [CrossRef]
- Rashad, A.M.; Khan, W.A.; EL-Kabeir, S.M.; EL-Hakiem, A. Mixed convective flow of micropolar nanofluid across a horizontal cylinder in saturated porous medium. Appl. Sci. 2019, 9, 5241. [Google Scholar] [CrossRef]
- Duan, Z.P.; He, B.S.; Duan, Y.Y. Sphere drag and heat transfer. Sci. Rep. 2015, 5, 12304. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Wang, C.; Qi, M.; Ren, W. Particle image velocimetry analysis of plane flow field induced by drill string planetary motion based on superposition principle. J. Pet. Sci. Eng. 2018, 170, 121–129. [Google Scholar] [CrossRef]
- Yao, J.; Lou, W.; Shen, G.; Guo, Y.; Xing, Y. Influence of inflow turbulence on the flow characteristics around a circular cylinder. Appl. Sci. 2019, 9, 3595. [Google Scholar] [CrossRef]
- He, W.; Pérez, J.M.; Yu, P.; Li, L.K. Non-modal stability analysis of low-Re separated flow around a NACA 4415 airfoil in ground effect. Aerosp. Sci. Technol. 2019, 92, 269–279. [Google Scholar] [CrossRef]
- Fan, Y.; Bao, Y.; Ling, C.; Chu, Y.; Tan, X.; Yang, S. Experimental study on the thermal management performance of air cooling for high energy density cylindrical lithium-ion batteries. Appl. Therm. Eng. 2019, 155, 96–109. [Google Scholar] [CrossRef]
- Liang, H.; Duan, R.Q. Effect of lateral end plates on flow crossing a yawed circular cylinder. Appl. Sci. 2019, 9, 1590. [Google Scholar] [CrossRef]
- Hong, L.; Wang, C.Y. Annular axisymmetric stagnation flow on a moving cylinder. Int. J. Eng. Sci. 2009, 47, 141–152. [Google Scholar] [CrossRef]
- Ticoş, C.M.; Ticoş, D.; Williams, J.D. Pushing microscopic matter in plasma with an electron beam. Plasma Phys. Control. Fusion 2019, 62, 025003. [Google Scholar] [CrossRef]
- Subiantoro, A.; Ooi, K.T. Investigation of electroosmotically induced pressure gradient in rectangular capillaries. Int. J. Eng. Sci. 2019, 145, 103172. [Google Scholar] [CrossRef]
- Alben, S.; Shelley, M.; Zhang, J. Drag reduction through self-similar bending of a flexible body. Nature 2002, 420, 479–481. [Google Scholar] [CrossRef] [PubMed]
- Manzoor, R.; Khalid, A.; Khan, I.; Baleanu, D.; Nisar, K.S. Numerical simulation of drag reduction on a square rod detached with two control rods at various gap spacing via lattice Boltzmann method. Symmetry 2020, 12, 475. [Google Scholar] [CrossRef]
- Sarıoğlu, M.; Akansu, Y.E.; Yavuz, T. Control of flow around square cylinders at incidence by using a rod. AIAA J. 2015, 43, 1419–1426. [Google Scholar] [CrossRef]
- Samad, A.; Garrett, S.J. On the stability of boundary-layer flows over rotating spheroids. Int. J. Eng. Sci. 2014, 82, 28–45. [Google Scholar] [CrossRef]
- Goldstein, S. Modern Developments in Fluid Dynamics: An Account of Theory and Experiment Relating to Boundary Layers, Turbulent Motion and Wakes; Clarendon Press: Oxford, UK, 1938. [Google Scholar]
- Lin, Y.J.; Miau, J.J.; Tu, J.K.; Tsai, H.W. Nonstationary, three-dimensional aspects of flow around circular cylinder at critical Reynolds numbers. AIAA J. 2011, 49, 1857–1870. [Google Scholar] [CrossRef]
- Rai, M.M. Detached shear-layer instability and entrainment in the wake of a flat plate with turbulent separating boundary layers. J. Fluid Mech. 2015, 774, 5–36. [Google Scholar] [CrossRef]
- Wang, X.D.; Liu, Y.N.; Wang, L.Y.; Ding, L.; Hu, H. Numerical study of nacelle wind speed characteristics of a horizontal axis wind turbine under time-varying flow. Energies 2019, 12, 3993. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chhabra, R.P. Combined effects of fluid shear-thinning and yield stress on heat transfer from an isothermal spheroid. Int. J. Heat Mass Transf. 2016, 93, 803–826. [Google Scholar] [CrossRef]
- Will, J.B.; Kruyt, N.P.; Venner, C.H. An experimental study of forced convective heat transfer from smooth, solid spheres. Int. J. Heat Mass Transf. 2017, 109, 1059–1067. [Google Scholar] [CrossRef]
- Ellendt, N.; Lumanglas, A.M.; Moqadam, S.I.; Mädler, L. A model for the drag and heat transfer of spheres in the laminar regime at high temperature differences. Int. J. Therm. Sci. 2018, 133, 98–105. [Google Scholar] [CrossRef]
- Williamson, C.H. Vortex dynamics in the cylinder wake. Ann. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Wagner, D.J. Vortex shedding and transition frequencies associated with flow around a circular cylinder. AIAA J. 2003, 41, 542–544. [Google Scholar] [CrossRef]
- Jethani, Y.; Kumar, K.; Sameen, A.; Mathur, M. Local origin of mode-B secondary instability in the flow past a circular cylinder. Phys. Rev. Fluids 2018, 3, 103902. [Google Scholar] [CrossRef]
- Yu, S.; Tang, T.; Li, J.; Yu, P. Effect of Prandtl number on mixed convective heat transfer from a porous cylinder in the steady flow regime. Entropy 2020, 22, 184. [Google Scholar] [CrossRef]
- Wang, Y.; Tuo, H.; Li, L.; Zhao, Y.; Qin, H.; An, C. Dynamic simulation of installation of the subsea cluster manifold by drilling pipe in deep water based on OrcaFlex. J. Pet. Sci. Eng. 2018, 163, 67–78. [Google Scholar] [CrossRef]
- Heshamudin, N.S.; Katende, A.; Rashid, H.A.; Ismail, I.; Sagala, F.; Samsuri, A. Experimental investigation of the effect of drill pipe rotation on improving hole cleaning using water-based mud enriched with polypropylene beads in vertical and horizontal wellbores. J. Pet. Sci. Eng. 2019, 179, 1173–1185. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Alabi, S.B.; Dosunmu, A. Settling velocity of drill cuttings in drilling fluids: A review of experimental, numerical simulations and artificial intelligence studies. Powder Technol. 2018, 339, 728–746. [Google Scholar] [CrossRef]
- Movahedi, H.; Shad, S.; Mokhtari-Hosseini, Z.B. Modeling and simulation of barite deposition in an annulus space of a well using CFD. J. Pet. Sci. Eng. 2018, 161, 476–496. [Google Scholar] [CrossRef]
- Leth-Espensen, A.; Li, T.; Glarborg, P.; Løvås, T.; Jensen, P.A. The influence of size and morphology on devolatilization of biomass particles. Fuel 2020, 264, 116755. [Google Scholar] [CrossRef]
- Kuethe, A.M.; Chow, C.Y. Foundations of Aerodynamics: Bases of Aerodynamic Design; John Wiley and Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Li, D.; Li, S.; Xue, Y.; Yang, Y.; Su, W.; Xia, Z.; Shi, Y.; Lin, H.; Duan, H. The effect of slip distribution on flow past a circular cylinder. J. Fluids Struct. 2014, 51, 211–224. [Google Scholar] [CrossRef]
- Duan, Z.P.; He, B.S. Extended Reynolds analogy for slip and transition flow heat transfer in microchannels and nanochannels. Int. Commun. Heat Mass Transf. 2014, 56, 25–30. [Google Scholar] [CrossRef]
- Antonia, R.A.; Rajagopalan, S. Determination of drag of a circular cylinder. AIAA J. 1990, 28, 1833–1834. [Google Scholar] [CrossRef]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums; Pitt Press: Cambridge, UK, 1851. [Google Scholar]
- Oseen, C.W. Uber die Stokes’ sche Formel und Uber eine verwandte Aufgabe in der Hydrodynamik. Arkiv Mat. Astron. Och Fysik 1910, 6, 1. [Google Scholar]
- Lamb, H. XV. On the uniform motion of a sphere through a viscous fluid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1911, 21, 112–121. [Google Scholar] [CrossRef]
- Van Dyke, M. Perturbation Methods in Fluid Mechanics; Parabolic Press: Stanford, CA, USA, 1975. [Google Scholar]
- Tomotika, S.; Aoi, T. An expansion formula for the drag on a circular cylinder moving through a viscous fluid at small Reynolds numbers. Q. J. Mech. Appl. Math. 1951, 4, 401–406. [Google Scholar] [CrossRef]
- Proudman, I.; Pearson, J.R.A. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 1957, 2, 237–262. [Google Scholar] [CrossRef]
- Kaplun, S. Low Reynolds number flow past a circular cylinder. J. Math. Mech. 1957, 595–603. [Google Scholar] [CrossRef]
- Tamada, K.O.; Miura, H.; Miyagi, T. Low-Reynolds-number flow past a cylindrical body. J. Fluid Mech. 1983, 132, 445–455. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary-Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Dryden, H.L.; Hill, G.C. Wind Pressure on Circular Cylinders and Chimneys; US Government Printing Office: Washington, DC, USA, 1930. [Google Scholar]
- Delany, N.K.; Sorensen, N.E. Low-speed drag of cylinders of various shapes. NACA Tech. 1953. [Google Scholar]
- Tritton, D.J. Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 1959, 6, 547–567. [Google Scholar] [CrossRef]
- Roshko, A. Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 1961, 10, 345–356. [Google Scholar] [CrossRef]
- Achenbach, E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5 × 106. J. Fluid Mech. 1968, 34, 625–639. [Google Scholar] [CrossRef]
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Achenbach, E. Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 1971, 46, 321–335. [Google Scholar] [CrossRef]
- Drag Coefficient—Wikipedia. Available online: https://en.wikipedia.org/wiki/Drag_coefficient (accessed on 16 January 2020).
- Barati, R.; Neyshabouri, S.A.A.S. Comment on “Summary of frictional drag coefficient relationships for spheres: Evolving solution strategies applied to an old problem”. Chem. Eng. Sci. 2018, 181, 90–91. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Khan, W.A.; Culham, J.R.; Yovanovich, M.M. Fluid flow around and heat transfer from an infinite circular cylinder. Trans. ASME J. Heat Transf. 2005, 127, 785–790. [Google Scholar] [CrossRef]
- Kramers, H. Heat transfer from spheres to flowing media. Physica 1946, 12, 61–80. [Google Scholar] [CrossRef]
- Fand, R.M. Heat transfer by forced convection from a cylinder to water in crossflow. Int. J. Heat Mass Transf. 1965, 8, 995–1010. [Google Scholar] [CrossRef]
- Siddiqui, O.K.; Shuja, S.Z.; Zubair, S.M. Assessment of thermo-fluid analogies for different flow configurations: The effect of Prandtl number, and laminar-to-turbulent flow regimes. Int. J. Therm. Sci. 2018, 129, 145–170. [Google Scholar] [CrossRef]
- Gupta, A.S.; Thodos, G. Direct analogy between mass and heat transfer to beds of spheres. AIChE J. 1963, 9, 751–754. [Google Scholar] [CrossRef]
- Friend, W.L.; Metzner, A.B. Turbulent heat transfer inside tubes and the analogy among heat, mass, and momentum transfer. AIChE J. 1958, 4, 393–402. [Google Scholar] [CrossRef]
- Hughmark, G.A. Momentum, heat, and mass transfer analogy for turbulent flow in circular pipes. Ind. Eng. Chem. Fundam. 1969, 8, 31–35. [Google Scholar] [CrossRef]
- Krantz, W.B.; Wasan, D.T. Heat, mass, and momentum transfer analogies for the fully developed turbulent flow of power law fluids in circular tubes. AIChE J. 1971, 17, 1360–1367. [Google Scholar] [CrossRef]
- Sureshkumar, R. Effects of polymer stresses on analogy between momentum and heat transfer in drag-reduced turbulent channel flow. Phys. Fluids 2018, 30, 035106. [Google Scholar]
- Dong, Q.; Wang, C.; Xiong, C.; Li, X.; Wang, H.; Ling, T. Investigation on the cooling and evaporation behavior of Semi-Flexible Water Retaining Pavement based on laboratory test and thermal-mass coupling analysis. Materials 2019, 12, 2546. [Google Scholar] [CrossRef]
- Yoon, H.S.; Lee, J.B.; Seo, J.H.; Park, H.S. Characteristics for flow and heat transfer around a circular cylinder near a moving wall in wide range of low Reynolds number. Int. J. Heat Mass Transf. 2010, 53, 5111–5120. [Google Scholar] [CrossRef]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Sanitjai, S.; Goldstein, R.J. Heat transfer from a circular cylinder to mixtures of water and ethylene glycol. Int. J. Heat Mass Transf. 2004, 47, 4785–4794. [Google Scholar] [CrossRef]
- Perkins, H.C., Jr.; Leppert, G. Forced convection heat transfer from a uniformly heated cylinder. Trans. ASME J. Heat Transf. 1962, 84, 257–261. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).